Abstract
The cocrystallization technique has been widely applied in the fields of energetic materials (EMs) to settle the inherent trade-off between high energy and low sensitivity in current high-energy molecules. Despite its widespread application, the mechanistic understanding of cocrystals growing from solutions remains largely underexplored. This paper presents a mechanistic model grounded in the spiral growth mechanism to predict the crystal morphologies of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) and 7H-trifurazano [3,4-b:3′,4′-f:3″,4″-d]azepine (TFAZ) cocrystals. In this model, it was assumed that CL-20 and TFAZ molecules incorporated into the crystal lattice simultaneously from solution as preformed growth units. The binding energies between the CL-20 molecule and TFAZ molecule were calculated to determine the most potential growth units. The predicted morphologies closely align with the experimental determinations supporting the model’s validity. Furthermore, the study found that the crystal habits were significantly influenced by the choice of solvents, due to variations in interfacial energetics affecting the growth process.
1. Introduction
Cocrystallization is a versatile approach that pairs target molecules with carefully selected coformers to create materials possessing tailored properties. Originally focused on predictable intermolecular interactions between functional groups, this field has significantly advanced to encompass the design of intricate multi-component cocrystals [1,2,3,4,5,6]. In the domain of energetic materials, cocrystallization has proven to be a powerful strategy for modifying the stability and energetic performance (e.g., energy, propagation velocity, and pressure) of existing high-energy molecules (HEMs) [7,8,9]. This approach enables the effective integration of the physicochemical properties from at least two types of HEMs within a single crystal lattice, thereby influencing fundamental characteristics such as chemical purity, stability, shape and size distribution, crystal polymorphism, and defect density [10]. Among these attributes, crystal morphology is critical in determining the functional performance and the practical applications of crystallization products [11,12,13,14]. For instance, in energetic materials, crystal morphology significantly affects sensitivity and safety; spherical crystal habits generally exhibit lower impact and friction sensitivities compared to needle-shaped or plate-shaped crystals of similar size [14,15]. This highlights the importance of optimizing crystal morphology under controlled crystallization conditions to enhance the safety and efficiency of high-energy molecule production. Consequently, engineering crystal morphology is a crucial aspect of manufacturing energetic materials.
During the crystallization process, the crystal growth morphology is determined not only by the external growth conditions (e.g., solvent, supersaturation, temperature, and additives/impurities) but also by the internal structure of the crystal lattice (e.g., molecular arrangement and intermolecular interactions in the solid state). In order to engineer the growth morphologies of the crystalline solids scientifically, fundamental crystal growth mechanisms, together with the impacts of the growth conditions on the ultimate crystal habits, have been extensively explored with significant efforts. Supported by computational simulations, crystal growth models have been successfully applied to crystal morphology prediction, including the Bravais–Friedel–Donnay–Harker (BFDH) rule [16,17,18], the periodic bond chain (PBC) theory [19,20,21], the attachment energy (AE) model and its modifications (the MAE model) [22,23], kinetic Monte Carlo Simulations (kMC) [24,25,26], the spiral growth model [27], and the two-dimensional (2D) nucleation and growth model [28]. Among these theoretical models, it is well established that faceted crystals usually grow through layer-by-layer growth mechanisms, such as 2D nucleation and growth or the spiral growth mechanism, which capture the influences of growth environments (such as solvents, temperature, and supersaturation). These layered growth mechanisms has been used successfully to predict the crystal morphologies of a wide range of organic molecules (e.g., HEMs, pharmaceuticals, and solvates) grown from vapor or solutions [27,28,29,30,31,32,33]. By understanding and applying these models, researchers can predict and control the morphologies of crystals, which is critical for optimizing their properties for specific applications.
2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) is currently the most powerful energetic molecule, and it has attracted worldwide interest in recent years [34]. However, its high energy content is inherently accompanied by excessive sensitivity to external stimuli, such as friction, impact, or shock waves, severely limiting its commercial applications. To address this issue, cocrystallization with relatively insensitive coformers has been employed to develop a series of CL-20-based cocrystals with varying stoichiometric ratios. These cocrystals exhibit altered properties, including improved sensitivity, density, energetic performance, and thermal stability [35]. Thus, cocrystallization has been proven to be a powerful technique for tuning the properties of CL-20-based materials.
Despite its potential, the present preparation approaches primarily rely on the trial-and-error method, lacking the capability of directional design or full-scale preparation of cocrystals. Mechanistic modeling offers a powerful tool to understand the relationship between molecular and crystal structures, providing fundamental insight into potential shape modification at the molecular level. However, the growth mechanisms of energetic cocrystals in solvents remain unclear, and crystal habit predictions for energetic cocrystals using mechanistic models have not been reported. To address this gap, this study employs the spiral growth model to predict the cocrystal morphologies of CL-20/7H-trifurazano [3,4-b:3′,4′-f:3″,4″-d]azepine (TFAZ) grown from different solvents. These predictions aim to provide a fundamental theoretical understanding of cocrystals grown from solutions and to guide the engineering of energetic cocrystal materials.
2. The Spiral Growth Mechanism
The steady-state crystal growth morphology, which has no relevance to the primary seed shape [36], can be predicted with the perpendicular growth rates of all the crystal faces existing on the final habit. With the Frank–Chernov condition [37], the crystal habit is calculated as
where is the perpendicular growth rate of face i and is the perpendicular distance between face i and the crystal center. Under the spiral growth mechanism, the growth rate of each crystal face can be estimated with the step height h (the interplanar distance or a multiple of ) and the spiral rotation time .
In real systems, crystal faces are naturally imperfect and usually contain screw dislocations, which can act as continuous sources for generating step edges through a spiral mechanism. Once the length of a spiral edge reaches a certain value , it will start to grow, and the corresponding step velocity remains constant [38,39]. The critical length of edge i is given by
where is the growth unit width along edge i, is the mean value of the kink energy, and is the supersaturation ratio. The step velocity of an edge can be expressed as follows: [29]
where is the propagation distance when one layer of the growth unit is incorporated into the edge, is the kink density, and is the kink rate, representing the net incorporation rate of the growth units into the kink sites [29,40]. The outwards advance of one step edge sequentially gives rise to an adjacent edge, which also starts to grow after its length reaches the critical value . The repetition of the above process finally leads to the formation of a spiral away from the initial screw dislocation. Therefore, the rotation time for a convex spiral can be expressed as follows: [27]
where is the angle between edge i and edge i + 1.
For crystals growing from solution, the existence of solvent molecules has a significant impact on the fundamental solid-state interactions. These solvent molecules interact with both the crystal surface and the solute molecules, modifying the interfacial energies and thus influencing the growth dynamics and morphology of the crystal. The solvent-modified interfacial energies can be estimated with the van Oss, Chaudhury and Good (vOCG) model [41,42,43].
where subscripts c and s represent the crystal and solvent, d corresponds to the dispersive interaction, AB denotes the acid-base interaction, and +/− refers to the electron-accepting/electron-donating component. The interfacial energies for the solvent phase can be obtained using empirical correlations of solubility parameters [44],
where is the molar volume, and refers to the components of the solubility parameters (e.g., dispersion, h-bonding, and polarization). The solubility parameters for the solvents used in the present work are shown in Table 1.

Table 1.
Solvent information: molar volume (, ml/moL), dispersive solubility parameter (, ), polar solubility parameter (, ), and hydrogen-bonding solubility parameter (, ).
3. Computational Details
The layer-by-layer growth mechanisms (spiral growth and 2D nucleation and growth mechanisms) are incorporated into a prototype software framework, ADDICT 12, using the fundamental solid state and solution chemistry [27,28,29]. To predict and engineer the growth morphologies of a specific crystal polymorph with ADDICT, the initial step involves defining the growth unit. For the CL-20/TFAZ cocrystal growing from a supersaturated solution, it was assumed that CL-20 and the coformer molecules retained their primary binding sites in the solution, allowing them to simultaneously attach into the solid state together. The molar ratio of the CL-20/TFAZ cocrystal is 1:1; thus, the growth unit is a hetero-dimer consisting of one CL-20 molecule and one TFAZ molecule, stabilized by noncovalent interactions. The strongest intermolecular interaction strength stands for the optimal selection to be the most potential hetero-dimer growth units. The intermolecular interactions within the lattice were calculated with the AMBER force field implemented in ADDICT [45,46]. The partial charges for all the atoms were obtained using Gaussian 03 [47] with the restrained electronic potential (RESP) model [48]. After identifying the growth units in the crystal unit cell, all the total sums of the inter-atomic interactions between pairs of growth units were analyzed to determine the PBCs, which were selected using the rules proposed by Hartman and Perdok [22]. Crystal faces with at least two PBCs were defined as flat faces (F faces), which grew via the spiral growth mechanism at low supersaturation. Each PBC in the F faces grows as a step edge of the spiral with the direction of the steps flowing across the entire surface. The relative growth rate for each F face was calculated with established mechanistic equations to predict the steady-state growth shape. Finally, ADDICT visualized the PBCs, spiral structures on each F face, and the overall crystal habits.
4. Results and Discussion
The experimentally observed morphology of the CL-20/TFAZ cocrystal, as reported by Liu, is demonstrated in Figure 1a [49]. This cocrystal was grown from isopropyl acetate at room temperature through slow evaporation, resulting in a stick-like shape with flat surfaces. The space group of the CL-20/TFAZ cocrystal is P21, containing two CL-20 molecules and two TFAZ molecules in the crystal unit cell. The lattice parameters are a = 8.288 (2) Å, b = 11.555 (3) Å, c = 11.805 Å, and β = 91.11(<1)° (CSD refcode HIVGAW01 was employed in this work) [49]. Figure 1b shows the predicted morphology of the CL-20/TFAZ cocrystal using the BFDH model, which was applied via the Materials Studio software 6.1 [50]. According to this model, the {0 0 1} faces were dominant due to the relatively larger interplanar spacing, as detailed in Table 2. The hierarchy of the habit facets’ importance is {0 0 1} > {1 0 0} > {0 1 1} = {0 1} > {1 1 0} = { 1 0} > {1 0 }. On the other hand, the AE model, also implemented using the Materials Studio software 6.1, provides an alternative prediction of the crystal shape, as shown in Figure 1c. While the AE model’s prediction closely resembles that of the BFDH model, it additionally highlights the emergence of the {1} and {1} face families with small surface areas.
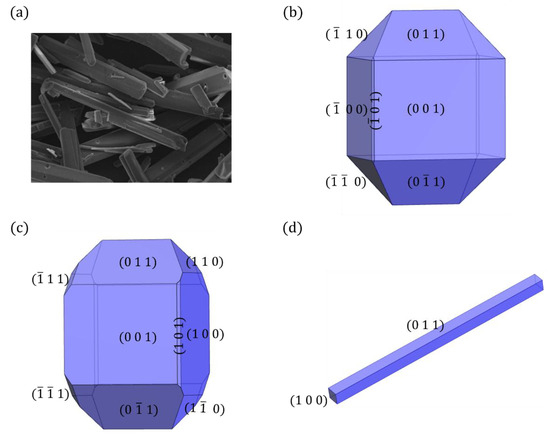
Figure 1.
Comparison of (a) the experimentally observed crystal morphology of the CL-20/TFAZ cocrystal grown from isopropyl acetate with predicted crystal morphologies by (b) BFDH, (c) AE, and (d) the spiral growth model.

Table 2.
Interplanar spacing (d, in Å) and attachment energy (, in kcal/mol) of CL-20/TFAZ cocrystal.
With the AMBER force field, the binding energy between the CL-20 and TFAZ molecules in the CL-20/TFAZ hetero-dimer was computed to be −12.74 kcal/mol. Within the unit cell, there are two dimeric growth units, with CL-20 molecules existing in the γ-formed conformer (see Figure 2a) [51]. As shown in Figure 2a, two different types of intermolecular interactions were identified within this dimer [49]. One type is the hydrogen-bonding interaction, which is formed between a H atom of the CL-20 molecule and a N atom in the furazan ring of the TFAZ molecule. The other type is the π-π stacking interaction, referring to the intermolecular stacking between the lone-pair electrons around each O atom of the NO2 functional group of CL-20 and the π-bonded structure of the furazan ring in TFAZ. Actually, the interaction region indicator (IRI) distribution isosurfaces further validated the significance of this π-π stacking, highlighting its crucial contribution to the stabilization of the dimer (as shown in Figure 2b) [52,53].
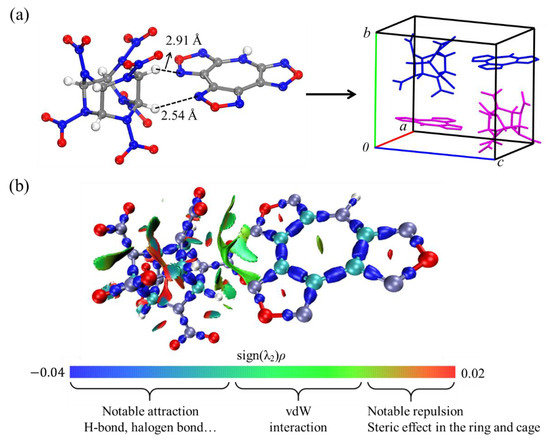
Figure 2.
(a) Unit cell of CL-20/TFAZ cocrystal containing two dimers. (b) B3LYP/def2-svp calculated isosurface of IRI = 1.0 with mapped on the isosurface (VMD image) [54].
After defining the growth unit, the aggregate interactions between the growth units in the crystal lattice were computed to identify the strong repeated interaction directions, known as periodic bond chains (PBCs). For the CL-20/TFAZ cocrystal, eight different bonding interactions were found throughout the entire crystal system, with the binding energy ranging from −25.83 to −1.41 kcal/mol, which formed six different PBCs. The average energy per bond (in the solid state and in isopropyl acetate) for each PBC is given in Table S1. Six face families with two or more PBCs were identified, {0 1 1}, {1 0 }, {0 2 0}, {0 0 1}, { 1 1 }, {1 0 0}, and the bonding structures for different crystal faces are illustrated in Figure 3, where the red and blue dots represent the mass centers of the two different growth units. Utilizing the hetero-dimer as the growth unit and applying the spiral mechanistic growth model, the crystal shape of the CL-20/TFAZ cocrystal grown from isopropyl acetate was predicted (see Figure 1d), with intermediate data provided in Table S2. The predicted morphology aligns well with the experimental habit, which was observed to be a stick-like shape (see Figure 1a). This consistency between predicted and observed morphologies validates the computational model and the understanding of the crystallization process.
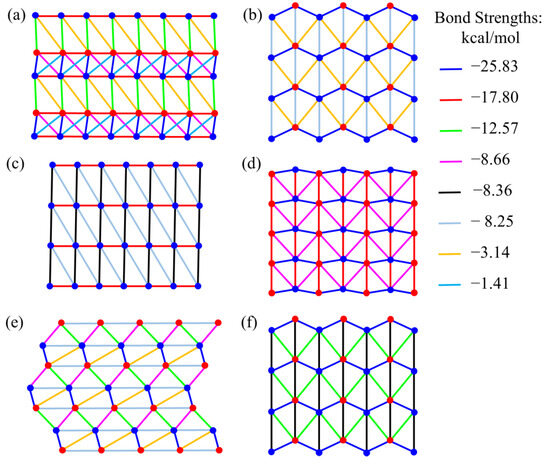
Figure 3.
Bonding structures of different F faces for CL-20/TFAZ cocrystal: (a) {0 1 1} face, (b) {1 0 } face, (c) {0 2 0} face, (d) {0 0 1} face, (e) {1 1 } face, (f) {1 0 0} face.
In terms of crystals growing from solution, the presence of solvent molecules plays a significant role in engineering the crystal morphology and provides substantial opportunities to design the crystal habits. The surface energetics of the same crystal face vary depending on the surrounding solvent molecules. Additionally, the same solvent will modify the surface energetics of different crystal faces to varying extents, which results in the appearance and disappearance of specific crystal faces and ultimately influences the steady-state morphology. Based on the good agreement between the predictions and the experimental determinations, the influence of solvents on the steady-state morphologies of the CL-20/TFAZ cocrystal was explored with the spiral growth model. The solvents were classified into three groups: nonpolar (hexane and n-heptane); polar without hydroxyl groups (n-butyl acetate and acetone); and polar with hydroxyl groups (methanol and propionic acid). As shown in Figure 4, the CL-20/TFAZ cocrystal showed needle-like habits when grown from nonpolar hexane and n-heptane solvents. However, the relative growth rates of the {1 0 0} and {1 0 } faces decreased dramatically in n-butyl acetate and acetone solvents (see Table 3), which led to a transition from needle-like to stick-like habits. In acetone, the surrounding faces include two face families, {1 0 0} and {1 0 }. With further reduction in the relative growth rates of {1 0 0} and {1 0 } faces, the predicted growth habit of the CL-20/TFAZ cocrystal in methanol was observed to be cuboid, while in propionic acid the crystal shape was closer to cubic. These changes in morphology are attributed to the interaction between the solvent molecules and the exposed functional groups (C=N, N-H and NO2) at the surfaces (see Figure S1), which had varying degrees of influence on different crystal faces (see intermediate data in Tables S3–S8), enabling desirable modifications to the crystal habits with suitable solvents.
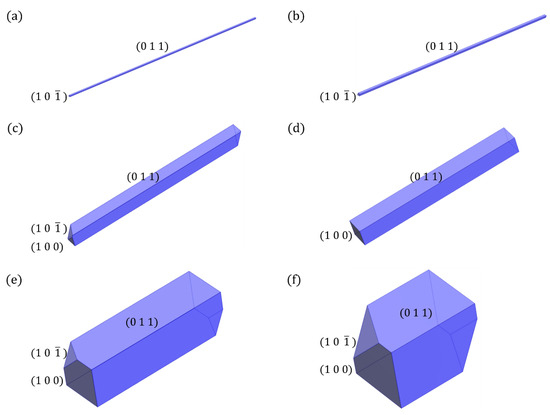
Figure 4.
Predicted crystal morphologies of CL-20/TFAZ cocrystal grown from (a) hexane, (b) n-heptane, (c) n-butyl acetate, (d) acetone, (e) methanol, (f) propionic acid.

Table 3.
Predicted relative growth rates of CL-20/TFAZ cocrystal grown from hexane, n-heptane, n-butyl acetate, acetone, methanol, propionic acid.
5. Conclusions
The crystal habits of CL-20/TFAZ cocrystals grown from different solvents were predicted with a mechanistic growth model. It was assumed in the model that prior to incorporation into the crystal lattice, CL-20 and TFAZ molecules formed hetero-dimers, which then solidified in a bonded and preformed state. Considering that cocrystals are typically stabilized by nonbonding interactions such as hydrogen bonds, halogen bonds, π-π stacking, p-π stacking, or Van der Waals forces, the binding energies between the component molecules play a critical role in determining the most potential growth units. Based on this model, the predicted crystal habits of CL-20/TFAZ cocrystals closely matched the experimentally observed morphologies. Through the strategic selection of solvents, the crystal morphologies of CL-20/TFAZ were effectively modified from needle-like habits to cubic shapes. This theoretical framework provides a robust tool for engineering HEM cocrystals with tailored crystal chemistry, offering valuable insights into the underlying molecular growth mechanisms. Moreover, the applicability of this model extends beyond the CL-20/TFAZ system, as it can be readily adapted to other cocrystal systems.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/compounds5010006/s1, Table S1: Average energetic interactions (kcal/mol) between CL-20/TFAZ dimers of each periodic bond chains (PBCs) in the solid state and isopropyl acetate; Table S2: Detailed results: CL-20/TFAZ cocrystal grown from isopropyl acetate with the vOCG solvent model; Table S3: Detailed results: CL-20/TFAZ cocrystal grown from hexane with the vOCG solvent model; Table S4: Detailed results: CL-20/TFAZ cocrystal grown from n-heptane with the vOCG solvent model; Table S5: Detailed results: CL-20/TFAZ cocrystal grown from n-butyl acetate with the vOCG solvent model; Table S6: Detailed results: CL-20/TFAZ cocrystal grown from acetone with the vOCG solvent model; Table S7: Detailed results: CL-20/TFAZ cocrystal grown from methanol with the vOCG solvent model; Table S8: Detailed results: CL-20/TFAZ cocrystal grown from propionic acid with the vOCG solvent model; Figure S1: Molecular arrangements on (a) {0 1 1} face, (b) {1 0 } face, (c) {0 2 0} face, (d) {0 0 1} face, (e) {1 1 } face, (f) {1 0 0} face.
Author Contributions
Y.S.: conceptualization, data curation, writing—original draft preparation, reviewing and editing, figures—visualization, and drawing; L.Y.: data curation, software, writing—reviewing and editing; Y.W. and N.-T.S.: final editing, and approval of the draft for submission. All authors have read and agreed to the published version of the manuscript.
Funding
This work was by financially funded by the National Natural Science Foundation of China (no. 22073080).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We thank Yang Wang from Yangzhou University for his very helpful suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, J.; Sarma, B.; Evans, J.M.B.; Myerson, A.S. Pharmaceutical Crystallization. Cryst. Growth Des. 2011, 11, 887–895. [Google Scholar] [CrossRef]
- Qiao, N.; Li, M.; Schlindwein, W.; Malek, N.; Davies, A.; Trappitt, G. Pharmaceutical cocrystals: An overview. Int. J. Pharm. 2011, 419, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Wu, S.; Macaringue, E.G.J.; Zhang, T.; Gong, J.; Wang, J. Recent Progress in Continuous Crystallization of Pharmaceutical Products: Precise Preparation and Control. Org. Process Res. Dev. 2020, 24, 1785–1801. [Google Scholar] [CrossRef]
- Ejarque, D.; Calvet, T.; Font-Bardia, M.; Pons, J. Structural Landscape of α-Acetamidocinnamic Acid Cocrystals with Bipyridine-Based Coformers: Influence of Crystal Packing on Their Thermal and Photophysical Properties. Cryst. Growth Des. 2024, 24, 1746–1765. [Google Scholar] [CrossRef] [PubMed]
- Ejarque, D.; Calvet, T.; Font-Bardia, M.; Pons, J. Virtual assessment achieved two binary cocrystals based on a liquid and a solid pyridine derivative with modulated thermal stabilities. CrystEngComm 2023, 25, 4798–4811. [Google Scholar] [CrossRef]
- Ejarque, D.; Calvet, T.; Font-Bardia, M.; Pons, J. Cocrystals Based on 4,4′-bipyridine: Influence of Crystal Packing on Melting Point. Crystals 2021, 11, 191. [Google Scholar] [CrossRef]
- Landenberger, K.B.; Matzger, A.J. Cocrystal Engineering of a Prototype Energetic Material: Supramolecular Chemistry of 2,4,6-Trinitrotoluene. Cryst. Growth Des. 2010, 10, 5341–5347. [Google Scholar] [CrossRef]
- Millar, D.I.A.; Maynard-Casely, H.E.; Allan, D.R.; Cumming, A.S.; Lennie, A.R.; Mackay, A.J.; Oswald, I.D.H.; Tang, C.C.; Pulham, C.R. Crystal engineering of energetic materials: Co-crystals of CL-20. CrystEngComm 2012, 14, 3742–3749. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Yang, Z.-J.; Nie, F.; Yan, Q.-L. Recent advances on the crystallization engineering of energetic materials. Energ. Mater. Front. 2020, 1, 141–156. [Google Scholar] [CrossRef]
- Pawar, N.; Saha, A.; Nandan, N.; Parambil, J.V. Solution Cocrystallization: A Scalable Approach for Cocrystal Production. Crystals 2021, 11, 303. [Google Scholar] [CrossRef]
- Heng, J.Y.Y.; Bismarck, A.; Lee, A.F.; Wilson, K.; Williams, D.R. Anisotropic Surface Energetics and Wettability of Macroscopic Form I Paracetamol Crystals. Langmuir 2006, 22, 2760–2769. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.G.; Sun, C.H.; Qiao, S.Z.; Zou, J.; Liu, G.; Smith, S.C.; Cheng, H.M.; Lu, G.Q. Anatase TiO2 single crystals with a large percentage of reactive facets. Nature 2008, 453, 638–641. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.-C.; Zhou, J.-S.; Sun, J.; Qiu, Y.; Wei, D.-Z.; Shen, Y.-L. Study of the crystal shape and its influence on the anti-tumor activity of tumor necrosis factor-related apoptosis-inducing ligand (Apo2L/TRAIL). Cryst. Res. Technol. 2008, 43, 888–893. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, C.; Li, H.; Zhou, Y.; Xu, J.; Xu, R.; Li, J.; Luo, Y. Occupancy Model for Predicting the Crystal Morphologies Influenced by Solvents and Temperature, and Its Application to Nitroamine Explosives. Cryst. Growth Des. 2013, 13, 282–290. [Google Scholar] [CrossRef]
- Duan, X.; Wei, C.; Liu, Y.; Pei, C. A molecular dynamics simulation of solvent effects on the crystal morphology of HMX. J. Hazard. Mater. 2010, 174, 175–180. [Google Scholar] [CrossRef]
- Bravais, A. Études Cristallographiques; Gauthier-Villars: Paris, France, 1866. [Google Scholar]
- Friedel, G. Etudes sur la loi de Bravais. Bull. Soc. Franc. Miner 1907, 30, 326–455. [Google Scholar] [CrossRef]
- Donnay, J.D.H.; Harker, D. A new law of crystal morphology extending the law of Bravais. Am. Miner. 1937, 22, 446–467. [Google Scholar]
- Hartman, P.; Perdok, W.G. On the relations between structure and morphology of crystals. I. Acta Cryst. 1955, 8, 49–52. [Google Scholar] [CrossRef]
- Hartman, P.; Perdok, W. On the relations between structure and morphology of crystals. II. Acta Cryst. 1955, 8, 521–524. [Google Scholar] [CrossRef]
- Hartman, P.; Perdok, W.G. On the relations between structure and morphology of crystals. III. Acta Cryst. 1955, 8, 525–529. [Google Scholar] [CrossRef]
- Hartman, P.; Bennema, P. The attachment energy as a habit controlling factor: I. Theoretical considerations. J. Cryst. Growth 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Lu, J.J.; Ulrich, J. An improved prediction model of morphological modifications of organic crystals induced by additives. Cryst. Res. Technol. 2003, 38, 63–73. [Google Scholar] [CrossRef]
- Mazal, T.; Doherty, M.F. Modeling Morphologies of Organic Crystals via Kinetic Monte Carlo Simulations: Noncentrosymmetric Growth Units. Cryst. Growth Des. 2024, 24, 3756–3770. [Google Scholar] [CrossRef]
- Padwal, N.A.; Doherty, M.F. Step Velocity Growth Models for Molecular Crystals: Two Molecules in the Unit Cell. Cryst. Growth Des. 2024, 24, 4368–4379. [Google Scholar] [CrossRef]
- Padwal, N.A.; Mazal, T.; Doherty, M.F. Modern Modeling and Simulation Approaches for Morphology Predictions of Molecular Crystals. Ind. Eng. Chem. Res. 2024, 63, 18401–18410. [Google Scholar] [CrossRef]
- Snyder, R.C.; Doherty, M.F. Predicting crystal growth by spiral motion. Proc. R. Soc. A 2009, 465, 1145–1171. [Google Scholar] [CrossRef]
- Tilbury, C.J.; Doherty, M.F. Modeling layered crystal growth at increasing supersaturation by connecting growth regimes. AIChE J. 2017, 63, 1338–1352. [Google Scholar] [CrossRef]
- Kuvadia, Z.B.; Doherty, M.F. Spiral Growth Model for Faceted Crystals of Non-Centrosymmetric Organic Molecules Grown from Solution. Cryst. Growth Des. 2011, 11, 2780–2802. [Google Scholar] [CrossRef]
- Shim, H.-M.; Koo, K.-K. Molecular Approach to the Effect of Interfacial Energy on Growth Habit of ε-HNIW. Cryst. Growth Des. 2016, 16, 6506–6513. [Google Scholar] [CrossRef]
- Li, J.; Tilbury, C.J.; Kim, S.H.; Doherty, M.F. A design aid for crystal growth engineering. Prog. Mater. Sci. 2016, 82, 1–38. [Google Scholar] [CrossRef]
- Sun, Y.; Tilbury, C.J.; Reutzel-Edens, S.M.; Bhardwaj, R.M.; Li, J.; Doherty, M.F. Modeling Olanzapine Solution Growth Morphologies. Cryst. Growth Des. 2018, 18, 905–911. [Google Scholar] [CrossRef]
- Sun, Y.; Reutzel-Edens, S.M.; Bhardwaj, R.M.; Doherty, M.F. Crystal Morphology Modeling of Solvates and Hydrates of Organic Molecular Crystals: Olanzapine Solvate and Dihydrate. Cryst. Growth Des. 2021, 21, 4871–4877. [Google Scholar] [CrossRef]
- Nielsen, A.T.; Chafin, A.P.; Christian, S.L.; Moore, D.W.; Nadler, M.P.; Nissan, R.A.; Vanderah, D.J.; Gilardi, R.D.; George, C.F.; Flippen-Anderson, J.L. Synthesis of polyazapolycyclic caged polynitramines. Tetrahedron 1998, 54, 11793–11812. [Google Scholar] [CrossRef]
- Liu, G.; Li, H.; Gou, R.; Zhang, C. Packing Structures of CL-20-Based Cocrystals. Cryst. Growth Des. 2018, 18, 7065–7078. [Google Scholar] [CrossRef]
- Zhang, Y.; Sizemore, J.P.; Doherty, M.F. Shape evolution of 3-dimensional faceted crystals. AIChE J. 2006, 52, 1906–1915. [Google Scholar] [CrossRef]
- Chernov, A. The kinetics of the growth forms of crystals. Sov. Phys. Cryst. 1963, 7, 728–730. [Google Scholar]
- Kaischew, R.; Budevski, E. Surface processes in electrocrystallization. Contemp. Phys. 1967, 8, 489–516. [Google Scholar] [CrossRef]
- Voronkov, V.V. Dislocation mechanism of growth with a low kink density. Sov. Phys. Cryst. 1973, 18, 19–223. [Google Scholar]
- Tilbury, C.J.; Joswiak, M.N.; Peters, B.; Doherty, M.F. Modeling Step Velocities and Edge Surface Structures during Growth of Non-Centrosymmetric Crystals. Cryst. Growth Des. 2017, 17, 2066–2080. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Good, R.J. A Theory for the Estimation of Surface and Interfacial Energies. I. Derivation and Application to Interfacial Tension. J. Phys. Chem. 1957, 61, 904–909. [Google Scholar] [CrossRef]
- Tilbury, C.J.; Green, D.A.; Marshall, W.J.; Doherty, M.F. Predicting the Effect of Solvent on the Crystal Habit of Small Organic Molecules. Cryst. Growth Des. 2016, 16, 2590–2604. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Interfacial Lifshitz-van der Waals and polar interactions in macroscopic systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Kaelble, D.H. Physical Chemistry of Adhesion; Wiley-Interscience: Hoboken, NJ, USA, 1971. [Google Scholar]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Cheatham, T.E.; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Crowley, M.; Walker, R.C.; Zhang, W. Amber 10; University of California: San Francisco, CA, USA, 2008. [Google Scholar]
- Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; et al. Gaussian 03, Revision C. 02; Gaussian: Wallingford, CT, USA, 2003. [Google Scholar]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Liu, N.; Duan, B.; Lu, X.; Zhang, Q.; Xu, M.; Mo, H.; Wang, B. Preparation of CL-20/TFAZ cocrystals under aqueous conditions: Balancing high performance and low sensitivity. CrystEngComm 2019, 21, 7271–7279. [Google Scholar] [CrossRef]
- Material Studio, version 6.1. Software for Technical Computation. Accelrys Inc.: San Diego, CA, USA, 2011.
- Zhu, S.-F.; Zhang, S.-H.; Gou, R.-J.; Wu, C.-L.; Han, G.; Jia, H.-Y. Understanding the Effect of Solvent on the Growth and Crystal Morphology of MTNP/CL-20 Cocrystal Explosive: Experimental and Theoretical Studies. Cryst. Res. Technol. 2018, 53, 1700299. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chem. Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).