1. Introduction
Plant-parasitic nematodes are recognized as major agricultural pathogens and are known to attack plants and cause great economic losses in crops worldwide [
1,
2,
3]. Among plant-parasitic nematodes, there are sedentary endoparasites, which include the genera
Heterodera and
Globodera (cyst nematodes) and
Meloidogyne, which are species better known as root-knot nematodes. Vegetables and ornamental crops are usually among the most susceptible cultivated plants that are affected by root-knot nematodes [
4]. Among root-knot nematodes,
Meloidogyne javanica is one of the most damaging plant parasites, often causing heavy losses, especially in plants grown in coarse-textured sandy soils. Nowadays, alternatives including the use of chemical substances, agricultural practices for managing pests, and the disease incorporation of organic amendments are either environmentally unacceptable or technically demanding. Thus, resistant varieties may potentially provide the most effective means of controlling nematode invasion. Despite the aforementioned control methods, the use of biological control agents such as the obligate hyperparasitic bacterium
Pasteuria penetrans [
5,
6,
7] has been recognized as one of the most effective biological control agents against root-knot nematodes [
8,
9], showing quite promising results [
10,
11,
12]. The potential use of
P. penetrans as a biological control agent against important plant-parasitic species has been widely studied in the past [
13,
14,
15,
16]. These studies include the distribution rate, host range, host specificity, as well as biotic and abiotic factors [
17,
18,
19,
20]. To date, it has been mentioned that successful parasitism depends on the attachment of 5–10 spores per juvenile (J2), which is sufficient to initiate infection without reducing the ability of the nematode to invade the root system [
21,
22,
23]. However, studies have shown that there may be little or no root invasion if there are more than 15 spores attached to the nematode’s body, inferring that spore attachment will affect the ability of J2s to locate and/or invade the root [
24,
25,
26]. The results of these studies imply high variances in the numbers of spores attached to the nematode’s body but no attempt has been made to examine this variability in detail, e.g., as shown by the target parameter of variability. This research is important since plant protectionists could use it as a prediction model to decide whether infected nematodes can cause plant damage and thus, yield losses.
Studies focused on the biology of
P. penetrans mentioned that, during the infective stage, the endospores of
P. penetrans attach to the extremal nematode body wall (cuticle) of free-living of
Meloidogyne populations. As observed in many relevant studies [
27,
28], as soon as J2s are attracted by the root exudates of a host plant, the nematodes begin to become attached by the bacterium spores which penetrate the nematode’s cuticle and begin to grow and develop within the invaded nematode [
6,
29,
30]. Eventually, the female nematode body becomes filled with spores [
10,
30]. As it has been remarkably noted, each infected female may contain up to 2.5 million spores [
31], which are finally released back into the soil environment.
Overall, in this study, the main objective was to calculate the P. penetrans spore attachment process as a distribution, providing a model that allows the variance to be divided into components and offer an explanation in vitro and in planta.
3. Discussion
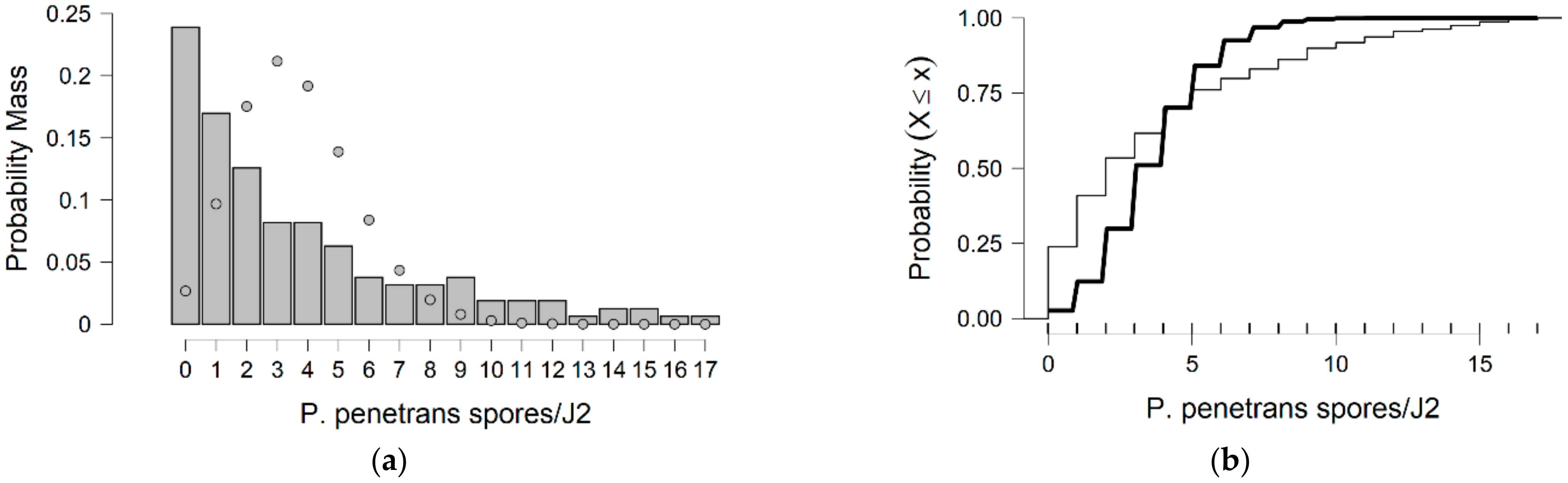
Poisson model is usually used to model data. If the observed variability in counts is much larger than the mean, a phenomenon termed overdispersion occurs, and the negative binomial model is often used as a replacement for overdispersed count data.
The application of the Poisson and negative binomial distributions for modeling
P. penetrans attachment data was also studied by Vagelas et al. [
24]. In the aforementioned research [
24], evidence is provided of the
P. penetrans attachment counts being characterized by a significantly larger variance than the mean. This phenomenon in biology is called “overdispersion” [
36]. In addition to the aforementioned study [
24], the results of the presented study are in agreement with other relevant research studies [
23,
24,
25,
26], which concluded that in analyzing
P. penetrans attachment counts, the variance is significantly larger than the mean, and negative binomial distribution is the most appropriate model to fit the observed data. All previous studies [
23,
24,
25,
26] which modeled
P. penetrans overdispersed attachment with data set in water bioassays only provided the simplest answer to the issues that the negative binomial distribution is the only model to explain data variability regarding the overdispersion of
P. penetrans. This research provided evidence that apart from in the water bioassay,
P. penetrans overdispersion is related to soil counts suggesting that the negative binomial distribution is the most appropriate model for solving the overdispersion problem.
Overdispersed data can lead to underestimated standard errors and inflated test statistics and in such circumstances, the negative binomial model can be utilized.
In more detail, the data presented in this study were collected from the observed values of P. penetrans spore’s attachment to nematodes and the predicted values were mainly developed by the Poisson and negative binomial distributions. The P. penetrans spore’s attachment was modeled at one concentration (5000 spores), in water and the soil bioassay, at four times of exposure (1, 3, 6, and 9 h) and (12, 24, 26, and 48 h), respectively. In the water bioassay, the modeling approaches discussed above confirmed that the Poisson distribution is a sufficient model for nematode populations limited to 1 h of exposure. Interestingly, the mean is equal to the variance suggesting ‘under-dispersion’. The same results were presented for the loam soil bioassay, suggesting the ‘under-dispersion’ phenomenon.
The negative binomial distribution is considered the most appropriate model to fit the data sets for the sandy loam soil and in the water bioassay at 3, 6, and 9 h of exposure. The data show that for sandy loam soil and in a water bioassay, the negative binomial distribution can model ‘overdispersed’ data sets. It is well known that, in nature, several distributions—which were devised for series in which the variance is significantly higher than the mean—showed that the ‘overdispersion’ phenomenon is mainly explained by the negative binomial model [
34,
36,
37,
38,
39,
40] or other discrete distributions such as the extended biparametric Waring and the univariate generalized Waring distributions [
41,
42,
43,
44].
In general, for the inference of the count data, the four most commonly used statistical model distributions are the Poisson, negative binomial, hurdle, and zero-inflated regression models. The hurdle and zero-inflated regression models are used to handle the distribution of the count outcome with excess zeroes, a phenomenon that did not occur in our data. The negative binomial model addresses the issue of overdispersion by including a dispersion parameter that relaxes the presumption of equal mean and variance in the distribution.
In this research, soil data show that, after 36 h of J2s exposure to
P. penetrans spores, high numbers of
P. penetrans spores/nematodes were observed and the negative binomial distribution was proposed as the most efficient model for overdispersed data sets, particularly for sandy loam soil. A thorough classification of the negative binomial distribution could be evidence of nematodes encountering clumps of spores. This is true as the odds ratio is 2.831, indicating that these nematodes encounter clumps of nearly three spores, an important result which corrects previous research studies [
22,
25,
26]. Moreover, in the sandy loam soil bioassay, it was demonstrated that those clumps of
P. penetrans spores affected the nematodes invasion rate.
In this paper, we focused on determining the number of
P. penetrans attached to J2s cuticle. From this study, it was assumed that the water bioassay observation agrees with the study completed by sandy loam soil, suggesting that when J2s encumbered with >15 spores/juvenile, a possible halt of nematode in the soil could be caused. The same results were reported by Davies et al. [
24], where it was commented that when J2s encumbered with >15 spores/juvenile, resulting in a reduction in the invasion level of >70%. The same observation was also mentioned in a previous research study completed by the authors [
25,
26], where it was shown that the
P. penetrans spores attached to the nematode cuticle appeared to have a significant impact on nematode’s movement (nematode turns, etc.,) which may play a significant role in the nematode distribution and mobility. These results are also observed in the soil. Our data present that when nematodes are encumbered with 3–10 spores of
P. penetrans then they are always overdispersed. On the other hand, when nematodes are encumbered with >10
P. penetrans spores, the invasion rate is less than 70%, a result which corrects a previous research study [
22,
26].
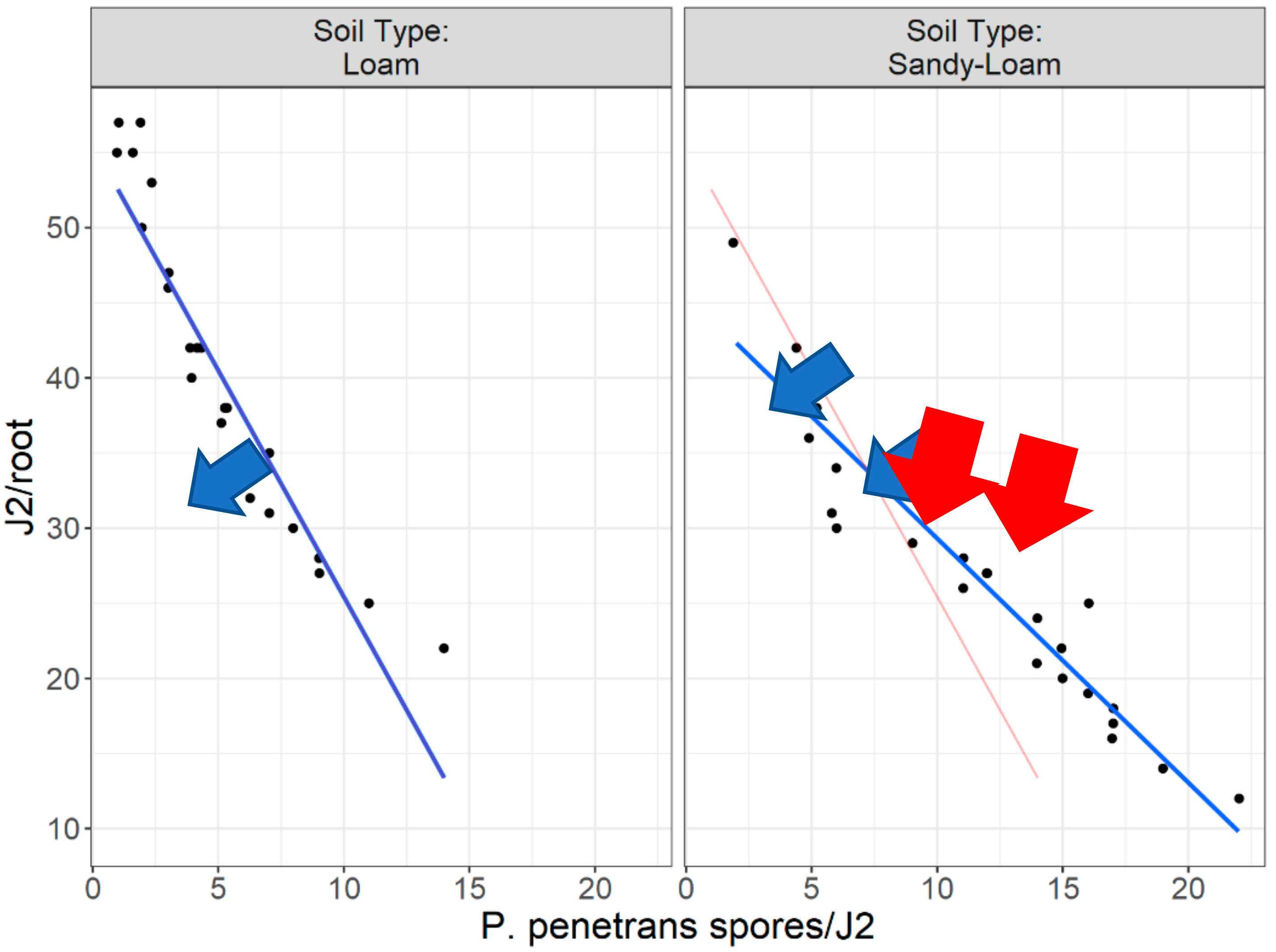
In this research, there is evidence that the soil type, (particularly the sandy soil), appears to have a significant impact on P. penetrans spore’s attachment and thus nematode invasion. Based upon this, significant data are presented suggesting that fewer nematodes invade plant roots when they are encumbered with 3–10 or 4.5–8 P. penetrans spores.
This impact of the soil type also significantly affected the nematodes‘ establishment on the tomato root system when J2s were encumbered with 6–7 P. penetrans spores, and possibly immobilized them in the soil when encumbered with >12 or 15 P. penetrans spores, especially in the sandy loam soil.
In the examination of the variability of the attachment among sandy loam and loam soil, the negative binomial was not the most appropriate model to fit the loam bioassay data, suggesting an ‘under-dispersion’ or a probability of a failure [
45,
46] of
P. penetrans spores attachment due to the stress environment occurred in the loam soil. A possible explanation caused the low rate of
P. penetrans attachment at the loam soil may be due to sand contents. Sandy soils may exhibit an increasing rate of
P. penetrans spores’ attachment whereas the absence of sand in loam soil causes attachment failure in clumps of spores. This can be seen as a particular case of our research concluded that the failure rate of attachment, e.g., nematodes being encumbered with fewer than three spores, is characterized by an increasing rate of invasion. At this point, we proposed that the gamma (γ) distribution can be used for modeling this phenomenon. Gamma (γ) distribution (as well as Weibull distribution, which was introduced as a second model in our data) may be considered as an under-dispersed extension of Poisson distribution. It is clear that if data exhibit overdispersion, then the variance is larger than the mean. On the other hand, if the data are under-dispersed and if mean = variance = λ, then the number of events in a given time period of length t follows a Poisson distribution with parameter λt. Whereas the Poisson distribution is the answer to this issue, any one step of Poisson mixture distributions assumes that there are only two sources of variability, the negative binomial distribution (which is a Poisson–gamma (γ) mixture) and the gamma (γ) distribution [
44,
47]. Based on that conclusion, it is necessary to mention here that, as the distribution of
P. penetrans spores attachment is exposed to variance data (which make it of great interest for modeling overdispersed count data sets), a serious draw back to the variance decomposition occurs (as shown in
Figure 13 and
Figure 14), and it is difficult to determine which model is the most appropriate for referring to data proneness (e.g., the clumps of spores).
The estimates in the
x and
y axes of
Figure 15 and
Figure 16 are of interest as the variance is a multiple of the mean which is consistent with the negative binomial model. The linear regression plots presented with
Figure 17 and
Figure 18 clearly support (with the “Ghost Line”) the hypothesis that the reduction in the invasion level (by approximately 70%) is observed when J2s are encumbered with more than seven (7)
P. penetrans spores. Moreover, the generalized linear modeling plot in
Figure 18 clearly reflects the relationship between nematodes invasion (J2s/root) and J2s encumbered with
P. penetrans spores (
P. penetrans spores/J2) in two soil types (sandy loam and loam soil), suggesting that the sand content affects the reduction in the invasion level. Furthermore, the high positive coefficient value of sandy loam soil (6.375) clearly indicates that more
P. penetrans spores are attached in the sandy loam soil. The coefficient of 6.375 (
Table 8) is not only positive but also significant from the coefficient of 0.808 (
Table 8), suggesting that the Poisson model is not perfect. Again, the gamma (γ) distribution (
p = 0.123) followed by the Weibull distribution (
p = 0.083) of
Figure 20 confirms that, apart from the negative binomial distribution, the gamma (γ) distribution jointly models the effects of liability (variance) and proneness (a better distribution for the others), especially the coefficient of the sandy loam soil. Thus, the following hypothesis is considered that the reduction in the invasion level (approximately by 70%) is observed when J2s were encumbered with 4.5–8
P. penetrans spores as estimated with the Wilcoxon signed rank test (
Table 10) and further confirmed with the cubic line of
Figure 21.