Next Article in Journal
Sodium Nitrite-Related Fatalities: Are We Facing a New Trend? Case Report and Literature Review
Previous Article in Journal
From Laws and Court Rulings to Daily Clinical Practice: The Role of Forensic Experts in Modelling Informed Consent Disclosure for Health Treatment
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forensic Sciences
Volume 5
Issue 3
10.3390/forensicsci5030041
forensicsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Validation of Subadult Age and Stature Estimation Methods Using a Contemporary Japanese Sample

by
Elaine Y. Chu
*,
Amariah J. Treviño
and
Marissa E. Vasquez
Department of Anthropology, Texas State University, San Marcos, TX 78666, USA
*
Author to whom correspondence should be addressed.
Forensic Sci. 2025, 5(3), 41; https://doi.org/10.3390/forensicsci5030041
Submission received: 30 May 2025 / Revised: 21 August 2025 / Accepted: 27 August 2025 / Published: 3 September 2025
Browse Figures
Versions Notes

Abstract

Background/Objectives: Methods of estimating the biological profile in forensic anthropology must meet criteria set forth by standards for admissibility in legal proceedings. Subadult biological profile methods have not been as extensively validated due to limited sources of subadult skeletal reference data. Methods: Data for the contemporary Japanese validation sample were collected from full-body, postmortem computed tomography (PMCT) scans (n = 118). Ten subadult age and stature estimation methods using long bone lengths were validated for accuracy, precision, and bias. The methods included both linear and nonlinear regression. Results: Nonlinear regression methods yielded high validation accuracy and precision for age (>90%; <2.5 cm) and stature (>95.89%; <17 cm) and performed better than linear regression methods. Most methods do not meet criteria set by the American Academy of Forensic Sciences (AAFS) Standards Board (ASB) or the American National Standards Institute (ANSI). Conclusions: As skeletal data become increasingly accessible, it is important to continue to validate currently available methods for estimating aspects of the subadult biological profile while also prioritizing the creation of new population-specific and generic methods applicable for forensic casework. Particular focus should lie on improving reference skeletal material variation, appropriate statistical modeling, and adherence to standards in forensic anthropology. Recommendations for choosing the most appropriate method, given a subadult forensic case, are provided.

1. Introduction

Age and stature estimation are two aspects of the subadult biological profile that are strongly related to growth and development [1,2,3,4,5], making them useful in forensic anthropological casework, as they can achieve the high accuracy and precision expected in medicolegal settings [6,7]. When considering which methods to use for a biological profile report, including for subadults, methods should meet a certain set of standards set within the field of forensic anthropology by the American Academy of Forensic Sciences (AAFS) Standards Board (ASB) as well as the American National Standards Institute (ANSI)—these include high testing or cross-validated accuracy, high precision, and validation [8,9,10]. A lack of subadult representation in currently available skeletal collections has not only restricted the creation of contemporaneous methods for estimating the subadult biological profile [11,12] but also hindered the validation of pre-existing methods for use in current forensic anthropological casework [13]. As a result, few methods [14] are currently available that meet the standards.
An additional layer of complexity is the homogeneity of skeletal collections often used for creating methods in forensic anthropology [15], thus necessitating targeted validations of methods for individuals who are not from the same geographic region as the reference sample. Asians are considered one of the fastest-growing minorities in the United States [16], further justifying the importance of considering which methods are applicable for Asian remains. While population-specific methods for Japanese adult individuals are numerous [17,18,19,20,21,22], the same cannot be said for the subadult biological profile. Differences in the trajectories of growth and development between Japanese and European individuals, for example, have been previously reported [23,24,25,26]. Until population-specific subadult methods can be created for Japanese individuals, it is important to assess which methods are most applicable for forensic anthropological casework in Japan or for individuals from similar geographic regions.
Virtual anthropology has created a new avenue for diversifying skeletal reference data for method creation and validation, including for subadults [12,27,28,29,30]. Biological data on shape and size, such as linear measurements, macroscopic observations, and landmark configurations derived from three-dimensional (3D) computed tomography (CT) scans, are comparable to those obtained from physical specimens, making them an accurate and precise substitute for acquiring skeletal reference data [27,31,32,33,34,35,36]. As such, virtual anthropology is not only an alternative source for skeletal reference material for research, but also an alternative means of forensic anthropological application for disaster victim identification, trauma analysis, and generating a biological profile [29,32,37,38,39].
The current study aims to validate ten known subadult age and stature estimation methods utilizing long bone lengths on a contemporary Japanese sample obtained from postmortem CT (PMCT) images. Methods using only the long bones are specifically validated here, as their shafts tend to preserve better compared to epiphyses and are easier to recover than dentition [40,41,42]. Validation accuracy and precision of each method will be evaluated, and recommendations for which methods are appropriate for use in forensic anthropological casework are provided. Current standards for estimating age [43] and stature [44] from skeletal remains (henceforth “Standards”) are set by the Academy Standards Board of the American Academy of Forensic Sciences and are used to evaluate the applicability of different methods in forensic anthropology.

2. Materials and Methods

2.1. Samples

In collaboration with the Education and Research Center of Legal Medicine at Chiba University, PMCT scans were analyzed for a sample of 118 Japanese individuals (51 females and 67 males) aged between birth and 25 years (Figure 1). The upper age range was chosen with the consideration that maturity of the full skeleton (i.e., when growth and development stop) is reached around 25 years with the fusion of the medial clavicle [45] and obliteration of epiphyseal growth lines [46]. Specifications for imaging protocols have been described elsewhere [18,20]. For each individual, available demographic information included biological sex, age at death, and cadaveric stature, which were all collected per intake procedures at Chiba University. PMCT images were processed using 3D Slicer [47] to generate 3D models of the humerus, radius, ulna, femur, tibia, and fibula. Using Amira-Avizo3DTM software (version 2024.2), developed by ThermoFisher Scientific (Waltham, MA, USA), each long bone was virtually measured using the protocol established by Stull and Corron [48]. These measurements included diaphyseal lengths, following the protocol for measuring using AmiraTM by Stull and Corron [48], or maximum lengths, following definitions for dry bone measurements from Langley and colleagues [49]. Descriptive statistics on all measurements used in this study are provided in the Supplementary Material Table S1.

2.2. Subadult Age and Stature Estimation Methods

Ten methods were validated using the contemporary Japanese sample in this study [1,13,50,51,52,53,54,55,56]. All methods differ in reference sample age range, sample size by sex, and population (Table 1). Both linear and nonlinear regression are featured among the methods. All methods using linear regression follow a simple format:
y = mx + b,
where y is either the estimated age or stature, m is the slope, b is the intercept, and x is the long bone length. Methods that provide interval estimates using linear equations all use the standard error of the estimate to calculate varying levels of confidence intervals [1,13,14,50,57]. The two methods that use nonlinear regression do so in different ways. The age estimation method from Stull and colleagues [56], also known as MCP-S-Age, uses a mixed cumulative probit algorithm that follows a Bayesian framework for estimating an age posterior density distribution [58]. The point estimate for age is reported as the mean of the distribution, and MCP-S-Age also returns a 95% credible interval, a Bayesian version of a prediction interval [59], of the density distribution [56,58]. The stature estimation method from Chu and Stull [51], otherwise known as KidStats: Stature (KS: Stature), uses a three-parameter asymptotic exponential equation to estimate stature and provides a 95% prediction interval. Finally, the method from Brits and colleagues [1] is unique in that they provide two different equations for each long bone: one using diaphyseal lengths and one using maximum lengths. This approach allows for better coverage for estimating stature in the (older) transitioning ages (e.g., 10–17 years) where the epiphyses are fusing to the diaphysis [1]. In contrast, KS: Stature allows for either type of measurement to be used in their models and does not differentiate between measurement types [51]. Four out of the ten methods [1,13,51,56] were created using virtual samples, whereas the others were created using dry bone reference samples [14,50,52,53,54,55]. Additionally, stature estimation methods vary on whether living stature [1,14,55] or cadaveric stature [13,51] is being estimated. Prior research has demonstrated large differences (4.3 cm) between living and cadaveric statures [60]; however, as stature is typically reported as an estimated range, it is expected that the range covered by methods that provide methods for estimating stature intervals should encompass both living and cadaveric statures.
Validation of each method first used applicable subsets of the contemporary Japanese sample in accordance with the age ranges used by each method (Table 1). For example, the first validation of Smith [14] only included n = 17 Japanese individuals aged between 3 and 10 years. Second, age and stature were also estimated for the full Japanese validation sample (aged 0–25 years) to evaluate the applicability of these methods when age is unknown or must be estimated. The rationale for the use of a sample age range that extends beyond the lower and/or upper bounds of each method is to provide consistency in the sample size and evaluation of method performance. It is difficult to truly compare different methods when, as previously mentioned, the truncated sample size for evaluating Smith [14] is n = 17, whereas the truncated sample size for evaluating Murray and colleagues [13] is n = 53. Age and stature ranges were calculated when guidance on how to calculate intervals was provided, which included six out of ten methods (see Table 1). Sex-specific models were not validated in this study, as sex estimation of subadult remains has only recently become accurate for limited age ranges [61,62,63,64,65].

2.3. Method Comparisons

The applicability of each method for use on Japanese subadult remains was evaluated using different measures of accuracy and precision for both the truncated age ranges (i.e., reference sample age ranges) and the full validation sample. Compiling the results from all tests provides guidance for recommendations on which methods are most appropriate for use in forensic anthropological casework involving Japanese subadults. All analyses were conducted using R version 4.4.1 [66] and RStudio version 2023.06.1+524 [67].
Validation accuracy was calculated as the proportion of individuals whose known age or stature fell within the estimated interval provided by each method. The breadth of the range estimates produced by each method was evaluated to provide additional context for validation accuracy. For example, a method could be 99% accurate but produce forensically uninformative age estimates, where the predicted range of an individual aged 3 is estimated to be between 2 and 12 years. While technically accurate, an age estimate spanning 10 years would not assist in narrowing the number of potential missing persons reports [56].
Precision was evaluated in two ways, as each provides varying insights on how point estimates compare to known information. Mean squared error (MSE), which is the average squared distance the point estimate is from the known age or stature, is used to evaluate the overall error of a method and has been previously recommended for validating age estimation methods for adults [10]. While it is useful to evaluate the general amount of error produced by a method, it does not provide any guidance on whether there is any bias in the estimates. Patterns of bias (i.e., whether a method over- or underestimates age or stature) were visualized using Bland–Altman plots [68,69].

3. Results

Validation accuracy and precision of each method in this study are summarized for age (Table 2) and stature (Table 3). Methods reporting high validation accuracy and lower MSE values (i.e., higher precision) were considered better performing and more applicable to the Japanese validation sample.

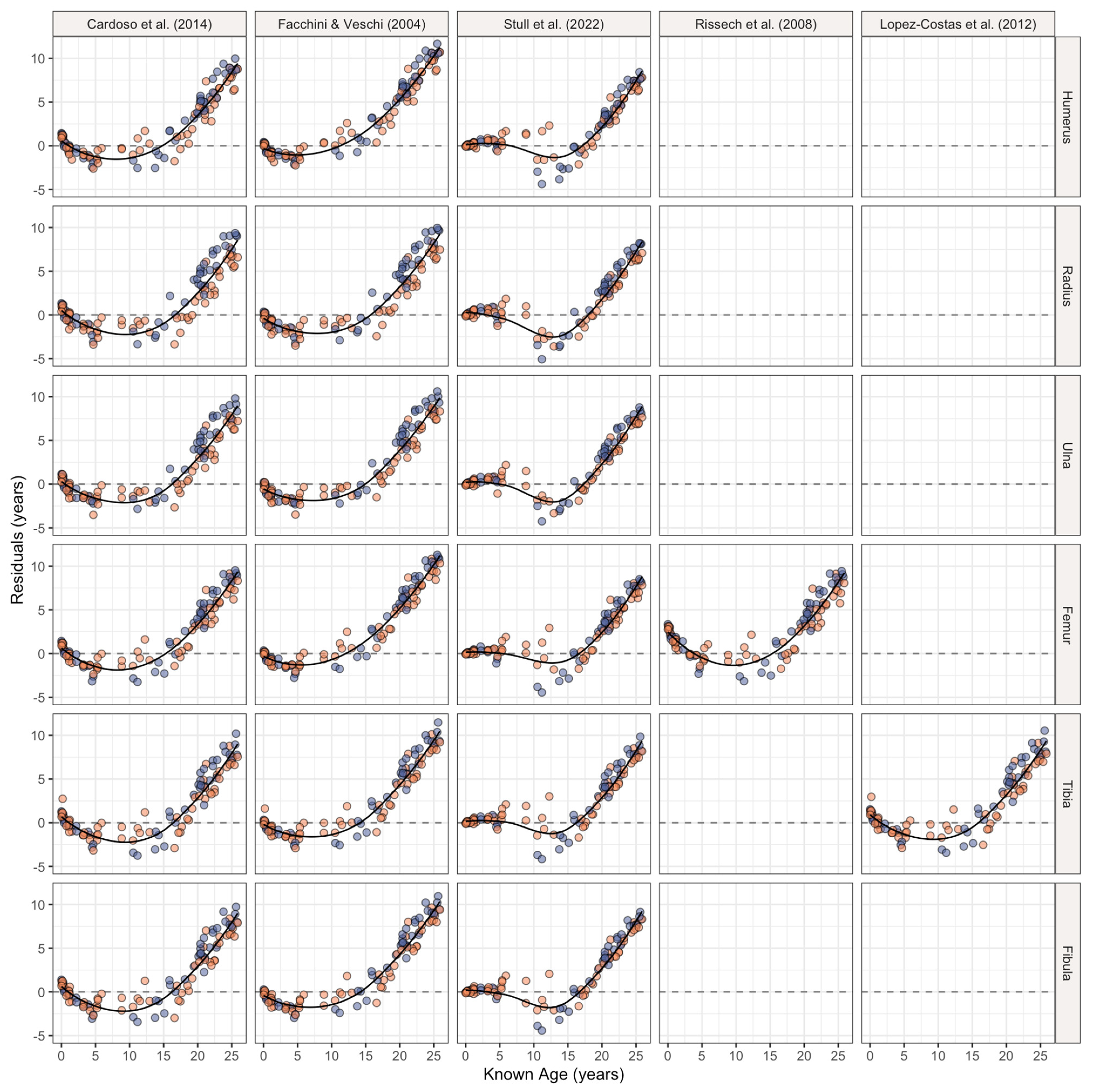
3.1. Age Estimation Methods

Estimates provided by linear equations from Cardoso and colleagues [50] using the truncated sample resulted in validation accuracies ranging from 89.09 to 96.36% and MSE values ranging from 1.23 to 1.92 years. Estimates using the full sample showed lower accuracies of 52.99–60.00% and increased MSE ranging from 14.28 to 17.60 years. The average generated 95% confidence interval for both the truncated and overall samples was 4.59 years. The MCP-S-Age method by Stull and colleagues [56] produced validation accuracies of 85.00–96.72% and MSE ranging from 1.35 to 2.10 years using the truncated sample. The average 95% credible interval for the truncated sample was 3.18 years. The full sample yielded lower accuracies of 61.74–71.79% and increased MSE values of 11.72–14.97 years. The average generated 95% credible interval for the full sample was 5.18 years. Validation accuracy could not be evaluated for the remaining three methods, as they did not provide guidance for calculating age intervals. However, for Facchini & Veschi [52], linear equation estimates produced MSE values ranging from 0.95 to 2.12 years for the truncated sample and 17.36–28.40 years for the full sample. The tibia length equation from López-Costas and colleagues [53] produced an MSE of 1.82 years for the truncated sample and 16.38 years for the full sample. Finally, the femur length equation from Rissech and colleagues [54] produced an MSE of 3.19 years for the truncated sample and 17.23 years for the full sample. On average, the linear methods provided by Cardoso and colleagues [50] produced a validation accuracy of 92.43% and MSE of 1.66 years for the truncated sample (n = 55; 0–13 years) and a validation accuracy of 47.49% and MSE of 15.78 years for the full sample. The nonlinear methods provided by MCP-S-Age [54] produced an average validation accuracy of 90.87% and MSE of 1.55 years for the truncated sample (n = 60 or n = 61; 0–16 years) and a validation accuracy of 67.29% and MSE of 13.27 years for the full sample.
Bias in the age estimates generated by each method for the full Japanese validation sample is presented as Bland–Altman plots in Figure 2. A general trend of initial underestimation (trending above zero) followed by overestimation (trending below zero) and then again underestimation of age is observed by most methods. However, the degree and timing of over- and underestimation vary by method. MCP-S-Age [56] point estimates maintain the least amount of bias in age for the longest time, demonstrating a trendline hovering around zero until age five, before overestimating age from five to 17 years and then underestimating age until 25 years. All methods produce age estimates within two to three years of known age until age 10 and within five years of known age until age 20. From ages 20–25, all methods underestimate age by five or more years, with increasing bias as age increases. Results suggest that the application of age estimation using long bone lengths may be extended beyond the current 12–17 age restriction of all methods to about 20 years, with expectations of lower precision.

3.2. Stature Estimation Methods

Stature estimation methods by Brits and colleagues [1] use either diaphyseal or maximum length measurements of the lower limb. Diaphyseal linear models using the truncated sample ranged from 26.67 to 43.75%, and MSE values ranged from 33.14 to 38.14 cm. The full sample resulted in accuracies of 45.22–56.14% and MSE values ranging between 16.41 and 37.57 cm. The maximum length linear models produced 0.00% accuracy for all models using the truncated sample, with MSE values ranging from 163.59 to 175.61 cm. The full sample resulted in accuracies of 6.83–20.00% and MSE ranging from 108.20 to 117.84 cm. The KS: Stature method by Chu and Stull [51] estimates stature using either linear or nonlinear regression. Linear estimates using the truncated sample resulted in validation accuracies ranging from 91.78 to 98.63% and MSE values ranging from 19.76 to 30.33 cm. The full sample resulted in improved accuracies ranging from 94.02 to 99.15% and lower MSE ranging from 17.91 to 28.81 cm. Nonlinear models using the truncated sample resulted in validation accuracies ranging from 95.89 to 98.63% and MSE values ranging from 12.22 to 16.85 cm. The full sample produced accuracies ranging from 94.87 to 98.28% and MSE values of 12.30–18.15 cm. For Murray and colleagues [13], linear models using the truncated sample resulted in accuracy ranging from 92.45 to 100% and MSE values ranging from 11.31 to 16.45 cm. The full sample resulted in accuracies ranging from 69.23 to 81.90% and MSE ranging from 36.79 to 64.56 cm. For Smith [14], linear models using the truncated sample produced accuracies ranging from 47.06 to 82.35% with MSE values ranging from 15.24 to 28.04 cm. The full sample produced validation accuracies of 49.12–81.03% and MSE values of 17.57–32.86 cm. Validation accuracy could not be evaluated for the femur method by Robbins Schug and colleagues [55]. However, the method yielded an MSE of 15.92 cm for the truncated sample and 29.38 cm for the full sample. On average, the linear methods (see Table 3) produced a validation accuracy of 68.26% and MSE of 40.02 cm for the truncated sample and a validation accuracy of 69.19% and MSE of 38.95 cm for the full sample. The nonlinear methods provided by Chu and Stull [51] produced an average validation accuracy of 97.59% and MSE of 13.92 cm for the truncated sample and a validation accuracy of 97.41% and MSE of 14.36 cm for the full sample. Among all methods, stature estimates from linear regression equations by Brits and colleagues [1] and Chu and Stull [51] are the only cases of improved performance when transitioning from truncated sample metrics and full sample metrics, which explains the marginal improvement of the global linear method validation accuracy and precision observed for the full sample compared to the truncated sample.
Bias in the stature estimates generated by each method using the full Japanese sample is presented using Bland–Altman plots (Figure 3). Each method generates a different trend in estimation bias and varies in timing. Nonlinear equations from KS: Stature [51] generate relatively little bias in stature estimates (trends hovering around zero) for the entire Japanese validation sample. Linear equations by KS: Stature [51] demonstrate an underestimation of stature by 5 cm until age 12, followed by relatively low levels of bias from 12 to 25 years. Stature estimates from Smith [14] initially overestimate stature from birth until two years, followed by an underestimation of stature that either stabilizes around 5 cm or falls back around zero bias from 15 to 25 years. Murray and colleagues’ [13] and Robbins Schug and colleagues’ [55] equations both initially show little bias in stature estimates from birth until five years, followed by an overestimation of stature of around 5–10 cm from 5 to 25 years. Finally, Brits and colleagues’ [1] equations using diaphyseal lengths show different patterns based on long bone length. Trendlines for estimates from the femur and lower limb (femur + tibia) follow similar patterns, with greater underestimation of stature from birth to 10 years and then relatively low levels of bias, with the trendline hovering around zero for ages 10–25. The trendline for estimates from the tibia shows an initial overestimation of stature until age five and then an underestimation of stature, stabilizing around 5 cm from ages 5–25. All estimates generated by maximum length equations from Brits and colleagues [1] show an underestimation of stature of greater magnitude than most other methods, with trendlines hovering around 10 cm. All methods tend to generate point estimates with greater bias for males (orange-filled circles) than females (blue-filled circles), with few exceptions (Figure 3).

4. Discussion

The present study is the first to validate ten selected age and stature estimation methods utilizing long bone lengths on a Japanese subadult sample. In some cases, this study is the first instance of method validation [1,50,51,52,55,56], moving these methods one step closer to inclusion in forensic anthropological casework in line with current legal standards [6,7,9,43,44]. The Japanese sample used in this study serves two functions: (1) as a validation sample completely distinct from the reference samples from which each method was trained, and (2) to evaluate which methods are most applicable to forensic casework regarding Japanese individuals until population-specific or global methods can be created (Figure 4). Methods were evaluated in terms of validation accuracy, precision, and bias of generated output, both for the truncated ages following reference sample age ranges from each method and the entire Japanese validation sample.

4.1. Subadult Age Estimation

Five subadult age estimation methods using long bone lengths were validated in this study. The published standard regarding age estimation in forensic anthropological casework only mentions the use of diaphyseal dimensions (i.e., lengths and breadths) for infant and child age estimation [43] (p. 3) and does not provide specific citations for appropriate methods. It is therefore up to the practitioner to decide which methods to apply to a subadult case. Age-related guidelines for age estimation methods are cyclical in nature, as it is difficult to know whether diaphyseal dimensions and/or methods should be used for age estimation without already estimating a general age based on other factors, such as dental development or epiphyseal fusion [3,70,71,72,73]. While the five age estimation methods validated in this study include individuals beyond infancy and childhood (see Table 1), they all have a restricted age range in consideration of epiphyseal fusion [50,52,53,54,56].
All methods demonstrated a marked improvement in precision of age estimates, changing from a maximum MSE of 28 years to a maximum MSE of three years when restricting the Japanese validation sample to ages matching reference data age ranges (Table 2). Results confirm that methods are more precise when used within the confines of reference sample demographics, which should be considered when selecting a method [43]; however, this again poses a cyclical issue of knowing age before applying an age estimation method. This study therefore also evaluated the applicability of subadult age estimation methods beyond the age ranges of the reference samples, as is more realistic in forensic casework where age is unknown. As demonstrated in Figure 2, all methods were still able to produce age estimates within five years of known age until 20 years, pointing to the potential of long bone measurements to contribute to age estimation beyond younger (<12) age ranges. Understanding the utility of long bones in the subadult biological profile is important because long bones are more likely to be recovered from forensic contexts [40]. Still, subadult age estimation methods using dentition and epiphyses are far more numerous in the literature [2,74]. These findings suggest that the utility of long bone lengths for subadult age estimation may extend beyond the start of epiphyseal fusion and that maximum length measurements should also be considered for integration in future methods.
Validation accuracy could only be calculated for two out of five methods, Cardoso and colleagues [50] and MCP-S-Age [56], as they are the only two that provided guidance on how to calculate age ranges using their method (Table 3). Methods that do not provide a means for calculating age intervals, and therefore accuracy, do not meet the criteria of the current standards [43]. While both methods failed to reach above 80% validation accuracy for the entire Japanese validation sample, they achieved 88% validation accuracy or better when considering only the age ranges used in the reference samples. These findings indicate that methods for subadult age estimation using long bone lengths are most applicable to individuals aged from birth to 16 years. The Bland–Altman plot (Figure 2) suggests that extending the applicable age range of these methods to 20 years does not significantly impact the precision of the point estimates, and therefore estimated age ranges, keeping the bias within 2.5 years.
In general, Cardoso and colleagues [50] achieved an average truncated validation accuracy of 92.43% for individuals aged from birth to 13, while MCP-S-Age [56] achieved an average truncated validation accuracy of 90.89% for individuals aged from birth to 16. In method evaluation, it is also important to reiterate that the approaches for calculating age ranges also differ between the methods. Cardoso and colleagues [50] calculate 95% confidence intervals by multiplying the mean standard error for each equation by two and adding or subtracting that value from the point estimate generated by the linear equation. While confidence intervals are noted as acceptable means for calculating age ranges for forensic anthropology casework [43], others have noted that confidence intervals are only applicable to the reference sample and should not be applied to new data [56,57,74]. This recommendation should be taken into consideration by practitioners, especially when faced with unknown individuals who may not fit the same demographics as a method’s reference sample, as is the case in the current study. Stull and colleagues [56] provide a 95% credible interval, which is akin to a prediction interval but using a Bayesian framework [58,59], which also meets the criteria set forth by Standards [43].
When evaluating precision, bias, and validation accuracy, the authors recommend using MCP-S-Age [56] for subadult age estimation using long bone lengths, especially when a general age below 12 years cannot be ascertained using other developmental indicators. However, it should be noted that the equations from Cardoso and colleagues [50] may also be used in forensic casework once guidance for calculating a prediction interval is provided.

4.2. Subadult Stature Estimation

Five subadult stature estimation methods using long bone lengths were validated in this study. Published standards regarding stature estimation in forensic anthropological casework provide only one recommendation for subadult stature estimation [44], which is Smith [14]. The reference sample age range for Smith [14] is from three to 10 years, making it unclear whether stature should be estimated for individuals outside that age range (e.g., from birth to three years or 10–25). All other stature estimation methods validated in this study (see Table 1) include age ranges outside of that of Smith [14]. To the author’s knowledge, Smith [14] has only been validated one other time by Cardoso [75] in comparison to other stature estimation studies from archeological and historic samples [76,77]. Cardoso found that of the three methods, Smith’s [14] method produced the smallest residual, meaning the smallest distance between known stature and estimated stature. As the current study focuses on contemporary forensic casework, methods provided by Telkkä and colleagues [77] and Feldesman [76] were not validated in the present study because their samples are incompatible. The research presented here is also important as the first validation of four of the five stature estimation methods tested here.
All methods demonstrated a marked improvement in precision (between 3.66 cm and 32.90 cm MSE) of subadult stature estimation for truncated age ranges compared to full age ranges, except for estimates produced by KS: Stature [51] and Brits and colleagues [1]. Improved precision using the full sample for KS: Stature [51] is most likely because while the reference age range extends from birth to 20 years, there does not appear to be any additional bias for stature estimates from 20 to 25 years (Figure 3). Further investigation of the stature estimates produced by Brits and colleagues [1] revealed that while most stature estimates yielded low residuals (differences between estimated stature and known stature), there were a few individuals whose stature was estimated to be 10 cm or larger than their known stature—therefore compounding the amount of error observed in the MSE value. Additionally, the age range of the maximum length reference sample (10–17 years) still showed significant underestimation of stature for the Japanese sample, while younger ages (<5) actually revealed less bias in stature estimates, especially when using the diaphyseal length equations (Figure 3). While fluctuations in bias (over- and underestimation) in stature estimates are observed for all methods (Figure 3), a general stabilization or reduction in bias occurs around age 12; thus, it does not appear that stature estimates become worse as age increases after 12 years. These findings suggest that all stature estimation methods validated in this study may be applied to individuals outside the reference sample age range, to individuals as old as 25 years.
Validation accuracy could be calculated for all methods except for Robbins Schug and colleagues’ [55] femur method. Again, KS: Stature [51] methods were able to achieve a validation accuracy of 91.78% or greater for both the truncated and full Japanese validation samples, whereas Murray and colleagues [13] and Smith [14] achieved a maximum of 81.89% validation accuracy for the full sample. However, when evaluating only the truncated age range, Murray and colleagues’ [13] methods achieved 92.25% or greater validation accuracy, and Smith’s [14] methods achieved a maximum validation accuracy of 82.35%. In contrast, Brits and colleagues’ [1] estimates yielded low (0.00–56.14%) validation accuracy. These results suggest that there may be significant differences in the relationships between long bone length and stature for the Smith [14] sample (i.e., the Denver Growth Study) versus the more contemporary samples for Murray and colleagues [13] and KS: Stature [51]. In fact, there may be some overlap in reference individuals between Murray and colleagues [13] and KS: Stature [51], which both use data from the New Mexico Decedent Image Database [78,79]. Beyond the fact that the validation sample is of Japanese origin, which does not match the reference samples used for the stature estimation methods, stark differences in the accuracy of stature estimates between methods also suggest secular change in overall stature [80,81,82,83]. Previous research into the secular change in Japanese individuals has also demonstrated similar limb-to-stature ratios but differences in absolute stature when compared to individuals from the United States [24,25,84].
Evaluating the precision and accuracy of stature estimates also extends beyond reference age ranges. For example, the large MSE values from Brits and colleagues’ [1] methods suggest that the reference sample of Black South African individuals is not as appropriate for stature estimation of Japanese individuals compared to the largely Western European samples represented by the other stature estimation methods (see Table 1). Stature estimates from Brits and colleagues [1] also had the lowest accuracy rates, suggesting that the difference in proportions between Black South African individuals and Japanese individuals is much more pronounced than that of individuals from the United States or Western Europe.
As is true with subadult age estimation, the subadult stature estimation methods differed in their calculation of a stature interval. Smith [14] and Murray and colleagues [13] both recommend calculating a 95% confidence interval by either multiplying the standard error of estimate by two or 1.96, respectively, and adding or subtracting that value from the point estimate. These resulted in estimated intervals ranging between 7.88 cm and 12.64 cm for Smith [14] and intervals ranging from 14.62 cm to 17.44 cm for Murray and colleagues [13]. Similarly, Brits and colleagues [1] recommend adding or subtracting the standard error of estimate from the point estimate. However, no additional multiplication is recommended, meaning that the estimated intervals only capture 47.50% of the distribution instead, resulting in much narrower ranges (between 6.32 cm and 7.54 cm). Standards recommend the reporting of a 90% (or higher) prediction interval and make no mention of confidence intervals [44]. KS: Stature [51] equations provide 95% prediction intervals, ranging from 16.9 cm to 18.90 cm for nonlinear models and 20.4 cm to 24.5 cm for linear models. While the ranges provided by KS: Stature [51] and Murray and colleagues [13] are much wider compared to those from Smith [14], prediction intervals are always larger than confidence intervals to account for variation in a population that is not captured by a reference sample [75]. Still, as Smith [14] also notes, to what extent is stature estimation helpful in narrowing missing persons reports for subadults when the estimated stature range covers half to almost an entire foot? The standard for stature estimation includes a caveat that stature estimation should never be the sole criterion for exclusion when narrowing missing persons reports [44], suggesting that stature is not the most identifying aspect of the adult or subadult biological profile.
When evaluating precision, bias, and validation accuracy, the authors recommend using KS: Stature [51] for subadult estimation using long bone lengths. Not only did KS: Stature [51] produce the highest validation accuracy, but it also demonstrated the least amount of bias (Figure 3) across the full validation sample age range, especially when using the nonlinear models. However, it should be noted that the equations provided by Murray and colleagues [13] also produced high validation accuracies that show their ability to accurately estimate stature for Japanese individuals. However, Murray and colleagues [13] do not provide a means of calculating a 95% prediction interval, which is the required criterion for standards [44].

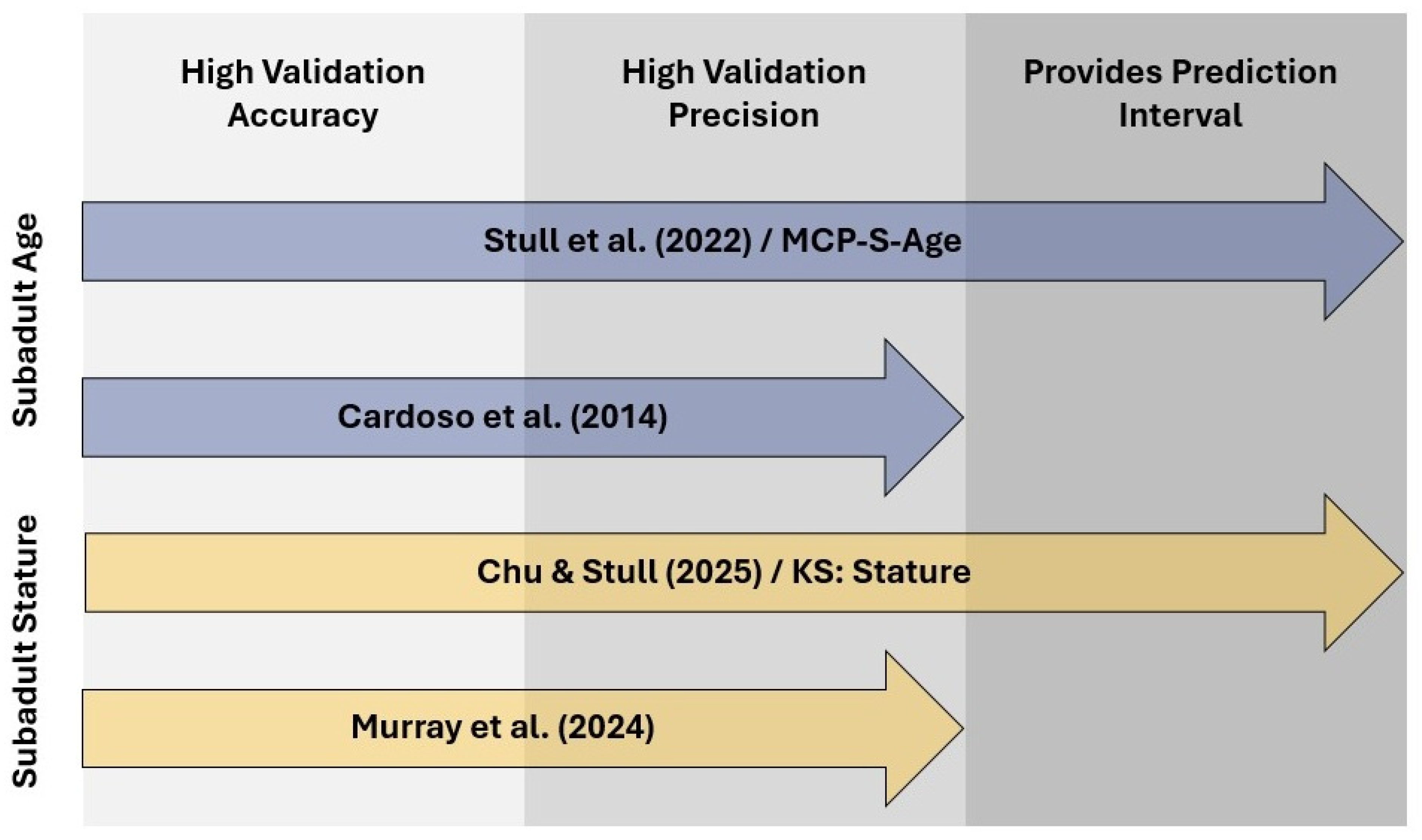
4.3. Recommendations

When considering which methods to use for forensic anthropological analysis and subsequent reporting, it is important to consider several factors. Results of this study suggest that the best-performing methods for use in Japanese forensic anthropological casework regarding subadults are the MCP-S-Age method from Stull and colleagues [56] for age estimation and the nonlinear KS: Stature methods from Chu and Stull [51] for stature estimation. These conclusions were not made solely based on high accuracy and precision for the Japanese validation sample but also due to additional context and considerations—applicable to all cases of subadult remains, regardless of presumed geographic origin—that are outlined below.
1.
Appropriate reference samples
Table 1 demonstrates the prevalence of methods for estimating the subadult biological profile trained on WEIRD (“Westernized, Educated, Industrial, Rich, and Democratic”) reference data—a common theme in forensic anthropology as a discipline [15] but also prevalent in other fields [85,86,87]. Poor stature estimates produced by Brits and colleagues’ [1] equations on the Japanese validation sample further the dialog on the importance of diversifying skeletal reference material for the applicability of non-WEIRD individuals, either through population-specific methods or moving towards global models that capture greater variation. Different aspects of the subadult biological profile may require different considerations. Research has demonstrated that generic equations may outperform population-specific equations for estimating adult stature [88]. As demonstrated in this study, however, reference sample demographics do not consist only of geographic origin or genetic history but also temporality. For example, patterns of growth and development have been shown to vary by location, socioeconomic status, and secular change [23,89,90]. It is therefore important to continue to strive for more diverse and contemporaneous sources of subadult skeletal reference data to (1) create and test generic subadult methods against population-specific ones and (2) verify that current methods of estimating the subadult biological profile are accurate for groups that differ geographically from the reference samples. The methods developed by Stull and colleagues [56], Chu and Stull [51], and Murray and colleagues [13] were all trained on subsets of the New Mexico Decedent Image Database [78,79], which is more diverse and temporally relevant to the Japanese validation study.
2.
Statistical methods that reflect biology
Growth and development are not a linear process. However, subadult methods have only recently begun to incorporate nonlinear statistical approaches to estimating aspects of the biological profile [71,91,92]. The subadult biological profile methods validated in this study rely on the strong relationship between long bone length and chronological age or stature. Neither of these relationships is linear (Figure 5), which is supported by the fact that the two nonlinear methods, MCP-S-Age [56] and KS: Stature [51], outperformed the linear methods validated in this study when evaluating the full Japanese validation sample. While linear methods validated in this study did perform with high validation accuracy and precision for their respective truncated samples (Table 2 and Table 3), they are restricted to the narrow age ranges for which the methods can be applied. As previously mentioned, this also requires the practitioner to make prior assessments on whether the age of the unknown individual falls within a method’s reference sample age range before utilizing a method. In addition, the rigidity of linear regression is prone to over- and underestimating age and stature at different points over the process of growth and development (i.e., age), as is observed in Figure 2 and Figure 3. As age increases, the relationships modeled by subadult age and stature methods using long bone lengths change (Figure 5). However, linear regression assumes an infinitely continuous process, which is why a marked increase in the amount of bias for all linear methods was observed in the present study (Figure 2 and Figure 3) and the marked decrease in validation accuracy and precision when comparing performance using the truncated and full samples (Table 2 and Table 3). The validation of KS: Stature [51] provides a stark demonstration of the difference in performance between linear and nonlinear stature estimation equations, as the method provides both. While validation accuracies for the linear and nonlinear equations produced by KS: Stature were similar for both the truncated and full samples, precision improved by roughly 5–15 cm when comparing linear to nonlinear point estimates (Table 3).
3.
Consult Standards
The role of published standards is to provide best-practice guidelines for all practitioners of forensic anthropology [9,93,94]. It is important to follow recommendations for method selection, such as the choice of appropriate reference materials, but also how to report estimates for the biological profile, which may differ based on age, sex, stature, or population affinity. For example, the Standard for Age Estimation in Forensic Anthropology is more relaxed in their recommendations, only specifying the following: “An age estimate shall be reported as an interval, per method specification (e.g., 95% confidence interval, 95% prediction interval, two-standard deviation range, posterior probabilities) [emphasis added]…the point estimate shall not be used in isolation without consideration of the interval (e.g., to answer the question of whether an individual has attained the age of majority)” [43] (p. 4). In contrast, the Standard for Stature Estimation in Forensic Anthropology is more specific in their recommendation: “…a 90% (or greater) prediction interval [emphasis added] should be reported” [44] (p. 3). Many of the methods validated in this study do not meet the current guidelines set by their respective standards, as they either (a) do not provide a means for calculating an interval (for age estimation) or (b) do not provide a means for calculating a prediction interval (for stature estimation). Practitioners should consider these factors when selecting methods for forensic anthropological casework.
While results of this validation study present MCP-S-Age [56] and KS: Stature [51] as the most appropriate for the Japanese validation sample, it is important to also note the other now-validated methods that may still be considered for forensic anthropological casework. The age estimation method from Cardoso and colleagues [50] still produced high validation accuracy for individuals between birth and 13 years, making it an appropriate method for practitioners who believe the unknown individual to fall within that age range and specific reference population. Stature estimates produced by Murray and colleagues’ [13] equations also produced high validation accuracy for individuals within their reference demographic age range (birth to 12 years), suggesting the applicability of the method in forensic anthropological casework. While the current method from Murray and colleagues [13] only provides guidance for calculating the 95% confidence intervals, which is not in line with published standards, methods for reporting a prediction interval from pre-existing equations can be explored. In the case where the demographics of the reference data used by Cardoso and colleagues [50] and Murray and colleagues [13] may be more appropriate, the authors also recommend that their methods be considered.

4.4. Limitations, Considerations, and Future Directions

Limitations of this study include the geographic distance of Japan from the rest of the countries/populations used as reference data for each method and the small sample sizes of the Japanese sample per age cohort. However, the present validation sample size (n = 118) is larger than the reference sample sizes of some of the methods in this study (Table 1) and other subadult validation studies [13,75]. Another consideration in the design of this project is the choice of including ages ranging from birth to 25 years. As observed by all methods validated in this sample, the designation of “subadult” appears to terminate around 18 years, with the exception of KS: Stature [51], which terminates at 20 years. While 18 years is a common legal age of majority, this cut-off point for distinguishing subadults from adults is arbitrary in biology, as there is no biological basis for establishing 18 years as a boundary for adulthood. For this project, the validation sample age range extended beyond 18 years to 25 years, following the concept that adulthood begins at the cessation of skeletal growth and development. As such, 25 years was chosen because it coincides with the final stages of medial clavicle fusion [45] and obliteration of epiphyseal growth lines [46], which would suggest that the period of skeletal growth and development has subsided. The inclusion of validation individuals beyond the legal age of majority cut-off also allows for variation (e.g., potential acceleration or deceleration) in the trajectory of growth and development of Japanese individuals compared to the method reference populations. Finally, with ever-increasing diversity and prevalence of subadult skeletal reference data through virtual anthropology [12,29,30], future validation samples may better reflect reference sample demographics for a more comprehensive study. Additionally, increasing subadult Japanese reference data may result in population-specific methods of age and stature estimation, with the final goal of incorporating all data into global models where geographic origin is not considered an a priori requirement [51,56,88].

5. Conclusions

The goal of the present study was to validate subadult age and stature estimation methods commonly found in the literature on a contemporary Japanese sample to broadly establish method applicability in forensic casework for subadults and, specifically, to provide recommendations for methods most applicable for Japanese individuals. For nine out of the ten methods explored in this study, this is the first instance of method validation, which is an important step in meeting the criteria for medicolegal casework [6,7,43,44]. Methods that utilized reference data that were more demographically diverse and produced wider interval estimates performed better in terms of point estimate precision and validation accuracy. Secular change appears to have a more nuanced effect on stature estimation than age estimation, and nonlinear regression generally outperformed linear regression. Method validation remains an important, but often overlooked, aspect of forensic anthropological research. It is therefore imperative that validation studies continue to test the applicability of methods on diverse demographic samples and, until more comprehensive methods can be created and validated, explore the extent to which methods may be applied to individuals falling outside the demographic boundaries of the reference sample.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/forensicsci5030041/s1, Table S1: Descriptive statistics of length measurements for the truncated Japanese validation sample, by age-year cohorts and sex. Mean lengths and sample size are provided, with standard deviations represented within the parentheses. All measurements are presented in millimeters (mm). Note that some age/sex combinations do not have any data and are denoted with NA. Standard deviations that are NA are due to a sample size of one.

Author Contributions

Conceptualization, E.Y.C. and A.J.T.; Methodology, E.Y.C.; Formal analysis, E.Y.C. and A.J.T.; Investigation, E.Y.C. and A.J.T.; Resources, E.Y.C.; Data curation, E.Y.C. and A.J.T.; Writing—original draft, E.Y.C., A.J.T. and M.E.V.; Writing—review & editing, M.E.V.; Visualization, E.Y.C.; Supervision, E.Y.C.; Project administration, E.Y.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted according to the guidelines of the Declaration of Helsinki and was determined not human subjects research according to the Code of Federal Regulations (45 CRF 46.102: Protection of Human Subjects) and the Institutional Review Board of the Division of Research at Texas State University (Reference #05-871-700).

Informed Consent Statement

Patient consent was waived because of the retrospective research design.

Data Availability Statement

The dataset presented in this article is not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to elainechu@txstate.edu.

Acknowledgments

Thank you to our collaborators at the Education and Research Center of Legal Medicine at Chiba University, including: Hirotaro Iwase, Chiba Fumiko, Maiko Yoshida, and Yukiko Uemura. Additional thanks to Briana T. New for providing insightful comments and edits to a prior version of the manuscript that resulted in impactful improvements.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
3DThree-dimensional
CTComputed tomography
PCMTPostmortem computed tomography
AAFSAmerican Academy of Forensic Sciences
ASBAAFS Standards Board
ANSIAmerican National Standards Institute

References

  1. Brits, D.M.; Bidmos, M.A.; Manger, P.R. Stature estimation from the femur and tibia in Black South African sub-adults. Forensic Sci. Int. 2017, 270, 277.e1–277.e10. [Google Scholar] [CrossRef] [PubMed]
  2. Corron, L.; Marchal, F.; Condemi, S.; Adalian, P. A critical review of sub-adult age estimation in biological anthropology: Do methods comply with published recommendations? Forensic Sci. Int. 2018, 288, 328.e1–328.e9. [Google Scholar] [CrossRef]
  3. Cunningham, C.A. Skeletal age estimation in juveniles and subadults. In Age Estimation; Adserias-Garriga, J., Ed.; Academic Press: London, UK, 2019; pp. 41–54. [Google Scholar] [CrossRef]
  4. Langley, N.R. Stature estimation. In Forensic Anthropology: A Comprehensive Introduction, 2nd ed.; Langley, N.R., Tersigni-Tarrant, M.T.A., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 195–203. [Google Scholar]
  5. Rissech, C.; Márquez-Grant, N.; Turbón, D. A collation of recently published Western European formulae for age estimation of subadult skeletal remains: Recommendations for forensic anthropology and osteoarchaeology. J. Forensic Sci. 2013, 58, S163–S168. [Google Scholar] [CrossRef]
  6. Grivas, C.R.; Komar, D.A. Kumho, Daubert, and the nature of scientific inquiry: Implications for forensic anthropology. J. Forensic Sci. 2008, 53, 771–776. [Google Scholar] [CrossRef]
  7. Lesciotto, K.M. The impact of Daubert on the admissibility of forensic anthropology expert testimony. J. Forensic Sci. 2015, 60, 549–555. [Google Scholar] [CrossRef]
  8. Bethard, J.D.; DiGangi, E.A. From the laboratory to the witness stand: Research trends and method validation in forensic anthropology. In Forensic Anthropology and the United States Judicial System, 1st ed.; Fulginiti, L.C., Hartnett-McCann, K., Galloway, A., Eds.; Wiley: Hoboken, NJ, USA, 2019; pp. 41–52. [Google Scholar] [CrossRef]
  9. Fleischman, J.M.; Pierce, M.L.; Crowder, C.M. Transparency in forensic anthropology through the implementation of quality assurance practices. In Forensic Anthropology and the United States Judicial System, 1st ed.; Fulginiti, L.C., Hartnett-McCann, K., Galloway, A., Eds.; Wiley: Hoboken, NJ, USA, 2019; pp. 70–88. [Google Scholar] [CrossRef]
  10. Valsecchi, A.; Irurita Olivares, J.; Mesejo, P. Age estimation in forensic anthropology: Methodological considerations about the validation studies of prediction models. Int. J. Legal Med. 2019, 133, 1915–1924. [Google Scholar] [CrossRef]
  11. Campanacho, V.; Alves Cardoso, F.; Ubelaker, D.H. Documented skeletal collections and their importance in forensic anthropology in the United States. Forensic Sci. 2021, 1, 228–239. [Google Scholar] [CrossRef]
  12. Stull, K.E.; Corron, L.K. The Subadult Virtual Anthropology Database (SVAD): An accessible repository of contemporary subadult reference data. Forensic Sci. 2022, 2, 20–36. [Google Scholar] [CrossRef]
  13. Murray, N.J.; Spake, L.; Cervantes, M.; Albanese, J.; Cardoso, H.F. New More Generic and Inclusive Regression Formulae for the Estimation of Stature from Long Bone Lengths in Children. Forensic Sci. 2024, 4, 62–75. [Google Scholar] [CrossRef]
  14. Smith, S.L. Stature estimation of 3–10-year-old children from long bone lengths. J. Forensic Sci. 2007, 52, 538–546. [Google Scholar] [CrossRef]
  15. Go, M.C.; Yukyi, N.; Chu, E.Y. On WEIRD anthropologists and their white skeletons. Forensic Anthropol. 2021, 4, 145–160. [Google Scholar] [CrossRef]
  16. Budiman, A.; Ruiz, N.G. Key Facts About Asian Americans, a Diverse and Growing Population. Available online: https://www.pewresearch.org/short-reads/2021/04/29/key-facts-about-asian-americans/ (accessed on 29 May 2025).
  17. Chiba, F.; Inokuchi, G.; Hoshioka, Y.; Sakuma, A.; Makino, Y.; Torimitsu, S.; Yamaguchi, R.; Saitoh, H.; Kono, M.; Iwase, H. Age estimation by evaluation of osteophytes in thoracic and lumbar vertebrae using postmortem CT images in a modern Japanese population. Int. J. Legal Med. 2022, 136, 261–267. [Google Scholar] [CrossRef]
  18. Chiba, F.; Makino, Y.; Torimitsu, S.; Motomura, A.; Inokuchi, G.; Ishii, N.; Hoshioka, Y.; Abe, H.; Yamaguchi, R.; Sakuma, A.; et al. Stature estimation based on femoral measurements in the modern Japanese population: A cadaveric study using multidetector computed tomography. Int. J. Legal Med. 2018, 132, 1485–1491. [Google Scholar] [CrossRef]
  19. Hishmat, A.M.; Michiue, T.; Sogawa, N.; Oritani, S.; Ishikawa, T.; Fawzy, I.A.; Hashem, M.A.M.; Maeda, H. Virtual CT morphometry of lower limb long bones for estimation of the sex and stature using postmortem Japanese adult data in forensic identification. Int. J. Legal Med. 2015, 129, 1173–1182. [Google Scholar] [CrossRef]
  20. Kira, K.; Chiba, F.; Makino, Y.; Torimitsu, S.; Yamaguchi, R.; Tsuneya, S.; Motomura, A.; Yoshida, M.; Saitoh, N.; Inokuchi, G.; et al. Stature estimation by semi-automatic measurements of 3D CT images of the femur. Int. J. Legal Med. 2023, 137, 359–377. [Google Scholar] [CrossRef] [PubMed]
  21. Ogawa, Y.; Imaizumi, K.; Miyasaka, S.; Yoshino, M. Discriminant functions for sex estimation of modern Japanese skulls. J. Forensic Leg. Med. 2013, 20, 234–238. [Google Scholar] [CrossRef]
  22. Torimitsu, S.; Nakazawa, A.; Flavel, A.; Iwase, H.; Makino, Y.; Hisham, S.; Franklin, D. Estimation of population affinity using cranial measurements acquired in multidetector computed tomography images of Japanese and Malay individuals. Int. J. Legal Med. 2025, 139, 863–873. [Google Scholar] [CrossRef]
  23. Eveleth, P.B.; Tanner, J.M. Worldwide Variation in Human Growth, 2nd ed.; Cambridge University Press: London, UK, 1991. [Google Scholar]
  24. Greulich, W.W. A comparison of the physical growth and development of American-born and native Japanese children. Am. J. Phys. Anthropol. 1957, 15, 489–515. [Google Scholar] [CrossRef]
  25. Kimura, K. Studies on growth and development in Japan. Am. J. Phys. Anthropol. 1984, 27, 179–213. [Google Scholar] [CrossRef]
  26. Kondo, S.; Eto, M. Physical growth studies on Japanese-American children in comparison with native Japanese. In Comparative Studies on Human Adaptability of Japanese, Caucasians, and Japanese Americans; Horvath, S.M., Kondo, S., Matsui, H., Yoshimura, H., Eds.; University of Tokyo Press: Tokyo, Japan, 1975; Volume 1, pp. 13–45. [Google Scholar]
  27. Brough, A.L.; Rutty, G.N.; Black, S.; Morgan, B. Post-mortem computed tomography and 3D imaging: Anthropological applications for juvenile remains. Forensic Sci. Med. Pathol. 2012, 8, 270–279. [Google Scholar] [CrossRef] [PubMed]
  28. Dedouit, F.; Savall, F.; Mokrane, F.Z.; Rousseau, H.; Crubézy, E.; Rougé, D.; Telmon, N. Virtual anthropology and forensic identification using multidetector CT. BJR 2014, 87, 20130468. [Google Scholar] [CrossRef]
  29. Franklin, D.; Blau, S. Physical and virtual sources of biological data in forensic anthropology: Considerations relative to practitioner and/or judicial requirements. In Statistics and Probability in Forensic Anthropology; Academic Press: London, UK, 2020; pp. 17–45. [Google Scholar] [CrossRef]
  30. Stock, M.K.; Stull, K.E.; Garvin, H.M.; Klales, A.R. Development of modern human subadult age and sex estimation standards using multi-slice computed tomography images from medical examiner’s offices. In Developments in X-Ray Tomography X; SPIE: Bellingham, WA, USA, 2016; Volume 99670E, pp. 48–61. [Google Scholar] [CrossRef]
  31. Abegg, C.; Balbo, I.; Dominguez, A.; Grabherr, S.; Campana, L.; Moghaddam, N. Virtual anthropology: A preliminary test of macroscopic observation versus 3D surface scans and computed tomography (CT) scans. Forensic Sci. Res. 2021, 6, 34–41. [Google Scholar] [CrossRef]
  32. Brough, A.L.; Morgan, B.; Robinson, C.; Black, S.; Cunningham, C.; Adams, C.; Rutty, G.N. A minimum data set approach to post-mortem computed tomography reporting for anthropological biological profiling. Forensic Sci. Med. Pathol. 2014, 10, 504–512. [Google Scholar] [CrossRef] [PubMed]
  33. Colman, K.L.; de Boer, H.H.; Dobbe, J.G.; Liberton, N.P.; Stull, K.E.; van Eijnatten, M.; Streekstra, G.J.; Oostra, R.J.; van Rijn, R.R.; van der Merwe, A.E. Virtual forensic anthropology: The accuracy of osteometric analysis of 3D bone models derived from clinical computed tomography (CT) scans. Forensic Sci. Int. 2019, 304, 109963. [Google Scholar] [CrossRef] [PubMed]
  34. Corron, L.; Marchal, F.; Condemi, S.; Chaumoitre, K.; Adalian, P. Evaluating the consistency, repeatability, and reproducibility of osteometric data on dry bone surfaces, scanned dry bone surfaces, and scanned bone surfaces obtained from living individuals. BMSAP 2017, 29, 33–53. [Google Scholar] [CrossRef]
  35. Franklin, D.; Swift, L.; Flavel, A. ‘Virtual anthropology’ and radiographic imaging in the Forensic Medical Sciences. Egypt. J. Forensic Sci. 2016, 6, 31–43. [Google Scholar] [CrossRef]
  36. Jerković, I.; Bašić, Ž.; Bareša, T.; Krešić, E.; Hadžić, A.A.; Dolić, K.; Ćavar Borić, M.; Budimir Mršić, D.; Čavka, M.; Šlaus, M.; et al. The repeatability of standard cranial measurements on dry bones and MSCT images. J. Forensic Sci. 2022, 67, 1938–1947. [Google Scholar] [CrossRef]
  37. Brough, A.L.; Morgan, B.; Rutty, G.N. Postmortem computed tomography (PMCT) and disaster victim identification. Radiol. Med. 2015, 120, 866–873. [Google Scholar] [CrossRef]
  38. Kolpan, K.E.; Vadala, J.; Dhanaliwala, A.; Chao, T. Utilizing augmented reality for reconstruction of fractured, fragmented and damaged craniofacial remains in forensic anthropology. Forensic Sci. Int. 2024, 357, 111995. [Google Scholar] [CrossRef] [PubMed]
  39. Oriola, L.S.; Oller, N.A.; Martínez-Abadías, N. Virtual anthropology: Forensic applications to cranial skeletal remains from the Spanish Civil War. Forensic Sci. Int. 2022, 341, 111504. [Google Scholar] [CrossRef]
  40. Manifold, B.M. Intrinsic and extrinsic factors involved in the preservation of non-adult skeletal remains in archaeology and forensic science. Bull. Int. Assoc. Paleodont. 2012, 6, 51–69. Available online: https://hrcak.srce.hr/95443 (accessed on 15 May 2025).
  41. Manifold, B.M. Skeletal preservation of children’s remains in the archaeological record. Homo 2015, 66, 520–548. [Google Scholar] [CrossRef]
  42. Stojanowski, C.M.; Seidemann, R.M.; Doran, G.H. Differential skeletal preservation at Windover Pond: Causes and consequences. Am. J. Phys. Anthropol. 2002, 119, 15–26. [Google Scholar] [CrossRef]
  43. ANSI/ASB Standard 133; Standard for Age Estimation in Forensic Anthropology. 1st ed. AAFS Standards Board, LLC: Colorado Springs, CO, USA, 2024.
  44. ANSI/ASB Standard 045; Standard for Stature Estimation in Forensic Anthropology. 1st ed. AAFS Standards Board, LLC: Colorado Springs, CO, USA, 2019.
  45. Langley, N.R. The lateral clavicular epiphysis: Fusion timing and age estimation. Int. J. Legal Med. 2016, 130, 511–517. [Google Scholar] [CrossRef]
  46. Black, S.; Scheuer, L. Age changes in the clavicle: From the Early Neonatal Period to Skeletal Maturity. Int. J. Osteoarchaeol 1996, 6, 425–434. [Google Scholar] [CrossRef]
  47. Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef] [PubMed]
  48. Stull, K.E.; Corron, L.K. Subadult Virtual Anthropology Database (SVAD) Data Collection Protocol: Epiphyseal Fusion, Diaphyseal Dimensions, Dental Development Stages, Vertebral Neural Canal Dimensions. 2021. Available online: https://zenodo.org/records/5348392 (accessed on 29 May 2025).
  49. Langley, N.R.; Jantz, L.M.; Ousley, S.D.; Jantz, R.L.; Milner, G. Data Collection Procedures for Forensic Skeletal Material 2.0; University of Tennessee: Knoxville, TN, USA; Lincoln Memorial University: Harrogate, TN, USA, 2016. [Google Scholar]
  50. Cardoso, H.F.; Abrantes, J.; Humphrey, L.T. Age estimation of immature human skeletal remains from the diaphyseal length of the long bones in the postnatal period. Int. J. Legal Med. 2014, 128, 809–824. [Google Scholar] [CrossRef] [PubMed]
  51. Chu, E.Y.; Stull, K.E. An investigation of the relationship between long bone measurements and stature: Implications for estimating skeletal stature in subadults. Int. J. Legal Med. 2025, 139, 441–453. [Google Scholar] [CrossRef]
  52. Facchini, F.; Veschi, S. Age determination on long bones in a skeletal subadults sample (b-12 years). Coll. Anthropol. 2004, 28, 89–98. Available online: https://hrcak.srce.hr/4889 (accessed on 15 May 2025).
  53. López-Costas, O.; Rissech, C.; Trancho, G.; Turbón, D. Postnatal ontogenesis of the tibia. Implications for age and sex estimation. Forensic Sci. Int. 2012, 214, 207.e1–207.e11. [Google Scholar] [CrossRef]
  54. Rissech, C.; Schaefer, M.; Malgosa, A. Development of the femur—Implications for age and sex determination. Forensic Sci. Int. 2008, 180, 1–9. [Google Scholar] [CrossRef] [PubMed]
  55. Robbins Schug, G.; Gupta, S.; Cowgill, L.W.; Sciulli, P.W.; Blatt, S.H. Panel regression formulas for estimating stature and body mass from immature human skeletons: A statistical approach without reference to specific age estimates. J. Archaeol. Sci. 2013, 40, 3076–3086. [Google Scholar] [CrossRef]
  56. Stull, K.E.; Chu, E.Y.; Corron, L.K.; Price, M.H. Subadult age estimation using the mixed cumulative probit and a contemporary United States population. Forensic Sci. 2022, 2, 741–779. [Google Scholar] [CrossRef]
  57. Heskes, T. Practical confidence and prediction intervals. In Advances in Neural Information Processing Systems; Mozer, M.C., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1996; Volume 9, Available online: https://proceedings.neurips.cc/paper_files/paper/1996/file/7940ab47468396569a906f75ff3f20ef-Paper.pdf (accessed on 15 May 2025).
  58. Stull, K.E.; Chu, E.Y.; Corron, L.K.; Price, M.H. Mixed cumulative probit: A multivariate generalization of transition analysis that accommodates variation in the shape, spread and structure of data. R. Soc. Open Sci. 2023, 10, 220963. [Google Scholar] [CrossRef]
  59. Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
  60. Cardoso, H.F.; Marinho, L.; Albanese, J. The relationship between cadaver, living and forensic stature: A review of current knowledge and a test using a sample of adult Portuguese males. Forensic Sci. Int. 2016, 258, 55–63. [Google Scholar] [CrossRef]
  61. Auchter, L.E.; Stull, K. Development and Validation of a Subadult Sex Estimation Method Using Pelvic Metrics. Forensic Anthropol. 2025, 8, 19. [Google Scholar] [CrossRef]
  62. Blake, K.A. A test of sex estimation in subadults using the elevation of the auricular surface from four samples of known age and sex. J. Forensic Sci. 2019, 64, 1129–1134. [Google Scholar] [CrossRef]
  63. Garvin, H.M.; Stock, M.K.; Marciniec, K.A.; Mohamed, M.M.; Ternent, E.; Cirillo, L.E.; Stull, K.E. Sex estimation of the subadult ilium prior to acetabular fusion. J. Forensic Sci. 2021, 66, 2113–2125. [Google Scholar] [CrossRef] [PubMed]
  64. Klales, A.R.; Burns, T.L. Adapti-ng and applying the Phenice (1969) adult morphological sex estimation technique to subadults. J. Forensic Sci. 2017, 62, 747–752. [Google Scholar] [CrossRef]
  65. Stull, K.E.; L’Abbé, E.N.; Ousley, S.D. Subadult sex estimation from diaphyseal dimensions. Am. J. Phys. Anthropol. 2017, 163, 64–74. [Google Scholar] [CrossRef]
  66. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 29 May 2025).
  67. RStudio: Integrated Development Environment for R. Available online: http://www.posit.co/ (accessed on 29 May 2025).
  68. Bland, J.M.; Altman, D.G. Comparing methods of measurement: Why plotting difference against standard method is misleading. Lancet 1995, 346, 1085–1087. [Google Scholar] [CrossRef]
  69. Giavarina, D. Understanding bland altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef]
  70. AlQahtani, S.J.; Hector, M.P.; Liversidge, H.M. Brief communication: The London atlas of human tooth development and eruption. Am. J. Phys. Anthropol. 2010, 142, 481–490. [Google Scholar] [CrossRef]
  71. De Tobel, J.; Fieuws, S.; Hillewig, E.; Phlypo, I.; Van Wijk, M.; de Haas, M.B.; Politis, C.; Verstraete, K.L.; Thevissen, P.W. Multi-factorial age estimation: A Bayesian approach combining dental and skeletal magnetic resonance imaging. Forensic Sci. Int. 2020, 306, 110054. [Google Scholar] [CrossRef]
  72. Kamnikar, K.R.; Herrmann, N.P.; Plemons, A.M. New approaches to juvenile age estimation in forensics: Application of transition analysis via the Shackelford et al. method to a diverse modern subadult sample. Hum. Biol. 2018, 90, 11–30. [Google Scholar] [CrossRef] [PubMed]
  73. Stull, K.E.; Corron, L.K.; Price, M.H. Subadult age estimation variables: Exploring their varying roles across ontogeny. In Remodeling Forensic Skeletal Age; Algee-Hewitt, B.F.B., Kim, J., Eds.; Academic Press: London, UK, 2021; pp. 49–73. [Google Scholar] [CrossRef]
  74. Corron, L.; Adalian, P.; Condemi, S.; Marchal, F.; Navega, D. Sub-adult aging method selection (SAMS): A decisional tool for selecting and evaluating sub-adult age estimation methods based on standardized methodological parameters. Forensic Sci. Int. 2019, 304, 109897. [Google Scholar] [CrossRef]
  75. Cardoso, H.F. A test of three methods for estimating stature from immature skeletal remains using long bone lengths. J. Forensic Sci. 2009, 54, 13–19. [Google Scholar] [CrossRef]
  76. Feldesman, M.R. Femur/stature ratio and estimates of stature in children. Am. J. Phys. Anthropol. 1991, 87, 447–459. [Google Scholar] [CrossRef]
  77. Telkkä, A.; Palkama, A.; Virtama, P. Prediction of stature from radiographs of long bones in children. J. Forensic Sci. 1962, 7, 474–479. [Google Scholar]
  78. Berry, S.D.; Edgar, H.J. A new resource for pathology informatics: The New Mexico decedent image database. J. Pathol. Inform. 2021, 12, 44. [Google Scholar] [CrossRef]
  79. Edgar, H.J.H.; Daneshvari Berry, S.; Moes, E.; Adolphi, N.L.; Bridges, P.; Nolte, K.B. New Mexico Decedent Image Database. Office of the Medical Investigator, University of New Mexico. 2020. Available online: http://nmdid.unm.edu/ (accessed on 29 May 2025).
  80. Bogin, B. Secular changes in childhood, adolescent and adult stature. Nestle Nutr. Inst. Workshop Ser. 2013, 71, 115–126. [Google Scholar] [CrossRef]
  81. Jantz, R.L.; Jantz, L.M.; Devlin, J.L. Secular changes in the postcranial skeleton of American whites. Hum. Biol. 2016, 88, 65–75. [Google Scholar] [CrossRef]
  82. Klepinger, L.L. Stature, maturation variation and secular trends in forensic anthropology. J. Forensic Sci. 2001, 46, 788–790. [Google Scholar] [CrossRef]
  83. Shin, D.H.; Oh, C.S.; Kim, Y.S.; Hwang, Y.I. Ancient-to-modern secular changes in Korean stature. Am. J. Phys. Anthropol. 2012, 147, 433–442. [Google Scholar] [CrossRef]
  84. Bogin, B. Patterns of Human Growth, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
  85. Apicella, C.; Norenzayan, A.; Henrich, J. Beyond WEIRD: A review of the last decade and a look ahead to the global laboratory of the future. Evol. Hum. Behav. 2020, 41, 319–329. [Google Scholar] [CrossRef]
  86. Gjesdal, A. The WEIRDEST People in the World: How the West Became Psychologically Peculiar and Particularly Prosperous, by Joseph Henrich. New York: Farrar, Straus, and Giroux, 2020. In Business Ethics Quarterly; Cambridge University Press: Cambridge, UK, 2023; Volume 33, pp. 244–247. [Google Scholar] [CrossRef]
  87. Henrich, J.; Heine, S.J.; Norenzayan, A. Most people are not WEIRD. Nature 2010, 466, 29. [Google Scholar] [CrossRef]
  88. Albanese, J.; Tuck, A.; Gomes, J.; Cardoso, H.F. An alternative approach for estimating stature from long bones that is not population-or group-specific. Forensic Sci. Int. 2016, 259, 59–68. [Google Scholar] [CrossRef]
  89. Bielicki, T.; Welon, Z. Growth data as indicators of social inequalities: The case of Poland. Am. J. Phys. Anthropol. 1982, 25, 153–167. [Google Scholar] [CrossRef]
  90. Bogin, B.; Loucky, J. Plasticity, political economy, and physical growth status of Guatemala Maya children living in the United States. Am. J. Phys. Anthropol. 1997, 102, 17–32. [Google Scholar] [CrossRef]
  91. Stull, K.E.; L’Abbé, E.N.; Ousley, S.D. Using multivariate adaptive regression splines to estimate subadult age from diaphyseal dimensions. Am. J. Phys. Anthropol 2014, 154, 376–386. [Google Scholar] [CrossRef] [PubMed]
  92. Wang, J.; Wang, M.; Shen, S.; Guo, Y.; Fan, L.; Ji, F.; Tao, J. Testing nonlinear equations for dental age evaluation in a population of eastern China. Legal Med. 2021, 48, 101793. [Google Scholar] [CrossRef] [PubMed]
  93. Langley, N.R.; Tersigni-Tarrant, M.A.; Passalacqua, N.V.; Crowder, C.M.; Garvin, H.M.; McQuade, W.E.P.; Martinez, M.S.; Pilloud, M.A. The future of forensic anthropology practice and education: Competencies, certification, and licensure. Am. J. Biol. Anthropol. 2025, 183, e70034. [Google Scholar] [CrossRef]
  94. Passalacqua, N.; Pilloud, M.A.; Congram, D. Forensic anthropology as a discipline. Biology 2021, 10, 691. [Google Scholar] [CrossRef] [PubMed]
Forensicsci 05 00041 g001
Figure 1. Age distribution and sample size of the Japanese validation sample, separated by sex.
Figure 1. Age distribution and sample size of the Japanese validation sample, separated by sex.
Forensicsci 05 00041 g001
Forensicsci 05 00041 g002
Figure 2. Bland–Altman plot demonstrating bias in predicted age generated by each method (columns) and by each long bone (rows) for the entire Japanese validation sample. Female = blue-filled circles. Male = orange-filled circles. A LOESS trendline (black solid line) is used to demonstrate the pattern of bias across known age (x-axis). Residuals (y-axis) were calculated as predicted age subtracted from known age. Age is overestimated when the trendline falls below zero and is underestimated when the trendline is above zero [50,52,53,54,56].
Figure 2. Bland–Altman plot demonstrating bias in predicted age generated by each method (columns) and by each long bone (rows) for the entire Japanese validation sample. Female = blue-filled circles. Male = orange-filled circles. A LOESS trendline (black solid line) is used to demonstrate the pattern of bias across known age (x-axis). Residuals (y-axis) were calculated as predicted age subtracted from known age. Age is overestimated when the trendline falls below zero and is underestimated when the trendline is above zero [50,52,53,54,56].
Forensicsci 05 00041 g002
Forensicsci 05 00041 g003
Figure 3. Bland–Altman plot demonstrating bias in predicted stature generated by each method (columns) and by each long bone (rows) for the entire Japanese validation sample. Female = blue-filled circles. Male = orange-filled circles. A LOESS trendline (black solid line) is used to demonstrate the pattern of bias across known age (x-axis) to show bias in stature estimates as age increases. Residuals (y-axis) were calculated as predicted stature subtracted from known stature. Stature is overestimated when the trendline falls below zero and is underestimated when the trendline is above zero [1,13,14,51,55].
Figure 3. Bland–Altman plot demonstrating bias in predicted stature generated by each method (columns) and by each long bone (rows) for the entire Japanese validation sample. Female = blue-filled circles. Male = orange-filled circles. A LOESS trendline (black solid line) is used to demonstrate the pattern of bias across known age (x-axis) to show bias in stature estimates as age increases. Residuals (y-axis) were calculated as predicted stature subtracted from known stature. Stature is overestimated when the trendline falls below zero and is underestimated when the trendline is above zero [1,13,14,51,55].
Forensicsci 05 00041 g003
Forensicsci 05 00041 g004
Figure 4. Recommended methods for subadult age (purple) and subadult stature (yellow) estimation for cases regarding Japanese individuals. Methods were chosen based on validation accuracy, validation precision, and meeting the standards outlined by the ASB/ANSI [13,43,44,50,51,56].
Figure 4. Recommended methods for subadult age (purple) and subadult stature (yellow) estimation for cases regarding Japanese individuals. Methods were chosen based on validation accuracy, validation precision, and meeting the standards outlined by the ASB/ANSI [13,43,44,50,51,56].
Forensicsci 05 00041 g004
Forensicsci 05 00041 g005
Figure 5. Relationship between femur length (x-axis) and age (top, y-axis) or stature (bottom, y-axis). A LOESS line (black solid line) was fit to each relationship for combined sex. A linear regression (red dashed line) was also fit to each relationship for combined sex. Females = blue-filled circles. Males = orange-filled circles.
Figure 5. Relationship between femur length (x-axis) and age (top, y-axis) or stature (bottom, y-axis). A LOESS line (black solid line) was fit to each relationship for combined sex. A linear regression (red dashed line) was also fit to each relationship for combined sex. Females = blue-filled circles. Males = orange-filled circles.
Forensicsci 05 00041 g005
Table 1. Summary of methods validated in the present study. Methods that provide interval estimates are indicated with an “x”.
Table 1. Summary of methods validated in the present study. Methods that provide interval estimates are indicated with an “x”.
MethodReference Sample Age Range
(in Years)		Reference Sample Size by SexReference Sample PopulationsRegression TypeProvides
Interval
Estimates
Age Estimation methods
Cardoso et al. [50]0–13
F: 72
M: 122		Portuguese and EnglishLinearx
Facchini & Veschi [52]0–12F: 70
M: 79		ItalianLinear
Lόpez-Costas et al. [53]0–17F: 26
M: 31		Portuguese and EnglishLinear
Rissech et al. [54]0–16F: 52
M: 35		Portuguese, English,
Spanish, and Scottish		Linear
Stull et al. [56]/
MCP-S-Age		0–16F: 405
M: 526		American (U.S.)Nonlinearx
Stature Estimation Methods
Brits et al. [1]10–17F: 30
M: 29		Black South AfricanLinearx
Chu & Stull [51]/
KS: Stature		0–20F: 401
M: 589		American (U.S.)Linear and Nonlinearx
Murray et al. [13]0–12F: 79
M: 73		American (U.S.)Linearx
Robbins Schug et al. [55]0.5–11.520
individuals, sex unknown		American (U.S.)Linear
Smith [14]3–10F: 36
M: 31		American (U.S.)Linearx
Table 2. Validation of age estimation methods using long bone length. Validation accuracy could only be calculated for Cardoso and colleagues [50] and Stull and colleagues [56]. Validation accuracy could not be calculated for the remaining methods because methods for calculating interval estimates were not provided. Mean squared error (MSE) is the average squared distance between the point estimate and the known age.
Table 2. Validation of age estimation methods using long bone length. Validation accuracy could only be calculated for Cardoso and colleagues [50] and Stull and colleagues [56]. Validation accuracy could not be calculated for the remaining methods because methods for calculating interval estimates were not provided. Mean squared error (MSE) is the average squared distance between the point estimate and the known age.
MethodLong BoneTruncated Sample SizeAccuracy (%)MSE
(in Years)		Full Sample SizeAccuracy (%)MSE
(in Years)
Cardoso et al. [50]Humerus5594.551.2311755.5617.60
Radius5592.731.781156014.28
Ulna5596.361.6211659.4815.65
Femur5590.911.5911752.9917.12
Tibia5589.091.9211554.7814.97
Fibula5590.911.8011456.1415.05
Facchini & Veschi [52]Humerus53-0.95117-28.40
Radius532.1211517.36
Ulna531.8911620.23
Femur531.1611727.65
Tibia531.4611522.04
Fibula531.7011421.59
Lόpez-Costas et al. [53]Tibia64-1.82115-16.38
Rissech et al. [54]Femur60-3.19117-17.23
Stull et al. [56]/
MCP-S-Age		Humerus6193.441.5011771.7912.18
Radius6085.002.1011566.9611.72
Ulna6091.671.5411669.8313.28
Femur6088.331.4011763.2513.23
Tibia6190.161.3511561.7414.97
Fibula6196.721.4411470.1814.22
Table 3. Validation of stature estimation methods using long bone length. Validation accuracy could not be calculated for Robbins Schug et al. [55] because a method for calculating interval estimates was not provided. Mean squared error (MSE) is the average squared distance between the point estimate and the known stature.
Table 3. Validation of stature estimation methods using long bone length. Validation accuracy could not be calculated for Robbins Schug et al. [55] because a method for calculating interval estimates was not provided. Mean squared error (MSE) is the average squared distance between the point estimate and the known stature.
MethodLong BoneTruncated Sample SizeAccuracy (%)MSE
(in cm)		Full Sample SizeAccuracy (%)MSE
(in cm)
Brits et al. [1]
Diaphyseal		Femur1526.6738.1411753.8520.96
Tibia1643.7533.1411545.2237.57
Lower
(Femur + Tibia)		1526.6735.1911456.1416.41
Brits et al. [1]
Maximum 		Femur150.00167.901176.83108.20
Tibia160.00163.5911520.00117.84
Lower
(Femur + Tibia)		150.00175.611148.77114.20
Chu & Stull [51]/
KS: Stature
Linear		Humerus7391.7829.5211794.0228.81
Radius7295.8330.3311597.3926.42
Ulna7395.8925.3311697.4124.49
Upper
(Humerus + Radius)		7294.4427.6211595.6523.62
Femur7398.6319.7611799.1517.91
Tibia7397.2625.4811598.2623.21
Fibula7398.6322.5911498.2520.32
Lower
(Femur + Tibia)		7298.6121.4211499.1218.32
Chu & Stull [51]/
KS: Stature
Nonlinear		Humerus7395.8915.1011794.8718.15
Radius7297.2216.8511598.2614.96
Ulna7398.6312.5711698.2814.36
Upper
(Humerus + Radius)		7298.6113.3411598.2613.62
Femur7395.8912.7111796.5813.21
Tibia7397.2615.8511597.3915.75
Fibula7398.6312.7011498.2512.63
Lower
(Femur + Tibia)		7298.6112.2211497.3712.30
Murray et al. [13]Humerus5394.3412.8511773.5049.51
Radius5396.2316.1111571.3064.56
Ulna53100.0011.3111681.9040.47
Femur5392.4515.0911769.2344.48
Tibia5396.2316.4511578.2636.79
Robbins Schug et al. [55]Femur37-15.92117-29.38
Smith [14]Humerus1782.3524.5411775.2125.84
Radius1782.3519.2711572.1731.40
Ulna1782.3515.2411681.0320.51
Femur1752.9428.0411778.6317.57
Tibia1764.7121.2911557.3930.38
Fibula1758.8222.2311449.1232.86
Lower
(Femur + Tibia)		1747.0622.4711461.1420.12
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chu, E.Y.; Treviño, A.J.; Vasquez, M.E. Validation of Subadult Age and Stature Estimation Methods Using a Contemporary Japanese Sample. Forensic Sci. 2025, 5, 41. https://doi.org/10.3390/forensicsci5030041

AMA Style

Chu EY, Treviño AJ, Vasquez ME. Validation of Subadult Age and Stature Estimation Methods Using a Contemporary Japanese Sample. Forensic Sciences. 2025; 5(3):41. https://doi.org/10.3390/forensicsci5030041

Chicago/Turabian Style

Chu, Elaine Y., Amariah J. Treviño, and Marissa E. Vasquez. 2025. "Validation of Subadult Age and Stature Estimation Methods Using a Contemporary Japanese Sample" Forensic Sciences 5, no. 3: 41. https://doi.org/10.3390/forensicsci5030041

APA Style

Chu, E. Y., Treviño, A. J., & Vasquez, M. E. (2025). Validation of Subadult Age and Stature Estimation Methods Using a Contemporary Japanese Sample. Forensic Sciences, 5(3), 41. https://doi.org/10.3390/forensicsci5030041

Article Metrics

Back to TopTop