A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples and Scoring
2.2. Statistical Methodology
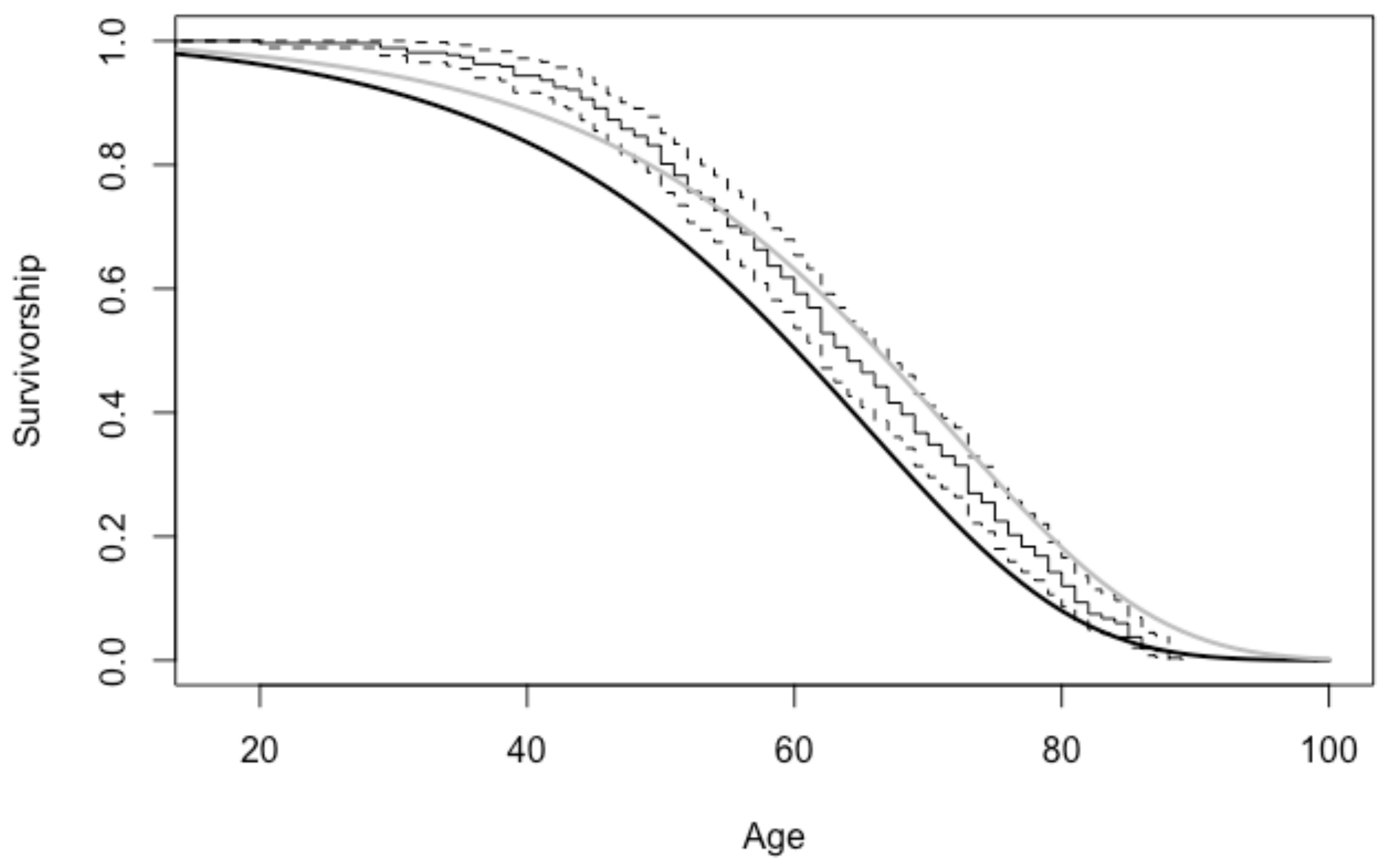
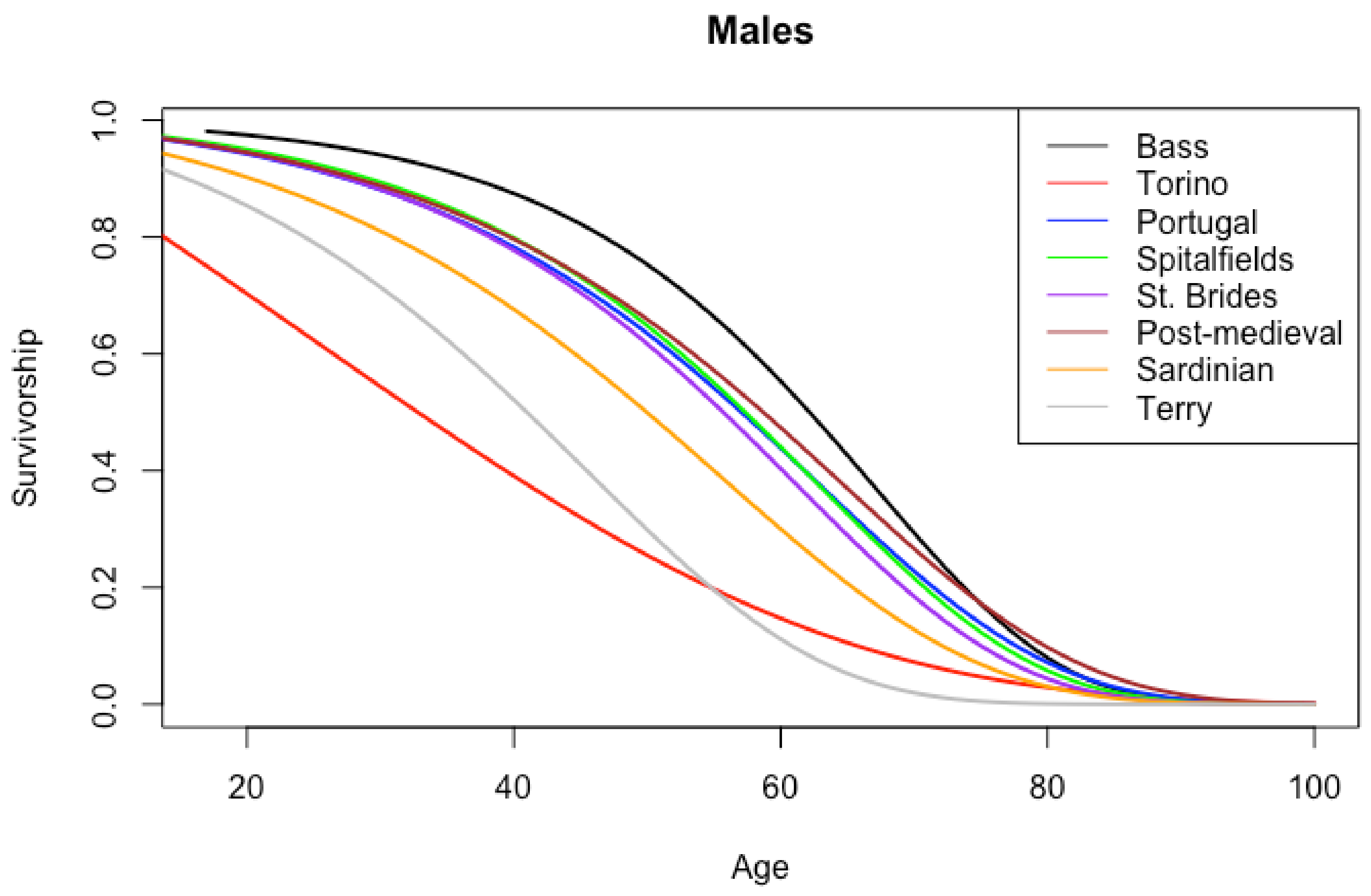
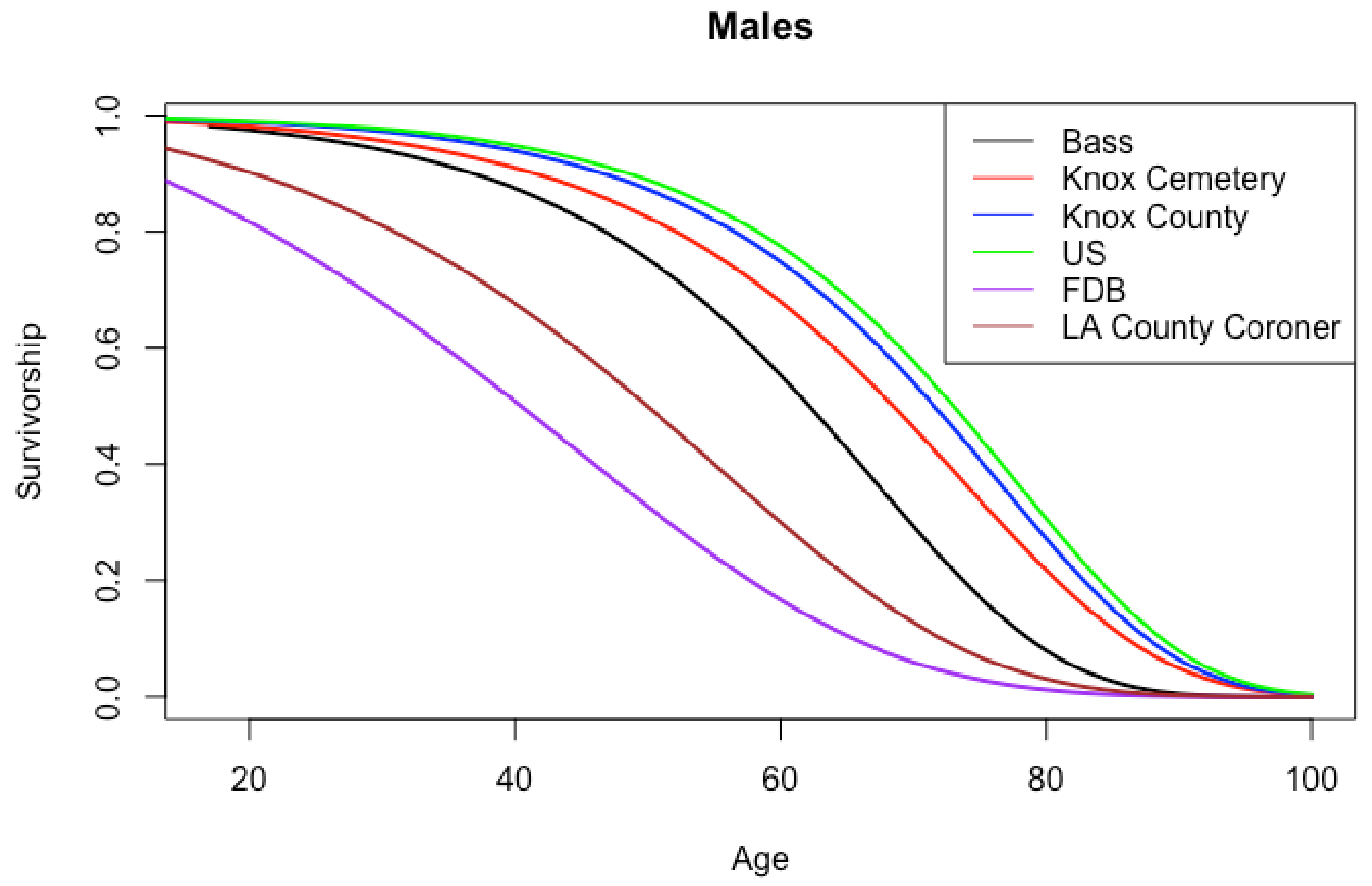
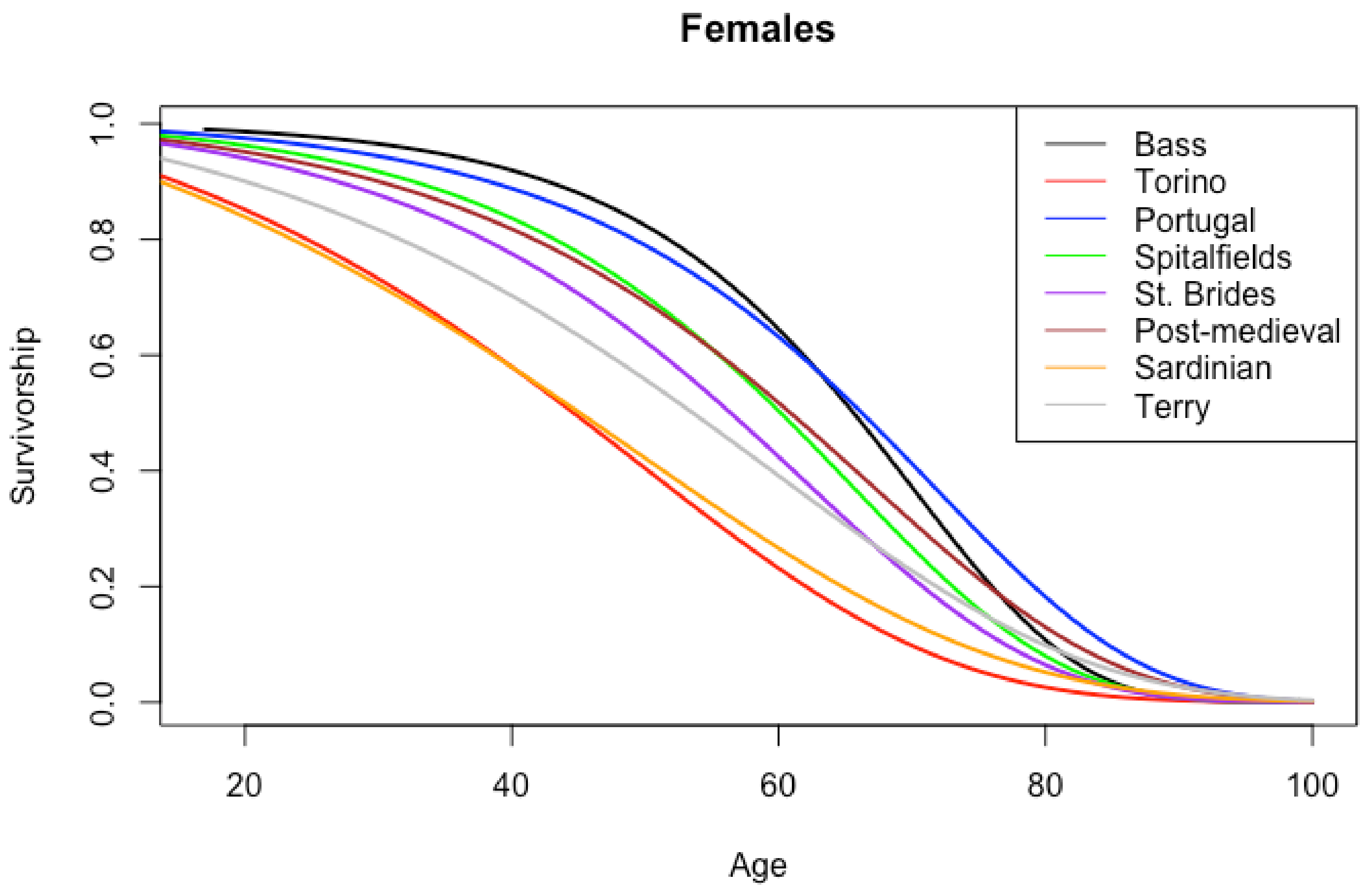
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bocquet-Appel, J.-P.; Masset, C. Farewell to Paleodemography. J. Hum. Evol. 1982, 11, 321–333. [Google Scholar] [CrossRef]
- Boldsen, J.; Milner, G.; Konigsberg, L.; Wood, J. Transition Analysis: A New Method for Estimating Age from Skeletons. In Paleodemography: Age Distributions from Skeletal Samples; Hoppa, R.D., Vaupel, J.W., Eds.; Cambridge University Press: Cambridge, UK, 2002; pp. 73–108. [Google Scholar]
- Godde, K.; Hens, S.M. Age-at-Death Estimation in an Italian Historical Sample: A Test of the Suchey-Brooks and Transition Analysis Methods. Am. J. Phys. Anthropol. 2012, 149, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Godde, K.; Hens, S.M. Modeling Senescence Changes of the Pubic Symphysis in Historic Italian Populations: A Comparison of the Rostock and Forensic Approaches to Aging Using Transition Analysis. Am. J. Phys. Anthropol. 2015, 156, 466–473. [Google Scholar] [CrossRef] [PubMed]
- Kimmerle, E.H.; Konigsberg, L.W.; Jantz, R.L.; Baraybar, J.P. Analysis of Age-at-Death Estimation through the Use of Pubic Symphyseal Data. J. Forensic Sci. 2008, 53, 558–568. [Google Scholar] [CrossRef] [PubMed]
- Konigsberg, L.W.; Herrmann, N.P.; Wescott, D.J.; Kimmerle, E.H. Estimation and Evidence in Forensic Anthropology: Age-at-Death. J. Forensic Sci. 2008, 53, 541–557. [Google Scholar] [CrossRef] [PubMed]
- Hens, S.M.; Godde, K. Auricular Surface Aging: Comparing Two Methods That Assess Morphological Change in the Ilium with Bayesian Analyses. J. Forensic Sci. 2016, 61 (Suppl. S1), S30–S38. [Google Scholar] [CrossRef]
- Godde, K. The Use of Informative Priors in Bayesian Modeling Age-at-Death; a Quick Look at Chronological and Biological Age Changes in the Sacroiliac Joint in American Males. AIMS Public Health 2017, 4, 278. [Google Scholar] [CrossRef]
- Nikita, E.; Xanthopoulou, P.; Kranioti, E. An Evaluation of Bayesian Age Estimation Using the Auricular Surface in Modern Greek Material. Forensic Sci. Int. 2018, 291, 1–11. [Google Scholar] [CrossRef]
- Lovejoy, C.; Meindl, R.; Pryzbeck, T. Chronological Metamorphosis of the Auricular Surface of the Ilium: A New Method for the Determination of Adult Skeletal Age at Death. Am. J. Phys. Anthropol. 1985, 68, 15–28. [Google Scholar] [CrossRef]
- Murray, K.; Murray, T. A Test of the Auricular Surface Aging Techniques. J. Forensic Sci. 1991, 36, 1163–1169. [Google Scholar] [CrossRef]
- Martrille, L.; Ubelaker, D.H.; Cattaneo, C.; Seguret, F.; Tremblay, M.; Baccino, E. Comparison of Four Skeletal Methods for the Estimation of Age at Death on White and Black Adults. J. Forensic Sci. 2007, 52, 302–307. [Google Scholar] [CrossRef]
- Saunders, S.R.; Fitzgerald, C.; Rogers, T.; Dudar, C.; McKillop, H. A Test of Several Methods of Skeletal Age Estimation Using a Documented Archaeological Sample. Can. Soc. Forensic Sci. J. 1992, 25, 97–118. [Google Scholar] [CrossRef]
- Bedford, M.E.; Russell, K.F.; Lovejoy, C.O.; Meindl, R.S.; Simpson, S.W.; Stuart-Macadam, P.L. Test of the multifactorial aging method using skeletons with known ages-at-death from the grant collection. Am. J. Phys. Anthropol. 1993, 91, 287–297. [Google Scholar] [CrossRef]
- Falys, C.G.; Schutkowski, H.; Weston, D.A. Auricular Surface Aging: Worse than Expected? A Test of the Revised Method on a Documented Historic Skeletal Assemblage. Am. J. Phys. Anthropol. 2006, 130, 508–513. [Google Scholar] [CrossRef]
- Storey, R. An elusive paleodemography? A comparison of two methods for estimating the adult age distribution of deaths at late Classic Copan, Honduras. Am. J. Phys. Anthropol. 2007, 132, 40–47. [Google Scholar] [CrossRef]
- Rougé-Maillart, C.; Vielle, B.; Jousset, N.; Chappard, D.; Telmon, N.; Cunha, E. Development of a Method to Estimate Skeletal Age at Death in Adults Using the Acetabulum and the Auricular Surface on a Portuguese Population. Forensic Sci. Int. 2009, 188, 91–95. [Google Scholar] [CrossRef]
- Schmitt, A. Age-at-Death Assessment Using the Os Pubis and the Auricular Surface of the Ilium: A Test on an Identified Asian Sample. Int. J. Osteoarchaeol. 2004, 14, 1–6. [Google Scholar] [CrossRef]
- Hens, S.M.; Rastelli, E.; Belcastro, G. Age Estimation from the Human Os Coxa: A Test on a Documented Italian Collection. J. Forensic Sci. 2008, 53, 1040–1043. [Google Scholar] [CrossRef]
- Buckberry, J.L.; Chamberlain, A.T. Age Estimation from the Auricular Surface of the Ilium: A Revised Method. Am. J. Phys. Anthropol. 2002, 119, 231–239. [Google Scholar] [CrossRef]
- Hens, S.M.; Belcastro, M.G. Auricular Surface Aging: A Blind Test of the Revised Method on Historic Italians from Sardinia. Forensic Sci. Int. 2012, 214, 209.e1–209.e5. [Google Scholar] [CrossRef]
- Mulhern, D.M.; Jones, E.B. Test of revised method of age estimation from the auricular surface of the ilium. Am. J. Phys. Anthropol. 2005, 126, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Algee-Hewitt, B.F.B. Age-at-Death Patterns and Transition Analysis Trends for Three Asian Populations: Implications for [Paleo]Demography. Am. J. Biol. Anthropol. 2022, 177, 207–222. [Google Scholar] [CrossRef]
- Braga, J.; Heuze, Y.; Chabadel, O.; Sonan, N.K.; Gueramy, A. Non-Adult Dental Age Assessment: Correspondence Analysis and Linear Regression versus Bayesian Predictions. Int. J. Legal. Med. 2005, 119, 260–274. [Google Scholar] [CrossRef] [PubMed]
- Daubert v. Merrell Dow Pharmaceuticals, Inc., 509 U.S. 579; United States Court of Appeals for the Ninth Circuit: San Francisco, CA, USA, 1993.
- Shirley, N.R.; Wilson, R.J.; Meadows Jantz, L. Cadaver Use at the University of Tennessee’s Anthropological Research Facility. Clin. Anat. 2011, 24, 372–380. [Google Scholar] [CrossRef]
- Cardoso, H.F.V. Brief Communication: The Collection of Identified Human Skeletons Housed at the Bocage Museum (National Museum of Natural History), Lisbon, Portugal. Am. J. Phys. Anthropol. 2006, 129, 173–176. [Google Scholar] [CrossRef]
- Hens, S.M.; Godde, K.; Macak, K.M. Iron Deficiency Anemia, Population Health and Frailty in a Modern Portuguese Skeletal Sample. PLoS ONE 2019, 14, e0213369. [Google Scholar] [CrossRef]
- Natural History Museum, London. Human Comparative Collection. Available online: https://www.nhm.ac.uk/our-science/collections/palaeontology-collections/human-comparative-collection.html (accessed on 18 July 2022).
- Kim, J.; Algee-Hewitt, B.F.B.; Konigsberg, L.W. Inferring Age at Death for Japanese and Thai Skeletal Samples under a Bayesian Framework of Analysis: A Test of Priors and Their Effects on Estimation. Forensic Anthropol. 2019, 2, 273–292. [Google Scholar] [CrossRef]
- Hens, S.M.; Godde, K. New Approaches to Age Estimation Using Palatal Suture Fusion. J. Forensic Sci. 2020, 65, 1406–1415. [Google Scholar] [CrossRef]
- WORD. Wellcome Osteological Database. Available online: https://www.museumoflondon.org.uk/collections/other-collection-databases-and-libraries/centre-human-bioarchaeology/osteological-database (accessed on 27 January 2020).
- Godde, K.; Hens, S.M. An Epidemiological Approach to the Analysis of Cribra Orbitalia as an Indicator of Health Status and Mortality in Medieval and Post-Medieval London under a Model of Parasitic Infection. Am. J. Phys. Anthropol. 2021, 174, 631–645. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Garvin, H.M.; Passalacqua, N.V. Current Practices by Forensic Anthropologists in Adult Skeletal Age Estimation. J. Forensic Sci. 2012, 57, 427–433. [Google Scholar] [CrossRef]
- Fenelon, A. Geographic Divergence in Mortality in the United States. Popul. Dev. Rev. 2013, 39, 611–634. [Google Scholar] [CrossRef]
- Wilmoth, J.; Boe, C.; Barbieri, M. Geographic Differences in Life Expectancy at Age 50 in the United States Compared with Other High-Income Countries. In International Differences in Mortality at Older Ages: Dimensions and Sources; Crimmins, E., Preston, S.H., Cohen, B., Eds.; National Academies Press: Washington, DC, USA, 2010; pp. 333–366. [Google Scholar]
- Fenelon, A.; Preston, S.H. Estimating Smoking-Attributable Mortality in the United States. Demography 2012, 49, 797–818. [Google Scholar] [CrossRef]
- Ezzati, M.; Friedman, A.B.; Kulkarni, S.C.; Murray, C.J.L. The Reversal of Fortunes: Trends in County Mortality and Cross-County Mortality Disparities in the United States. PLoS Med. 2008, 5, e66. [Google Scholar] [CrossRef]
- James, W.; Cossman, J.; Wolf, J.K. Persistence of Death in the United States: The Remarkably Different Mortality Patterns between America’s Heartland and Dixieland. Demogr. Res. 2018, 39, 897–910. [Google Scholar] [CrossRef]
- Miller, C.E.; Vasan, R.S. The Southern Rural Health and Mortality Penalty: A Review of Regional Health Inequities in the United States. Soc. Sci. Med. 2021, 268, 113443. [Google Scholar] [CrossRef]
- Singh, G.K.; Siahpush, M. Widening Rural–Urban Disparities in Life Expectancy, U.S. 1969–2009. Am. J. Prev. Med. 2014, 46, e19–e29. [Google Scholar] [CrossRef]
- Wami, W.; Walsh, D.; Hennig, B.D.; McCartney, G.; Dorling, D.; Galea, S.; Sampson, L.; Dundas, R. Spatial and Temporal Inequalities in Mortality in the USA 1968–2016. Health Place 2021, 70, 102586. [Google Scholar] [CrossRef]
- Wang, H.; Schumacher, A.E.; Levitz, C.E.; Mokdad, A.H.; Murray, C.J. Left behind: Widening Disparities for Males and Females in US County Life Expectancy 1985–2010. Popul. Health Metr. 2013, 11, 8. [Google Scholar] [CrossRef]
- Kulkarni, S.C.; Levin-Rector, A.; Ezzati, M.; Murray, C.J. Falling behind: Life Expectancy in US Counties from 2000 to 2007 in an International Context. Popul. Health Metr. 2011, 9, 16. [Google Scholar] [CrossRef]
- Cullen, M.R.; Cummins, C.; Fuchs, V.R. Geographic and Racial Variation in Premature Mortality in the U.S.: Analyzing the Disparities. PLoS ONE 2012, 7, e32930. [Google Scholar] [CrossRef]
- Paulozzi, L.J. Does Inadequate Diet during Childhood Explain the Higher High Fracture Rates in the Southern United States? Osteoporos Int. 2010, 21, 417–423. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.K.; Sempos, C.T.; Barton, C.N.; Vanderveen, J.E.; Yetley, E.A. Effectiveness of Food Fortification in the United States: The Case of Pellagra. Am. J. Public Health 2000, 90, 727–738. [Google Scholar] [PubMed]
- Bethony, J.; Brooker, S.; Albonico, M.; Geiger, S.M.; Loukas, A.; Diemert, D.; Hotez, P.J. Soil-Transmitted Helminth Infections: Ascariasis, Trichuriasis, and Hookworm. Lancet 2006, 367, 1521–1532. [Google Scholar] [CrossRef]
- Howard, G. Why Do We Have a Stroke Belt in the Southeastern United States? A Review of Unlikely and Uninvestigated Potential Causes. Am. J. Med. Sci. 1999, 317, 160–167. [Google Scholar] [CrossRef]
- Lanska, D.J.; Kuller, L.H. The Geography of Stroke Mortality in the United States and the Concept of a Stroke Belt. Stroke 1995, 26, 1145–1149. [Google Scholar] [CrossRef]
- Starr, M.C.; Montgomery, S.P. Soil-transmitted helminthiasis in the United States: A systematic review—1940–2010. Am. J. Trop. Med. Hyg. 2011, 85, 680. [Google Scholar] [CrossRef]

| Age Interval | American | Portuguese | Spitalfields |
|---|---|---|---|
| Males/Females | Males/Females | Males/Females | |
| 16–19 | 1/0 | 5/5 | 2/2 |
| 20–29 | 7/3 | 18/22 | 5/5 |
| 30–39 | 44/12 | 20/10 | 14/9 |
| 40–49 | 72/30 | 34/12 | 8/11 |
| 50–59 | 83/57 | 49/39 | 15/22 |
| 60–69 | 80/67 | 35/43 | 25/19 |
| 70–79 | 50/60 | 33/66 | 13/16 |
| 80–89 | 35/38 | 27/43 | 2/9 |
| 90–99 | 0/0 | 0/5 | 2/0 |
| Total | 372/267 | 221/245 | 86/93 |
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 2.97 | 19.45 | 3.05 | 21.17 |
| II-III | 3.28 | 26.47 | 3.37 | 29.16 |
| III-IV | 3.55 | 34.89 | 3.62 | 37.38 |
| IV-V | 3.81 | 45.18 | 3.86 | 47.29 |
| V-VI | 4.08 | 59.28 | 4.03 | 56.45 |
| VI-VII | 4.29 | 72.91 | 4.16 | 63.87 |
| VII-VIII | 4.53 | 92.75 | 4.40 | 81.80 |
| ST DEV | 0.25 | 0.23 | ||
| b | 4.04 | 4.28 | ||
| Log-likelihood | −303.65 | −324.73 | ||
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 3.04 | 20.96 | 3.14 | 23.26 |
| II-III | 3.55 | 34.86 | 3.61 | 36.95 |
| III-IV | 3.86 | 47.31 | 3.91 | 49.82 |
| IV-V | 4.40 | 81.63 | 4.43 | 83.92 |
| ST DEV | 0.40 | 0.43 | ||
| b | 2.52 | 2.30 | ||
| Log-likelihood | −258.58 | −293.02 | ||
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 2.93 | 18.69 | 3.04 | 20.84 |
| II-III | 3.29 | 26.94 | 3.51 | 33.42 |
| III-IV | 3.75 | 42.55 | 3.83 | 45.98 |
| IV-V | 4.00 | 54.36 | 4.01 | 55.08 |
| ST DEV | 0.32 | 0.29 | ||
| b | 3.12 | 3.50 | ||
| Log-likelihood | −205.14 | −181.16 | ||
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 3.47 | 32.14 | 3.55 | 34.81 |
| II-III | 4.32 | 75.47 | 4.21 | 67.04 |
| ST DEV | 0.52 | 0.47 | ||
| b | 1.92 | 2.11 | ||
| Log-likelihood | −192.38 | −204.25 | ||
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 3.46 | 31.73 | 3.33 | 27.89 |
| II-III | 3.78 | 43.71 | 3.63 | 37.82 |
| ST DEV | 0.53 | 0.47 | ||
| b | 1.89 | 2.14 | ||
| Log-likelihood | −167.89 | −119.71 | ||
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 3.63 | 37.76 | 3.54 | 34.53 |
| II-III | 4.58 | 97.24 | 4.22 | 68.01 |
| ST DEV | 0.74 | 0.49 | ||
| b | 1.35 | 2.04 | ||
| Log-likelihood | −214.93 | −207.04 | ||
| Parameter | Estimate | Age at Transition | Estimate | Age at Transition |
|---|---|---|---|---|
| MALES | FEMALES | |||
| I-II | 2.96 | 19.25 | 3.04 | 20.96 |
| II-III | 3.25 | 25.84 | 3.38 | 29.48 |
| III-IV | 3.50 | 32.98 | 3.55 | 34.92 |
| IV-V | 3.77 | 43.54 | 3.73 | 41.74 |
| V-VI | 4.00 | 54.73 | 3.94 | 51.48 |
| VI-VII | 4.26 | 71.03 | 4.20 | 66.90 |
| ST DEV | 0.30 | 0.30 | ||
| b | 3.30 | 3.29 | ||
| Log-likelihood | −293.97 | −278.58 | ||
| Phase | HPD | 75% HPDR | 90% HPDR | 95% HPDR |
|---|---|---|---|---|
| MALES | ||||
| 63.44% Realized Accuracy | 83.87% Realized Accuracy | 88.98% Realized Accuracy | ||
| I | 18.00 | 18.00–25.24 | 18.00–29.15 | 18.00–31.91 |
| II | 25.18 | 18.71–33.95 | 18.00–39.25 | 18.00–43.31 |
| III | 34.85 | 25.2–48.2 | 22.01–55.12 | 20.26–59.78 |
| IV | 47.04 | 34.45–63.50 | 30.20–71.39 | 27.79–76.45 |
| V | 61.79 | 46.74–78.51 | 41.19–85.46 | 37.96–89.66 |
| VI | 73.28 | 57.96–88.06 | 51.75–93.81 | 48.01–97.23 |
| VII | 81.36 | 66.74–94.44 | 60.41–99.39 | 56.47–102.34 |
| VIII | 89.14 | 75.72–100.64 | 69.60–104.95 | 65.68–107.50 |
| FEMALES | ||||
| 65.17% Realized Accuracy | 85.39% Realized Accuracy | 91.39% Realized Accuracy | ||
| I | 18.00 | 18.00–26.07 | 18.00–30.15 | 18.00–32.99 |
| II | 27.77 | 20.53–37.61 | 18.26–42.33 | 18.00–46.27 |
| III | 37.94 | 27.96–51.49 | 24.58–58.49 | 22.68–63.27 |
| IV | 49.78 | 37.14–66.03 | 32.80–73.73 | 30.32–78.67 |
| V | 61.38 | 47.06–77.78 | 41.83–84.77 | 38.78–89.04 |
| VI | 69.65 | 54.76–85.02 | 48.98–91.18 | 45.53–94.88 |
| VII | 78.55 | 63.52–92.41 | 57.21–97.68 | 53.35–100.81 |
| VIII | 89.10 | 75.15–100.91 | 68.80–105.26 | 64.76–107.83 |
| Phase | HPD | 75% HPDR | 90% HPDR | 95% HPDR |
|---|---|---|---|---|
| MALES | ||||
| 62.10% Realized Accuracy | 79.03% Realized Accuracy | 82.26% Realized Accuracy | ||
| I | 18.00 | 18.0–27.9 | 18.00–33.52 | 18.00–37.62 |
| II | 26.01 | 18.04–37.69 | 18.00–45.99 | 18.00–51.78 |
| III | 35.63 | 24.04–52.85 | 20.56–61.58 | 18.75–67.09 |
| IV | 48.89 | 33.73–68.74 | 28.79–77.53 | 26.05–82.83 |
| V | 62.67 | 45.38–80.84 | 38.99–87.96 | 35.30–92.15 |
| VI | 73.36 | 55.94–89.12 | 48.76–94.96 | 44.46–98.39 |
| VII | 85.00 | 68.86–98.19 | 61.43–102.93 | 56.73–105.69 |
| FEMALES | ||||
| 50.56% Realized Accuracy | 64.79% Realized Accuracy | 71.16% Realized Accuracy | ||
| I | 18.00 | 18.00–29.89 | 18.00–36.4 | 18.00–41.12 |
| II | 30.17 | 20.19–45.36 | 18.00–53.57 | 18.00–60.24 |
| III | 40.48 | 27.42–59.57 | 23.43–69.00 | 21.29–74.91 |
| IV | 50.11 | 34.67–70.38 | 29.65–79.29 | 26.85–84.62 |
| V | 61.88 | 44.29–80.81 | 37.92–88.22 | 34.27–92.54 |
| VI | 73.38 | 55.31–89.61 | 47.93–95.55 | 43.54–99.01 |
| VII | 86.43 | 69.86–99.59 | 62.13–104.23 | 57.21–106.92 |
| Method | CI | Number of Successes | Number of Failures | p-Value | Probability of Success | Bias |
|---|---|---|---|---|---|---|
| MALES | ||||||
| LJ | 75% | 236 | 136 | <0.0001 | 0.63 | 7.95 |
| LJ | 90% | 312 | 60 | 0.0003 | 0.84 | 8.33 |
| LJ | 95% | 331 | 41 | <0.0001 | 0.89 | 8.62 |
| BC | 75% | 231 | 141 | <0.0001 | 0.62 | 10.85 |
| BC | 90% | 294 | 78 | <0.0001 | 0.79 | 10.77 |
| BC | 95% | 306 | 66 | <0.0001 | 0.82 | 11.49 |
| FEMALES | ||||||
| LJ | 75% | 174 | 93 | 0.0004 | 0.65 | 7.99 |
| LJ | 90% | 228 | 39 | 0.0183 | 0.85 | 8.04 |
| LJ | 95% | 244 | 23 | 0.0109 | 0.91 | 8.09 |
| BC | 75% | 135 | 132 | <0.0001 | 0.51 | −10.91 |
| BC | 90% | 173 | 94 | <0.0001 | 0.65 | −11.02 |
| BC | 95% | 190 | 77 | <0.0001 | 0.71 | −11.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hens, S.M.; Godde, K. A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples. Forensic Sci. 2022, 2, 682-695. https://doi.org/10.3390/forensicsci2040051
Hens SM, Godde K. A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples. Forensic Sciences. 2022; 2(4):682-695. https://doi.org/10.3390/forensicsci2040051
Chicago/Turabian StyleHens, Samantha M., and Kanya Godde. 2022. "A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples" Forensic Sciences 2, no. 4: 682-695. https://doi.org/10.3390/forensicsci2040051
APA StyleHens, S. M., & Godde, K. (2022). A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples. Forensic Sciences, 2(4), 682-695. https://doi.org/10.3390/forensicsci2040051






