Abstract
Nuclear fuel cladding serves as the primary barrier to the release of radioactive fission products and is subjected to high-temperature and high-pressure environments during both normal reactor operation and accident scenarios such as loss of coolant accidents (LOCAs). Predicting the burst behavior of cladding is essential for ensuring structural integrity, especially under varying heating rates—an aspect inadequately addressed in existing empirical models. In this study, a finite element-based damage model is developed to simulate the ballooning and burst behavior of Zircaloy-4 cladding. The model incorporates creep deformation, stress triaxiality, and time-dependent damage accumulation. Material behavior is characterized using experimentally determined creep constants and the model is calibrated against burst test data from the literature. A new heating-rate-dependent burst correlation is proposed based on model outputs. The results indicate that increasing the heating rate raises the burst temperature due to reduced exposure time in the temperature regime where creep damage accumulates significantly. The model accurately reproduces burst behavior across a wide range of internal pressures (1–10 MPa) and heating rates (5–100 °C/s). The newly developed correlation improves predictive capability in accident analysis tools and can be directly implemented into safety analysis codes for Indian pressurized heavy water reactors (PHWRs), contributing to enhanced reactor safety evaluations.
1. Introduction
Analysis of progressive (i.e., time dependent) deformation of fuel bundles, pressure tube, calandria tube, and coolant channels of pressurized heavy water reactors (PHWR) is one of the important aspects of severe accident research for these types of reactors. Various types of accident scenarios are postulated during analysis, and it must be shown that the barrier to radioactive release is maintained in these scenarios. The fuel clad or fuel pin is the first barrier to radioactive high-temperature, heat-producing oxide fuel pellets. Due to accumulation of fission gas inside the clad and high-heat-generating pellets, the fuel clad can deform by ballooning when the external surface is not cooled sufficiently during a postulated loss of coolant accident (LOCA) scenario. The objective of this work is to study the ballooning deformation behavior of fuel clad when subjected to different loading conditions such as internal pressure and heating rates producing high temperature in the wall of fuel clad. The burst behavior of clad is often a matter of interest for the safety analysts, and hence, this aspect is also investigated in this work.
The creep deformation and the corresponding ballooning and burst behavior of nuclear fuel clad has been studied extensively both experimentally and numerically [1,2,3,4,5,6,7]. Feria et al. [1] and Aragón et al. [2] have studied the ballooning deformation of clad assuming a design basis accident (DBA), i.e., loss of coolant accident (LOCA). They have used the severe accident code FRAPTRAN for simulation of clad deformation behavior. The burst behavior of Fe-based alloy cladding tube was studied under LOCA condition in Ref. [3].
Campello et al. [4] have studied the steady-state creep behavior of Zircaloy-4 claddings under LOCA condition and those of FeCrAl-ODS (oxide dispersion strengthened) cladding have been studied extensively by Narukawa et al. [5]. The deformation and burst behavior of Cr-coated Zircaloy cladding under DBA/LOCA conditions have been studied in Refs. [6,7]. A similar study was also found in the works of Kim et al. [8] and Lee et al. [9].
The validation process of the phenomena of clad ballooning and burst during LOCA conditions has been carried out extensively in Refs. [10,11,12,13], where in situ test data has been used. The code ‘BISON’ has been used extensively to study the deformation behavior of clad in Refs. [10,11,12,13,14,15]. The details of development and validation of another severe accident code ‘ENIGMA’ (used for prediction of deformation behavior of zirconium-based cladding materials) are presented by Rossiter and Peakman [13].
The deformation and burst behavior of FeCrAl-based C26M cladding under simulated LOCA conditions have been studied in Ref. [12]. Garrison et al. [16] studied the burst characteristics of an accident-tolerant FeCrAl cladding under temperature transients. The creep deformation behavior of a nuclear-grade C26M2 FeCrAl alloy accident-tolerant fuel cladding was studied through burst test in Ref. [17].
The results of the numerical simulation of an accident-tolerant fuel clad deformation during LOCA are presented in Ref. [18]. The thermo-mechanical deformation behavior of Zircaloy-4 clad under simulated post-DNB (departure from nucleate boiling) conditions are presented in Ref. [19]. The ballooning and burst characteristics of chromium-coated Zircaloy clad was studied numerically by Ma et al. [20] and a numerical study of PWR (pressurized water reactor) fuel rod cladding ballooning and burst behavior was presented by Zhang et al. [21].
The deformation and burst characteristics of oxide dispersion-strengthened FeCrAl cladding were studied in Refs. [22,23]. The deformation and burst behavior of Zircaloy-4 cladding tube (with internal hydride) were studied experimentally by Kamerman [24]. He used internal pressure and high-temperature loading to characterize the deformation and burst behavior of clad. In situ deformation measurements of Zircaloy-4 cladding tube under various transient heating conditions and the results of the study of the corresponding strain evolution have been presented by researchers in Refs. [25,26,27,28,29].
Various techniques, such as optical image analysis and digital image correlation (DIC), etc., have been used for accurate measurement of strain during the creep deformation process. An extensive review of the progress of research work concerning the study and modeling of high-temperature thermo-mechanical deformation behaviors of Cr-coated cladding and FeCrAl claddings under LOCA conditions are presented in Refs. [30,31].
The bi-axial creep deformation behavior of thin-walled clads are studied in Refs. [32,33]. The thermal creep fracture of a Zr1%Nb cladding alloy has been studied by Sklenicka et al. [34]. Zircaloy-4 coupons have been irradiated using proton beams and the corresponding irradiation-assisted creep deformation of the alloy has been studied in Ref. [35]. Creep tests on Zircaloy-4 fuel claddings have been conducted by Choi et al. [36] and the corresponding deformation behavior has been studied. Various failure criteria for nuclear fuel cladding, which fail by the mechanism of creep rupture, have been presented in Refs. [37,38].
The phenomenon of hydrogen embrittlement and the associated failure characteristics of Zircaloy-4 cladding have been studied recently by Deng et al. [39]. They have used the damage model (i.e., Gurson–Tverggard–Needleman’s porous plasticity model) to simulate the failure of fuel clad. The influence of assembly structural features of light water reactors on cladding burst behavior under LOCA conditions has been studied by Schappel and Capps [40].
The deformation behavior of fuel clad of Indian PHWR was studied in Ref. [41]. Several burst experiments have been recently carried out in Ref. [42] using Zircaloy-4 fuel clad of Indian PHWR. The above researchers have presented the burst temperature and burst time of fuel clad as a function of burst stress. Chung and Kassner [43] have also presented an extensive experimental database, which contains clad burst data for various pressure magnitudes and heating rate conditions. Rosinger [44] have used this database in their work to predict the failure of Zircaloy-4 fuel sheathing during postulated LOCA conditions.
Several experimental techniques have been developed to investigate the fracture and failure behavior of Zircaloy cladding tubes under diverse loading and environmental conditions, providing valuable insight into crack initiation, propagation, and damage evolution. The Pin-Loaded Tension (PLT) method [45,46,47,48] used sharply notched pins to study axial crack growth under tensile loading. Additionally, the Internal Conical Mandrel method [49] was developed to simulate fuel-pellet-induced distortion by forcing a tapered mandrel into axially cracked tubes, mimicking pellet-cladding mechanical interaction (PCMI). Furthermore, the effect of anisotropy in fracture toughness of Zircaloy-4 material was determined in [50]. These approaches highlight the importance of studying failure mechanisms under constrained multi-axial conditions, providing insights that inform the present work’s damage model, which incorporates stress triaxiality, creep deformation, and heating rate effects to simulate burst behavior in Zircaloy-4 cladding.
From a detailed study of the literature, it was observed that various types of correlations have been proposed in the literature, which are mainly empirical in nature. These correlations usually express clad burst stress as a function of burst temperature, which are exponential decay type, and the constants vary depending upon the material of interest, manufacturing conditions of the clad, and the temperature range.
The effect of heating rate on clad burst behavior has not been taken into account explicitly in these correlations. Hence, the objective of this work is to develop a heating-rate-dependent correlation, which can represent the clad burst temperature as a function of applied stress for various heating rates. For this purpose, a material damage-based model has been proposed and validated with experimental data available in the literature so that the same can be used for its extensive application in the development of an appropriate correlation for predicting the burst behavior of Indian PHWR Zircaloy-4 fuel clad.
This paper has been organized into seven sections. After a brief description of the problem, a reactor Channel Configuration and Experimental Approach is provided in Section 2. The material properties used in the finite element (FE) analysis of ballooning and the burst behavior of fuel clad are presented in Section 3, followed by the details of FE analysis in Section 4. The results are presented in Section 5, which are followed by a discussion regarding the development of a suitable burst correlation in Section 6. Some of the important conclusions are reported in Section 7.
2. Reactor Channel Configuration and Experimental Approach
A schematic representation of a typical reactor coolant channel in a pressurized heavy water reactor (PHWR) is shown in Figure 1a. This channel assembly comprises several key components including the calandria tube, pressure tube, and the centrally located fuel bundles. Each fuel bundle consists of multiple fuel pins which in turn house stacked cylindrical fuel pellets responsible for the generation of thermal energy during reactor operation.
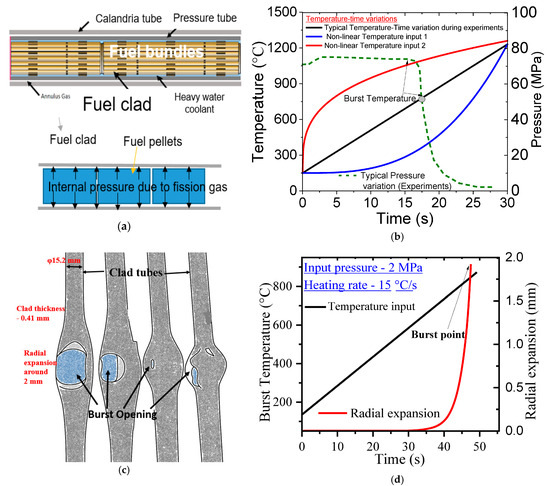
Figure 1.
(a) Schematic arrangement of fuel pins and fuel bundles inside the pressure tube enclosed by calandria tube in a typical pressurized heavy water reactor and the loading condition of fuel clad. (b) Typical variation in temperature in different regions of clad tube during clad burst experiment and corresponding time variation in internal pressure. (c) Typical localized ballooning and burst of clad tube in the experiment. (d) Radial expansion of clad tube corresponding to temperature input with heating rate of 15 °C/s.
To experimentally replicate the high-temperature failure mechanisms of nuclear fuel cladding under accident conditions, a controlled heating and pressurization setup is used. In this setup, a section of the cladding tube is subjected to internal pressurization simulating fission gas buildup while the tube is externally heated using electrical current. This heating method allows for a uniform and controlled temperature rise across the clad wall.
Figure 1b shows a representative time-history of temperature and pressure variations during a burst test. A sudden drop in internal pressure is typically observed when localized creep deformation leads to rupture of the cladding as shown by the failure points in Figure 1c. These bursts result from the accumulation of thermal and mechanical damage due to creep at elevated temperatures and stress levels. The radial expansion of the clad tube corresponding to typical input temperature is shown in Figure 1d. It can be observed that the expansion occurs rapidly after reaching 600 °C, further leading to burst of the clad tube.
It is seen from the temperature profiles in Figure 1b that the heating rate can follow either linear or non-linear paths, particularly under severe accident conditions. This introduces significant variability in the temperature–time path leading to clad failure. Empirical correlations that relate burst stress and burst temperature typically assume fixed heating rates and, therefore, do not adequately capture the path-dependent nature of the actual thermal loading. Consequently, such correlations may yield inaccurate predictions when applied to real accident scenarios.
Given this limitation, it becomes essential to adopt a physics-based micromechanical framework capable of incorporating heating rate effects into the burst prediction. The motivation for the present study is to address this gap by developing and validating a damage model that can explicitly account for the influence of different heating rates on the ballooning and burst behavior of Zircaloy-4 fuel cladding. This approach aims to improve the predictive accuracy of burst phenomena under a wide range of accident relevant thermal conditions.
3. Material Data Used in Finite Element Analysis of Fuel Clad Deformation
For simulation of burst behavior of nuclear fuel clad, finite element analysis with an elastic–plastic–creep constitutive model for the material has been used. The material properties of Zircaloy-4 fuel clad have been used in the simulation. One of the important aspects of material constitutive models is that of creep deformation. For simulation of creep deformation behavior, Norton’s constitutive law has been used, where the rate of creep strain is a function of equivalent stress ‘σ’ and temperature T (in K) as shown in Equation (1), and A, n, and c are being the steady-state or secondary creep deformation constants of the material.
To evaluate the parameters of the model, creep experiments have been carried out using Zircaloy-4 as the material of the specimens and the creep strain as a function of time has been evaluated at different temperatures and applied stress values. A typical variation in the data of creep strain as a function of time is shown in Figure 2.
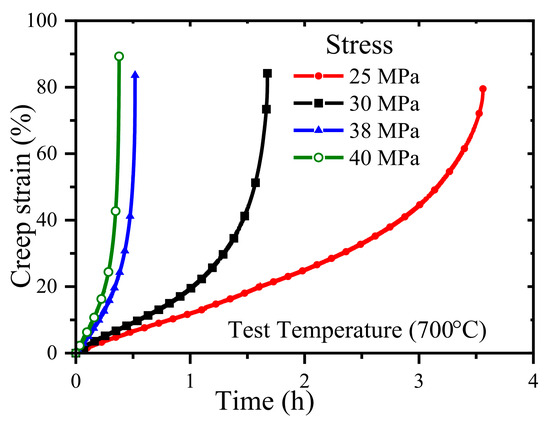
Figure 2.
Variation in creep strain as a function of time for Zircaloy-4 fuel clad of Indian PHWR as obtained from experiment.
It can be observed that the creep deformation of the specimens falls predominantly in the secondary range and the onset of tertiary occurs earlier for higher values of applied stress. This is similar to typical creep deformation of similar types of Zirconium-based alloys. Using data of tests conducted at several temperatures and stress values, the correlation between creep strain rate (in the secondary regime), as a function of applied stress and temperature, has been evaluated. The details can be found elsewhere [41]. It was also observed that the material constants A, n, and c are dependent on the range of temperature, as this material undergoes phase change at higher temperatures [42]. The values of the material constants A, n, and c are provided in Table 1.

Table 1.
Material parameters for modeling of creep deformation of Zircaloy-4 fuel clad in FE analysis.
Moderate n-values (4.9–4.2) are observed in the temperature range of 600 °C to 850 °C. This range reflects typical dislocation climb/glide-controlled creep where strain rate is strongly stress-dependent. The drop in the magnitude of n between 850 and 1000 °C signifies a creep regime transition from dislocation-dominated to diffusion-controlled or grain-boundary sliding mechanisms. This behavior is consistent with known phase transformation and creep characteristics of Zircaloy-4. Such data is critical for accurately simulating burst behavior in high-temperature accident scenarios where Zircaloy-4 may experience varying mechanisms depending on the thermal path. These data are used in finite element analysis of fuel clad for simulating the ballooning and burst behavior. The initiation of burst of fuel clad has been simulated with the help of a material damage model, which shall be discussed in later sections.
4. Description of Finite Element Model Used in Simulation of Ballooning and Burst Behavior of Fuel Clad
As discussed in Section 1, the cylindrical fuel clad deforms locally by creep and balloons at a location as shown in Figure 1c. In order to simulate this deformation behavior, the cylindrical clad has been modeled using axisymmetric analysis. The geometry of the fuel clad is shown in Figure 3a. The outer diameter of the clad is 15.2 mm and the thickness is 0.4 mm. The FE axisymmetric model of the clad is shown in Figure 3b. The FE mesh contains 8-noded higher order quadratic elements. The mesh was refined adaptively in regions of expected high stress and strain gradients specifically around the mid-length of the tube where ballooning and burst were observed experimentally. The axial and radial element sizes were selected based on mesh convergence studies, which involved refining the mesh until further refinement resulted in less than 1% change in critical output parameters such as maximum von-Mises stress at clad burst temperature and its corresponding creep strain. A typical result of convergence of maximum von-Mises stress for internal pressure of 4 MPa at the burst temperature is shown in Figure 3c. It can be seen that after a total of 1000 elements (3221 nodes), there is not much change in the maximum von-Mises stress; hence, this mesh is used for further studies. This final mesh included sufficient density (approximately 100 elements (0.6 mm length) along the axial direction and 10 elements (0.04 mm length) along the radial direction) to capture the evolving deformation and damage fields during the burst event with high resolution. This mesh configuration ensured a balance between computational efficiency and numerical accuracy and the simulation results were further validated against experimental burst data showing good agreement.
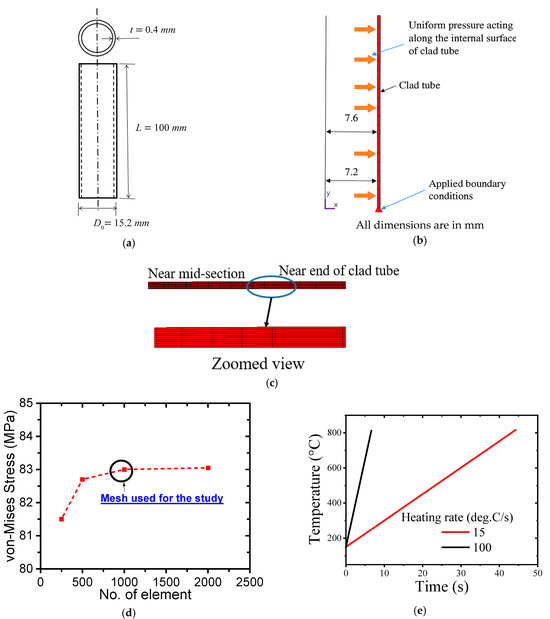
Figure 3.
(a) Geometry of fuel clad of Indian PHWR used in the finite element analysis. (b) Axisymmetric finite element model of fuel clad with internal pressure. (c) Mesh used for the study with its zoomed view near transition of elements. (d) Mesh convergence study for determining the final mesh to be used. (e) Typical variation in temperature of clad as a function of time during burst test for two specified heating rates.
The loading and boundary conditions for the fuel clad are shown in Figure 3b. Internal pressure is applied and the clad is subjected to a temperature history, as shown in Figure 3d. This temperature history is similar to those used in experiments as reported in Ref. [42]. The creep material properties used in the FE analysis are shown in Table 1. The results of clad deformation history and associated changes in von Mises equivalent stress and equivalent creep strain values are discussed in detail in the next section. In addition, the burst behavior is modeled with the help of a damage model, as discussed later.
5. Results of FE Analysis, Prediction of Burst Initiation and Experimental Validation
In this section, the results of clad deformation and creep strain accumulation in the fuel clad are shown for various types of loading conditions (i.e., internal pressure and temperature histories, represented in terms of constant heating rates). Figure 4a shows the radial deformation contour of the clad at the time step of 45 s for the constant heating rate of 15 °C/s. The internal pressure is 3.1 MPa. The maximum radial deformation is 5.3 mm, as can be seen from Figure 4a. It has been seen that the radial deformation profile observed in FE simulation is similar to that of the experimental clad tube, as shown in Figure 4a. The corresponding contour for von Mises equivalent stress is shown in Figure 4b and the maximum value of this parameter is 65 MPa.
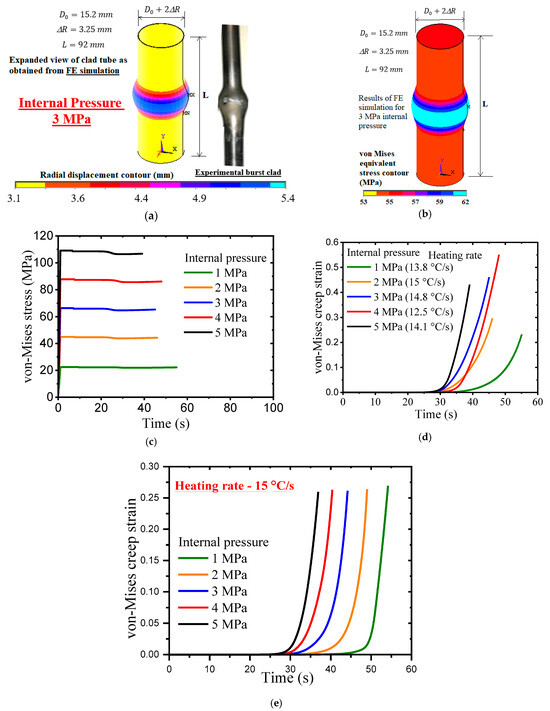
Figure 4.
(a) Results of radial deformation profile of the fuel clad, as obtained from FE simulation showing ballooning behavior. (b) Contour of von Mises stress in the axisymmetric model of fuel clad for simulation at an internal pressure of 3.1 MPa. (c) Variation in von Mises stress at the maximum location as a function of time for variation values of internal pressure ranging from 1 to 5 MPa and heating rate of 15 °C/s. (d) Variation in equivalent creep strain with time for variation combinations of internal pressure and heating rates. (e) Variation in equivalent creep strain for a constant heating rate of 15 °C/s.
It may be noted that the maximum values of von Mises equivalent stress increase with the increase in applied magnitude of internal pressure, as shown in Figure 4c. The corresponding creep strain accumulation with time for various combinations of internal pressure and heating rates are shown in Figure 4d. It may be observed that creep strain accumulation starts after a threshold time of 30 s (approximately) as this much time is required for the temperature in the clad to reach 600 °C (approximately), as can be seen from Figure 3c. The creep deformation becomes significant only after the temperature in the clad exceeds 600 °C, as can be seen from the material constants presented in Table 1.
The creep deformation of Zircaloy-4 clad is insignificant below the temperature of 600 °C. Again, the rate of creep strain accumulation is higher for higher values of internal pressure when the heating rates are similar, as can be seen from Figure 4d. However, when the heating rate is lower, i.e., 12.5 °C/s, the creep strain accumulation in the clad is initially slower, even for higher values of applied internal pressure (i.e., 4 MPa), when compared to the corresponding strain accumulation for 2 MPa internal pressure and 15 °C/s heating rate case. This can be explained based on corresponding temperature history in the clad. To isolate the influence of internal pressure from that of heating rate, a set of simulations was conducted where the heating rate was held constant at 15 °C/s while the internal pressure was varied across different cases. As shown in Figure 4e, the results reveal a consistent trend, i.e., the burst time of the clad tube increases progressively as the applied internal pressure decreases under this fixed temperature loading condition. This behavior is attributed to the lower stress levels at reduced pressures, which in turn delay the accumulation of creep strain and material damage necessary to trigger burst. These results reinforce the understanding that for a given temperature ramp, the mechanical loading (pressure) plays a dominant role in determining the rate of creep damage evolution and the timing of failure initiation.
Initially, the temperature in the clad with a lower heating rate is less, and hence, the creep strain accumulation is less even for higher stress value. However, once temperature exceeds the threshold value, both temperature and stress values contribute to creep strain accumulation, and hence, the creep strain increases rapidly for 4 MPa internal pressure when compared to that of clad with 2 MPa internal pressure and 15 °C/s heating rate. Hence, it can be concluded that both heating rate and internal pressure values play a role in creep strain accumulation and the corresponding material damage, which leads to the initiation of micro-crack and eventual burst in the clad. However, the process of simulation of creep damage requires information regarding stress triaxiality and creep strain. A model for simulation of clad burst is presented in the following paragraphs.
The process of creep damage accumulation occurs by void growth and coalescence [43,51], and hence, the corresponding damage variable can be described using a model similar to that of Rice and Tracey’s void growth law, as presented in Ref. [51]. In this work, a new damage variable ‘D’ is proposed, which is a function of stress triaxiality (i.e., ratio of hydrostatic stress to von Mises equivalent stress ) and the inelastic strain increment as shown in Equation (2). The cumulative damage variable ‘D’ is obtained by integrating the expression until the instant of clad burst, as observed in the experiment. The value of damage variable ‘D’ characterizing burst in the clad is denoted as ‘’ and this value is initially calibrated from experimental data.
The constant 0.283 represents the void growth rate factor for a spherical void in an idealized plastic matrix under triaxial stress conditions [43]. Using time-dependent history of von Mises equivalent stress and equivalent creep strain increment, as presented in Figure 4c,d, the evolution of damage variable ‘D’ in the Indian PHWR fuel clad is calculated for internal pressure of 2 MPa and the heating rate of 15 °C/s. The corresponding result is shown in Figure 5. The burst of Zircaloy fuel clad corresponding to this loading condition occurs at 45 s, as reported in the experiment carried out in Ref. [42]. Corresponding to this time and the above loading condition, the critical damage parameter ‘’ has been estimated to be 0.12. This value of critical damage parameter is a material property, and hence, it has been used in subsequent FE simulations to predict the burst behavior of Zircaloy-4 fuel clad for various combinations of internal pressure loading and heating rates. The critical damage value is inferred from the timing of experimentally observed burst, rather than direct imaging of internal damage accumulation. In situ imaging techniques (e.g., X-ray tomography or DIC) can be used in future works to directly correlate model predictions with real-time damage evolution in cladding tubes.
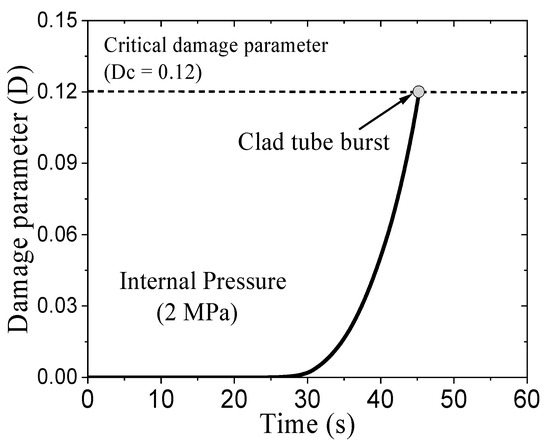
Figure 5.
Evolution of damage parameter ‘D’ as a function of time, as obtained from FE simulation, for an internal pressure of 2 MPa and determination of critical value from time of clad burst, as observed in experiment.
The results of FE simulation for various values of internal pressure ranging from 5 to 10 MPa are shown in Figure 6a. In these simulations, the heating rate is kept constant at 15 °C/s and the corresponding variation in temperature with time is shown in Figure 3c. As can be seen from Figure 6a, the damage parameter accumulates after a threshold time step as it required some time for the wall temperature in the clad to exceed 600 °C.
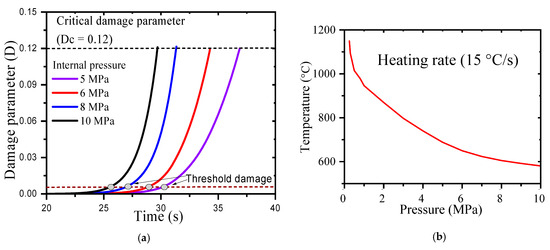
Figure 6.
(a) Variation in damage parameter with time for different values of internal pressure in the clad showing threshold damage after which the damage accumulation accelerates rapidly. (b) Variation in temperature at instant of burst (i.e., corresponding to attainment of critical damage parameter in the FE simulation) as a function of burst pressure.
The damage accumulation occurs in an exponentially increasing manner and corresponds to the critical damage value of 0.12; the time is noted for each magnitude of internal pressure. The corresponding temperature at the instant of simulated clad burst can be found from Figure 3c, as the heating rate is known. Using the above procedure, the temperature of clad at the instant of burst (called burst temperature) is plotted against the internal pressure applied in the clad (called burst pressure) and this data is shown in Figure 6b. This variation depends upon heating rate, as can be seen from subsequent discussions, as the creep damage accumulation depends upon clad temperature history, which is in turn dependent upon the heating rate.
The results of the FE simulation have been validated with experimental data from the literature [42] and a comparison of the same is shown in Figure 7. The clad burst temperature is plotted as a function of burst pressure (i.e., applied internal pressure) in Figure 7a and it can be observed that the burst temperature is inversely dependent upon the burst pressure for a given heating rate (i.e., linear variation in temperature with time). The higher burst pressure induces higher stresses in the clad; hence, the damage accumulation occurs faster, leading to burst at less time, and hence, lesser temperature.
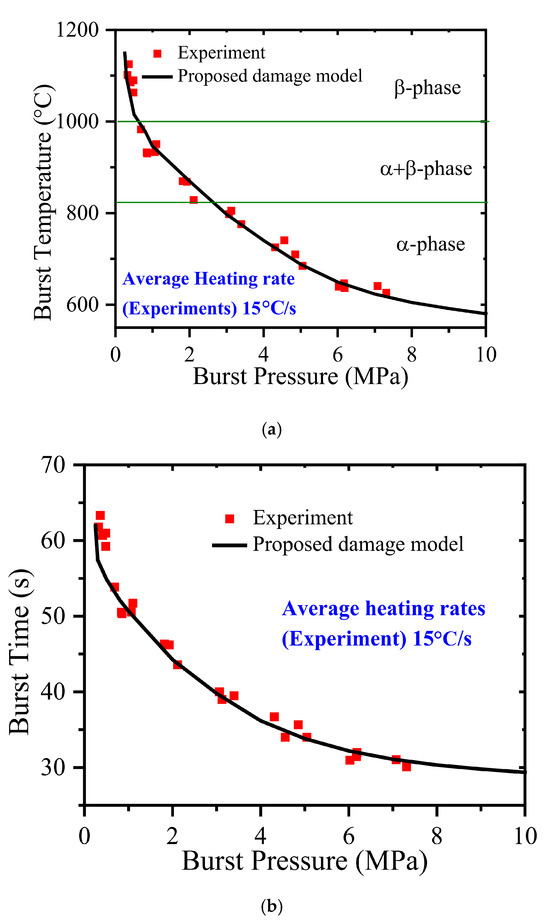
Figure 7.
Comparison of predicted (a) burst temperature vs. burst pressure data and (b) burst time vs. burst pressure data with corresponding experimental data taken from the literature [42].
A similar observation is also seen in Figure 7b, where the time to clad burst is plotted against burst pressure and the dependence is similar to that of burst temperature. The results of the proposed damage model for both burst temperature vs. burst pressure and burst time vs. burst pressure are also compared with corresponding experimental data taken from the literature [42]. It may be observed that the current damage model is able to model the experimentally observed clad burst behavior very satisfactorily, and hence, this serves as a predictive tool in the modeling of clad deformation during severe accident scenarios.
Moreover, this damage model can be used to simulate clad burst behavior even for different constant and variable heating rates, which may be encountered during severe accident progression in the reactor core. It may be noted that the researchers use various types of empirical correlations between burst temperature and burst stress, which is not suitable for the integrity analysis of fuel clad for variable heating rate scenarios, as discussed later. On the other hand, the effect of heating rate on clad burst correlation is absent in the typical empirical correlations, as presented in Ref. [42].
These correlations use an exponential decay type correlation between burst temperature and burst stress, and the constants usually vary for different temperature zones as these are derived from experimental data corresponding to given loading conditions, and hence, these may not be applicable in generalized loading scenarios. These limitations have been tackled through this new damage model. Later, a heating-rate-dependent burst temperature vs. burst stress correlation has also been proposed, which shall be very useful for the practitioners and safety analysts.
The effect of heating rate on clad burst behavior has been simulated by varying the heating rate from 15 °C/s to 100 °C/s. Various magnitudes of internal pressure varying from 1 MPa to 10 MPa have been used in the FE simulation. The typical variations in von Mises equivalent stress and equivalent creep strain with time are shown for the two different heating rates in Figure 8a,b. The creep strain accumulation is faster for a higher heating rate, as can be seen from Figure 8b.
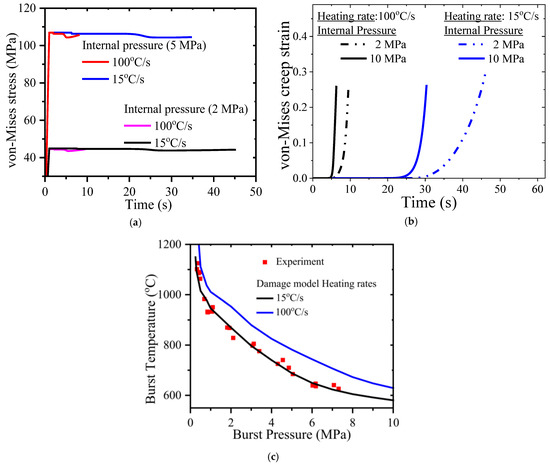
Figure 8.
Evolution of (a) von Mises stress and (b) equivalent creep strain at the maximum location of the clad with time for two different heating rates and internal pressure values. (c) Variation in burst temperature as a function of burst pressure for Zircaloy-4 fuel clad, as predicted by the damage model for two different heating rates and its comparison with experiment from literature [42].
Moreover, the internal pressure also has a profound effect on creep strain accumulation. Higher internal pressure produces higher stress values in the clad, as can be seen from Figure 8a, and this in turn leads to faster creep strain accumulation, as observed in Figure 8b. Using a similar principle (as discussed earlier) to calculate burst temperature and burst pressure, the variation in burst temperature as a function of burst pressure for the two different heating rates are evaluated and the corresponding data are presented in Figure 8c.
It may be noted that the clad burst behavior is highly dependent upon the heating rate. However, as discussed earlier, the effect of heating rate is not considered in the empirical correlations available in the literature (example, Ref. [42]), and hence, this remains a limitation of the existing correlations. For this purpose, a new heating-rate-dependent correlation has been proposed in this work, which uses the results of the damage model to derive the new correlation.
To elucidate this point, a typical experimental database for burst stress vs. burst temperature, as taken from Ref. [42], is shown in Figure 9a. The data points have been fitted with different types of correlations in the different temperature regimes. However, the functional forms of all these correlations remain exponential decay type, with constants deferring for each zone of temperature, as shown in Figure 9a. Another set of experimental data points have been taken from Ref. [43], which shows the variations in clad burst temperature with burst pressure values for two different heating rates in Figure 9b.
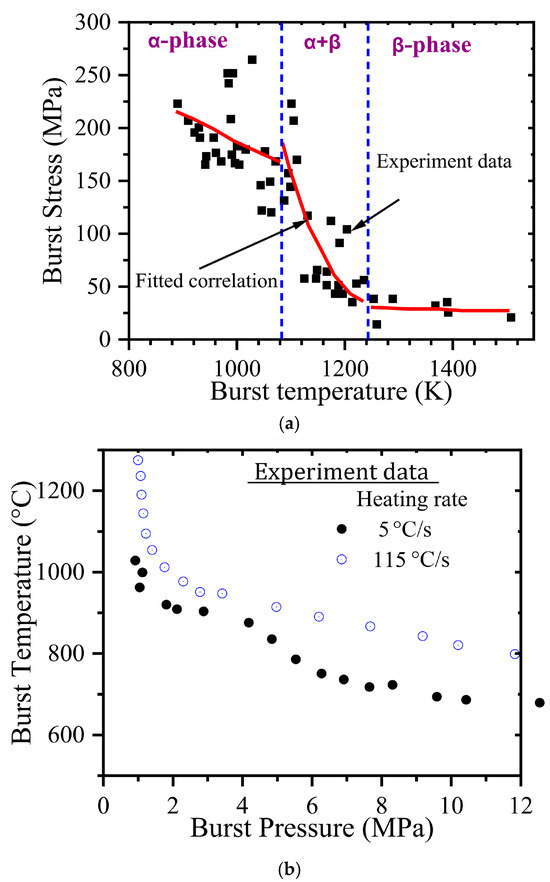
Figure 9.
(a) Burst stress as a function of burst pressure as obtained from experimental data taken from literature [42] along with the fitted exponential correlation. (b) Burst temperature vs. burst pressure data as taken from literature [43] for two different heating rates.
One notable observation in this data is that significant differences in the clad burst temperature vs. burst pressure behavior are observed for the two different heating rates of 5 °C/s and 115 °C/s, respectively. The higher heating rate produces higher burst temperature for a given applied internal pressure value. This is similar to the results of our FE simulation, as discussed earlier and presented in Figure 8c. In order to quantify the effect of heating rate on burst temperature vs. burst pressure behavior of fuel clad, the damage model, as developed in this work, has been applied and the results have been correlated to a normalized heating rate as discussed later in detail.
The effect of heating rate on clad burst behavior is also reported in Ref. [44]; however, no such correlation linking clad burst temperature to the heating rate and applied stress can be found in the literature. Figure 10 shows the variation in burst temperature as a function of initially applied stress (or engineering stress) for different heating rates ranging from 1 °C/s to 100 °C/s. It can be seen from this figure that the heating rates elevate the temperature at the time of clad burst if the applied stress is kept constant.
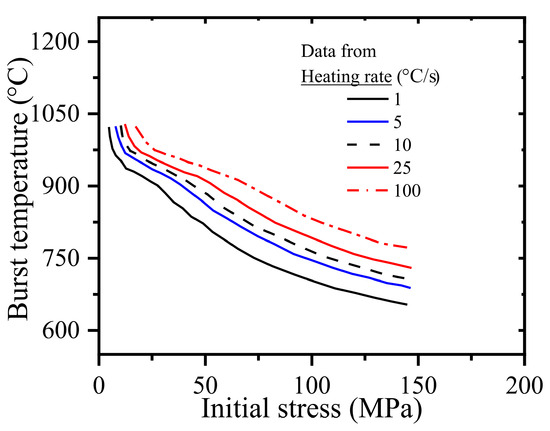
Figure 10.
Burst temperature vs. initially applied stress as predicted by Rosinger [44] using an empirical model for various heating rates.
As the higher heating rate reduces the corresponding time duration for strain accumulation for a given temperature range, the creep damage accumulation becomes less for this temperature range, and hence, a higher temperature is required for creep damage accumulation to reach the desired critical magnitude, which in turn initiates micro-crack and corresponding burst in the clad. Using the material data for Indian PHWR fuel clad, as presented in Table 1, FE simulations have been carried out for different heating rates ranging from 5 °C/s to 100 °C/s.
The corresponding initial stress values (controlled with the help of internal pressure) have varied from 1 MPa to 180 MPa, covering a very wide range of applied stress and heating rates. The results of burst temperature and initial stress are plotted in Figure 11 for different heating rates varying from a slow heating rate of 5 °C/s to a very fast heating rate of 100 °C/s. The results show an inverse type dependence of burst temperature on initial stress for a fixed heating rate, and with increased heating rate, the burst temperature becomes more for a given applied stress. This is similar to our earlier discussion of corresponding results from the literature; however, this result corresponds to the material properties of Indian PHWR fuel clad and this has been predicted through our proposed damage model.
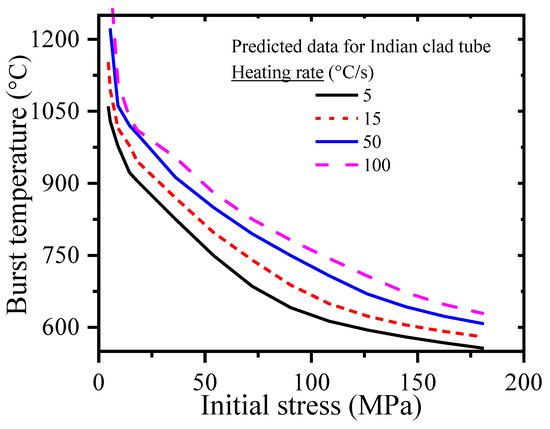
Figure 11.
Burst temperature vs. initially applied stress as predicted by current damage model for various heating rates for Indian clad.
Figure 12 shows a comparative analysis of burst temperature as a function of initial stress for two different cladding materials, i.e., Indian PHWR Zircaloy-4 clad tube (lines) and CANDU Zircaloy clad tube (symbols). It visualizes how heating rate and initial stress influence the burst behavior providing both experimental and simulation data. As the initial stress increases, the burst temperature decreases. Higher heating rates result in higher burst temperatures for the same stress level due to reduced time for creep damage accumulation. Both simulated (Indian) and CANDU data exhibit similar dependence on stress and heating rate, validating the physical realism of the proposed damage model. CANDU data consistently show higher burst temperatures compared to the Indian data at equivalent stress levels, possibly due to differences in cladding fabrication, microstructure, or experimental setup. The close agreement in trend between simulation (Indian) and CANDU data supports the applicability and robustness of the developed model across different reactor designs.
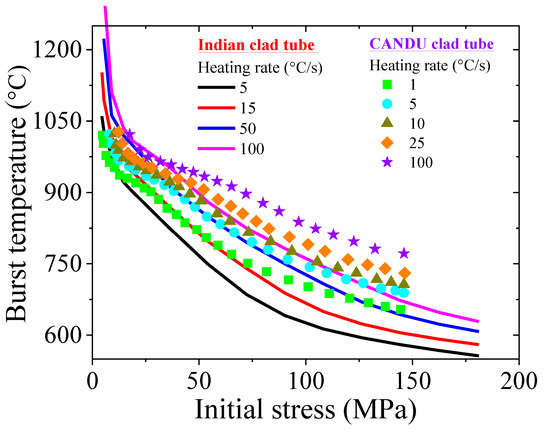
Figure 12.
Comparison of burst temperature vs. initially applied stress as predicted by current damage model for various heating rates for Indian clad and Rosinger data [44].
6. Discussion
As discussed earlier, the finite element-based damage model can be used to predict the clad burst behavior for any type of high-temperature loading scenarios. It can also simulate the heating rate effect on clad burst behavior or, in other words, the effect of temperature history (either linear or non-linear variation with time) is inbuilt in the formulation. This model has also been validated against experimental data, as presented in Figure 7. However, for simplicity and ease of use for the practitioners, a new heating-rate-dependent correlation has been developed additionally in this work using the new damage model. This type of correlation is also helpful for severe accident codes, which rely on its simplicity in order to perform simulations of severe accident progression of core components efficiently.
Initially, the heating rate of 5 °C/s was chosen as the reference heating rate, as this is one of the lowest heating rates encountered in typical experimental data for heating rates in the literature. This reference data shall be used later to develop the heating-rate-dependent clad burst correlation. Figure 13a shows the variation in burst temperature (Tb) vs. engineering burst stress (the same as the initially applied equivalent stress) for the reference heating rate of 5 °C/s. The data points have been fitted with a correlation, as shown in Figure 13a.
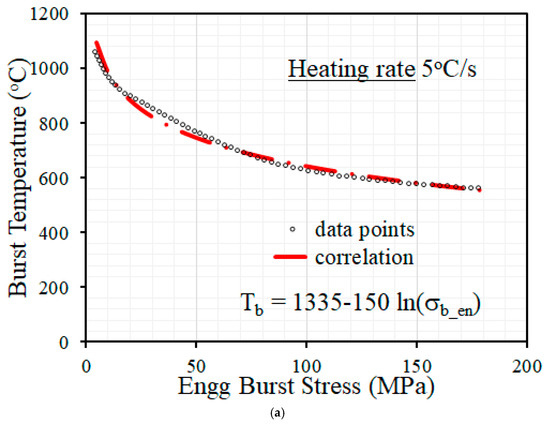
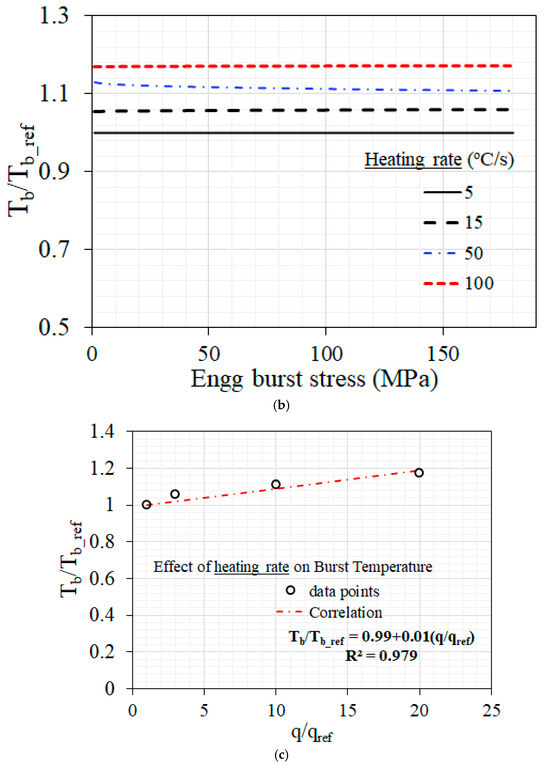
Figure 13.
(a) Variation in burst temperature with engineering burst stress for the reference heating rate of 5 °C/s and corresponding reference correlation for clad burst behavior. (b) Variation in normalized burst temperature with engineering burst stress for different heating rates varying from 5 °C/s to 100 °C/s. (c) Variation in normalized burst temperature with normalized heating rate and the corresponding proposed correlation.
Later, similar simulations have been carried out for several heating rates varying from 15 °C/s to 100 °C/s. The corresponding burst temperature vs. engineering burst stress data have been used to derived the normalized burst temperature, expressed as , where denotes the burst temperature for any heating rate and corresponds to the burst temperature for the reference heating rate of 5 °C/s. The variation in the normalized burst temperature with burst stress is shown in Figure 13b.
It can be observed that this normalized burst temperature is almost independent of the applied engineering burst stress. However, the normalized burst temperature increases with heating rate, as can be seen from Figure 13b. Later, the heating rate has also been normalized with the reference data, corresponding to that of 5 °C/s heating rate. The normalized heating rate is defined as , where is the actual heating rate in °C/s and corresponds to the reference heating rate of 5 °C/s.
The variation of with is shown in Figure 13c. The data points from simulation have been fitted with a correlation, as shown in Figure 13c. Hence, the new heating-rate-dependent clad burst correlation, as developed in this work, can be summarized as follows in Equation (3) below.
In order to use this correlation, the use first calculates the value of as a function of . Later, using information regarding heating rate and reference heating rate = 5 °C/s, the value of normalized burst temperature is calculated, from which the actual clad burst temperature can be calculated using the first line of Equation (3).
7. Conclusions
In this work, the ballooning and burst behavior of nuclear fuel clad due to high temperature creep deformation and associated damage accumulation has been investigated using a material damage model. This model can predict the burst temperature as a function of burst stress for different heating rates. In addition, a new correlation has also been developed based on the results of a new damage model, which can predict the burst behavior of clad as a function of heating rate. Such kinds of burst correlations are not available in the literature. The following conclusions can be derived from this work.
- The creep damage accumulation depends upon the history of temperature and stress variation in the clad and the stress triaxiality in the clad is an important factor, which promotes creep damage accumulation in the material.
- For a given heating rate, higher applied pressure results in lower temperature at clad burst as the applied stress is higher, which can lead to higher creep strain accumulation at a given temperature.
- A threshold magnitude of burst time and burst temperature is observed, both in experimental data from the literature, and from the results of the current simulation, which corresponds to the clad temperature of the order of 600 °C, approximately. This corresponds to the temperature below which creep deformation of Indian PHWR Zircaloy-4 fuel clad is negligible.
- Clad burst temperature increases with heating rate for a given value of applied stress. This can be explained based on temperature variation with time for different heating rates. For a higher heating rate, there is less time available for creep deformation at a given temperature range, and hence, the clad needs to attain higher temperature in order to accumulate creep damage corresponding to the critical value needed for initiation of clad burst.
- A new heating-rate-dependent correlation has been developed in this work, which can be used by the practitioners as well as by the engineers using the severe accident analysis program in order to simulate the clad deformation and burst behavior in a realistic manner, when heating rate varies during the accident progression.
Author Contributions
Conceptualization, M.K.S.; methodology, A.S. and M.K.S.; software, A.S.; validation, A.S. and M.K.S.; formal analysis, A.S. and M.K.S.; investigation, A.S. and M.K.S.; resources, M.K.S.; data curation, A.S. and M.K.S.; writing—original draft preparation, A.S. and M.K.S.; writing—review and editing, M.K.S.; visualization, A.S.; supervision, M.K.S.; project administration, M.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data shall be available on request.
Acknowledgments
The authors acknowledge the support of Head, Reactor Safety Division, Bhabha Atomic Research Centre, Mumbai, India for his kind encouragement for this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feria, F.; Aragón, P.; Herranz, L. Assessment of cladding ballooning during DBA-LOCAs with FRAPTRAN. Ann. Nucl. Energy 2023, 195, 110194. [Google Scholar] [CrossRef]
- Aragón, P.; Feria, F.; Herranz, L.E.; Schubert, A.; Van Uffelen, P. Enhancing cladding mechanical modelling during DBA/LOCA accidents with FRAPTRAN: The TUmech one-dimensional model. Prog. Nucl. Energy 2024, 171, 105189. [Google Scholar] [CrossRef]
- Massey, C.P.; Terrani, K.A.; Dryepondt, S.N.; Pint, B.A. Cladding burst behavior of Fe-based alloys under LOCA. J. Nucl. Mater. 2016, 470, 128–138. [Google Scholar] [CrossRef]
- Campello, D.; Tardif, N.; Moula, M.; Baietto, M.; Coret, M.; Desquines, J. Identification of the steady-state creep behavior of Zircaloy-4 claddings under simulated Loss-Of-Coolant Accident conditions based on a coupled experimental/numerical approach. Int. J. Solids Struct. 2017, 115–116, 190–199. [Google Scholar] [CrossRef]
- Narukawa, T.; Kondo, K.; Fujimura, Y.; Kakiuchi, K.; Udagawa, Y.; Nemoto, Y. Behavior of FeCrAl-ODS cladding tube under loss-of-coolant accident conditions. J. Nucl. Mater. 2023, 582, 154467. [Google Scholar] [CrossRef]
- Aragón, P.; Feria, F.; Herranz, L.E.; Schubert, A.; Van Uffelen, P. Fuel performance modelling of Cr-coated Zircaloy cladding under DBA/LOCA conditions. Ann. Nucl. Energy 2024, 211, 110950. [Google Scholar] [CrossRef]
- Sweet, R.; Mouche, P.; Bell, S.; Kane, K.; Capps, N. Chromium-coated cladding analysis under simulated LOCA burst conditions. Ann. Nucl. Energy 2022, 176, 109275. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, J.W.; Kim, H.; Lee, S.-U. Prediction of ballooning and burst for nuclear fuel cladding with anisotropic creep modeling during Loss of Coolant Accident (LOCA). Nucl. Eng. Technol. 2021, 53, 3379–3397. [Google Scholar] [CrossRef]
- Li, W.; Chen, H.; Wu, X.; Duan, Q.; Su, G. Simulation of nuclear fuel clad high-temperature ballooning under loss-of-coolant accident conditions considering anisotropic creep. Ann. Nucl. Energy 2024, 203, 110500. [Google Scholar] [CrossRef]
- Capps, N.; Ridley, M.; Yan, Y.; Bell, S.; Kane, K. BISON validation to in situ cladding burst test and high-burnup LOCA experiments. Ann. Nucl. Energy 2023, 191, 109905. [Google Scholar] [CrossRef]
- Pastore, G.; Williamson, R.; Gardner, R.; Novascone, S.; Tompkins, J.; Gamble, K.; Hales, J. Analysis of fuel rod behavior during loss-of-coolant accidents using the BISON code: Cladding modeling developments and simulation of separate-effects experiments. J. Nucl. Mater. 2021, 543, 152537. [Google Scholar] [CrossRef]
- Sweet, R.; Massey, C.; Hirschhorn, J.; Bell, S.; Kane, K. Wrought FeCrAl alloy (C26M) cladding behavior and burst under simulated loss-of-coolant accident conditions. Nucl. Eng. Des. 2024, 431, 113712. [Google Scholar] [CrossRef]
- Lee, S.K.; Capps, N.A.; Brown, N.R. BISON analysis of FeCrAl and Zircaloy cladding deformation during simulated BWR cyclic dryout conditions. J. Nucl. Mater. 2023, 576, 154243. [Google Scholar] [CrossRef]
- Rossiter, G.; Peakman, A. Development and validation of Loss of Coolant Accident (LOCA) simulation capability in the ENIGMA fuel performance code for zirconium-based cladding materials. Nucl. Eng. Des. 2023, 416, 112767. [Google Scholar] [CrossRef]
- Verma, L.; Clifford, I.; Konarski, P.; Scolaro, A.; Ferroukhi, H. OFFBEAT V&V studies for REBEKA tests on cladding ballooning and burst during LOCA conditions. Ann. Nucl. Energy 2024, 208, 110773. [Google Scholar] [CrossRef]
- Garrison, B.; Cinbiz, M.; Gussev, M.; Linton, K. Burst characteristics of advanced accident-tolerant FeCrAl cladding under temperature transient testing. J. Nucl. Mater. 2022, 560, 153488. [Google Scholar] [CrossRef]
- Joshi, P.; Kombaiah, B.; Cinbiz, M.; Murty, K. Characterization of stress-rupture behavior of nuclear-grade C26M2 FeCrAl alloy for accident-tolerant fuel cladding via burst testing. Mater. Sci. Eng. A 2020, 791, 139753. [Google Scholar] [CrossRef]
- Kane, K.; Bell, S.; Capps, N.; Garrison, B.; Shapovalov, K.; Jacobsen, G.; Deck, C.; Graening, T.; Koyanagi, T.; Massey, C. The response of accident tolerant fuel cladding to LOCA burst testing: A comparative study of leading concepts. J. Nucl. Mater. 2022, 574, 154152. [Google Scholar] [CrossRef]
- Jailin, T.; Tardif, N.; Desquines, J.; Chaudet, P.; Coret, M.; Baietto, M.-C.; Georgenthum, V. Thermo-mechanical behavior of Zircaloy-4 claddings under simulated post-DNB conditions. J. Nucl. Mater. 2020, 531, 151984. [Google Scholar] [CrossRef]
- Ma, Z.; Shirvan, K.; Wu, Y.; Su, G. Numerical investigation of ballooning and burst for chromium coated zircaloy cladding. Nucl. Eng. Des. 2021, 383, 111420. [Google Scholar] [CrossRef]
- Zhang, X.; Li, G.; Gao, R.; Zhao, X.; Yao, P. Numerical study on PWR fuel rod cladding ballooning and burst behavior with the thermo-mechanical coupling finite element method. Int. J. Adv. Nucl. React. Des. Technol. 2025, 7, 7–18. [Google Scholar] [CrossRef]
- Yano, Y.; Sekio, Y.; Tanno, T.; Kato, S.; Inoue, T.; Oka, H.; Ohtsuka, S.; Furukawa, T.; Uwaba, T.; Kaito, T.; et al. Ultra-high temperature creep rupture and transient burst strength of ODS steel claddings. J. Nucl. Mater. 2019, 516, 347–353. [Google Scholar] [CrossRef]
- Massey, C.P.; Kane, K.A.; Sweet, R.T.; Bell, S.B.; Dryepondt, S.N.; Burns, J.; Nelson, A.T. Microstructure dependent burst behavior of oxide dispersion–strengthened FeCrAl cladding. Mater. Des. 2023, 234, 112307. [Google Scholar] [CrossRef]
- Kamerman, D. The deformation and burst behavior of Zircaloy-4 cladding tubes with hydride rim features subject to internal pressure loads. Eng. Fail. Anal. 2023, 153, 107547. [Google Scholar] [CrossRef]
- Bell, S.; Kane, K.; Ridley, M.; Garrison, B.; Johnston, B.; Capps, N. In-situ determination of strain during transient burst testing and the temperature dependence of Zircaloy-4 claddings. J. Nucl. Mater. 2024, 591, 154910. [Google Scholar] [CrossRef]
- Choi, G.-H.; Kim, D.-H.; Shin, C.-H.; Kim, J.Y.; Kim, B.J. In-situ deformation measurement of Zircaloy-4 cladding tube under various transient heating conditions using optical image analysis. Nucl. Eng. Des. 2020, 370, 110859. [Google Scholar] [CrossRef]
- Gussev, M.; Byun, T.; Yamamoto, Y.; Maloy, S.; Terrani, K. In-situ tube burst testing and high-temperature deformation behavior of candidate materials for accident tolerant fuel cladding. J. Nucl. Mater. 2015, 466, 417–425. [Google Scholar] [CrossRef]
- Kim, D.-H.; Choi, G.-H.; Kim, H.; Lee, C.; Lee, S.-U.; Hong, J.-D.; Kim, H.-S. Measurement of Zircaloy-4 cladding tube deformation using a three-dimensional digital image correlation system with internal transient heating and pressurization. Nucl. Eng. Des. 2020, 363, 110662. [Google Scholar] [CrossRef]
- Ridley, M.; Massey, C.; Bell, S.; Capps, N. High temperature creep model development using in-situ 3-D DIC techniques during a simulated LOCA transient. Ann. Nucl. Energy 2023, 193, 110012. [Google Scholar] [CrossRef]
- Yin, C.; Su, G.; Qian, L.; Xiong, Q.; Liu, Y.; Wu, Y.; Du, S.; Zhang, J.; Xiao, Z. Research progress in high-temperature thermo-mechanical behaviors for modelling Cr-coated cladding under loss-of-coolant accident condition. Nucl. Eng. Des. 2025, 439, 114125. [Google Scholar] [CrossRef]
- Qian, L.; Liu, Y.; Huang, T.; Chen, W.; Du, S.; Yin, C.; Xiong, Q. Research progress in high-temperature thermo-mechanical behavior for modelling FeCrAl cladding under loss-of-coolant accident condition. Prog. Nucl. Energy 2023, 164, 104848. [Google Scholar] [CrossRef]
- Murty, K.L.; Seok, C.; Kombaiah, B. Burst and Biaxial Creep of Thin-Walled Tubing of Low c/a-Ratio HCP Metals. Procedia Eng. 2013, 55, 443–450. [Google Scholar] [CrossRef]
- Xin, J.; Yuyu, L.; Libin, Z. Thermal creep behavior of CZ cladding under biaxial stress state. Nucl. Eng. Technol. 2020, 52, 2901–2909. [Google Scholar] [CrossRef]
- Sklenicka, V.; Kral, P.; Kucharova, K.; Kvapilova, M.; Dvorak, J.; Kloc, L. Thermal creep fracture of a Zr1%Nb cladding alloy in the α and (α + β) phase regions. J. Nucl. Mater. 2021, 553, 152950. [Google Scholar] [CrossRef]
- Moore, B.; Topping, M.; Long, F.; Daymond, M. Stress and temperature dependence of irradiation creep in zircaloy-4 studied using proton irradiation. J. Nucl. Mater. 2024, 603, 155383. [Google Scholar] [CrossRef]
- Choi, G.-H.; Shin, C.-H.; Kim, J.Y.; Kim, B.J. Circumferential steady-state creep test and analysis of Zircaloy-4 fuel cladding. Nucl. Eng. Technol. 2021, 53, 2312–2322. [Google Scholar] [CrossRef]
- Limon, R.; Lehmann, S. A creep rupture criterion for Zircaloy-4 fuel cladding under internal pressure. J. Nucl. Mater. 2004, 335, 322–334. [Google Scholar] [CrossRef]
- Han, M.; Liu, H.; Zhang, W.; Zhang, Y.; Luo, S. A failure criterion for nuclear fuel cladding due to internal gas. Nucl. Eng. Des. 2025, 434, 113909. [Google Scholar] [CrossRef]
- Deng, Y.; Liao, H.; He, Y.; Yin, Y.; Pellegrini, M.; Su, G.; Okamoto, K.; Wu, Y. Investigation on hydrogen embrittlement and failure characteristics of Zr-4 cladding based on the GTN method. Nucl. Mater. Energy 2023, 36, 101463. [Google Scholar] [CrossRef]
- Schappel, D.; Capps, N. Impact of LWR assembly structural features on cladding burst behavior under LOCA conditions. Nucl. Eng. Des. 2024, 418, 112887. [Google Scholar] [CrossRef]
- Syed, A.; Samal, M.; Chattopadhyay, J. Determination of critical material damage parameter for Indian clad tube burst behavior under severe accident scenario. Procedia Struct. Integr. 2024, 60, 195–202. [Google Scholar] [CrossRef]
- Sawarn, T.K.; Banerjee, S.; Pandit, K.; Anantharaman, S. Study of clad ballooning and rupture behavior of fuel pins of Indian PHWR under simulated LOCA condition. Nucl. Eng. Des. 2014, 280, 501–510. [Google Scholar] [CrossRef]
- Chung, H.M.; Kassner, T.F. Deformation Characteristics of Zircaloy Cladding in Vacuum and Steam Under Transient Heating Conditions: Summary Report; Argonne National Laboratory: Lemont, IL, USA, 1978. [Google Scholar]
- Rosinger, H. A model to predict the failure of zircaloy-4 fuel sheathing during postulated loca conditions. J. Nucl. Mater. 1984, 120, 41–54. [Google Scholar] [CrossRef]
- Samal, M.K.; Sanyal, G.; Chakravartty, J.K. An experimental and numerical study of the fracture behaviour of tubular specimens in a pin-loading-tension set-up. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 224, 1–12. [Google Scholar] [CrossRef]
- Samal, M.; Sanyal, G.; Chakravartty, J. Estimation of fracture behavior of thin walled nuclear reactor fuel pins using Pin-Loading-Tension (PLT) test. Nucl. Eng. Des. 2010, 240, 4043–4050. [Google Scholar] [CrossRef]
- Sanyal, G.; Samal, M.; Chakravartty, J.; Ray, K.; Suri, A.; Banerjee, S. Prediction of J–R curves of thin-walled fuel pin specimens in a PLT setup. Eng. Fract. Mech. 2011, 78, 1029–1043. [Google Scholar] [CrossRef]
- Sanyal, G.; Samal, M.K. Fracture behavior of thin-walled Zircaloy fuel clad tubes of Indian pressurized heavy water reactor. Int. J. Fract. 2012, 173, 175–188. [Google Scholar] [CrossRef]
- Syed, A.; Samal, M.K.; Chattopadhyay, J.; Dutta, P. Fracture toughness evaluation of axially-cracked tubular thin-walled specimens of Zircaloy-4 and its implications for integrity analysis of nuclear fuel clad. Theor. Appl. Fract. Mech. 2019, 106, 102449. [Google Scholar] [CrossRef]
- Samal, M.; Syed, A.; Chattopadhyay, J.; Ram, A.; Paul, B.; Reddy, M. Effect of texture on crack initiation toughness and the corresponding anisotropy in ductile fracture resistance of thin Zircaloy-4 sheets of Indian PHWR core component. J. Nucl. Mater. 2020, 535, 152189. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).