Next Article in Journal
On Ballooning and Burst Behavior of Nuclear Fuel Clad Considering Heating Rate Effect: Development of a Damage Model, a Burst Correlation and Experimental Validation
Previous Article in Journal
Transient Response of an Infinite Isotropic Magneto-Electro-Elastic Material with Multiple Axisymmetric Planar Cracks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Solids
Volume 6
Issue 4
10.3390/solids6040055
solids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

DFT Study of Oxygen Ion Migration in Mg-Doped Cubic Zirconia

by
Zhussupbek M. Salikhodzha
1,
Guldari B. Bairbayeva
1,*,
Anatoli I. Popov
1,2,
Raigul N. Kassymkhanova
1,
Keleshek B. Zhangylyssov
1,
Elena Popova
3,* and
Marina Konuhova
2
1
Institute of Physical and Technical Sciences, Faculty Transport and Energy, L.N. Gumilyov Eurasian National University, 13 Kazhymukan St., Astana 010000, Kazakhstan
2
Institute of Solid-State Physics, University of Latvia, LV-1063 Riga, Latvia
3
Department of Physics, University of Maryland, College Park, MD 20742-4111, USA
*
Authors to whom correspondence should be addressed.
Solids 2025, 6(4), 55; https://doi.org/10.3390/solids6040055
Submission received: 19 July 2025 / Revised: 12 September 2025 / Accepted: 17 September 2025 / Published: 25 September 2025
Browse Figures
Versions Notes

Abstract

This work presents a theoretical investigation of ionic conductivity in cubic zirconia (c-ZrO2) doped with magnesium, using density functional theory (DFT) with the hybrid B3LYP functional as implemented in the CRYSTAL23 software package. It was found that the spatial arrangement of magnesium atoms and oxygen vacancies significantly affects the energy barriers for oxygen ion migration. Configurations with magnesium located along and outside the migration path were analyzed. The results show that when Mg2+ is positioned along the migration trajectory and near an oxygen vacancy, stable defect complexes are formed with minimal migration barriers ranging from 0.96 to 1.32 eV. An increased number of Mg atoms can lead to a further reduction in the barrier, although in certain configurations the barriers increase up to 3.0–4.6 eV. When doping occurs outside the migration path, the energy profile remains symmetric and moderate (0.9–1.1 eV), indicating only a weak background influence. These findings highlight the critical role of coordinated distribution of Mg atoms and oxygen vacancies along the migration pathway in forming efficient ion-conducting channels. This insight offers potential for designing high-performance zirconia-based electrolytes for solid oxide fuel cells and sensor applications.

1. Introduction

Zirconium dioxide (ZrO2) is a promising oxide material widely used in solid oxide fuel cells, lithium-ion batteries, photocatalysis, and optoelectronics due to its high thermal and chemical stability, ionic conductivity, and mechanical strength [1,2,3,4]. ZrO2 nanoparticles exhibit activity in the photodegradation of organic pollutants [2] and are employed in batteries to enhance anode stability and prevent degradation [3,4]. In addition, ZrO2 is in demand in catalysis and as a dielectric material in thin-film structures [5,6,7,8], highlighting its versatility and importance among modern functional materials [9,10,11,12,13,14]. The ZrO2 is also one of the most promising materials for nuclear engineering [15,16,17,18,19], and when doped, it is an effective phosphor for many luminescent applications [20,21,22].
ZrO2 is a wide-bandgap semiconducting oxide with a polymorphic structure that exists under atmospheric pressure in three allotropic modifications [23,24]: monoclinic (m-ZrO2) [25], tetragonal (t-ZrO2), and cubic (c-ZrO2). The monoclinic phase (baddeleyite) is thermodynamically stable at room temperature, while the transitions to the tetragonal and cubic modifications occur at 1478 K and 2650 K, respectively [26,27]. Controlling the phase stability of ZrO2 is crucial for its application in ceramics, including solid oxide fuel cells (SOFCs), dental materials, and jewelry [28,29,30,31,32,33,34,35,36,37].
Pure zirconium dioxide is characterized by a low concentration of oxygen vacancies, which limits its ionic conductivity. The activation energy for ion transport is determined by the sum of the vacancy formation energy and the migration energy barrier. Various dopants are used to enhance conductivity and stabilize specific phases. The most common dopant elements include Yb [38], Ce [39,40], and Y [41], as well as Al, Ca, Eu, Mg, Na, Sc, and Tb [42]. For example, the addition of 10 mol% Sc stabilizes the cubic c-ZrO2 phase, resulting in high ionic conductivity [43]. Doping with Al allows tuning of the bandgap width and enhances the absorption coefficient in the tetragonal phase of ZrO2 [44], while lanthanide ions not only stabilize the ZrO2 phase but also modulate its optical emission properties [45,46,47,48,49].
Doping ZrO2 with magnesium oxide (MgO) leads to the formation of oxygen vacancies, which enhances ionic conductivity. Studies show that MgO doping affects the polymorphic transformations and mechanical properties of ZrO2. It has been established that low concentrations of MgO stabilize the tetragonal phase, while higher concentrations promote the transition to the cubic phase. The strengthening of the material is associated with phase transitions, increased dislocation density, and the formation of intergranular MgO inclusions [50].
Previous DFT studies have shown that sulfur doping increases the formation energy of oxygen vacancies and raises the migration barrier, resulting in reduced ionic conductivity [51]. The effect of MgO on the radiation resistance of ZrO2 was also investigated in [52], where it was demonstrated that an optimal concentration of 0.10 mol% MgO leads to the formation of a substitutional phase Zr0.9Mg0.1O2, which reduces deformation and enhances the material’s strength. Studies on the defect structure of ZrO2 [53] revealed that polyalanines form chains of oxygen vacancies, which may act as conductive filaments in ReRAM devices, enabling resistive switching through oxygen migration. Moreover, doping ZrO2 with impurity ions affects the system’s total energy, contributing to phase stabilization and improved ionic conductivity, which is important for applications in solid oxide fuel cells [54].
Despite numerous studies on zirconia modeling, the question of how the spatial arrangement of Mg atoms relative to the oxygen migration path affects ionic conductivity remains unresolved. It is unclear whether substitution along the migration pathway enhances conductivity through direct interaction with vacancies or, conversely, creates obstacles due to local structural distortion.
In this work, a theoretical investigation of ionic conductivity in cubic zirconia (c-ZrO2) stabilized with magnesium was carried out using density functional theory (DFT) with the hybrid B3LYP correlation-exchange (XC) functional. The study focuses on the influence of oxygen vacancies and the spatial positioning of magnesium dopants on the energy profile of oxygen ion migration. The scientific novelty of this work lies in the comparative analysis of two doping strategies and in identifying the decisive role of the local coordination environment in forming effective oxygen migration pathways, which can be applied in the design of next-generation oxide electrolytes.

2. Materials and Methods

The ideal crystal of cubic zirconium dioxide (c-ZrO2) has a face-centered cubic structure with space group symmetry Fm-3m (225). The ZrO2 crystal structure corresponds to a fluorite-type arrangement formed in the cubic space group Fm-3m. Zr4+ atoms are coordinated by eight O2− atoms in a body-centered cubic configuration, with a Zr–O bond length of 2.20 Å. Each O2− ion is bonded to four equivalent Zr4+ atoms, forming an OZr4 tetrahedral coordination polyhedron with shared angles and edges [55].
In this study, density functional theory (DFT) [56,57] was employed using the hybrid B3LYP [58,59] functional implemented in the CRYSTAL23 software package [60]. A 2 × 2 × 2 supercell of cubic zirconia (c-ZrO2) containing 96 atoms was used as the model system (see Figure 1). In all calculations, the following basis sets were employed: Zr—Zr_SC_HAYWSC-3111(32111df) G, O—O_8-411, and Mg—Mg_8-511d1G. All basis sets were taken from the CRYSTAL23 library. (https://www.crystal.unito.it/basis_sets.html, accessed on 30 August 2025). In CRYSTAL, restricted (closed shell) calculations are used by default, which is appropriate for ZrO2 since Zr4+ and O2− ions have fully filled outer shells and electrons are paired.
To calculate the structural and electronic properties, total energy calculations were performed without geometry optimization. The initial lattice parameter was set to a = 5.10 Å [61], and the calculated band gap was 5.28 eV, which is comparable to the experimental value of 6.1 eV [62].
To accurately model ionic conductivity in cubic zirconia (c-ZrO2), the calculations were carried out without performing full geometry optimization of atomic positions and lattice parameters. This approach preserved the target structure required for subsequent studies of ionic transport. The system was modeled using density functional theory (DFT) with strict convergence criteria: an energy threshold of 10−6 eV, a gradient threshold of 4.5 × 10−4 eV/Å, and a maximum atomic displacement of 1.8 × 10−3 Å. These settings ensured high precision in calculating the structural and energetic characteristics of the system. Oxygen vacancies were created in the calculations by removing oxygen atoms from the lattice. To provide a clearer picture of how oxygen vacancies and Mg substitutions affect the crystal lattice, Table 1 summarizes the local distortions and the resulting average symmetries for different defect configurations. The data highlights the transition from the ideal cubic structure to tetragonal or rhombohedral distortions upon vacancy formation, as well as the restoration of cubic symmetry at higher Mg concentrations. It should be noted that these symmetrical changes are local in nature, while the overall bulk structure remains cubic since full geometric optimization was not performed.
Thus, the correlation between migration barriers and structural symmetry emphasizes that both the type and distribution of defects play a decisive role in defining ionic conductivity in ZrO2-based systems.
These defects were modeled to investigate their key role in ionic conductivity, as they form possible migration pathways for oxygen ions in the material.
In addition, in crystalline materials, a distinction is usually made between stoichiometric and non-stoichiometric defects. The first group includes, for example, Frenkel and Schottky defects, where the overall cation-to-anion ratio is preserved despite local disorder. In contrast, oxygen vacancies in cubic ZrO2 are non-stoichiometric defects, since their formation changes the cation-to-anion ratio and leads to a deviation from the ideal stoichiometry [63]. Magnesium dopants were introduced into the system by substituting some of the zirconium atoms, allowing the investigation of magnesium’s influence on ionic conductivity. Magnesium in the structure can shift the positions of vacancies and create new defect pathways, affecting oxygen ion migration and, consequently, the material’s conductivity.
These calculations involving magnesium doping and oxygen vacancies provide a basis for further analysis of ionic conductivity in c-ZrO2, which is important for developing advanced materials for solid oxide fuel cells and other applications. The analysis of the system’s total energy as a function of oxygen vacancy concentration and magnesium content allowed us to examine the influence of defects on the phase stability and electronic properties of zirconia.

3. Results

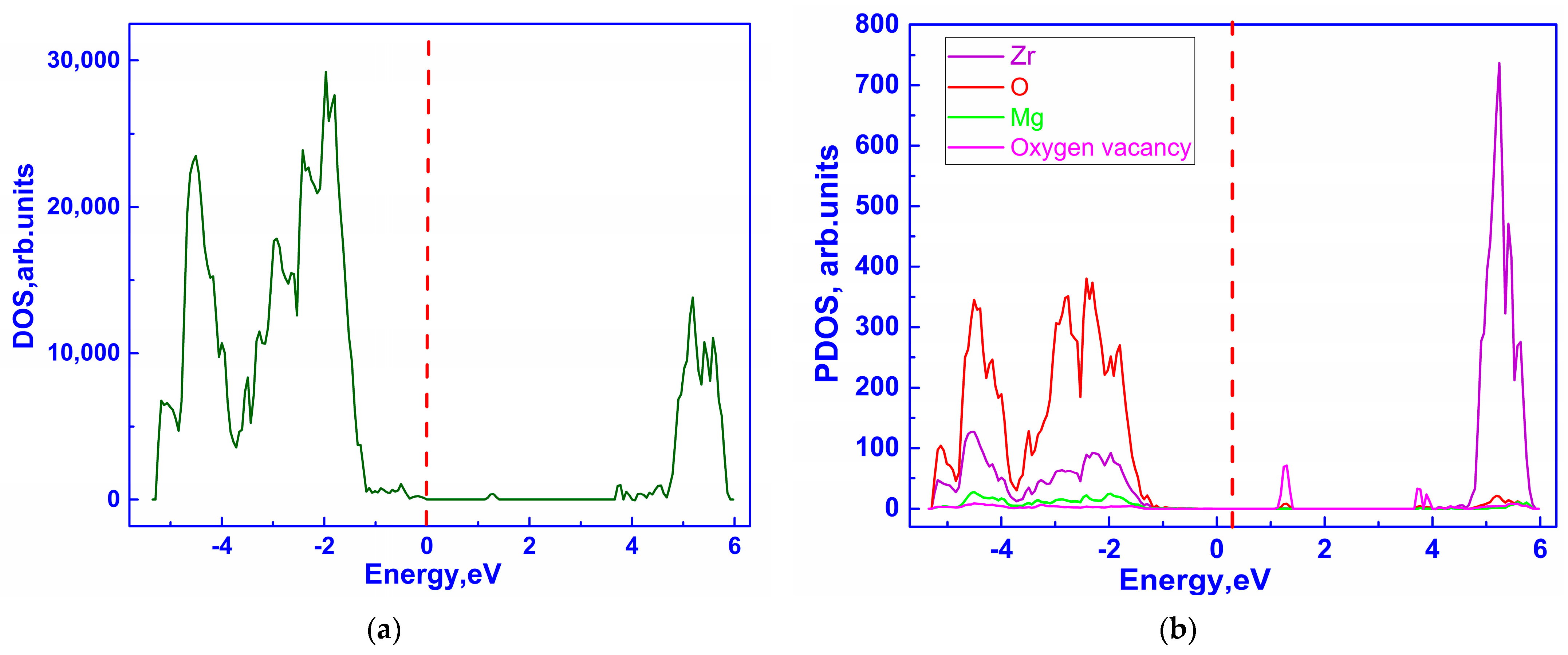
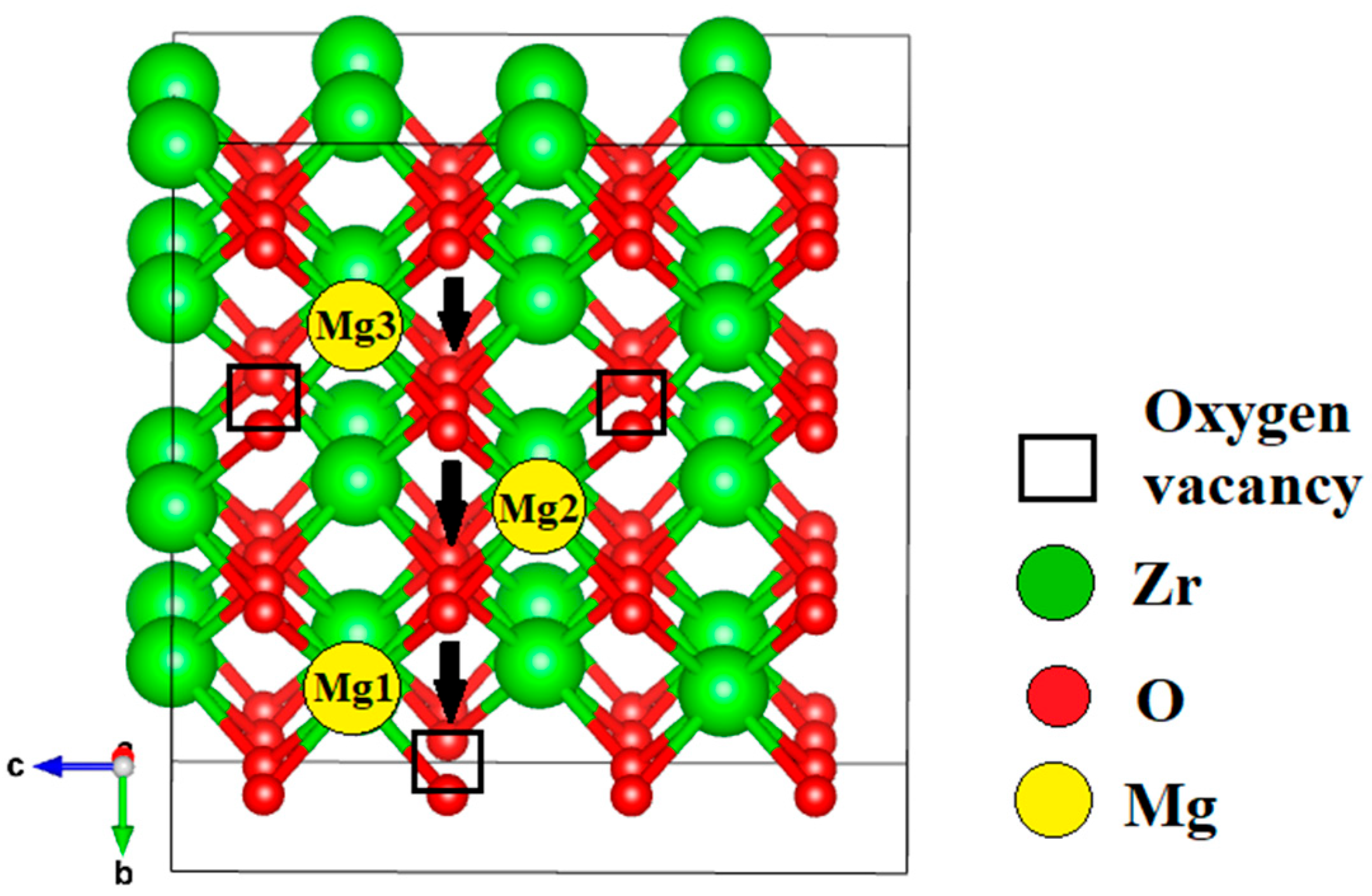
3.1. Investigation of the Electronic Properties of Magnesium-Stabilized Cubic Zirconia

It is well known that the creation of oxygen vacancies in ZrO2 contributes to structural stabilization and enhances ionic conductivity. These vacancies are modeled from first principles by removing one or more oxygen atoms from the supercell.
The modeling is carried out using standard density functional theory (DFT) methods. Total and partial densities of electronic states (DOS and PDOS) are calculated using the hybrid B3LYP functional. The valence electron configurations are 4d25s2 for zirconium and 2s22p4 for oxygen. Oxygen vacancies are modeled within a cubic ZrO2 supercell containing 96 atoms. The geometric parameters of the nearest atoms are not optimized.
As shown in Figure 2, in pristine ZrO2, the valence band is primarily composed of oxygen 2p orbitals, with a maximum around −4.5 eV, while the conduction band starts above the Fermi level and includes contributions from Zr 4d states. Upon the creation of an oxygen vacancy, an additional narrow localized state appears near the bottom of the conduction band, associated with the remaining paired electron.
In the PDOS spectra (Figure 2), the formation of a single oxygen vacancy in ZrO2 leads to the appearance of a localized state approximately 0.1 eV below the Fermi level. At the same time, the vacancy contributes negligibly to the valence band. The main contributions to the valence and conduction bands originate from oxygen (O 2p) and zirconium (Zr 4d) atoms, respectively. These findings align with the general model of defect state formation in oxide dielectrics and demonstrate the potential role of vacancies in enabling ionic conductivity.
With an increase in the concentration of oxygen vacancies in ZrO2 to three per supercell, the total density of states retains the typical oxide profile with a wide band gap (Figure 3). However, in the PDOS projected onto the vacancy sites, a localized state appears within the band gap (approximately 0.1–0.5 eV below the Fermi level), associated with the defects. In the configurations shown in Figure 2 and Figure 4, the removed oxygen atoms and the positions of Zr atoms substituted by Mg are illustrated in Figure 3.
The height and width of the peaks indicate an accumulation of defect states that maintain a discrete character, suggesting that the vacancies are spatially separated. This confirms their influence on ionic conductivity.
Figure 5 presents the total and partial density of states (DOS and PDOS) for a zirconia structure containing one magnesium substitutional atom and one oxygen vacancy. The upper part of the valence band is primarily formed by oxygen 2p electrons, while the conduction band is mainly composed of zirconium 4d electrons. As shown in the PDOS, magnesium contributes minimally to the electronic structure of the system, which is consistent with its Mg2+ electronic configuration and the absence of unoccupied d-states.
It is clearly observed that the defect states associated with the oxygen vacancy are in the lower part of the conduction band (approximately 1.3 eV above the Fermi level). The position of the oxygen vacancy state has shifted compared to the undoped system.
Figure 6 shows the total and partial density of states (DOS and PDOS) for a zirconia system containing two oxygen vacancies and two magnesium atoms. As in previous cases, the valence band is mainly formed by oxygen 2p orbitals, while the conduction band consists primarily of zirconium 4d states. The presence of oxygen vacancies leads to the formation of defect levels in the upper part of the band gap, which in this system are located closer to the conduction band edge—approximately 4.5–5.5 eV above the Fermi level.
These defect states exhibit greater intensity than in the case with a single vacancy, indicating a cumulative effect of electron localization as the number of vacancies increases. The contribution of magnesium atoms near the Fermi level remains minimal, confirming their role as compensating dopants that influence charge neutrality but do not directly participate in the formation of the band structure. Thus, double magnesium substitution stabilizes the vacancies, shifting their associated states into the conduction band region.
Figure 7 presents the total and partial density of electronic states (DOS and PDOS) for a zirconia system containing three oxygen vacancies and three magnesium atoms. The total DOS shows a characteristic separation between the valence and conduction bands with a wide band gap. As seen in the PDOS, the contribution from oxygen vacancies forms a clearly defined narrow state located near the bottom edge of the conduction band, approximately 5.5–6.0 eV above the Fermi level.
This indicates that as the concentration of vacancies increases, the energy level of the associated states shifts upward while maintaining a localized character. Additional magnesium substitution compensates for the excess charge, but the contribution from Mg remains minimal in both the valence and conduction bands. Thus, an increase in the number of defects enhances localization effects and may promote the formation of new channels for ionic conduction.
The atomic configurations corresponding to Figure 5, Figure 6 and Figure 7, indicating the removed oxygen atoms and the positions of Zr atoms substituted by Mg, are illustrated in Figure 8.
An analysis of the total and partial density of states (DOS and PDOS) was conducted for ZrO2 systems with one and three oxygen vacancies and varying numbers of Mg atoms. It was shown that the electronic structure is strongly dependent on the defect configuration.
In the system with a single vacancy, a localized state appears below the Fermi level, which may hinder ionic conductivity. The addition of one Mg atom shifts this state above the Fermi level and reduces its intensity, indicating charge compensation and state delocalization, thereby promoting improved oxygen mobility.
With an increase in the number of Mg atoms and vacancies to 2 and 3, further suppression of localized states is observed, while the contribution of Mg to the valence and conduction bands remains minimal, confirming its role as a charge compensator.
In the case of three vacancies without magnesium, pronounced unoccupied states are detected above the Fermi level—an indication of electronic traps. Their disappearance upon Mg introduction highlights the stabilizing effect of substitution.
Thus, configurations with a Mg:VO ratio close to 1:1 are the most effective for enhancing ionic conductivity by eliminating localized states and creating favorable pathways for oxygen migration. The results are consistent with literature data on perovskites [64,65] and emphasize the importance of targeted defect engineering in designing ZrO2-based ion-conducting materials.

3.2. Investigation of Ionic Conductivity

Defects significantly influence the chemical and physical properties of metal oxides. Point and bulk defects often determine their catalytic, electrical, optical, and mechanical activity. Surface oxygen vacancies play a key role in heterogeneous catalysis. The oxygen vacancy formation energy on the surface (Eovac) serves as an important parameter for predicting the catalytic properties of oxide materials.
To model an oxygen vacancy, one oxygen atom was removed from the supercell. The vacancy formation energy was calculated using the following expression:
E F = E d + E O − E p
where EF—is the oxygen vacancy formation energy, Ed—is the total energy of the defective system, EO—is the energy of an isolated oxygen atom, and Ep—is the total energy of the pristine (defect-free) system.
The oxygen vacancy formation energy (Eovac) is an important parameter that determines the catalytic activity of metal oxides. Estimating these energies can support the development of promising catalysts using data-driven approaches. In the present study, Eovac values were determined for c-ZrO2. It is known that Eovac is strongly influenced by the band gap width, lattice formation energy, and electron affinity.
The oxygen vacancy formation energy was calculated as the difference between the total energies of the defective supercell and the ideal crystal, considering the chemical potential of an oxygen atom, defined as the energy of a single O atom in its ground state.
The calculated oxygen vacancy formation energy is 12.6 eV, which is consistent with the typical overestimation of bond strength inherent to hybrid functionals. Since all subsequent calculations (including substitutional defects and defect complexes) were performed using the B3LYP functional, the use of this value ensures methodological consistency and allows for a reliable comparison of the relative energetic characteristics of different configurations.

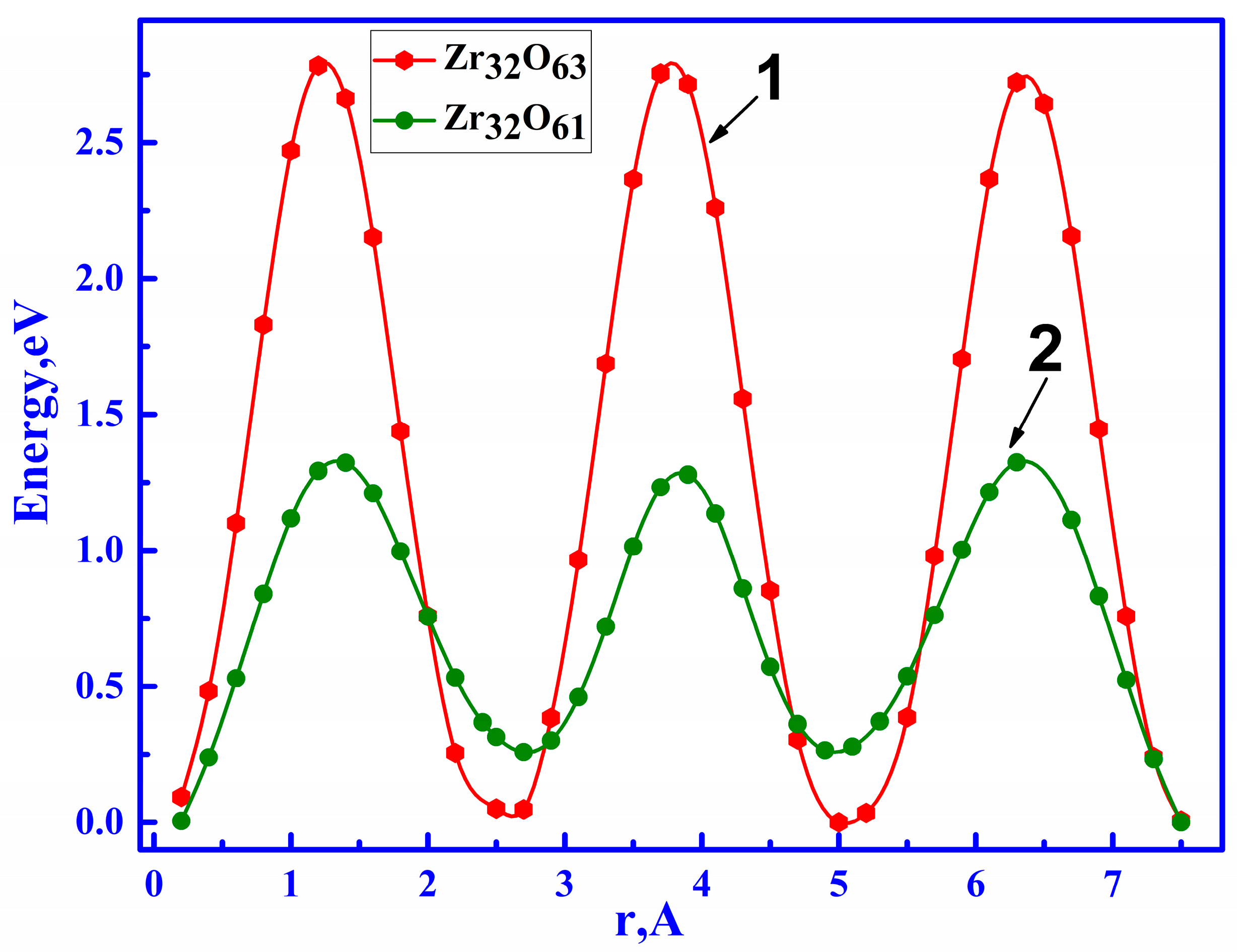
3.2.1. Ionic Conductivity via Oxygen Vacancy-Mediated Oxygen Ion Migration

In this study, we examined the mechanism of oxygen migration in the defective structure of c-ZrO2. A 96-atom supercell was constructed, in which one oxygen atom was initially removed to create a vacancy. Subsequently, an oxygen atom from the upper layer was gradually displaced in 0.2 Å steps until it filled the oxygen vacancy at approximately 2.5 Å. This process was repeated for other layers of the structure (Figure 9, curve 1). At each step, the total energy of the system was calculated.
In the graph presented here and in subsequent analyses, the vertical axis represents the relative total energy of the system. It was found that the system’s energy reaches a minimum when the oxygen atom occupies the vacancy and increases when it is near zirconium atoms. The dependence of the total energy on the oxygen atom’s position exhibits a sinusoidal pattern, indicating the presence of periodic energy barriers and stable configurations within the structure. Figure 9 shows the energy profile along the oxygen ion migration path in defective cubic zirconia (c-ZrO2) through vacancy sites. Curve 1 in Figure 9 corresponds to the migration of an oxygen ion into a single vacancy site (Figure 3a), while curve 2 represents migration through three oxygen vacancies (Figure 3b). The energy maxima observed at distances of 1.2–1.4 Å, 3.7–3.9 Å, and 6.3 Å indicate energy barriers that arise when the oxygen atom passes through a zirconium plane, interacting with Zr atoms and increasing the system’s energy
The energy minimum, observed at 2.5 Å, 5 Å, and 7.5 Å, corresponds to positions where the oxygen atom sequentially occupies vacant sites, leading to system stabilization and energy minimization.
A comparison of the migration barriers for an oxygen ion in a structure with one vacancy (2.7 eV) and along a path with three vacancies (1.32 eV) reveals a reduction of 1.4 eV.
It should be noted that aligning multiple oxygen vacancies along a single trajectory is statistically unlikely. Nevertheless, the results confirm that the formation of oxygen vacancies significantly lowers the energy barriers for oxygen migration, thereby enhancing the material’s ionic conductivity.

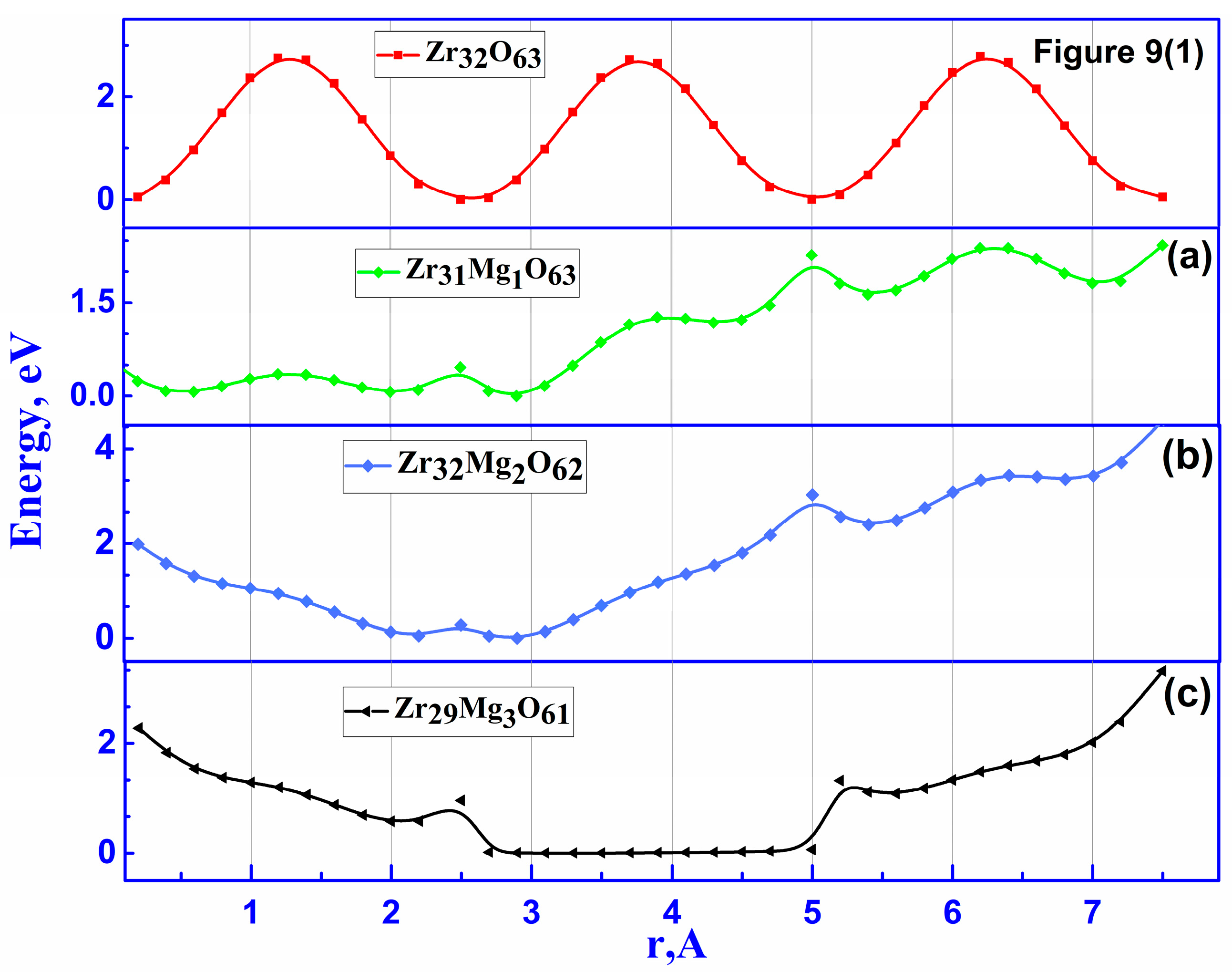
3.2.2. Ionic Conductivity of ZrO2 Stabilized with MgO Aligned Along the Migration Path

To assess the effect of doping on the stability and ionic conductivity of zirconia, the energetic characteristics of systems containing one, two, and three magnesium atoms substituting zirconium atoms near a pre-existing oxygen vacancy were calculated. The total energy of the system consistently decreased with an increasing number of magnesium atoms: −173,907.27 eV for one Mg, −176,028.56 eV for two, and −178,150.40 eV for three, indicating an increase in the thermodynamic stability of complex defects Zr32−xMgxO64−x with higher dopant concentrations. These values are significantly lower than the energy of the system with a single vacancy (−169,733.80 eV) and the undoped system (−1,395,245.93 eV), confirming the energetic favorability of forming complex defects.
The substituting Mg2+ atoms aligned along the oxygen migration path lie in the same (100) crystallographic plane. This arrangement contributes to stabilizing the system containing oxygen vacancies (Figure 8).
In Figure 10a, the profile of the relative total energy during oxygen migration in the Zr31Mg1O63 system (with one Mg atom aligned along the migration path) shows a shift in the positions of energy minima and maxima compared to the undoped structure. The graph illustrates the energy variation as a function of the oxygen ion’s displacement coordinate.
At the points corresponding to vacancies (2.5 Å, 5.0 Å, and 7.5 Å), where deep minima were ideally expected, local maxima are instead observed: 0.462 eV, 2.264 eV, and 2.424 eV, respectively. This indicates that the Mg2+ ion located near the trajectory disrupts the symmetry of the potential curve and distorts the local electrostatic field. In the initial segment (0–2 Å), the energy gradually decreases, reaching a minimum of 0.067 eV at 2.0 Å, but then instead of further decreasing, it rises. At 3.7–3.9 Å and 6.3–6.4 Å, where the oxygen ion passes near zirconium, the energy increases to 1.26 and 2.37 eV, respectively. Similarly, when passing through the Mg-Zr planes (1.2–1.4 Å), the energy is approximately ~0.35 eV, which corresponds to the energy maximum in the undoped system with oxygen vacancies.
From the dependence of the system’s total energy on the distance with one magnesium atom, it is seen that the total energy is lower compared to pure ZrO2, indicating the thermodynamic stability of the defect structure. In the migration within the initial structure with a single oxygen vacancy, the maximum barriers reach ~2.7 eV. Thus, magnesium doping leads to a decrease in the total energy of the system and a reduction in migration barriers, although it is accompanied by a shift in critical points and a disruption of the migration path symmetry.
In Figure 10b, the dependence of the total energy of the system on the oxygen ion migration distance in the Zr30Mg2O62 structure, where two zirconium atoms are replaced by magnesium along the migration path, is shown.
In the interval from 0.2 to 2.5 Å, a monotonic decrease in energy from 1.98 to 0.27 eV is observed with a local minimum of 0.048 eV at 2.2 Å and an absolute minimum (0 eV) at 2.9 Å. The minima at 2.2–2.9 Å are explained by the stable localization of oxygen near the vacancy.
Values at 1.4 Å and 3.9 Å, corresponding to the passage of oxygen through the Mg–Zr and Zr–Zr coordination planes, are characterized by local energy bends: at 1.4 Å, the energy is 0.774 eV, and at 3.9 Å—1.18 eV. This indicates the interaction of oxygen with nearby magnesium and zirconium atoms, creating local distortions in the electrostatic field of the lattice.
At 5.0 Å (the second vacancy), there is a sharp energy rise to 3.03 eV, indicating an increase in the potential energy of the electrostatic field. The oxygen ion exits the potential well corresponding to the vacancy and crosses the zirconium plane (at 5.4 Å—energy 2.39 eV). The maximum barrier of 4.62 eV is observed at 7.5 Å, which is associated with the completion of the migration path.
In Figure 10c, the dependence of the reduced total energy of the Zr29Mg3O61 system corresponding to the oxygen ion migration along a trajectory with three magnesium ions is shown. In the initial region (0.2–2.5 Å), where the ion passes through the magnesium–zirconium planes, the energy gradually decreases from 2.27 eV to 0.96 eV. From 2.7 Å to 4.7 Å, a deep potential well is observed with energy ranging from 0.01664 eV to 0.03447 eV, which corresponds to the ion passing near Mg ions. However, when exiting this region (r > 5 Å), as the oxygen begins to leave the Mg influence zone and approaches the zirconium planes, the energy sharply increases. At 5.2 Å, the energy is 1.32 eV and continues to rise to 3.31 eV at 7.5 Å. Despite the relatively high final barrier, the system with three magnesium atoms exhibits the lowest total energy among all studied configurations, indicating its high stability. This emphasizes that with increasing Mg concentration, the system becomes more stable, but the electrostatic field becomes less symmetric, and the barriers may increase again in certain regions.
The analysis revealed that local substitution of zirconium atoms with magnesium near an oxygen vacancy has a significant impact on both the thermodynamic stability of the structure and the energy profile of oxygen ion migration. As the number of Mg atoms increases, the total energy of the system decreases consistently, indicating the formation of more stable configurations: −173,907.27 eV (1 Mg), −176,028.57 eV (2 Mg), −178,150.4 (3 Mg).
However, migration energy profiles exhibit a complex dependence on the number and arrangement of the dopant atoms (Table 2). With one Mg atom, the energy barriers shift but remain moderate compared to the undoped system (2.7 eV). In the case of two Mg atoms, deep potential wells are formed, but the end of the migration path shows a sharp energy increase up to 4.62 eV, indicating hindered migration. The third configuration, with three Mg atoms, offers the best stabilization of oxygen near the vacancy (energies ~0 eV), but is also accompanied by a rise in the energy barrier to 3.3 eV at the later stage of migration.
Thus, optimal ionic conductivity is achieved by balancing the number and spatial arrangement of dopant atoms: excessive magnesium can enhance local stabilization but may disrupt the uniformity of the migration channel, increasing energy barriers at the final stages of migration.

3.2.3. Ionic Conductivity of ZrO2 Stabilized with MgO with Spatially Distributed Mg Ions

As a continuation of the investigation into the effect of magnesium doping on ionic conductivity in cubic zirconia (c-ZrO2), a series of models were examined in which Mg atoms substituted zirconium atoms outside the oxygen ion migration trajectory. In the structures with Mg doping positioned away from the migration path, the magnesium atoms replace zirconium in various planes, primarily oriented along (001) and (100). Two Mg2+ ions are localized within the same (001) plane at z = 2.5645 Å, while the first Mg atom is displaced to the plane at z = 7.6936 Å, corresponding to another parallel (001) plane. This arrangement of magnesium ions, removed from the migration trajectory, eliminates their direct interaction with oxygen vacancies and limits their effect on the total system energy to background electrostatic influences (Figure 11).
Three configurations were selected for calculation: Zr31Mg1O63, Zr30Mg2O62, and Zr29Mg3O61, in which one, two, and three Mg atoms, respectively, substitute zirconium atoms outside the oxygen ion migration path, thus avoiding direct interaction with vacancies. The total energies of these systems were −173,905.54 eV, −176,760.58 eV, and −178,149.75 eV, respectively. This indicates that increasing MgO concentration contributes to thermodynamic stabilization.
From Figure 12a, corresponding to the Zr31Mg1O63 configuration, the overall shape of the energy profile resembles the energy variation during oxygen ion migration via vacancies. The minimum energy is observed at 2.85 Å and equals 0 eV, indicating the position of the oxygen vacancy.
At other points, such as 1.2–1.4 Å, the energy reaches 0.92 and 0.90 eV, respectively, while near 3.65–3.85 Å, maxima of 0.99–1.01 eV are observed, despite the absence of direct interaction from the Mg atom. Further along, at 5.85–6.25 Å, the energy rises again to 0.94–1.12 eV.
This behavior indicates that the Mg atom, located outside the migration path, does not exert a significant stabilizing effect on the migration trajectory but does alter the electrostatic field. In contrast to the case where Mg ions are aligned along the migration path, the graph displays a sinusoidal pattern, and the peak energy values do not exceed 1.12 eV.
Figure 12b shows the dependence of the reduced total energy of the system corresponding to the Zr30Mg2O62 configuration, in which two magnesium atoms substitute zirconium atoms outside the migration path. At distances corresponding to the position of the vacancy, small potential barriers are observed. The minimum energy is reached at 2.9 Å and equals 0 eV, while the maximum occurs at distances of 1.2 Å (1.3 eV), 3.8 Å (0.85 eV), 5.0 Å (1.1 eV), 6.4 Å (1.3 eV), and 7.5 Å (1.1 eV). The placement of Mg2+ outside the migration path reduces the height of the energy barrier compared to when Mg2+ is located along the path.
Figure 12c shows the dependence of the reduced total energy of the system corresponding to the Zr29Mg3O61 configuration. Here, three magnesium atoms substitute for zirconium outside the oxygen migration path. The energy along the trajectory fluctuates within 0.0–1.05 eV, with an absolute minimum at 2.9 Å (0 eV), corresponding to the position of the oxygen vacancy. Additional energy minima are observed at 0.2 Å (0.05 eV), 2.2 Å (0.13 eV), and 5.4–5.6 Å (~0.26 eV), indicating stabilization of the oxygen ion near these points. Maxima are observed at 1.2 Å (1.01 eV), 2.5 Å (0.5 eV), 3.7 Å (0.9 eV), 5.0 Å (1.05 eV), 6.4 Å (0.85 eV), and 7.5 Å (1.05 eV), indicating moderate energy barriers. Thus, introducing three Mg atoms outside the migration path preserves the symmetry of the electrostatic field and lowers the energy amplitude, providing a stable oxygen migration pathway.
The analysis of the influence of magnesium substitutions on the total energy of the oxygen migration system in the ZrO2 structure has shown that the nature and effectiveness of the modification directly depend on both the number of Mg2+ ions and their spatial arrangement relative to the migration pathway.
When magnesium ions are located outside the migration trajectory, the variation in the normalized total energy becomes smooth, and the maximum energy barriers are 0.9 eV and 1.3 eV, respectively (Table 3). The results of the performed calculations show that the spatial positioning of the implanted magnesium ions outside the migration path significantly reduces the height of the potential barriers. Overall, increasing the number of Mg2+ ions, when optimally positioned either along or outside the trajectory, contributes to a decrease in the energy barriers.

4. Discussion

The creation of a single oxygen vacancy in cubic ZrO2 leads to the formation of defect levels within the band gap and a reduction in the energy barrier for oxygen ion migration. A particularly significant factor is the presence of lattice oxygen atoms along the migration pathway—when these are absent, the barrier is considerably reduced, facilitating ionic conductivity. These findings are consistent with theoretical studies that emphasize the critical role of vacancies in zirconia-based oxide systems [66,67].
When zirconium atoms are substituted with magnesium along the oxygen migration pathway, stable complex defects are formed, as evidenced by the consistent decrease in the system’s total energy with increasing Mg content. However, the migration energy profiles exhibit a nonlinear dependence on the number and position of dopant atoms along the channel. For instance, with one Mg atom, a moderate reduction in the barrier to 1.27 eV is observed; with two Mg atoms, a sharp increase in the primary barrier to 3.03 eV occurs midway through the path; and with three Mg atoms, the most balanced behavior is achieved—a continuous channel is formed with nearly zero energy and moderate barriers of 0.96–1.32 eV, providing optimal conditions for migration. These differences are explained by local lattice distortions and charge redistribution induced by different doping configurations along the channel [68].
In contrast, substituting zirconium with magnesium outside the oxygen migration pathway also leads to a decrease in the system’s total energy with increasing Mg content but does not cause significant changes in the migration energy landscape. With two and three substitutions outside the migration channel, the barriers remain moderate (with a maximum of 0.96–1.3 eV), the profile maintains symmetry, and no sharp local distortions are observed. This indicates that such doping exerts only a background electrostatic effect and smooths the potential landscape. Similar conclusions are presented in studies on the role of vacancies and their correlation with doping in oxide systems [67].
Table 4 summarizes the relative energies (ΔE) of different defect configurations in cubic ZrO2, calculated with respect to the ideal Zr32O64 supercell. The results show that the creation of oxygen vacancies alone leads to an increase in the total energy, indicating destabilization of the structure. In contrast, substitution of Zr by Mg in combination with oxygen vacancies significantly lowers the system energy, thus stabilizing the defective configurations. A comparison between Mg atoms placed along the migration pathway and outside of it demonstrates that the “along pathway” configurations are slightly more favorable, with energy differences of less than 3 eV depending on the number of Mg substitutions.
In contrast, Mg substitution along with the migration trajectory can either enhance or hinder conductivity, depending on the number and distribution of the substitutions. Considering the experimental impossibility of aligning Mg substitutions strictly along a specific migration channel direction, the most effective approach is to introduce the maximum possible amount of Mg substitutions throughout the crystal volume in combination with oxygen vacancies. This strategy enables the formation of a continuous, energetically favorable path for oxygen migration. These conclusions align with computational results on perovskites, where the importance of coordinated defect structure tuning for achieving high ionic conductivity is emphasized [69], as well as with modeling studies demonstrating the impact of rhodium and silver doping on oxygen behavior in oxide and perovskite systems [70,71,72], and the significance of the local electronic environment near vacancies and color centers in fluoride [73,74] and oxides [75,76,77].
It should be noted that all calculations presented here were performed at 0 K and therefore do not account for the direct influence of thermal vibrations on the migration barriers. At elevated temperatures typical for solid oxide fuel cells (800–1200 K), thermal fluctuations reduce the absolute values of the barriers and accelerate oxygen transport. Nevertheless, as shown in molecular dynamics studies [78,79], the relative trends induced by defects and substitutions are preserved even at high temperatures. Therefore, the DFT results at 0 K can be regarded as a reliable baseline for analyzing the impact of vacancies and substitutions on ionic conductivity in ZrO2.

5. Conclusions

The obtained results are of great importance for understanding the mechanisms of crystalline structure stabilization in ZrO2 and can be applied in the development of materials for solid oxide fuel cells (SOFCs) and oxygen sensors.
Thus, the main objective of this study has been achieved. A fundamental relationship has been established between the number and spatial distribution of magnesium substitutions and the shape of the energy landscape for oxygen migration. The findings confirm that controlled defect distribution (vacancies and substitutions) is a key factor in optimizing ionic conductivity in zirconia, opening new prospects for the targeted design of solid oxide electrolytes and sensing materials.

Author Contributions

Conceptualization, Z.M.S., G.B.B. and A.I.P.; methodology, Z.M.S., G.B.B., A.I.P., E.P. and M.K.; software, Z.M.S., G.B.B. and R.N.K.; validation, R.N.K. and K.B.Z.; formal analysis, K.B.Z.; investigation, Z.M.S., G.B.B., R.N.K., E.P. and M.K.; writing—original draft preparation Z.M.S., G.B.B., R.N.K. and K.B.Z.; writing—review and editing Z.M.S., A.I.P., G.B.B., E.P. and M.K.; visualization, R.N.K.; supervision, project administration, Z.M.S. and A.I.P.; funding acquisition, Z.M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP19680240). In addition, M. K and A.I.P. were supported by EUROfusion Enabling Research Project ENR-MAT.02. ISSP-UL- “New dielectric functional materials and interfaces (DFMI)—Theoretical and Experimental analysis.” This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). The views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.

Data Availability Statement

The data will be available upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
DFTDensity functional theory
DOSA function that describes the number of electronic states at each energy level that are available to be occupied in a system.
PDOSA decomposition of the total DOS into contributions from specific atoms or orbitals helps to understand which atoms or orbitals contribute to particular energy levels.
B3LYPA hybrid Density Functional Theory (DFT) functional that combines Becke’s three-parameter exchange functional with the Lee-Yang-Parr correlation functional.

References

  1. Danilov, V.P.; Borisova, E.S.; Shukshin, V.E.; Runina, K.I.; Strekalov, P.V.; Mayakova, M.N.; Petrova, O.B. Structure and optical properties of ZrO2–Sc2O3 solid solution system obtained by the coprecipitation method. Glass Ceram. 2025, 81, 428–437. [Google Scholar] [CrossRef]
  2. Sathya, A.; Anburaj, D.B.; Porkalai, V.; Muthuvel, A.; Al-Zaqri, N. Hydrothermal synthesis of ZrO2 nanoparticles: Study on structural, optical, morphology properties, and photocatalyst activity. Phys. Solid State 2025, 67, 196–206. [Google Scholar] [CrossRef]
  3. Fu, S.; Zhang, J.; Chen, X.; Wang, Z.; Zhao, Y. Oxygen defect-rich CeO2−x@ZrO2 Mott–Schottky electrocatalyst with tunable interfacial charge redistribution for accelerated sulfur redox kinetics in lithium–sulfur batteries. Chem. Eng. J. 2025, 512, 162371. [Google Scholar] [CrossRef]
  4. Jin, H.-B.; Zhang, Z.-H.; Ma, P.; Li, H.-B. Synergically enhancing lithium-ion storage performance of silicon anode by designing shelled structure with reduced graphene oxide and ZrO2. Rare Met. 2025, 44, 2393–2404. [Google Scholar] [CrossRef]
  5. Jammee, R.; Kolganov, A.; Groves, M.C.; Pidko, E.A.; Sydora, O.L.; Conley, M.P. C–H bond activation by sulfated zirconium oxide is mediated by a sulfur-centered Lewis superacid. Angew. Chem. Int. Ed. 2024, 63, e202421699. [Google Scholar] [CrossRef]
  6. Florez, J.; Diaz-Uribe, C.E.; Vallejo, W.; Duran, F.; Puello, E.; Salazar, J.; Zarate, X.; Schott, E. Study of methylene blue removal and photocatalytic degradation on zirconia thin films modified with Mn-Anderson polyoxometalates. Dalton Trans. 2025, 54, 2471–2482. [Google Scholar] [CrossRef] [PubMed]
  7. Han, W.; Lin, L.; Cen, Z.; Ke, Y.; Xu, Q.; Zhu, J.; Mei, X.; Xia, Z.; Zheng, X.; Wang, Y.; et al. Production of branched alkanes by upcycling of waste polyethylene over controlled acid sites of SO4/ZrO2–Al2O3 catalyst. Angew. Chem. Int. Ed. 2025, 64, e202417923. [Google Scholar] [CrossRef]
  8. Huang, Q.A.; Cao, Y.; Satou, K.; Murayama, H.; Yoshizawa, A.; Yamamoto, E.; Nakayama, A.; Ishida, T.; Kitagawa, Y.; Ishimaru, Y.; et al. Active and stable Au/ZrO2 catalysts for isomerization of allylic esters: A practical application of heterogeneous gold catalysis. Appl. Catal. B Environ. Energy 2025, 373, 125351. [Google Scholar] [CrossRef]
  9. Yang, Z.; Liu, T.; Wang, H.; Zhang, Z.; Yin, H.; Wang, S.; Waterhouse, G.I.N.; Wang, X.; Ma, C.; Li, P. Synergistic Adsorption-Catalysis Regulation Effect for Carbon Dioxide Over Hierarchically-Structured Cu/Zro2 Nts; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
  10. Luo, J.; Yao, C.; Zhou, Y.; Qian, Y.; Wang, L.; Lu, C.; Li, X. Facile Oxygen Functionalization Strategy for Mediating the Activity–Stability Trade-Off for Metal Encapsulated Catalysts. Surf. Interfaces 2025, 72, 107209. [Google Scholar] [CrossRef]
  11. Li, M.; Wang, S.; Dong, M.; Wang, J.; Fan, W. Effect of metal-support interaction on catalytic performance of Pd/ZrOx in CO2 hydrogenation to formate. Chem. Res. Chin. Univ. 2025, 41, 529–538. [Google Scholar]
  12. Lee, S.H.; Lee, T.Y.; Lim, H.H.; Cho, J.W.; An, C.; Chae, S.C. Symmetry engineering in antiferroelectric ZrO2 thin films via split-up behavior. ACS Appl. Electron. Mater. 2025, 7, 2146–2152. [Google Scholar] [CrossRef]
  13. Wang, J.; Yang, X.; Song, X.-F.; Li, C.; Zhu, H.-F. The influence of Ce element doping on the mechanical properties of ZrO2 ceramic from first-principles calculations. Solid State Ion. 2025, 424, 116865. [Google Scholar] [CrossRef]
  14. Yuan, J.; Dai, J.-Q.; Zhao, M.-W.; Zhong, Y.-Y.; Deng, D.-W. First-principles study on thermodynamic stability and electronic structures of the ferroelectric binary HfO2 and ZrO2 (001) polar surfaces. Surf. Interfaces 2025, 42, 105523. [Google Scholar] [CrossRef]
  15. Kadyrzhanov, K.K.; Kozlovskiy, A.A.; Konuhova, M.; Popov, A.I.; Shlimas, D.D.; Borgekov, D.B. Determination of gamma radiation shielding efficiency by radiation-resistant composite ZrO2–Al2O3–TiO2–WO3–Nb2O5 ceramics. Opt. Mater. 2024, 154, 115752. [Google Scholar] [CrossRef]
  16. Kozlovskiy, A.L.; Konuhova, M.; Shlimas, D.I.; Borgekov, D.B.; Zdorovets, M.V.; Shakirziyanov, R.I.; Garanin, Y.A.; Volodina, N.O.; Popov, A.I. Study of the effect of nanostructured grains on the radiation resistance of zirconium dioxide ceramics during gas swelling under high-dose irradiation with helium ions. ES Mater. Manuf. 2024, 24, 1165. [Google Scholar] [CrossRef]
  17. Kenzhina, I.E.; Kozlovskiy, A.L.; Begentayev, M.; Blynskiy, P.; Tolenova, A.; Popov, A.I. Study of phase transformations in ZrO2 ceramics stabilized by Y2O3 and their role in changing strength characteristics and heat resistance. Sustainability 2025, 17, 4284. [Google Scholar] [CrossRef]
  18. Kozlovskiy, A.L.; Konuhova, M.; Borgekov, D.B. Study of irradiation temperature effect on radiation-induced polymorphic transformation mechanisms in ZrO2 ceramics. Opt. Mater. 2024, 156, 115994. [Google Scholar] [CrossRef]
  19. Imanova, G. Modeling defect formation in nano-ZrO2 under He and H+ irradiation. Mod. Phys. Lett. B 2024, 38, 2450206. [Google Scholar] [CrossRef]
  20. Costantini, J.M.; Gutierrez, G.; Lelong, G.; Guillaumet, M.; Rahman, M.M.; Yasuda, K. Raman spectroscopy study of damage in swift heavy ion-irradiated ceramics. J. Raman Spectrosc. 2022, 53, 1614–1624. [Google Scholar] [CrossRef]
  21. Liu, Y.; Zhu, Y.; Shen, T.; Chai, J.; Niu, L.; Li, S.; Jin, P.; Zheng, H.; Wang, Z. Irradiation response of Al2O3–ZrO2 ceramic composite under He ion irradiation. J. Eur. Ceram. Soc. 2021, 41, 2883–2891. [Google Scholar] [CrossRef]
  22. Dauletbekova, A.; Zvonarev, S.; Nikiforov, S.; Akilbekov, A.; Shtang, T.; Karavannova, N.; Akylbekova, A.; Ishchenko, A.; Akhmetova-Abdik, G.; Baymukhanov, Z.; et al. Luminescence properties of ZrO2:Ti ceramics irradiated with electrons and high-energy Xe ions. Materials 2024, 17, 1307. [Google Scholar] [CrossRef]
  23. Bandarenka, H.; Burko, A.; Laputsko, D.; Dronina, L.; Kovalchuk, N.; Podelinska, A.; Shapel, U.; Popov, A.I.; Bocharov, D. Ultraviolet exposure improves SERS activity of graphene-coated Ag/ZrO2 substrates. Crystals 2023, 13, 1570. [Google Scholar] [CrossRef]
  24. Nikiforov, S.V.; Kortov, V.S.; Kiryakov, A.N.; Konev, S.F.; Men’shenina, A.A. Increasing the luminescence yield of zirconia. Tech. Phys. Lett. 2017, 43, 1074–1076. [Google Scholar] [CrossRef]
  25. Swami, S.K.; Khan, J.I.; Dutta, V.; Lee, J.; Laquai, F.; Chaturvedi, N. Spray-deposited aluminum-doped zinc oxide as an efficient electron transport layer for inverted organic solar cells. ACS Appl. Energy Mater. 2023, 6, 2906–2913. [Google Scholar] [CrossRef]
  26. Kate, R.S.; Deokate, R.J. Effect of cobalt doping on electrochemical properties of sprayed nickel oxide thin films. Mater. Sci. Energy Technol. 2020, 3, 830–839. [Google Scholar] [CrossRef]
  27. Ricca, C.; Ringuedé, A.; Cassir, M.; Adamo, C.; Labat, F. A comprehensive DFT investigation of bulk and low-index surfaces of ZrO2 polymorphs. J. Comput. Chem. 2015, 36, 9–21. [Google Scholar] [CrossRef] [PubMed]
  28. Shin, H.; Benali, A.; Luo, Y.; Crabb, E.; Lopez-Bezanilla, A.; Ratcliff, L.E.; Jokisaari, A.M.; Heinonen, O. Zirconia and hafnia polymorphs: Ground-state structural properties from diffusion Monte Carlo. Phys. Rev. Mater. 2018, 2, 075001. [Google Scholar] [CrossRef]
  29. Rajesh, G.; Akilandeswari, S.; Govindarajan, D.; Thirumalai, K. Enhancement of photocatalytic activity of ZrO2 nanoparticles by doping with Mg for UV light photocatalytic degradation of methyl violet and methyl blue dyes. J. Mater. Sci. Mater. Electron. 2020, 31, 4058–4072. [Google Scholar] [CrossRef]
  30. Marfin, A.Y.; Nikiforov, S.V.; Ananchenko, D.V.; Zyryanov, S.S.; Yakovlev, G.A.; Denisov, E.I. Thermoluminescence of monoclinic ZrO2 after electron irradiation. AIP Conf. Proc. 2022, 2466, 030012. [Google Scholar]
  31. Sredojević, D.; Lazić, V.; Pirković, A.; Periša, J.; Murafa, N.; Spremo-Potparević, B.; Živković, L.; Topalović, D.; Zarubica, A.; Krivokuća, M.J.; et al. Toxicity of silver nanoparticles supported by surface-modified zirconium dioxide with dihydroquercetin. Nanomaterials 2022, 12, 3195. [Google Scholar] [CrossRef]
  32. Osinkin, D.A.; Antonova, E.P.; Lesnichyova, A.S.; Tropin, E.S.; Chernov, M.E.; Chernov, E.I.; Farlenkov, A.S.; Khodimchuk, A.V.; Eremin, V.A.; Kovrova, A.I.; et al. Application of promising electrode materials in contact with a thin-layer ZrO2-based supporting electrolyte for solid oxide fuel cells. Energies 2020, 13, 1190. [Google Scholar] [CrossRef]
  33. Qi, S.; Porotnikova, N.M.; Ananyev, M.V.; Kuzmin, A.V.; Eremin, V.A.; Pankratov, A.A.; Molchanova, N.G.; Reznitskikh, O.G.; Farlenkov, A.S.; Vovkotrub, E.G.; et al. High-temperature glassy-ceramic sealants SiO2–Al2O3–BaO–MgO and SiO2–Al2O3–ZrO2–CaO–Na2O for solid oxide electrochemical devices. Trans. Nonferrous Met. Soc. China 2016, 26, 2916–2924. [Google Scholar] [CrossRef]
  34. Farlenkov, A.S.; Ananyev, M.V.; Eremin, V.A.; Porotnikova, N.M.; Kurumchin, E.K. Particle coarsening influence on oxygen reduction in LSM–YSZ composite materials. Fuel Cells 2015, 15, 131–139. [Google Scholar]
  35. Nikiforov, S.; Dauletbekova, A.; Gerasimov, M.; Kasatkina, Y.; Denisova, O.; Lisitsyn, V.; Golkovski, M.; Akylbekova, A.; Bazarbek, A.-D.; Akilbekov, A.; et al. Thermoluminescent and dosimetric properties of zirconium dioxide ceramics irradiated with high doses of pulsed electron beam. Crystals 2023, 13, 1585. [Google Scholar] [CrossRef]
  36. Ananchenko, D.V.; Nikiforov, S.V.; Sobyanin, K.V.; Konev, S.F.; Dauletbekova, A.K.; Akhmetova-Abdik, G.; Akilbekov, A.T.; Popov, A.I. Paramagnetic defects and thermoluminescence in irradiated nanostructured monoclinic zirconium dioxide. Materials 2022, 15, 8624. [Google Scholar] [CrossRef]
  37. Borik, M.A.; Bredikhin, S.I.; Bublik, V.T.; Kulebyakin, A.V.; Kuritsyna, I.E.; Lomonova, E.E.; Milovich, P.O.; Myzina, V.A.; Osiko, V.V.; Ryabochkina, P.A.; et al. Structure and conductivity of yttria- and scandia-doped zirconia crystals grown by skull melting. J. Am. Ceram. Soc. 2017, 100, 5536–5547. [Google Scholar] [CrossRef]
  38. Gayathri, P.; Balasubramani, V.; Balraju, P.; Sayed, M.A.; Shkir, M. Ultra-high photosensitivity response in MIS SBDs enabled by Zn-integrated ZrO2@Zn interfacial layers for photovoltaic devices. Phys. B Condens. Matter 2025, 714, 417506. [Google Scholar]
  39. Aboraia, A.M.; Sharaf, I.M.; Alradaddi, S.; Trabelsi, A.B.G.; Alkallas, F.H. Advanced supercapacitors benefit from the electrode material Gd-Enhanced Cubic-ZrO2. Phys. B Condens. Matter 2025, 714, 417519. [Google Scholar]
  40. Cheng, Z.; Ren, H.; Wang, Y.; Ta, S.; Zhang, P.; Yang, Y.; Xu, S.; Goodman, B.A.; Deng, W. Effects of Yb2O3 as stabilizer and sensitizer on the luminescence properties of cubic ZrO2 single crystals. Cryst. Growth Des. 2022, 22, 5481–5488. [Google Scholar]
  41. Thammachart, M.; Meeyoo, V.; Risksomboon, T.; Osuwan, S. Catalytic activity of CeO2–ZrO2 mixed oxide catalysts prepared via sol–gel technique: CO oxidation. Catal. Today 2001, 68, 53–61. [Google Scholar] [CrossRef]
  42. Li, P.; Chen, I.-W.; Penner-Hahn, J.E. Effect of dopants on zirconia stabilization—An X-ray absorption study: II, tetravalent dopants. J. Am. Ceram. Soc. 1994, 77, 1281–1288. [Google Scholar] [CrossRef]
  43. Winczewski, J.P.; Zeiler, S.; Gabel, S.; Maestre, D.; Merle, B.; Gardeniers, J.; Arce, A.S. Additive manufacturing of 3D yttria-stabilized zirconia microarchitectures. Mater. Des. 2024, 238, 112701. [Google Scholar] [CrossRef]
  44. Feng, Y.; Wu, J.; Chi, Q.; Li, W.; Yu, Y.; Fei, W. Recent advances in design and applications of heteroatom-doped carbon with single-atom active sites. Chem. Rev. 2020, 120, 1710–1766. [Google Scholar] [CrossRef]
  45. Haering, C.; Roosen, A.; Schichl, H.; Schnöller, M. Mechanical properties of tape-cast electrolyte substrates for solid oxide fuel cells. Solid State Ion. 2005, 176, 261–268. [Google Scholar] [CrossRef]
  46. King, A.; Singh, R.; Anand, R.; Behera, S.K.; Nayak, B.B. Phase and luminescence behaviour of Ce-doped zirconia nanopowders for latent fingerprint visualisation. Optik 2021, 242, 167087. [Google Scholar] [CrossRef]
  47. Xie, Y.; Ma, Z.; Liu, L.; Su, Y.; Zhao, H.; Liu, Y.; Zhang, Z.; Duan, H.; Li, J.; Xie, E. Enhanced photocatalytic activity in ZrO2–TiO2 nanocomposite films deposited by magnetron sputtering. Appl. Phys. Lett. 2010, 97, 141916. [Google Scholar] [CrossRef]
  48. Furasova, A.D.; Ivanovski, V.; Yakovlev, A.V.; Milichko, V.A.; Vinogradov, V.V.; Vinogradov, A.V. Inkjet fabrication of highly efficient luminescent Eu-doped ZrO2 nanostructures. Nanoscale 2017, 9, 13069–13078. [Google Scholar] [CrossRef] [PubMed]
  49. Winczewski, J.; Herrera, M.; Cabriel, C.; Izeddin, I.; Gabel, S.; Merle, B.; Arce, A.S.; Gardeniers, H. Additive manufacturing of 3D luminescent ZrO2:Eu3+ architectures. Adv. Opt. Mater. 2022, 10, 2102758. [Google Scholar] [CrossRef]
  50. Kurakhmedov, A.E.; Morzabayev, A.K.; Tleubay, I.; Berguzinov, A.; Kozlovskiy, A.L. Study of the mechanisms of polymorphic transformations in zirconium dioxide upon doping with magnesium oxide, as well as establishing the relationship between structural changes and strength properties. Ceramics 2023, 6, 1164–1178. [Google Scholar] [CrossRef]
  51. Malyi, O.I.; Wu, P.; Kulish, V.V.; Bai, K.; Chen, Z. Formation and migration of oxygen and zirconium vacancies in cubic zirconia and zirconium oxysulfide. Solid State Ion. 2012, 212, 117–122. [Google Scholar] [CrossRef]
  52. Kurakhmedov, A.E.; Alin, M.; Temir, A.M.; Ivanov, I.A.; Bikhert, Y.V.; Ungarbayev, Y.O.; Zdorovets, M.V.; Kozlovskiy, A.L. Study of the effect of doping ZrO2 ceramics with MgO to increase the resistance to polymorphic transformations under the action of irradiation. Nanomaterials 2021, 11, 3172. [Google Scholar] [CrossRef]
  53. Perevalov, T.V.; Islamov, D.R. Oxygen polyvacancies as conductive filament in zirconia: First principle simulation. ECS Trans. 2017, 80, 357–362. [Google Scholar] [CrossRef]
  54. Xue, Q.; Huang, X.; Wang, L.; Zhang, H.; Zhang, J. Computational and experimental investigations of defect interaction and ionic conductivity in doped zirconia. Phys. Rev. Appl. 2018, 10, 014032. [Google Scholar] [CrossRef]
  55. Dhingra, A.; Thakur, O.P.; Pandey, R. Structure–property relationship and electronic structure calculation of cubic YSZ solid electrolyte for electrochemical applications. J. Electron. Mater. 2025, 54, 1949–1960. [Google Scholar] [CrossRef]
  56. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
  57. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  58. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  59. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
  60. Erba, A.; Desmarais, J.K.; Casassa, S.; Civalleri, B.; Dona, L.; Bush, I.J.; Searle, B.; Maschio, L.; Edith-Dazr, L.; Cossard, A.; et al. CRYSTAL23: A program for computational solid-state physics and chemistry. J. Chem. Theory Comput. 2022, 19, 6891–6932. [Google Scholar] [CrossRef]
  61. Muhammad, I.D.; Awang, M. Modelling the interatomic potential of cubic zirconia. Appl. Mech. Mater. 2013, 446–447, 151–157. [Google Scholar] [CrossRef]
  62. French, R.H.; Glass, S.J.; Ohuchi, F.S.; Xu, Y.-N.; Ching, W.Y. Experimental and theoretical determination of the electronic structure and optical properties of three phases of ZrO2. Phys. Rev. B 1994, 49, 5133–5142. [Google Scholar] [CrossRef] [PubMed]
  63. Kröger, F.A. The Chemistry of Imperfect Crystals, 2nd ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1974; Volume 2. [Google Scholar]
  64. Li, W.; Sunarso, J.; Yang, Y.; Chen, Y.; Ge, C.; Wang, W.; Guo, Y.; Ran, R.; Zhou, W. Strategies for improving oxygen ionic conducting in perovskite oxides and their practical applications. Energy Rev. 2024, 3, 100085. [Google Scholar] [CrossRef]
  65. Rauf, S.; Hanif, M.B.; Mushtaq, N.; Tayyab, Z.; Ali, N.; Shah, M.Y.; Javed, Q.; Rasool, K.; Khan, M.A.; Xu, W. Modulating the energy band structure of the Mg-doped Sr0.5Pr0.5Fe0.2Mg0.2Ti0.6O3−δ electrolyte with boosted ionic conductivity and electrochemical performance for solid oxide fuel cells. ACS Appl. Mater. Interfaces 2022, 14, 43067–43084. [Google Scholar] [CrossRef] [PubMed]
  66. Kulish, V.V.; Malyi, O.I.; Persson, C.; Wu, P. Evaluation of phosphorene as anode material for Na-ion batteries: A first-principles study. Phys. Chem. Chem. Phys. 2015, 17, 13921–13928. [Google Scholar] [CrossRef]
  67. Hinuma, Y.; Graciani, J.; Stacchiola, D.; Senanayake, S.D.; Rodríguez, J.A.; Ganduglia-Pirovano, M.V. Density functional theory calculations of oxygen vacancy formation and subsequent molecular adsorption on zirconia surfaces. J. Phys. Chem. C 2018, 122, 1687–1696. [Google Scholar] [CrossRef]
  68. Han, Z.-K.; Liu, W.; Gao, Y. Advancing the understanding of oxygen vacancies in ceria: Insights into their formation, behavior, and catalytic roles. JACS Au 2025, 5, 1549–1569. [Google Scholar] [CrossRef]
  69. Emery, A.A.; Wolverton, C. High-throughput DFT calculations of formation energy, stability, and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data 2017, 4, 160124. [Google Scholar] [CrossRef]
  70. Kaptagay, G.A.; Satanova, B.M.; Abuova, A.U.; Konuhova, M.; Zakiyeva, Z.Y.; Tolegen, U.Z.; Koilyk, N.O.; Abuova, F.U. Effect of rhodium doping for photocatalytic activity of barium titanate. Opt. Mater. X 2025, 25, 100382. [Google Scholar] [CrossRef]
  71. Inerbaev, T.M.; Abuova, A.U.; Zakiyeva, Z.Y.; Abuova, F.U.; Mastrikov, Y.A.; Sokolov, M.; Gryaznov, D.; Kotomin, E.A. Effect of Rh doping on optical absorption and oxygen evolution reaction activity on BaTiO3 (001) surfaces. Molecules 2024, 29, 2707. [Google Scholar] [CrossRef]
  72. Abuova, A.U.; Mastrikov, Y.A.; Kotomin, E.A.; Kawazoe, Y.; Inerbaev, T.M.; Akilbekov, A.T. First-principles modeling of Ag adsorption on the LaMnO3 (001) surfaces. Solid State Ion. 2015, 273, 46–50. [Google Scholar] [CrossRef]
  73. Abuova, F.U.; Kotomin, E.A.; Lisitsyn, V.M.; Akilbekov, A.T.; Piskunov, S. Ab initio modeling of radiation damage in MgF2 crystals. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2014, 326, 314–317. [Google Scholar] [CrossRef]
  74. Dauletbekova, A.; Abuova, F.; Akilbekov, A.; Kotomin, E.; Piskunov, S. First-principles modeling of the H color centers in MgF2 crystals. Phys. Status Solidi C 2013, 10, 160–164. [Google Scholar] [CrossRef]
  75. Zhukovskii, Y.F.; Platonenko, A.; Piskunov, S.; Kotomin, E.A. Ab initio simulations on migration paths of interstitial oxygen in corundum. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2016, 374, 29–34. [Google Scholar] [CrossRef]
  76. Kaewmeechai, C.; Strand, J.; Shluger, A.L. Structure and migration mechanisms of oxygen interstitial defects in β-Ga2O3. Phys. Status Solidi B 2025, 263, 2400652. [Google Scholar] [CrossRef]
  77. Usseinov, A.B.; Akilbekov, A.T.; Kotomin, E.A.; Karipbayev, Z.T. First-principles calculations of CO2 adsorption on the (10-10) ZnO surface. AIP Conf. Proc. 2019, 2174, 020181. [Google Scholar] [CrossRef]
  78. Kilo, M.; Argirusis, C.; Borchardt, G.; Jackson, R.A. Oxygen diffusion in yttria-stabilised zirconia—Experimental results and molecular dynamics calculations. Phys. Chem. Chem. Phys. 2003, 5, 2219–2224. [Google Scholar] [CrossRef]
  79. Momenzadeh, L.; Belova, I.V.; Murch, G.E. Analysis of thermotransport and thermal and ionic conductivity in doped lanthanum gallate (LSGM) using molecular dynamics. Solid State Ion. 2022, 377, 115881. [Google Scholar] [CrossRef]
Solids 06 00055 g001
Figure 1. Structure of c-ZrO2.
Figure 1. Structure of c-ZrO2.
Solids 06 00055 g001
Solids 06 00055 g002
Figure 2. DOS (a) and PDOS (b) of Zr32O63.
Figure 2. DOS (a) and PDOS (b) of Zr32O63.
Solids 06 00055 g002
Solids 06 00055 g003
Figure 3. Structure of c-ZrO2 with one oxygen vacancy (a) and with three oxygen vacancies (b) along the oxygen migration path.
Figure 3. Structure of c-ZrO2 with one oxygen vacancy (a) and with three oxygen vacancies (b) along the oxygen migration path.
Solids 06 00055 g003
Solids 06 00055 g004
Figure 4. DOS (a) and PDOS (b) of Zr32O61.
Figure 4. DOS (a) and PDOS (b) of Zr32O61.
Solids 06 00055 g004
Solids 06 00055 g005
Figure 5. DOS (a) and PDOS (b) of Zr31Mg1O63.
Figure 5. DOS (a) and PDOS (b) of Zr31Mg1O63.
Solids 06 00055 g005
Solids 06 00055 g006
Figure 6. DOS (a) and PDOS (b) of Zr30Mg2O62.
Figure 6. DOS (a) and PDOS (b) of Zr30Mg2O62.
Solids 06 00055 g006
Solids 06 00055 g007
Figure 7. DOS (a) and PDOS (b) of Zr29Mg3O61.
Figure 7. DOS (a) and PDOS (b) of Zr29Mg3O61.
Solids 06 00055 g007
Solids 06 00055 g008
Figure 8. Oxygen migration along the trajectory with substitution of one, two, and three Zr atoms by Mg in c-ZrO2.
Figure 8. Oxygen migration along the trajectory with substitution of one, two, and three Zr atoms by Mg in c-ZrO2.
Solids 06 00055 g008
Solids 06 00055 g009
Figure 9. Dependence of the relative total energy of the system on the distance in the c-ZrO2 structure with one oxygen vacancy (1) and three oxygen vacancies (2).
Figure 9. Dependence of the relative total energy of the system on the distance in the c-ZrO2 structure with one oxygen vacancy (1) and three oxygen vacancies (2).
Solids 06 00055 g009
Solids 06 00055 g010
Figure 10. Dependence of the total energy of the system on the oxygen migration distance with substitution of one (a), two (b), and three (c) Zr atoms with Mg in c-ZrO2. The top graph (previously labeled as Figure 9(1)) corresponds to the structure Zr32O63 with one oxygen vacancy.
Figure 10. Dependence of the total energy of the system on the oxygen migration distance with substitution of one (a), two (b), and three (c) Zr atoms with Mg in c-ZrO2. The top graph (previously labeled as Figure 9(1)) corresponds to the structure Zr32O63 with one oxygen vacancy.
Solids 06 00055 g010
Solids 06 00055 g011
Figure 11. Oxygen migration with substitution of one, two, and three Zr atoms by Mg outside the migration trajectory in c-ZrO2.
Figure 11. Oxygen migration with substitution of one, two, and three Zr atoms by Mg outside the migration trajectory in c-ZrO2.
Solids 06 00055 g011
Solids 06 00055 g012
Figure 12. Dependence of the reduced total energy of the system during oxygen migration with substitution of one (a), two (b), and three (c) Zr atoms by Mg in c-ZrO2. The top graph (previously labeled as Figure 9(1)) corresponds to the structure Zr32O63 with one oxygen vacancy.
Figure 12. Dependence of the reduced total energy of the system during oxygen migration with substitution of one (a), two (b), and three (c) Zr atoms by Mg in c-ZrO2. The top graph (previously labeled as Figure 9(1)) corresponds to the structure Zr32O63 with one oxygen vacancy.
Solids 06 00055 g012
Table 1. Local symmetry changes in cubic ZrO2 with oxygen vacancies and Mg substitutions (near and outside vacancy sites).
Table 1. Local symmetry changes in cubic ZrO2 with oxygen vacancies and Mg substitutions (near and outside vacancy sites).
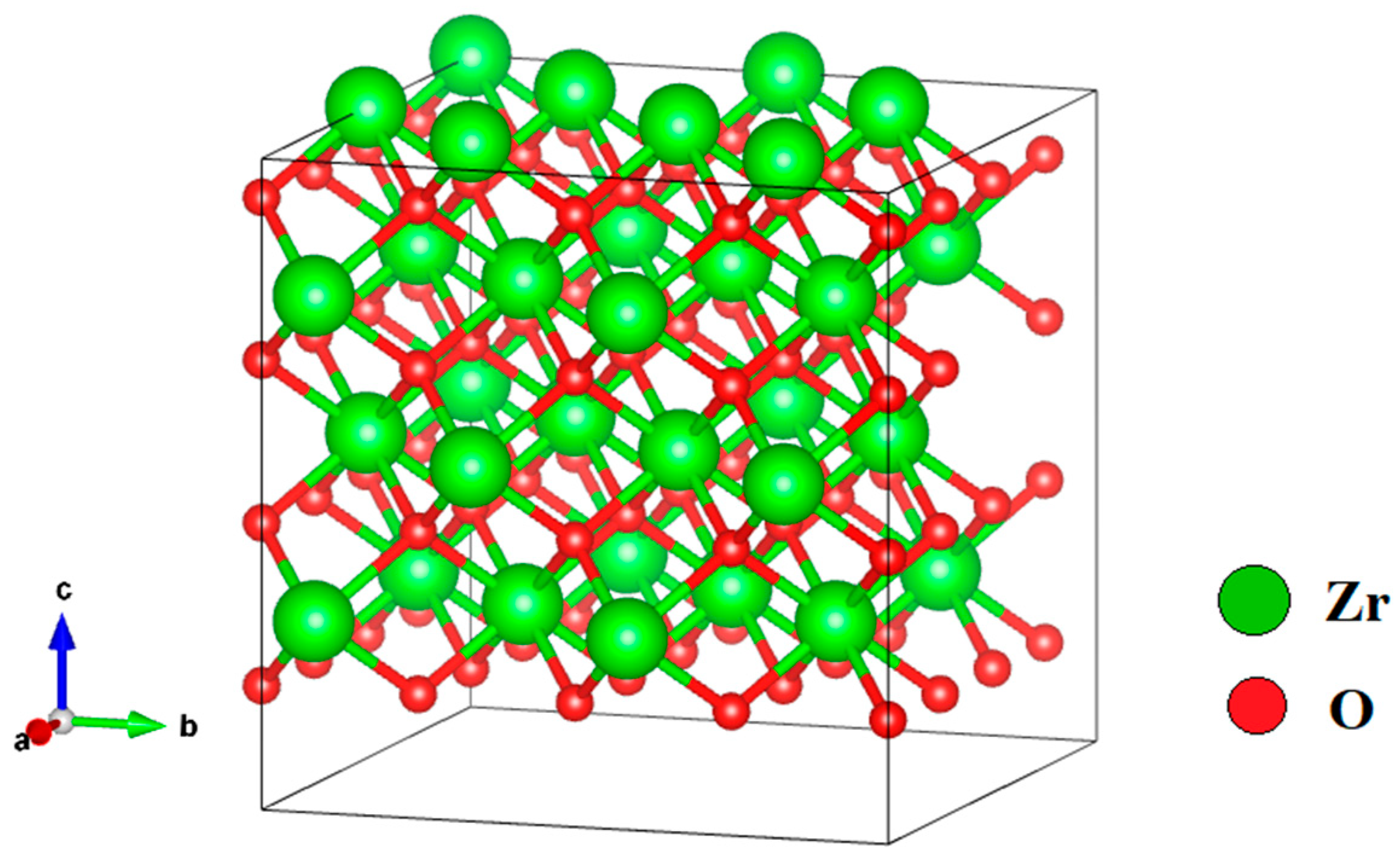
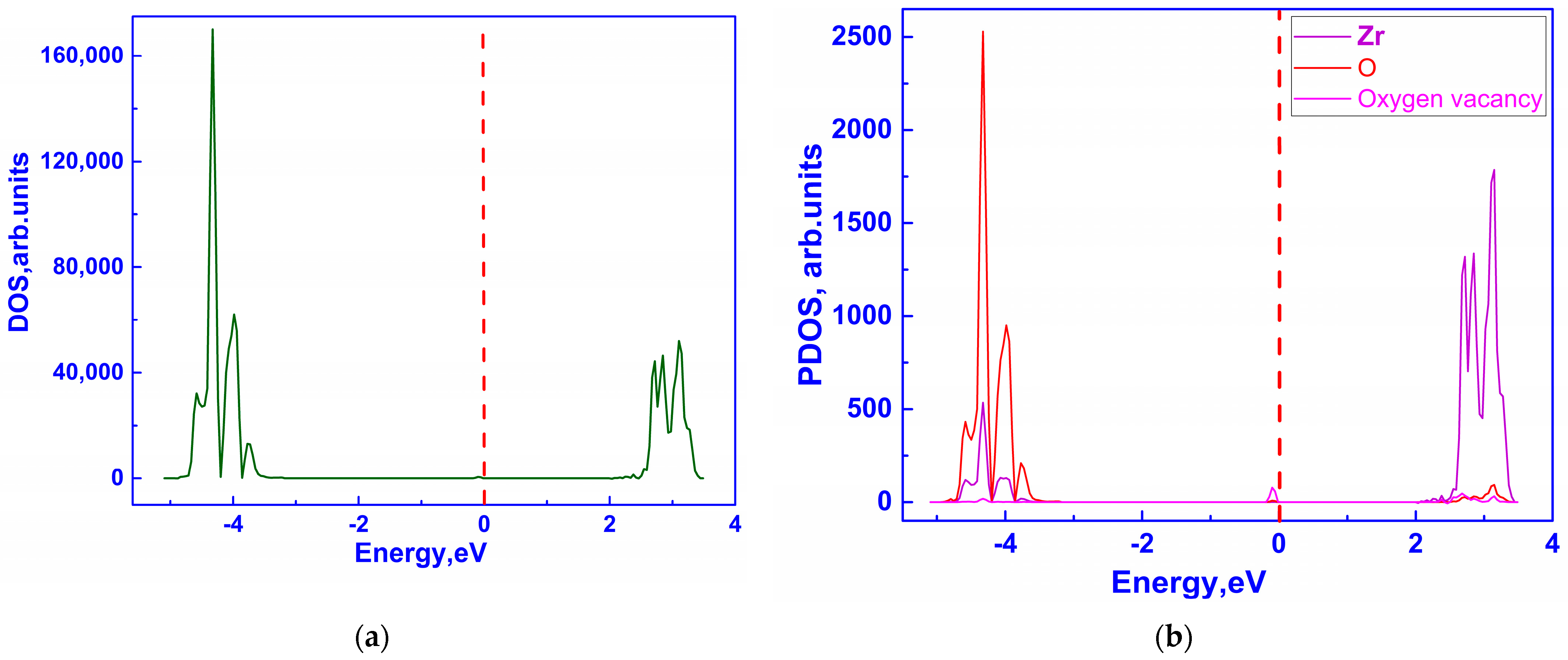
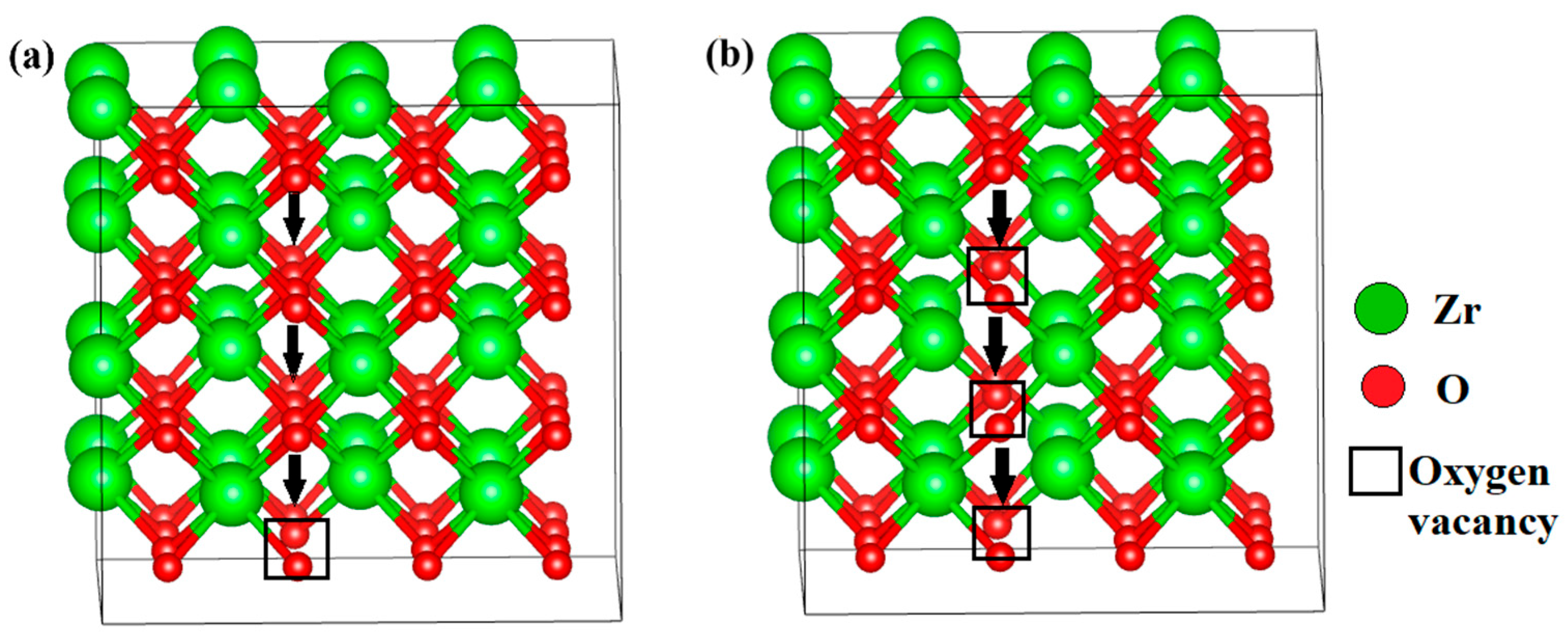
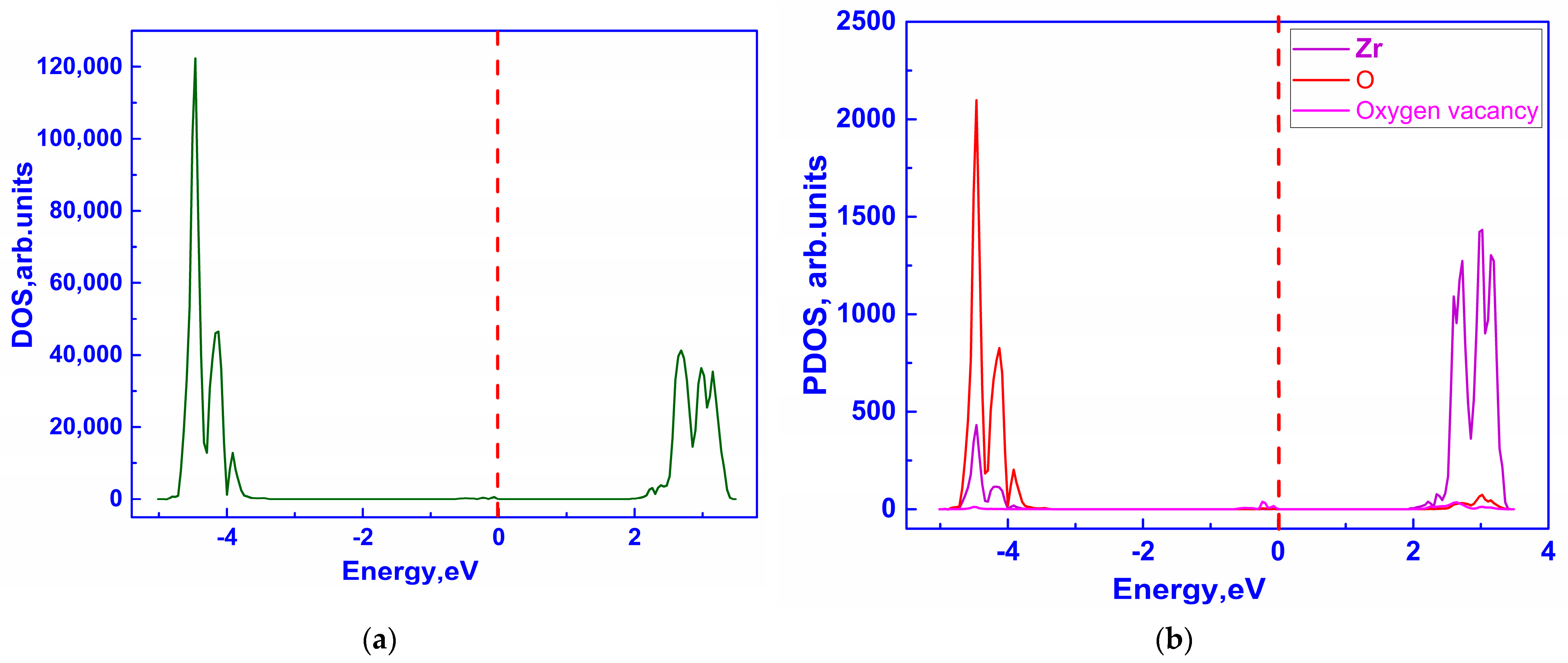
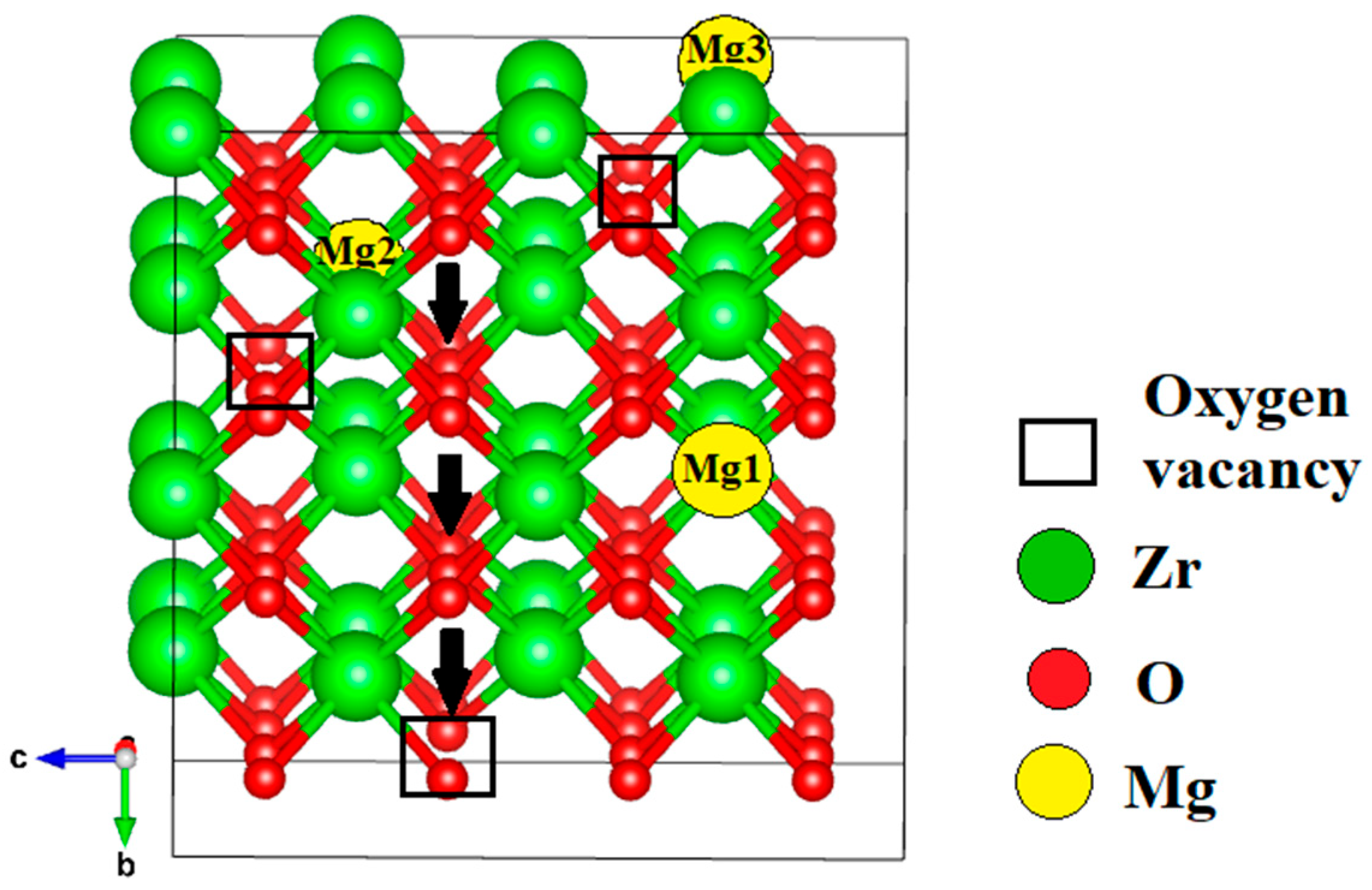
ConfigurationLocal EffectAverage SymmetrySpace GroupLattice Change
Zr32O64 (ideal)Perfect cubic latticeCubicFm-3ma = b = c
Zr32O63 (1 VO)Zr shifts toward vacancy; distortionLocally tetragonalLocal tetragonal/rhombohedralLocal anisotropy
Zr32O61 (3 VO)Vacancy chain ⟨001⟩; elongationTetragonalP42/nmcc/a > 1
Mg near VO (1–3)Mg–VO dipoles; stronger distortions; high Mg restores cubicTetragonal → Cubic-likeP42/nmc → Fm-3mc/a > 1 → ≈ 1
Mg outside VO (1–3)Weak background effect; lattice stableMostly cubicFm-3ma ≈ b ≈ c
Table 2. Energy barriers for oxygen migration in c-ZrO2 with different numbers and arrangements of Mg atoms.
Table 2. Energy barriers for oxygen migration in c-ZrO2 with different numbers and arrangements of Mg atoms.
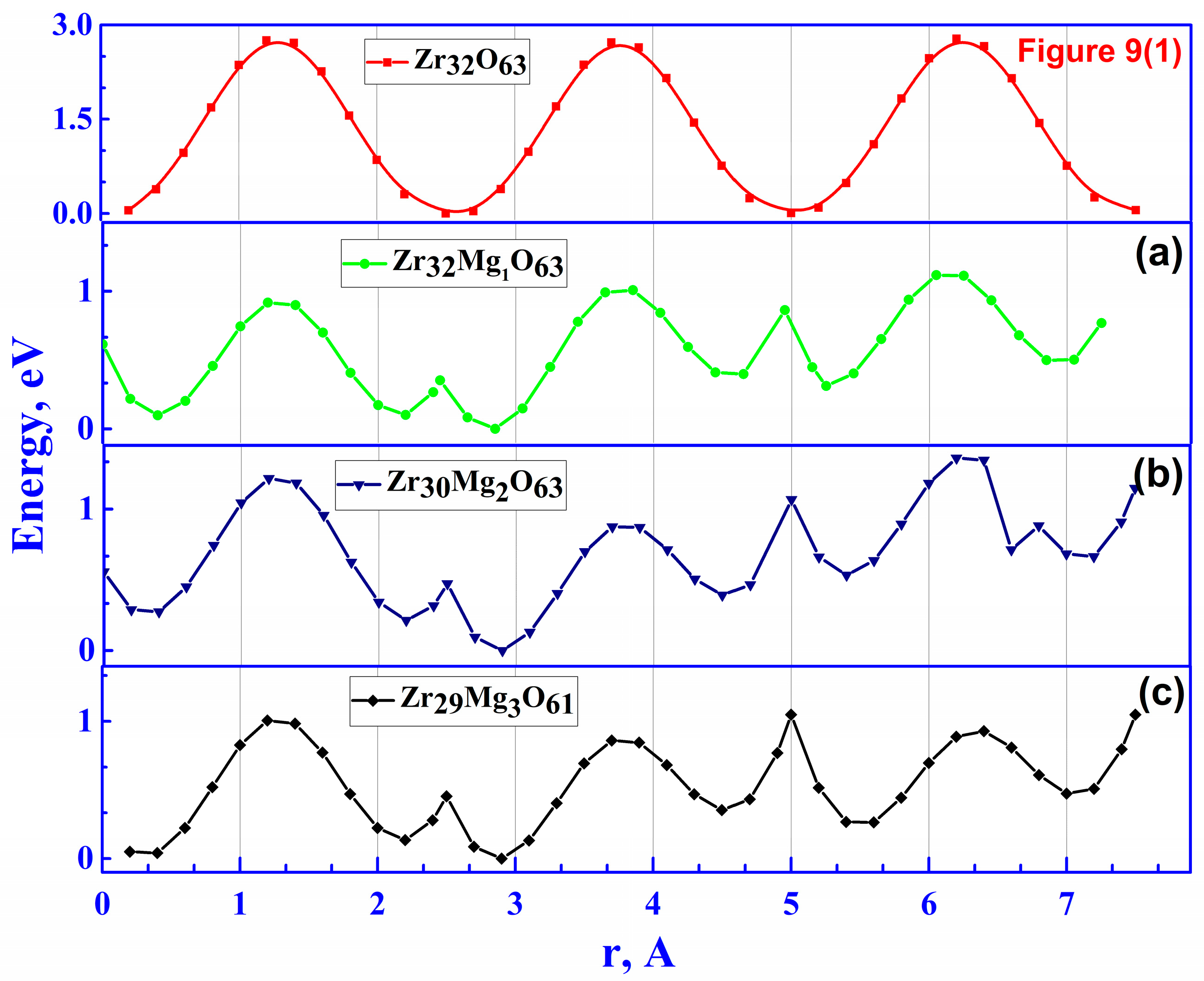
Doping ConfigurationNumber of MgMin. Barrier, eVMax. Barrier, eV
Zr31Mg1O6310.42.4
Zr30Mg2O6220.53.1
Zr29Mg3O6130.81.32
Table 3. Energy Barriers for Oxygen Migration in c-ZrO2 with Different Numbers and Positions of Mg Atoms.
Table 3. Energy Barriers for Oxygen Migration in c-ZrO2 with Different Numbers and Positions of Mg Atoms.
Doping ConfigurationNumber of MgMin. Barrier, eVMax. Barrier, eV
Zr31Mg1O6310.41.12
Zr30Mg2O6220.51.34
Zr29Mg3O6130.51.05
Table 4. Total energies of the ZrO2 system for different numbers of oxygen vacancies and Mg dopants (along and outside the migration pathway).
Table 4. Total energies of the ZrO2 system for different numbers of oxygen vacancies and Mg dopants (along and outside the migration pathway).
ConfigurationMg PositionTotal Energy (eV)ΔE = Econfig − EZr32O64 (eV)
Zr32O64 −171,752.370.00
Zr32O63 −169,742.54+2009.83
Zr32O61 −165,599.06+6153.31
Zr31Mg1O63along pathway−173,916.22−2163.85
Zr30Mg2O62−176,037.62−4285.25
Zr29Mg3O61−178,159.57−6407.20
Zr31Mg1O63outside pathway−173,914.32−2161.95
Zr30Mg2O62−176,034.90−4282.53
Zr29Mg3O61−178,158.75−6406.38
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Salikhodzha, Z.M.; Bairbayeva, G.B.; Popov, A.I.; Kassymkhanova, R.N.; Zhangylyssov, K.B.; Popova, E.; Konuhova, M. DFT Study of Oxygen Ion Migration in Mg-Doped Cubic Zirconia. Solids 2025, 6, 55. https://doi.org/10.3390/solids6040055

AMA Style

Salikhodzha ZM, Bairbayeva GB, Popov AI, Kassymkhanova RN, Zhangylyssov KB, Popova E, Konuhova M. DFT Study of Oxygen Ion Migration in Mg-Doped Cubic Zirconia. Solids. 2025; 6(4):55. https://doi.org/10.3390/solids6040055

Chicago/Turabian Style

Salikhodzha, Zhussupbek M., Guldari B. Bairbayeva, Anatoli I. Popov, Raigul N. Kassymkhanova, Keleshek B. Zhangylyssov, Elena Popova, and Marina Konuhova. 2025. "DFT Study of Oxygen Ion Migration in Mg-Doped Cubic Zirconia" Solids 6, no. 4: 55. https://doi.org/10.3390/solids6040055

APA Style

Salikhodzha, Z. M., Bairbayeva, G. B., Popov, A. I., Kassymkhanova, R. N., Zhangylyssov, K. B., Popova, E., & Konuhova, M. (2025). DFT Study of Oxygen Ion Migration in Mg-Doped Cubic Zirconia. Solids, 6(4), 55. https://doi.org/10.3390/solids6040055

Article Metrics

Back to TopTop