Preliminary Modeling of Single Pulp Fiber Using an Improved Mass–Spring Method
Abstract
1. Introduction
2. Methodology
2.1. Modeling of Single Fiber
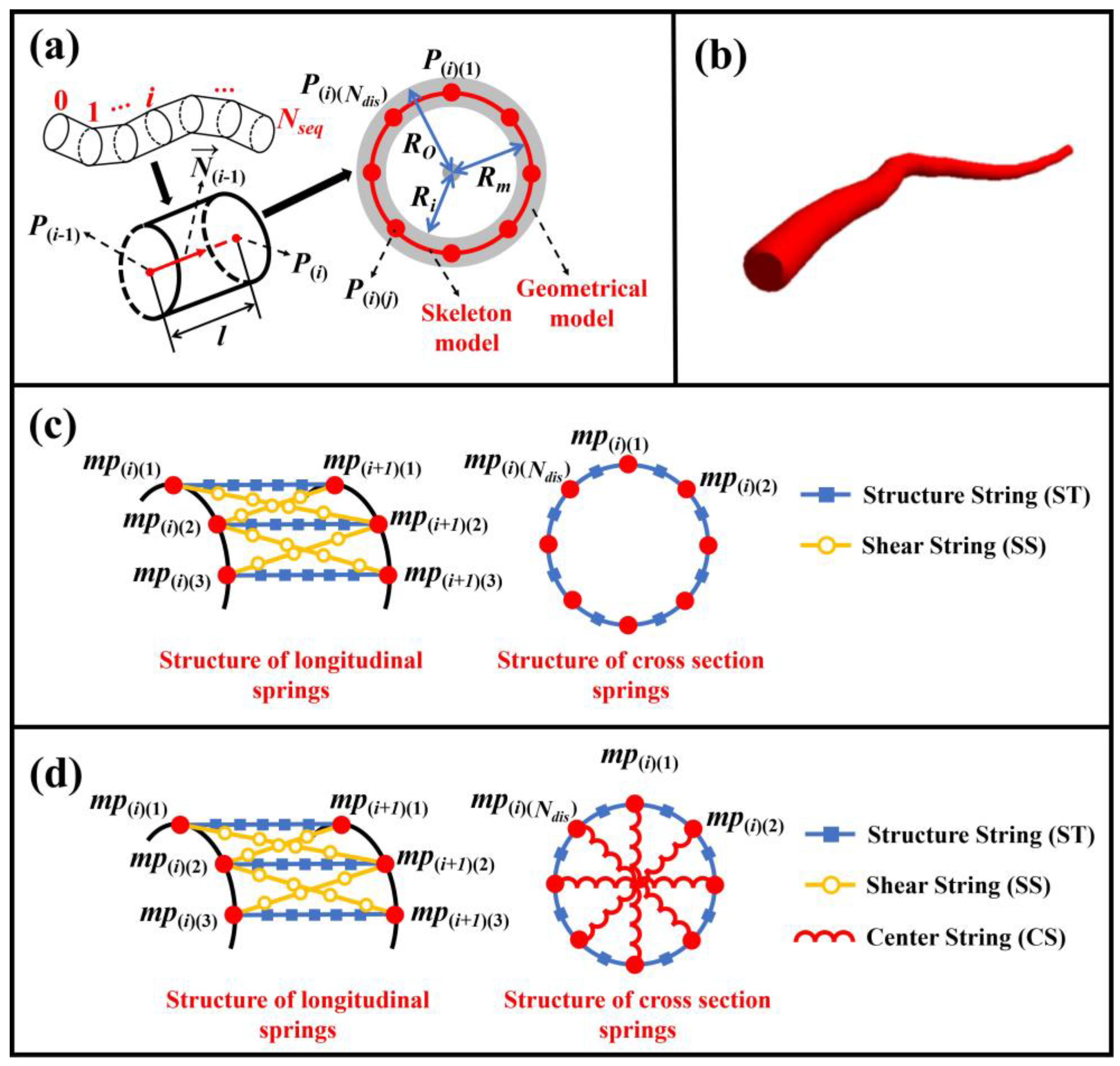
2.1.1. Geometric Model of Single Pulp Fiber
2.1.2. Mass–Spring Model of Single Pulp Fiber
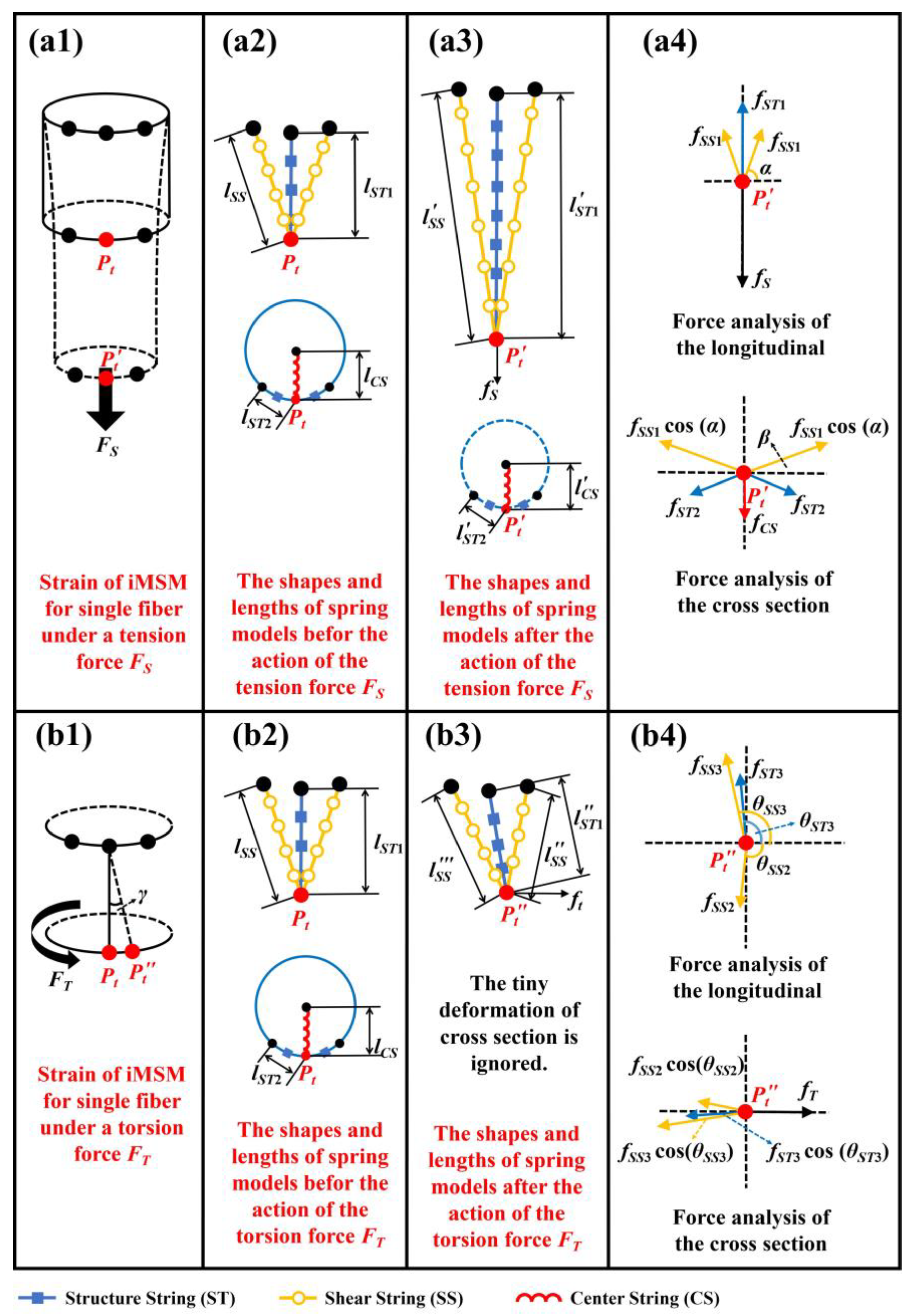
2.1.3. Parameters Calculation Model of iMSM
2.2. Simulating Single Pulp Fiber Properties Based on iMSM
2.2.1. Calculation Model of iMSM
2.2.2. Solving Method of Calculation Model of iMSM
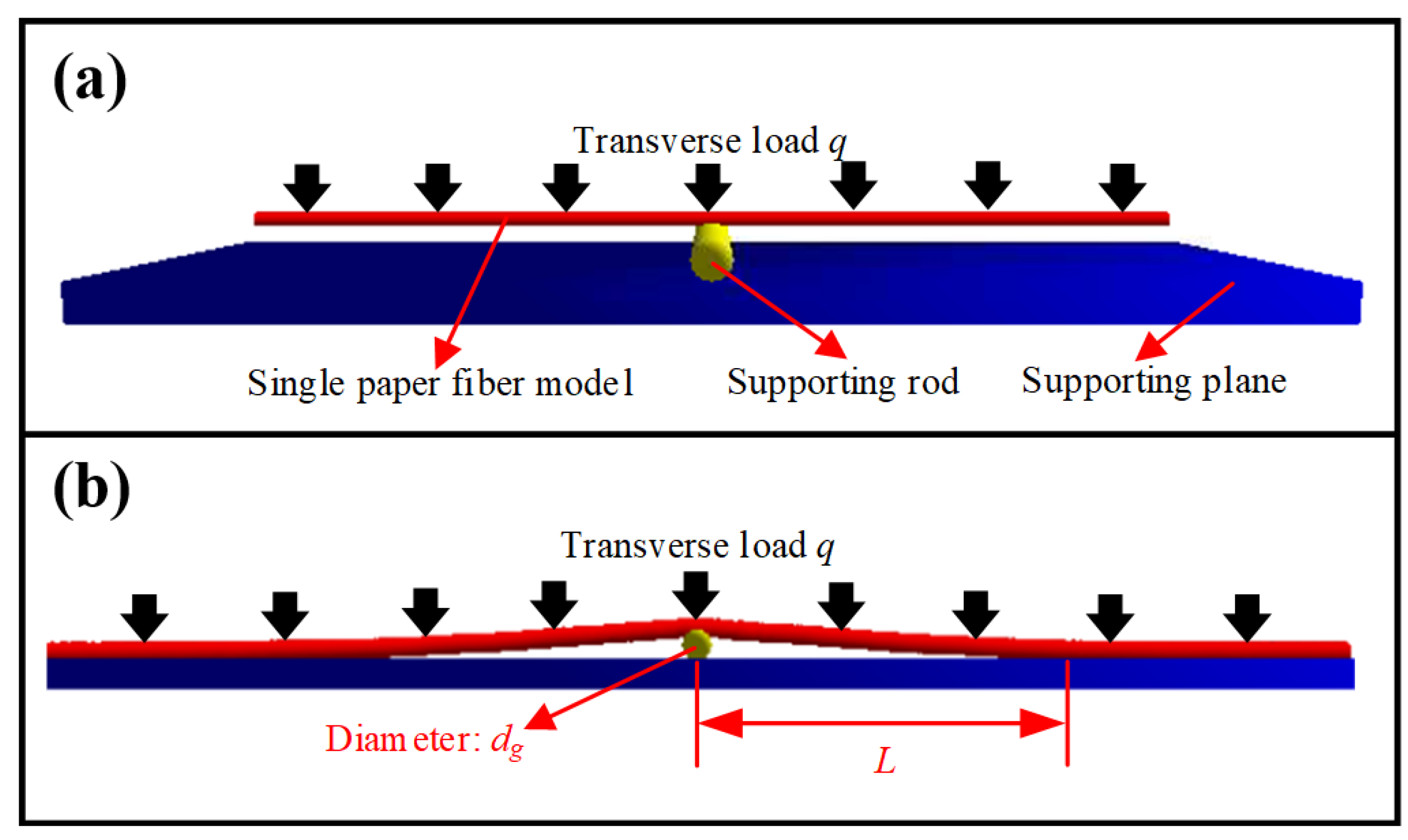
3. Modeling and Simulation of Single Paper Fiber
3.1. Modeling Parameters of Single Paper Fiber
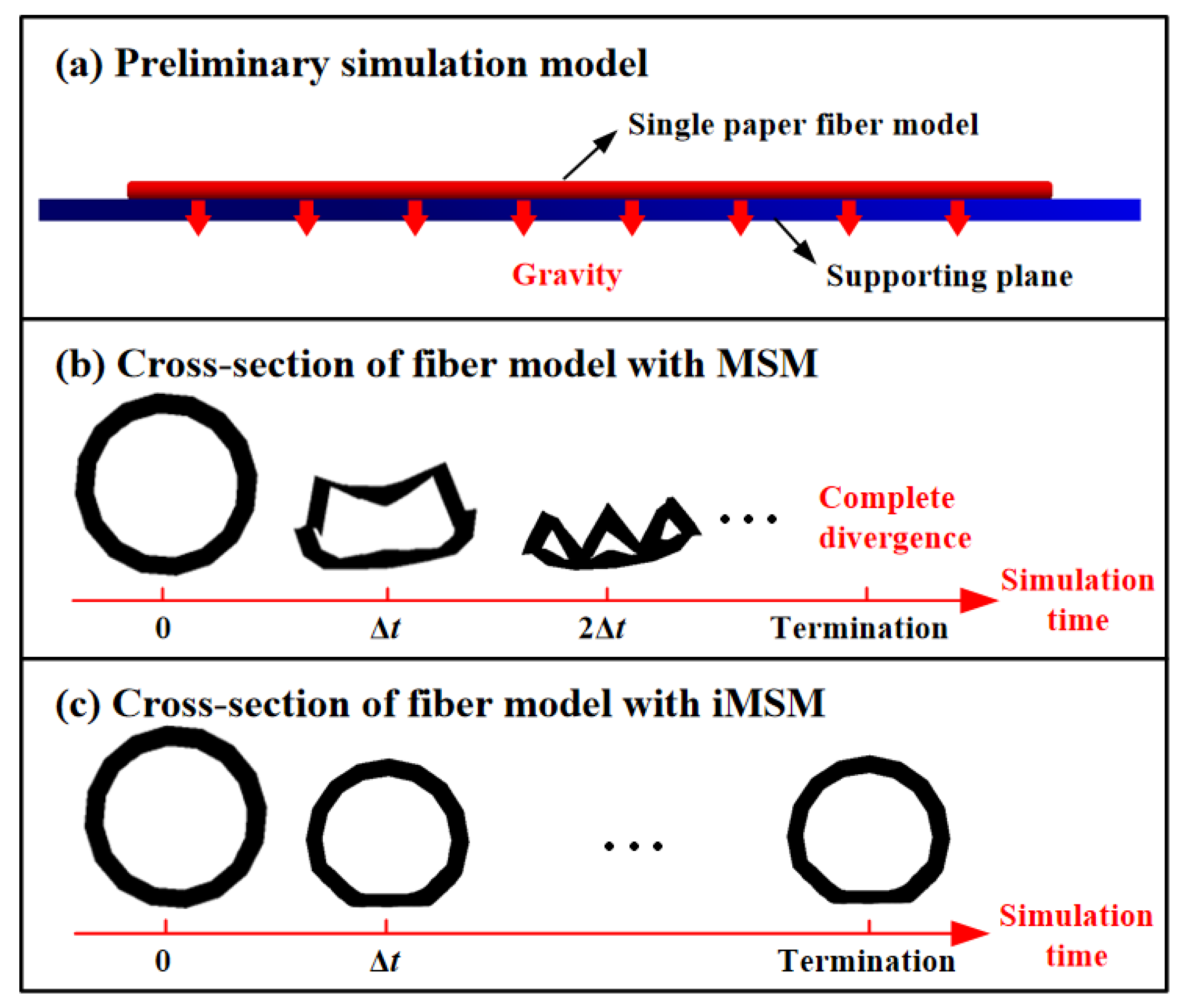
3.2. Preliminary Simulation with MSM and iMSM
3.3. Modeling Results of Single Fiber Model with iMSM
3.4. Validating Single Fiber Model with iMSM
3.4.1. Validating Model with iMSM
3.4.2. Evaluation Criterion for Model Validation
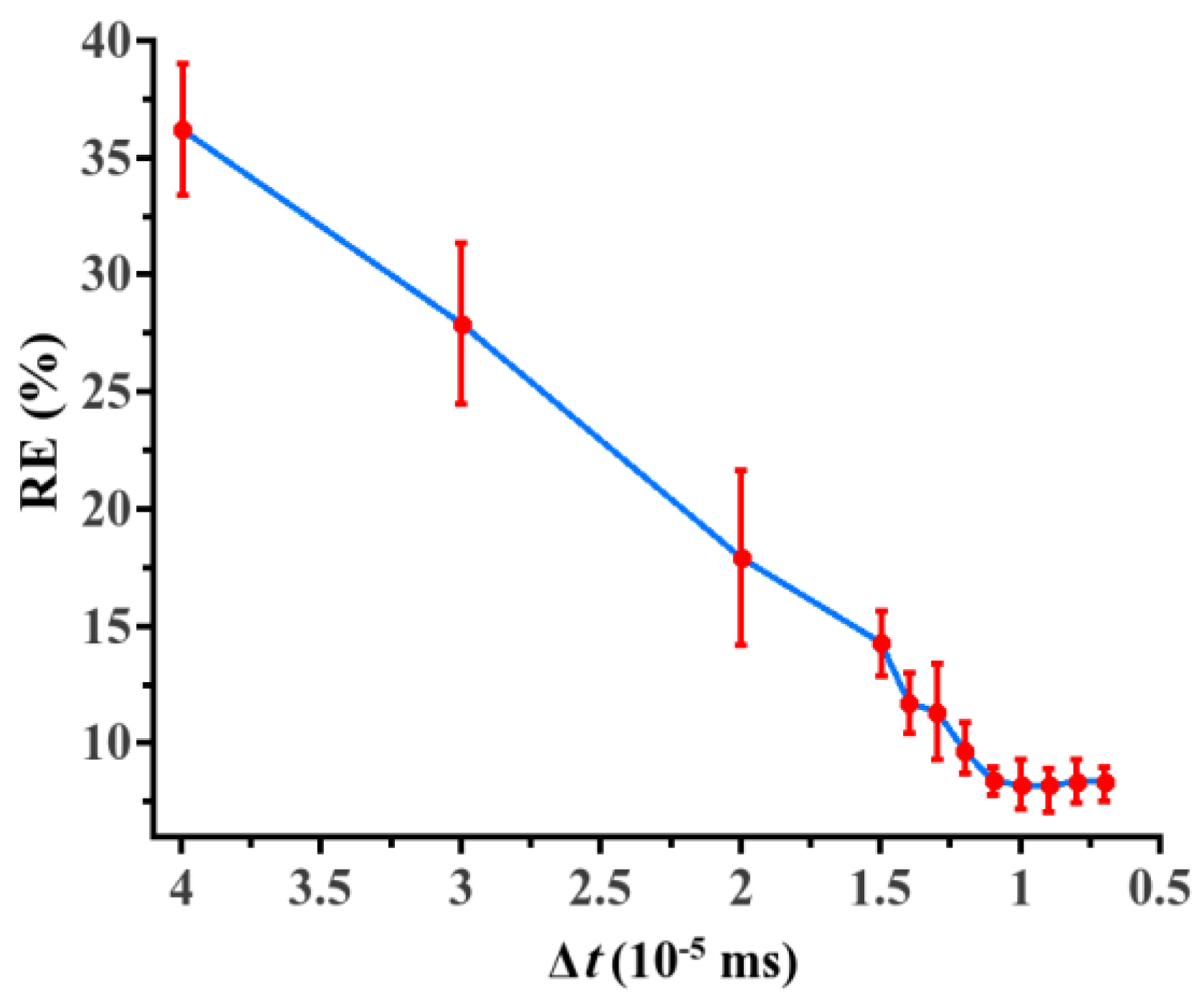
3.4.3. Determination of the Simulation Step
3.5. Validating the Response of a Single Paper Fiber Model with iMSM
3.5.1. Fiber Morphology Verification During Dynamic Simulation Process
3.5.2. Single Fiber Model Elastic Modulus Verification
4. Conclusions and Perspective
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simon, J.-W. A Review of Recent Trends and Challenges in Computational Modeling of Paper and Paperboard at Different Scales. Arch. Comput. Methods Eng. 2020, 28, 2409–2428. [Google Scholar] [CrossRef]
- Kortschot, K. The role of the fibre in the structural hierarchy of paper. In The Fundamentals of Papermaking Materials; Baker, C.F., Ed.; Symp: Cambridge, UK, 1997; pp. 351–399. [Google Scholar]
- Hagman, A.; Nygårds, M. Thermographical Analysis of Paper During Tensile Testing and Comparison to Digital Image Correlation. Exp. Mech. 2016, 57, 325–339. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.J.; Opara, U.L. Analysis of the creep behaviour of ventilated corrugated paperboard packaging for handling fresh produce—An experimental study. Food Bioprod. Process. 2019, 117, 126–137. [Google Scholar] [CrossRef]
- Hussain, S.; Coffin, D.W.; Todoroki, C. Investigating Creep in Corrugated Packaging. Packag. Technol. Sci. 2017, 30, 757–770. [Google Scholar] [CrossRef]
- Linvill, E.; Östlund, S. The Combined Effects of Moisture and Temperature on the Mechanical Response of Paper. Exp. Mech. 2014, 54, 1329–1341. [Google Scholar] [CrossRef]
- Köstner, V.; Ressel, J.; Sadlowsky, B.; Borocz, P. Measuring the creep behaviour of corrugated board by cascade and individual test rig. J. Appl. Pack Res. 2018, 10, 46–61. [Google Scholar]
- Bronkhorst, C. Modelling paper as a two-dimensional elastic–plastic stochastic network. Int. J. Solids Struct. 2003, 40, 5441–5454. [Google Scholar] [CrossRef]
- Lavrykov, S.; Ramarao, B.V.; Lindström, S.B.; Singh, K.M. 3D network simulations of paper structure. Nord. Pulp Pap. Res. J. 2012, 27, 256–263. [Google Scholar] [CrossRef]
- Kulachenko, A.; Uesaka, T. Direct simulations of fiber network deformation and failure. Mech. Mater. 2012, 51, 1–14. [Google Scholar] [CrossRef]
- Tojaga, V.; Kulachenko, A.; Östlund, S.; Gasser, T.C. Modeling multi-fracturing fibers in fiber networks using elastoplastic Timoshenko beam finite elements with embedded strong discontinuities—Formulation and staggered algorithm. Comput. Methods Appl. Mech. Eng. 2021, 384, 113964. [Google Scholar] [CrossRef]
- Timm, H.; Stegemann, J.; Küppers, M. Photosynthetic induction strongly affects the light compensation point of net photosynthesis and coincidentally the apparent quantum yield. Trees 2001, 16, 47–62. [Google Scholar] [CrossRef]
- Corte, H.; Kallmes, O.J. Statistical geometry of a fibrous network. In The Formation and Structure of Paper; Bolam, F., Ed.; FRC: Manchester, UK, 1961; pp. 13–46. [Google Scholar]
- Balberg, I.; Binenbaum, N. Computer study of the percolation threshold in a two-dimensional anisotropic system of conducting sticks. Phys. Rev. B 1983, 28, 3799–3812. [Google Scholar] [CrossRef]
- Stockie, J.M.; Green, S.I. Simulating the Motion of Flexible Pulp Fibres Using the Immersed Boundary Method. J. Comput. Phys. 1998, 147, 147–165. [Google Scholar] [CrossRef]
- Eichhorn, S.J.; Sampson, W.W. Statistical geometry of pores and statistics of porous nanofibrous assemblies. J. R. Soc. Interface 2005, 2, 309–318. [Google Scholar] [CrossRef]
- Deng, M.; Dodson, C. Paper: An Engineered Stochastic Structure; Tappi Press: Atlanta, GA, USA, 1994. [Google Scholar]
- Kahkonen, S. Elasticity and Stiffness Evolution in Random Fiber Networks. Master’s Thesis, University of Jyvaskyla, Westphalia, Finland, October 2003. [Google Scholar]
- Sampson, W.W. A model for fibre contact in planar random fibre networks. J. Mater. Sci. 2004, 39, 2775–2781. [Google Scholar] [CrossRef]
- Kawamura, F.; Ohira, T.; Kikuchi, Y. Constituents from the roots of Taxus cuspidata. J. Wood Sci. 2004, 50, 548–551. [Google Scholar] [CrossRef]
- Tornberg, A.-K.; Gustavsson, K. A numerical method for simulations of rigid fiber suspensions. J. Comput. Phys. 2006, 215, 172–196. [Google Scholar] [CrossRef]
- Vincent, R.; Rueff, M.; Voillot, C. 3-D computational simulation of paper handsheet structure and prediction of apparent density. TAPPI J. 2009, 8, 10–17. [Google Scholar] [CrossRef]
- Conceição, E.; Curto, J.; Simões Portugal, A. Coding a simulation model of the 3D structure of paper. In Lecture Notes in Computer Science, International Symposium Computational Modeling of Objects Represented in Images; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6026, pp. 299–310. [Google Scholar]
- Shaghaghi, T.; Ghadrdan, M.; Tolooiyan, A. Design and Optimisation of Drainage Systems for Fractured Slopes Using the XFEM and FEM. Simul. Model. Pr. Theory 2020, 103, 102110. [Google Scholar] [CrossRef]
- Beraki, M.; Trovão, J.P.; Perdigão, M. Characterization of variable inductors using finite element analysis. Simul. Model. Pr. Theory 2019, 97, 101952. [Google Scholar] [CrossRef]
- Borodulina, S.; Kulachenko, A.; Tjahjanto, D. Constitutive modeling of a paper fiber in cyclic loading applications. Comput. Mater. Sci. 2015, 110, 227–240. [Google Scholar] [CrossRef]
- Motamedian, H.R.; Kulachenko, A. Rotational Constraint between Beams in 3-D Space. Mech. Sci. 2018, 9, 373–387. [Google Scholar] [CrossRef]
- Motamedian, H.R.; Kulachenko, A. Simulating the hygroexpansion of paper using a 3D beam network model and concurrent multiscale approach. Int. J. Solids Struct. 2019, 161, 23–41. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Zheng, W.; Yang, B. Real-time simulation of virtual palpation system. IoP 2019, 234, 1–6. [Google Scholar] [CrossRef]
- Vassilev, T. Mass-Spring Cloth Simulation with Shape Matching; ACM Press: New York, NY, USA, 2017; pp. 257–264. [Google Scholar] [CrossRef]
- Ren, D.; Chen, Y.; Lin, B.; Zeng, F.; Huang, J.; Wang, J. Modelling and simulation of vessel surgery based on Mass-Spring. In Proceedings of the 2017 International Conference on Mechanical, Aeronautical and Automotive Engineering (ICMAA 2017), Singapore, 13–14 May 2017; pp. 1–4. [Google Scholar]
- Mozafary, V.; Payvandy, P. Study and comparison techniques in fabric simulation using mass spring model. Int. J. Cloth. Sci. Technol. 2016, 28, 634–689. [Google Scholar] [CrossRef]
- Yan, D.; Li, K. Measurement of wet fiber flexibility by confocal laser scanning microscopy. J. Mater. Sci. 2007, 43, 2869–2878. [Google Scholar] [CrossRef]
- Hibbeler, R. Mechanics of Materials, 8th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Hong, Y.; Hou, Q.; Xie, H. Action Mechanism of High-Shear Fiber Kneader Treatment on the Aspen BCTMP Fiber Morphology. Adv. Mater. Res. 2010, 113-116, 689–693. [Google Scholar] [CrossRef]
- Heyden, S. Network Modelling for the Evaluation of Mechanical Properties of Cellulose Fiber Fluff. Ph.D. Thesis, Lund University, Lund, Sweden, March 2000. [Google Scholar]
- Inin, D.; Cengiz, N. Stability of a Spring-Mass system with generalized piecewise constant argument. In Proceedings of the Progress on Difference Equations and Discrete Dynamical Systems, 2019 International Conference on Difference Equations and Applications, Istanbul, Turkey, 22–26 July 2019; Springer: Cham, Switzerland, 2021; Volume 341, pp. 213–229. [Google Scholar] [CrossRef]
- Qi, L.; Huang, S.; Fu, G.; Zhou, S.; Jiang, X. On the mechanics of curved flexoelectric microbeams. Int. J. Eng. Sci. 2018, 124, 1–15. [Google Scholar] [CrossRef]
- Steadman, R.; Luner, P. The effect of wet fibre flexibility on sheet apparent density. In Papermaking Raw Materials, Trans. of the VIIIth Fund. Res. Symp, Oxford, UK, 1985; Punton, V., Ed.; MEP: London, UK, 2018; pp. 311–337. [Google Scholar]


| Types of Paper Fiber | Diameter d (μm) | Wall Thickness w (μm) | Elastic Modulus E (GPa) | Shear Modulus G (GPa) |
|---|---|---|---|---|
| Aspen CTMP | 7.62 | 2.24 | 17.17 | 7.15 |
| Aspen BCTMP | 6.73 | 2.39 | 2.27 | 0.95 |
| Birch BCTMP | 10.35 | 3.09 | 2.38 | 0.99 |
| Spruce BKP | 3.80 | 1.36 | 1.47 | 0.61 |
| Fiber Type | Simulation Parameters | |||
|---|---|---|---|---|
| Number of Discretized Points Ndis | Number of Segments Nseq | Number of Mass Points Nmp | Number of Springs Ns | |
| Aspen CTMP | 32 | 507 | 16,256 | 64,896 |
| Aspen BCTMP | 16 | 317 | 5952 | 23,744 |
| Birch BCTMP | 32 | 438 | 14,048 | 56,064 |
| Spruce BKP | 16 | 670 | 10,736 | 42,880 |
| Types of Single Paper Fiber | External Transverse Loads q (μN·μm−1) | Experimental Elastic Modulus E (GPa) | Simulated Elastic Modulus (GPa) | RE of E (%) | Simulation Time (Min) |
|---|---|---|---|---|---|
| Aspen CTMP | 1 | 17.17 | 15.79 | 8.03 | 2.80 |
| 1.5 | 15.48 | 9.83 | 2.65 | ||
| 2 | 16.07 | 6.41 | 2.60 | ||
| 2.5 | 16.12 | 6.13 | 2.52 | ||
| Averaged of Aspen CTMP | 15.87 | 7.60 | 2.64 | ||
| Aspen BCTMP | 1 | 2.27 | 2.01 | 11.54 | 1.14 |
| 1.5 | 2.06 | 9.40 | 1.08 | ||
| 2 | 2.04 | 10.20 | 1.00 | ||
| 2.5 | 2.02 | 10.80 | 0.95 | ||
| Averaged of Aspen BCTMP | 2.03 | 10.49 | 1.04 | ||
| Birch BCTMP | 1 | 2.38 | 2.57 | 8.18 | 2.26 |
| 1.5 | 2.55 | 7.04 | 2.19 | ||
| 2 | 2.55 | 7.20 | 2.14 | ||
| 2.5 | 2.63 | 10.63 | 2.08 | ||
| Averaged of Birch BCTMP | 2.58 | 8.29 | 2.17 | ||
| Spruce BKP | 1 | 1.47 | 1.27 | 11.51 | 2.08 |
| 1.5 | 1.33 | 6.85 | 1.90 | ||
| 2 | 1.34 | 6.23 | 1.72 | ||
| 2.5 | 1.35 | 5.86 | 1.57 | ||
| Averaged of Spruce BKP | 1.32 | 7.61 | 1.82 | ||
| Averaged relative error of E for all fibers | 8.49 | 1.92 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Shen, W.; Coffin, D.W.; Song, T.; Bloch, J.-F.; Corriou, J.-P. Preliminary Modeling of Single Pulp Fiber Using an Improved Mass–Spring Method. Solids 2025, 6, 50. https://doi.org/10.3390/solids6030050
Liu Y, Shen W, Coffin DW, Song T, Bloch J-F, Corriou J-P. Preliminary Modeling of Single Pulp Fiber Using an Improved Mass–Spring Method. Solids. 2025; 6(3):50. https://doi.org/10.3390/solids6030050
Chicago/Turabian StyleLiu, Yin, Wenhao Shen, Douglas W. Coffin, Tao Song, Jean-Francis Bloch, and Jean-Pierre Corriou. 2025. "Preliminary Modeling of Single Pulp Fiber Using an Improved Mass–Spring Method" Solids 6, no. 3: 50. https://doi.org/10.3390/solids6030050
APA StyleLiu, Y., Shen, W., Coffin, D. W., Song, T., Bloch, J.-F., & Corriou, J.-P. (2025). Preliminary Modeling of Single Pulp Fiber Using an Improved Mass–Spring Method. Solids, 6(3), 50. https://doi.org/10.3390/solids6030050








