Abstract
Noncoplanar spin textures give rise not only to unusual magnetic structures but also to emergent electromagnetic responses stemming from scalar spin chirality, such as the topological Hall effect. In this study, we theoretically investigate nonreciprocal transport phenomena induced by noncoplanar magnetic orderings through microscopic model analyses. By focusing on meron–antimeron spin textures that exhibit local scalar spin chirality while maintaining vanishing global chirality, we demonstrate that the electronic band structure becomes asymmetrically modulated, which leads to the emergence of nonreciprocal transport. The present mechanism arises purely from the noncoplanar magnetic texture itself and requires neither net magnetization nor relativistic spin–orbit coupling. We further discuss the potential relevance of our findings to the compound Gd2PdSi3, which has been suggested to host a meron–antimeron crystal phase at low temperatures.
1. Introduction
Noncoplanar spin textures have garnered significant attention in condensed matter physics owing to their ability to generate emergent electromagnetic responses. These complex spin structures are stabilized through a variety of mechanisms, as extensively discussed in recent studies [1,2]. The microscopic key ingredient of these emergent electromagnetic responses lies in the scalar spin chirality, which is defined as a triple scalar product of spins, i.e., , where denotes the spin at site i, which naturally arises from noncoplanar spin textures [3,4,5,6]. Acting as an effective magnetic field on conduction electrons, the scalar spin chirality enables various ferromagnetic-structure-driven phenomena in systems without net magnetization or relativistic spin–orbit coupling. A prominent example is the topological Hall effect [7,8,9,10,11,12,13,14,15], which has been experimentally observed in materials hosting noncoplanar spin textures, such as skyrmion crystals [16,17,18,19,20,21,22] and other complex chiral spin states [23,24,25,26].
Previous investigations have primarily focused on noncoplanar spin textures accompanying a nonzero net scalar spin chirality, as these configurations naturally support the topological Hall effect. However, another class of noncoplanar spin textures exists that is characterized by finite local scalar spin chirality but zero net chirality over the entire system. A representative example is the meron–antimeron crystal, which is obtained by shifting a relative phase among the constituent spin density waves in a skyrmion crystal [27,28]; a meron corresponds to a topological spin texture with half-integer skyrmion number, while an antimeron is its counterpart with the opposite skyrmion number [29,30,31,32,33]. When arranged periodically, these textures form meron–antimeron crystals with vanishing global scalar spin chirality but finite local chirality. Such meron–antimeron crystals have been suggested or observed in compounds including Gd2PdSi3 [27], Co8Zn9Mn3 [34], and GdRu2Ge2 [35].
Although the meron–antimeron crystal does not give rise to a topological Hall effect due to its zero net scalar spin chirality, it can exhibit a different transport phenomenon, nonlinear nonreciprocal transport, wherein the resistance depends on the direction of current flow without requiring conventional semiconducting junctions [36,37,38,39,40,41,42]. Recent studies have shown that such nonreciprocity can emerge when the spatial distribution of the local scalar spin chirality breaks both the spatial inversion and time-reversal symmetries [43,44]. This mechanism is fundamentally distinct from nonreciprocity induced by the interplay between relativistic spin–orbit coupling and the magnetic field in noncentrosymmetric chiral/polar materials [36,37], thereby broadening the range of candidate materials.
In the present study, we theoretically examine the emergence of nonreciprocal transport arising from meron–antimeron spin textures via a microscopic model analysis. Using a tight-binding model that hosts the meron–antimeron crystal on a two-dimensional triangular lattice, we demonstrate that the electronic band structure under the meron–antimeron crystal exhibits asymmetric dispersions in terms of the wave vector. Subsequent calculations of the Drude-type nonlinear conductivity reveal the presence of nonlinear nonreciprocal transport along the y direction, with no such behavior along the x direction. We emphasize that this nonreciprocal transport is purely triggered by the noncoplanar magnetic structure, requiring neither net magnetization nor relativistic spin–orbit coupling. Finally, we discuss the experimental implications of our findings for the skyrmion-hosting compound Gd2PdSi3, where the nature of the zero-field phase—whether it is a single-Q spiral state or a meron–antimeron crystal—is still under debate. Our results serve as a promising platform to identify the underlying magnetic phase in Gd2PdSi3.
The remainder of this paper is organized as follows: In Section 2, we introduce the tight-binding model and define the meron–antimeron spin textures on the triangular lattice. Then, after presenting the asymmetric band structure in the absence of the spin–orbit coupling in Section 3, we show the behavior of nonlinear nonreciprocal transport in Section 4. We discuss the experimental relevance of our results, with emphasis on Gd2PdSi3, in Section 5. Finally, we conclude our results in Section 6.
2. Model
We consider a s-d-type tight-binding model comprising itinerant electrons and localized spins on a two-dimensional triangular lattice. The s-d Hamiltonian is given by
where and are the creation and annihilation operators, respectively, for an itinerant electron with spin at the lattice site i, and represents an ith classical localized spin of unit magnitude, i.e., . The first term in Equation (1) describes the kinetic energy of itinerant electrons, including nearest-neighbor hopping with amplitude . The second term in Equation (1) describes the onsite exchange interaction between the spin of itinerant electrons, expressed as , and the localized spin , mediated by the coupling constant J. Here, denotes the vector of Pauli matrices. The sign of J is inconsequential in the present context, since the localized spins are treated as classical vectors. For the numerical analyses presented in Section 3 and Section 4, we set as the unit of energy and choose . The different choices of and J do not alter the following results at the qualitative level. The s-d model has been widely employed in the study of transport phenomena in systems with topological spin textures [45,46,47,48,49,50,51,52], owing to its capacity to accommodate and stabilize a variety of spin configurations, such as the skyrmion crystal [53,54,55,56,57,58,59,60], hedgehog crystal [61], and other noncoplanar magnetic states [62,63,64,65], through large-scale numerical simulations.
Here, we consider a fixed spin configuration of localized spins. Specifically, we employ the meron–antimeron crystal spin texture, which consists of a superposition of triple-Q spin density waves, expressed as [66]
where ; we choose three ordering wave vectors connected by threefold rotational symmetry of the triangular lattice, where , , and , with does not exhibit loss of generality (the lattice constant of the triangular lattice is set as unity). denotes the relative phase among triple-Q spin density waves; we set , , and so that a noncoplanar spin texture has neither a net magnetization nor a scalar spin chirality, as detailed below [67]. The normalization constant ensures the unit magnitude of spin, , at every site.
Figure 1a illustrates the spin configuration of the meron–antimeron crystal. The spin configuration includes approximately three distinct types of magnetic vortices. The first is an in-plane vortex, characterized by the absence of a z-component in the spin, centered around regions where . The second is a meron-like vortex, exhibiting a skyrmion number of , centered around regions where . The third is an antimeron-like vortex, possessing a skyrmion number of , centered around regions where . The number of spins pointing in the positive z direction is equal to that of those pointing in the negative z direction, leading to cancelation of the net magnetization along the z axis.
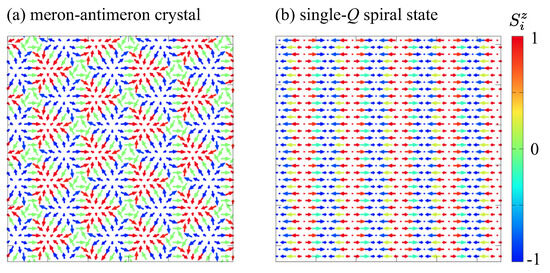
Figure 1.
Real-space spin configurations of (a) the meron–antimeron crystal and (b) the single-Q spiral state. The arrows represent the direction of spin moments, and their color indicates the z-spin component. The meron–antimeron crystal is represented by a superposition of three spiral waves at , , and with , while the single-Q spiral state is characterized by a single spiral wave at . The effective time-reversal symmetry combined with the translational operation is broken in (a), while it is preserved in (b).
Figure 2 shows the spatial distribution of the scalar spin chirality, which reflects the local topological nature of the spin configuration. The scalar spin chirality, which is defined as (, and k are in a counterclockwise order), is calculated for each triangle plaquette . By comparing with the spin configuration in Figure 1a, one can identify that the meron-like (antimeron-like) vortices correspond to regions with negative (positive) scalar spin chirality, while the in-plane vortices yield zero scalar spin chirality. By summing the scalar spin chirality around each meron (antimeron)-like vortex, the topological number of () is obtained by following the formula in Ref. [68], whose expression is explicitly given by
where is the number of magnetic unit cells. is given by
Consequently, both the net scalar spin chirality and net skyrmion number vanish in the meron–antimeron crystal structure. The stabilization mechanism of this meron–antimeron spin configuration on the triangular lattice has been clarified only in noncentrosymmetric systems with the Dzyaloshinskii–Moriya interaction [66]; the stability in the centrosymmetric case has not been clarified yet. Since we focus on the qualitative behavior of nonlinear nonreciprocal transport under the meron–antimeron crystal, we assume the transport property under the fixed spin configuration for simplicity.
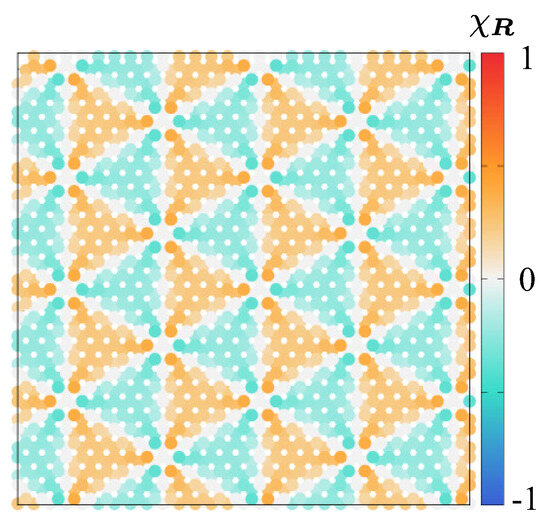
Figure 2.
Real-space scalar spin chirality configuration of the meron–antimeron crystal.
For comparison, we also examine a single-Q spiral state, whose spin configuration is defined by
The real-space spin configuration of the single-Q spiral state is shown in Figure 1b. Due to its coplanar spin texture, this spin configuration does not exhibit any local scalar spin chirality on individual triangular plaquettes, in stark contrast to the meron–antimeron crystal.
3. Electronic Band Structure
Under the spin configurations in Figure 1a,b, we calculate the corresponding Fermi surfaces at the chemical potential . Figure 3a displays the Fermi surfaces in the first magnetic Brillouin zone for the meron–antimeron crystal. While the overall shape retains an approximate sixfold symmetry, subtle symmetry breaking is evident. Specifically, the Fermi surfaces remain invariant under the mirror operation but not under , indicating an asymmetric structure along the direction. Meanwhile, the threefold rotational symmetry is preserved in the Fermi surfaces. To satisfy such a transformation, the lowest-order functional form of the asymmetric band deformation in the limit is given by the third-order function of rather than the linear order of . In this case, the functional form is given by , which plays a key role in the nonlinear nonreciprocal transport discussed in Section 4. It is noted that this asymmetric band modulation is purely driven by noncoplanar magnetic textures of the meron–antimeron crystal, as the present model excludes the effect of the relativistic spin–orbit coupling [43,44,69]. In contrast, the Fermi surfaces for the single-Q spiral state in Figure 3b exhibit a twofold symmetry and are symmetric under both and , indicating the absence of asymmetric modulations and nonlinear transport.
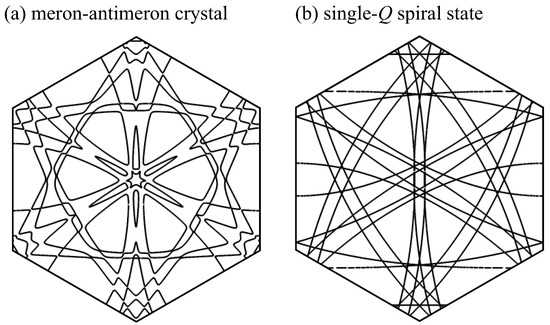
Figure 3.
Fermi surfaces of (a) the meron–antimeron crystal and (b) the single-Q spiral state at , , and .
From a symmetry viewpoint, asymmetric deformations of the Fermi surfaces in the meron–antimeron crystal are attributed to the simultaneous breaking of spatial inversion and time-reversal symmetries. Indeed, the spin configuration in Figure 1a is not invariant under both symmetry operations. This symmetry breaking is clearly manifested in the spatial distribution of the scalar spin chirality, as shown in Figure 2; their color pattern is reversed under either operation. Furthermore, the breaking of sixfold rotational symmetry is important to obtain the asymmetric band modulations in the plane. Similar asymmetric modulations have also been obtained in the case of electronic systems [70,71,72,73,74,75] and magnonic systems [76,77,78,79,80] once the symmetry conditions in terms of the spatial inversion and time-reversal symmetries are satisfied.
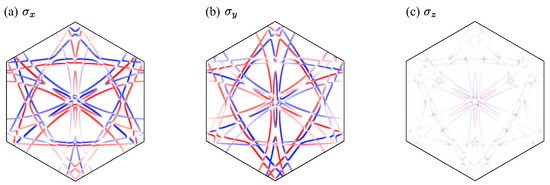
In addition to the asymmetric modulations of the electronic bands, the system under the meron–antimeron spin texture exhibits antisymmetric spin splitting. As shown in Figure 4a–c, the spin polarizations in each component are characterized as a momentum functional form of , , and , respectively. The first two terms correspond to Rashba-type spin splitting, , typically associated with a polar field along the z direction, as observed at surfaces and interfaces. The third term corresponds to Ising-type spin splitting, commonly arising under a trigonal crystal field, as found in materials such as MoS2 [81,82]. However, the mechanism required to induce antisymmetric spin splitting in the present system is different from that in the above studies [81,82]; the noncoplanar magnetic ordering provides an internal mean field that gives rise to spin splitting, even in the absence of relativistic spin–orbit coupling [43]. In other words, this mechanism is rooted in the magnetic texture itself rather than in relativistic effects, which is conceptually aligned with the emerging field of noncentrosymmetric noncollinear altermagnetism, which explores systems exhibiting antisymmetric spin splitting without conventional spin–orbit interactions [83,84,85,86,87]. In contrast, the single-Q spiral state exhibits antisymmetric spin polarization only in the y-spin component, following the functional form . This effect originates from the vector spin chirality in the plane [84,88], and lacks the antisymmetric spin polarization in the x- and z-spin components.
4. Nonlinear Nonreciprocal Transport
Reflecting the asymmetric band modulation along the direction in the meron–antimeron crystal, nonlinear nonreciprocal transport along the y direction is anticipated [41,89]. To quantify this response, we calculate the second-order nonlinear conductivity , defined via the relation , where and denote the electric current and electric field in the y direction, respectively. The calculation is based on the Drude-type mechanism by focusing on the intraband process, where the conductivity is expressed as [90,91]
with being the energy eigenvalue and the Fermi distribution function for the band index n, obtained by the exact diagonalization of the Hamiltonian in Equation (1) incorporating the meron–antimeron crystal spin texture. represents the derivative in terms of the wave vector . Here, e, , ℏ, , and represent the electron charge, the relaxation time, the reduced Planck constant, the number of sites within the magnetic unit cell (=48), and the number of supercells, respectively, where we set and . In the following calculation, we set the temperature to . Although we consider the DC component here, qualitatively similar results to and are expected for the AC component with the frequency .
Figure 5a shows a contour plot of as a function of the electron filling per site (with denoting full filling) and the molecular field . The results reveal that becomes nonzero in almost all of the parameter regions, ranging from positive (red) to negative (blue) values. The parameter dependence on filling and the molecular field is generally nontrivial, as exemplified in the case of in Figure 5b, due to multi-band effects stemming from the multi-sublattice structure. This suggests that both electron filling and field strength are key tuning parameters for optimizing the nonlinear response: the former can be controlled via electron or hole doping, while the latter can be varied through temperature. Under the present model parameters, the maximum absolute value of is found near and . Notably, in the low- and high-filling regions behaves in a relatively monotonic way, since the shape of the Fermi surface becomes simple in these regimes.
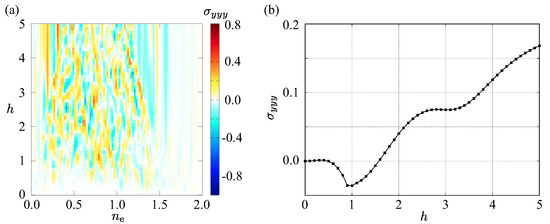
Figure 5.
(a) Nonlinear nonreciprocal conductivity against the filling and the molecular field h. (b) h dependence of at .
Let us briefly estimate the quantitative value of . By supposing the linear conductivity to be and , the ratio [m/A], which is independent of the relaxation time in the clean limit, is estimated to be for [eV], where the dimensions of and are given by [A/V] and [Am/V2], respectively. This value is comparable to the values in the two-dimensional material systems, such as a few-layer WTe2 and strained WSe2 [92].
5. Experimental Relevance
Finally, we comment on the experimental relevance of our results to the compound Gd2PdSi3, in which the skyrmion crystal was discovered under external magnetic fields despite the centrosymmetric crystal structure [27,93,94,95,96]. However, the nature of the low-field magnetic phase remains unresolved, even after detailed resonant X-ray scattering (RXS) measurements. Two main candidates have been proposed: the meron–antimeron crystal and the single-Q spiral state. Distinguishing between these two is particularly challenging using RXS due to the presence of multi-domain structures in the sample, which obscure the signatures of each magnetic configuration [27].
The present results offer two promising approaches for identifying the low-field magnetic phase in Gd2PdSi3. One approach involves measuring the second-order nonlinear conductivity. As shown in our analysis, the meron–antimeron crystal yields finite nonlinear nonreciprocal conductivity characterized by a nonzero , while the single-Q spiral state exhibits vanishing nonlinear conductivity due to the presence of effective time-reversal symmetry. Another promising method is spin-resolved angle-resolved photoemission spectroscopy, which enables direct observation of antisymmetric spin polarization in the band structure. In the meron–antimeron crystal, the antisymmetric spin polarization manifests in a pattern described by ( is the numerical constant), whereas it simplifies to in the single-Q spiral state when the effect of the relativistic spin–orbit is small. In particular, even in the multi-domain structure, the single-Q state is not expected to show antisymmetric spin polarization along the z-axis, in contrast to the case of the meron–antimeron crystal.
6. Conclusions
In conclusion, we have theoretically demonstrated that nonlinear nonreciprocal transport can emerge purely from noncoplanar magnetic textures, specifically those forming a meron–antimeron crystal structure, without requiring net magnetization or relativistic spin–orbit coupling. By employing a microscopic tight-binding model on the two-dimensional triangular lattice, we showed that the meron–antimeron spin configuration induces asymmetric band deformations and antisymmetric spin splitting in the electronic structure, both of which are qualitatively distinct from those observed in the single-Q spin configuration. This asymmetry is a consequence of the simultaneous breaking of spatial inversion and time-reversal symmetries, driven by the spatial distribution of the local scalar spin chirality. We further calculated the second-order nonlinear conductivity tensor based on the Drude-type mechanism, and revealed its strong dependence on both the electron filling and the strength of the molecular field. Our results suggest that nonlinear nonreciprocal transport can be maximized under specific model parameter conditions, which can be tuned via temperature or carrier doping. Lastly, we discussed the potential experimental relevance of our findings to Gd2PdSi3, a centrosymmetric compound that has been suggested to host the meron–antimeron crystal phase at a zero magnetic field. Our proposed method of using nonlinear nonreciprocal transport and/or spin-resolved angle-resolved photoemission spectroscopic measurements enables us to distinguish the meron–antimeron crystal from the single-Q spiral state, which could be helpful in determining a low-field magnetic phase diagram in Gd2PdSi3.
Funding
This research was supported by JSPS KAKENHI (Grants Numbers JP22H00101, JP22H01183, JP23H04869, and JP23K03288) and by JST CREST (JPMJCR23O4) and JST FOREST (JPMJFR2366). Parts of the numerical calculations were performed on the supercomputing systems at ISSP, the University of Tokyo.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Kalmeyer, V.; Laughlin, R.B. Equivalence of the resonating-valence-bond and fractional quantum Hall states. Phys. Rev. Lett. 1987, 59, 2095–2098. [Google Scholar] [CrossRef]
- Domenge, J.C.; Sindzingre, P.; Lhuillier, C.; Pierre, L. Twelve sublattice ordered phase in the J1 − J2 model on the kagomé lattice. Phys. Rev. B 2005, 72, 024433. [Google Scholar] [CrossRef]
- Bulaevskii, L.N.; Batista, C.D.; Mostovoy, M.V.; Khomskii, D.I. Electronic orbital currents and polarization in Mott insulators. Phys. Rev. B 2008, 78, 024402. [Google Scholar] [CrossRef]
- Al-Hassanieh, K.A.; Batista, C.D.; Ortiz, G.; Bulaevskii, L.N. Field-Induced Orbital Antiferromagnetism in Mott Insulators. Phys. Rev. Lett. 2009, 103, 216402. [Google Scholar] [CrossRef] [PubMed]
- Loss, D.; Goldbart, P.M. Persistent currents from Berry’s phase in mesoscopic systems. Phys. Rev. B 1992, 45, 13544–13561. [Google Scholar] [CrossRef]
- Ye, J.; Kim, Y.B.; Millis, A.J.; Shraiman, B.I.; Majumdar, P.; Tešanović, Z. Berry Phase Theory of the Anomalous Hall Effect: Application to Colossal Magnetoresistance Manganites. Phys. Rev. Lett. 1999, 83, 3737–3740. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the Kagomé Lattice: Chiral Spin State Based A Ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef] [PubMed]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Machida, Y.; Nakatsuji, S.; Maeno, Y.; Tayama, T.; Sakakibara, T.; Onoda, S. Unconventional anomalous Hall effect enhanced by a noncoplanar spin texture in the frustrated Kondo lattice Pr2Ir2O7. Phys. Rev. Lett. 2007, 98, 057203. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Takatsu, H.; Yonezawa, S.; Fujimoto, S.; Maeno, Y. Unconventional anomalous Hall effect in the metallic triangular-lattice magnet PdCrO2. Phys. Rev. Lett. 2010, 105, 137201. [Google Scholar] [CrossRef]
- Ueland, B.; Miclea, C.; Kato, Y.; Ayala-Valenzuela, O.; McDonald, R.; Okazaki, R.; Tobash, P.; Torrez, M.; Ronning, F.; Movshovich, R.; et al. Controllable chirality-induced geometrical Hall effect in a frustrated highly correlated metal. Nat. Commun. 2012, 3, 1067. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. J. Exp. Theor. Phys. 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Shindou, R.; Nagaosa, N. Orbital Ferromagnetism and Anomalous Hall Effect in Antiferromagnets on the Distorted fcc Lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef]
- Martin, I.; Batista, C.D. Itinerant Electron-Driven Chiral Magnetic Ordering and Spontaneous Quantum Hall Effect in Triangular Lattice Models. Phys. Rev. Lett. 2008, 101, 156402. [Google Scholar] [CrossRef] [PubMed]
- Akagi, Y.; Motome, Y. Spin Chirality Ordering and Anomalous Hall Effect in the Ferromagnetic Kondo Lattice Model on a Triangular Lattice. J. Phys. Soc. Jpn. 2010, 79, 083711. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Multiple-Q instability by (d-2)-dimensional connections of Fermi surfaces. Phys. Rev. B 2014, 90, 060402. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.H.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef]
- Brey, L.; Fertig, H.; Côté, R.; MacDonald, A. Skyrme and meron crystals in quantum Hall ferromagnets. Phys. Scr. 1996, 1996, 154. [Google Scholar] [CrossRef]
- Ezawa, M. Compact merons and skyrmions in thin chiral magnetic films. Phys. Rev. B 2011, 83, 100408. [Google Scholar] [CrossRef]
- Lin, S.Z.; Saxena, A.; Batista, C.D. Skyrmion fractionalization and merons in chiral magnets with easy-plane anisotropy. Phys. Rev. B 2015, 91, 224407. [Google Scholar] [CrossRef]
- Tan, A.; Li, J.; Scholl, A.; Arenholz, E.; Young, A.T.; Li, Q.; Hwang, C.; Qiu, Z.Q. Topology of spin meron pairs in coupled Ni/Fe/Co/Cu(001) disks. Phys. Rev. B 2016, 94, 014433. [Google Scholar] [CrossRef]
- Bera, S.; Mandal, S.S. Theory of the skyrmion, meron, antiskyrmion, and antimeron in chiral magnets. Phys. Rev. Res. 2019, 1, 033109. [Google Scholar] [CrossRef]
- Yu, X.Z.; Koshibae, W.; Tokunaga, Y.; Shibata, K.; Taguchi, Y.; Nagaosa, N.; Tokura, Y. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 2018, 564, 95–98. [Google Scholar] [CrossRef]
- Yoshimochi, H.; Takagi, R.; Ju, J.; Khanh, N.; Saito, H.; Sagayama, H.; Nakao, H.; Itoh, S.; Tokura, Y.; Arima, T.; et al. Multistep topological transitions among meron and skyrmion crystals in a centrosymmetric magnet. Nat. Phys. 2024, 20, 1001. [Google Scholar] [CrossRef]
- Rikken, G.; Raupach, E. Observation of magneto-chiral dichroism. Nature 1997, 390, 493–494. [Google Scholar] [CrossRef]
- Rikken, G.L.J.A.; Fölling, J.; Wyder, P. Electrical Magnetochiral Anisotropy. Phys. Rev. Lett. 2001, 87, 236602. [Google Scholar] [CrossRef] [PubMed]
- Seki, S.; Okamura, Y.; Kondou, K.; Shibata, K.; Kubota, M.; Takagi, R.; Kagawa, F.; Kawasaki, M.; Tatara, G.; Otani, Y.; et al. Magnetochiral nonreciprocity of volume spin wave propagation in chiral-lattice ferromagnets. Phys. Rev. B 2016, 93, 235131. [Google Scholar] [CrossRef]
- Giordano, A.; Verba, R.; Zivieri, R.; Laudani, A.; Puliafito, V.; Gubbiotti, G.; Tomasello, R.; Siracusano, G.; Azzerboni, B.; Carpentieri, M.; et al. Spin-Hall nano-oscillator with oblique magnetization and Dzyaloshinskii-Moriya interaction as generator of skyrmions and nonreciprocal spin-waves. Sci. Rep. 2016, 6, 36020. [Google Scholar] [CrossRef]
- Yokouchi, T.; Hoshino, S.; Kanazawa, N.; Kikkawa, A.; Morikawa, D.; Shibata, K.; Arima, T.h.; Taguchi, Y.; Kagawa, F.; Nagaosa, N.; et al. Current-induced dynamics of skyrmion strings. Sci. Adv. 2018, 4, eaat1115. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M. Nonlinear nonreciprocal transport in antiferromagnets free from spin-orbit coupling. Phys. Rev. B 2022, 106, 014420. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M. Nonreciprocal Transport in Noncoplanar Magnetic Systems without Spin–Orbit Coupling, Net Scalar Chirality, or Magnetization. J. Phys. Soc. Jpn. 2022, 91, 094704. [Google Scholar] [CrossRef]
- Calderón, M.J.; Brey, L. Skyrmion strings contribution to the anomalous Hall effect in double-exchange systems. Phys. Rev. B 2001, 63, 054421. [Google Scholar] [CrossRef]
- Yanagihara, H.; Salamon, M.B. Skyrmion Strings and the Anomalous Hall Effect in CrO2. Phys. Rev. Lett. 2002, 89, 187201. [Google Scholar] [CrossRef] [PubMed]
- Onoda, M.; Tatara, G.; Nagaosa, N. Anomalous Hall effect and skyrmion number in real and momentum spaces. J. Phys. Soc. Jpn. 2004, 73, 2624–2627. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I. Antiferromagnetic skyrmion crystals: Generation, topological Hall, and topological spin Hall effect. Phys. Rev. B 2017, 96, 060406. [Google Scholar] [CrossRef]
- Mohanta, N.; Dagotto, E.; Okamoto, S. Topological Hall effect and emergent skyrmion crystal at manganite-iridate oxide interfaces. Phys. Rev. B 2019, 100, 064429. [Google Scholar] [CrossRef]
- Göbel, B.; Akosa, C.A.; Tatara, G.; Mertig, I. Topological Hall signatures of magnetic hopfions. Phys. Rev. Res. 2020, 2, 013315. [Google Scholar] [CrossRef]
- Göbel, B.; Schimpf, L.; Mertig, I. Topological orbital Hall effect caused by skyrmions and antiferromagnetic skyrmions. Commun. Phys. 2025, 8, 17. [Google Scholar] [CrossRef]
- Banerjee, S.; Rowland, J.; Erten, O.; Randeria, M. Enhanced Stability of Skyrmions in Two-Dimensional Chiral Magnets with Rashba Spin-Orbit Coupling. Phys. Rev. X 2014, 4, 031045. [Google Scholar] [CrossRef]
- Ozawa, R.; Hayami, S.; Motome, Y. Zero-Field Skyrmions with a High Topological Number in Itinerant Magnets. Phys. Rev. Lett. 2017, 118, 147205. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Skyrmion Crystal from RKKY Interaction Mediated by 2D Electron Gas. Phys. Rev. Lett. 2020, 124, 207201. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kathyat, D.S.; Kumar, S. Antiferromagnetic skyrmions and skyrmion density wave in a Rashba-coupled Hund insulator. Phys. Rev. B 2021, 103, 134424. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Eto, R.; Mochizuki, M. Dynamical switching of magnetic topology in microwave-driven itinerant magnet. Phys. Rev. B 2021, 104, 104425. [Google Scholar] [CrossRef]
- Miyazaki, Y. Equivariant neural networks for spin dynamics simulations of itinerant magnets. Mach. Learn. Sci. Technol. 2023, 4, 045006. [Google Scholar] [CrossRef]
- Eto, R.; Mochizuki, M. Theory of Collective Excitations in the Quadruple-Q Magnetic Hedgehog Lattices. Phys. Rev. Lett. 2024, 132, 226705. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; van den Brink, J. Frustration-Induced Insulating Chiral Spin State in Itinerant Triangular-Lattice Magnets. Phys. Rev. Lett. 2010, 105, 216405. [Google Scholar] [CrossRef]
- Barros, K.; Kato, Y. Efficient Langevin simulation of coupled classical fields and fermions. Phys. Rev. B 2013, 88, 235101. [Google Scholar] [CrossRef]
- Barros, K.; Venderbos, J.W.F.; Chern, G.W.; Batista, C.D. Exotic magnetic orderings in the kagome Kondo-lattice model. Phys. Rev. B 2014, 90, 245119. [Google Scholar] [CrossRef]
- Chern, G.W.; Barros, K.; Wang, Z.; Suwa, H.; Batista, C.D. Semiclassical dynamics of spin density waves. Phys. Rev. B 2018, 97, 035120. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Meron-antimeron crystals in noncentrosymmetric itinerant magnets on a triangular lattice. Phys. Rev. B 2021, 104, 094425. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Locking of skyrmion cores on a centrosymmetric discrete lattice: Onsite versus offsite. Phys. Rev. Res. 2021, 3, 043158. [Google Scholar] [CrossRef]
- Berg, B.; Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Eto, R.; Pohle, R.; Mochizuki, M. Low-Energy Excitations of Skyrmion Crystals in a Centrosymmetric Kondo-Lattice Magnet: Decoupled Spin-Charge Excitations and Nonreciprocity. Phys. Rev. Lett. 2022, 129, 017201. [Google Scholar] [CrossRef]
- Volkov, B.; Gorbatsevich, A.; Kopaev, Y.V.; Tugushev, V. Macroscopic current states in crystals. Zh. Eksp. Teor. Fiz 1981, 81, 742. [Google Scholar]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Maksimov, P.A.; Zhu, Z.; White, S.R.; Chernyshev, A.L. Anisotropic-Exchange Magnets on a Triangular Lattice: Spin Waves, Accidental Degeneracies, and Dual Spin Liquids. Phys. Rev. X 2019, 9, 021017. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Okuma, N. Nonreciprocal superposition state in antiferromagnetic optospintronics. Phys. Rev. B 2019, 99, 094401. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403. [Google Scholar] [CrossRef]
- Hayami, S. Mechanism of antisymmetric spin polarization in centrosymmetric multiple-Q magnets based on effective chiral bilinear and biquadratic spin cross products. Phys. Rev. B 2022, 105, 024413. [Google Scholar] [CrossRef]
- Brekke, B.; Sukhachov, P.; Giil, H.G.; Brataas, A.; Linder, J. Minimal Models and Transport Properties of Unconventional p-Wave Magnets. Phys. Rev. Lett. 2024, 133, 236703. [Google Scholar] [CrossRef]
- Sukhachov, P.; Linder, J. Impurity-induced Friedel oscillations in altermagnets and p-wave magnets. Phys. Rev. B 2024, 110, 205114. [Google Scholar] [CrossRef]
- Soori, A. Crossed Andreev reflection in collinear p-wave magnet/triplet superconductor junctions. Phys. Rev. B 2025, 111, 165413. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Cheon, S.; Lee, H.W.; Cheong, S.W. Nonreciprocal spin waves in a chiral antiferromagnet without the Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2018, 98, 184405. [Google Scholar] [CrossRef]
- Ideue, T.; Hamamoto, K.; Koshikawa, S.; Ezawa, M.; Shimizu, S.; Kaneko, Y.; Tokura, Y.; Nagaosa, N.; Iwasa, Y. Bulk rectification effect in a polar semiconductor. Nat. Phys. 2017, 13, 578. [Google Scholar] [CrossRef]
- Wakatsuki, R.; Saito, Y.; Hoshino, S.; Itahashi, Y.M.; Ideue, T.; Ezawa, M.; Iwasa, Y.; Nagaosa, N. Nonreciprocal charge transport in noncentrosymmetric superconductors. Sci. Adv. 2017, 3, e1602390. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Kaplan, D.; Zhang, Z.; Holder, T.; Cao, N.; Wang, A.; Zhou, X.; Zhou, F.; Jiang, Z.; Zhang, C.; et al. Quantum-metric-induced nonlinear transport in a topological antiferromagnet. Nature 2023, 621, 487–492. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.R.; Sugawara, H.; Matsuda, T.D.; Sato, H.; Mallik, R.; Sampathkumaran, E.V. Magnetic anisotropy, first-order-like metamagnetic transitions, and large negative magnetoresistance in single-crystal Gd2PdSi3. Phys. Rev. B 1999, 60, 12162–12165. [Google Scholar] [CrossRef]
- Hirschberger, M.; Spitz, L.; Nomoto, T.; Kurumaji, T.; Gao, S.; Masell, J.; Nakajima, T.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; et al. Topological Nernst Effect of the Two-Dimensional Skyrmion Lattice. Phys. Rev. Lett. 2020, 125, 076602. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3 (R = Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).