Abstract
Phase equilibria studies were performed in the Li2O-SiO2 system for heat-treated samples using Scanning Electron Microscope (SEM) and X-Ray Diffraction (XRD). The temperature of the eutectic reaction (Liq. ⇌ Li4SiO4 + Li2SiO3) was experimentally determined at 1289 K using Differential Thermal Analysis (DTA). No evidences of the Li6Si2O7 formation was found by the experimental investigation and therefore, it was not considered. Heat capacity of the Li8SiO6 phase was measured using Differential Scanning Calorimetry (DSC). Solid phases of the Li2O-SiO2 system were described as stoichiometric compounds and liquid phases by two-sublattice partially ionic liquid model. Four stoichiometric intermediate compounds were considered to be stable (Li8SiO6, Li4SiO4, Li2SiO3 and Li2Si2O5). The polymorphic transformation in Li2Si2O5 phase was accounted and the metastable liquid miscibility gap on SiO2-rich side was reproduced. The calculated phase diagram satisfactorily agrees with the experimental phase equilibria as well as calculated thermodynamic properties reproduces experimental values within uncertainty limits.
1. Introduction
The demand for lithium-ion batteries (LIBs) for use in electric vehicles and other applications has grown substantially in recent years, leading to an increased focus on the development of methods for recycling and recovering the raw materials used in these batteries [1]. The electrodes in LIBs have a limited number of cycles, meaning that they can only be used a certain number of times before they lose their effectiveness. As a result, researchers have been investigating ways to recycle the materials used in these electrodes so that they can be reused, reducing waste and conserving resources.
The first cathode materials used in LIBs were produced using the LiCoO2 compound. To recycle the Co and Li in these materials, pyrometallurgical methods have been applied. These methods involve heating the materials in a reducing atmosphere, which allows the separation between Co and Li. At low partial pressures of oxygen, metals like Co, Ni, and Cu are reduced from their oxides and dissolved in the metallic alloy, while Li2O reacts with the oxide slag to form the LiAlO2 phase [2]. The Li concentrated in LiAlO2 phase is separated after the slag crystallization. For this process, the slag is mainly composed of aluminum oxide (Al2O3) and silica (SiO2), while calcium oxide (CaO) is introduced as a flux.
The new generation of LIBs contains Mn either in the form Li(NixMny)O2 solid solution or in form of spinel phase LiMn2O4 [3]. Pyrometallurgical processes can also be applied to recycle Li from the cathode materials. Reduction smelting occurs at an oxygen partial pressure at which Co, Ni, and Cu are completely part of the metallic alloy, while Li and most of Mn are concentrated in the slag. The introduction of Mn in the slag system induces the preferential crystallization of LiMn2O4 over LiAlO2. Therefore, the selection of a suitable slag system is crucial for improving the efficiency for recycling process [4]. A new method of spent LIBs based on smelting reduction of the MnOx-SiO2-Al2O3 slag system was suggested by Guo et al. [5]. Pyrolusite (a MnO2 enriched slag) was used as the major flux, and as a result of this process, Co-Ni-Cu-Fe alloy and Mn-rich slag containing Li were separated.
The CALPHAD method has been successfully employed to determine potential chemical compositions and process conditions for optimizing the separation of desirable phases from the slag [6,7]. Recently, the electrochemical properties and cell performance of LIBs were predicted based on thermodynamic calculations [8]. Therefore, investigations of phase diagrams among the Li2O, SiO2, Al2O3 and MnOx oxides are an important step towards creating a tool for simulating the maximal separation of Li2O from the metal alloy [9]. A review of the literature indicated some inconsistencies in pseudo-binary systems, as for example the Li2O-SiO2 system. In the present work, thermodynamic parameters of the Li2O-SiO2 system were optimized using the CALPHAD approach, and liquid was described using a two-sublattice partially ionic liquid model.
2. Literature Review
The phase equilibria in Li2O-SiO2 system was constructed based on experimental data by Kracek [10] for the first time. In this study, the samples were prepared using Li2CO3 and quartz as starting raw-materials for solid state reactions. DTA measurements were conducted to determine the temperatures of phase transformations. Three intermediate compounds were identified: Li4SiO4, Li2SiO3, and Li2Si2O5. Kracek [10] reported that the Li4SiO4 phase melts incongruently at 1528 K, while Li2SiO3 melts congruently at 1474 K. At 1297 K (with a SiO2 mole fraction of 0.28), an eutectic reaction Liq. ⇌ Li4SiO4 + Li2SiO3 was proposed. Additionally, an incongruent melting behavior was suggested for the Li2Si2O5 phase at 1306 K. No experimental data were provided for the Li2O-rich region.
Skokan et al. [11] studied the phase relations in the Li2O-rich side. According with their results, the Li8SiO6 phase was found to be stable up to 1105 K. To stabilize this compound, the samples were prepared by solid state reaction using dried oxides (Li2O, Li4SiO4 and SiO2) under controlled atmospheric conditions, in order to avoid the interaction with CO2 and H2O from the air. At elevated temperatures, Li8SiO6 decomposes into Li2O and Li4SiO4. Additionally, an eutectic reaction, Liq. ⇌ Li4SiO4 + Li2O, was proposed at 1265 K based on experimental results obtained using DTA methods. The thermal expansion coefficients were obtained for the Li4SiO4, Li2SiO3 and Li8SiO6 phases.
Claus et al. [12] experimentally investigated the Li4SiO4-Li2SiO3 region within the Li2O-SiO2 system. The study was performed in a temperature range of 1273 to 1573 K using techniques such as DTA, high-temperature calorimetry and XRD. Accoriding to them [12], Li4SiO4 and Li2SiO3 phases melt congruently at temperatures of 1531K and 1482 K, respectively. A high-temperature phase (Li6Si2O7) was proposed to melt incongruently at 1303 K and decomposes eutectoidically at 1293 K. Large effects were obtained in their DTA results, and then, Claus et al. [12] proposed the existence of two invariant reactions in a narrow temperature range.
It should be noted that all intermediate compounds are stoichiometric and no homogeneity ranges in these compounds were identified experimentally.
Based on the experimental results obtained by Kracek [10], Kim and Saunders [13] performed the first thermodynamic modeling for the Li2O-SiO2 system. A subregular solution model was employed to describe the liquid. For the calculations, the critical point obtained by Moriya et al. [14] at a temperature of 1275 K and a SiO2-rich composition was used. Moreover, the liquidus data provided by Moriya et al. [14] were incorporated. The calculated liquidus curves demonstrated reasonable agreement with the experimental data across most of the composition range. According to [13], the Li4SiO4 phase melts congruently, contradicting the phase diagram proposed by Kracek [10].
Recently, Konar et al. [15] performed a new assessment of thermodynamic functions for the Li2O-SiO2 system using the Modified Quasichemical Model (MQM) in the pair approximation for the liquid phase. The compound Li6Si2O7 was treated as stable and the polymorphic transformation for the Li2Si2O5 phase was taken into account. The metastable miscibility gap for liquid close to the SiO2 side was well reproduced accordingly to experimental data from [14,16]. Konar et al. [15] reviewed the thermodynamic experimental data and indicated that heat capacities are availible in the literature, except for the Li8SiO6 phase. For that phase, Neumann-Kopp rule was applied to derive heat capacity. Furthermore, Konar et al. [15] fitted the heat capacities with a rather complicated equations, especially to describe the second order transition for the Li4SiO4 phase.
The crystallographic data of the stable phases in the Li2O-SiO2 system [17,18,19,20,21,22,23,24,25,26,27] are presented in Table 1. It is important to mention that these data were used to support the XRD analysis in the present work.

Table 1.
Crystallographic data of the solid phases in the Li2O-SiO2 system.
Literature data agree very well about the congruent melting of the intermediate phases, the metastable miscibility gap for glass in SiO2-rich side, the polymorphic transformation for Li2Si2O5 phase and nature of most invariant reactions. However, uncertainties in the Li2O-Li2SiO3 section were observed concerning the available literature data. Firstly, the stability of Li6Si2O7 was proposed by Claus et al. [12] and reproduced by [15] at a small range of temperature, although in experimental studies performed by several works [11,13,28] this compound was not found. Secondly, thermodynamic data about Li8SiO6 is unclear and its stability is still under discussion [11], especially because the difficulty to produce this compound. Taking into account these uncertainties and the necessity to develop a new thermodynamic database for Li-ion recycling [29], a new optimization is presented in this work based on two-sublattice partially ionic liquid model for liquid description.
3. Thermodynamic Models
3.1. Stoichiometric Compounds
Equation (1) describes the Gibbs energy function for stoichiometric compounds and its temperature dependence. All the temperatures and Gibbs energies are given in Kelvin and Joule per mole, respectively.
where is the enthalpy of formation at room temperature, is the standard entropy and CP is the heat capacity. Furthermore, the heat capacities can be calculated using Maier-Kelley polynomial function [30], as shown in Equation (2):
3.2. Ionic Liquid
The two-sublattice partially ionic liquid model [31,32] was applied for the liquid in the Li2O-SiO2 system. The species distribution is represented by the formula (Li+1, Si+4)P (O−2, Va, , )Q, where P and Q denote the number of sites on each sublattice, adjusted based on the composition to maintain electroneutrality. This model can be applied to both metallic and oxide melts. In the absence of oxygen, the anionic sublattice remains vacant, resulting in the model being equivalent to the substitutional solution model that considers interactions between metallic atoms.
The partially ionic two-sublattice model was formulated as part of the Compound Energy Formalism (CEF) [33], a commonly utilized model in CALPHAD evaluations. CEF is employed to describe the Gibbs energy of a solution phase with several species occupying multiple crystallographic sites. The Gibbs energy (Gm) can be calculated using Equation (3) for the two-sublattice partially ionic liquid model:
where srfGm corresponds to the mechanical mixture, cnfSm is the configurational entropy and exGm represents the excess energy of mixing. The expression to calculate srfGm is shown in Equation (4).
where yi is the site fraction of the species i and G represents the Gibbs energy of end-members. The configurational entropy can be calculated according to Equation (5).
The excess Gibbs energy contribution, exGm, here represents the deviation from the ideal behavior and is defined below as shown in Equation (4), where the parameter L is related to interactions between constituents according to their respective sublattices.
4. Methodology
4.1. Sample Preparation and Microstructural Characterization
The samples of the Li2O-SiO2 system were prepared by solid-state reaction from high-purity oxide powders (Li2O min. 99.99% and SiO2 99.995%, 40 mesh, Alfa Aesar). The samples were mixed in Ar controlled atmosphere inside a glovebox, to avoid interaction between sample and air. The samples were wrapped in a Pt-foil and inserted in tubes of quartz. The quartz tubes were removed from the glovebox and sealed with controlled amount of Ar inside. No interaction with air occurred during this process. After that, the samples were respectively heat-treated at 1073 K, 1173 K, 1273 K and 1278 K by 8 h, 4 h, 2 h and 2 h in a muffle furnace (NABERTHERM), in order to achieve a pseudo-equilibrium state. After heat treatment, the quartz tubes were quenched in air and the samples were characterized.
X-ray diffraction (XRD) investigations were carried out using an URD6 X-ray diffractometer with radiation ( = 1.54056 Å) and radiation ( = 1.54437 Å). ICSD (Inorganic Crystal Structure Database, 2017) [34] was used for interpretation of the powder diffraction patterns. Qualitative and quantitative analyses of the XRD patterns were performed by Rietveld analysis using Topas software (BRUKER, https://www.bruker.com/en/products-and-solutions/diffractometers-and-x-ray-microscopes/x-ray-diffractometers/diffrac-suite-software/diffrac-topas.html).
The metallographic preparation was performed according to the following procedure: the samples were cold-mounted in epoxy resin, grounded with SiC abrasive paper (P320 up to P2400), polished with colloidal silica (0.05 μm), cleaned with ethanol and dried with hot air. The microstructural examination was done using Scanning Electron Microscope SEM (JEOL JSM-7800 Field Emission Gun, JEOL, Ltd., Tokyo, Japan) equipped with an Energy-dispersive X-ray spectroscopy (EDX).
4.2. Thermal Analysis and Calorimetry
Temperatures of the solid-state transformations and melting behavior were determined by TG-DTA SETSYS Evolution-1750 (SETARAM, Caluire, France) using a B-type tricouple DTA rod (PtRh 6%/30% thermocouple). The ceramic specimens placed in open Pt crucibles were heated and cooled under a dynamic air atmosphere at rates of 10 and 30 K/min, respectively. Also, the microsctructures obtained after melting by DTA were characterized by SEM/EDX. Mass loss was controlled during DTA measurements.
The heat capacity of the Li8SiO6 phase was experimentally measured using a DSC 8000 (Perkin Elmer Inc., Rodgau, Germany). The classical three-step continuous method was applied in the temperature range from 210 K to 570 K. The pressed disks were measured in a Pt/Rh crucible under flowing argon atmosphere (20 mL/min). Calibrations were done with a certified standard sapphire.
5. Results
5.1. Experimental Results
Table 2 provides the nominal compositions for the samples alongside with the respective phases identified by XRD for each condition of heat treatment. The phase quantities are presented in vol.%, and their corresponding lattice parameters were determined through Rietveld analysis, as detailed in Table 2. Microstructural investigations using SEM/BSE were used to support the XRD findings, although quantitative determination of phase compositions was not experimentally determined due to the low atomic mass of Li. Details regarding the temperatures and durations of the respective heat treatments can also be found in Table 2. A subset of XRD outcomes is shown in Figure 1, while selected SEM/BSE micrographs are presented in Figure 2.

Table 2.
Sample compositions in the Li2O-SiO2 system and phase identification by XRD results verified by SEM/BSE along with results of Rietveld analysis.
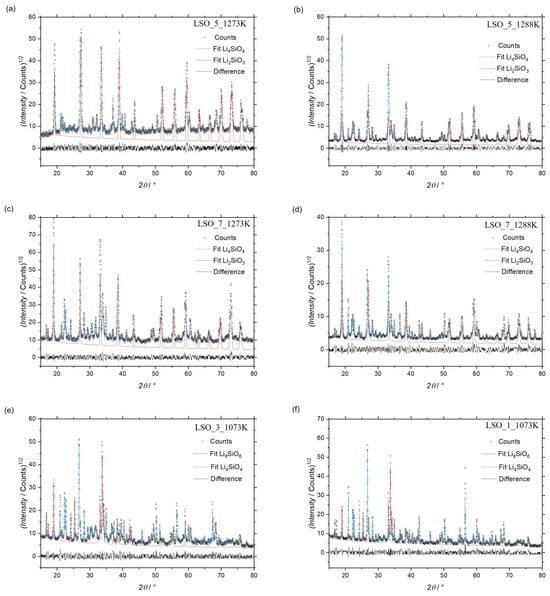
Figure 1.
Diffractograms from XRD after heat treatments: (a) sample LSO_5 at 1273 K; (b) sample LSO_5 at 1288 K; (c) sample LSO_7 at 1273 K; (d) sample LSO_7 at 1288 K; (e) sample LSO_3 at 1073 K; (f) sample LSO_1 at 1073 K.

Figure 2.
SEM-BSE images after heat treatments: (a) sample LSO_5 at 1273 K for 2 h; (b) sample LSO_5 at 1288 K for 2 h; (c) sample LSO_7 at 1273 K for 2 h; (d) sample LSO_7 at 1288 K for 2 h; (e) sample LSO_4 at 1273 K for 2 h; (f) sample LSO_3 at 1073 K for 8 h.
Samples marked as LSO_1, LSO_2 and LSO_3 were prepared to determine the phase equilibria in the Li2O-rich region and stability of the Li8SiO6 phase was confirmed. Moreover, sample marked as LA_3 was used to approximately determine heat capacity of that phase using DSC.
Samples marked as LSO_4, LSO_5 and LSO_7 were produced to investigate the section Li4SiO4-Li2SiO3 and the possible stability of the Li6Si2O7 phase. However, formation of this phase was not observed in the present study.
SEM/BSE micrographs presented in Figure 2a,b show the microstructures of the sample labeled LSO_5 heat-treated at 1273 K and 1288 K for 2 h, respectively. According to those micrographs accounting with the XRD results showed in Figure 1a,b, no evidences of the Li6Si2O7 phase were found. Only Li4SiO4 and Li2SiO3 phases were observed. Li2SiO3 phase is identified as the light-gray contrast, while the Li4SiO4 phase corresponds to the dark-grey contrast in the SEM/BSE micrographs of the Figure 2a,b.
Sample LSO_5 was melted in DTA and the results are shown in Figure 3. The temperature of the eutectic reaction was experimentally determined with onset at 1289 K, as shown in Figure 3b. The effects observed from the heating, as well as the effect observed in the cooling are quite narrow and well defined. No second or even third reaction could be associated to these effects. The SEM/BSE micrograph after melting Figure 3b indicates the eutectic reaction (Liq. ⇌ Li4SiO4 + Li2SiO3), although it seems to be difficult the visualization of a more clear eutectic-type microstructure due to the low difference in contrast between the phases. It should be noted that microstructure of eutectic reaction is not available in literature and the conclusion of eutectic character of reaction is based on substantial decrease of melting temperature in comparison with congruent melting of Li4SiO4 and Li2SiO3 compounds. Based on the results of the present work (DTA and XRD study), the Li6Si2O7 phase should be treated as metastable (as it was suggested by Meshalkin [28]). Probably, observation of [12] can be explained by stabilization of this phase by impurities. The effect with onset at 873 K is linked to the second-order transformation in the Li4SiO4 phase, which occurs due to the movement of rotation and translation of atoms along the crystal. The temperature obtained for such transformation is in agreement with literature data from [35,36].
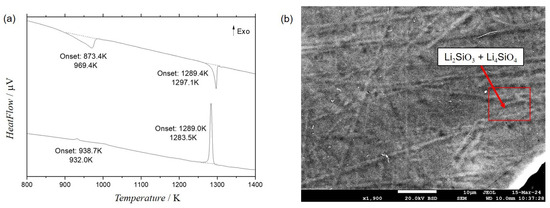
Figure 3.
Experimental results obtained for LSO_5: (a) DTA results with effects at 873.4 K and 1289.4 K associated respectively to the second-order transition for Li4SiO4 phase and the eutectic reaction Liq. ⇌ Li4SiO4 + Li2SiO3 and (b) SEM/BSE micrograph after melting.
Similar results to the LSO_5 were obtained for the samples labeled by LSO_4 and LSO_7. XRD results of sample LSO_7 showed in Figure 1c,d indicate the presence of Li4SiO4 and Li2SiO3 after heat treatment at 1273 and 1288 K. No remaining peaks are found in these results. The SEM/BSE micrographs of sample LSO_7 showed in Figure 2c,d agree with their respective XRD results. Moreover, some regions of sample LSO_7 after heat treatment at 1288 K seems to be melted as shown in Figure 2d, which is in agreement with micrograph of sample LSO_5 at same heat treatment conditions. It is important to mention that these samples were heat-treated almost at the same temperature of the beginning of the eutectic reaction, as indicated by the DTA results in Figure 3b. Due to the small difference of composition, microstructure of sample LSO_4 after heat treatment at 1273 K is almost the same to the microstructure of sample LSO_7, as shown in Figure 2e.
The SEM/BSE micrograph and the respective XRD data of sample LSO_3 heat-treated at 1073 K for 8 h indicates a microstructure formed by Li4SiO4 and Li8SiO6 phases, as shown in the Figure 1e and Figure 2f. Same results were obtained for samples LSO_1 and LSO_2 heat-treated at the same conditions. XRD data of sample LSO_1 is shown in Figure 1f. Since Li2O has a high volatility, a large evaporation occurred during the heat treatment for this group of samples, which it can be explain the volume of pores observed in the SEM/BSE micrograph of Figure 2f. As result of Li2O evaporation, the equilibria shifted from the two-phase field between Li2O and Li8SiO6 to the two-phase field between Li8SiO6 + Li4SiO4 phases.
Results of SEM/BSE and XRD for the samples LSO_1 and LSO_2 heat-treated at 1173 K for 4 h showed a Li4SiO4 single-phase microstructure. As result of Li evaporation, the equilibria shifted in direction of Li4SiO4 composition. At this temperature, Li8SiO6 is not stable. Therefore, the temperature of the perictectoid reaction (Li2O + Li4SiO4 ⇌ Li8SiO6) is between 1073 K and 1173 K, as proposed before by Skokan et al. [11].
Figure 4 shows the heat capacities as function of the temperature for the (a) Li8SiO6, (b) Li4SiO4, (c) Li2SiO3 and (d) Li2Si2O5 phases. The open circles in Figure 4a were obtained experimentally by DSC, while the continuous line indicates the calculated curve using Maier-Kelley polynomial for the Li8SiO6 phase. Since it is difficult to produce a single-phase sample for this compound, the sample with higher amount of Li8SiO6 determined by XRD (LSO_3) was used for the DSC measurement. Also, the volume fraction of second phase (Li4SiO4) was accounted and its contribution to heat capacity was considered. Heat capacity of the Li8SiO6 phase deviates slightly, but it agrees within uncertainty limits to the calculated heat capacity using the Neumann-Kopp rule, as shown in Figure 4a.
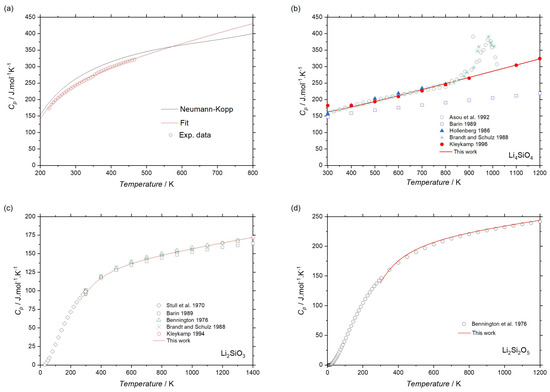
Figure 4.
Heat capacities curves of the (a) Li8SiO6, (b) Li4SiO4 [35,36,37,38,39], (c) Li2SiO3 [36,39,40,41,42] and (d) Li2Si2O5 [41] phases.
The Maier-Kelley coefficients were calculated for the Li4SiO4 phase using experimental data obtained by Brandt and Schulz [36] using DSC from 298.15 up to 800 K and data from Kleykamp [35] using drop calorimetry (DC) for temperatures higher than 800 K. Experimental data from Asou et al. [37] using DC, Hollenberg [38] using DSC, as well as estimated data from Barin [39] were also used for comparison. Data from these authors are in a good agreement with each other, except from data of Barin [39], which are lower than obtained in experiments [35,36,37,38] with the the difference increasing with temperature grows. Therefore the experimental data which are in a good mutual agreement were selected to fit heat capacity in the present work. A peak in an interval of temperature between 800–1000 K was experimentally observed explained by the second order transition for the Li4SiO4 phase. Same transformation was also found in DTA data of Figure 3. To ensure a more meaningful modeling and avoid the inclusion of parameters lacking physical significance in curve optimization, the Maier-Kelley polynomial was employed, complemented by a concise description suitable for the temperature range under consideration.
Experimental data obtained using DC by Kleykamp [40] and adiabatic calorimetry (AC) data of Bennington [41] were used to fit the heat capacity of the Li2SiO3 and Li2Si2O5 phases, as shown in Figure 4c and d, respectively. Experimental values of heat capacity for the Li2SiO3 phase from different authors [36,39,42] were also plotted in Figure 4c. It should be noted that experimental data for all three phases are in a good mutual agreement and well reproduced by fitted equations.
5.2. Thermodynamic Modeling
The optimization of thermodynamic parameters was conducted using the Thermo-Calc software (https://thermocalc.com/) [43], employing the PARROT module within the CALPHAD approach [44]. Subsequent computations of the phase diagram and thermodynamic properties for the Li2O-SiO2 system were executed using the POLY-3 module. Throughout the optimization process, specific weights were assigned to each type of experimental data, considering the uncertainties associated with individual experimental methods. Detailed thermodynamic parameters are provided in Table 3, while corresponding thermodynamic functions are outlined in Table 4. Gibbs energy expressions for the Li-O system were sourced from Chang et al. [45] and for the Si-O system from Dumitrescu and Sundman [46]. SGTE data [47] was used for pure elements. All of the solid phases were treated as stoichiometric and two-sublattice partially ionic liquid model was adopted for liquid description. Detailed information concerning the thermodynamic models applied to our modeling are presented on Section 3. The calculated phase diagram of the Li2O-SiO2 system with parameters optimized in the present work is shown in Figure 5.

Table 3.
Thermodynamic description for the Li2O-SiO2 system.

Table 4.
Thermodynamic description for the Li2O-SiO2 system.
As mentioned above, the stability of Li6Si2O7 phase was not experimentally confirmed in the present study taking into account the data obtained by DTA, XRD and by microstructural characterization of heat-treated samples at 1288 K. Therefore, this phase was not considered in our thermodynamic modeling. Instead of three invariant reactions for the section between Li4SiO4-Li2SiO3 (i- Liq. + Li2SiO3 ⇌ Li6Si2O7; ii- Liq. ⇌ Li4SiO4 + Li6Si2O7; iii- Li6Si2O7⇌ Li4SiO4 + Li2SiO3;) as proposed by Claus et al. [12] and reproduced by Konar et al. [15], the present description proposes only one invariant reaction Liq. ⇌ Li4SiO4 + Li2SiO3 as shown in (Figure 5), which agrees with data from Kracek [10] and Meshalkin et al. [28].
The phase diagram was effectively reproduced within uncertainty limits, as shown in Figure 5. Discrepancies observed between the calculated liquidus lines and experimental data can be attributed to higher uncertainties of determination of liquidus temperatures compared to invariant reactions using DTA. Especially uncertainty of liquidus determination is increased in case of Li2O evaporation during melting and therefore shift the composition of sample towards the SiO2 side.
The metastable liquid miscibility gap of the Li2O-SiO2 system was calculated to be in agreement with the experimental data from Moriya et al. [14], Haller et al. [16] and calculations of Kim et al. [13]. The metastable miscibility gap is shown also in Figure 5 close to the SiO2-side. The formation of metastable miscibility gaps between SiO2 and oxides formed by alkali metals (e.g., Na2O and K2O) were already reported by Wu et al. [48].
The calculated values of thermodynamic properties like enthalpy of formation and standard entropy at room temperatures are listed in the Table 5. No significant deviations were observed in comparison with experimental data [41,42,49,50,51,52]. Our calculated values are also compared with the values obtained by Konar et al. [15], and except for the Li8SiO6 phase, the thermodynamic properties are in good agreement. For the Li8SiO6 and Li4SiO4 phases, the Gibbs energies were calculated and comparison with estimated data from Migge [53] was done in temperature range between 700 to 1100 K, as shown in Figure 6. For both phases, the Gibbs energies are in good agreement with data of [53].

Table 5.
Standard enthalpy and entropy of formation of the Li2O-SiO2 compounds at 298 K.
Experimentally heat capacity data for the intermediate phases were used to develop the thermodynamic database. Effects of the second order transition for the heat capacity of the Li4SiO4 phase was not considered in the present work for the reasons previously discussed in Section 5.1, although an increase of entropy is resulted from this transformation. However, it does not affect significantly the modeling on this region of the phase diagram.
The data for invariant reactions calculated with the thermodynamic parameters optimized in the present work are compared with temperatures experimentally determined by different methods like quenching method from [10,54], DTA from [11,12,54,55,56], drop calorimetry from [35], KEMS from [51], DSC from [41,57] and assessment from [15] in Table 6. Results of calculations for the eutectic reaction (Liq. ↔ Li4SiO4 + Li2SiO3) are almost 30 K higher than our experimental value of 1289K obtained by DTA. It seems to be difficult to fit substantial temperature difference between the congruent melting of the Li4SiO4 and Li2SiO3 phases and eutectic reaction without distortion of other parts of diagram using models accepted in the present work. The calculated phase diagram using thermodynamic parameters optimized in the present work reproduces well the polymorphic transformation of Li2Si2O5 phase, the congruent melting for the intermediate compounds like Li4SiO4, Li2SiO3 and Li2Si2O5, as well as most of the invariant reactions from literature data (Table 6).

Table 6.
Invariant and congruent reactions in the Li2O-SiO2 system and their respective temperatures.
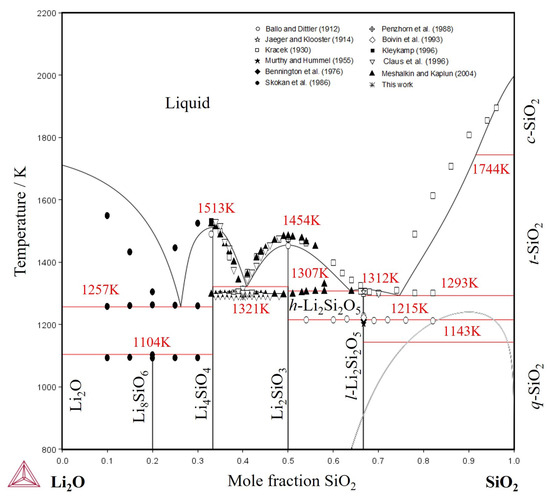
Figure 5.
Phase diagram of the Li2O-SiO2 system calculated with thermodynamic parameters obtained in this work [10,11,12,28,35,41,54,55,56,57].
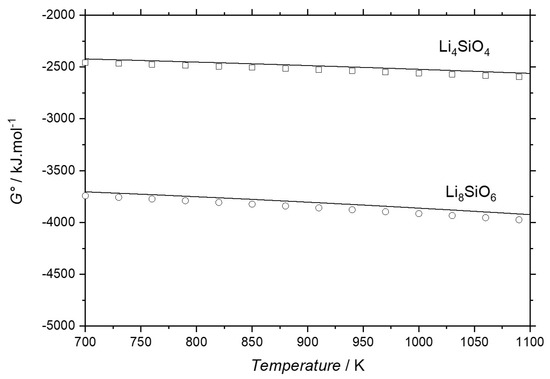
Figure 6.
Calculated Gibbs energies for the Li8SiO6 and Li4SiO4 phases in comparison to estimated data from Migge [53].
Figure 7 shows the calculated ln a(Li2O) in liquid as function of the SiO2 content for two different temperatures (1473 K and 1673 K) in comparison with estimated values of Charles [58] based on the liquidus behavior within the Li2O-SiO2 system. It can be observed that the Li2O activity increases with the temperature increase.
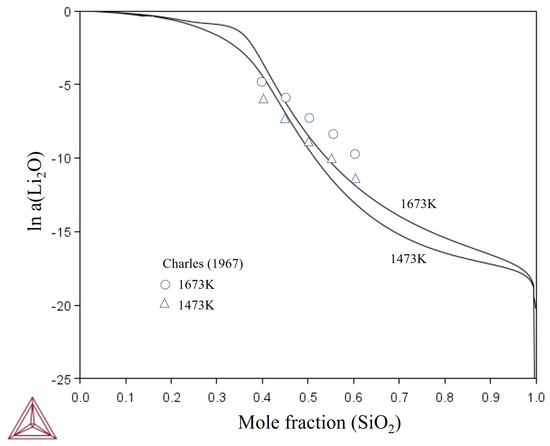
Figure 7.
Calculated activity of Li2O for liquid in comparison to data obtained by Charles [58].
The obtained experimental results and literature data were used to derive a thermodynamic database for the Li2O-SiO2 system. The experimental data are well reproduced by calculations using the thermodynamic database. The presented thermodynamic database in this work is a subsystem of the larger system Li2O-Al2O3-SiO2-MnOx, which is one of the important foundations for simulation of Li-recycling processes.
6. Conclusions
Phase equilibria of the Li2O-SiO2 system were experimentally investigated using XRD, SEM and DTA. Heat capacity of the Li8SiO6 phase was experimentally determined using DSC. The CALPHAD method was employed to derive thermodynamic descriptions for the Li2O-SiO2 system, resulting in the reproduction of the phase diagram and available thermodynamic properties. The Gibbs energies of the Li8SiO6, Li4SiO4, Li2SiO3, l-Li2Si2O5 and h-Li2Si2O5 phases were modeled as stoichiometric compounds and two-sublattice partially ionic liquid model was applied for the liquid description. The metastable miscibility gap of liquid phase in the SiO2 rich side was calculated and reproduced accounting literature data. The calculated phase diagram using optimized parameters obtained in this study aligns with both our experimental findings and existing literature. Furthermore, it accurately reproduces available experimental thermodynamic data within acceptable margins of uncertainty. The derived thermodynamic description is part of a high order system database (Li2O-SiO2-Al2O3-MnOx) for further applications in Li recycling processes.
Author Contributions
Conceptualization, D.A.d.A. and O.F.; methodology, D.A.d.A.; software, D.A.d.A. and O.F.; validation, O.F.; formal analysis, O.F.; investigation, D.A.d.A.; resources, O.F.; data curation, D.A.d.A.; writing—original draft preparation, D.A.d.A. and O.F.; writing—review and editing, D.A.d.A. and O.F.; visualization, D.A.d.A. and O.F.; supervision, O.F.; project administration, O.F.; funding acquisition, O.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by DFG (Deutsche Forschungsgemeinschaft) grant number in frame of the subproject SPP-2315: EnAM (Engineered Artificial Minerals)—A01 Project ID 470392360.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors gratefully acknowledge the technical assistance from the employees of the Institute of Materials Science (TU Freiberg), namely M. Löffler, M. Kriegel, B. Wahl and K. Becker.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Elwert, T.; Goldmann, D.; Strauss, K.; Schirmer, T. Phase composition of high lithium slags from the recycling of lithium ion batteries. World Metall.-Erzmetall. 2012, 65, 163–171. [Google Scholar]
- Schirmer, T.; Qiu, H.; Li, H.; Goldmann, D.; Fischlschweiger, M. Li-distribution in compounds of the Li2O-MgO-Al2O3-SiO2-CaO system — A first survey. Metals 2020, 10, 1633. [Google Scholar] [CrossRef]
- Cupid, D.; Reif, A.; Seifert, H. Enthalpy of formation of Li1+ xMn2-xO4 (0 < x < 0.1) spinel phases. Thermochim. Acta 2015, 599, 35–41. [Google Scholar]
- Schnickmann, A.; De Abreu, D.A.; Fabrichnaya, O.; Schirmer, T. Stabilization of Mn4+ in synthetic slags and identification of important slag forming phases. Minerals 2024, 14, 368. [Google Scholar] [CrossRef]
- Guoxing, R.; Songwen, X.; Meiqiu, X.; Bing, P.; Youqi, F.; Fenggang, W.; Xing, X. Recovery of valuable metals from spent lithium-ion batteries by smelting reduction process based on MnO-SiO2-Al2O3 slag system. In Advances in Molten Slags, Fluxes, and Salts, Proceedings of the 10th International Conference on Molten Slags, Fluxes, and Salts 2016, Seattle, WC, USA, 22–25 May 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 211–218. [Google Scholar]
- Liu, H.; Zhang, W.; Guan, Z.; Li, N.; Wang, J.; Zhang, S.; Du, Y.; Wang, J.; Dang, F. Thermodynamic Perspective: Insights into the Capacity Increase Phenomenon and Regulation of the Capacity Tendency of MnO for Lithium-Ion Battery Anodes. ACS Appl. Energy Mater. 2021, 4, 12662–12670. [Google Scholar] [CrossRef]
- Li, N.; Li, D.; Zhang, W.; Chang, K.; Dang, F.; Du, Y.; Seifert, H. Development and application of phase diagram for Li-ion batteries using CALPHAD approach. Prog. Nat. Sci. Mater. Inter. 2019, 29, 265–276. [Google Scholar] [CrossRef]
- Haccuria, E.; Hayes, P.; Jak, E. Phase equilibria studies of the MnO-Al2O3-SiO2 system in equilibrium with metallic alloy. Part 1: Development of technique and determination of liquidus isotherms between 1423 and 1523 K. Int. J. Mat. Res. 2014, 105, 941–952. [Google Scholar] [CrossRef]
- Xiao, S.; Ren, G.; Xie, M.; Pan, B.; Fan, Y.; Wang, F.; Xia, X. Recovery of valuable metals from spent lithium-ion batteries by smelting reduction process based on MnO–SiO2–Al2O3 slag system. J. Sustain. Metall. 2017, 3, 703–710. [Google Scholar] [CrossRef]
- Kracek, F. The binary system Li2O–SiO2. J. Phys. Chem. 1930, 34, 2641–2650. [Google Scholar] [CrossRef]
- Skokan, A.; Wedemeyer, H.; Vollath, D.; Günther, E. Thermal properties and application of potential lithium silicate breeder materials. In Fusion Technology 1986. 2 v; International Atomic Energy Agency: Vienna, Austria, 1986. [Google Scholar]
- Claus, S.; Kleykamp, H.; Smykatz-Kloss, W. Phase equilibria in the Li4SiO2-Li2SiO2 region of the pseudobinary Li2O-SiO2 system. J. Nucl. Mater. 1996, 230, 8–11. [Google Scholar] [CrossRef]
- Kim, S.; Sanders, T., Jr. Thermodynamic modeling of phase diagrams in binary alkali silicate systems. J. Am. Ceram. Soc. 1991, 74, 1833–1840. [Google Scholar] [CrossRef]
- Moriya, Y. Phase Separation and Crystallization Process in Glasses. Osaka Kogyo Gijutsu Shikenjo Hokoku 1971, 339, 1–101. [Google Scholar] [CrossRef]
- Konar, B.; Van Ende, M.; Jung, I. Critical evaluation and thermodynamic optimization of the Li-O, and Li2O-SiO2 systems. J. Eur. Ceram. Soc. 2017, 37, 2189–2207. [Google Scholar] [CrossRef]
- Haller, W.; Blackburn, D.; Simmons, J. Miscibility Gaps in Alkali-Silicate Binaries—Data and Thermodynamic Interpretation. J. Am. Ceram. Soc. 1974, 57, 120–126. [Google Scholar] [CrossRef]
- Watanabe, A.; Kobayashi, G.; Matsui, N.; Yonemura, M.; Kubota, A.; Suzuki, K.; Hirayama, M.; Kanno, R. Ambient pressure synthesis and H- conductivity of LaSrLiH2O2. Electrochemistry 2017, 85, 88–92. [Google Scholar] [CrossRef]
- Hofmann, R.; Hoppe, R. Ein neues Oxogermanat: Li8GeO6= Li8O2 [GeO4].(Mit einer Bemerkung über Li8SiO6 und Li4GeO4). Z. Für Anorg. Und Allg. Chem. 1987, 555, 118–128. [Google Scholar] [CrossRef]
- Völlenkle, H.; Wittmann, A.; Nowotny, H. The crystal structure of Li 6[Si2O7]. Monatshefte Für Chem./Chem. Mon. 1969, 100, 295–303. [Google Scholar] [CrossRef]
- Grasso, M.L.; Blanco, M.V.; Cova, F.; Gonzalez, J.A.; Larochette, P.A.; Gennari, F.C. Evaluation of the formation and carbon dioxide capture by Li4SiO4 using in situ synchrotron powder X-ray diffraction studies. Phys. Chem. Chem. Phys. 2018, 20, 26570–26579. [Google Scholar] [CrossRef] [PubMed]
- Völlenkle, H. Verfeinerung der kristallstrukturen von Li2SiO3 und Li2GeO3. Z. Für Krist.-Cryst. Mater. 1981, 154, 77–82. [Google Scholar] [CrossRef]
- De Jong, B.; Slaats, P.; Super, H.; Veldman, N.; Spek, A. Extended structures in crystalline phyllosilicates: Silica ring systems in lithium, rubidium, cesium, and cesium/lithium phyllosilicate. J. Non-Cryst. Solids 1994, 176, 164–171. [Google Scholar] [CrossRef]
- Smith, R.; Howie, R.; West, A.; Aragon-Pina, A.; Villafuerte-Castrejon, M. The structure of metastable lithium disilicate, Li2Si2O5. Acta Crystallogr. Sect. 1990, 46, 363–365. [Google Scholar] [CrossRef]
- Lee, S.; Xu, H.; Xu, H.; Neuefeind, J. Crystal structure of moganite and its anisotropic atomic displacement parameters determined by synchrotron X-ray diffraction and X-ray/neutron pair distribution function analyses. Minerals 2021, 11, 272. [Google Scholar] [CrossRef]
- Tucker, M.; Keen, D.; Dove, M. A detailed structural characterization of quartz on heating through the α–β phase transition. Mineral. Mag. 2001, 65, 489–507. [Google Scholar] [CrossRef]
- Schmahl, W.; Swainson, I.; Dove, M.; Graeme-Barber, A. Landau free energy and order parameter behaviour of the α/β phase transition in cristobalite. Z. Für Krist. 1992, 201, 125–145. [Google Scholar] [CrossRef]
- Kihara, K.; Matsumoto, T.; Imamura, M. High-order thermal-motion tensor analyses of tridymite. Z. Für Krist.-Cryst. Mater. 1986, 177, 39–52. [Google Scholar] [CrossRef]
- Meshalkin, A.; Kaplun, A. Phase Equilibria in the Range 33.33–58 mol% SiO2 of the Li2O-SiO2 System. Russ. J. Inorg. Chem. 2004, 49, 772–774. [Google Scholar]
- de Abreu, D.A.; Löffler, M.; Kriegel, M.J.; Fabrichnaya, O. Experimental Investigation and Thermodynamic Modeling of the Li2O–Al2O3 System. J. Phase Equilibria Diffus. 2024, 45, 36–55. [Google Scholar] [CrossRef]
- Maier, C.; Kelley, K. An equation for the representation of high-temperature heat content data1. J. Am. Chem. Soc. 1932, 54, 3243–3246. [Google Scholar] [CrossRef]
- Hillert, M.; Jansson, B.; Sundman, B. Others A two-sublattice model for molten solutions with different tendency for ionization. Metall. Trans. 1985, 16, 261–266. [Google Scholar] [CrossRef]
- Sundman, B. Modification of the two-sublattice model for liquids. Calphad 1991, 15, 109–119. [Google Scholar] [CrossRef]
- Hillert, M. The compound energy formalism. J. Alloys Compd. 2001, 320, 161–176. [Google Scholar] [CrossRef]
- Belsky, A.; Hellenbrandt, M.; Karen, V.; Luksch, P. New developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in support of materials research and design. Acta Crystallogr. Sect. Struct. Sci. 2002, 58, 364–369. [Google Scholar] [CrossRef] [PubMed]
- Kleykamp, H. Enthalpy, heat capacity, second-order transitions and enthalpyof fusion of Li4SiO4 by high-temperature calorimetry. Thermochim. Acta 1996, 287, 191–201. [Google Scholar] [CrossRef]
- Brandt, R.; Schulz, B. Specific heat of some Li-compounds. J. Nucl. Mater. 1988, 152, 178–181. [Google Scholar] [CrossRef]
- Asou, M.; Terai, T.; Takahashi, Y. High-temperature enthalpy-increment measurements and derived heat capacity of lithium orthosilicate (Li4SiO4) at temperatures from 300 K to 1000 K. J. Chem. Thermodyn. 1992, 24, 273–280. [Google Scholar] [CrossRef]
- Hollenberg, G.W. A transformation in lithium orthosilicate. J. Nucl. Mater. 1981, 103, 591–595. [Google Scholar] [CrossRef]
- Barin, I.; Platzki, G. Thermochemical Data of Pure Substances; Wiley Online Library: Hoboken, NJ, USA, 1989. [Google Scholar]
- Kleykamp, H. Enthalpies and heat capacities of Li2SiO3 and Li2ZrO3 between 298 and 1400 K by drop calorimetry. Thermochim. Acta 1994, 237, 1–12. [Google Scholar] [CrossRef]
- Bennington, K.; Ferrante, M.; Stuve, J. Thermodynamic Properties of two Lithium Silicates (Li2SiO3 and Li2Si2O5); US Department of the Interior, Bureau of Mines: Pittsburgh PA, USA, 1976.
- Stull, D.; Hildenbrand, D.; Oetting, F.; Sinke, G. Low-temperature heat capacities of 15 inorganic compounds. J. Chem. Eng. Data 1970, 15, 52–56. [Google Scholar] [CrossRef]
- Andersson, J.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar]
- Sundman, B.; Lukas, H.; Fries, S. Computational Thermodynamics: The Calphad Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Chang, K.; Hallstedt, B. Thermodynamic assessment of the Li–O system. Calphad 2011, 35, 160–164. [Google Scholar] [CrossRef]
- Dumitrescu, L.; Sundman, B. A thermodynamic reassessment of the Si-Al-O-N system. J. Eur. Ceram. Soc. 1995, 15, 239–247. [Google Scholar] [CrossRef]
- Dinsdale, A. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Wu, P.; Eriksson, G.; Pelton, A. Optimization of the thermodynamic properties and phase diagrams of the Na2O–SiO2 and K2O–SiO2 systems. J. Am. Ceram. Soc. 1993, 76, 2059–2064. [Google Scholar] [CrossRef]
- Ihle, H.; Penzhorn, R.; Schuster, P. The thermochemistry of lithium silicates in view of their use as breeder materials. Fusion Eng. Des. 1989, 8, 393–397. [Google Scholar] [CrossRef]
- Asano, M.; Kubo, K.; Nakagawa, H. Determination of heats of formation for solid and liquid lithium metasilicates by vaporization method. J. Nucl. Sci. Technol. 1983, 20, 1051–1053. [Google Scholar] [CrossRef][Green Version]
- Penzhorn, R.; Ihle, H.; Schuster, P.; Zmbov, K. The evaporation process of solid lithium metasilicate. J. Nucl. Mater. 1988, 155, 471–475. [Google Scholar] [CrossRef]
- Asano, M.; Nakagawa, H. Vaporization of lithium metasilicate in a graphite Knudsen cell. J. Nucl. Mater. 1989, 161, 190–196. [Google Scholar] [CrossRef]
- Migge, H. Estimation of free energies for Li8SiO6 and Li4SiO4 and calculation of the phase diagram of the Li-Si-O system. J. Nucl. Mater. 1988, 151, 101–107. [Google Scholar] [CrossRef]
- Ballo, R.; Dittler, E. Die binären Systeme: Li2SiO3: Al2(SiO3)3, Li4SiO4: Al4(SiO4)3, LiAlO2: SiO2 und Die Lithium-Aluminiumsilikatmineralien. Z. Für Anorg. Chem. 1912, 76, 39–69. [Google Scholar] [CrossRef]
- Jaeger, F.M.; Van Klooster, H.S. Studies in the field of silicate chemistry. I.Compounds of lithia with silica. Versl. Gewone Vergad. Afd. Natuurkd. K. Ned. Akad. Wet. 1914, 22, 900–923. [Google Scholar]
- Murthy, M.; Hummel, F. Phase equilibria in the system lithium metasilicate-forsterite–silica. J. Am. Ceram. Soc. 1955, 38, 55–59. [Google Scholar] [CrossRef]
- Boivin, P.; Berthelay, J.; Blanc, Y.; Coulet, A.; Castanet, R. Determination of temperature and enthalpy of melting of alkali disilicates by differential calorimetric analysis. J. Mater. Sci. 1993, 28, 1834–1838. [Google Scholar] [CrossRef]
- Charles, R. Activities in Li2O-, Na2O, and K2O-SiO2 Solutions. J. Am. Ceram. Soc. 1967, 50, 631–641. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).