Next Article in Journal
Iron-Containing Nickel Cobalt Sulfides, Selenides, and Sulfoselenides as Active and Stable Electrocatalysts for the Oxygen Evolution Reaction in an Alkaline Solution
Previous Article in Journal
Investigation of In-Situ Low Copper Alloying of 316L Using the Powder Bed Fusion Process
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Solids
Volume 4
Issue 3
10.3390/solids4030011
solids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

On the RE2TiAl3 (RE = Y, Gd–Tm, Lu) Series—The First Aluminum Representatives of the Rhombohedral Mg2Ni3Si Type Structure

by
Elias C. J. Gießelmann
1,
Stefan Engel
1,
Israa M. El Saudi
1,
Lars Schumacher
2,
Mathis Radzieowski
2,
Josef Maximilian Gerdes
2 and
Oliver Janka
1,*
1
Anorganische Festkörperchemie, Universität des Saarlandes, Campus C4.1, 66386 Saarbrücken, Germany
2
Institut für Anorganische und Analytische Chemie, Universität Münster, Corrensstrasse 28/30, 48149 Münster, Germany
*
Author to whom correspondence should be addressed.
Solids 2023, 4(3), 166-180; https://doi.org/10.3390/solids4030011
Submission received: 2 June 2023 / Revised: 21 June 2023 / Accepted: 28 June 2023 / Published: 5 July 2023
Browse Figures
Versions Notes

Abstract

:
Several ternary rare-earth metals containing titanium aluminum intermetallics in the RE2TiAl3 series (RE = Y, Gd–Lu) have been synthesized from the elements using arc-melting techniques. All compounds crystallize in the trigonal crystal system with rhombohedral space group R3m (Z = 3) and lattice parameters ranging between a = 582–570 and c = 1353–1358 pm. They adopt the Mg2Ni3Si-type structure, which is an ordered superstructure of the cubic Laves phase MgCu2 and has been observed for Al intermetallics for the first time. Tetrahedral [TiAl3] entities that are connected over all corners form a network where the empty [TiAl3] tetrahedra exhibit a full Ti/Al ordering based on the single crystal results. The Al atoms are arranged into 63 Kagomé nets, while the Ti atoms connect these nets over the triangular units. In the cavities of this three-dimensional arrangement, the RE cations can be found forming a distorted diamond-type substructure. Magnetic measurements revealed that Y2TiAl3 and Lu2TiAl3 are Pauli paramagnetic substances, in line with the metallic character. The other compounds exhibit paramagnetism with antiferromagnetic ordering at a maximum Néel temperature of TN = 26.1(1) K for Gd2TiAl3.

Graphical Abstract

1. Introduction

The Laves phases of general composition AB2, named after Fritz Laves, belong to the most prominent structure types in the field of intermetallic compounds [1,2,3]. The Pearson database [4] lists over 4000 (pseudo) binary compounds in the cubic MgCu2 (Fd3m) or the hexagonal MgZn2 and MgNi2 (both P63/mmc)-type structures [5]. The majority of these compounds contain a rare-earth element; therefore, the magnetic properties of these materials have been studied in great detail [6]. Their structures usually do not show larger homogeneity ranges and can be regarded as packing dominated as illustrated by the fact that, for example, NeHe2 [7] and ArNe2 [8] can be observed under high-pressure conditions and adopt the MgZn2-type structure. Moreover, Ar(H2)2 was reported to form the hexagonal Laves phase at high pressure [9], while Xe(N2)2 adopts the cubic MgCu2-type structure [10]. The ideal size ratio of the constituent elements A and B is rA/rB = (3/2)1/2 ≈ 1.225. In all three binary Laves phases, the B atoms form empty B4 tetrahedra that exhibit different connectivities, always forming a network, with the A atoms in the respective cavities. In the MgCu2-type structure, however, only corner-sharing Cu4 tetrahedra are present; in the MgZn2-type structure, two tetrahedra are connected over a common face, and the remaining corners are used to form strands [001]. Finally, in MgNi2, both connection modes can be found. In addition to these basic types, different (highly complex) stacking variants have been reported [11]. Based on these binary structure types, ordered ternary compounds can be derived. The Mg2Cu3Si (P63/mmc)-type structure [12], for example, allows for an ordering on the two crystallographic Zn sites of the hexagonal MgZn2-type structure. Besides the prototype, aluminum compounds (e.g., Ce2RuAl3 [13], the RE2TAl3 series with RE = Y, La–Nd, Sm, Gd–Lu and T = Ru, Rh, Ir [14], U2Cu3Al [15] or the solid solution Ti2Ni1–xAl3+x [16]) along with gallides (U2Fe3Ga [17], Eu2IrGa3 [18], Nb2Cu1.1Ga2.9 [19], and Ho2Ru2Ga2 [20]), silicides (e.g., the Sc2T3Si and Ti2T3Si series with T = Cr, Mn, Fe, Co, and Ni [21,22,23]), and germanides (U2T3Ge series with T = Mn, Fe, Co [24,25,26,27], Mn2Cu3Ge [28], and Mn2Co3Ge [29]) have been reported. The cubic MgCu4Sn-type structure (F43m) [30] is a ternary ordered variant of the cubic MgCu2 type, where magnesium/tin ordering takes place on the former Mg site. Exemplarily, the rare-earth-containing series RENi4In (RE = Sc, Y, La–Nd, Sm, Gd–Tm) [31], RENi4Au (RE = Sc, Y, Gd–Lu) [32,33], RECu4Ag (RE = La–Nd, Sm, Gd–Tm) [34], and RECu4Au (RE = Gd–Er) [35] should be mentioned. Furthermore, Yb6Ir5Ga7 [36] represents a √3 × √3 superstructure of the hexagonal MgZn2-type structure, allowing for a coloration of the tetrahedral strands of the prototype. To date, the iridium gallides RE6Ir5Ga7 (RE = Sc, Y, Nd, Sm, Gd–Lu) [36,37] and the RE6T5Al7 series (RE = Sc, Y, Ce–Nd, Sm, Gd–Lu, T = Ru, Ir) [38] have been reported. Finally, a rhombohedral ordered variant of the MgCu2 type is observed for the Mg2Ni3Si (R3m) type structure [39], realized, e.g., for the gallides RE2Rh3Ga (RE = Y, La–Nd, Sm, Gd–Er) [40], the silicides RE2Rh3Si (RE = Ce, Pr, Er) [41,42,43] and U2Ru3Si [44], or the germanides RE2T3Ge (RE = Y, Pr, Sm, Er) [41,45], U2Ru3Ge [44], and Ca2Pd3Ge [46]. More information on superstructures of the Laves phases can be found in a recent review article [47].
With respect to application, titanium and aluminum-based materials are of great interest since they belong to the group of light-weight alloys [48]. Therefore, the binary phase diagram Ti/Al is probably one of the best investigated ones [49,50,51,52,53]. Several binary intermetallics have been identified in this system, of which TiAl2 and TiAl3 are too brittle to be of technical importance; however, α2-Ti3Al and γ-TiAl are of crucial importance to the field of titanium-based alloys [54,55].
Here, we report on the synthesis and structural and magnetic characterization of the RE2TiAl3 series (RE = Y, Gd–Tm, Lu), the first aluminum intermetallics adopting the rhombohedral Mg2Ni3Si-type structure. However, as seen for many aluminum series, they form an anti-type arrangement within the network in comparison to the [Ni3Si] one, that is, the prototype.

2. Materials and Methods

Synthesis: The compounds of the RE2TiAl3 (RE = Y, Gd–Tm, Lu) series were synthesized by arc-melting the elements, using rare-earth ingots (Onyxmet, 99.9%), titanium chips (Onyxmet, 99.9%), and aluminum turnings (Onyxmet, 99.99%). All starting materials were weighed in the ideal stoichiometry of 2:1:3 (RE:Ti:Al). The reactants were arc-melted under an argon atmosphere of about 800 mbar [56]. The obtained buttons were remelted several times to increase the homogeneity. All samples were weighed after arc-melting; the mass loss is <0.5%. The samples were subsequently enclosed in evacuated quartz tubes and annealed in a second step (923 or 1123 K, 7 to 12 d) to increase their overall phase purity and homogeneity. The Tm2TiAl3 sample was transferred to an Al2O3 crucible and annealed for 3 h in an induction furnace (Trumpf Hüttinger, TruHeat 5010, Freiburg, Germany). The annealing led to X-ray pure samples, suitable for physical property measurements. All samples obtained by these processes show metallic luster and are stable under ambient conditions over months.
SEM-EDX data: Semiquantitative EDX analyses of the bulk samples were conducted on a JEOL 7000F (Jeol, Freising, Germany) equipped with an EDAX Genesis 2000 EDX detector (EDAX, Unterschleissheim, Germany). Investigations of the single crystals were conducted on a Zeiss Evo MA10 (Zeiss, Jena, Germany) scanning electron microscope with an Oxford Instrument EDX detector using REF3, TiO2, and Al2O3 as internal standards. The crystals used for the structure determination were measured on their glass fibers in the variable pressure (VP) mode of the instrument under 60 Pa N2 atmosphere.
X-Ray diffraction: The annealed polycrystalline samples were analyzed by powder X-ray diffraction. Powder X-ray diffraction (PXRD) patterns of the pulverized samples were recorded at room temperature on a D8-A25-Advance diffractometer (Bruker, Karlsruhe, Germany) in Bragg–Brentano θ-θ-geometry (goniometer radius 280 mm) with Cu Kα-radiation (λ = 154.0596 pm). A 12 µm Ni foil working as Kβ filter and a variable divergence slit were mounted at the primary beam side. A LYNXEYE detector with 192 channels was used at the secondary beam side. Experiments were carried out in a 2θ range of 6 to 130° with a step size of 0.013° and a total scan time of 1 h.
Small fragments of the annealed and crushed samples of Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 were glued to thin quartz fibers using beeswax. The crystallite quality was checked by Laue photographs on a Buerger precession camera (white molybdenum radiation; imaging plate system, Fujifilm, BAS-READER 1800, Minato, Japan). Intensity data sets of suitable single crystals were collected at room temperature, either on an IPDS-II (graphite-monochromatized MoKα radiation; λ = 0.71073 pm; oscillation mode) or on a Bruker D8 Venture diffractometer (graphite-monochromatized MoKα radiation; λ = 0.71073 pm) equipped with a μ-focus source.
CCDCs 1939725-1939727 contain the supplementary crystallographic data for this paper. The data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/structures.
Physical property measurements: Annealed pieces of the respective X-ray pure RE2TiAl3 (RE = Y, Gd–Tm, Lu) samples were attached to the sample holder rod of a Vibrating Sample Magnetometer (VSM) using Kapton foil for measuring the magnetization M(H,T) in a Quantum Design (San Diego, CA, USA) Physical Property Measurement System (PPMS). All samples were investigated in the temperature range of 2.5–300 K with applied external magnetic fields of up to 80 kOe.

3. Results and Discussion

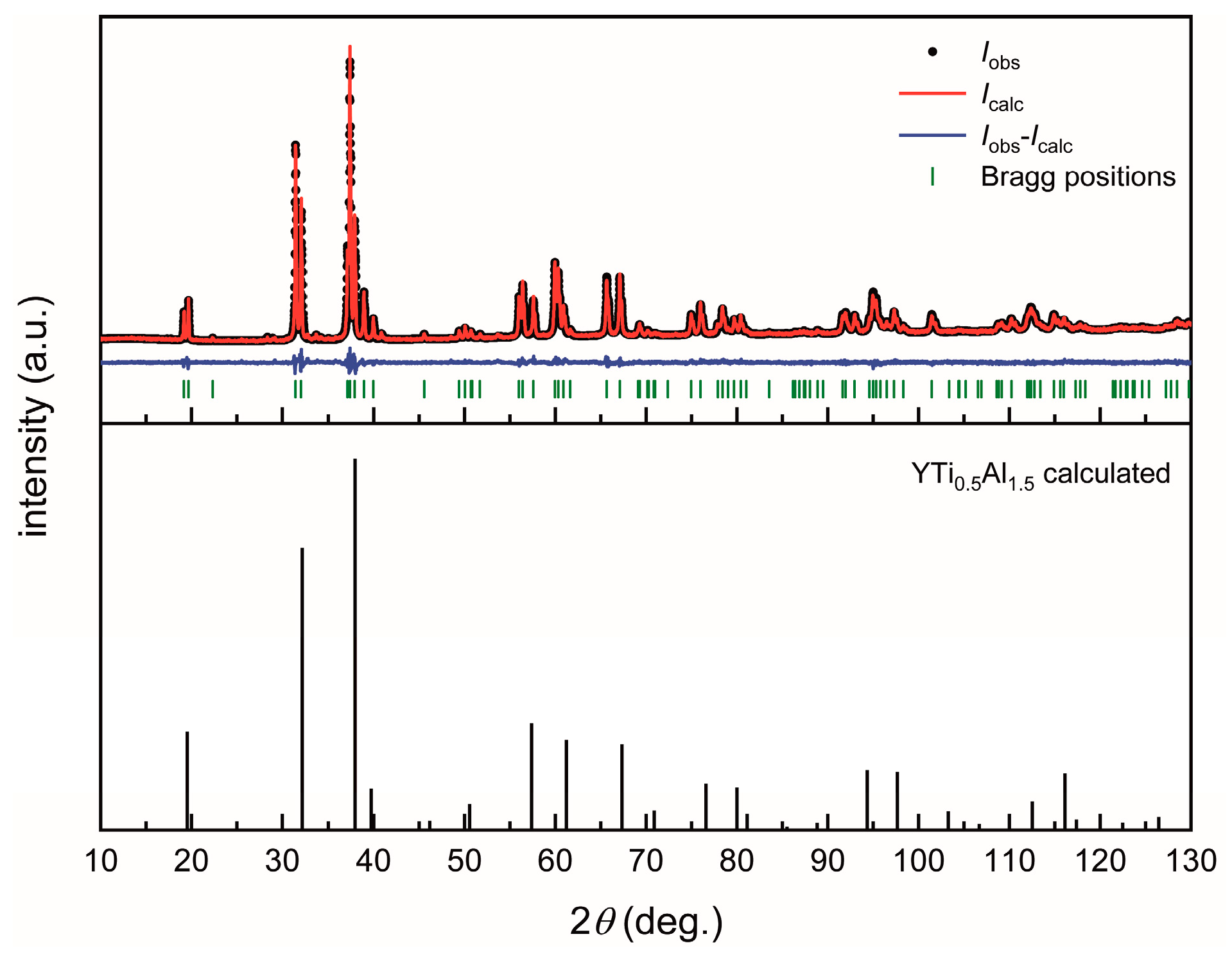
3.1. Structure Refinement

The obtained single crystal data sets showed a rhombohedral lattice; space group R3m was found to be correct during the structure refinement. Isotypism to the Mg2Ni3Si-type structure was evident from both single crystal and powder X-ray diffraction experiments. Starting values for the structure refinement were obtained using the SuperFlip [57] program package, implemented in Jana2006 [58,59]. All atomic positions and anisotropic displacement parameters were subsequently refined, again using Jana2006. Occupancy parameters of all crystallographic sites were individually refined in separate series of least-squares refinements to check for the correct composition. No mixing, especially of Ti and Al, was observed. The final difference Fourier syntheses were contourless. Details on the measurements, refined atomic parameters, displacement parameters, and interatomic distances can be found in Table 1, Table 2, Table 3 and Table 4.

3.2. SEM-EDX Data

EDX investigations of the bulk samples were carried out exemplarily on Er2TiAl3, Tm2TiAl3, and Lu2TiAl3. The experimentally determined averaged element ratios (Table 5) were obtained from five spot measurements and one area measurement and are in good agreement with the ideal compositions. The crystals of Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 measured on the diffractometer were analyzed semi-quantitatively using a SEM in combination with EDX (Table 5). No impurity elements heavier than sodium (detection limit of the instrument) were observed. The experimentally determined averaged element ratios were obtained from five spot measurements and are in good agreement with the ideal compositions. Differences originate from the conchoidal fractures of the crystallites and the non-perfect perpendicular orientation of the crystals to the beam.

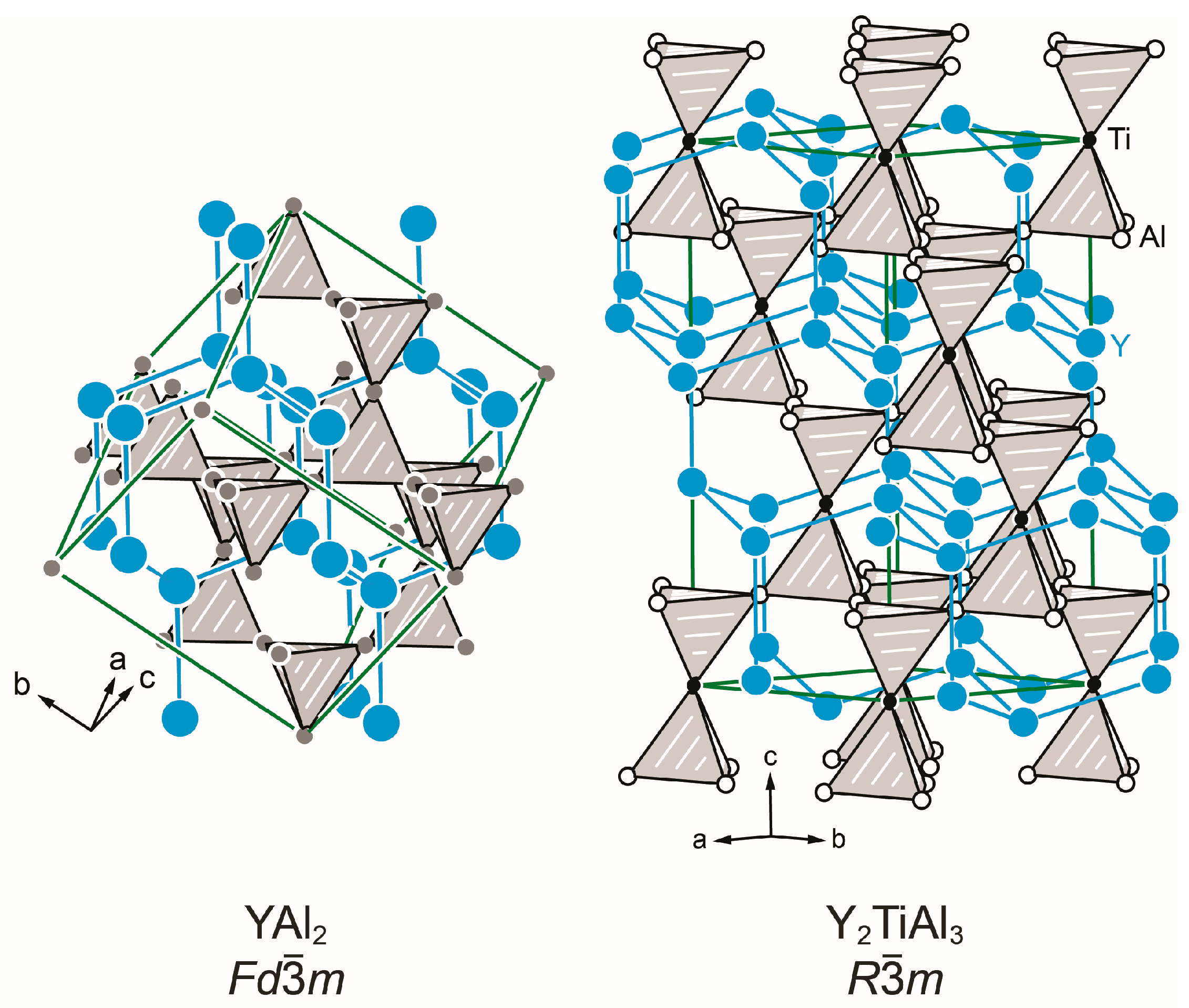
3.3. Crystal Chemistry

The rare-earth compounds of the RE2TiAl3 series (RE = Y, Gd–Tm, Lu) crystallize in the trigonal Mg2Ni3Si-type structure with space group R3m and Z = 3. The lattice parameters and unit cell volumes (Table 6) decrease from the gadolinium to the lutetium compound, as expected due to the lanthanide contraction (Figure 1, Table 6). Y2TiAl3 exhibits lattice parameters similar to those of Tb2TiAl3, in line with the comparable ionic radii of the trivalent cations (Y3+: 106 pm; Tb3+ 104 pm; CN = 8 [60]). In Figure 2, a comparison of the Rietveld fit of the experimental diffraction pattern of Y2TiAl3 using the trigonal Mg2Ni3Si type and the cubic MgCu2-type structure is shown. The rhombohedral distortion is easily visible in the diffraction patterns due to the splitting of the reflections (Figures S1–S6, Tables S1–S6).
Table 1. Crystallographic data and structure refinement information for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3, space group R3m, Z = 3, Mg2Ni3Si type determined from single crystal X-ray diffraction data. All data sets were collected at room temperature.
Table 1. Crystallographic data and structure refinement information for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3, space group R3m, Z = 3, Mg2Ni3Si type determined from single crystal X-ray diffraction data. All data sets were collected at room temperature.
Formula Y2TiAl3Gd2TiAl3Tb2TiAl3
CCDC number193972519397271939726
Molar mass, g mol−1306.6443.3446.7
Lattice parameterssee Table 6
Density calc., g cm−34.045.775.90
Crystal size, µm 50 × 40 × 3530 × 25 × 1040 × 40 × 20
Diffractometer IPDS-IIIPDS-IIBruker CCD
Wavelength; λ, pmMoKα; 71.073MoKα; 71.073MoKα; 71.073
Transmission ratio (min/max)0.2943/0.41020.5295/0.76730.3054/0.5561
Detector distance, mm607040
Exposure time, min10300.167
Integr. param. A, B, EMS14.0; −1.0; 0.03016.0; –4.0; 0.030–
F(000), e417567573
Range in hkl±9; −8, +9, ±21±8; ±8, ±20±7; ±8, −17, +20
θmin, θmax, deg4.4/34.94.4/33.34.4/32.0
Linear absorption coeff., mm−124.727.629.7
Total no. of reflections28891579826
Independent reflections/Rint229/0.0510212/0.0696190/0.0143
Reflections with I ≥ 3σ(I)/Rσ191/0.0168175/0.0275181/0.0122
Data/parameters229/11212/11190/11
R1/wR2 for I ≥ 3σ(I)0.0177/0.03570.0208/0.02140.0105/0.0259
R1/wR2 for all data0.0286/0.03930.0317/0.02210.0111/0.0260
Goodness-of-fit on F21.231.161.03
Extinction schemeLorentzian isotropic [61]
Extinction coefficient160(50)58(19)350(20)
Diff. Fourier residues /e– Å−3−1.32/+1.01−1.81/+1.40−0.37/+1.06
Table 2. Atom positions and equivalent isotropic displacement parameters (pm2) for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 determined from single crystal X-ray diffraction data. Ueq is defined as one-third of the trace of the orthogonalized Uij tensor.
Table 2. Atom positions and equivalent isotropic displacement parameters (pm2) for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 determined from single crystal X-ray diffraction data. Ueq is defined as one-third of the trace of the orthogonalized Uij tensor.
AtomWyckoff
Position		xyzUeq
Y2TiAl3
Y6c000.37244(4)89(1)
Ti3a00075(2)
Al9d1/201/288(3)
Gd2TiAl3
Gd6c000.37333(3)81(1)
Ti3a00067(5)
Al9d1/201/284(7)
Tb2TiAl3
Tb6c000.37348(1)64(1)
Ti3a00054(2)
Al9d1/201/269(3)
Table 3. Anisotropic displacement parameters (pm2) for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 determined from single crystal X-ray diffraction data. Coefficients Uij of the anisotropic displacement factor tensor of the atoms are defined by −2π2[(ha*)2U11 + … + 2hka*b*U12].
Table 3. Anisotropic displacement parameters (pm2) for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 determined from single crystal X-ray diffraction data. Coefficients Uij of the anisotropic displacement factor tensor of the atoms are defined by −2π2[(ha*)2U11 + … + 2hka*b*U12].
AtomU11U22U33U12U13U23
Y2TiAl3
Y86(2)U1194(2)43(1)0U13
Ti79(3)U1166(4)40(1)0U13
Al84(3)86(4)95(5)43(2)5(2)10(1)
Gd2TiAl3
Gd79(2)U1184(2)40(1)0U13
Ti74(5)U1154(9)37(3)0U13
Al77(6)80(11)95(10)40(5)4(6)8(13)
Tb2TiAl3
Tb62(1)U1169(1)31(1)0U13
Ti55(3)U1152(4)28(1)0U13
Al74(3)68(5)64(4)34(2)2(2)5(3)
Table 4. Interatomic distances (pm) for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 determined from single crystal X-ray diffraction data. All distances of the first coordination spheres are listed. All standard uncertainties were less than 0.1 pm.
Table 4. Interatomic distances (pm) for Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 determined from single crystal X-ray diffraction data. All distances of the first coordination spheres are listed. All standard uncertainties were less than 0.1 pm.
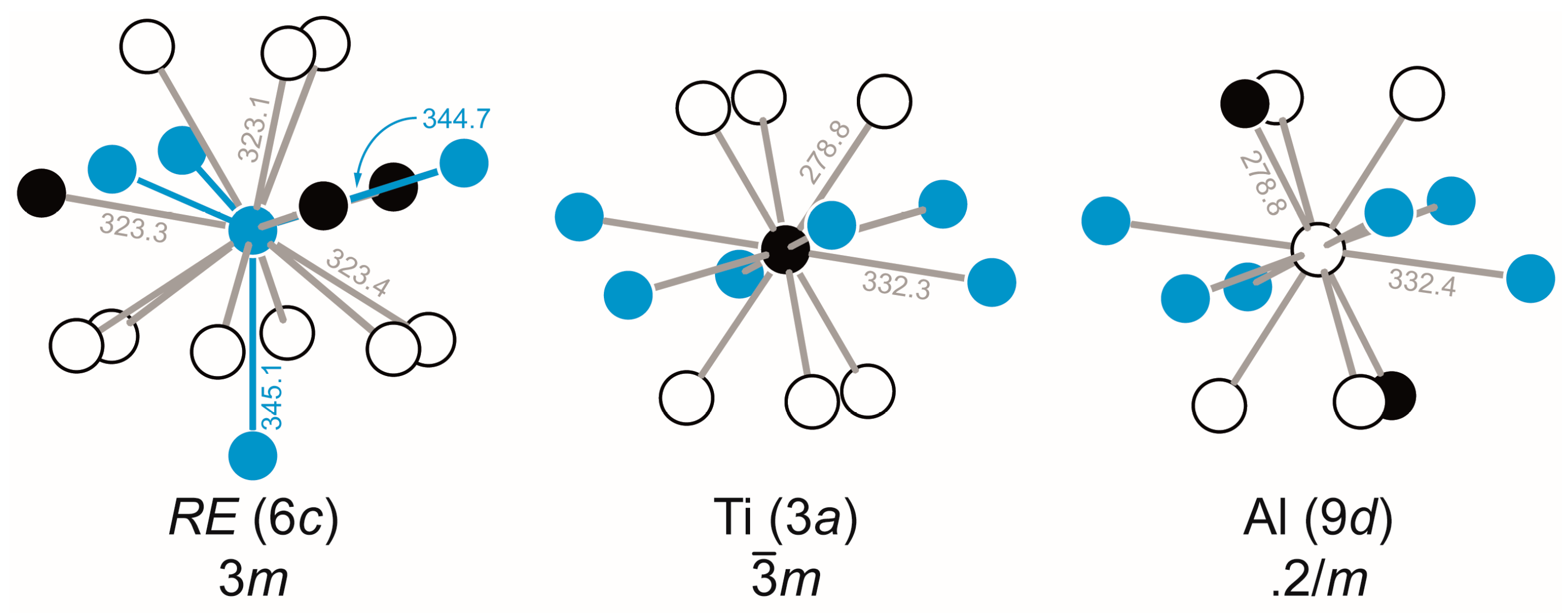
Y2TiAl3Gd2TiAl3Tb2TiAl3
Y:3Al323.1Gd:3Al325.4Tb:3Al324.1
3Ti332.3 6Al333.1 6Al331.3
6Al332.4 3Ti333.8 3Ti332.1
3Y344.7 1Gd344.1 1Tb342.2
1Y345.1 3Gd346.8 3Tb345.1
Ti:6Al278.8Ti:6Al279.9Ti:6Al278.6
6Y332.3 6Gd333.8 6Tb332.1
Al:2Ti278.8Al:2Ti279.9Al:2Ti278.6
4Al284.1 4Al285.2 4Al283.7
2Y323.1 2Gd325.4 2Tb324.1
4Y332.4 4Gd333.1 4Tb331.3
Table 5. SEM-EDX data of the rhombohedral RE2TiAl3 series. Standard deviations are ±2 at.-%.
Table 5. SEM-EDX data of the rhombohedral RE2TiAl3 series. Standard deviations are ±2 at.-%.
CompoundRE (at.-%)Ti (at.-%)Al (at.-%)
Ideal composition33.316.750.0
Single crystal data
Y2TiAl3361648
Gd2TiAl3341650
Bulk sample data
Er2TiAl3361450
Tm2TiAl3321652
Lu2TiAl3371548
Table 6. Lattice parameters of the rhombohedral RE2TiAl3 series (RE = Y, Gd–Tm, Lu), space group R3m, Z = 3, Mg2Ni3Si type, determined by powder X-ray diffraction. P denotes powder data, SC single crystal data.
Table 6. Lattice parameters of the rhombohedral RE2TiAl3 series (RE = Y, Gd–Tm, Lu), space group R3m, Z = 3, Mg2Ni3Si type, determined by powder X-ray diffraction. P denotes powder data, SC single crystal data.
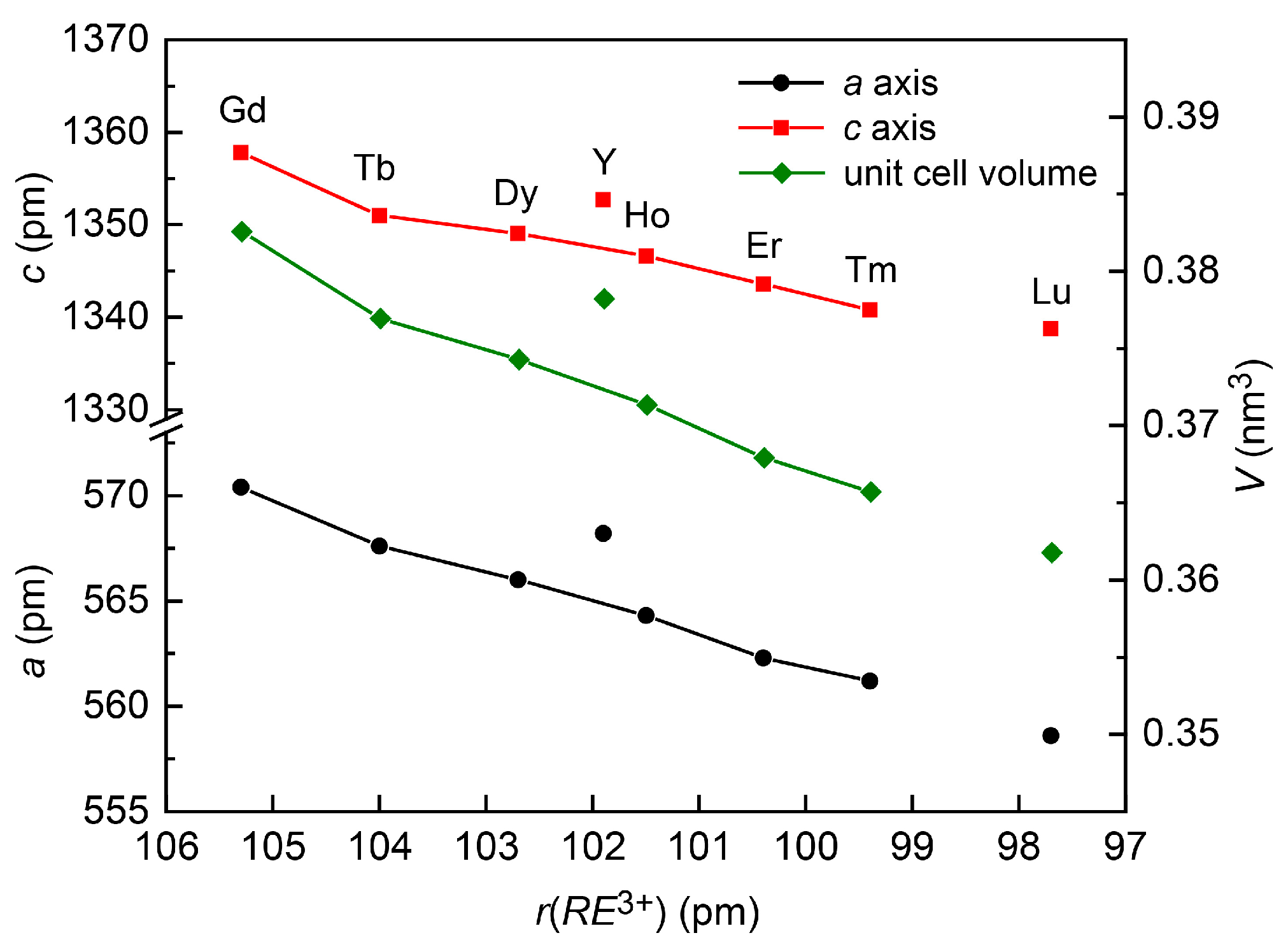
Compounda (pm)c (pm)V (nm³)
Y2TiAl3 P568.29(4)1353.0(1)0.3784
Y2TiAl3 SC568.22(7)1352.9(2)0.3783
Gd2TiAl3 P569.81(5)1359.6(2)0.3823
Gd2TiAl3 SC570.45(5)1358.0(1)0.3827
Tb2TiAl3 P567.55(6)1351.0(3)0.3769
Tb2TiAl3 SC567.39(6)1352.4(2)0.3771
Dy2TiAl3 P565.90(6)1349.1(2)0.3742
Ho2TiAl3 P564.86(3)1347.5(1)0.3723
Er2TiAl3 P563.10(3)1344.3(1)0.3691
Tm2TiAl3 P559.61(9)1341.3(3)0.3638
Lu2TiAl3 P558.37(4)1338.2(1)0.3613
The following discussion of the crystal structure and the interatomic distances is based on the single crystal data obtained for Y2TiAl3. As the crystal structure (Figure 3) can be derived from the cubic Laves phase (MgCu2 type, Fd3m), the structural relationship is fairly obvious. A group–subgroup scheme according to the Bärnighausen formalism for the structural relationship of CeRh2 and Ce2Rh3Ga has been provided in the literature [40]. As in the MgCu2-type structure, only two crystallographic positions are occupied (Mg on 8a, 0,0,0; Cu on 16c, 3/8, 3/8, 3/8) and no distinct ordering is possible. A translationengleiche transition of index 4 leads to the structure of Mg2Ni3Si in the rhombohedral crystal system and space group R3m. This allows for a decoupling of the lattice parameters along with the possibility of atomic ordering (16c splits into 3a and 9d). In addition, Mg atoms (6c) gain a free z parameter allowing the adjustment of interatomic distances. A recent review article [47] summarizes the information on the superstructures of Laves phases.
The tetrahedral entities in the cubic structure type are connected over all corners, forming a network, however, by only one crystallographic position. In rhombohedral Y2TiAl3, a splitting of this single position takes places, allowing full Ti/Al ordering in the empty [TiAl3] tetrahedra. The Al atoms form 63 Kagomé nets, while the Ti atoms connect these nets over the triangles. In the cavities of this three-dimensional arrangement, the RE cations can be found. They form a distorted cubic diamond-type substructure, as highlighted in Figure 3. The coordination environments of the Ti and Al atoms are depicted in Figure 4. In the network, Ti–Al distances of 279 pm can be found, longer than the sum of the covalent radii (Ti + Al = 132 + 125 = 257 pm [60]), suggesting moderate bonding interactions. In the binary compounds TiAl (tetragonal CuAu type, P4/mmm [62]) and Ti3Al (hexagonal Mg3Cd type, P63/mmc [63]), interatomic distances of 283 and 286 + 289 pm are observed, respectively, while in the only thus far known ternary compound Y6Ti4Al43 (hexagonal Ho6Mo4Al43 type, P63/mcm [64]), Ti–Al distances of 259–287 pm are found. The Y atoms in Y2TiAl3 are surrounded by 16 atoms in the shape of a Frank–Kasper polyhedra [65,66] according to Y@Al9Y4Ti3 (Figure 4, top), while Ti and Al both exhibit icosahedra coordination environments (Figure 4, middle and bottom). The Ti atoms are surrounded octahedrally by the Al atoms along with six Y atoms (Y@Al6Y6), the Al atoms by four Al, two Ti, and six Y atoms (Al@Al4Ti2Y6). The Y–Ti distances are 332 pm, while the Y–Al distances range between 323 and 332 pm, suggesting rather weak interactions when compared to the sum of the covalent radii (Y + Ti = 162 + 132 = 294 pm; Y + Al = 162 + 125 = 287 pm [60]). In YAl2 (cubic MgCu2 type, Fd3m [67,68]), heteroatomic Y–Al distances of 325 pm can be observed, which suggest rather low interactions. Since no binary phases in the system Y/Ti exist; only the comparison with Y6Ti4Al43 [64] is possible. The shortest Y–Ti distance is 354 pm, also suggesting very weak to no bonding interactions, while Y–Al distances between 308 and 344 pm are observed. In Y2TiAl3, two different Y–Y distances (344.7 and 345.2 pm) are observed, due to the distortion of the cubic MgCu2-type structure. In cubic YAl2 [67,68], only one distance of 340 pm is found.
Attempts to extend the series of the RE2TiAl3 compounds to the larger elements (RE = La-Nd, Sm, Eu) were not successful. For the lanthanum compound, a synthesis under the same conditions as described above resulted in a mixture of the binary compounds LaAl2 (MgCu2 type), LaAl (CeAl type) and elemental titanium (Mg type). The refined powder pattern is shown in Figure S7 (Table S7).

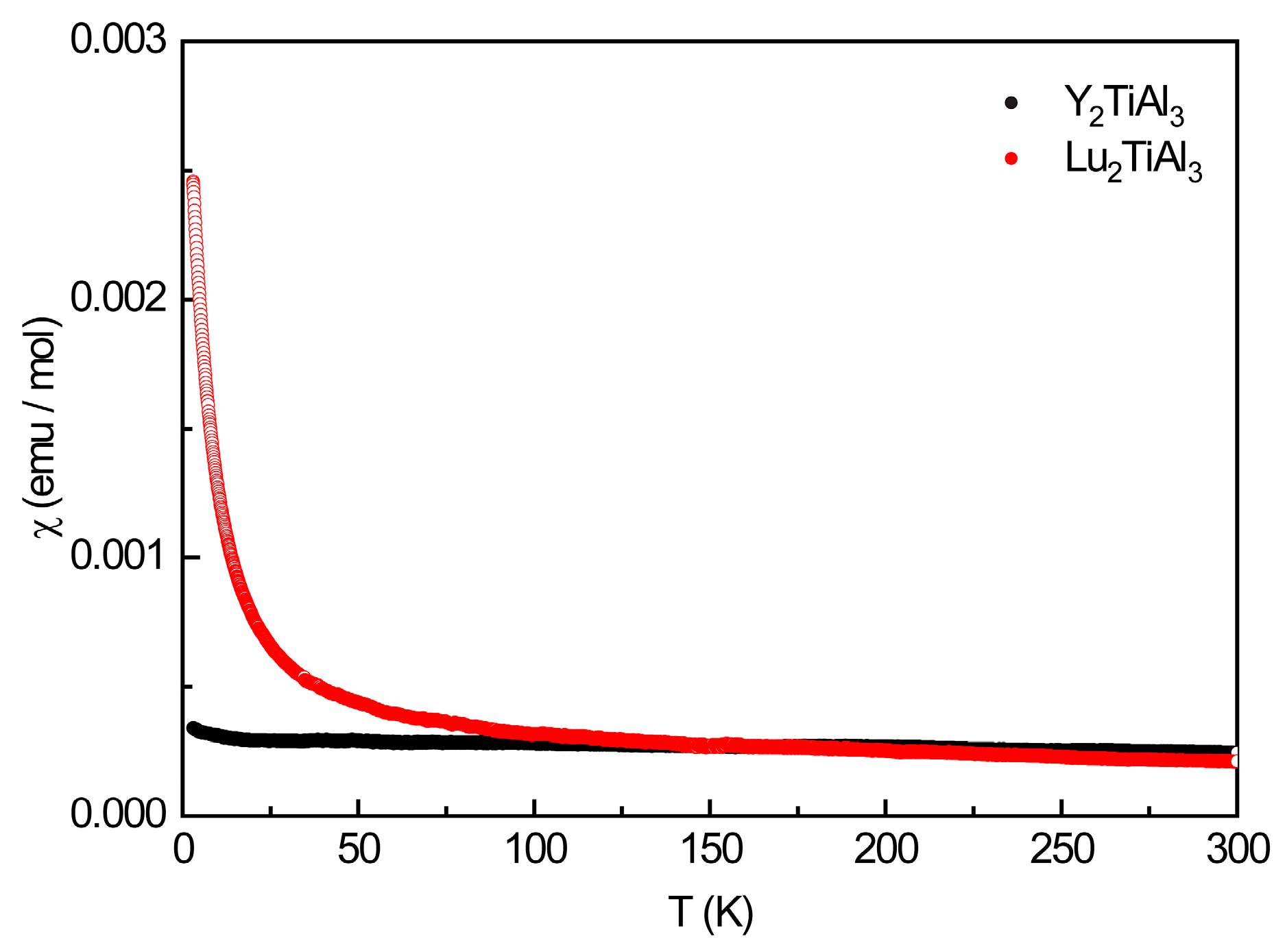
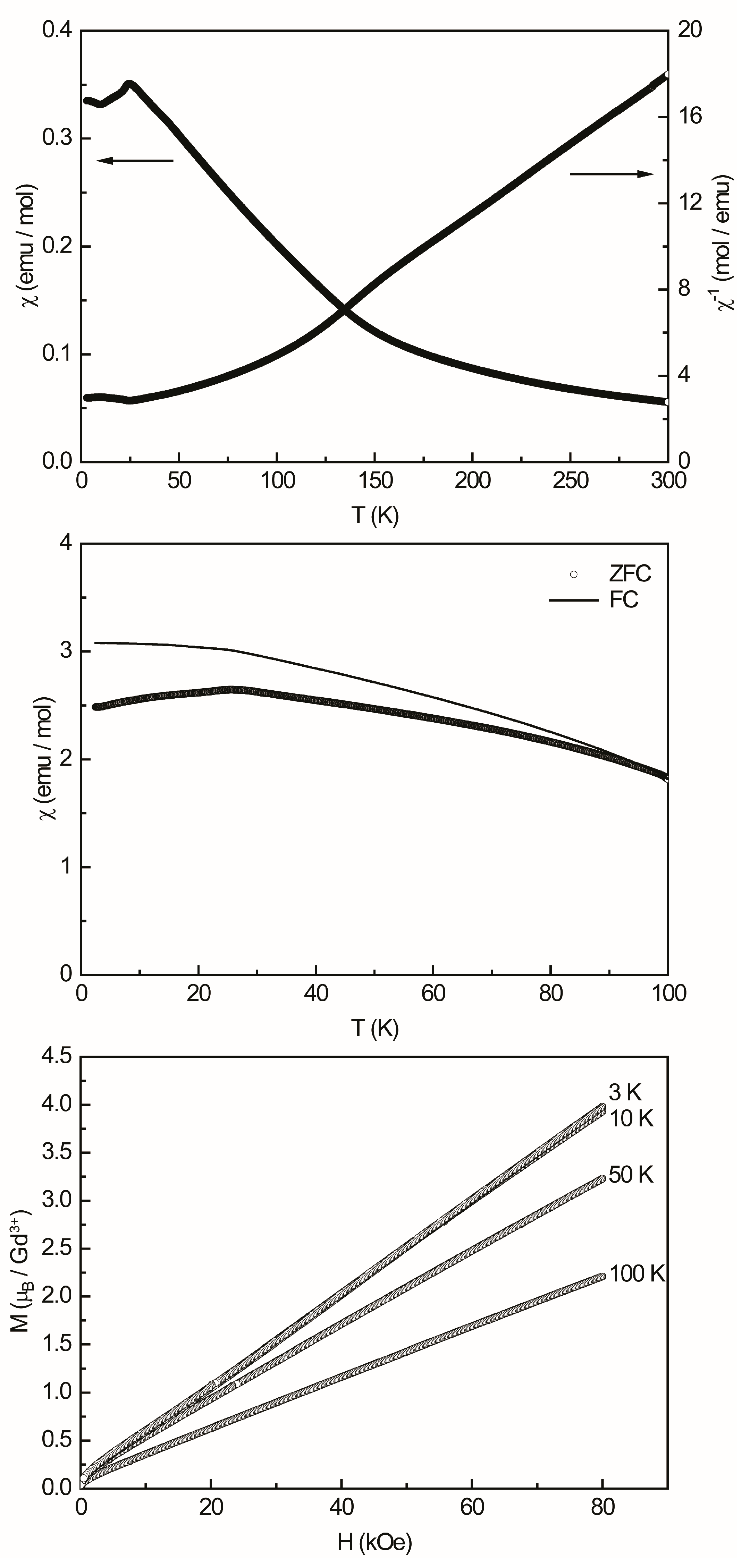
3.4. Physical Properties

The physical properties of the RE2TiAl3 series (Table 7; RE = Y, Gd–Tm, Lu) were determined by susceptibility and magnetization experiments. While Y2TiAl3 and Lu2TiAl3 exhibit Pauli paramagnetism, in line with their metallic character and the absence of (unpaired) f-electrons, all other compounds are paramagnetic. The temperature dependence of the magnetic susceptibility of Y2TiAl3 and Lu2TiAl3 is depicted in Figure 5. The susceptibility exhibits positive values over the whole investigated temperature region and reaches χ(300 K) = +2.48(1) × 10−4 emu mol−1 (Y2TiAl3) and χ(300 K) = +2.14(1) × 10−4 emu mol−1 (Lu2TiAl3), indicating that the Pauli paramagnetism overcompensates the intrinsic diamagnetism.
The magnetic data of Gd2TiAl3 is depicted in Figure 6. The ZFC (zero-field-cooled) investigations at high field (10 kOe) were conducted in the temperature range of 3–300 K and are shown in the top panel. From the inverse susceptibility, the effective magnetic moment was determined to μeff = 7.89(1) μB, well in line with the theoretical moment of μeff,calc = 7.94 μB for a free Gd3+ cation. The paramagnetic Curie temperature is θP = +20.8(1) K, indicating dominant ferromagnetic interactions in the paramagnetic temperature regime. From the low-field 100 Oe ZFC/FC (zero-field-cooled/field-cooled) measurements, an antiferromagnetic ordering was derived with a Néel temperature of TN = 26.1(1) K. The rather strong bifurcation, along with the high residual magnetization, however, indicates that the investigated sample could contain ferromagnetic impurities. Samples of the same composition but from different batches exhibit a similar behavior. Therefore, homogeneity ranges within the samples are suspected. One impurity might be GdAl2 [69], which exhibits ferromagnetic ordering below TC = 170 K. Therefore, pure GdAl2 cannot be the impurity but the solid solution GdTixAl2–x could be responsible for the magnetic behavior. Since these compounds crystallize in the cubic MgCu2-type structure, trace impurities are invisible in the powder X-ray patterns, since the reflections overlap with those of rhombohedral Gd2TiAl3 (Figure 2). However, since ferromagnetic transitions are significantly stronger compared to antiferromagnetic ones (factor 1000 to 10,000), only traces of the respective impurity can be present. The magnetization isotherms (Figure 6, bottom) finally exhibit a steep increase already at low magnetic fields. This is an additional indication of the presence of ferromagnetic impurities. The 50 and 100 K isotherms are linear, as expected for a paramagnetic material; those measured at 3 and 10 K show a very weak curvature that could indicate an upcoming spin-reorientation at even higher fields. The comparatively low saturation magnetization of μsat = 3.98(1) μB reached at 3 K and 80 kOe also underlines a strong antiferromagnetic ground state. Similar effects have been observed, e.g., for GdPtGe2 [70] or Gd3Pt4Ge6 [71]. Usually, Gd intermetallics reach (nearly) the theoretical full saturation magnetization μsat,theo = 7 μB according to gJ × J, as seen, e.g., for GdAl2 [72], Gd3Al2 [72], Gd2RhAl3 [14], or GdPt6Al3 [73].
Er2TiAl3 could be obtained in nearly pure form; the magnetic data are depicted in Figure 7. The effective magnetic moment was determined to be μeff = 9.73(1) μB and is slightly enhanced compared to the theoretical moment of μeff,calc = 9.58 μB for a free Er3+ cation; the paramagnetic Curie temperature is θP = −6.5(1) K, indicating antiferromagnetic interactions in the paramagnetic temperature regime. An antiferromagnetic ordering was derived from the low-field zero-field-cooled measurements (Figure 7, middle) with a Néel temperature of TN = 17.6(1) K; however, again a bifurcation is visible, suggesting traces of ferromagnetic impurities. The magnetization isotherms (Figure 7, bottom) at 50 and 100 K isotherms are linear, as expected for a paramagnetic material; the ones measured at 3 and 10 K show an S-shape with a curvature that indicates a spin-reorientation at a critical field of Hcrit = 20.7(5) kOe, determined by the derived value of the 3 K isotherm. The saturation magnetization of μsat = 4.46(1) μB reaches 3 K and 80 kOe, which is below the expected value of μsat,theo = 9 μB according to gJ × J.
Table 7. Physical properties of the RE2TiAl3 (RE = Y, Gd–Tm; Lu) series: TN, Néel temperature; µexp, experimental magnetic moment; µeff, effective magnetic moment; θP, paramagnetic Curie temperature; µsat, experimental saturation magnetization; gJ × J, theoretical saturation magnetization.
Table 7. Physical properties of the RE2TiAl3 (RE = Y, Gd–Tm; Lu) series: TN, Néel temperature; µexp, experimental magnetic moment; µeff, effective magnetic moment; θP, paramagnetic Curie temperature; µsat, experimental saturation magnetization; gJ × J, theoretical saturation magnetization.
CompoundTN (K)µexp (µB)µeff (µB)θP (K)µsat (µB per RE3+)gJ × J (µB per RE3+)
Y2TiAl3Pauli-paramagnetic, non-superconducting, χ(300 K) = +2.48(1) × 10−4 emu mol−1
Gd2TiAl326.1(1)7.98(1)7.94+20.8(1)3.98(1)7
Tb2TiAl324.0(1)10.04(1)9.72+31.7(1)3.58(1)9
Dy2TiAl326.1(1)11.14(1)10.65−0.29(1)7.98(1)10
Ho2TiAl310.3(1)10.85(1)10.61+0.72(1)7.36(1)10
Er2TiAl317.6(1)9.73(1)9.58−6.5(1)4.46(1)9
Tm2TiAl310.8(1)7.69(1)7.61−7.3(1)3.46(1)7
Lu2TiAl3Pauli-paramagnetic, non-superconducting, χ(300 K) = +2.14(1) × 10−4 emu mol−1

4. Conclusions

In this paper, we present the synthesis as well as structural and magnetic characterization of the RE2TiAl3 series with RE = Y, Gd–Tm, and Lu. These compounds adopt the rhombohedral Mg2Ni3Si-type structure and are the first representations in the field of aluminum intermetallics. The crystal structures of Y2TiAl3, Gd2TiAl3, and Tb2TiAl3 have been refined from single crystal X-ray diffraction data and clearly indicate the formation of the rhombohedral structure. Powder X-ray diffraction experiments underline this observation as the diffraction patterns exhibit the expected splitting of reflections based on the transition from the cubic to the rhombohedral crystal system. Powder patterns of selected members of the series have been refined using the Rietveld method. All compounds have been characterized by magnetic susceptibility and magnetization experiments. While Y2TiAl3 and Lu2TiAl3 exhibit a nearly temperature independent behavior in line with the expected Pauli paramagnetism, the other compounds of the series show a stable trivalent oxidation state of the rare-earth atoms. All compounds exhibit antiferromagnetic transitions at lower temperatures; however, sometimes traces of ferromagnetic impurities can be observed. These originate from impurities that crystallize in the cubic MgCu2-type structure and have to be considered solid solutions according to RETixAl2–x. Even small traces of these compounds provide visible features in the magnetic data since ferromagnetic transitions are significantly stronger than antiferromagnetic ones. An identification of these impurities is impossible since their reflections overlap with those of the rhombohedral main phase. Finally, the valence electron concentration (VEC) also shows an intriguing feature. The title compounds exhibit a VEC of 19 e– (2× 3e– + 4e– + 3× 3e–), while all other compounds that adopt the Mg2Ni3Si-type structure, including the prototype itself, exhibit VECs between 36 and 39. The stability of the aluminum representatives will be investigated by quantum-chemical calculations in the future.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/solids4030011/s1, Figure S1: Rietveld refinement of Y2TiAl3; Figure S2: Rietveld refinement of Dy2TiAl3; Figure S3: Rietveld refinement of Ho2TiAl3; Figure S4: Rietveld refinement of Er2TiAl3; Figure S5: Rietveld refinement of Tm2TiAl3; Figure S6: Rietveld refinement of Lu2TiAl3; Figure S7: Rietveld refinement of nominal La2TiAl3; Table S1: Rietveld refinement of Y2TiAl3; Table S2: Rietveld refinement of Dy2TiAl3; Table S3: Rietveld refinement of Ho2TiAl3; Table S4: Rietveld refinement of Er2TiAl3; Table S5: Rietveld refinement of Tm2TiAl3; Table S6: Rietveld refinement of Lu2TiAl3; Table S7: Rietveld refinement of nominal La2TiAl3.

Author Contributions

Conceptualization, O.J.; methodology, E.C.J.G., S.E., M.R., J.M.G. and L.S.; analysis, E.C.J.G., S.E., I.M.E., L.S. and O.J.; investigation, E.C.J.G., S.E., I.M.E., M.R., J.M.G. and L.S.; writing—original draft preparation, E.C.J.G. and M.R.; writing—review and editing, E.C.J.G. and O.J.; visualization, E.C.J.G.; supervision, O.J.; project administration, O.J.; funding acquisition, O.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the German Research Foundation DFG, grant numbers JA 1891-10-1 and INST 256/349-1.

Data Availability Statement

CCDCs 1939725-1939727 contain the supplementary crystallographic data for this paper. The data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/structures.

Acknowledgments

We thank Rolf-Dieter Hoffmann and Jutta Kösters for the collection of the single crystal intensity data and Jörg Schmauch for the help with the SEM/EDX investigations. Instrumentation and technical assistance for this work were provided by the Service Center X-ray Diffraction, with financial support from Saarland University and the German Science Foundation (project number INST 256/349-1).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Paufler, P.; Gustav, E.R. Schulze’s pioneering work on Laves phases. Z. Kristallogr. 2006, 221, 311. [Google Scholar] [CrossRef]
  2. Fischer, W.; Fritz, H. Laves—An ideal for generations. Z. Kristallogr. 2006, 221, 305. [Google Scholar] [CrossRef]
  3. Parthé, E.; Fritz, H. Laves—100 years young. Z. Kristallogr. 2006, 221, 301. [Google Scholar] [CrossRef]
  4. Villars, P.; Cenzual, K. (Eds.) Pearson’s Crystal Data: Crystal Structure Database for Inorganic Compounds; (release 2022/23); ASM International®: Materials Park, OH, USA, 2023. [Google Scholar]
  5. Laves, F.; Witte, H. Der Einfluß von Valenzelektronen auf die Kristallstruktur ternärer Magnesiumlegierungen. Metallwirtsch. Metallwiss. Metalltech. 1936, 15, 840–842. [Google Scholar]
  6. Gschneidner, K.A., Jr.; Pecharsky, V.K. Binary rare earth Laves phases—An overview. Z. Kristallogr. 2006, 221, 375–381. [Google Scholar] [CrossRef]
  7. Fukui, H.; Hirao, N.; Ohishi, Y.; Baron, A.Q.R. Compressional behavior of solid NeHe2 up to 90 GPa. J. Phys. Condens. Matter 2010, 22, 095401. [Google Scholar] [CrossRef] [PubMed]
  8. Dewaele, A.; Rosa, A.D.; Guignot, N. Argon-neon binary diagram and ArNe2 Laves phase. J. Chem. Phys. 2019, 151, 124708. [Google Scholar] [CrossRef]
  9. Ji, C.; Goncharov, A.F.; Shukla, V.; Jena, N.K.; Popov, D.; Li, B.; Wang, J.; Meng, Y.; Prakapenka, V.B.; Smith, J.S.; et al. Stability of Ar(H2)2 to 358 GPa. Proc. Natl. Acad. Sci. USA 2017, 114, 3596–3600. [Google Scholar] [CrossRef]
  10. Laniel, D.; Weck, G.; Loubeyre, P. Xe(N2)2 compound to 150 GPa: Reluctance to the formation of a xenon nitride. Phys. Rev. B 2016, 94, 174109. [Google Scholar] [CrossRef]
  11. Komura, Y.; Kitano, Y. Long-period stacking variants and their electron-concentration dependence in the Mg-base Friauf-Laves phases. Acta Crystallogr. 1977, B33, 2496–2501. [Google Scholar] [CrossRef]
  12. Witte, H. Untersuchungen im System Magnesium-Kupfer-Silicium mit besonderer Berücksichtigung des Schnittes MgCu2-MgSi2. Z. Angew. Mineral. 1938, 1, 255–268. [Google Scholar]
  13. Mishra, T.; Hoffmann, R.-D.; Schwickert, C.; Pöttgen, R. Structure Refinement and Magnetic Properties of Ce2RuAl3 and a Group-Subgroup Scheme for Ce5Ru3Al2. Z. Naturforsch. 2011, 66b, 771–776. [Google Scholar] [CrossRef]
  14. Eustermann, F.; Stegemann, F.; Gausebeck, S.; Janka, O. Structural and Magnetic Investigations of the Pseudo Ternary RE2TAl3 series (RE = Sc, Y, La–Nd, Sm, Gd–Lu; T = Ru, Rh, Ir)—Size Dependent Formation of Two Different Structure Types. Z. Naturforsch. 2018, 73b, 819–830. [Google Scholar] [CrossRef]
  15. Blazina, Z.; Ban, Z. The Crystal Structures of U2Cu3Al and UCuAl2, and their Relationship with Some Other Phases in the System U-Cu-Al. Z. Naturforsch. 1981, 35b, 1162–1165. [Google Scholar]
  16. Huneau, B.; Rogl, P.; Zeng, K.; Schmid-Fetzer, R.; Bohn, M.; Bauer, J. The ternary system Al–Ni–Ti Part I: Isothermal section at 900 °C; Experimental investigation and thermodynamic calculation. Intermetallics 1999, 7, 1337–1345. [Google Scholar] [CrossRef]
  17. Zelinskii, A.V.; Fedorchuk, A.O.; Zelinska, O.Y. Synthesis and crystal structure of the compounds UMn1.43Ga0.57 and U2Fe3Ga. Visn. Lviv. Derzh. Univ. Ser. Khim. 2013, 54, 92–97. [Google Scholar]
  18. Sichevych, O.; Prots, Y.; Schnelle, W.; Schmidt, M.; Grin, Y. Crystal structure of dieuropium trigallium iridium, Eu2Ga3Ir. Z. Kristallogr. NCS 2006, 221, 263–264. [Google Scholar] [CrossRef]
  19. Mykhalichko, O.; Gladyshevskii, E.I.; Hlukhyy, V.; Fässler, T.F. Synthesis and crystal structure of the compound Nb2Cu1.10Ga2.90. Visn. Lviv. Derzh. Univ. Ser. Khim. 2009, 50, 89–93. [Google Scholar]
  20. Myakush, O.R.; Fedorchuk, A.A. Crystal structure and electrical properties of HoRuGa compound. Visn. Lviv. Derzh. Univ. Ser. Khim. 2004, 44, 62–66. [Google Scholar]
  21. Yan, X.L.; Chen, X.-Q.; Grytsiv, A.; Witusiewicz, V.T.; Rogl, P.; Podloucky, R.; Giester, G. On the ternary Laves phases {Sc,Ti}2M3Si (M = Cr, Mn, Fe, Co, Ni) with MgZn2-type. J. Alloys Compd. 2007, 429, 10–18. [Google Scholar] [CrossRef]
  22. Kotur, B.Y. Crystal structure of Sc2M3Si (where M = Fe, Co, Ni) compounds. Dopov. Akad. Nauk Ukr. RSR 1977, A39, 164–165. [Google Scholar]
  23. Bardos, D.I.; Gupta, K.P.; Beck, P.A. Ternary Laves Phases with Transition Elements and Silicon. Trans. Metall. Soc. AIME 1961, 221, 1087–1088. [Google Scholar]
  24. Henriques, M.S.; Berthebaud, D.; Lignie, A.; El Sayah, Z.; Moussa, C.; Tougait, O.; Havela, L.; Gonçalves, A.P. Isothermal section of the ternary phase diagram U–Fe–Ge at 900 °C and its new intermetallic phases. J. Alloys Compd. 2015, 639, 224–234. [Google Scholar] [CrossRef]
  25. Hoffmann, R.-D.; Pöttgen, R.; Chevalier, B.; Gaudin, E.; Matar, S.F. The ternary germanides UMnGe and U2Mn3Ge. Solid State Sci. 2013, 21, 73–80. [Google Scholar] [CrossRef]
  26. Soudé, A.; Tougait, O.; Pasturel, M.; Kaczorowski, D.; Noël, H.; Roisnel, T. Characterization of the novel intermetallic compounds U2Co3Ge, U6Co12Ge4 and U6Co12Ge4C. J. Alloys Compd. 2011, 509, 5447–5452. [Google Scholar] [CrossRef]
  27. Henriques, M.S.; Tougait, O.; Noel, H.; Pereira, L.C.J.; Waerenborgh, J.C.; Gonçalves, A.P. Evidence of uranium magnetic ordering on U2Fe3Ge. Solid State Commun. 2008, 148, 159–162. [Google Scholar] [CrossRef]
  28. Teslyuk, M.Y.; Gladyshevskii, E.I. Crystal structure of MnCu1.5Ge0.5 ternary compound. Visn. Lviv. Derzh. Univ. Ser. Khim. 1963, 6, 42–45. [Google Scholar]
  29. Kuz’ma, Y.B.; Gladyshevskii, E.I. Crystal structure of the compound Mn2Co3Ge. Dopov. Akad. Nauk Ukr. RSR 1963, A25, 205–208. [Google Scholar]
  30. Gladyshevskii, E.I.; Krypyakevych, P.I.; Teslyuk, M.Y. Crystal structure of the ternary phase Cu4MgSn. Dokl. Akad. Nauk. SSSR 1952, 85, 81–84. [Google Scholar]
  31. Zaremba, V.I.; Baranyak, V.M.; Kalychak, Y.M. Crystal structure of the RNi4In compounds. Visn. Lviv. Derzh. Univ. Ser. Khim. 1984, 25, 18–19. [Google Scholar]
  32. Felner, I. Magnetic properties of RAuNi4 rare earth compounds. Solid State Commun. 1977, 21, 267–268. [Google Scholar] [CrossRef]
  33. Dwight, A.E. Crystal structure of RENi4Au compounds and unitcell constants in the YCo5-YNi5-YCu5 series. J. Less-Common Met. 1975, 43, 117–120. [Google Scholar] [CrossRef]
  34. Takeshita, T.; Malik, S.K.; Wallace, W.E. Crystal structure of RCu4Ag and RCu4Al (R = Rare Earth) intermetallic compounds. J. Solid State Chem. 1978, 23, 225–229. [Google Scholar] [CrossRef]
  35. Kaneko, T.; Arai, S.; Abe, S.; Kamigaki, K. Magnetic properties of cubic RAuCu4 (R = Gd, Tb, Dy, Ho and Er) intermetallic compounds. J. Phys. Soc. Jpn. 1986, 55, 4441–4447. [Google Scholar] [CrossRef]
  36. Seidel, S.; Pöttgen, R. Yb6Ir5Ga7—A MgZn2 Superstructure. Z. Anorg. Allg. Chem. 2017, 643, 261–265. [Google Scholar] [CrossRef]
  37. Eustermann, F.; Pominov, A.; Pöttgen, R. Rare Earth (RE) Gallides with Closely Related Compositions: REIrGa and RE6Ir5Ga7. Z. Anorg. Allg. Chem. 2018, 644, 1297–1303. [Google Scholar] [CrossRef]
  38. Eustermann, F.; Stegemann, F.; Radzieowski, M.; Janka, O. Intermetallic RE6T5Al7 Phases (RE = Sc, Y, Ce–Nd, Sm, Gd–Lu, T = Ru, Ir)—Diversity in their Magnetic, Magnetocaloric and Critical Properties. Inorg. Chem. 2019, 58, 16211–16226. [Google Scholar] [CrossRef]
  39. Noréus, D.; Eriksson, L.; Göthe, L.; Werner, P.E. Structure determination of Mg2SiNi3. J. Less-Common Met. 1985, 107, 345–349. [Google Scholar] [CrossRef]
  40. Seidel, S.; Janka, O.; Benndorf, C.; Mausolf, B.; Haarmann, F.; Eckert, H.; Heletta, L.; Pöttgen, R. Ternary rhombohedral Laves phases RE2Rh3Ga (RE = Y, La–Nd, Sm, Gd–Er). Z. Naturforsch. 2017, 72b, 289–303. [Google Scholar] [CrossRef]
  41. Cenzual, K.; Chabot, B.; Parthé, E. Y2Rh3Ge, a rhombohedral substitution variant of the MgCu2 type. J. Solid State Chem. 1987, 70, 229–234. [Google Scholar] [CrossRef]
  42. Lipatov, A.; Gribanov, A.; Grytsiv, A.; Safronov, S.; Rogl, P.; Rousnyak, J.; Seropegin, Y.; Giester, G. The ternary system cerium–rhodium–silicon. J. Solid State Chem. 2010, 183, 829–843. [Google Scholar] [CrossRef]
  43. Kaczorowski, D.; Lipatov, A.; Gribanov, A.; Seropegin, Y. Low-temperature magnetic and electrical transport properties of some ternary Ce–Rh–Si compounds. J. Alloys Compd. 2011, 509, 6518–6521. [Google Scholar] [CrossRef]
  44. Vernière, A.; Lejay, P.; Bordet, P.; Chenavas, J.; Brison, J.P.; Haen, P.; Boucherle, J.X. Crystal structures and physical properties of some new ternary compounds U2T3X (T = Ru, Os; X = Si, Ge). J. Alloys Compd. 1994, 209, 251–255. [Google Scholar] [CrossRef]
  45. Morozkin, A.V. New ternary compounds in the Sm–Rh–Ge system. J. Alloys Compd. 2004, 385, L1–L2. [Google Scholar] [CrossRef]
  46. Doverbratt, I.; Ponou, S.; Lidin, S. Ca2Pd3Ge, a new fully ordered ternary Laves phase structure. J. Solid State Chem. 2013, 197, 312–316. [Google Scholar] [CrossRef]
  47. Gießelmann, E.; Pöttgen, R.; Janka, O. Laves phases: Superstructures induced by coloring and distortions. Z. Anorg. Allg. Chem. 2023, e202300109. [Google Scholar] [CrossRef]
  48. Janka, O. Metallic Light-Weight Alloys: Al, Ti, Mg; Pöttgen, R., Jüstel, T., Strassert, C., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2022. [Google Scholar]
  49. Massalski, T.B.; Okamoto, H.; Subramanian, P.R.; Kacprzak, L. Binary Alloy Phase Diagrams, 2nd ed.; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
  50. Okamoto, H. Al-Ti (aluminum-titanium). J. Phase Equilibria 1993, 14, 120–121. [Google Scholar] [CrossRef]
  51. Raghavan, V. Al-Ti-V (Aluminum-Titanium-Vanadium). J. Phase Equilibria Diffus. 2005, 26, 276–279. [Google Scholar] [CrossRef]
  52. Batalu, D.; Coşmeleaţǎ, G.; Aloman, A. Critical analysis of the Ti-Al phase diagrams. U.P.B. Sci. Bull. Ser. B 2006, 68, 77–90. [Google Scholar]
  53. Schuster, J.C.; Palm, M. Reassessment of the binary Aluminum-Titanium phase diagram. J. Phase Equilibria Diffus. 2006, 27, 255–277. [Google Scholar] [CrossRef]
  54. Peters, M.; Hemptenmacher, J.; Kumpfert, J.; Leyens, C. Structure and Properties of Titanium and Titanium Alloys in Titanium and Titanium Alloys: Fundamentals and Applications; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2003. [Google Scholar]
  55. Sauthoff, G. Intermetallics in Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2012. [Google Scholar]
  56. Pöttgen, R.; Gulden, T.; Simon, A. Miniaturisierte Lichtbogenapperatur für den Laborbedarf. GIT Labor-Fachz. 1999, 43, 133–136. [Google Scholar]
  57. Palatinus, L.; Chapuis, G. SUPERFLIP—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Crystallogr. 2007, 40, 786–790. [Google Scholar] [CrossRef]
  58. Petříček, V.; Dušek, M.; Palatinus, L. (Eds.) The Crystallographic Computing System; JANA 2006; Institute of Physics of the Czech Academy of Sciences: Praha, Czech Republic, 2006. [Google Scholar]
  59. Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar] [CrossRef]
  60. Emsley, J. The Elements; Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
  61. Becker, P.J.; Coppens, P. Extinction within the limit of validity of the Darwin transfer equations. I. General formalism for primary and secondary extinction and their applications to spherical crystals. Acta Crystallogr. 1974, A30, 129–147. [Google Scholar] [CrossRef]
  62. Duwez, P.E.; Taylor, J.L. Crystal Structure of TiAl. Trans. Am. Inst. Min. Metall. Pet. Eng. 1952, 194, 70–71. [Google Scholar] [CrossRef]
  63. Ence, E.; Margolin, H. Compounds in the Titanium-Rich Region of the Ti-Al System. Trans. Am. Inst. Min. Metall. Pet. Eng. 1957, 209, 484–485. [Google Scholar] [CrossRef]
  64. Niemann, S.; Jeitschko, W. Ternary aluminides A6T4Al43 with A = Y, Nd, Sm, Gd-Lu, Th, U and T = Cr, Mo, W. Z. Metallkd. 1994, 85, 345–349. [Google Scholar]
  65. Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures. Acta Crystallogr. 1959, 12, 483–499. [Google Scholar] [CrossRef]
  66. Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. I. Definitions and basic principles. Acta Crystallogr. 1958, 11, 184–190. [Google Scholar] [CrossRef]
  67. Compton, V.B.; Matthias, B.T. Laves phase compounds of rare earths and hafnium with noble metals. Acta Crystallogr. 1959, 12, 651–654. [Google Scholar] [CrossRef]
  68. Gießelmann, E.C.J.; Engel, S.; Kostusiak, W.; Zhang, Y.; Herbeck-Engel, P.; Kickelbick, G.; Janka, O. Raman and NMR spectroscopic and theoretical investigations of the cubic Laves-phases REAl2 (RE = Sc, Y, La, Yb, Lu). Dalton Trans. 2023, 52, 3391–3402. [Google Scholar] [CrossRef] [PubMed]
  69. Zhou, G.F.; Bakker, H. Mechanically induced structural and magnetic changes in the GdAl2 Laves phase. Phys. Rev. B 1995, 52, 9437–9445. [Google Scholar] [CrossRef] [PubMed]
  70. Janka, O.; Hoffmann, R.D.; Heying, B.; Pöttgen, R. Structural phase transitions in YPtGe2 and GdPtGe2. Dalton Trans. 2018, 47, 6075–6088. [Google Scholar] [CrossRef] [PubMed]
  71. Eustermann, F.; Eilers-Rethwisch, M.; Renner, K.; Hoffmann, R.-D.; Pöttgen, R.; Janka, O. Magnetic properties of the germanides RE3Pt4Ge6 (RE = Y, Pr, Nd, Sm, Gd–Dy). Z. Naturforsch. 2017, 72b, 855–864. [Google Scholar] [CrossRef]
  72. Staliński, B.; Pokrzywnicki, S. Magnetic Properties of Gadolinium-Aluminium Intermetallic Compounds. Phys. Status Solidi B 1966, 14, K157–K160. [Google Scholar] [CrossRef]
  73. Eustermann, F.; Stegemann, F.; Renner, K.; Janka, O. Platinum Triangles in the Pt/Al Framework of the Intermetallic REPt6Al3 (RE = Ce-Nd, Sm, Gd, Tb) Series. Z. Anorg. Allg. Chem. 2017, 643, 1836–1843. [Google Scholar] [CrossRef]
Solids 04 00011 g001
Figure 1. Trigonal lattice parameters and unit cell volumes of the RE2TiAl3 (RE = Y, Gd–Tm, Lu) series (Mg2Ni3Si type) plotted versus the ionic radii of the trivalent RE3+ cations. The connection between the data points is a guide to the eye.
Figure 1. Trigonal lattice parameters and unit cell volumes of the RE2TiAl3 (RE = Y, Gd–Tm, Lu) series (Mg2Ni3Si type) plotted versus the ionic radii of the trivalent RE3+ cations. The connection between the data points is a guide to the eye.
Solids 04 00011 g001
Solids 04 00011 g002
Figure 2. Rietveld refinement of Y2TiAl3 (top) in the trigonal Mg2Ni3Si-type structure in comparison with (bottom) the cubic MgCu2-type structure.
Figure 2. Rietveld refinement of Y2TiAl3 (top) in the trigonal Mg2Ni3Si-type structure in comparison with (bottom) the cubic MgCu2-type structure.
Solids 04 00011 g002
Solids 04 00011 g003
Figure 3. Unit cells of YAl2 (left) and Y2TiAl3 (right). Yttrium, titanium, and aluminum atoms are depicted as blue, black, and open white circles, respectively. The empty [Al4] and [TiAl3] tetrahedra in YAl2 and Y2TiAl3 and the diamond-related substructure formed by the Y atoms are highlighted.
Figure 3. Unit cells of YAl2 (left) and Y2TiAl3 (right). Yttrium, titanium, and aluminum atoms are depicted as blue, black, and open white circles, respectively. The empty [Al4] and [TiAl3] tetrahedra in YAl2 and Y2TiAl3 and the diamond-related substructure formed by the Y atoms are highlighted.
Solids 04 00011 g003
Solids 04 00011 g004
Figure 4. Coordination environments surrounding the Y, Ti, and Al atoms in the crystal structure of Y2TiAl3. Yttrium, titanium, and aluminum atoms are depicted as blue, black, and open white circles, respectively. Wyckoff sites, site symmetries, and interatomic distances (in pm) are given.
Figure 4. Coordination environments surrounding the Y, Ti, and Al atoms in the crystal structure of Y2TiAl3. Yttrium, titanium, and aluminum atoms are depicted as blue, black, and open white circles, respectively. Wyckoff sites, site symmetries, and interatomic distances (in pm) are given.
Solids 04 00011 g004
Solids 04 00011 g005
Figure 5. Temperature dependence of the magnetic susceptibility of Y2TiAl3 (black) and Lu2TiAl3 (red) measured with an applied external field of 10 kOe.
Figure 5. Temperature dependence of the magnetic susceptibility of Y2TiAl3 (black) and Lu2TiAl3 (red) measured with an applied external field of 10 kOe.
Solids 04 00011 g005
Solids 04 00011 g006
Figure 6. Magnetic data of Gd2TiAl3. (top) Temperature dependence of the magnetic and inverse magnetic susceptibility (χ and χ−1 data) measured with an applied external field of 10 kOe; (middle) zero-field-cooled/field-cooled (ZFC/FC) measurements measured with an applied external field of 100 Oe; (bottom) magnetization isotherms recorded at 3, 10, 50, and 100 K.
Figure 6. Magnetic data of Gd2TiAl3. (top) Temperature dependence of the magnetic and inverse magnetic susceptibility (χ and χ−1 data) measured with an applied external field of 10 kOe; (middle) zero-field-cooled/field-cooled (ZFC/FC) measurements measured with an applied external field of 100 Oe; (bottom) magnetization isotherms recorded at 3, 10, 50, and 100 K.
Solids 04 00011 g006
Solids 04 00011 g007
Figure 7. Magnetic data of Er2TiAl3. (top) Temperature dependence of the magnetic and inverse magnetic susceptibility (χ and χ−1 data) measured with an applied external field of 10 kOe; (middle) zero-field-cooled/field-cooled (ZFC/FC) measurements measured with an applied external field of 100 Oe; (bottom) magnetization isotherms recorded at 3, 10, 50, and 100 K.
Figure 7. Magnetic data of Er2TiAl3. (top) Temperature dependence of the magnetic and inverse magnetic susceptibility (χ and χ−1 data) measured with an applied external field of 10 kOe; (middle) zero-field-cooled/field-cooled (ZFC/FC) measurements measured with an applied external field of 100 Oe; (bottom) magnetization isotherms recorded at 3, 10, 50, and 100 K.
Solids 04 00011 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gießelmann, E.C.J.; Engel, S.; El Saudi, I.M.; Schumacher, L.; Radzieowski, M.; Gerdes, J.M.; Janka, O. On the RE2TiAl3 (RE = Y, Gd–Tm, Lu) Series—The First Aluminum Representatives of the Rhombohedral Mg2Ni3Si Type Structure. Solids 2023, 4, 166-180. https://doi.org/10.3390/solids4030011

AMA Style

Gießelmann ECJ, Engel S, El Saudi IM, Schumacher L, Radzieowski M, Gerdes JM, Janka O. On the RE2TiAl3 (RE = Y, Gd–Tm, Lu) Series—The First Aluminum Representatives of the Rhombohedral Mg2Ni3Si Type Structure. Solids. 2023; 4(3):166-180. https://doi.org/10.3390/solids4030011

Chicago/Turabian Style

Gießelmann, Elias C. J., Stefan Engel, Israa M. El Saudi, Lars Schumacher, Mathis Radzieowski, Josef Maximilian Gerdes, and Oliver Janka. 2023. "On the RE2TiAl3 (RE = Y, Gd–Tm, Lu) Series—The First Aluminum Representatives of the Rhombohedral Mg2Ni3Si Type Structure" Solids 4, no. 3: 166-180. https://doi.org/10.3390/solids4030011

APA Style

Gießelmann, E. C. J., Engel, S., El Saudi, I. M., Schumacher, L., Radzieowski, M., Gerdes, J. M., & Janka, O. (2023). On the RE2TiAl3 (RE = Y, Gd–Tm, Lu) Series—The First Aluminum Representatives of the Rhombohedral Mg2Ni3Si Type Structure. Solids, 4(3), 166-180. https://doi.org/10.3390/solids4030011

Article Metrics

Back to TopTop