Numerical Investigation of the Influence of Fatigue Testing Frequency on the Fracture and Crack Propagation Rate of Additive-Manufactured AlSi10Mg and Ti-6Al-4V Alloys
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Processing and Characterization
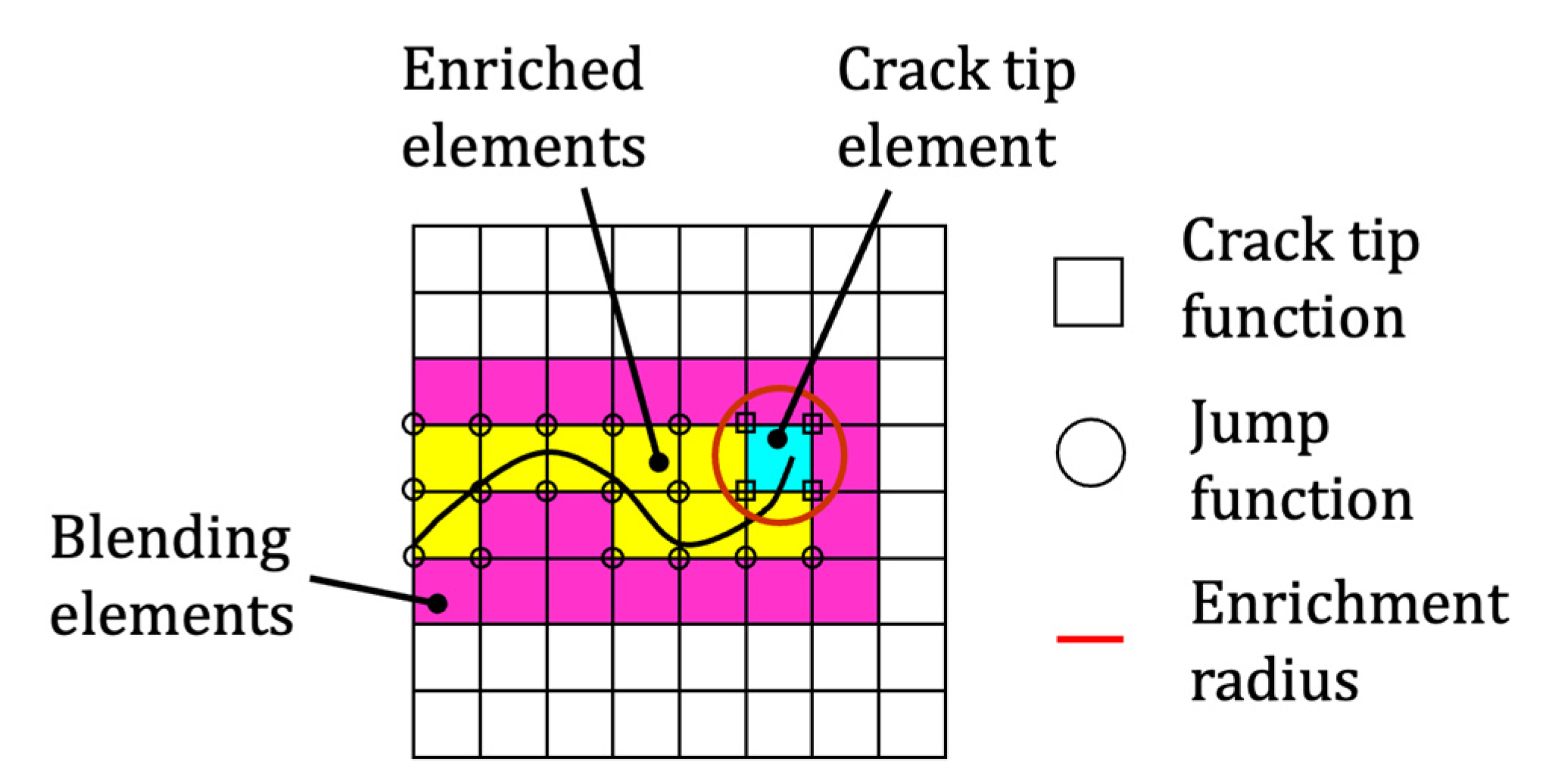
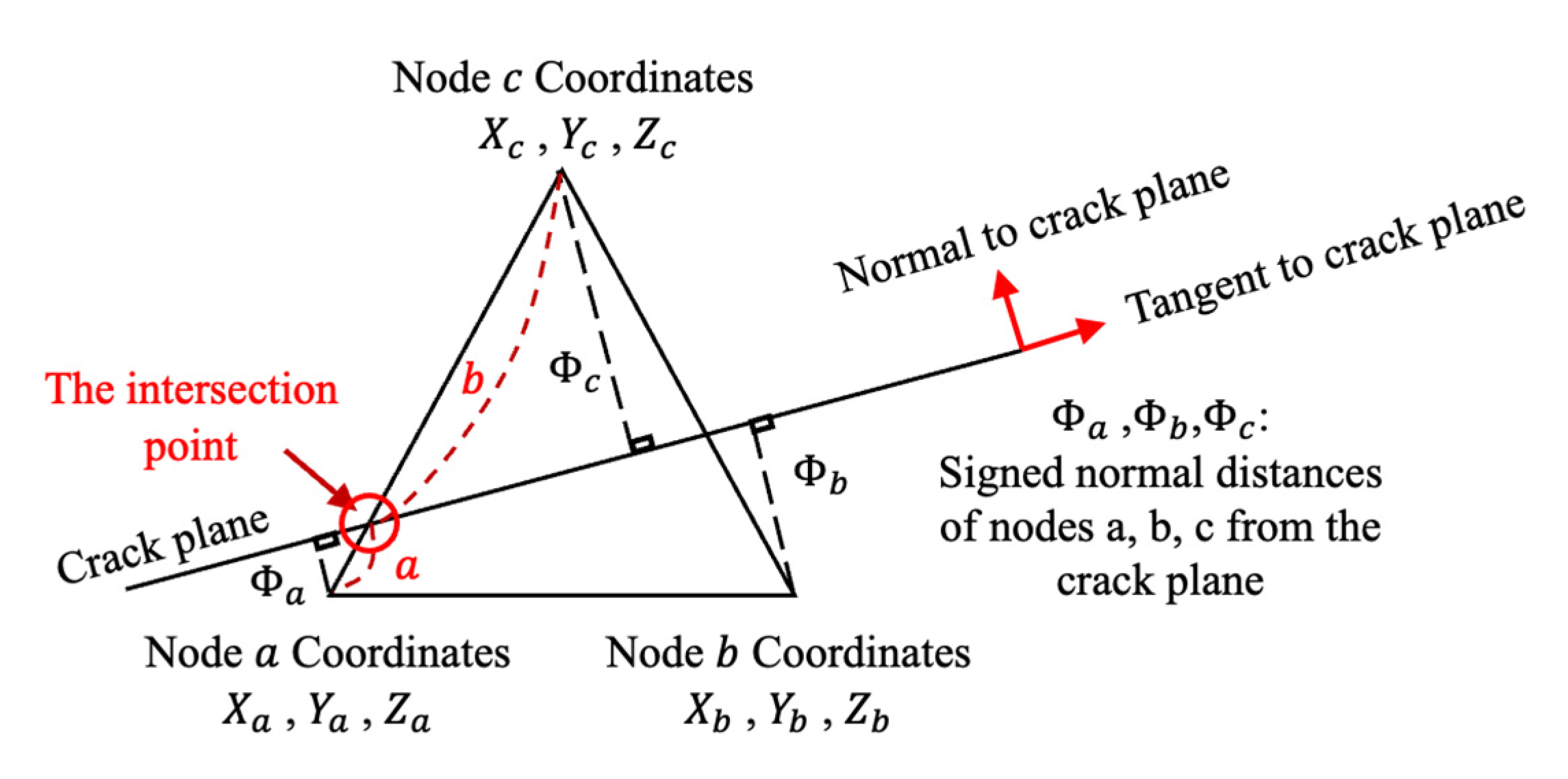
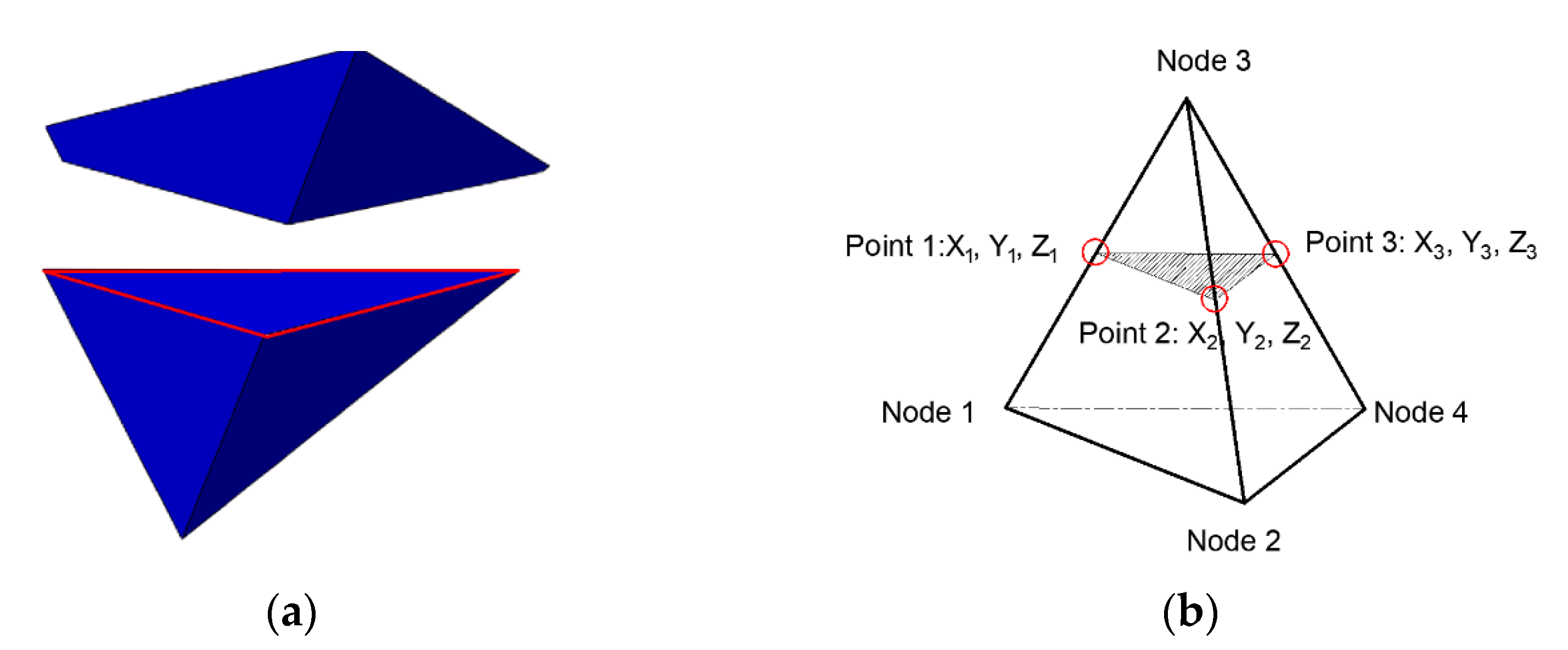
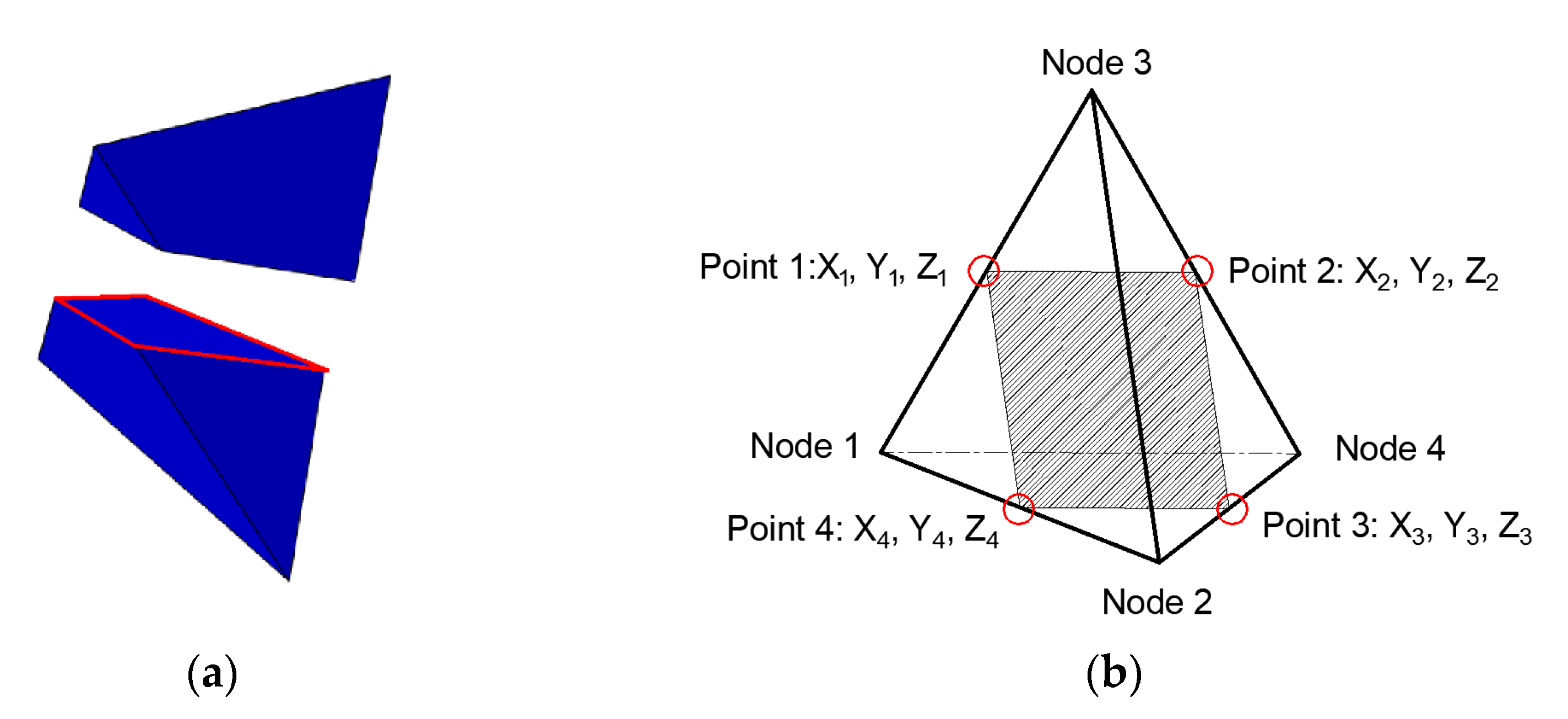
2.2. The Extended Finite Element Method
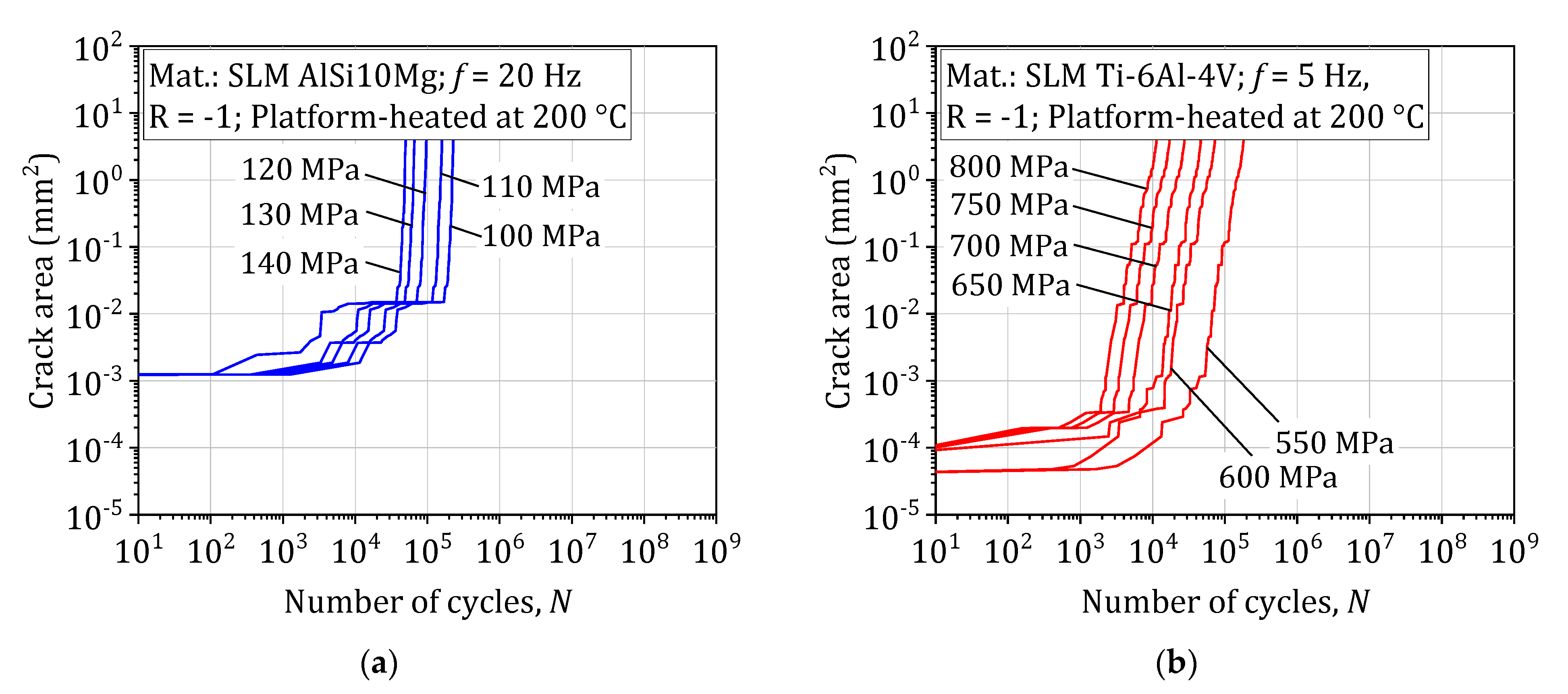
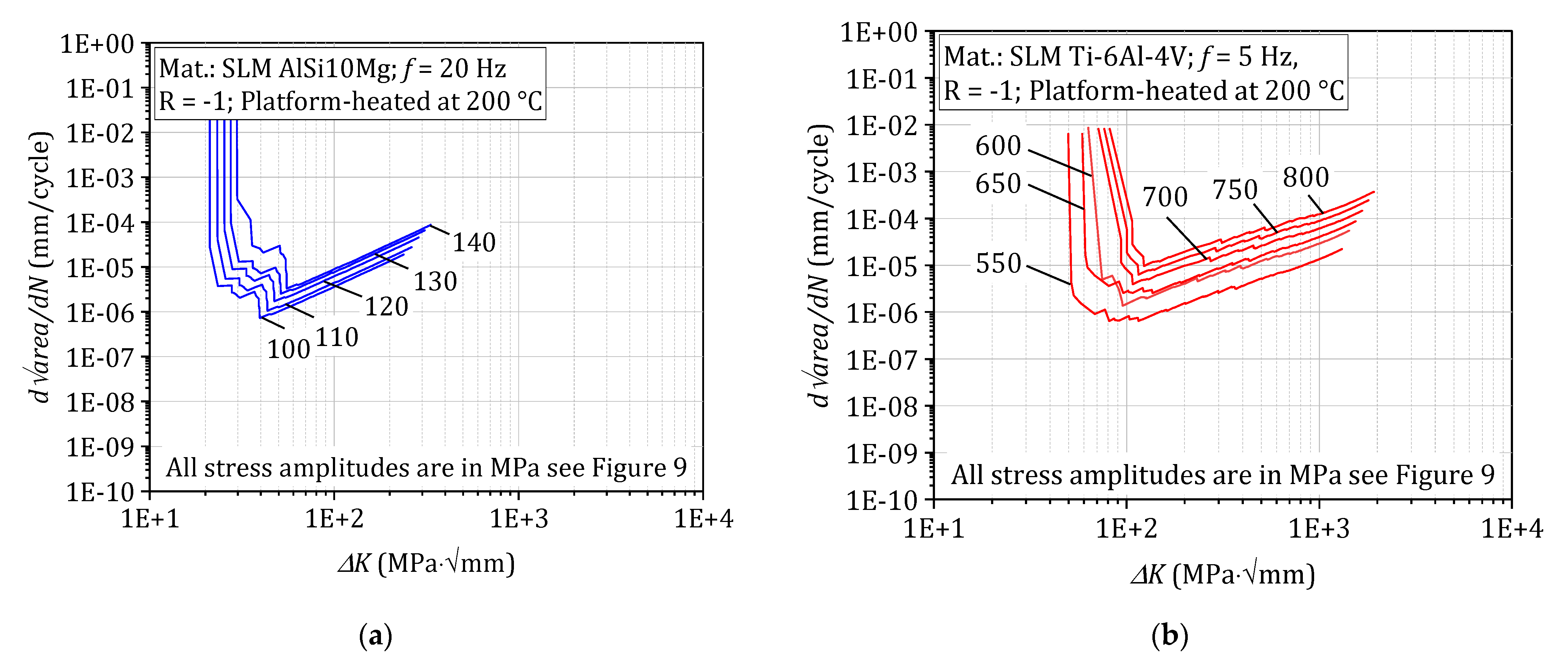
3. Results
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Hartman, A.; Schijve, J. The effects of environment and load frequency on the crack propagation law for macro fatigue crack growth in aluminium alloys. Eng. Fract. Mech. 1970, 1, 615–631. [Google Scholar] [CrossRef]
- Takeo, Y.; Kiyoshi, S. The effect of frequency on fatigue crack propagation rate and striation spacing in 2024-T3 aluminium alloy and SM-50 steel. Eng. Fract. Mech. 1976, 8, 81–88. [Google Scholar] [CrossRef]
- Meyn, D.A. An analysis of frequency and amplitude effects on corrosion fatigue crack propagation in Ti-8Al-1Mo-1V. Metall. Trans. 1971, 2, 853–865. [Google Scholar] [CrossRef]
- Zhu, X.; Jones, J.W.; Allison, J.E. Effect of frequency, environment, and temperature on fatigue behavior of E319 cast aluminum alloy: Stress-controlled fatigue life response. Metall. Mater. Trans. A 2008, 39, 2681–2688. [Google Scholar] [CrossRef]
- Zhu, X.; Jones, J.W.; Allison, J.E. Effect of frequency, environment, and temperature on fatigue behavior of E319 cast-aluminum alloy: Small-crack propagation. Metall. Mater. Trans. A 2008, 39, 2666–2680. [Google Scholar] [CrossRef] [Green Version]
- Gingell, A.D.B.; King, J.E. The effect of frequency and microstructure on corrosion fatigue crack propagation in high strength aluminium alloys. Acta Mater. 1997, 45, 3855–3870. [Google Scholar] [CrossRef]
- Mayer, H.; Papakyriacou, M.; Pippan, R.; Stanzl-Tschegg, S. Influence of loading frequency on the high cycle fatigue properties of AlZnMgCu1.5 aluminium alloy. Mater. Sci. Eng. A 2001, 314, 48–54. [Google Scholar] [CrossRef]
- Takezono, S.; Satoh, M. Effect of stress frequency on fatigue crack propagation in titanium. J. Eng. Mater. Technol. 1982, 104, 257–261. [Google Scholar] [CrossRef]
- Morrissey, R.; McDowell, D.L.; Nicholas, T. Frequency and stress ratio effects in high cycle fatigue of Ti-6Al-4V. Int. J. Fatigue 1999, 21, 679–685. [Google Scholar] [CrossRef]
- Takeuchi, E.; Furuya, Y.; Nagashima, N.; Matsuoka, S. The effect of frequency on the giga-cycle fatigue properties of a Ti-6Al-4V alloy. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 599–605. [Google Scholar] [CrossRef]
- Awd, M.; Johannsen, J.; Chan, T.; Merghany, M.; Emmelmann, C.; Walther, F. Improvement of fatigue strength in lightweight selective laser melted alloys by in situ and ex situ composition and heat treatment. In TMS 2020 149th Annual Meeting & Exhibition Supplemental Proceedings; The Minerals, Metals & Materials Series; Springer International Publishing: Cham, Switzerland, 2020; pp. 115–126. ISBN 978-3-030-36295-9. [Google Scholar]
- Siddique, S.; Imran, M.; Wycisk, E.; Emmelmann, C.; Walther, F. Fatigue assessment of laser additive manufactured AlSi12 eutectic alloy in the very high cycle fatigue (VHCF) range up to 1E9 cycles. Mater. Today Proc. 2016, 3, 2853–2860. [Google Scholar] [CrossRef]
- Siddique, S.; Awd, M.; Tenkamp, J.; Walther, F. High and very high cycle fatigue failure mechanisms in selective laser melted aluminum alloys. J. Mater. Res. 2017, 32, 4296–4304. [Google Scholar] [CrossRef]
- Awd, M.; Siddique, S.; Hajavifard, R.; Walther, F. Comparative study of defect-based and plastic damage-based approaches for fatigue lifetime calculation of selective laser melted AlSi12. In Proceedings of the 7th International Conference on Fracture Fatigue and Wear, Ghent, Belgium, 9–10 July 2018; Abdel Wahab, M., Ed.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2019; pp. 297–313. ISBN 9789811304101. [Google Scholar]
- Awd, M.; Stern, F.; Kampmann, A.; Kotzem, D.; Tenkamp, J.; Walther, F. Microstructural characterization of the anisotropy and cyclic deformation behavior of selective laser melted AlSi10Mg structures. Metals 2018, 8, 825. [Google Scholar] [CrossRef] [Green Version]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Tabor, D. The hardness of solids. Rev. Phys. Technol. 1970, 1, 145–179. [Google Scholar] [CrossRef]
- Kushch, V.I.; Dub, S.N.; Litvin, P.M. Determination of the young modulus from elastic section of the Berkovich indenter loading curve. J. Superhard Mater. 2007, 29, 228–234. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Awd, M.; Siddique, S.; Johannsen, J.; Emmelmann, C.; Walther, F. Very high-cycle fatigue properties and microstructural damage mechanisms of selective laser melted AlSi10Mg alloy. Int. J. Fatigue 2019, 124, 55–69. [Google Scholar] [CrossRef]
- Schneider-Maunoury, C.; Albayda, A.; Bartier, O.; Weiss, L.; Mauvoisin, G.; Hernot, X.; Laheurte, P. On the use of instrumented indentation to characterize the mechanical properties of functionally graded binary alloys manufactured by additive manufacturing. Mater. Today Commun. 2020, 25, 101451. [Google Scholar] [CrossRef]
- Lu, L.; Dao, M.; Kumar, P.; Ramamurty, U.; Karniadakis, G.E.; Suresh, S. Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proc. Natl. Acad. Sci. USA 2020, 117, 7052–7062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kese, K.O.; Alvarez, A.-M.; Karlsson, J.K.-H.; Nilsson, K.H. Experimental evaluation of nanoindentation as a technique for measuring the hardness and Young’s modulus of Zircaloy-2 sheet material. J. Nucl. Mater. 2018, 507, 267–275. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Bouhala, L.; Shao, Q.; Koutsawa, Y.; Younes, A.; Núñez, P.; Makradi, A.; Belouettar, S. An XFEM crack-tip enrichment for a crack terminating at a bimaterial interface. Eng. Fract. Mech. 2013, 102, 51–64. [Google Scholar] [CrossRef]
- Awd, M.; Labanie, M.F.; Moehring, K.; Fatemi, A.; Walther, F. Towards deterministic computation of internal stresses in additively manufactured materials under fatigue loading: Part I. Materials 2020, 13, 2318. [Google Scholar] [CrossRef] [PubMed]
- Awd, M.; Siddique, S.; Walther, F. Microstructural damage and fracture mechanisms of selective laser melted Al-Si alloys under fatigue loading. Theor. Appl. Fract. Mech. 2020, 106, 102483. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 4th ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2017; ISBN 978-1-4987-2813-3. [Google Scholar]
- Carpinteri, A.; Paggi, M. Are the Paris’ law parameters dependent on each other? Frat. Ed Integrità Strutt. 2008, 1, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.S. Analysing the fatigue crack growth in structural details. Eng. Fract. Mech. 1996, 53, 345–361. [Google Scholar] [CrossRef]
- Cotterell, B.; Rice, J.R. Slightly curved or kinked cracks. Int. J. Fract. 1980, 16, 155–169. [Google Scholar] [CrossRef]
- Dunham, W. Journey through Genius: The Great Theorems of Mathematics; Penguin Books: New York, NY, USA, 1991; ISBN 978-0-14-014739-1. [Google Scholar]
- Smith, M. Abaqus/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2009. [Google Scholar]
- Jeon, S.-W.; Lee, K.-W.; Kim, J.Y.; Kim, W.J.; Park, C.-P.; Kwon, D. Estimation of fracture toughness of metallic materials using instrumented indentation: Critical indentation stress and strain model. Exp. Mech. 2017, 57, 1013–1025. [Google Scholar] [CrossRef]
- Sansoz, F.; Ghonem, H. Effects of loading frequency on fatigue crack growth mechanisms in α/β Ti microstructure with large colony size. Mater. Sci. Eng. A 2003, 356, 81–92. [Google Scholar] [CrossRef]
- Rege, K.; Lemu, H.G. A review of fatigue crack propagation modelling techniques using FEM and XFEM. IOP Conf. Ser. Mater. Sci. Eng. 2017, 276, 012027. [Google Scholar] [CrossRef]
- Leiting Dong, S.N.A. Fracture & fatigue analyses: SGBEM-FEM or XFEM? Part 2: 3D Solids. Comput. Modeling Eng. Sci. 2013, 90, 379–413. [Google Scholar] [CrossRef]
- Leiting Dong, S.N.A. Fracture & fatigue analyses: SGBEM-FEM or XFEM? Part 1: 2D Structures. Comput. Modeling Eng. Sci. 2013, 90, 91–146. [Google Scholar] [CrossRef]
- Bergara, A.; Dorado, J.I.; Martin-Meizoso, A.; Martínez-Esnaola, J.M. Fatigue crack propagation in complex stress fields: Experiments and numerical simulations using the extended finite element method (XFEM). Int. J. Fatigue 2017, 103, 112–121. [Google Scholar] [CrossRef]
- Grogan, D.M.; Leen, S.B.; Ó Brádaigh, C.M. An XFEM-based methodology for fatigue delamination and permeability of composites. Compos. Struct. 2014, 107, 205–218. [Google Scholar] [CrossRef]
- Feng, S.Z.; Li, W. An accurate and efficient algorithm for the simulation of fatigue crack growth based on XFEM and combined approximations. Appl. Math. Model. 2018, 55, 600–615. [Google Scholar] [CrossRef]
- Naderi, M.; Iyyer, N. Fatigue life prediction of cracked attachment lugs using XFEM. Int. J. Fatigue 2015, 77, 186–193. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, Y.; Li, Q.; Jin, F.; Nadakatti, M.M. Analysis of the initiation and propagation of fatigue cracks in the CRTS II slab track inter-layer using FE-SAFE and XFEM. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 678–690. [Google Scholar] [CrossRef]
- Bartaula, D.; Li, Y.; Koduru, S.; Adeeb, S. Simulation of fatigue crack growth using XFEM. In Proceedings of the Volume 3: Design and Analysis, Virtual, 3 August 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; p. V003T03A046. [Google Scholar]
- Nikfam, M.R.; Zeinoddini, M.; Aghebati, F.; Arghaei, A.A. Experimental and XFEM modelling of high cycle fatigue crack growth in steel welded T-joints. Int. J. Mech. Sci. 2019, 153–154, 178–193. [Google Scholar] [CrossRef]
- Martínez, J.C.; Vanegas Useche, L.V.; Wahab, M.A. Numerical prediction of fretting fatigue crack trajectory in a railway axle using XFEM. Int. J. Fatigue 2017, 100, 32–49. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, H. On damage accumulations in the cyclic cohesive zone model for XFEM analysis of mixed-mode fatigue crack growth. Comput. Mater. Sci. 2009, 46, 579–585. [Google Scholar] [CrossRef]
- Solob, A.; Grbović, A.; Božić, Ž.; Sedmak, S.A. XFEM based analysis of fatigue crack growth in damaged wing-fuselage attachment lug. Eng. Fail. Anal. 2020, 112, 104516. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, I.V.; Mishra, B.K. Fatigue crack growth simulations of plastically graded materials using XFEM and J-integral decomposition approach. Eng. Fract. Mech. 2019, 216, 106470. [Google Scholar] [CrossRef]
- Infante-García, D.; Qian, G.; Miguélez, H.; Giner, E. Analysis of the effect of out-of-phase biaxial fatigue loads on crack paths in cruciform specimens using XFEM. Int. J. Fatigue 2019, 123, 87–95. [Google Scholar] [CrossRef] [Green Version]







| Power | Scanning Speed | Spot Size | Hatching Distance | Layer Thickness | |
|---|---|---|---|---|---|
| P (W) | vs (mm/s) | D (mm) | ht (mm) | t (mm) | |
| AlSi10Mg | 350 | 1200 | 0.083 | 0.190 | 0.050 |
| Ti-6Al-4V | 240 | 1200 | 0.082 | 0.105 | 0.060 |
| mm/Cycle | [-] | |
|---|---|---|
| AlSi10Mg (20 Hz) | 4.2 × 10−5 | 1.2 |
| (20 kHz) | 7.6 × 10−7 | 1.2 |
| Ti-6Al-4V (5 Hz) | 2.1 × 10−6 | 1.685 |
| (20 kHz) | 1.22 × 10−8 | 1.685 |
| Experimental | Numerical | |
|---|---|---|
| AlSi10Mg | 41,288 | 51,463 |
| 140 MPa | ||
| 100 MPa | 220,475 | 234,895 |
| Ti-6Al-4V | ||
| 800 MPa | 13,113 | 12,316 |
| 500 MPa | 51,159,835 | 76,693,033 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awd, M.; Walther, F. Numerical Investigation of the Influence of Fatigue Testing Frequency on the Fracture and Crack Propagation Rate of Additive-Manufactured AlSi10Mg and Ti-6Al-4V Alloys. Solids 2022, 3, 430-446. https://doi.org/10.3390/solids3030030
Awd M, Walther F. Numerical Investigation of the Influence of Fatigue Testing Frequency on the Fracture and Crack Propagation Rate of Additive-Manufactured AlSi10Mg and Ti-6Al-4V Alloys. Solids. 2022; 3(3):430-446. https://doi.org/10.3390/solids3030030
Chicago/Turabian StyleAwd, Mustafa, and Frank Walther. 2022. "Numerical Investigation of the Influence of Fatigue Testing Frequency on the Fracture and Crack Propagation Rate of Additive-Manufactured AlSi10Mg and Ti-6Al-4V Alloys" Solids 3, no. 3: 430-446. https://doi.org/10.3390/solids3030030
APA StyleAwd, M., & Walther, F. (2022). Numerical Investigation of the Influence of Fatigue Testing Frequency on the Fracture and Crack Propagation Rate of Additive-Manufactured AlSi10Mg and Ti-6Al-4V Alloys. Solids, 3(3), 430-446. https://doi.org/10.3390/solids3030030







