1. Introduction
The isothermal, isotropic transformation from an amorphous to a crystalline phase, consisting of nucleation and growth of spherical domains, is usually well described by the
Kolmogorov–Johnson–Mehl–Avrami (
KJMA) model [
1,
2,
3]:
where
X is the fraction of material that has crystallized,
t is the time that has elapsed from the start of the process, v(
t,
τ) is the volume corresponding to the crystalline domains that were born at the
nucleation time τ, and
I(
τ) is the nucleation rate at
t =
τ. If we assume a constant nucleation rate, N
R, and a constant linear growth rate, k, Equation (1) reduces to what we will simply call the
Avrami exponential expression:
Though these two expressions were introduced about 80 years ago, they are still widely used to fit a great variety of experimental data, spanning metals and alloys [
1,
4], polymers [
2,
5], growth of cancerous cells [
6], etc. A few examples of critical reviews and/or alternatives to Avrami-like formulations are given in Refs. [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17].
The rate of transformation in Equation (2) is dictated by the product N
Rk
3. This suggests that increasing the growth rate, k
3, by a factor of 10 is the same as increasing the nucleation rate, N
R, by a factor of 10. Notice that the product N
Rk
3 can be achieved in innumerable ways: we could have a nucleation rate of 1000 N
R times a growth rate of k
3/1000 or N
R/1000 times 1000 k
3. In Equation (2), this is irrelevant due to the assumption that both rates remain constant along the transformation process. Nevertheless, we know that in reality, these two rates vary as crystallization progresses. Consider the process in which the domain growth rate is slowed by the proximity of other domains (phenomenon known as impingement). To some extent, it matters if for a given value of
X, we have a few large crystalline domains or a large number of small ones. When morphological details affect these two rates to a significant extent, Equation (1) would be better suited to deal with a crystallization kinetics involving time-dependent rates. We will follow a slightly different approach in order to study the roles of variations in these two rates. We will make use of an integral equation describing the isothermal crystallization kinetics that was introduced previously by the author to assess the relevance of phantom nuclei [
18]. In it, nucleation and growth rates explicitly depend on the degree of crystallization. It will be shown that varying the expression describing the growth rate as a function of
X has a much greater effect than varying the expression describing the nucleation rate as a function of
X, in clear contrast to the situation described for Equation (2) above in this paragraph. The reason for this is of a geometric nature, and we explain it in
Section 4.
To put our results in context, in
Appendix A, we show under which circumstances our integral equation transforms into three well-known models of isothermal crystallization, including Equations (1) and (2). To some extent, this lends support to our assertion that the asymmetry between the nucleation and growth rates contributes to the great success of Equations (1) and (2) in describing a wide range of experimental data.
2. Crystallization Kinetics Integral Equation
In developing our model, it is important to distinguish between two time variables:
- (1).
The time elapsed since the overall crystallization process started, beginning from a state of zero crystallization, is indicated by t.
- (2).
The nucleation time, τ, indicates the time at which a particular spherical crystalline domain, originating from a nucleus, begins its growth process. This way, we say that, at a time t, the growth interval for a spherical crystalline domain born at a nucleation time τ is (t–τ).
Let Vtot be the total volume of a sample and Vx(t) be the volume of material transformed at time t. Thus, we can define the crystallized fraction at time t as , with X(t = 0) = 0 and X(t = ∞) = 1. For simplicity, assume that the densities of non-crystallized (amorphous) and crystallized phases are the same.
Let us assume that at time
τ, a spherical domain initializes its growth with a constant and isotropic
radial growth rate, given by
where
r is the radius. That is, if growth is
unimpeded, the radius at time
t will be given by:
This is the kind of growth that is expected in the early stages of crystallization, when the spherical domains have little, if any, influence over each other. As the initial unimpeded growth continues, the volume of a crystalline domain born at time τ will be given by
We assume that, as the number and volume of spherical domains increase with time, growth will be increasingly diminished by the presence of close neighbors. In our formulation, this will be taken into account by the introduction of a
growth factor G[
X], with 0 ≤
G[
X] ≤ 1, such that now
k3G[
X] is an
instantaneous (
volumetric)
growth rate (
G[
X = 0] = 1 and
G[
X = 1] = 0). Thus, the volume of a crystalline domain born at a time
τ is now given by
For early stages of crystallization, we can consider that the nucleation rate is a constant, N
R, such that the number of nuclei born between time
t and
t + d
t is given by N
Rd
t. However, as in the case of the growth rate for later stages, we assume that the nucleation rate decreases as crystallinity increases. Thus, we propose an
instantaneous nucleation rate given by a function N
RI[
X], with 0 ≤
[
X] ≤ 1,
[
X = 0] = 1, and
[
X = 1] = 0. Thus, the number of crystalline domains born up to time
t is given by
We define
x(
t,
τ)
dτ as the fraction of the volume occupied by all the spherical domains born during the time interval from
τ to
τ +
dτ. Since the number of spherical domains born during this time interval is given by
, we have
X can be found by summing up the contributions from all spherical domains that have initiated growth within the time interval from 0 to
t:
Inserting Equation (6) into Equation (9):
where
. In Ref. [
18], the author made use of this integral equation to study the negligible contributions from phantom nuclei within the Avrami theory. In this paper, we use it to assess the relative importance of the growth and nucleation rates during the early and late stages of crystallization.
We assume that the evolution of
G and
I over time depends on the morphological properties of the system. Thus, we propose that
G and
I are functions that depend explicitly on
X and that they decrease monotonically from 1 to 0 as
X increases from 0 to 1. The following expressions will be used:
and
where
γ and
ν are the
growth and
nucleation exponents, respectively. By changing the values of these exponents, we can control how fast growth and nucleation rates decrease as
X increases.
3. Dependence of the Evolution of X on γ and ν
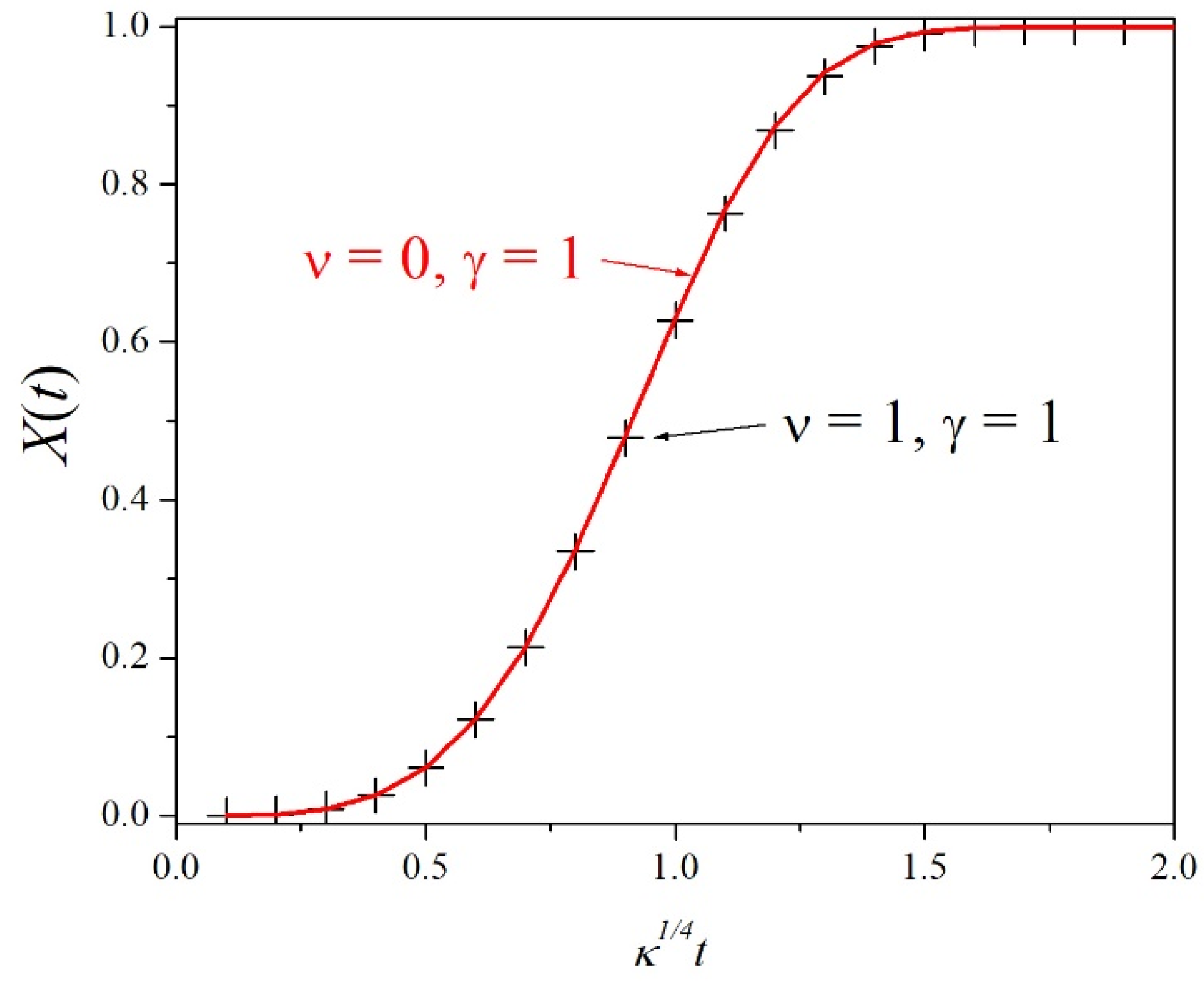
First, we consider the case in which
G and
I are proportional to (1 −
X), the untransformed fraction. This approximation is made by setting
γ = 1 and
ν = 1 in Equations (10)–(12). The + symbols in black in
Figure 1 show the time dependence of
X. Recalling that
x(
t,
τ)
dτ represents the fraction of volume occupied by all the spherical domains born during the time interval from
τ to
τ +
dτ, in
Figure 2 we show the relative values of
x(
t,
τ) versus time for crystalline domains born at different nucleation times
τ. As expected, the volume occupied by crystalline domains born in the early stages (
κ1/4τ = 0.001) is significantly larger than that of late comers (
κ1/4τ = 1). This point will turn out to be important for the discussions given below.
Figure 3 shows the rates d
x(
t,
τ)/d
t corresponding to the same
τ values. Again, we see the predominance of domains born in the early stages.
Next, we study the case for a time-independent
I (i.e.,
ν = 0), keeping the same growth exponent,
γ = 1. This case is important because it corresponds to the Avrami exponential expression, Equation (2) [
18]. Remarkably,
X(
t) is similar to one of the previous cases, as is shown by the red curve in
Figure 1. The curves shown in
Figure 4 and
Figure 5, corresponding to
x(
t,
τ) and d
x(
t,
τ)/d
t, respectively, are practically the same as those shown in
Figure 2 and
Figure 3. At first thought, this might seem remarkable, considering that for
ν = 1, nucleation decreases significantly for the late stages as
X increases, while it remains constant for
ν = 0. In the next section, we show that the reason is that, when referring to crystalline spherical domains,
early-born domains easily win the battle for volume. Even if we increase the exponent
ν further, let us say to 5 or 10, we still observe the same behavior as that depicted in
Figure 1. For two-dimensional crystallization, the difference between the
ν = 0 and
ν = 1 cases is larger, but still small [
18]. The conclusions drawn from the similarities between
Figure 2 and
Figure 3, on the one hand, and
Figure 4 and
Figure 5, on the other, are crucial in understanding the irrelevance of
phantom nuclei [
18], a topic that we do not touch here.
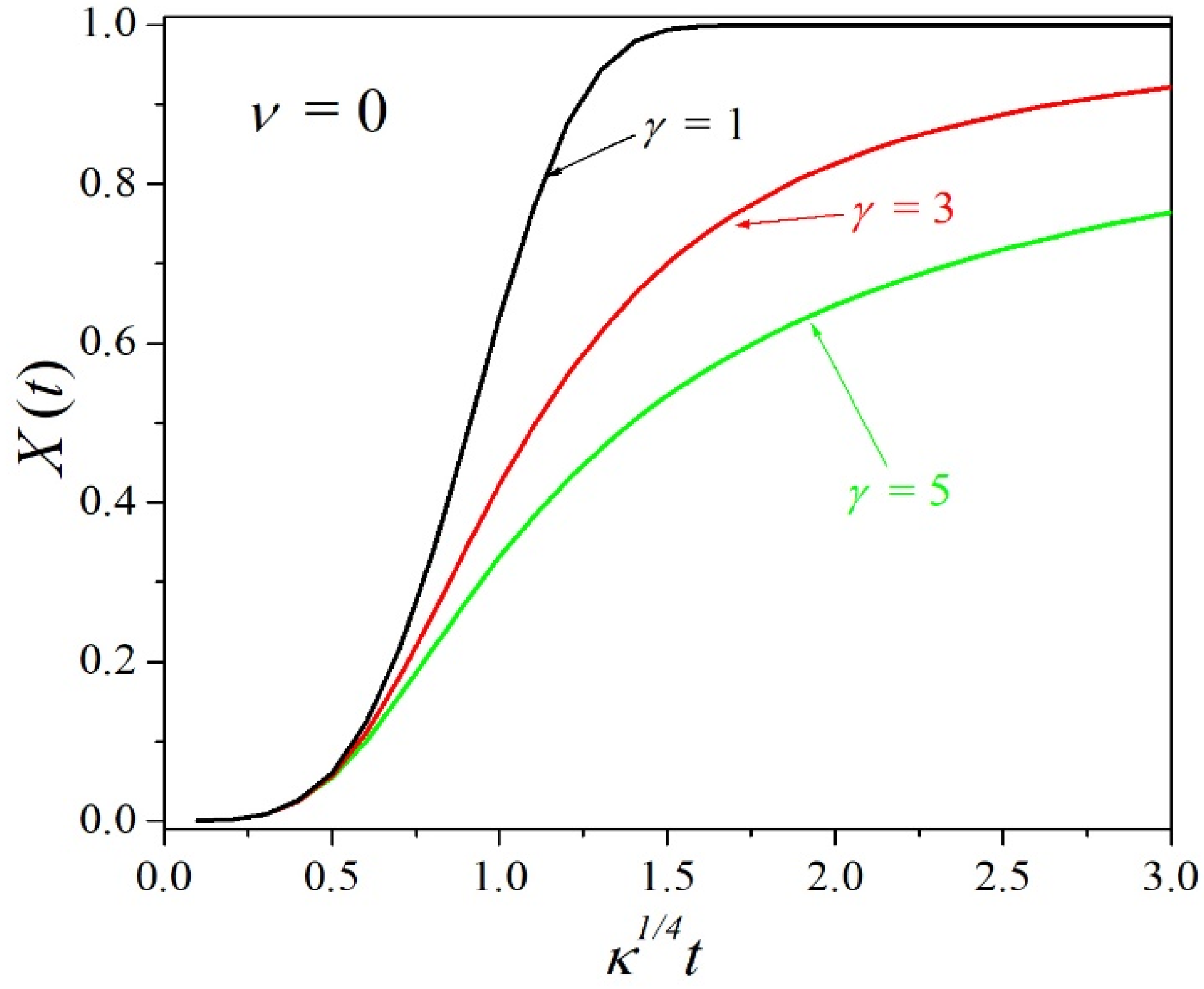
Now, let us study the effect of the variations in the growth exponent
γ on
X(
t). Having seen that the variations in the nucleation exponent
ν have a rather small effect on the crystallization rate, we choose to keep
ν = 0. The left-most curve in
Figure 6 corresponds to
γ = 1 (the Avrami exponential expression of
Figure 1, with
γ = 1 and
ν = 0), for which the growth rate is proportional to the untransformed fraction (1 −
X). For γ = 3 and 5, there is a noticeable slowdown of the growth rate for
X ≥ 0.1. This is in contrast to the similarity of the two curves in
Figure 1. The slow approach to the completion of the transformation, for
γ = 3 and 5, is what is known as a
long tail. It is shown in
Appendix A that for
γ ≠ 1 and
ν = 0, Equation (10) transforms into an expression proposed by Lee and Kim to study the transformation kinetics of Cu–Zn–Al shape memory alloys [
11].
In
Figure 7 and
Figure 8, we show
x(
t,
τ) and d
x(
t,
τ)/d
τ, respectively, as a function time, for
γ = 3 and
ν = 0. Since the growth rate now diminishes faster than when
γ = 1 (
Figure 1,
Figure 2,
Figure 3,
Figure 4 and
Figure 5), we see that the relative contributions to crystalline volume from domains born at
κ1/4τ = 0.1, 0.5, and 1 are now larger than for γ = 1 (see
Figure 2,
Figure 3,
Figure 4 and
Figure 5).
Figure 9 shows the domain volumes after completion of the crystallization process,
x(
t = ∞,
τ), as a function of birth time
τ, with ν = 0. For the Avrami case (
γ = 1), the domains born after
κ1/4τ = 1.0 have a negligible contribution. This is not the case for
γ = 3 and 5, in which case, at time
κ1/4τ = 1.0, the
old domains are smaller than for
γ = 1, leaving more room for
new domains to grow.
In these last two sections, we have considered a crystallization process consisting of nucleation and spherical growth, where growth and nucleation rates depend
explicitly on
X:
G(
X) and
I(
X). We found that, as would be expected, in its early stages, crystallization is governed by the product of both rates. However, as the transformation develops, the role of
I(
X) becomes quite insignificant compared to the role of
G(
X). This is clear if one notes that a
change in the function G(X) has a much larger effect on the evolution of X(
t)
than a similar change in I(
X). The reason for this is given in
Section 4.
5. Conclusions
We have studied the roles played by the crystalline domain growth rate and the nucleation rate in the calculations of the crystallized fraction, X(t), for systems that initially are characterized by an amorphous phase. We found that beyond the early stages of transformation, the role played by the domain growth rate is much more relevant than that played by the nucleation rate. As explained above, this contradicts Equation (2), which is a simplification of the KJMA model. To address this issue, we have made use of a formulation that considers crystallization as a process consisting of nucleation and growth of spherical crystalline domains and assumes that the nucleation and domain growth might be a function of the level of crystallization. It allowed us not just to calculate the overall level of crystallization but also to quantify the volume fraction corresponding to crystalline domains born at different nucleation times and levels of crystallization. This gave us a clear picture of the geometric factors responsible for the diminishing role of the nucleation rate as compared to that of the domain growth rate.
Within the framework of our integral formulation, we argue that the great success of Equations (1) and (2) in describing a wide range of experimental data is due, in part, to two features of the crystallization kinetics: (1) a growth rate G proportional to the amount of untransformed fraction (1 − X) is often a sound assumption, and (2) kinetics corresponding to different nucleation rate modes I(X) are described by similar expressions for cases of similar growth rates G(X). Future theoretical developments in the field of crystallization might benefit from taking into account the arguments and results presented above.