Solid State NMR for Nonexperts: An Overview of Simple but General Practical Methods
Abstract
1. Introduction
2. Chemical Shift Anisotropy
3. Cross-Polarization
4. Calculation of NMR Chemical Shifts
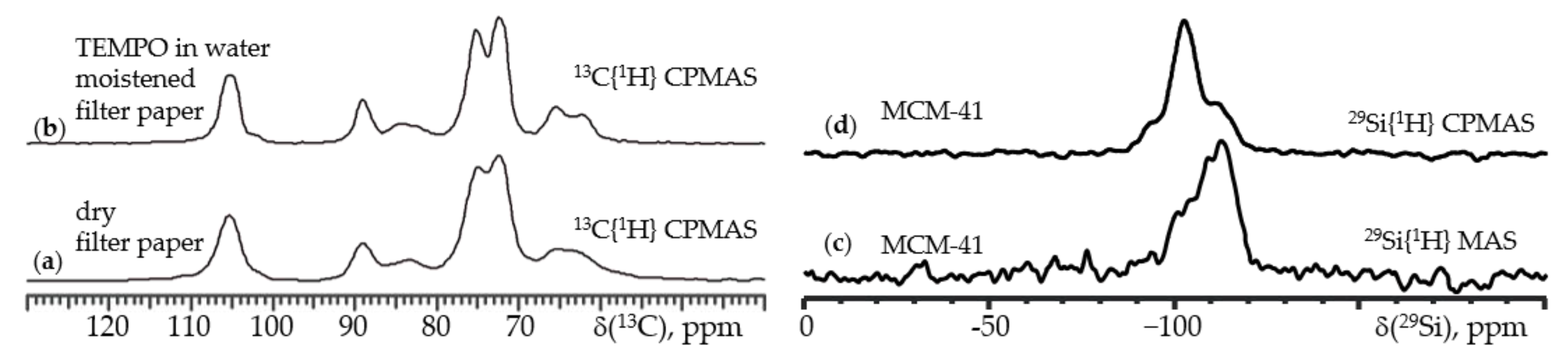
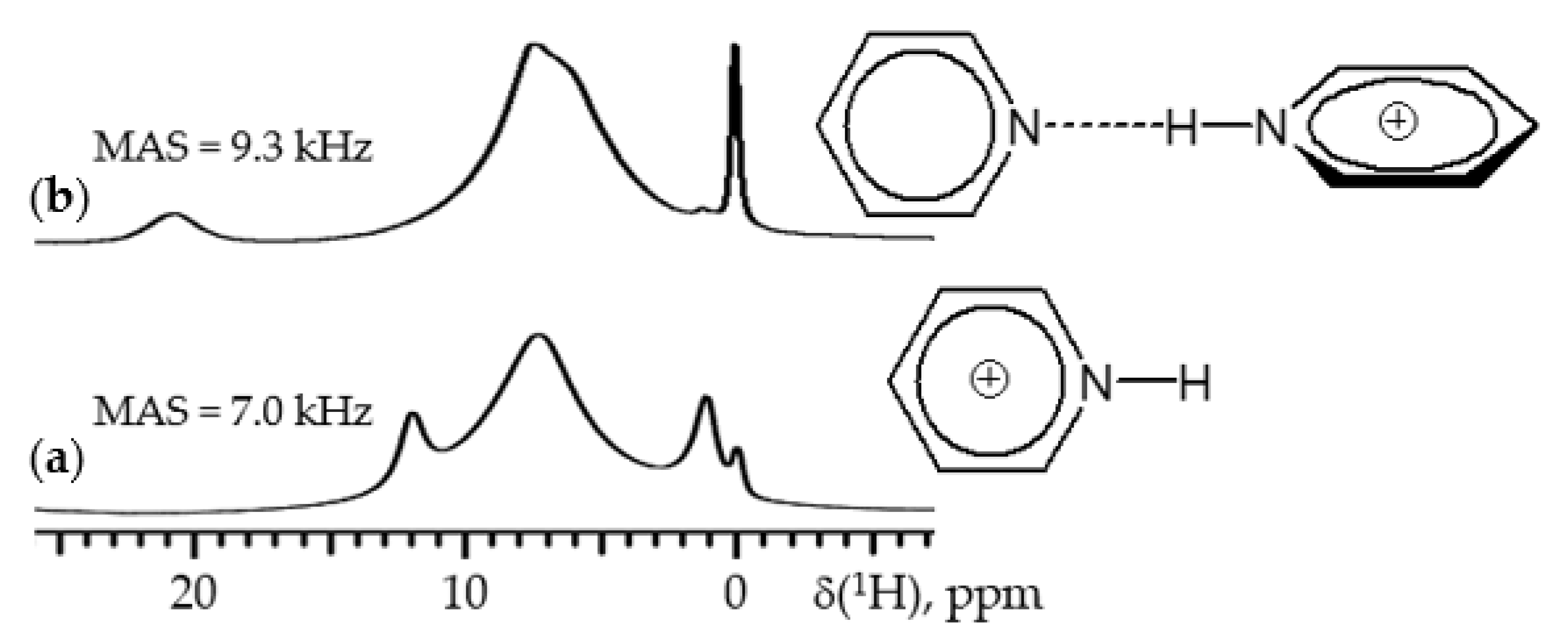
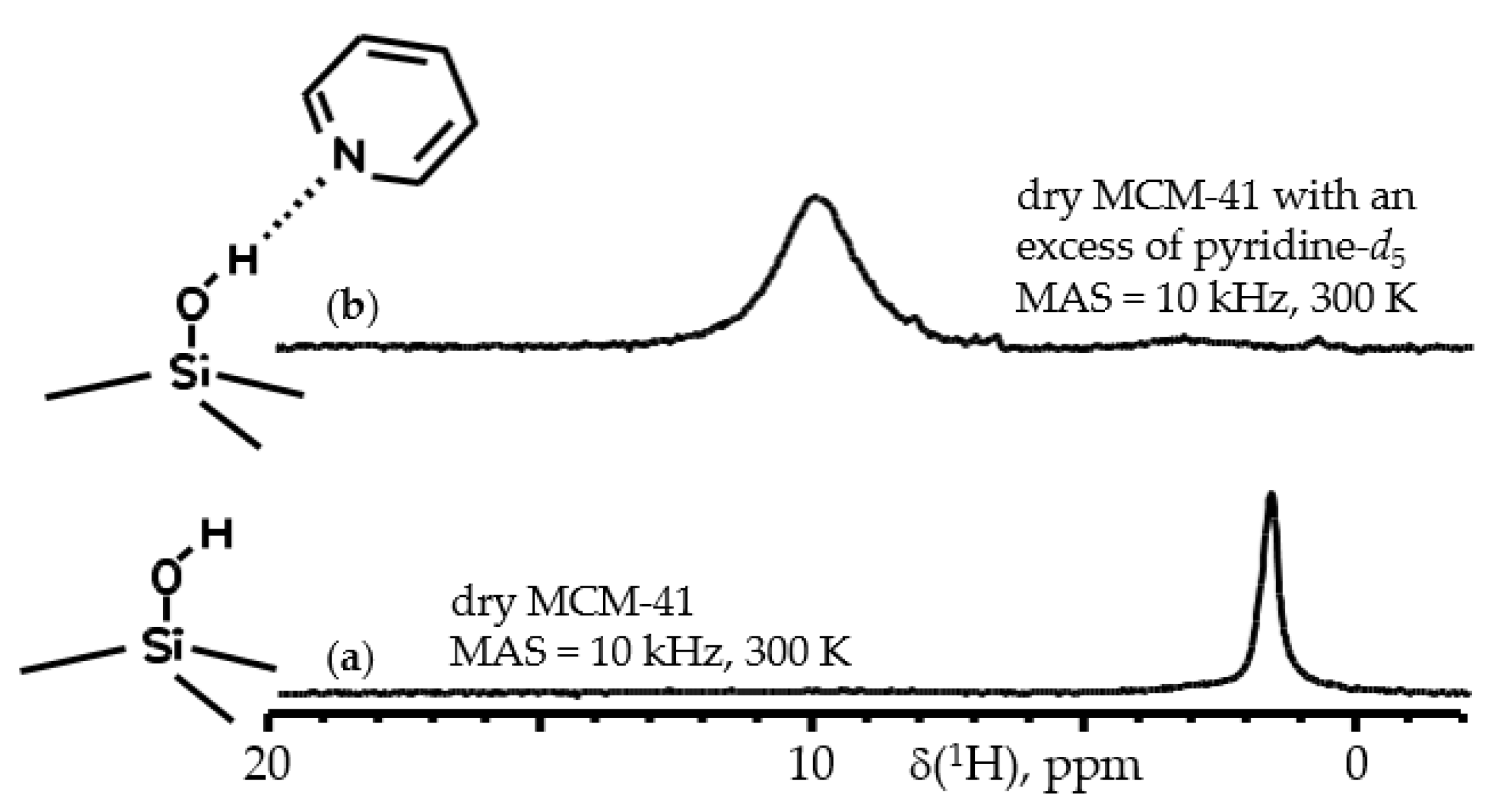
5. 1H NMR
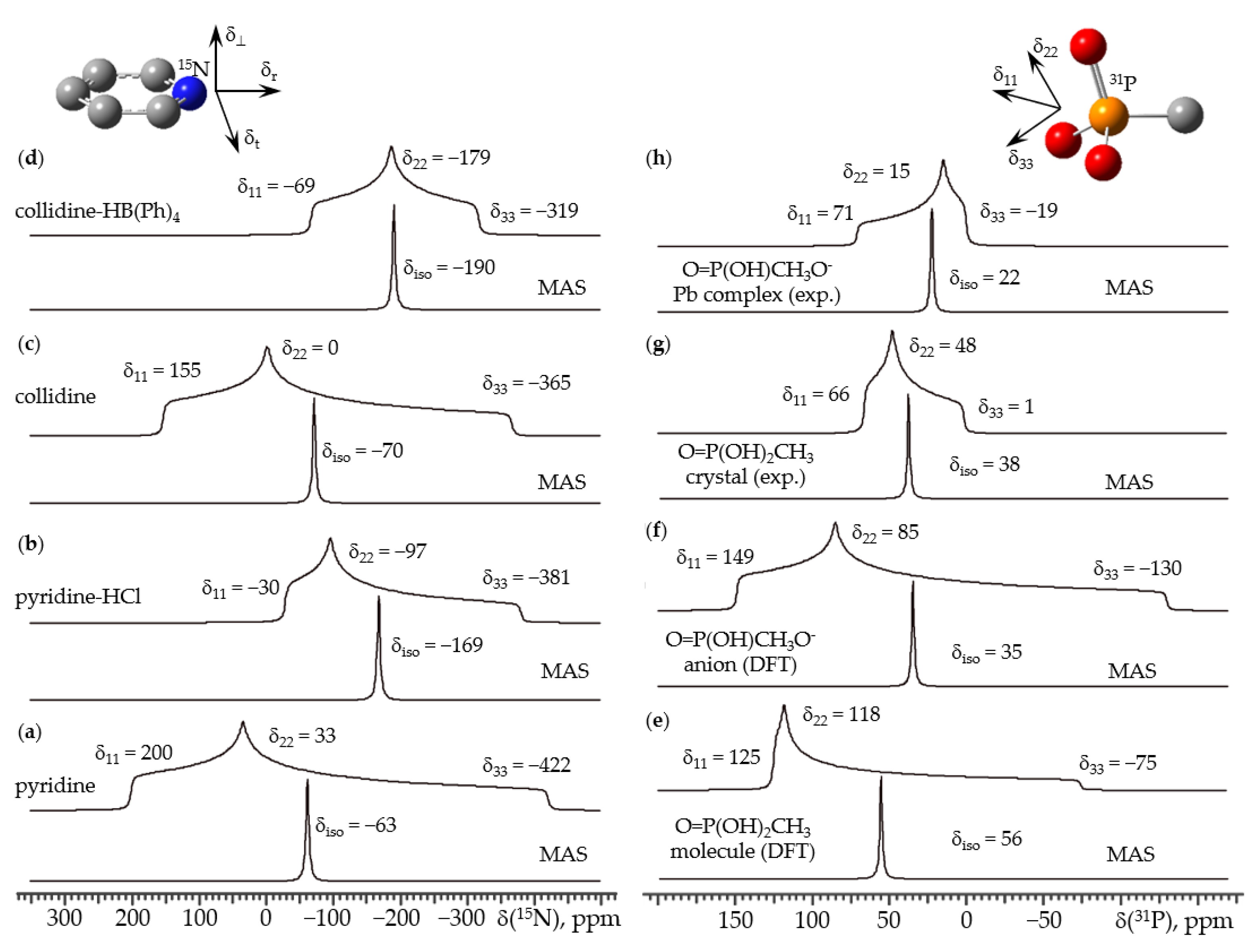
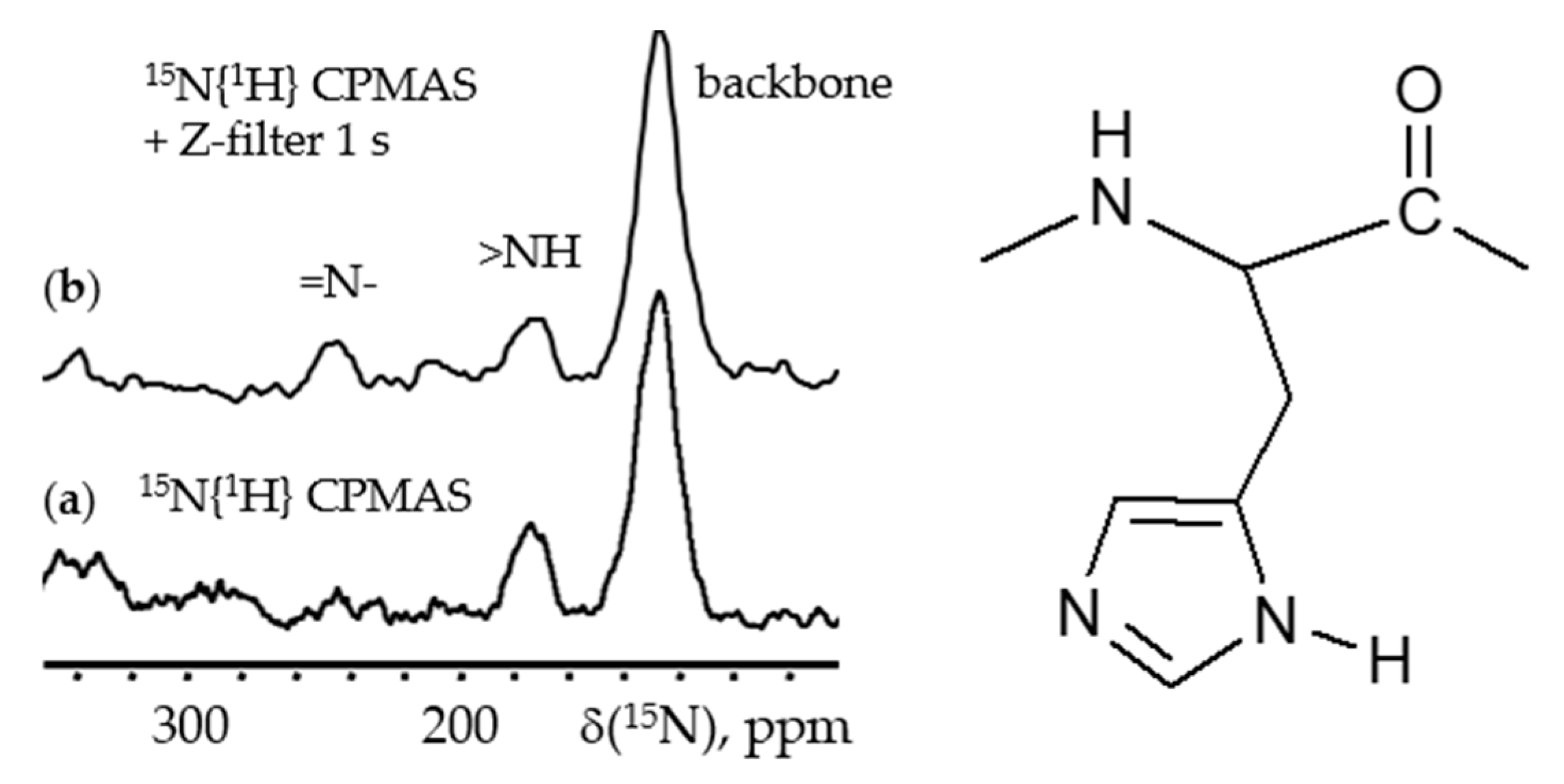
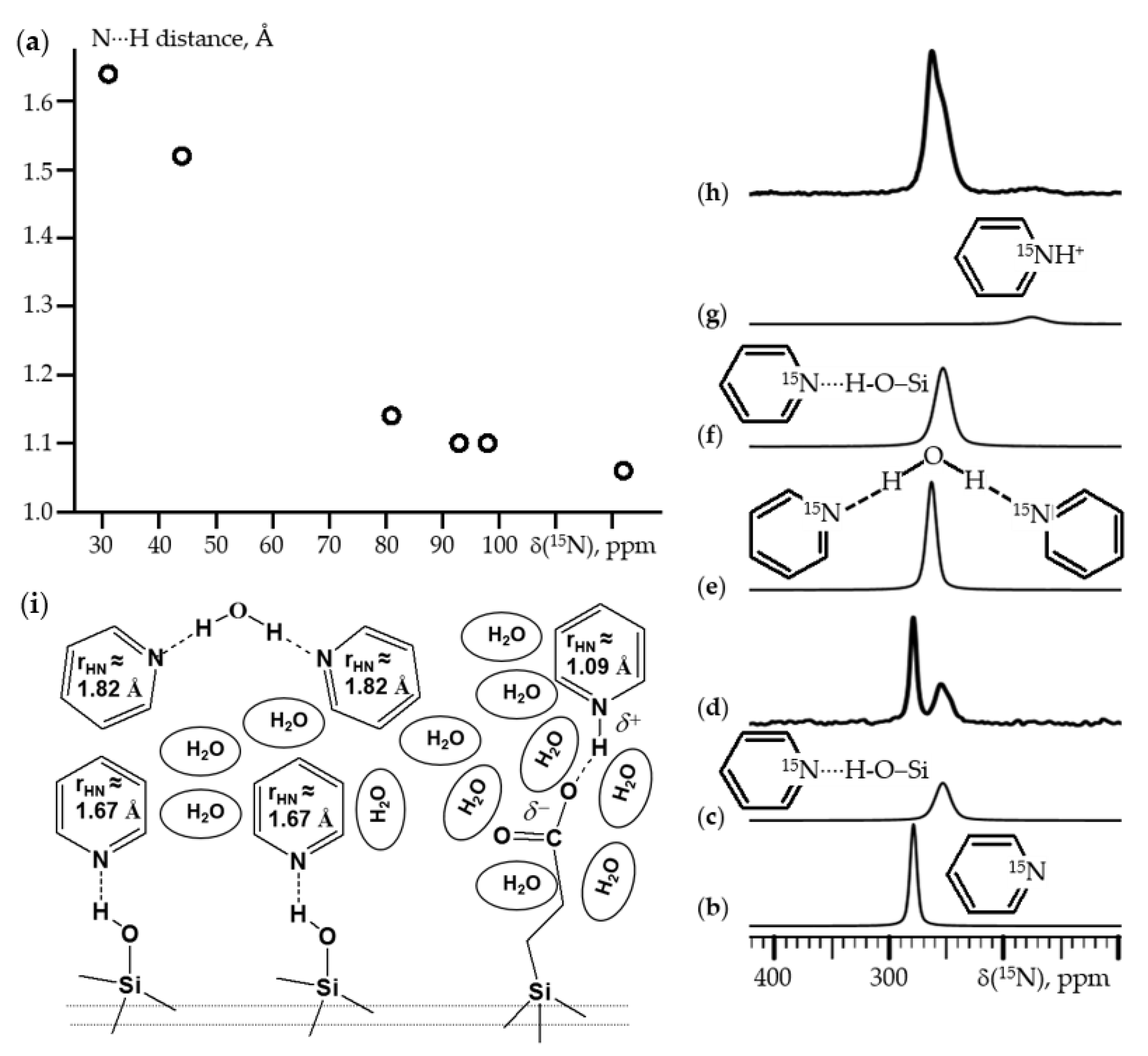
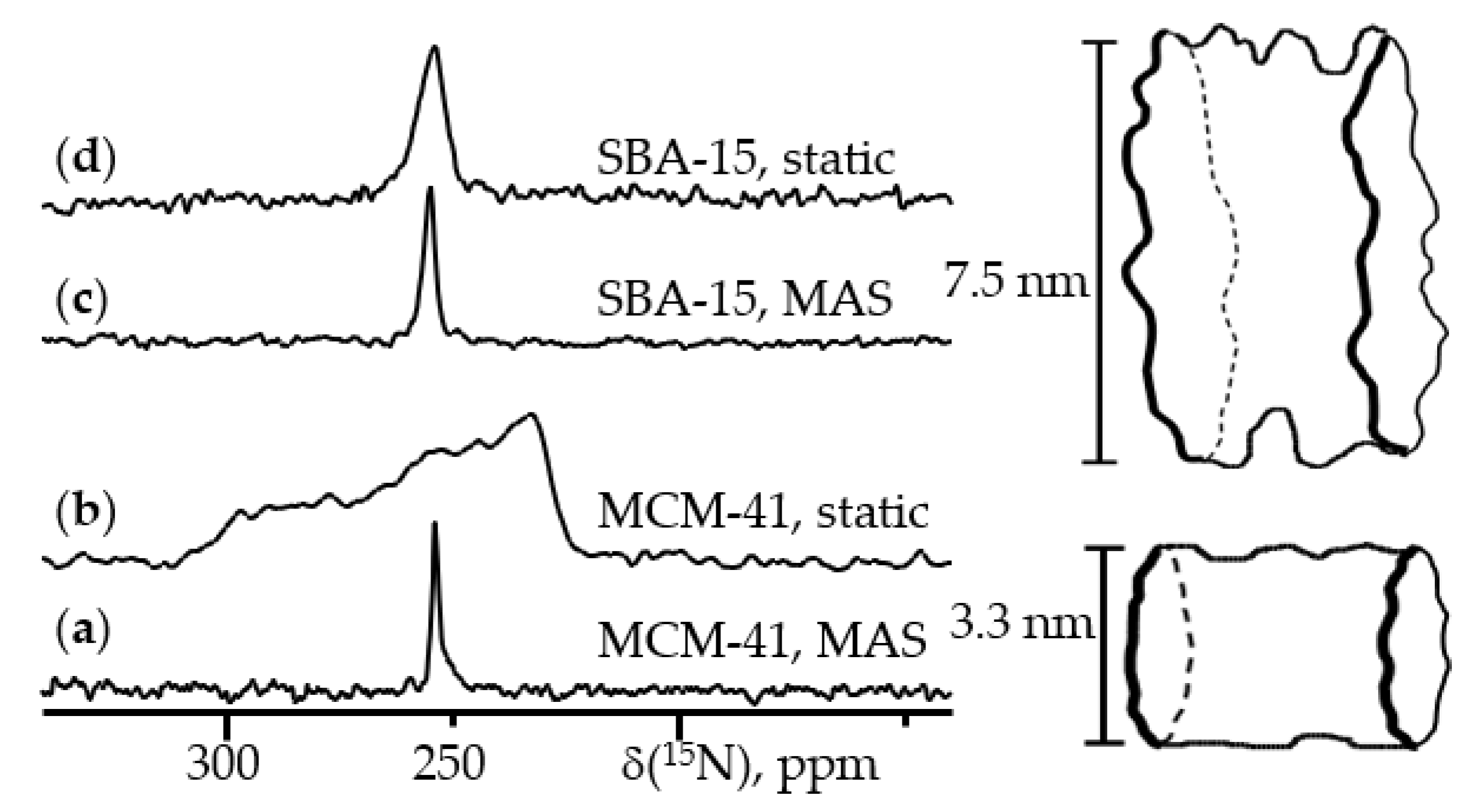
6. 15N NMR
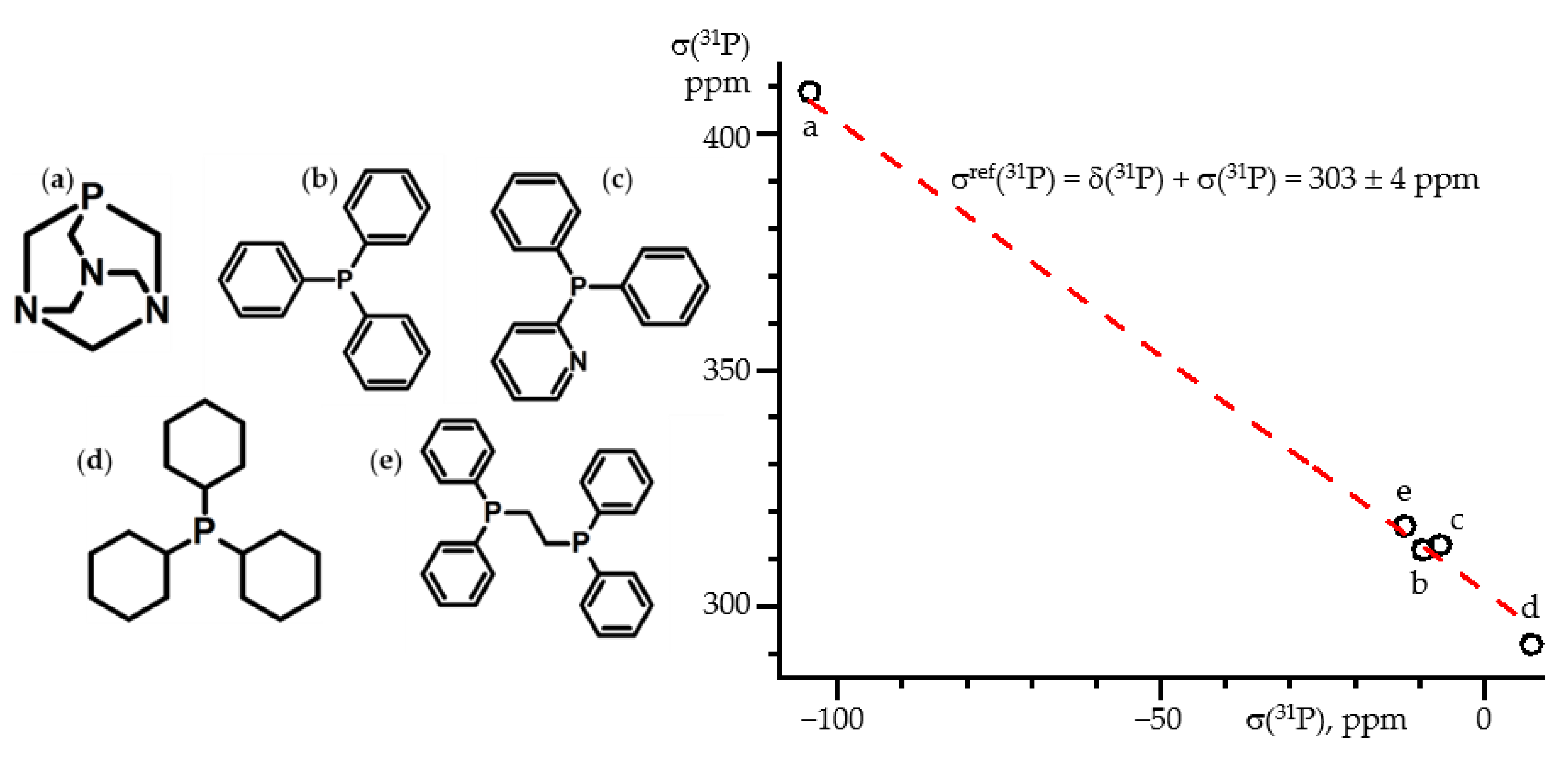
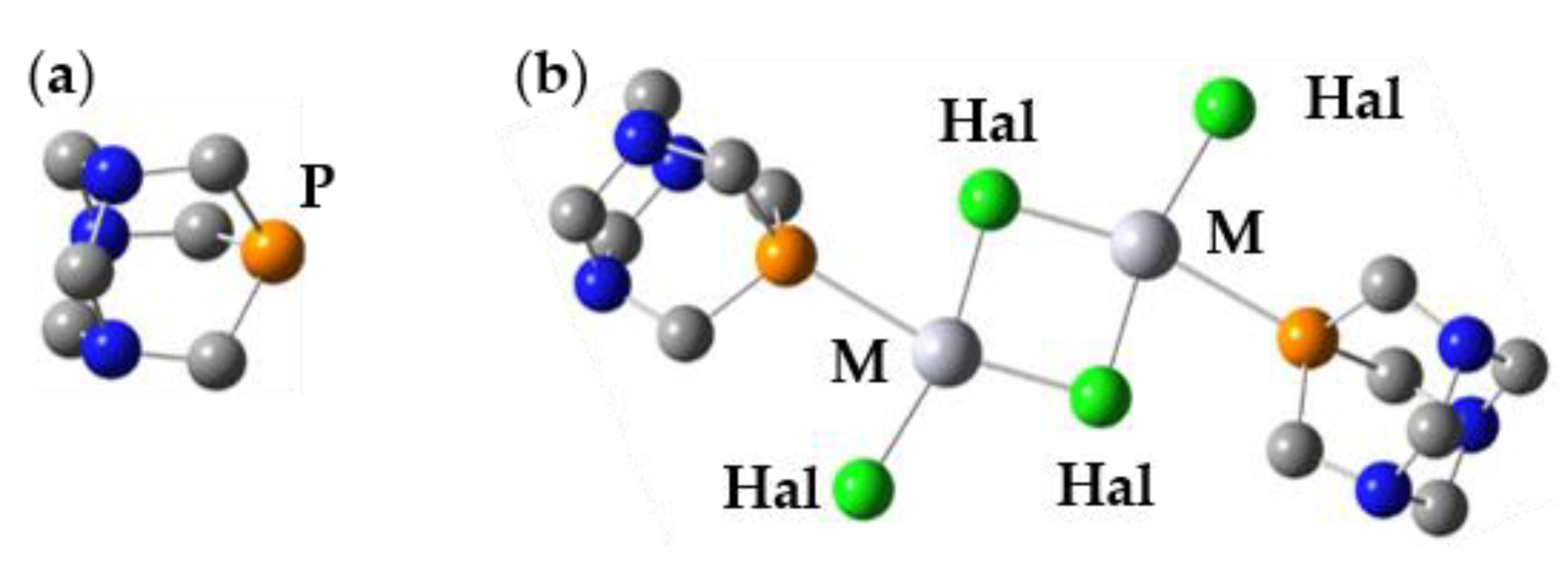
7. 31P NMR
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Porter, A.L.; Rafols, I. Is science becoming more interdisciplinary? Measuring and mapping six research fields over time. Scientometrics 2009, 81, 719–745. [Google Scholar] [CrossRef]
- Melnikova, D.L.; Badrieva, Z.F.; Kostin, M.A.; Maller, C.; Stas, M.; Buczek, A.; Broda, M.A.; Kupka, T.; Kelterer, A.-M.; Tolstoy, P.M.; et al. On Complex Formation between 5-Fluorouracil and β-Cyclodextrin in Solution and in the Solid State: IR Markers and Detection of Short-Lived Complexes by Diffusion NMR. Molecules 2020, 25, 5706. [Google Scholar] [CrossRef]
- Antonov, A.S.; Karpov, V.V.; Tupikina, E.Y.; Tolstoy, P.M.; Vovk, M.A. Aggregation Behavior of Lithionaphthalenes in Solution: Experimental and Theoretical Study. Organometallics 2020, 39, 3705–3714. [Google Scholar] [CrossRef]
- Jansen, D.; Gramüller, J.; Niemeyer, F.; Schaller, T.; Letzel, M.C.; Grimme, S.; Zhu, H.; Gschwind, R.M.; Niemeyer, J. What is the role of acid–acid interactions in asymmetric phosphoric acid organocatalysis? A detailed mechanistic study using interlocked and non-interlocked catalysts. Chem. Sci. 2020, 11, 4381–4390. [Google Scholar] [CrossRef]
- Lokesh, N.; Hioe, J.; Gramüller, J.; Gschwind, R.M. Relaxation Dispersion NMR to Reveal Fast Dynamics in Brønsted Acid Catalysis: Influence of Sterics and H-Bond Strength on Conformations and Substrate Hopping. J. Am. Chem. Soc. 2019, 141, 16398–16407. [Google Scholar] [CrossRef]
- Duer, M.J. (Ed.) Solid-State NMR Spectroscopy. Principles and Applications; Blackwell Science Ltd.: Oxford, UK, 2002. [Google Scholar]
- Bachmutov, V.I. Solid-State NMR in Materials Science. Principles and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Hodgkinson, P. (Ed.) Modern Methods in Solid-State NMR: A Practitioner’s Guide; The Royal Society of Chemistry: London, UK, 2018. [Google Scholar]
- Buntkowsky, G.; Vogel, M. Small Molecules, Non-Covalent Interactions, and Confinement. Molecules 2020, 25, 3311. [Google Scholar] [CrossRef]
- Brunner, E.; Rauche, M. Solid-state NMR spectroscopy: An advancing tool to analyse the structure and properties of metal–organic frameworks. Chem. Sci. 2020, 11, 4297–4304. [Google Scholar] [CrossRef]
- Gutmann, T.; Groszewicz, P.B.; Buntkowsky, G. Solid-state NMR of nanocrystals. Annu. Rep. NMR Spectrosc. 2019, 97, 1–82. [Google Scholar] [CrossRef]
- Smith, M.E. Recent progress in solid-state nuclear magnetic resonance of half-integer spin low-γ quadrupolar nuclei applied to inorganic materials. Magn. Reson. Chem. 2020, 1–44. [Google Scholar] [CrossRef]
- Bakhmutov, V.I. Strategies for Solid-State NMR Studies of Materials: From Diamagnetic to Paramagnetic Porous Solids. Chem. Rev. 2011, 111, 530–562. [Google Scholar] [CrossRef] [PubMed]
- Hodgkinson, P.; Wimperis, S. Solid-state NMR spectroscopy. Phys. Chem. Chem. Phys. 2009, 11, 6875. [Google Scholar] [CrossRef] [PubMed]
- Bryce, D.L.; Bernard, G.M.; Gee, M.; Lumsden, M.D.; Eichele, K.; Wasylishen, R.E. Practical Aspects of Modern Routine Solid-State Multinuclear Magnetic Resonance Spectroscopy: One-Dimensional Experiments. Can. J. Anal. Sci. Spectrosc. 2001, 46, 46–82. [Google Scholar] [CrossRef]
- Brown, S.P.; Spiess, W. Advanced Solid-State NMR Methods for the Elucidation of Structure and Dynamics of Molecular, Macromolecular, and Supramolecular Systems. Chem. Rev. 2001, 101, 4125–4156. [Google Scholar] [CrossRef] [PubMed]
- Albert, K. NMR investigations of stationary phases. J. Sep. Sci. 2003, 26, 215–224. [Google Scholar] [CrossRef]
- Gullion, T. Introduction to rotational-echo, double-resonance NMR. Concepts Magn. Reson. 1998, 10, 277–289. [Google Scholar] [CrossRef]
- Kaupp, M.; Bühl, M.; Malkin, V.G. (Eds.) Calculation of NMR and EPR Parameters; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Pilar, K.; Deng, Z.; Preefer, M.B.; Cooley, J.A.; Clément, R.; Seshadri, R.; Cheetham, A.K. Ab initio computation for solid-state 31P NMR of inorganic phosphates: Revisiting X-ray structures. Phys. Chem. Chem. Phys. 2019, 21, 10070–10074. [Google Scholar] [CrossRef]
- Grasa, P.; Baker, A.; Combes, C.; Rey, C.; Sarda, S.; Wright, A.J.; Smith, M.E.; Hanna, J.V.; Gervais, C.; Laurencin, D.; et al. From crystalline to amorphous calcium pyrophosphates: A solid state Nuclear Magnetic Resonance perspective. Acta Biomater. 2016, 31, 348–357. [Google Scholar] [CrossRef]
- Medvedev, A.G.; Churakov, A.V.; Prikhodchenko, P.V.; Lev, O.; Vener, M.V. Crystalline Peroxosolvates: Nature of the Coformer, Hydrogen-Bonded Networks and Clusters, Intermolecular Interactions. Molecules 2021, 26, 26. [Google Scholar] [CrossRef]
- Charpentier, T. The PAW/GIPAW approach for computing NMR parameters: A new dimension added to NMR study of solids. Solid State Nucl. Magn. Reson. 2011, 40, 1–20. [Google Scholar] [CrossRef]
- Solum, M.S.; Altmann, K.L.; Strohmeier, M.; Berges, D.A.; Zhang, Y.; Facelli, J.C.; Pugmire, R.J.; Grant, D.M. 15N Chemical Shift Principal Values in Nitrogen Heterocycles. J. Am. Chem. Soc. 1997, 119, 9804–9809. [Google Scholar] [CrossRef]
- Lorente, P.; Shenderovich, I.G.; Golubev, N.S.; Denisov, G.S.; Buntkowsky, G.; Limbach, H.-H. 1H/15N NMR Chemical Shielding, Dipolar 15N,2H Coupling and Hydrogen Bond Geometry Correlations in a Novel Serious of Hydrogen-Bonded Acid-Base Complexes of Collidine with Carboxylic Acids. Magn. Reson. Chem. 2001, 39, S18–S29. [Google Scholar] [CrossRef]
- Shenderovich, I.G. Effect of Noncovalent Interactions on the 31P Chemical Shift Tensor of Phosphine Oxides, Phosphinic, Phosphonic, and Phosphoric Acids, and Their Complexes with Lead(II). J. Phys. Chem. C 2013, 117, 26689–26702. [Google Scholar] [CrossRef]
- Andreeva, D.V.; Ip, B.; Gurinov, A.A.; Tolstoy, P.M.; Denisov, G.S.; Shenderovich, I.G.; Limbach, H.-H. Geometrical Features of Hydrogen Bonded Complexes Involving Sterically Hindered Pyridines. J. Phys. Chem. A 2006, 110, 10872–10879. [Google Scholar] [CrossRef] [PubMed]
- Lowe, I.J. Free Induction Decays of Rotating Solids. Phys. Rev. Lett. 1959, 2, 285–287. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Mauder, D.; Akcakayiran, D.; Buntkowsky, G.; Limbach, H.-H.; Findenegg, G.H. NMR Provides Checklist of Generic Properties for Atomic-Scale Models of Periodic Mesoporous Silicas. J. Phys. Chem. B 2007, 111, 12088–12096. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G.; Lesnichin, S.B.; Tu, C.; Silverman, D.N.; Tolstoy, P.M.; Denisov, G.S.; Limbach, H.-H. NMR Studies of Active-Site Properties of Human Carbonic Anhydrase II by using 15N-Labeled 4-Methylimidazole as a Local Probe and Histidine Hydrogen-Bond Correlations. Chem. Eur. J. 2015, 21, 2915–2929. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Shenderovich, I.G. Experimentally Established Benchmark Calculations of 31P NMR Quantities. Chemistry-Methods 2021, 1, 61–70. [Google Scholar] [CrossRef]
- Jensen, F. Segmented Contracted Basis Sets Optimized for Nuclear Magnetic Shielding. J. Chem. Theory Comput. 2015, 11, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G. Electric field effect on 31P NMR magnetic shielding. J. Chem. Phys. 2020, 153, 184501. [Google Scholar] [CrossRef] [PubMed]
- Nardo, V.M.; Cassone, G.; Ponterio, R.C.; Saija, F.; Sponer, J.; Tommasini, M.; Trusso, S. Electric-Field-Induced Effects on the Dipole Moment and Vibrational Modes of the Centrosymmetric Indigo Molecule. J. Phys. Chem. A 2020, 124, 10856–10869. [Google Scholar] [CrossRef] [PubMed]
- Cassone, G.; Sponer, J.; Trusso, S.; Saija, F. Ab initio spectroscopy of water under electric fields. Phys. Chem. Chem. Phys. 2019, 21, 21205–21212. [Google Scholar] [CrossRef]
- Dominikowska, J.; Palusiak, M. Tuning Aromaticity of para-Substituted Benzene Derivatives with an External Electric Field. ChemPhysChem 2018, 19, 590–595. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Provasi, P.F.; Pagola, G.I.; Ferraro, M.B. Electric field effects on nuclear magnetic shielding of the 1:1 and 2:1 (homo and heterochiral) complexes of XOOX′ (X, X′ = H, CH3) with lithium cation and their chiral dis-crimination. J. Chem. Phys. 2011, 135, 104116. [Google Scholar] [CrossRef]
- Del Bene, J.E.; Jordan, M.J.T. To What Extent Do External Fields and Vibrational and Isotopic Effects Influence NMR Coupling Constants Across Hydrogen Bonds? Two-Bond Cl-N Spin-Spin Coupling Constants (2hJCl-N) in Model ClH:NH3 Complexes. J. Phys. Chem. A 2002, 106, 5385–5392. [Google Scholar] [CrossRef]
- Ramos, M.; Alkorta, I.; Elguero, J.; Golubev, N.S.; Denisov, G.S.; Benedict, H.; Limbach, H.-H. Theoretical Study of the Influence of Electric Fields on Hydrogen-Bonded Acid−Base Complexes. J. Phys. Chem. A 1997, 101, 9791–9800. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Denisov, G.S. Adduct under Field—A Qualitative Approach to Account for Solvent Effect on Hydrogen Bonding. Molecules 2020, 25, 436. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Denisov, G.S. Modeling of Solute-Solvent Interactions Using an External Electric Field—From Tautomeric Equilibrium in Nonpolar Solvents to the Dissociation of Alkali Metal Halides. Molecules 2021, 26, 1283. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Denisov, G.S. Solvent effects on acid-base complexes. What is more important: A macroscopic reaction field or solute-solvent interactions? J. Chem. Phys. 2019, 150, 204505. [Google Scholar] [CrossRef] [PubMed]
- Struppe, J.; Quinn, C.M.; Sarkar, S.; Gronenborn, A.M.; Polenova, T. Ultrafast 1H MAS NMR Crystallography for Natural Abundance Pharmaceutical Compounds. Mol. Pharm. 2020, 17, 674–682. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.P. Applications of high-resolution 1H solid-state NMR. Solid State Nucl. Magn. Reson. 2012, 41, 1–27. [Google Scholar] [CrossRef]
- Paruzzo, F.M.; Emsley, L. High-resolution 1H NMR of powdered solids by homonuclear dipolar decoupling. J. Magn. Reson. 2019, 309, 106598. [Google Scholar] [CrossRef]
- Dudek, M.K.; Kazmierski, S.; Kostrzewa, M.; Potrzebowski, M.J. Solid-State NMR Studies of Molecular Crystals. Annu. Rep. NMR Spectrosc. 2018, 95, 1–81. [Google Scholar] [CrossRef]
- Mote, K.R.; Agarwal, V.; Madhu, P.K. Five decades of homonuclear dipolar decoupling in solid-state NMR: Status and outlook. Prog. Nucl. Magn. Reson. Spectrosc. 2016, 97, 1–39. [Google Scholar] [CrossRef]
- Vinogradov, E.; Madhu, P.K.; Vega, S. Strategies for high-resolution proton spectroscopy in solid-state NMR. Top. Curr. Chem. 2004, 246, 33–90. [Google Scholar] [CrossRef]
- Schnell, I.; Spiess, H.W. High-Resolution 1H NMR Spectroscopy in the Solid State: Very Fast Sample Rotation and Multiple-Quantum Coherences. J. Magn. Reson. 2001, 151, 153–227. [Google Scholar] [CrossRef]
- Gurinov, A.A.; Lesnichin, S.B.; Limbach, H.-H.; Shenderovich, I.G. How Short is the Strongest Hydrogen Bond in the Proton-Bound Homodimers of Pyridine Derivatives? J. Phys. Chem. A 2014, 118, 10804–10812. [Google Scholar] [CrossRef]
- Kong, S.; Borissova, A.O.; Lesnichin, S.B.; Hartl, M.; Daemen, L.L.; Eckert, J.; Antipin, M.Y.; Shenderovich, I.G. Geometry and Spectral Properties of the Protonated Homodimer of Pyridine in the Liquid and Solid States. A Combined NMR, X-ray Diffraction and Inelastic Neutron Scattering Study. J. Phys. Chem. A 2011, 115, 8041–8048. [Google Scholar] [CrossRef]
- Ip, B.C.K.; Andreeva, D.V.; Buntkowsky, G.; Akcakayiran, D.; Findenegg, G.H.; Shenderovich, I.G. NMR Study of Proton Transfer to Strong Bases on Inner Surfaces of MCM-41. Micropor. Mesopor. Mater. 2010, 134, 22–28. [Google Scholar] [CrossRef]
- Shenderovich, I.G.; Buntkowsky, G.; Schreiber, A.; Gedat, E.; Sharif, S.; Albrecht, J.; Golubev, N.S.; Findenegg, G.H.; Limbach, H.-H. Pyridine-15N A Mobile NMR Sensor for Surface Acidity and Surface Defects of Mesoporous Silica. J. Phys. Chem. B 2003, 107, 11924–11939. [Google Scholar] [CrossRef]
- Grünberg, B.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.-H.; Buntkowsky, G. Hydrogen Bonding of Water Confined in Mesoporous Silica MCM-41 and SBA-15 Studied by 1H Solid-State NMR. Chem. Eur. J. 2004, 10, 5689–5696. [Google Scholar] [CrossRef]
- Li, Z.; Rieg, C.; Beurer, A.-K.; Benz, M.; Bender, J.; Schneck, C.; Traa, Y.; Dyballa, M.; Hunger, M. Effect of aluminum and sodium on the sorption of water and methanol in microporous MFI-type zeolites and mesoporous SBA-15 materials. Adsorption 2021, 27, 49–68. [Google Scholar] [CrossRef]
- Breynaert, E.; Houlleberghs, M.; Radhakrishnan, S.; Grübel, G.; Taulelle, F.; Martens, J.A. Water as a tuneable solvent: A perspective. Chem. Soc. Rev. 2020, 49, 2557–2569. [Google Scholar] [CrossRef]
- Ok, S.; Hwang, B.; Liu, T.; Welch, S.; Sheets, J.M.; Cole, D.R.; Liu, K.-H.; Mou, C.-Y. Fluid Behavior in Nanoporous Silica. Front. Chem. 2020, 8, 734. [Google Scholar] [CrossRef] [PubMed]
- Veena, V.S.; Illath, K.; Lazar, A.; Vinod, C.P.; Ajithkumar, T.G.; Jayanthi, S. Distribution of water in the pores of periodic mesoporous organosilicates—A proton solid state MAS NMR study. Phys. Chem. Chem. Phys. 2018, 20, 29351. [Google Scholar] [CrossRef] [PubMed]
- Kumari, B.; Brodrecht, M.; Breitzke, H.; Werner, M.; Grünberg, B.; Limbach, H.-H.; Forg, S.; Sanjon, E.P.; Drossel, B.; Gutmann, T.; et al. Mixtures of Alcohols and Water confined in Mesoporous Silica: A Combined Solid-State NMR and Molecular Dynamics Simulation Study. J. Phys. Chem. C 2018, 122, 19540–19550. [Google Scholar] [CrossRef]
- Sebastiani, D. Ab-Initio Molecular Dynamics Simulations and Calculations of Spectroscopic Parameters in Hydrogen-Bonding Liquids in Confinement. Z. Phys. Chem. 2018, 232, 973–987. [Google Scholar] [CrossRef]
- Kristinaitytė, K.; Dagys, L.; Kausteklis, J.; Klimavicius, V.; Doroshenko, I.; Pogorelov, V.; Valevičienė, N.R.; Balevicius, V. NMR and FTIR studies of clustering of water molecules: From low-temperature matrices to nano-structured materials used in innovative medicine. J. Mol. Liq. 2017, 235, 1–6. [Google Scholar] [CrossRef]
- Shelyapina, M.G.; Silyukov, O.I.; Lushpinskaya, I.P.; Kurnosenko, S.A.; Mazur, A.S.; Shenderovich, I.G.; Zvereva, I.A. NMR Study of Intercalates and Grafted Organic Derivatives of H2La2Ti3O10. Molecules 2020, 25, 5229. [Google Scholar] [CrossRef]
- Klimavicius, V.; Dagys, L.; Chizhik, V.; Balevicius, V. CP MAS Kinetics Study of Ionic Liquids Confined in Mesoporous Silica: Convergence of Non-Classical and Classical Spin Coupling Models. Appl. Magn. Reson. 2017, 48, 673–685. [Google Scholar] [CrossRef]
- Buntkowsky, G.; Breitzke, H.; Adamczyk, A.; Roelofs, F.; Emmler, T.; Gedat, E.; Grünberg, B.; Xu, Y.; Limbach, H.-H.; Shenderovich, I.; et al. Structural and Dynamical Properties of Guest Molecules Confined in Mesoporous Silica Materials Revealed by NMR. Phys. Chem. Chem. Phys. 2007, 9, 4843–4853. [Google Scholar] [CrossRef]
- Vyalikh, A.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.-H.; Buntkowsky, G. Evidence of Microphase Separation in Controlled Pore Glasses. Solid State Nucl. Magn. Reson. 2005, 28, 117–124. [Google Scholar] [CrossRef]
- Gedat, E.; Schreiber, A.; Findenegg, G.H.; Shenderovich, I.; Limbach, H.-H.; Buntkowsky, G. Stray field gradient NMR reveals effects of hydrogen bonding on diffusion coefficients of pyridine in mesoporous silica. Magn. Reson. Chem. 2001, 39, S149–S157. [Google Scholar] [CrossRef]
- Neffati, R.; Judeinstein, P.; Rault, J. Freezing, melting and dynamics of supercooled water confined in porous glass. J. Phys. Condens. Matter 2020, 32, 465101. [Google Scholar] [CrossRef]
- Enninful, H.R.N.B.; Schneider, D.; Kohns, R.; Enke, D.; Valiullin, R. A novel approach for advanced thermoporometry characterization of mesoporous solids: Transition kernels and the serially connected pore model. Micropor. Mesopor. Mat. 2020, 309, 110534. [Google Scholar] [CrossRef]
- Werner, M.; Rothermel, N.; Breitzke, H.; Gutmann, T.; Buntkowsky, G. Recent Advances in Solid State NMR of Small Molecules in Confinement. Isr. J. Chem. 2014, 54, 60–73. [Google Scholar] [CrossRef]
- Sattig, M.; Reutter, S.; Fujara, F.; Werner, M.; Buntkowsky, G.; Vogel, M. NMR studies on the temperature-dependent dynamics of confined water. Phys. Chem. Chem. Phys. 2014, 16, 19229–19240. [Google Scholar] [CrossRef]
- Grünberg, B.; Grünberg, A.; Limbach, H.-H.; Buntkowsky, G. Melting of Naphthalene Confined in Mesoporous Silica MCM-41. Appl. Marn. Reson. 2013, 44, 189–201. [Google Scholar] [CrossRef]
- Szalontai, G. 1H NMR linewidths of small organic guest molecules physisorbed on different mesoporous silicas. J. Mol. Struct. 2020, 1205, 127646. [Google Scholar] [CrossRef]
- Torres Barthelemy, V.; Pérez-Hernández, N.; Shenderovich, I.G.; Tolstoy, P.M.; Denisov, G.S.; Limbach, H.-H. NMR-Detected Host-Guest Proton Exchange as a Tool to Explore Surface/Volume Ratios and Fluid Filling of Internal and External Spaces of Porous Solids containing Surface-OH-Groups. J. Phys. Chem. C 2020, 124, 22082–22095. [Google Scholar] [CrossRef]
- Gurinov, A.A.; Denisov, G.S.; Borissova, A.O.; Goloveshkin, A.S.; Greindl, J.; Limbach, H.-H.; Shenderovich, I.G. NMR Study of Solvation Effect on the Geometry of Proton-Bound Homodimers of Increasing Size. J. Phys. Chem. A 2017, 121, 8697–8705. [Google Scholar] [CrossRef] [PubMed]
- Limbach, H.-H.; Pietrzak, M.; Sharif, S.; Tolstoy, P.M.; Shenderovich, I.G.; Smirnov, S.N.; Golubev, N.S.; Denisov, G.S. NMR-Parameters and Geometries of OHN- and ODN Hydrogen Bonds of Pyridine-Acid Complexes. Chem. Eur. J. 2004, 10, 5195–5204. [Google Scholar] [CrossRef] [PubMed]
- Lesnichin, S.B.; Tolstoy, P.M.; Limbach, H.-H.; Shenderovich, I.G. Counteranion-Dependent Mechanisms of Intramolecular Proton Transfer in Aprotic Solution. Phys. Chem. Chem. Phys. 2010, 12, 10373–10379. [Google Scholar] [CrossRef]
- Chan-Huot, M.; Dos, A.; Zander, R.; Sharif, S.; Tolstoy, P.M.; Compton, S.; Fogle, E.; Toney, M.D.; Shenderovich, I.; Denisov, G.S.; et al. NMR Studies of Protonation and Hydrogen Bond States of Internal Aldimines of Pyridoxal 5′-Phosphate Acid−Base in Alanine Racemase, Aspartate Aminotransferase, and Poly-L-lysine. J. Am. Chem. Soc. 2013, 135, 18160–18175. [Google Scholar] [CrossRef]
- Limbach, H.-H.; Chan-Huot, M.; Sharif, S.; Tolstoy, P.M.; Shenderovich, I.G.; Denisov, G.S. Critical Hydrogen Bonds and Protonation States of Pyridoxal 5′-phosphate Revealed by NMR. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2011, 1814, 1426–1437. [Google Scholar] [CrossRef]
- Ip, B.C.K.; Shenderovich, I.G.; Tolstoy, P.M.; Frydel, J.; Denisov, G.S.; Buntkowsky, G.; Limbach, H.-H. NMR Studies of Solid Pentachlorophenol-4-Methylpyridine Complexes Exhibiting Strong OHN Hydrogen Bonds: Geometric H/D Isotope Effects and Hydrogen Bond Coupling Cause Isotopic Polymorphism. J. Phys. Chem. A 2012, 116, 11370–11387. [Google Scholar] [CrossRef]
- Bismarck, A.; Aranberri-Askargorta, I.; Springer, J.; Lampke, T.; Wielage, B.; Stamboulis, A.; Shenderovich, I.; Limbach, H.-H. Surface Characterization of Flax, Hemp and Cellulose Fibers; Surface Properties and the Water Uptake Behavior. Polym. Compos. 2002, 23, 872–894. [Google Scholar] [CrossRef]
- Gurinov, A.A.; Rozhkova, Y.A.; Zukal, A.; Čejka, J.; Shenderovich, I.G. Mutable Lewis and Brønsted Acidity of Aluminated SBA-15 as Revealed by NMR of Adsorbed Pyridine-15N. Langmuir 2011, 27, 12115–12123. [Google Scholar] [CrossRef]
- Akcakayiran, D.; Mauder, D.; Hess, C.; Sievers, T.K.; Kurth, D.G.; Shenderovich, I.; Limbach, H.-H.; Findenegg, G.H. Carboxylic Acid-Doped SBA-15 Silica as a Host for Metallo-supramolecular Coordination Polymers. J. Phys. Chem. B 2008, 112, 14637–14647. [Google Scholar] [CrossRef] [PubMed]
- Gurinov, A.A.; Mauder, D.; Akcakayiran, D.; Findenegg, G.H.; Shenderovich, I.G. Does Water Affect the Acidity of Surfaces? The Proton-Donating Ability of Silanol and Carboxylic Acid Groups at Mesoporous Silica. ChemPhysChem 2012, 13, 2282–2285. [Google Scholar] [CrossRef] [PubMed]
- Sharif, S.; Shenderovich, I.G.; González, L.; Denisov, G.S.; Silverman, D.N.; Limbach, H.-H. NMR and Ab initio Studies of Small Complexes Formed between Water and Pyridine Derivatives in Solid and Liquid Phase. J. Phys. Chem. A 2007, 111, 6084–6093. [Google Scholar] [CrossRef] [PubMed]
- Mauder, D.; Akcakayiran, D.; Lesnichin, S.B.; Findenegg, G.H.; Shenderovich, I.G. Acidity of Sulfonic and Phosphonic Acid-Functionalized SBA-15 under Almost Water-Free Conditions. J. Phys. Chem. C 2009, 113, 19185–19192. [Google Scholar] [CrossRef]
- Mulloyarova, V.V.; Ustimchuk, D.O.; Filarowski, A.; Tolstoy, P.M. H/D Isotope Effects on 1H-NMR Chemical Shifts in Cyclic Heterodimers and Heterotrimers of Phosphinic and Phosphoric Acids. Molecules 2020, 25, 1907. [Google Scholar] [CrossRef]
- Mulloyarova, V.V.; Giba, I.S.; Kostin, M.A.; Denisov, G.S.; Shenderovich, I.G.; Tolstoy, P.M. Cyclic Trimers of Phosphinic Acids in Polar Aprotic Solvent: Symmetry, Chirality and H/D Isotope Effects on NMR Chemical Shifts. Phys. Chem. Chem. Phys. 2018, 20, 4901–4910. [Google Scholar] [CrossRef]
- Machida, S.; Sohmiya, M.; Ide, Y.; Sugahara, Y. Solid-State 31P Nuclear Magnetic Resonance Study of Interlayer Hydroxide Surfaces of Kaolinite Probed with an Interlayer Triethylphosphine Oxide Monolayer. Langmuir 2018, 34, 12694–12701. [Google Scholar] [CrossRef] [PubMed]
- Seitz, A.E.; Hippauf, F.; Kremer, W.; Kaskel, S.; Scheer, M. Facile storage and release of white phosphorus and yellow arsenic. Nat. Commun. 2018, 9, 361. [Google Scholar] [CrossRef]
- Begimova, G.U.; Tupikina, E.Y.; Yu, V.K.; Denisov, G.S.; Bodensteiner, M.; Shenderovich, I.G. Effect of Hydrogen Bonding to Water on the 31P Chemical Shift Tensor of Phenyl- and Trialkylphosphine Oxides and a-Amino Phosphonates. J. Phys. Chem. C 2016, 120, 8717–8729. [Google Scholar] [CrossRef]
- Moussa, M.E.; Shelyganov, P.A.; Wegley, B.; Seidl, M.; Scheer, M. The Potential of the Diphosphorus Complex [Cp2W2(CO)4( η2-P2)] as an Organometallic Connecter in Supramolecular Chemistry. Eur. J. Inorg. Chem. 2019, 2019, 4241–4248. [Google Scholar] [CrossRef] [PubMed]
- Guenther, J.; Reibenspies, J.; Blümel, J. Synthesis and characterization of tridentate phosphine ligands incorporating long methylene chains and ethoxysilane groups for immobilizing molecular rhodium catalysts. Mol. Catal. 2019, 479, 110629. [Google Scholar] [CrossRef]
- Cluff, K.J.; Bhuvanesh, N.; Blümel, J. Monometallic Ni-0 and Heterobimetallic Ni-0/Au-I Complexes of Tripodal Phosphine Ligands: Characterization in Solution and in the Solid State and Catalysis. Chem. Eur. J. 2015, 21, 10138–10148. [Google Scholar] [CrossRef] [PubMed]
- Pazderski, L. 15N and 31P NMR Coordination Shifts in Transition Metal Complexes with Nitrogen- and Phosphorus-Containing Heterocycles. Annu. Rep. NMR Spectrosc. 2013, 80, 33–179. [Google Scholar] [CrossRef]
- Hubbard, P.J.; Benzie, J.W.; Bakhmutov, V.I.; Blümel, J. Disentangling Different Modes of Mobility of Triphenylphosphine Oxide Adsorbed on Alumina. J. Chem. Phys. 2020, 152, 054718. [Google Scholar] [CrossRef]
- Kharel, S.; Cluff, K.J.; Bhuvanesh, N.; Gladysz, J.A.; Blümel, J. Structures and Dynamics of Secondary and Tertiary Alkylphosphine Oxides Adsorbed on Silica. Chem. Asian J. 2019, 14, 2704–2711. [Google Scholar] [CrossRef]
- Hilliard, C.R.; Kharel, S.; Cluff, K.; Bhuvanesh, N.; Gladysz, J.; Bluemel, J. Structures and Unexpected Dynamic Properties of Phosphine Oxides Adsorbed on Silica Surfaces. Chem. Eur. J. 2014, 20, 17292–17295. [Google Scholar] [CrossRef]
- Shenderovich, I.G. For Whom a Puddle Is the Sea? Adsorption of Organic Guests on Hydrated MCM-41 Silica. Langmuir 2020, 36, 11383–11392. [Google Scholar] [CrossRef]
- Pires, E.; Fraile, J.M. Study of interactions between Brønsted acids and triethylphosphine oxide in solution by 31P NMR: Evidence for 2:1 species. Phys. Chem. Chem. Phys. 2020, 22, 24351–24358. [Google Scholar] [CrossRef]
- Ostras’, A.S.; Ivanov, D.M.; Novikov, A.S.; Tolstoy, P.M. Phosphine Oxides as Spectroscopic Halogen Bond Descriptors: IR and NMR Correlations with Interatomic Distances and Complexation Energy. Molecules 2020, 25, 1406. [Google Scholar] [CrossRef]
- Tupikina, E.Y.; Bodensteiner, M.; Tolstoy, P.M.; Denisov, G.S.; Shenderovich, I.G. P=O Moiety as an Ambidextrous Hydrogen Bond Acceptor. J. Phys. Chem. C 2018, 122, 1711–1720. [Google Scholar] [CrossRef]
- Arp, F.F.; Bhuvanesh, N.; Blümel, J. Hydrogen peroxide adducts of triarylphosphine oxides. Dalton Trans. 2019, 48, 14312–14325. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.H.; Lindhardt, D.; Bhuvanesh, N.; Blümel, J. Di(hydroperoxy)cycloalkanes Stabilized via Hydrogen Bonding by Phosphine Oxides: Safe and Efficient Baeyer−Villiger Oxidants. ACS Sustainable Chem. Eng. 2018, 6, 6829–6840. [Google Scholar] [CrossRef]
- Chernyshov, I.Y.; Vener, M.V.; Shenderovich, I.G. Local-structure effects on 31P NMR chemical shift tensors in solid state. J. Chem. Phys. 2019, 150, 144706. [Google Scholar] [CrossRef] [PubMed]
- Golubev, N.S.; Melikova, S.M.; Shchepkin, D.N.; Shenderovich, I.G.; Tolstoy, P.M.; Denisov, G.S. Interpretation of H/D Isotope Effects on NMR Chemical Shifts of [FHF]- Ion Based on Calculations of Nuclear Magnetic Shielding Tensor Surface. Z. Phys. Chem. 2003, 217, 1549–1563. [Google Scholar] [CrossRef]
- Fisher, K.J.; Alyea, E.C.; Shehnazarian, N. A 31P NMR Study of the Water Soluble Derivatives of 1,3,5-triaza-7-phosphaadamantane (PTA). Phosphorus Sulfur Silicon 1990, 48, 37–40. [Google Scholar] [CrossRef]
- Phillips, A.D.; Gonsalvi, L.; Romerosa, A.; Vizza, F.; Peruzzini, M. Coordination chemistry of 1,3,5-triaza-7-phosphaadamantane (PTA) Transition metal complexes and related catalytic, medicinal and photoluminescent applications. Coord. Chem. Rev. 2004, 248, 955–993. [Google Scholar] [CrossRef]
- Alyea, E.C.; Fisher, K.J.; Johnson, S. Synthesis, solid state 31P CP-MAS NMR, infrared and Raman studies of mercury(II) complexes of 1,3,5-triaza-7-phosphaadamantane (PTA). Can. J. Chem. 1989, 67, 1319–1323. [Google Scholar] [CrossRef]
- Smoleński, P.; Kirillov, A.M.; Guedes da Silva, M.F.C.; Pombeiro, A.J.L. Transformations of the Vaska-type complex trans- [RhCl(CO)(PTA)2] (PTA = 1,3,5-triaza-7-phosphaadamantane) during stepwise addition of HCl: Synthesis, characterization and crystal structure of trans-[RhCl2 (PTA)(PTAH)]. Inorg. Chim. Acta 2011, 378, 342–346. [Google Scholar] [CrossRef]
- Kirillov, A.M.; Smoleński, P.; Guedes da Silva, M.F.C.; Pombeiro, A.J.L. The First Copper Complexes Bearing the 1,3,5-Triaza-7- phosphaadamantane (PTA) Ligand. Eur. J. Inorg. Chem. 2007, 2007, 2686–2692. [Google Scholar] [CrossRef]
- Pellei, M.; Alidori, S.; Camalli, M.; Campi, G.; Lobbia, G.G.; Mancini, M.; Papini, G.; Spagna, R.; Santini, C. Copper(I)– organophosphine complexes of bis(3,5-dimethylpyrazol-1-yl)dithioacetate ligand. Inorg. Chim. Acta 2008, 361, 1456–1462. [Google Scholar] [CrossRef]
- Gavara, R.; Pinto, A.; Donamaria, R.; Olmos, M.E.; de Luzuriaga, J.M.L.; Rodriguez, L. Polarized Supramolecular Aggregates Based on Luminescent Perhalogenated Gold Derivatives. Inorg. Chem. 2017, 56, 11946–11955. [Google Scholar] [CrossRef]
- Bertrand, B.; Spreckelmeyer, S.; Bodio, E.; Cocco, F.; Picquet, M.; Richard, P.; Le Gendre, P.; Orvig, C.; Cinellu, M.A.; Casini, A. Exploring the potential of gold (III) cyclometallated compounds as cytotoxic agents: Variations on the CˆN theme. Dalton Trans. 2015, 44, 11911–11918. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G. 1,3,5-Triaza-7-Phosphaadamantane (PTA) as a 31P NMR Probe for Organometallic Transition Metal Complexes in Solution. Molecules 2021, 26, 1390. [Google Scholar] [CrossRef]
- Straasø, L.A.; Saleem, Q.; Hansen, M.R. A Toolbox of Solid-State NMR Experiments for the Characterization of Soft Organic Nanomaterials. Annu. Rep. NMR Spectrosc. 2016, 88, 307–383. [Google Scholar] [CrossRef]
- Jeziorna, A.; Kazmierski, S.; Paluch, P.; Skorupska, E.; Potrzebowski, M.J. Recent Progress in the Solid-State NMR Studies of Short Peptides: Techniques, Structure and Dynamics. Annu. Rep. NMR Spectrosc. 2014, 83, 67–143. [Google Scholar] [CrossRef]
- Jaeger, M.; Aspers, R.L.E.G. Covariance NMR and Small Molecule Applications. Annu. Rep. NMR Spectrosc. 2014, 83, 271–349. [Google Scholar] [CrossRef]
- Web of Science. Available online: www.webofknowledge.com (accessed on 31 March 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shenderovich, I.G.; Limbach, H.-H. Solid State NMR for Nonexperts: An Overview of Simple but General Practical Methods. Solids 2021, 2, 139-154. https://doi.org/10.3390/solids2020009
Shenderovich IG, Limbach H-H. Solid State NMR for Nonexperts: An Overview of Simple but General Practical Methods. Solids. 2021; 2(2):139-154. https://doi.org/10.3390/solids2020009
Chicago/Turabian StyleShenderovich, Ilya G., and Hans-Heinrich Limbach. 2021. "Solid State NMR for Nonexperts: An Overview of Simple but General Practical Methods" Solids 2, no. 2: 139-154. https://doi.org/10.3390/solids2020009
APA StyleShenderovich, I. G., & Limbach, H.-H. (2021). Solid State NMR for Nonexperts: An Overview of Simple but General Practical Methods. Solids, 2(2), 139-154. https://doi.org/10.3390/solids2020009







