Method for Monitoring the Condition of Steel Wire Ropes Based on the Analysis of Changes in the Linear Dimensions of Their Cross-Sections
Abstract
1. Introduction
- a substantial reduction of input size and computational burden;
- improved robustness to noise and visual distortions;
- interpretable numerical representation of geometric features;
- accurate detection of macroscopic deformations corresponding to visually discernible defects such as kinks, bends, and breaks.
2. Materials and Methods
2.1. Dataset and Image Acquisition
- Real images acquired in controlled laboratory conditions using a calibrated optical setup. These images capture industrial steel ropes in intact condition and with visually discernible surface defects.
- Synthetic images generated in Blender with strictly controlled defect geometry, illumination, and rope structure, providing tunable variability and precise labeling.
- verification of thickness-profile extraction accuracy under idealized conditions;
- visual assessment of class separability based on the extracted profile shape;
- analysis of robustness to visual perturbations—noise, illumination changes, and background nonuniformity—by controlled variation of imaging parameters.
2.2. Classification Model Selection
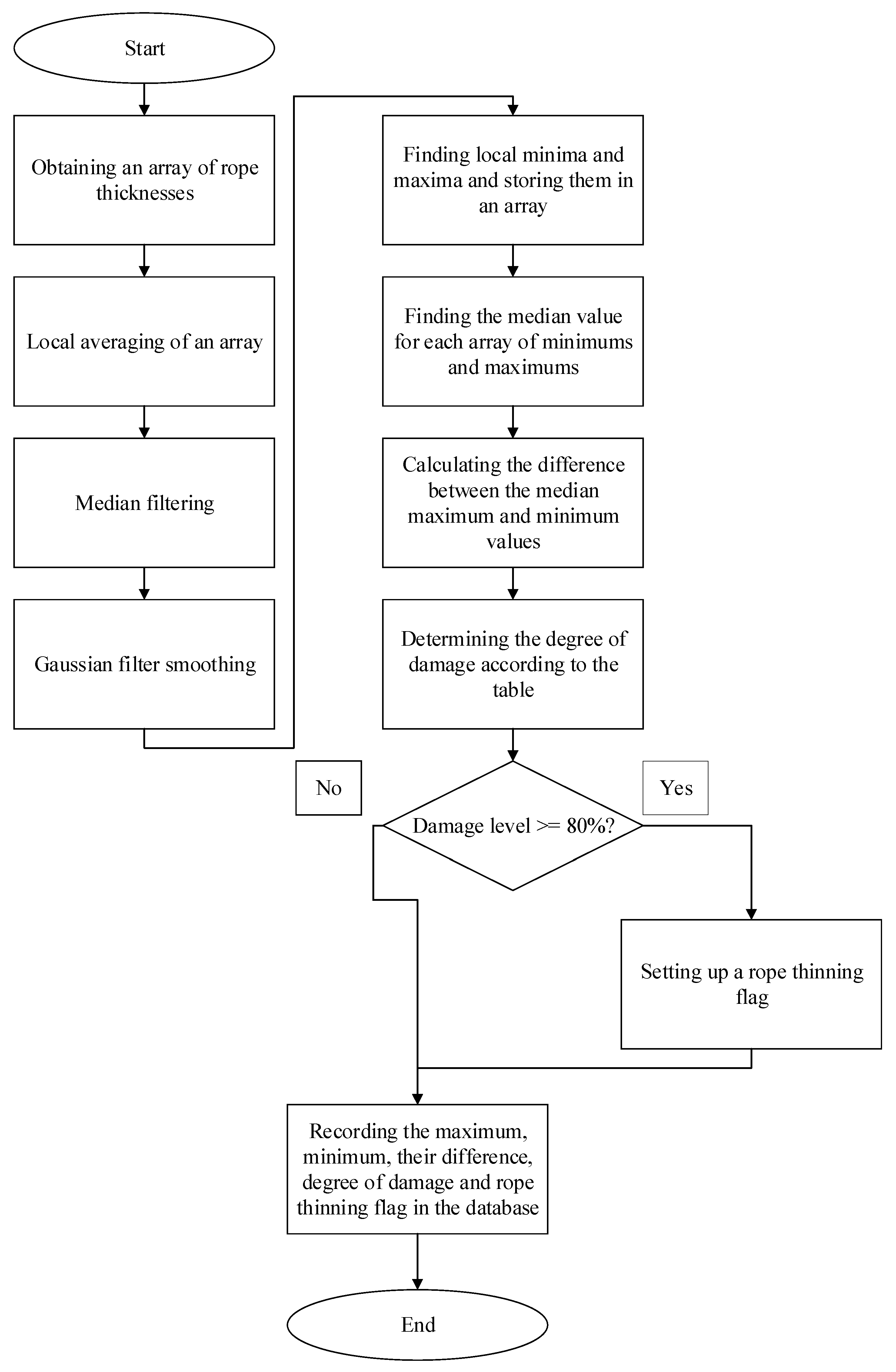
2.3. Defect Diagnosis Algorithm Based on Thickness Profile Analysis
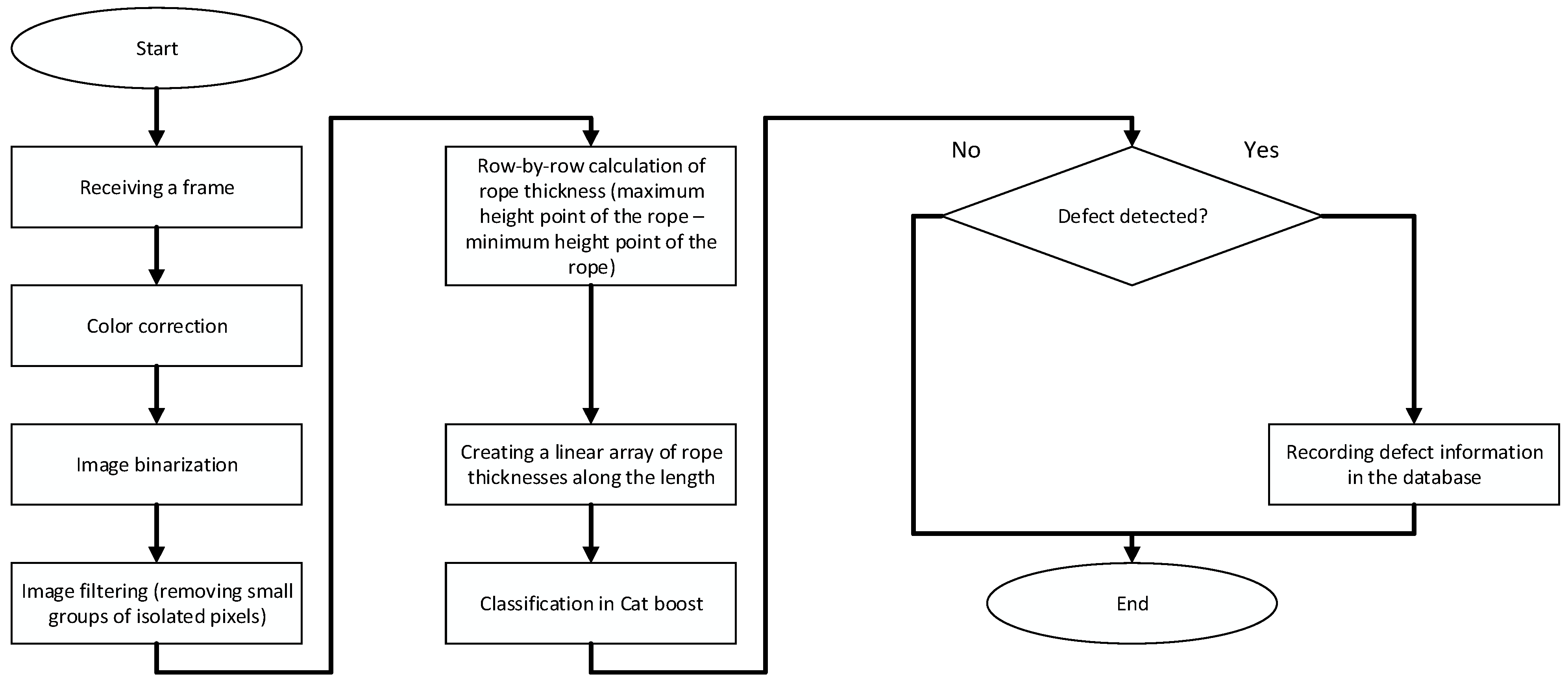
2.3.1. Image Acquisition and Preprocessing
2.3.2. Grayscale Conversion and Illumination Normalization
2.3.3. Adaptive Thresholding
2.3.4. Noise Suppression and Morphological Filtering
- Median filtering with a 3 × 3 kernel effectively removes impulse noise (e.g., salt-and-pepper) while preserving sharp object boundaries, which is essential for the subsequent thickness analysis.
- Connected-component analysis: each connected pixel group in the binary mask is labeled, and clusters with an area smaller than 50 pixels are removed as irrelevant. This threshold was chosen empirically based on a preliminary assessment of typical noise artifacts.
2.3.5. Thickness-Profile Computation and Construction
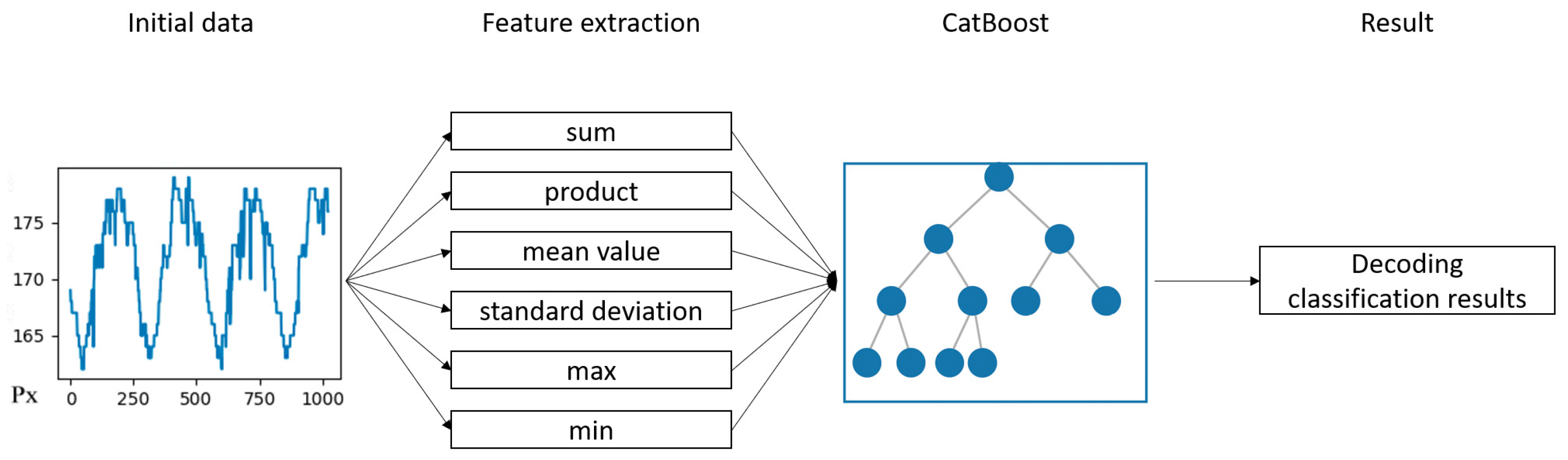
2.3.6. Rope-Condition Classification
- sum—the sum of all thickness values along the section; this can reflect the overall “rope volume” in the segment. If the segment is heavily worn, the sum tends to be lower;
- prod—the product of all thickness values; rarely used due to numerical instability (if any point is zero, the entire product collapses to zero). It can occasionally serve as an anomaly marker;
- mean—the average thickness, providing a baseline estimate of the nominal rope thickness; a decrease may indicate overall wear or local thinning;
- std—the standard deviation of the profile (overall variability/roughness); a high standard deviation suggests strong thickness fluctuations, potentially due to local damage or protruding wires;
- max, min—the extreme values capturing local deformations (e.g., bulges and constrictions).
2.3.7. Post-Processing and Result Logging
- the type of the detected defect;
- the coordinates of the defective segment along the rope;
- the timestamp of detection;
- the encoder-derived rope-length coordinate for the center of the processed window.
3. Results and Discussion
3.1. Verification on Synthetic Images
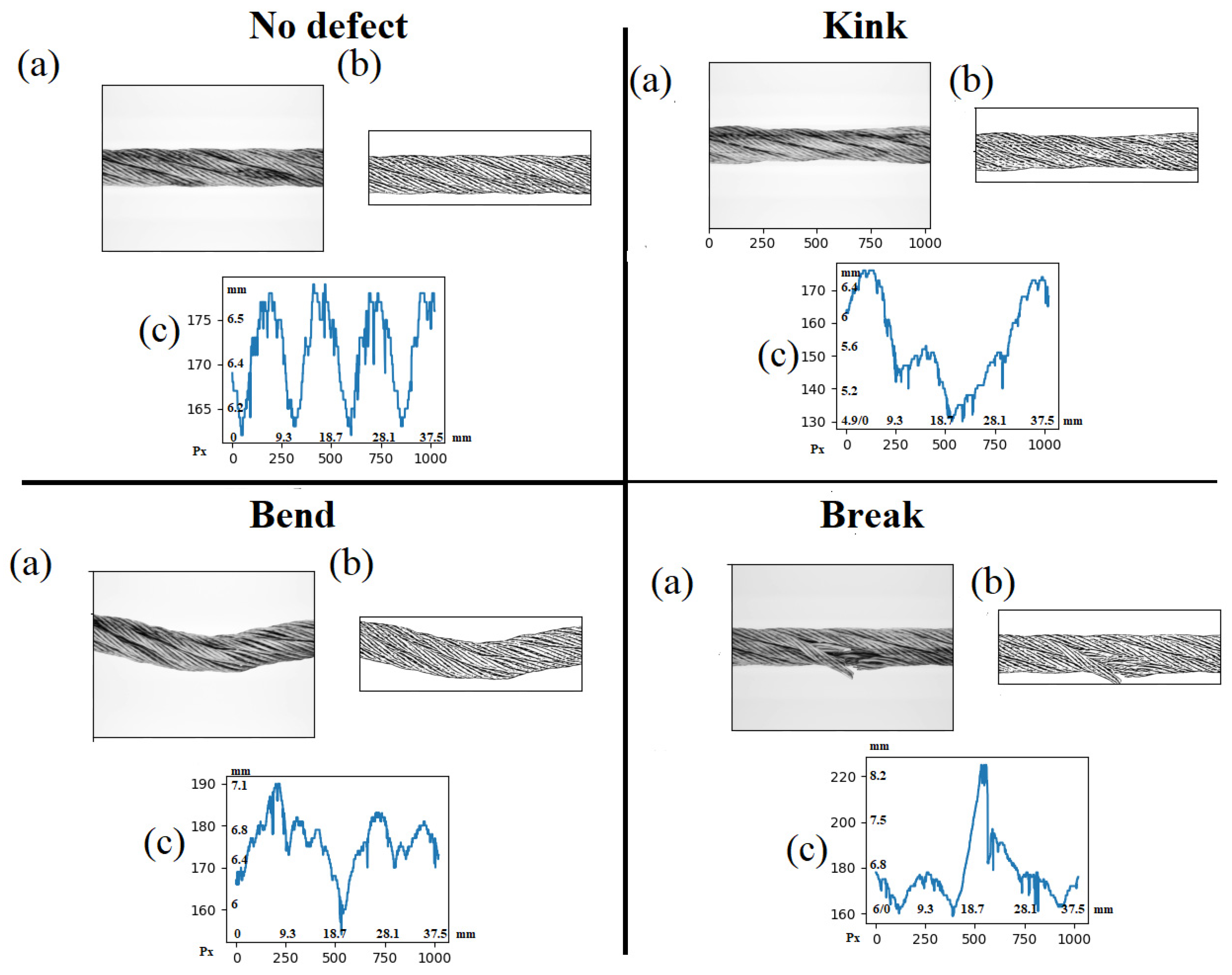
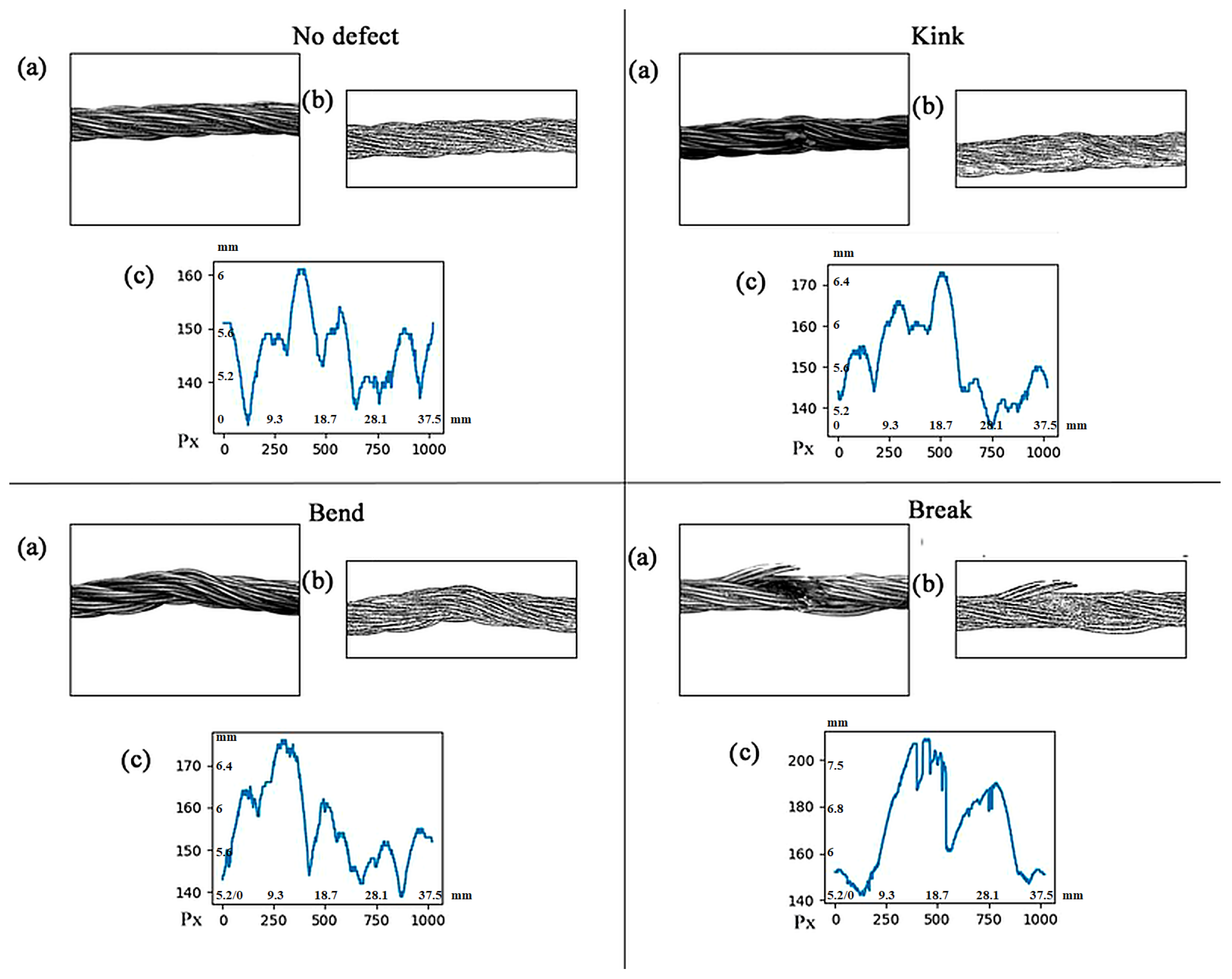
3.2. Testing on Real Rope Images
3.3. Profile-Based Representation of Diagnostic Classes
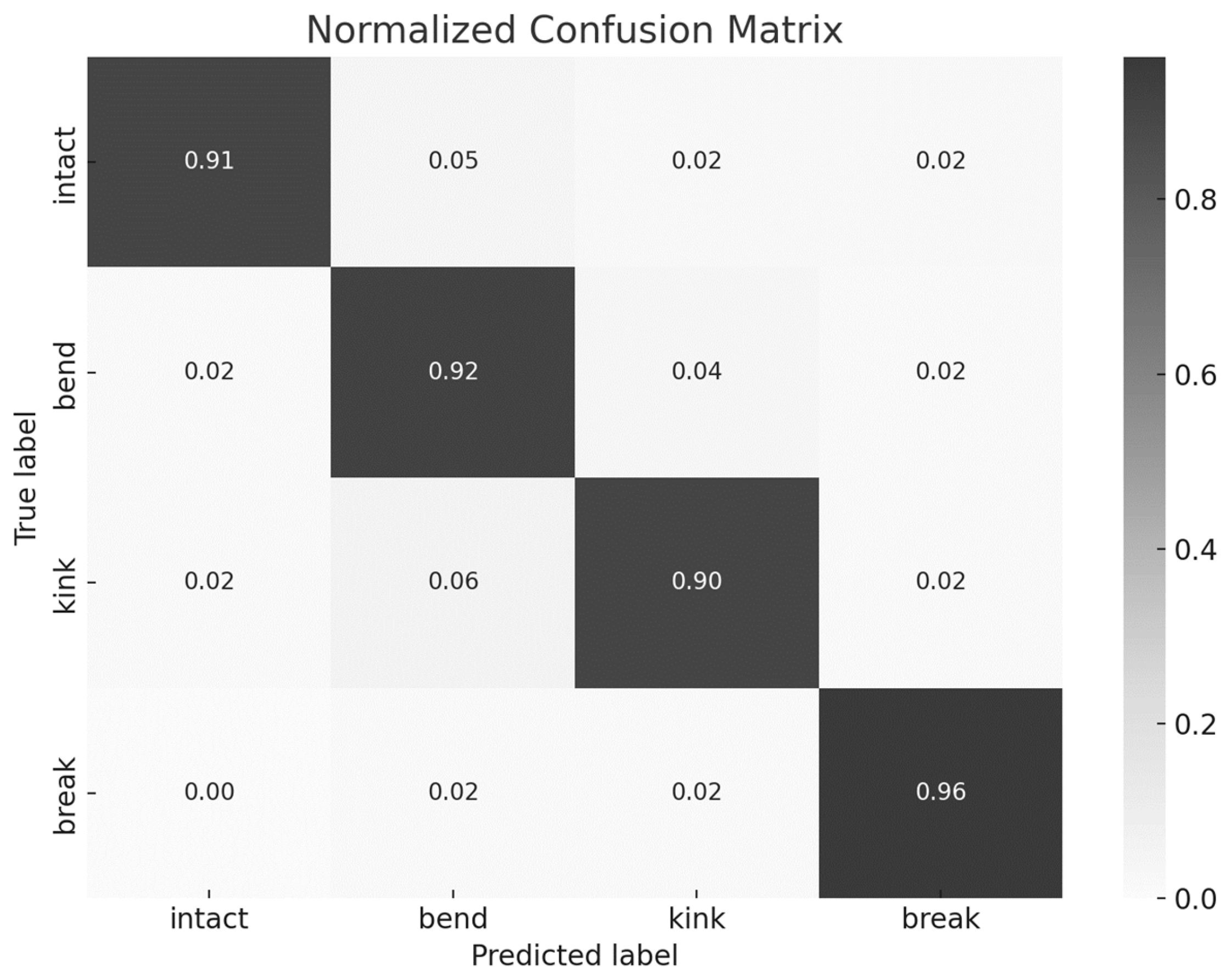
3.4. Classification and Evaluation of Diagnostic Accuracy
- Normal (no defects)
- With local thinning of 2.5%
- With local thinning of 5%
- With local thinning of 7.5%
- With local thinning of 10%
4. Conclusions
5. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mazurek, P.A. Comprehensive Review of Steel Wire Rope Degradation Mechanisms and Recent Damage Detection Methods. Sustainability 2023, 15, 5441. [Google Scholar] [CrossRef]
- Quiroz, V.E.; Calvopiña, D. Training of Highly Qualified Specialists in the Field of Software Development: Problems and Solutions in Higher Educational Institutions of Ecuador. ITM Web Conf. 2024, 59, 04008. [Google Scholar] [CrossRef]
- Tian, J.; Li, P.; Wang, W.; Ma, J.; Sun, G.; Wang, H. Quantitative Identification of Internal and External Wire Rope Damage Based on VMD-AWT Noise Reduction and PSO-SVM. Entropy 2022, 24, 981. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Cao, G. Wire rope lay length measurement based on DT-CWT. Measurement 2025, 256, 118041. [Google Scholar] [CrossRef]
- Maljaars, J.; Misiek, T. Fatigue Resistance of Steel Ropes: Failure Criterion. Steel Constr. 2021, 14, 196–204. [Google Scholar] [CrossRef]
- Ilyushin, Y.; Talanov, N. Evelopment of Methods and Models for Assessing Technical Condition of Mines and Underground Structures. Int. J. Eng. 2025, 38, 1659–1666. [Google Scholar] [CrossRef]
- Zhou, P.; Zhou, G.; Zhu, Z.; He, Z.; Ding, X.; Tang, C. A Review of Non-Destructive Damage Detection Methods for Steel Wire Ropes. Appl. Sci. 2019, 9, 2771. [Google Scholar] [CrossRef]
- Liu, S.; Tan, Q.; Zhang, Y. Shaft Diameter Measurement Using Structured Light Vision. Sensors 2015, 15, 19750–19767. [Google Scholar] [CrossRef]
- Wang, W.; Yang, H.; Chen, Y.; Huang, X.; Cao, J.; Zhang, W. Motion Analysis of Wire Rope Maintenance Device. Actuators 2023, 12, 392. [Google Scholar] [CrossRef]
- Gong, R.; Wang, Y.; Zhou, F.; Tang, B. Lubricating Grease Thickness Classification of Steel Wire Rope Surface Based on GEMR-MobileViT. Sensors 2025, 25, 2738. [Google Scholar] [CrossRef]
- Rani, A.; Ortiz-Arroyo, D.; Durdevic, P. A Survey of Vision-Based Condition Monitoring Methods Using Deep Learning: A Synthetic Fiber Rope Perspective. Eng. Appl. Artif. Intell. 2024, 136, 108921. [Google Scholar] [CrossRef]
- Skamyin, A.; Shklyarskiy, Y.; Lobko, K.; Dobush, V.; Sutikno, T.; Hatta, M.J. Impedance Analysis at High Harmonics. Indones. J. Electr. Eng. Comput. Sci. 2024, 33, 31–41. [Google Scholar] [CrossRef]
- Shklyarskiy, Y.E.; Lobko, K.K.; Kuznetsova, Y.N.; Vorobyev, M.S. Investigation of the Composite Motor Load in the Presence of Higher Harmonics in the Electrical Network. ENERGETIKA Proc. CIS High. Educ. Inst. Power Eng. Assoc. 2024, 67, 285–299. [Google Scholar] [CrossRef]
- Chazhoor, A.A.P.; Ho, E.S.L.; Gao, B.; Woo, W.L. A Review and Benchmark on State-of-the-Art Steel Defects Detection. SN Comput. Sci. 2024, 5, 114. [Google Scholar] [CrossRef]
- Bolshunov, A.V.; Ignatev, S.A.; Gorelik, G.D.; Krikun, N.S.; Vasilev, D.A.; Rakitin, I.V.; Shadrin, V.S. Comprehensive Studies of the Snow-Firn Layer in the Area of the Russian Antarctic Vostok Station. J. Min. Inst. 2025, 273, 52–64. [Google Scholar]
- Bolshunov, A.V.; Vasilev, D.A.; Dmitriev, A.N.; Ignatev, S.A.; Kadochnikov, V.G.; Krikun, N.S.; Serbin, D.V.; Shadrin, V.S. Results of Complex Experimental Studies at Vostok Station in Antarctica. J. Min. Inst. 2023, 263, 724–741. [Google Scholar]
- Ibrahim, A.A.M.S.; Tapamo, J.-R. A Survey of Vision-Based Methods for Surface Defects’ Detection and Classification in Steel Products. Informatics 2024, 11, 25. [Google Scholar] [CrossRef]
- Tchatchoua, P.; Graton, G.; Ouladsine, M.; Christaud, J.-F. Application of 1D ResNet for Multivariate Fault Detection on Semiconductor Manufacturing Equipment. Sensors 2023, 23, 9099. [Google Scholar] [CrossRef]
- Al-Selwi, S.M.; Hassan, M.F.; Abdulkadir, S.J.; Muneer, A.; Sumiea, E.H.H.; Alqushaibi, A.; Ragab, M.G. RNN-LSTM: From Applications to Modeling Techniques and Beyond—Systematic Review. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 102068. [Google Scholar] [CrossRef]
- Yang, T.; Li, J. Steel Surface Defect Detection Based on SSAM-YOLO. Int. J. Inf. Technol. Syst. Approach 2023, 16, 1–13. [Google Scholar] [CrossRef]
- Pardo, F.R.O.; Herrera, J.A.P.; Perez, M.C.R.; Cabascango, V.E.Q.; Urbano, A.P.M. Scientific Fundamentals for the Use of Serpentinized Rocks from the Eastern Region of Cuba. J. Phys. Conf. Ser. 2023, 2573, 012033. [Google Scholar] [CrossRef]
- Dey, D.; Haque, M.S.; Islam, M.M.; Aishi, U.I.; Shammy, S.S.; Mayen, M.S.A.; Noor, S.T.A.; Uddin, M.J. The proper application of logistic regression model in complex survey data: A systematic review. BMC Med. Res. Methodol. 2025, 25, 15. [Google Scholar] [CrossRef] [PubMed]
- Simakov, A.S.; Trifonova, M.E.; Gorlenkov, D.V. Virtual Analyzer of the Voltage and Current Spectrum of the Electric Arc in Electric Arc Furnaces. Russ. Metall. (Met.) 2021, 6, 713–719. [Google Scholar] [CrossRef]
- Shao, Z.; Ahmad, M.N.; Javed, A. Comparison of Random Forest and XGBoost Classifiers Using Integrated Optical and SAR Features for Mapping Urban Impervious Surface. Remote Sens. 2024, 16, 665. [Google Scholar] [CrossRef]
- Amaya-Tejera, N.; Gamarra, M.; Vélez, J.I.; Zurek, E. A Distance-Based Kernel for Classification via Support Vector Machines. Front. Artif. Intell. 2024, 7, 1287875. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Qian, H. CatBoost-Based Automatic Classification Study of River Network. ISPRS Int. J. Geo-Inf. 2023, 12, 416. [Google Scholar] [CrossRef]
- Mordia, R.; Verma, A.K. Visual Techniques for Defects Detection in Steel Products: A Comparative Study. Eng. Fail. Anal. 2022, 134, 106047. [Google Scholar] [CrossRef]
- El Hiouile, L.; Errami, A.; Azami, N. Toward Automatic Monitoring for Anomaly Detection in Open-Pit Phosphate Mines Using Artificial Vision: A Case Study of the Screening Unit. Mining 2023, 3, 645–658. [Google Scholar] [CrossRef]
- Cheremisina, O.V.; Balandinsky, D.A.; Gorbacheva, A.A.; Lysenko, M.R.; Yinzhou, L. Physicochemical Features of Action of Ethoxylated Esters of Phosphoric Acid with Different Degree of Ethoxylation in Conditions of Froth Flotation of Apatite. Colloids Surf. A Physicochem. Eng. Asp. 2024, 708, 135974. [Google Scholar] [CrossRef]
- Li, Z.; Wei, X.; Hassaballah, M.; Li, Y.; Jiang, X. A Deep Learning Model for Steel Surface Defect Detection. Complex Intell. Syst. 2024, 10, 885–897. [Google Scholar] [CrossRef]
- Bratskikh, D.S.; Romasheva, N.V.; Konopelko, A.Y.; Nikolaychuk, L.A. Model of Supply Chain Management in the Oil and Gas Industry Using Digital Technologies. Oil Ind. 2024, 7, 120–125. [Google Scholar] [CrossRef]
- Cacciari, I.; Ranfagni, A. Hands-On Fundamentals of 1D Convolutional Neural Networks—A Tutorial for Beginner Users. Appl. Sci. 2024, 14, 8500. [Google Scholar] [CrossRef]
- Lama, B.; Momayez, M. Review of Non-Destructive Methods for Rock Bolts Condition Evaluation. Mining 2023, 3, 106–120. [Google Scholar] [CrossRef]
- El Hiouile, L.; Errami, A.; Azami, N. Towards Mine 4.0: A Proposed Multi-Layered Architecture for Real-Time Surveillance and Anomaly Detection in an Open-Pit Phosphate Mine. Mining 2024, 4, 672–686. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; He, J.; Qiu, Y.; Liu, X.; Chen, L.; Yang, F.; Chen, B.; Tang, B.; Wang, Y. Steel Wire Rope Damage Width Identification Method Based on Residual Networks and Multi-Channel Feature Fusion. Machines 2024, 12, 744. [Google Scholar] [CrossRef]
- Beloglazov, I.; Plaschinsky, V. Development MPC for the Grinding Process in SAG Mills Using DEM Investigations on Liner Wear. Materials 2024, 17, 795. [Google Scholar] [CrossRef] [PubMed]
- Semykina, I.Y.; Kipervasser, M.V.; Gerasimuk, A.V. Study of Drive Currents for Lifting Bridge Cranes of Metallurgical Enterprises for Early Diagnosis of Load Excess Weight. J. Min. Inst. 2021, 247, 122–131. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Liu, S.; Ji, Z. Non-Destructive Testing of Wire Rope Algorithm Based on Lightweight YOLOv7-Tiny. In Proceedings of the International Conference on Algorithms, Software Engineering, and Network Security (ASENS 2024), Nanchang, China, 26–28 April 2024. [Google Scholar] [CrossRef]
- Yujra Rivas, E.; Vyacheslavov, A.; Gogolinskiy, K.V.; Sapozhnikova, K.; Taymanov, R. Deformation Monitoring Systems for Hydroturbine Head-Cover Fastening Bolts in Hydroelectric Power Plants. Sensors 2025, 25, 2548. [Google Scholar] [CrossRef]
- PB 10-382-00; Rules for the Design and Safe Operation of Hoisting Cranes. NPO OBT: Moscow, Russia, 2001.
- GOST 3241-91; Steel Wire Ropes. Technical Specifications. IPK Izdatelstvo Standartov: Moscow, Russia, 1993.
- GOST 30631-99; General Requirements for Machines, Instruments, and Other Technical Products Regarding Resistance to Mechanical Environmental Factors during Operation. State Committee of the Russian Federation for Standardization and Metrology: Moscow, Russia, 1999.
- RD 10-112-6-03; Guidelines for the Examination of Special Metallurgical Cranes. ZAO Ural Expert Center: Ekaterinburg, Russia, 2003.
- Zhou, M.; Lu, W.; Xia, J.; Wang, Y. Defect Detection in Steel Using a Hybrid Attention Network. Sensors 2023, 23, 6982. [Google Scholar] [CrossRef]
- Chu, Y.; Yu, X.; Rong, X. A Lightweight Strip Steel Surface Defect Detection Network Based on Improved YOLOv8. Sensors 2024, 24, 6495. [Google Scholar] [CrossRef]
- Ma, Y.; Yin, J.; Huang, F.; Li, Q. Surface Defect Inspection of Industrial Products with Object Detection Deep Networks: A Systematic Review. Artif. Intell. Rev. 2024, 57, 333. [Google Scholar] [CrossRef]




| Model | Robustness to Noise | Inference Speed | Hardware Requirements |
|---|---|---|---|
| 1D CNN | Medium | Moderate-speed | Medium |
| 1D ResNet | High | Low-speed | High |
| LSTM/BiLSTM | Medium | Low-speed | High |
| Transformer | High | Computationally intensive | Very High |
| MLP | Low | High-speed | Low |
| Logistic Regression | Low | High-speed | Low |
| SVM | Medium | Moderate-speed | Medium |
| Random Forest | High | Moderate-speed | Low |
| CatBoost | High | Moderate-speed | Low |
| Feature | Importance (Prediction Values Change) |
|---|---|
| max | 27.96 |
| std | 27.95 |
| sum | 26.23 |
| mean | 13.89 |
| min | 4.00 |
| prod | 0.00 |
| Defect Type | Visual Characteristics | Thickness-Profile Pattern |
|---|---|---|
| Intact (No Defects) | Uniform structure, homogeneous illumination, absence of artifacts | Stable line with fluctuations within 5–10% of the mean value |
| Kink | Sharp constriction, visible ruptures, disruption of wire lay | Peak or dip up to 30%, abrupt transitions |
| Bend | Smooth curvature, asymmetry of strands | Slow oscillations, amplitude up to 15%, no pronounced peaks |
| Break | Wire rupture, fragments, zero thickness in individual segments | Drop to zero, unstable shape, asymmetry |
| Rope Condition | ROC AUC | F1-Score | Precision | Recall | Balanced Accuracy |
|---|---|---|---|---|---|
| Break | 0.96 | 0.92 | 0.91 | 0.93 | 0.93 |
| Kink | 0.94 | 0.89 | 0.88 | 0.89 | 0.90 |
| Bend | 0.91 | 0.86 | 0.84 | 0.87 | 0.88 |
| Intact (No Defects) | 0.92 | 0.87 | 0.85 | 0.89 | 0.88 |
| Type Rope | Uniform Reduction in Rope Diameter (% of Nominal Diameter) | Degree Damage | % |
|---|---|---|---|
| Single-layer rope with organic core | Less than 6% | — | 0 |
| From 6% to 7% | Small | 20 | |
| From 7% to 8% | Average | 40 | |
| From 8% to 9% | High | 60 | |
| From 9% to 10% | Very high | 80 | |
| 10% or more | Culling | 100 | |
| Single-layer rope with a steel core or single-layer rope | Less than 3.5% | — | 0 |
| From 3.5% to 4.5% | Small | 20 | |
| From 4.5% to 5.5% | Average | 40 | |
| From 5.5% to 6.5% | High | 60 | |
| From 6.5% to 7.5% | Very high | 80 | |
| 7.5% or more | Culling | 100 | |
| Unspinning rope | Less than 1% | — | 0 |
| From 1% to 2% | Small | 20 | |
| From 2% to 3% | Average | 40 | |
| From 3% to 4% | High | 60 |
| Real Thinning | Classification Defect | Error (in Pixels) | Absolute Error (mm) | Relative Error (%) |
|---|---|---|---|---|
| 0% | norm | 4 | 0.15 | 2.5 |
| 2.5% | lung thinning | 3 | 0.11 | 1.9 |
| 5% | average thinning | 4 | 0.15 | 2.5 |
| 7.5% | moderate-severe | 5 | 0.19 | 2.5 |
| 10% | heavy thinning | 3 | 0.11 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulchitskiy, A.; Nikolaev, M. Method for Monitoring the Condition of Steel Wire Ropes Based on the Analysis of Changes in the Linear Dimensions of Their Cross-Sections. Mining 2025, 5, 79. https://doi.org/10.3390/mining5040079
Kulchitskiy A, Nikolaev M. Method for Monitoring the Condition of Steel Wire Ropes Based on the Analysis of Changes in the Linear Dimensions of Their Cross-Sections. Mining. 2025; 5(4):79. https://doi.org/10.3390/mining5040079
Chicago/Turabian StyleKulchitskiy, Aleksandr, and Mikhail Nikolaev. 2025. "Method for Monitoring the Condition of Steel Wire Ropes Based on the Analysis of Changes in the Linear Dimensions of Their Cross-Sections" Mining 5, no. 4: 79. https://doi.org/10.3390/mining5040079
APA StyleKulchitskiy, A., & Nikolaev, M. (2025). Method for Monitoring the Condition of Steel Wire Ropes Based on the Analysis of Changes in the Linear Dimensions of Their Cross-Sections. Mining, 5(4), 79. https://doi.org/10.3390/mining5040079









