Laboratory-Scale Drillstring Vibration Analysis

Abstract

Drillstring vibrations are detrimental to drill bits and downhole equipment, affecting drilling efficiency and operational cost in severe drillstring vibration cases. The complex behavior of drillstring vibration, including axial–torsional–lateral coupling and interactions among external forces, necessitated laboratory experiments to address challenges observed in the field. This review paper aims to provide practical insights into essential design considerations that support the effective development of laboratory-scale drillstring experiments. This study analyzes previous work on design methodologies, experimental configurations, measurement techniques, and downhole dynamic simulations. The comparative analysis, highlighting the key similarities and physical design novelties across different experiments, identifies that instrumentation limitations and incoherent downscaling approaches were among the primary setbacks from achieving realistic downscaled experimental models. Fewer studies have examined the interaction between flowing fluids and the drillstring to simulate realistic drilling operations. The study identifies unified experimental configurations across works that simulate similar drilling and vibration dynamics. A comprehensive summary of the foundational knowledge for research-objective-based design suggestions is presented to guide future laboratory-scale drilling vibration experimental design and innovation.

1. Introduction

Drillstring vibration is an unavoidable operational phenomenon, as drilling and exploration for energy extraction, such as hydrocarbons or geothermal energy, are destructive processes that cut through the Earth’s subsurface. Drilling vibration significantly reduces drilling efficiency and increases operational downtime. The drillstring consists of connected, long, slender drill pipes that transfer driving forces from the surface to a much heavier, shorter section of the drillstring, known as the bottom hole assembly (BHA) (Figure 1). This imbalanced physical configuration of the drillstring makes it prone to vibrations [1]. The BHA generally consists of drill collars, heavyweight drill pipes, drill bits, various mechanical tools, and measurement/logging while drilling (MWD/LWD) tools. The BHA is the most dynamically active portion of the drillstring. Various forces constantly act on the BHA, including centrifugal forces from rotation, periodic downhole impacts during drilling, continuous contact and friction with the wellbore, internal and external damping forces, and pressure fluctuations caused by circulating drilling mud [2,3,4]. Drilling vibrations increase the drillstring to wellbore contact frequency and accelerate drillstring component wear and failure [5,6]. High magnitudes of drillstring vibrations can interfere with MWD tools and increase dynamic stress per cycle, leading to premature fatigue failure [7,8].

Analyses of drillstring vibration behavior for vibration mitigation purposes trace back to the inception of rotary drilling operations in the 1930s [9]. Most drillstring vibration literature focuses on theoretical models [10,11,12]. However, only a few follow up with experimental tests to verify their models [13]. Finnie and Bailey [14] conducted one of the first experimental studies using a full-scale rig (i.e., a field-scale study) to investigate the vibration mechanisms for different modes via spectral analysis. They attached sensors and recorders in the lower sub of the drillstring, 50 ft below the rotary table, and collected the data through the top sub at the surface using a slip-ring connection. They discovered unexpected frequency signatures that could only be observed due to the coupling of torsional and lateral vibrations.

Researchers found discrepancies between theoretical and experimental findings in field-scale studies and urged the need for more experimental investigations with varying parameters [15,16]. Real-time downhole dynamic conditions are difficult to quantify using surface measurements, as they can often be misleading [17]. Conducting repetitive field experiments to investigate critical vibration phenomena, such as excessive stick–slip and whirl, is risky and resource-intensive, and may be impossible to predict analytically [18]. Thus, the adoption of small-scale or downscaled designs has gained increasing popularity in recent decades over field experiments due to their advantages of being accommodated within the laboratory environment.

Laboratory environments allow for the reproduction of critical vibrations under defined boundary conditions in a more controlled and safer setting. This enables high-resolution measurements of mechanical quantities, providing closer insight into the complex mechanisms of drillstring dynamics with downscaled designs. Therefore, laboratory studies of drillstring dynamics have become essential to complement theoretical studies [19]. The advent of modern downhole measurement tools has enabled the collection of reliable downhole drilling dynamics and vibration data from field operations, which can then be verified and replicated in laboratory experiments for in-depth analysis [20,21,22,23,24].

Several studies successfully established downscaled experimental facilities that incorporate sections of full-size BHAs for field-scale testing [25,26,27,28,29]. While such setups are designed for laboratory environments, they still require substantial power and resources to replicate field-scale drilling dynamics. In contrast, scaling down all components of the experimental assembly can significantly reduce power consumption and fabrication demands [30,31]. Throughout this paper, such configurations are referred to as laboratory-scale experiments.

Given the complexity of drillstring dynamics and the ongoing efforts to understand both uncoupled and coupled vibration mechanisms, experimental investigations are essential to bridge the gap between theoretical models and field data. Laboratory-scale setups provide a practical, controlled environment for such studies.

Most surveys on drillstring vibration studies focus either on mathematical modeling [32,33,34] or heuristic mitigation strategies [6,35], with limited attention to experimental design. While some works [36,37] incorporate machine learning and highlight experimental gaps, they lack a detailed discussion of physical experimental setups.

For example, Patil and Teodoriu [38] reviewed laboratory-scale torsional vibration experiments, identifying key design limitations such as neglecting distinctions in contact friction and drilling fluid damping. However, their discussion on design innovation remains limited. A review of stick–slip studies was presented in [38]; however, it offered limited detail into experimental setups, noting a lack of studies on bit–rock interaction and lithology effects.

Several experimental works [19,39] briefly reviewed past designs to justify their innovations. They highlighted issues such as high cost, lack of mechanical scaling, and impractical slenderness ratios, but did not explore design methodologies. A comprehensive survey was conducted across various vibration types, although it lacked a detailed experimental design and identified gaps in coupled-vibration studies [40].

Despite the current knowledge in the literature, no comprehensive review systematically examines the physical design of laboratory-scale experiments across all modes of drillstring vibration. Key gaps include the following: (1) the absence of a unified overview of experimental methodologies encompassing all drilling dynamics; (2) limited discussion of overlooked parameters such as drillstring–fluid interactions; and (3) the lack of a structured framework for downscaling principles and evaluating design innovation. This paper aims to address these deficiencies by offering critical design insights to accelerate and improve the efficiency of laboratory-scale drillstring vibration experiments.

2. Theoretical Background

To effectively understand and evaluate the experimental design methodologies discussed, it is essential first to establish a foundational understanding of drillstring vibration phenomena, the defining characteristics of laboratory-scale vibration experiments, and the principles of mechanical scaling.

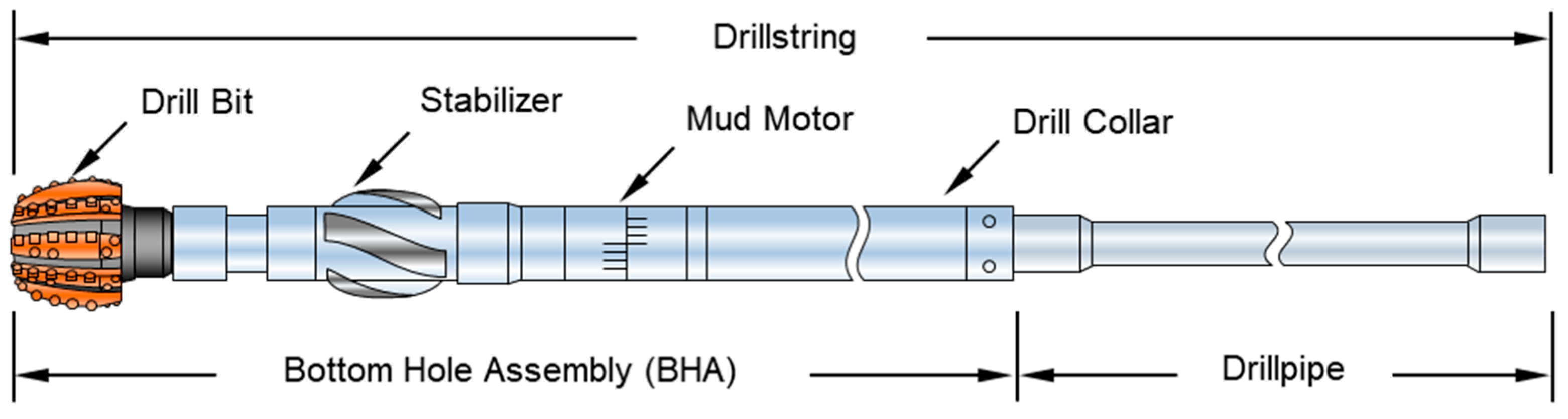
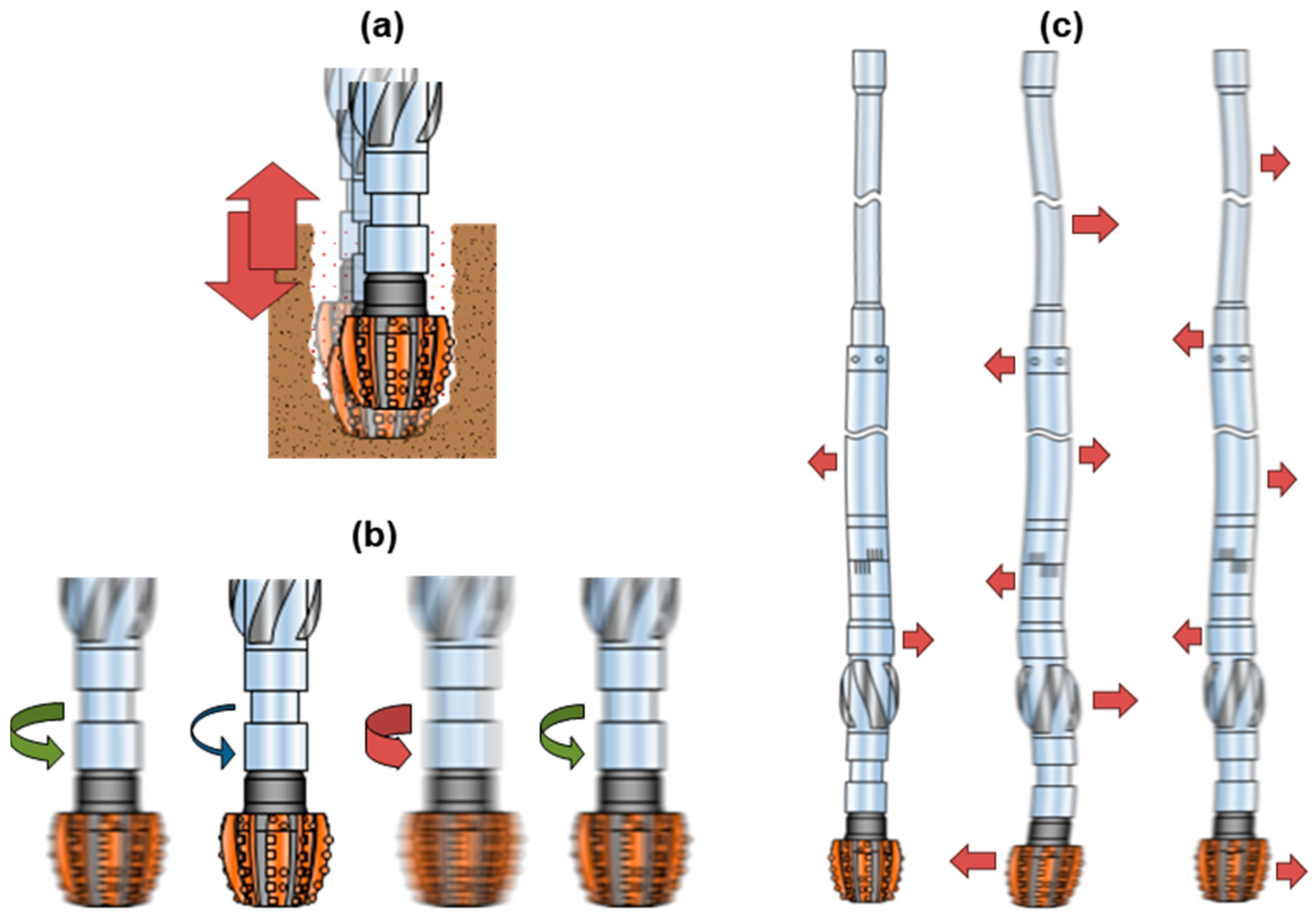
2.1. Drillstring Vibrations

The three basic or individual modes of drillstring vibrations are axial, torsional, and lateral. Axial vibration is the up-and-down motion of the drillstring during drilling, occurring in the longitudinal direction, which results in repetitive loss of contact between the bit and the rock formation, leading to the bit-bounce phenomenon in severe cases [25] (Figure 2a). Bit-bounce is more common in roller-cone drill bit operations. Torsional vibration results from periodic rotational accelerations and decelerations of the drill bit during drilling. In severe cases, the drill bit stops rotating for an instant (i.e., sticks) and then suddenly releases the stored rotational energy (i.e., slips) at a significantly higher angular velocity than the applied rotary speed [41] (Figure 2b). The stick–slip phenomenon occurs at every other rotation during drilling operations, as documented in prior studies [42]. Lateral, also known as transverse or bending vibration, is an oscillatory movement perpendicular to the drillstring axis [40] (Figure 2c).

The individual modes often couple and conjointly contribute to critical hindering vibration phenomena [43]. Three major coupled modes are axial–torsional, lateral–torsional, and lateral–axial. The primary causes of the vibration coupling phenomenon are high rotary speed, excessive driving torque, and steep wellbore inclination [32]. Axial–torsional coupling generates additional vibration chatter and accelerated drillstring degradation [44,45]. Experimental results have shown that lateral-axial vibration coupling leads to axial shortening or sinusoidal buckling of the drillstring [46,47]. Downhole lateral vibration causes the bit to walk around the wellbore, resulting in bouncing, rolling, sliding, or completely random lateral movements [48]. Periodic rolling or sliding of the BHA around a static wellbore contact point, without executing a complete circular motion, is called snaking motion. It is a frequent vibration phenomenon in horizontal and inclined wells [19]. There are two types of snaking motion: lateral up-and-down or side-to-side movement in a sinusoidal buckling configuration [49]. Eventually, if the bit’s center of rotation and the bit-face execute instantaneous complete revolutions around the wellbore, that forms a whirling motion of the BHA [50]. Whirl manifests as forward, backward, or chaotic motion, depending on the revolving direction of the bit-face [51]. The BHA revolves around the wellbore wall in the same direction as the bit rotation during forward whirling, rolls in the opposite direction during backward whirling, and follows random or planetary patterns during chaotic whirl motion. The drillstring experiences dynamic buckling along its length, e.g., sinusoidal buckling while snaking and helical buckling during whirling [52]. Buckling and whirling are widely recognized as the leading causes of borehole enlargement and drillstring failures [53].

2.2. Laboratory-Scale Experiments

Advances in empirical understanding through field-scale investigations have helped refine analytical models for studying drilling dynamics and the simplified mechanical representation of the drillstring structure, which are then adopted to fabricate downscaled models. Drillstring vibration is mathematically represented using a lumped-mass discrete system or continuous beam system [54]. In this manner, laboratory-scale drillstrings are represented as a single or multiple lumped masses connected by flexible strings [55], or as a continuous single or stepped beam-rotor system [56], between two pinned boundary conditions. In relation to field assembly, one supported end of the downscaled model represents the surface side, where the operating or surface parameters are applied to the drillstring. The applied external forces transfer to the other end of the downscaled model, which represents the downhole.

Most experiments model only a section of a drillstring or BHA to facilitate laboratory studies while maintaining relevance to practical drilling dynamics [19,57]. Both the drill pipe and BHA sections of the drillstring have been physically modeled together using a slender section connected to a larger, heavier assembly [55,58]. Steel pipes, rods, or flexible wires are the most common material choice for laboratory-scale models, as drillstring components are usually made of steel. The use of rigid, flexible alternative materials has become increasingly popular in recent decades, driven by market availability and experimental versatility [59]. For example, the minimum practical drillstring slenderness (length-to-diameter ratio) requirement reduces from 50:1 to 30:1 when a more flexible material, such as PVC, is used instead of steel in scaled experiments [60].

Two pinned supports are sufficient for models with short drillstring lengths [4]. However, additional lateral support or bounding rings are used to enhance test stability for setups with lengthy drillstring models [61]. In that case, circular or cylindrical bounding frames can effectively represent the wellbore and simulate wellbore contact dynamics. Confinement of drillstring in fluids allows for the study of the laboratory-scale interaction (FSI) between the drillstring and the drilling fluid [62,63].

The mechanisms that induce drilling dynamics may vary significantly across experiments, depending on the study’s focus. For example, downhole drill bit excitations can be simulated either by downscaled drill-bit drilling into rock samples [64] or by inducing axial/torsional excitation representing drill bit rock interaction [4,65].

In field-scale operations or under field conditions, the applied surface rotary speed usually ranges from 40 to 250 revolutions per minute (RPM), while the applied weight-on-bit (WOB) varies widely depending on rock hardness or formation type [66,67]. The drilling parameters are adjusted in laboratory-scale experiments depending on the downscaling relations. According to the mechanical similitude principle, geometrically downscaled drilling rigs typically require higher rotary speeds and lower WOB than the input parameters of a field condition to simulate similar drilling dynamics [4]. Thus, rotation and load are often applied to the drillstring models using small electromagnetic or hydraulic power systems [38].

Adopting a proper similitude principle in the experimental design establishes more realistic geometric, material, and dynamic scaling relations between the laboratory experiments and field operations [19]. Conducting dimensional analysis between the intended experimental model and a practical field-scale drillstring or BHA section is one of the initial steps in designing a downscaled model that adheres to the similitude principle. Several theoretical and numerical studies addressed dimensional analysis for downscaling field-scale drillstrings and drilling parameters [59,68,69,70,71]. However, most laboratory-scale experimental designs fail to articulate the underlying scaling laws or similitude principles, thereby limiting the applicability of their findings to real-world drillstring behavior [72].

2.3. Mechanical Scaling

Mechanically downscaled drillstring experiments adhere to the geometric, mechanical material property, and dynamics scaling relations to a field-scale drillstring prototype. The theoretical continuous-beam drillstring model often shapes the methodology for these experimental designs. The mechanical downscaling analysis is conducted according to the similitude principle, a concept used to design laboratory-scale dynamic models and to predict the behavior of a field-scale prototype [73]. Shyu [4] derived the similarity criteria for developing a downscaled BHA section.

Shyu [4] assumed the BHA to be a homogeneous beam and chose ten parameters that affect its lateral displacement during rotation (Equation (1)).

$$s=(l,d,D,E,\rho ,{\rho }_m,W,g,\varphi ,\Omega )$$

(1)

Here, s denotes the lateral displacement of the drill collar, l is the characteristic length of the drill collar, d is the drill collar’s outside diameter, D is the borehole diameter, E is the drill collar’s Young’s modulus, W is the WOB, g is gravity, $\varphi$ is the borehole deviation angle, Ω is the collar’s rotational speed, $\rho$ is drill collar density, and ${\rho }_m$ is mud density.

The Buckingham-π theorem [74] was used for dimensional analysis, yielding dimensionless scaling factors (Equations (2)–(4)) and corresponding scaled relations for the drilling parameters (Equations (5) and (6)).

$${\lambda }_1={\displaystyle \frac{l_M}{l_P}}$$

(2)

$${\lambda }_2={\displaystyle \frac{{(\rho -{\rho }_m)}_M}{{(\rho -{\rho }_m)}_P}}$$

(3)

$${\lambda }_3={\displaystyle \frac{E_M}{E_P}}$$

(4)

$${\displaystyle \frac{{\Omega }_M}{{\Omega }_P}}=\sqrt{{\displaystyle \frac{{\lambda }_3}{{\lambda }_2{\lambda }_1^2}}}$$

(5)

$${\displaystyle \frac{W_M}{W_P}}={\lambda }_1^2{\lambda }_3$$

(6)

Here, “P” and “M” subscripts denote the field-scale equivalent prototype and mechanically downscaled laboratory model.

2.4. Hydrodynamics Interactions

The earliest fundamental study of Jeffcott rotor dynamics under partial or complete fluid submersion addressed the influence of annular fluid columns on confined rotating systems, such as drillstrings. Fluid presence was generally modeled as an added lumped mass in the dynamic system [75]. Early investigations focused on the applicability of Stokes’ theory to hydrodynamic mass effects in annulus-confined rotors, concluding that denser annular fluids enhance damping performance for unbalanced rotor vibrations [62,76].

Drilling fluid flow imposes both viscous damping and hydrodynamic forces on the drillstring, yet most experiments assume these effects are constant or neglect them entirely [77]. In reality, circulating fluid exerts dynamic internal and external hydrodynamic forces that vary with fluid properties, flow regime, and annular pressure conditions [12,78]. To accurately capture these effects, force modeling should be integrated into vibration analysis rather than simplified as lumped mass terms [79,80]. These hydrodynamic forces can both dampen and excite drillstring vibrations [12]. Despite their significance, few experimental studies directly address FSI between circulating drilling fluid and the drillstring. While the dynamic impact of cross-directional flow around slender bodies, such as drillstrings, has been explored in various contexts [63,77,81,82], its application to drilling remains limited.

3. Drillstring Vibration Experiments

This paper focuses exclusively on reviewing the experimental investigations in which: (1) a representative drillstring or drillstring section was modeled and was subjected to subsurface drilling dynamics or downhole vibration simulation, (2) all test assembly components were scaled for laboratory use, (3) vibration mechanism, behavior or magnitudes were analyzed as the primary variable to meet the research objective and to conclude findings, and (4) had sufficient description of the design methodologies, experiment configurations, measurement techniques, and downhole dynamic simulation for the review analyses.

Drillstring vibration experiments are categorized into several distinct types, each tailored to capture specific aspects of drilling dynamics. The subsections are organized to reflect these variations, beginning with flexible disc-rotor models that simulate lateral motion via compliant connections, followed by rigid-body models that emphasize axial load transfer and bit–rock interaction. Hybrid designs integrate both flexible and rigid elements to represent the full drillstring behavior better. Mechanically scaled models adhere to similitude principles to replicate field-scale dynamics in laboratory settings. Hydrodynamic studies examine the influence of drilling fluids on vibration behavior, while objective, modular designs focus on customizable experimental setups for tool development and targeted investigations.

3.1. Flexible Disc-Rotor Models

A flexible disk-rotor system incorporates two-disk lumped masses connected by a flexible steel string. The top steel disk is rotated at a fixed center representing the steady rotation at the rotary table, and the bottom brass disk is free to move in lateral directions from its geometric center within a circular boundary representing the BHA and wellbore’s inside perimeter.

For example, Mihajlovic [58] validated a dynamic friction model that describes the effect of downhole contact friction on downhole instability and characterizes the coupled nature of friction-induced torsional and lateral vibrations. The experiment uses a brake mechanism with a small oil box with felt stripes to induce friction on the bottom disk. Unbalanced masses are added to the bottom disk to induce lateral vibration. They found that higher rotational speed increases the BHA-wellbore contact friction factor. However, at low rotation operations, lateral vibration can increase contact frequency and downhole friction.

Liao et al. [48] used a similar two-disk rotor model to develop a mathematical model to determine frictional stick–slip interactions that lead to lateral instability. The authors analyzed the effects of WOB and downhole friction on lateral displacement and compared the numerical results with experimental data. The authors claimed to have geometrically downscaled an actual drillstring system by a 25:1 ratio in their model, but provided no further description of the downscaling. They successfully produced bottom disk bouncing and rolling motions with stick–slip interactions to validate their proposed model.

From control strategies to mitigate drillstring vibration, Majeed et al. [83] validated their proposed self-tuning closed-loop control algorithm using the flexible disk-rotor model, demonstrating effectiveness in suppressing torsional vibration and stick–slip. Similarly, Ullah and Bohn [84] developed a dynamic surface control system that addresses both low- and high-frequency torsional oscillation (HFTO) without relying on a friction model. By treating bit–wellbore friction as model uncertainty via error equations, they compared their system performance with that of conventional PID controllers.

3.2. Rigid Body Models

Rigid body models are more suitable for handling high surface loading and transferring that as WOB from surface to downhole. These models are often adapted for bit interaction investigations involving physical drilling of rock samples with a drill bit.

For example, Elsayed and Raymond [44] experimentally investigated axial–torsional vibration coupling during hard rock drilling using a torsionally compliant, lab-scale drillstring with a Polycrystalline Diamond Compact (PDC) coring bit. Vibration characteristics were analyzed using amplitude and spectral methods under varying RPM, WOB, and ROP. A modular flywheel induced torsional compliance, and a hydraulic system applied field-representative loading. Results showed that stick–slip occurs at low RPM and high WOB, but can be mitigated through torsional compliance, while axial vibrations diminish at high WOB. Later, Raymond et al. [57] used the same facility to develop a model-based control system to mitigate the adverse effects of axial vibration during drilling. They simulated bit–rock interaction with bit-bounce and compared the axial-vibration-mitigation performance of an analog and a model-based control system. They concluded that model-based control systems with real-time feedback control are more effective in minimizing high-frequency vibrations.

Esmaeili et al. [85] investigated the effects of drillstring vibrations on ROP and drilling performance using a rock-drilling unit with double-cone drill bits. They presented an automated rig equipped with a programmable logic controller (PLC) and wireless measurement reporting units. The vibration magnitudes and ROP deviation were analyzed at varying RPM and WOB to determine the optimal drilling parameter range for the highest drilling performance. Their results showed that maintaining wellbore contact with a higher WOB, even at lower rotary speed, yields the most consistent ROP. Later, Esmaeili et al. [86] conducted experiments and demonstrated the potential of developing both linear and nonlinear prediction models using drilling parameters and drillstring vibration data for the fast and efficient determination of optimal drilling parameters. In an extended study, Elmgerbi et al. [87] used the test data from this experiment setup to validate their ROP optimization model using machine learning (ML) techniques.

Bavadiya et al. [64] investigated the drilling dynamics of PDC bits in soft sandstone under varying operational parameters, validating experimental results with an analytical model to assess the impact of vibrations on ROP. Their setup included a stiff aluminum drillstring with stabilizers, a custom two-cutter PDC bit, and a fluid delivery system via a swivel. An AC motor drove the rotation, while WOB was applied using an electro-pneumatic hoisting system [88]. The study found that increased axial vibration accelerated bit wear and torque, while higher rotary speeds induced greater lateral vibrations in hard sandstone. They recommended low RPM and WOB in hard formations to minimize lateral vibrations, noting that reducing RPM is more effective than lowering WOB for controlling axial vibrations.

In a recent work, Al Shekaili et al. [89] experimentally investigated bit bounce, stick–slip, and whirl under varying RPM, WOB, bit configurations, and downhole surface conditions (dry-clean, dry-unclean, wet-unclean). Their setup included a vertical, rigid drillstring with a heavier drill collar and a PDC bit, drilling into marble samples using pre-drilled shallow holes to simulate downhole conditions. Vibration analysis was performed using bivariate kernel estimation, spectral, and periodogram techniques. Results showed that higher RPM and WOB increased ROP but also amplified stick–slip and bit bounce. Moderate RPM and WOB yielded optimal drilling efficiency. The five-blade bit minimized lateral movement but increased TOB and wear, while the three-blade bit offered balanced performance. Poor borehole cleaning was linked to increased whirl formation.

3.3. Hybrid Designs

Some experimental studies combine both flexible and rigid models to benefit from representing both the flexible drill-pipe and rigid BHA section with substantial length, providing a complete drillstring representation. Because of the flexible drill-pipe section, a heavy axial load cannot be applied from the surface. Instead, free weights are added onto the BHA section to apply WOB.

For instance, Kapitaniak et al. [90] investigated the coupling among all vibration modes, emphasizing torsional vibration during buckling, using a modified stand drill. The experiment implemented bit–rock interaction using scaled bits and rock samples, examining the effect of WOB and RPM on vibration stability. A loosely mounted bearing at the BHA section served as a free rotation boundary and a stabilizer. The study utilized small commercial drill bits and rock samples, including sandstone, granite, and limestone. Subsequently, the authors experimentally investigated the effect of second-degree helical buckling on torsional vibration [91] and characterized parametric ranges for chaotic and periodic whirling for isolated backward and forward whirling [55]. In their endeavor, they presented, validated, and improved several mathematical models to describe the complex mechanism of each drillstring vibration mode and common torsional-lateral coupled vibration phenomena.

Liu et al. [92] investigated stick–slip, focusing on the role of WOB in controlling the system’s dynamics. They conducted numerical bifurcation analysis to identify favorable WOB ranges for controlling stick–slip conditions. Experimentally, they investigated the effects of frictional torque due to WOB, applied rotary speed, and geometric and mechanical properties of the drillstring, such as its stiffness, torsion, and damping constant, on stick–slip. They used a vertical assembly of flexible, connected pipes with integrated weight disks as the BHA, along with a custom downscaled metal tri-blade drill bit. They used a sand bed and rock samples for testing. The authors found that adjusting WOB increases the frictional torque, thereby increasing the spring constant and enabling an effective control strategy to suppress stick–slip.

3.4. Mechanically Scaled Models

Mechanically scaled experiment designs adhere to the mechanical similitude principle to relate the experimental dynamics and findings to a field-scale drillstring prototype.

For example, Shyu [4] derived the similitude criteria for developing a scaled BHA section to experimentally study lateral vibrations and demonstrated the comparative effectiveness of his experimental methodology by correlating it with field-scale tests. He investigated mechanisms of lateral vibration, whirling, and axial-lateral vibration coupling with his mechanically scaled experiment. The setup simulated forward and backward whirl, and spectral analysis was performed to identify the dominant vibration frequencies. The setup consisted of an acrylic rod as the BHA collar, and an electric motor and a shaker to provide constant rotation and axial bit-excitation. The experimental results validated the proposed model in predicting the lateral dominant frequencies causing forward and backward whirl. Westermann et al. [19] built a mechanically scaled experimental setup to determine the contact forces between the drillstring and wellbore. The experimental configuration replicated a BHA section between two stabilizers, based on field experiments that exhibited whirling. The system consisted of a connector pipe supported by a combination of fixed and floating bearings, with rotation and surface WOB provided by a motor and axial force module. Laboratory tests identified critical rotary speed and contact forces during backward whirl, showing a satisfactory correlation with field-scale observations.

In a related study, Lian et al. [93] examined the influence of WOB and rotary speed on horizontal drilling dynamics under wellbore constraints, focusing on lateral stability. Downhole WOB fluctuations, lateral vibration, and motion were compared across varying parameters, supported by numerical analysis of buckling shapes and wellbore contact forces. Lin et al. [94] extended this work by analyzing vibration magnitudes and whirling revolution speeds through spectral analysis. Their scaled setup used connected steel pipes with a cone bit and segmented organic glass wellbore encasings to house sensors. Rotation was applied from the surface via a motor, while WOB was introduced from the opposite end using a spring-loaded drilling block. The motor was mounted on a rolling support linked to a force transfer device. Results showed linear increases in WOB fluctuation and rotation frequency with rising input parameters. Axial and lateral vibration magnitudes increased with rotary speed, and lateral vibration reached critical levels under buckling. A significant rotary speed lag was observed between the drillstring ends, and whirl revolution speed rose with rotary input. Persistent stick–slip at the bit caused rotary speed to vary from zero to twice the surface input. Based on scaling relations, the authors recommended maintaining 37.5–50 RPM for stable field drilling, with the drillstring remaining in the lower-right quadrant of the wellbore and experiencing minimal contact frequency.

Ren et al. [52] investigated dynamic buckling in horizontal wells using a scaled experimental setup adapted from Shao et al. [95]. The drillstring was housed within a simulated wellbore, with a disk representing the bit attached at its end. The setup was designed to allow drilling fluid to circulate through the annulus; however, no fluid-flow tests were conducted. The study compared theoretical and experimental results for critical buckling loads and lateral vibration amplitudes, validating a mathematical model that accounts for drillstring–wellbore friction during dynamic buckling. Results showed that friction-induced buckling reduces the efficiency of WOB transfer. The drillstring exhibited snaking motion with sinusoidal buckling at lower rotary speeds and transitioned to spiral or helical buckling with whirl motion at higher speeds during loading.

Similarly, Wang et al. [96] investigated the lateral stability of a drillstring in inclined wells and verified their proposed mathematical model using Shao’s [97] similitude principle for scaling the experiment. They compared the lateral vibration amplitudes and frequencies at different rotary speeds, WOB, and a wellbore inclination of 79° (with respect to the vertical line) with those of a horizontal wellbore. They used an ABS engineering plastic pipe as a drillstring and an open-ended wellbore casing made of Lucite-e tube. The rotation was provided from the surface using a speed-regulated electromotor. They found that the effect of WOB and well inclination angle was insignificant compared to rotary speed.

Srivastava and Teodoriu [39] surveyed suitable materials and equipment for drillstring vibration experiments and introduced a new mechanically scaled facility. Sharma et al. [98] detailed this setup and demonstrated its capability to study torsional vibrations, where the experimental scaling analysis followed [19]. Stick–slip was manually induced using stepped surface rotation, and rotation and torque were measured. A continuous PVC drillstring was mounted vertically to simulate a J-shaped deviated well. Rotation was applied via a top-drive DC motor, while a stepper motor controlled WOB through hook load variation. An electromagnetic brake simulates bit sticking by engaging when the bit torque matches the surface torque. Results showed that more extended sticking periods at lower rotary speeds led to higher torsional vibration amplitudes due to energy accumulation. A minimum sensor resolution of 10 Hz was recommended for accurate torsional vibration analysis.

Li et al. [99] investigated the influence of well inclination, wellbore friction, measurement position, rotary speed, and WOB on the lateral motion and whirl formation mechanisms of the BHA. The experimental setup included a PMMA rod, an aluminum alloy near-bit stabilizer, and a bit to model the BHA, where dimensional analysis and scaling followed previous work [95,100,101]. Segmented wellbore sections housed sensors between openings, and multiple wellbore assemblies of different materials simulated varying frictional conditions. Results showed that using a stabilizer, lower rotary speed, increased wellbore friction, and higher inclination reduced lateral vibration. WOB had a greater impact on lateral vibration in vertical wells than in deviated wells. Additionally, higher friction, rotary speed, and WOB increased the likelihood of backward whirl, which, once formed, became a stable and persistent motion.

3.5. Hydrodynamics Studies

There are only a limited number of studies on the interaction between drilling fluid and drillstring vibrations. While these studies follow a similar investigation methodology, their experimental designs vary widely. Past challenges in instrumenting and measuring the drilling dynamics of a submerged drillstring model underscored the importance of studying the hydrodynamic effects of drilling fluid on drillstring vibration. Recent advances in sensor technology can solve these issues [102].

Berlioz et al. [65] investigated lateral instabilities during drilling by evaluating the effects of external forces and drilling fluid properties. Their setup used slender steel rods submerged in various fluids within plexiglass pipes of different diameters to simulate wellbore annulus clearances. A shaker generated axial force and rotary torque to simulate bit–rock interaction, while a two-plate brake mechanism transferred axial force to the drillstring and applied periodic torque through clutching action. Tests were conducted in both vertical and curved wellbore configurations. Vibration amplitudes were analyzed at harmonic frequencies of applied forces. Results showed that increased axial compression, higher fluid density and viscosity, and constant torque improved lateral stability. Similarly, Khulief and Sulaiman [18] used a uniform stainless-steel shaft enclosed in a Plexiglas tube to simulate the drillstring and wellbore. Torsional and axial excitations were applied using a magnetic tension brake and an electromagnetic shaker, respectively, to replicate bit–rock interaction. The setup enabled spectral analysis of natural frequencies and damping characteristics in different fluids, including air, turpentine oil, and water. They found that fluid damping factors depend on the BHA’s vibration frequency and decrease with lower WOB fluctuations and higher rotary speed.

Fluid–structure interaction (FSI) between drilling fluid circulation and a flexible drillstring was experimentally investigated using a vertically suspended, cantilevered flexible pipe housed within a partially enclosed rigid pipe, which was itself housed within a cylindrical reservoir [103]. Fluid was injected downward through the flexible pipe, while an upward flow through the annulus created cross-flow conditions. The rigid pipe’s length and position were adjustable to control the annular gap and eccentricity. Results showed that increasing pipe stiffness, enlarging the annular gap, and reducing flow velocity significantly reduced lateral vibrations and improved system stability.

The effects of fluid flow rate on drillstring vibrations were experimentally investigated using a setup that simulated drillstring rotation, axial excitation, and fluid circulation through a flexible PEX tube within a transparent acrylic casing [104]. Rotation was applied via a VFD-controlled motor, and axial bit excitation was introduced using an electromagnetic shaker at fixed amplitudes across a range of sweep frequencies. Water circulated downward through the drillstring and returned upward through the annulus. Spectral analysis showed that higher flow rates induced low-frequency vibrations but helped dampen high-frequency chatter and sudden spikes. In a subsequent study [24], they investigated the effects of laminar and turbulent annulus flow regimes, with and without rotation. Turbulent flow was more effective at reducing high-frequency vibrations and preventing whirling, while laminar flow suppressed low-frequency vibrations and lateral deflections.

The mechanism of fluid-induced vibrations caused by annulus multiphase flow during horizontal drilling into natural gas hydrate reservoirs was investigated, with emphasis on the effects of annular fluid velocity and gas content on drillstring lateral stability [78]. A nonlinear vibration model was developed to account for internal and external fluid forces, gravity, and bottom axial load. The experimental setup included a flexible plastic pipe inside a transparent horizontal wellbore, with rotation provided by a servo motor and axial excitation by a vibration generator. Water was pumped through the drillstring, while a gas mixture was injected from downhole, creating upward multiphase flow through the annulus. Results showed that higher annular fluid velocity increased vibration magnitude and reduced frequency, while higher gas content led to erratic lateral motion. The influence of fluid velocity on lateral vibration was found to be more significant than that of gas content.

3.6. Objective Modular Designs

Experimental models for tool development often feature modular and uniquely designed sections tailored to specific study objectives. These modules can simulate targeted drilling dynamics and are easily interchangeable. In some cases, the module itself represents the tool, while in others, a scaled-down prototype is attached to the drillstring model.

Isolated vibration studies are commonly conducted during the early stages of tool development and downscaled prototype testing of vibration-mitigation or agitator tools. One study designed two similar test rigs to evaluate the performance of a downscaled asymmetric damping tool (AVDT) under separate lateral and torsional vibration conditions [31]. Various prototype designs, placement locations, compression loads, and operational inclinations were tested, with comparisons made to concentric stabilizers. For lateral vibration tests, a single steel string was laterally supported at regular intervals within circular frames simulating the wellbore. Torsional vibration tests used a more slender steel string equipped with an inertia disk and shaft to represent the BHA and drill bit, with the shaft in constant contact with a steel wellbore to simulate torque and friction. Both assemblies were mounted on the same rig, which featured an inverted vertical configuration, where rotation was applied from the bottom and compression load from the top. Experimental results demonstrated that AVDT reduced lateral vibration by up to a factor of six compared to concentric stabilizers. Its asymmetric design also induced forward synchronous whirling (FSW), which generated parasitic torque and dampened torsional vibration during the slip phase of stick–slip. However, severe FSW could occur if the rotation frequency matched the drillstring’s harmonic frequency.

Coupled vibration studies have contributed to the development of tools that intentionally induce vibrations to enhance drilling performance and reduce stick–slip. One study tested an axial excitation tool using a tensioned steel string as the drillstring, with ball-bearing-supported cylinders simulating BHA inertia and a surrounding frame representing the wellbore [61]. Axial excitation was applied from the top using DC solenoids controlled by an AC inverter and variable driver, while torsional stiffness was adjusted via string tension. Results showed that stick–slip could be mitigated by applying high-frequency axial excitation or by matching the excitation force with the applied WOB.

The effectiveness of a downhole spring attachment as an axial shock absorber was evaluated by comparing WOB fluctuation and energy conversion efficiency across varying WOB levels, rotary speeds, spring stiffness, and tool positions on the BHA [105]. A vertical test assembly used a segmented ABS plastic pipe to represent the drillstring and incorporated the spring tool [106]. Results showed that the spring attachment reduced WOB fluctuation by 10–90%. Higher rotary speed and spring stiffness had a greater impact on lowering fluctuations than WOB or tool position. The relationship between spring stiffness and axial vibration was nonlinear; initial increases in stiffness reduced vibration, but excessive stiffness worsened it. Positioning the tool closer to the bit increased the risk of axial instability, though higher WOB helped counteract this effect.

Qualitative correlation between downhole lateral motion and vibration data from a drilling dynamics field recorder was investigated through spectral analysis of BHA motion and vibration signals [107]. The experiment used a horizontal setup with a redesigned BHA made of PVC pipe connected to a transparent acrylic wellbore casing, based on the same facility described in a previous study [102]. Rotation was applied using a VFD-controlled 3-phase AC motor, and bit interaction was simulated with an electromagnetic shaker. The field recorder was embedded near the downhole section of the BHA, and lateral motion was measured at the same axial position. Results showed that higher rotary speeds led to chaotic lateral motion, reflected in increased vibration magnitudes across all frequencies. In contrast, periodic BHA motion produced distinct vibration peaks at specific frequencies, with matched vibration magnitudes in both lateral directions during whirl.

4. Discussion

4.1. Comparative Summary

To enable a clear comparison of experimental strategies across different research efforts,

Table 1. Comparative summary of drillstring vibration experimentation, including vibration investigations, objectives, and approach.

Article	Mode	Phenomena	Objective	Approach	Instrumentation
[58]	Torsional, Lateral	Stick–slip, Whirl	Validating a dynamic friction model that describes the effect of downhole contact friction on the downhole instability and characterizes friction-induced torsional and lateral vibrations, and their coupled nature	Characterizing the nature of both torsional and lateral vibrations in terms of imposed BHA-wellbore friction and damping	Rotation at the motor and lower disk with encoders, lateral displacement with two Linear Variable Differential Transformer (LVDT) sensors, and brake friction force using a force sensor
[48]	Torsional, Lateral	Bit-Bounce, Stick–slip, Whirl	Developing a mathematical model to determine frictional stick–slip interactions that lead to lateral instability	Analyzing the effects of WOB and friction with stick–slip interactions on the lateral displacement and motion pattern, and comparing the numerical and experimental results	Rotation at both disks with two encoders, and lateral motion photographed
[83]	Torsional, Lateral	Stick–slip, Whirl	Verifying the self-tuning closed-loop control algorithm	Testing bit-whirl and bit-rotation stability at different rotations	Rotation of both disks using two encoders
[84]	Torsional	Stick–slip	Developing a dynamic surface control system to reduce high-frequency torsional oscillation	Defining error equations to describe bit to wellbore friction as model uncertainty	Top-drive rotation with an incremental encoder, BHA torque, and speed using Magtrol®
[44,57]	Axial, Torsional	Bit-Bounce, Stick–slip	Investigating axial and torsional vibration coupling during hard rock drilling with a PDC coring bit with a torsionally compliant laboratory-scale drillstring, and developing control strategies to mitigate bit-bounce effects	Simulating torsional and axial vibration phenomena, analyzing axial and torsional vibration characteristics in relation to drilling rotation, WOB, and ROP, and evaluating the performance of a control system	WOB is measured using the input parameter of the hydraulic system, axial displacement using a transducer, torsional vibration using a torsional displacement transducer, and accelerometers for system vibrations
[85,86,87]	Axial, Lateral	N/A	Experimentally evaluating drillstring vibration management with optimum drilling parameters to maximize ROP and drilling performance using an automated test rig	Comparing vibration magnitudes to ROP deviation as the drilling performance indicator over a range of WOB and RPM, and developing formation prediction and ROP optimization models with vibration data using ANN and ML	Top-drive rotation and torque with motor input frequency and power, WOB using load cell, ROP with servo-motor’s interface and ultrasonic sensor, and drillstring vibrations using accelerometers
[64,88]	Axial, Torsional, Lateral	N/A	Examining drilling dynamics of PDC bit on soft and hard sandstone samples for various drilling parameters	Comparing vibration responses for ranges of WOB and RPM, and validating experimental data with an analytical model for the effect of drilling parameters and vibration on ROP in soft rock formation	Lateral vibration, ROP, and rotation using individual laser/optical sensors, and individual sensors for torque, axial vibration, WOB, pressure, and flow rate
[89]	Axial, Torsional, Lateral	Bit-Bounce, Stick–Slip, Whirl	Developing detection approaches of bit bounce, whirling, and stick–slip in laboratory scale, and identifying controlling parameters to mitigate their adverse effects	Conducting bivariate kernel estimation, spectrum analysis, and periodogram analysis to evaluate the drilling dynamics and the impact of drillstring vibrations on drilling performance	Rotation and torsional fluctuation at surface and downhole using torque sensors, ROP and bit-bounce using laser sensors, WOB and bit-bounce using three load cells, and lateral movement using eddy current sensors
[55,90,91]	Axial, Torsional, Lateral	Stick–Slip, Buckling, Whirl	Developing an experimental setup to simulate all vibration modes in the same instance, and studying the coupled effect of lateral vibration on torsional vibration	Analyzing multiple bit–rock interactions in relation to various WOB, RPM, and different vibration phenomena	Surface and downhole rotation with encoders, lateral displacement with eddy current sensors, ROP with an LVDT, TOB using a force transducer, and WOB with a load cell below the rock samples
[92]	Torsional	Stick–Slip	Identifying stick–slip control method using WOB, rotary speed, and drillstring geometric and mechanical properties	Comparing the effects of frictional torque due to WOB, applied rotary speed, and geometric and mechanical properties of the drillstring, i.e., stiffness, torsion, and damping constant, on stick–slip	Rotation with encoders at the surface and downhole, and rotary speed fluctuation by using the motor’s current
[4]	Axial, Lateral	Whirl	Investigating mechanisms of lateral vibration, whirling, and axial-lateral vibration coupling	Simulating forward and backward whirling, and conducting spectral analysis to identify the dominant vibration frequencies for model verification	Lateral vibrations using two single-axis strain gauges attached to the drillstring using a slip-ring
[19]	Lateral	Whirl	Determining the contact force between the drillstring and wellbore during whirl	Analyzing the vibration responses of the drillstring with contact force between the drillstring and the wellbore	Lateral displacement using eddy-current sensors and contact forces using force sensors
[93,94]	Axial, Torsional, Lateral	Buckling, Whirl	Studying the effects of WOB and rotary speed on the dynamics of horizontal drilling and drilling stability	Comparing WOB and rotary speed fluctuation, and the effect of rotary speed on vibration magnitudes and whirl frequency	Axial force, torque, and lateral displacement using designated sensors, and a high-speed camera for drillstring motion
[52]	Lateral	Buckling, Whirl	Investigating the dynamic buckling of drillstring in horizontal wells and developing a mathematical model to address the drillstring to wellbore friction	Observing WOB transfer efficiency due to drillstring-wellbore friction, and comparing critical buckling loads and lateral vibration amplitudes between the theoretical and experimental results	Rotation with tachometer generator, WOB using a strain-type pressure sensor below the bit, axial and lateral displacement using eddy-current sensors
[96]	Axial, Torsional, Lateral	Buckling, Whirl	Investigating the lateral stability and motion of a drillstring in inclined wells and model verification	Comparing the lateral vibration amplitudes and frequency for different conditions, and a wellbore inclination of 79° compared to a horizontal wellbore	Axial force using a downhole force sensor, and lateral displacement using laser displacement sensors at three locations
[39,98]	Torsional	Stick–slip	Surveying experiment design and developing an experimental facility to study torsional vibration	Identifying good material and equipment choices to study drillstring vibration, and measuring torsional vibration responses during stick–slip at the bit	Surface and bit rotation with encoders, torque sensor, hook load using a load cell, axial displacement using a linear-potentiometer
[99]	Axial, Torsional, Lateral	Buckling, Whirl	Studying the effects of well inclination, well friction, measurement position, rotation speed, and WOB on the lateral motion and whirl formation mechanism	Comparing lateral movement magnitude, changes in whirl directions, and patterns	Torque input using torque sensors, WOB using a force sensor, and lateral displacement using optical proximity sensors
[65]	Lateral	Stick–slip, Whirl	Evaluating the effect of external forces and fluid properties on lateral instabilities	Comparing the vibration amplitudes at the harmonic frequencies to determine the effect of dogleg angle, torque, axial forces, and drilling fluids properties of ten different liquids on individual and coupled modes of lateral vibrations	Torque from both ends using torque meters, axial force with a force transducer, lateral displacement with proximity sensors, and optical sensors
[18]	Torsional	Stick–slip	Tuning and validating an elastodynamic model to describe the interaction between fluid and drillstring vibration	Determining the damping factor and natural frequency of the drillstring in the presence of three different liquids through spectral analysis	Lateral displacement using three eddy current probes at three measurements along the length, and rotation with motor speed control
[103]	Lateral	N/A	Interpreting the fluid structure interactions between drilling fluid circulation and drillstring	Investigating the effects of drillstring slenderness, material properties, and eccentricity on the lateral instability for different internal and external fluid flow	Lateral displacement using high-speed cameras, inlet fluid flow using magnetic flow meters, and confinement pressure using a Bourdon tube pressure gauge
[24,102,104,107]	Axial, Lateral	Whirl	Investigating the effects of circulating fluid flow on drillstring vibrations and lateral instability	Comparing spectral analysis of vibration responses and downhole lateral movement of the drillstring subjected to various rotary speeds, bit interaction, fluid flow, and annulus flow regimes	Rotation using an optic proximity sensor, lateral displacement using inductive sensors at three measurements along the length, tri-axial bit vibration using accelerometers, and fluid flow with flow meter
[78]	Lateral	N/A	Investigating the mechanism of fluid-induced vibrations by annulus multiphase flow in horizontal well drilling	Observed the effect of annular drilling fluid velocity and gas content on the drillstring’s lateral stability	Annular gas content with a gas flow meter, lateral displacement at three sections using an eddy current sensor
[31]	Torsional, Lateral	Stick–Slip, Whirl	Evaluating vibration mitigation performance of AVDT with downscaled prototypes	Comparing AVDT vibration mitigation performance for torsional and lateral vibrations using different prototype designs, i.e., placement location, compression load, and inclination	Rotation at top-drive and BHA with tachometer, shocks with accelerometer, WOB, and torque using motor output voltage and current
[61]	Torsional	Stick–Slip	Developing a downhole axial agitator tool for stick–slip mitigation	Comparing the change in torsional vibration and stick–slip while inducing axial excitation	Input rotation and torque with motor current-flow, drillstring rotation with tachometer generator, and WOB by correlating with hanging load spring extension using displacement sensors
[105,106]	Axial	Bit-bounce	Studying the effectiveness of a downhole spring attachment as an axial shock absorber tool	Comparing the level WOB fluctuation and energy conversion efficiency of the system for ranges of WOB, rotary speed, spring stiffness, and position on the BHA	Downhole load using a pressure sensor, axial displacement and vibration using a laser displacement sensor and an accelerometer, and lateral bit forces with force sensors

provides a structured overview of key drillstring vibration studies. Each entry categorizes the work by vibration mode (lateral, torsional, axial, or coupled), the physical phenomena investigated, the study’s primary objective, the methodological approach taken, and the instrumentation used. Furthermore,

Table 2. Comparison of experimental configurations, applied forces, and environment.

Article	Configuration	Dimensions – Length – Diameter	Applied Forces – Rotation – Axial load	Interactions – Bit–Rock/Torsional Resistance – Wellbore – Other Excitations
[58]	Vertical assembly of a two-disk rotor model with flexible steel	– 1.47 m – Upper disk 400 mm, string 2 mm, and lower disk 250 mm	– 200 rad/s, DC motor – 0.45 kg free-weight	– N/A – Brake system with a felt stripe for friction – N/A
[48]	Vertical assembly of a two-disk rotor model of a drillstring section with flexible steel	– N/A – 20 mm disks	– 400 RPM, Tunable speed motor – Free-weights	– Unbalanced loading – Cylindrical frame around the bottom disk – N/A
[83]	Vertical assembly of a two-disk rotor model with a flexible carbon steel string	– 1 m – N/A	– 87 RPM, DC motor – N/A	– N/A – Cylindrical frame around the bottom disk – N/A
[84]	Vertical assembly of a two-disk rotor model with a flexible carbon steel string	– 4.1 m – 6 × 4 mm (OD × ID)	– 0.8 Nm, Servo Motor – N/A	– N/A – N/A – N/A
[44,57]	Vertical assembly of a metal shaft with an inertia disk from the top-drive	– N/A – 76.2 mm	– 25–360 RPM, Belt drive and 25 hp hydraulic system – 227–1588 kg, Hydraulic actuator system	– 82.55 mm coring bit with three PDC cutters drilled into Sandstone and Granite rock cubes – N/A – Torsional compliance with an inertial disk
[85,86,87]	Vertical assembly of a metal shaft	– 0.52 m – 40 × 20 mm (OD × ID)	– 40–150 RPM, Servo Motor – 40–80 kg, Servo Motor-driven drawworks	– 50.8 mm and 76.2 mm diameter two double-cone drill bits drilled into Sandstone samples
[64,88]	Vertical assembly of aluminum pipe	– 0.91 m – 9.5 × 7.7 mm (OD × ID)	– 50–900 RPM, 1 HP AC motor – 4.5–22.7 kg, Electro pneumatic system	– 28.6 mm two-cutter PDC bit with 2 mm diameter nozzles into soft and hard Sandstone – N/A
[89]	Vertical assembly of connected steel pipes and a heavier cylinder at the end	– 0.6 m including the bit – 20 mm drill-pipe and 80 mm drill-collar	– 15–25 RPM, 24 V DC motor – 10–30 kg, Hydraulic pump actuator	– Several bits with a 130 mm diameter five-blade, and 78 mm and 110 mm diameter tri-blade PDC bits drilled into granite and marble rock samples – Loose bearing stabilizer – N/A
[55,90,91]	Vertical assembly of flexible string and rigid assembly model with weight disks as BHA	– N/A – 10 mm	– 0.5–1370 RPM, Electric motor – 89–223 kg, Free weights	– Rounded shaft rotated on 150 mm cube sandstone, granite, and limestone rock samples – Loose bearing stabilizer – N/A
[92]	Vertical assembly of flexible string and rigid assembly model with weight disks as BHA	– 0.84 m – 9.1 mm shaft and 5.16 mm disk	– 120 RPM, 12 V DC motor – Free weights	– Tri-blade metal bit on rock samples – Clamp holders – N/A
[4]	Vertical assembly of acrylic rod	– 1 m – 6.35 mm	– 150 RPM, Variable speed electric motor – 0.136 kg, Shaker	– N/A – N/A – N/A
[19]	Horizontal assembly of connected pipes	– 5.4 m – 44.5 × 19.5 mm (OD × ID)	– Drive motor – Surface force module	– Torsional spring module – 60 mm cylindrical floating frame around the middle of the drillstring – N/A
[93,94]	Horizontal assembly of connected steel pipes	– 25 m – 12 × 9 mm (OD × ID)	– 50–500 RPM, Electromotor – 0.2–0.6 MPa, Spring pressure load system	– Cone bit and formation rock – 20 mm segmented wellbore casing – N/A
[52]	Horizontal assembly	– 9.5 m – 17.78 × 5.7 mm (OD × ID)	– 0–300 RPM, Servo motor – 0–30 kg, Surface load	– A disk at the end of the drillstring interacts with the wellbore – 25 mm transparent wellbore – N/A
[96]	Horizontal and 79° inclined assembly, made of ABS engineering plastic pipe	– 10 m – 18 × 5.8 mm (OD × ID)	– 150–350 RPM, Electromotor – 0.1–2 kg, Load device	– N/A – 25 mm Lucite-e wellbore tube – N/A
[39,98]	Deviated assembly of a PVC string	– 15 m – 3.18 mm	– 50–200 RPM, DC motor – 0.5–1 kg, Surface hoisting system	– Electromagnetic brake – N/A – N/A
[99]	Vertical to horizontal, several inclined assemblies of polymethyl methacrylate (PMMA) rods, an aluminum alloy near-bit stabilizer, and a bit	– 2 m drill collar and 0.01 m stabilizer, 0.1 m away from the bit – 5 mm drill collar and 7 mm stabilizer	– 200–800 RPM, Servo motor – 0–0.07 kg, Loading screw	– 8 mm bit – Several 8 mm wellbore assemblies of different materials (PMMA, stainless steel, brass) – N/A
[65]	Vertical and a fixed curve deviated assembly with a 1° dogleg angle per 10 m	– 1.5 m vertical and 1.9 m deviated assembly 1.9 m – 3 mm	– 150 RPM, Electric motor – 0–20.4 kg, Shaker	– Brake systems and magnetic brakes – 8 mm plexiglass wellbore – Annulus circulation of ten liquids
[18]	Vertical assembly of stainless-steel shaft	– 1.44 m – 6 mm	– 150–400 RPM, DC motor – 0.2–1 kg, Shaker	– Magnetic tension break – Plexiglass wellbore – Different annulus fluids without circulation
[103]	Vertically cantilevered three different models of flexible pipes made of silicone rubber and Santoprene	– 0.441, 0.221, and 0.443 m – Two 16 × 6.35 mm (OD × ID) and one 13 × 9.5 mm (OD × ID)	– N/A – N/A	– N/A – Partial wellbore with optional annulus restriction – Water crossflow at multiple velocities
[24,102,104,107]	Horizontal assembly of a continuous PEX pipe with three stabilizer sections	– 5.93 m – 16 × 13 mm (OD × ID)	– 350–700 RPM, 3-phase AC motor – 0.6–5 mm at 30–120 Hz, Electromagnetic Shaker	– N/A – 57 mm acrylic wellbore – Complete fluid circulation at different flow velocities and regimes
[78]	Horizontal assembly of ABS engineering plastic pipe	– 10 m – 15 × 10 mm (OD × ID)	– 180 rad/min, Servo motor – 2 kg at 12 Hz, Vibration generator	– N/A – Transparent wellbore – Multiphase crossflow circulation with surface water and downhole gas injection
[31]	Vertical and 30° upside-down assembly with multiple supported sections of steel strings	– 2 m with 0.25 m support – One 5 mm string assembly, and the other with 1 mm, and 11 and 8 mm disks as BHA and bit	– 400 RPM, 12 V DC motor – 1–3.5 kg, Free weights	– 8 mm shaft with a steel bore – Several 18.66 mm circular frames support – N/A
[61]	Vertical assembly of steel string	– 1.25 m – 1 mm	– 1000 RPM, DC motor – 0.5 kg, Pneumatic actuator	– Unbalanced BHA loading – Cylindrical frame support – Axial excitation using DC solenoids
[105,106]	Vertical assembly of segmented ABS plastic pipes connected to a downhole axial shock absorber	– 13 m with 0.4 m shock absorber – 18 × 5 mm (OD × ID)	– 378 RPM, Adjustable speed motor – 0.5–2.5 kg	– N/A – 24 mm Lucite-e wellbore – N/A

provides a breakdown of the comparison of the experimental configurations used in those studies. Each entry outlines the physical configuration, including drillstring dimensions, applied forces, and interaction mechanisms. Depending on the experiment, the interaction may include bit–rock, wellbore, and other interactions, such as fluid–structure interaction or additional axial excitation. Dimensions and forces, or interactions not addressed in the respective studies, were indicated as ‘N/A’ in Table 2.

Practical experiments require the ability to vary input parameters, simulate drilling conditions, and capture system responses. However, physical constraints such as model size, material properties, and power requirements must be balanced with available resources. Instrumentation compatibility and market availability also influence design choices, as some sensors, like submersible types, can be costly or material-dependent.

While many studies overlook scaling effects, recent work has increasingly adopted the similitude principle to downscale field-scale systems. Dimensional analysis is used to establish geometric, material, and dynamic scaling relations, enabling experimental results to be extrapolated to field conditions.

Table 3. Summary of scaling ratios applied in laboratory models relative to field-scale drillstrings.

Articles	Geometric	Rotary Speed	WOB
[4]	18:1	1:5	27,248:1
[19]	4:1	-	-
[93,94]	8:1	1:8	64:1
[52]	10:1	1:3	9130:1
[96]	10:1	1:3	9130:1
[39,98]	30:1	1:1	-
[99]	43:1	1:4	130,000:1
[24,102,104,107]	17:1	1:2	3050:1
[78]	10:1	-	-
[105,106]	10:1	1:3	9130:1

summarizes field-to-laboratory scaling ratios of mechanically scaled experiments, rounded to whole digits, based on geometric, rotation speed, and WOB aspects.

Table 3 shows that greater geometric downscaling requires higher rotary speeds and increased power demands. Weight-on-bit (WOB) is significantly affected by model material, and using readily available materials can reduce fabrication time and maintenance costs.

4.2. Parametric Details

Most drillstring vibration experiments are conducted using vertical assemblies, particularly in studies involving lumped-mass models, hybrid configurations with flexible sections, and bit–rock interaction simulations. The vertical orientation replicates field-like conditions under gravity, maintaining tension in flexible sections and compression in heavy BHA components. It also facilitates adding weights and ensures structural stability. Horizontal assemblies are typically used to study lateral vibrations, buckling, and drillstring-wellbore interactions. These setups often involve long, mechanically scaled continuous beam models, which are more practical to accommodate horizontally. Inclined and curved assemblies are less common but have been used to examine the effects of drillstring-wellbore contact.

Lumped-mass models are generally compact, often under 1.5 m, and are not mechanically scaled. In contrast, continuous beam models frequently adopt mechanical scaling, ranging from 5 to 15 m in length and on average representing field-scale equivalents of approximately 110 m. Steel is the predominant material for drillstring construction, with slender pipes forming flexible sections and connected disks or pipes forming rigid components. Recent experiments increasingly use plastic materials, especially in scaled designs, though excessive connections may compromise model homogeneity. Typical nominal diameters are 1–2 mm for steel strings, 6 mm for slender shafts, and 13 mm for flexible plastic pipes.

Flexible assemblies are preferred for studying torsional and lateral vibrations, while rigid assemblies are necessary for evaluating drill bit performance under high torque and axial loads. Hybrid assemblies, combining flexible drill pipe sections with rigid BHA components, offer versatility for investigating multiple vibration modes.

Rotation is a primary surface drilling parameter, and experimental setups aim to replicate field conditions as closely as possible. Vertical assemblies typically use top drives to apply rotation, while horizontal setups apply rotation from the surface end of the drillstring. Most experiments employ speed-regulated electric motors, with a median test rotary speed of 250 RPM. No consistent correlation was observed between rotary speed and specific vibration modes.

Axial load and bit-excitation inducement methods vary across studies. Fixed loads are commonly applied, with rigid drillstrings capable of withstanding high compression forces; some experiments applied WOB up to 1588 kg. In contrast, flexible models typically operate under WOB below 2 kg due to buckling limitations. Hybrid assemblies often incorporate rigid BHA sections to apply WOB using free weights. Axial loads are implemented via hydraulic, pneumatic, or mechanical systems, either from the surface or downhole. Periodic axial loading is used to simulate WOB fluctuations and bit-excitation, often generated by electromagnetic shakers, enabling comparative spectral analysis between the induced excitation and system responses.

Bit–rock interaction is simulated using downscaled drill bits and reservoir rock samples. These setups generate downhole torque and torsional resistance to study torsional vibration and stick–slip behavior, typically using rigid drillstring structures. Brake systems are also employed to apply torsional resistance, with periodic braking used to simulate stick–slip dynamics.

Lateral vibration studies often use partial bounding rings or cylinders to restrict drillstring movement and simulate wellbore contact. Transparent encasings are occasionally used for visual monitoring, especially in fluid interaction studies. Some experiments vary wellbore material and friction to investigate contact dynamics, while rotor-disk models use confined downhole sections to simulate near-bit impact and friction.

Fluid interaction experiments typically submerge the drillstring in a static annular fluid column with predefined properties. To simulate field-like circulation, some setups use centrifugal pumps and swivel connections to inject fluid into the rotating drillstring and drain it from the annulus. Cross-directional continuous flow is essential for studying reciprocal interactions between fluid dynamics and drillstring vibrations. In one case, downhole gas production was simulated by injecting gas from the bottom of the assembly.

Torsional vibration studies typically focus on measuring and comparing rotary speed at both ends of the drillstring. High-resolution rotary encoders are commonly used for this purpose, while lower-resolution alternatives include tachometer generators and optical proximity sensors. Motor input speed is often inferred from current levels. Axial load and WOB are generally determined using free weights, hook load measurements, or pressure/load sensors positioned below the drilling block. Torque and torsion sensors, though precise, are rarely used due to cost and sensitivity. Instead, many studies simulate stick–slip conditions by applying pre-measured periodic torque. Wellbore frictional conditions are usually predefined by material selection, with force sensors used occasionally to measure contact forces.

Axial displacement and rate of penetration (ROP) are measured with single displacement sensors, while dual perpendicularly positioned sensors are used to capture lateral motion. Inductive displacement sensors and eddy-current probes are preferred for their sensitivity, though they require proximity and are susceptible to electromagnetic interference. To accommodate this, segmented wellbore encasings are sometimes used to allow sensor placement near the drillstring. Optical displacement sensors offer a greater range but are limited by refraction in transparent encasings and drilling fluids. High-speed cameras have also been employed for motion tracking.

Accelerometers are widely used for direct, high-resolution vibration and shock measurements. Available in single to tri-axial configurations, they must be fixed at specific axial positions. When mounted on rotating components, an angular transformation is required to interpret acceleration data. Accelerometers are particularly valuable for spectral analysis, enabling identification of natural frequencies and unwanted vibration modes.

5. Conclusions

This study delivers a comprehensive comparative assessment of 25 laboratory-scale experimental facilities by critically analyzing 37 published investigations on drillstring vibrations. The review reveals that only 28% of the studies focused on a single vibration mode, whereas 72% addressed multiple modes concurrently. In these multi-mode investigations, axial vibrations were examined in 44% of cases, torsional vibrations in 60%, and lateral vibrations in 76%. However, only 16% of the facilities were configured to capture all vibration modes simultaneously. Furthermore, while 84% of studies investigated at least one vibration phenomenon, only 52% considered coupled-mode interactions. Among individual phenomena, bit-bounce and dynamic buckling were the least explored, appearing in only 16% and 20% of studies, respectively. Fluid–structure interaction during drilling remains the most underrepresented dynamic factor, documented in merely two experimental facilities. Notably, mechanically scaled designs have gained prominence in recent years, driven by advancements in measurement technologies and material selection, with 80% of such investigations published within the past decade.

Experimental investigations into drillstring vibrations have evolved through a range of configurations, modeling approaches, and instrumentation strategies. Vertical assemblies are widely used for their ability to replicate field-relevant gravitational effects, while horizontal and inclined setups are tailored to explore specific phenomena such as lateral vibrations and buckling. Lumped-mass models offer simplified, computationally efficient representations, whereas continuous beam models enable more realistic simulations.

Material selection, particularly the increasing use of plastics in scaled models, reflects a balance between structural fidelity and practical constraints. Experimental methodologies vary in their implementation of rotation, axial loading, and bit excitation, with electromagnetic shakers and hydraulic systems commonly used to simulate drilling conditions. Measurement techniques range from rotary encoders and accelerometers to displacement sensors and high-speed cameras, each selected based on resolution requirements and physical limitations. While torque and friction measurements remain challenging due to sensor constraints, innovative strategies, such as predefined frictional interfaces and downhole loading systems, have yielded valuable insights.

Despite its importance, fluid interaction with the drillstring remains an experimentally limited area. Existing studies typically rely on static fluid columns or limited circulation setups, with only a few incorporating dynamic flow conditions or simulating downhole phenomena such as gas production. More comprehensive experimental work is needed to capture the reciprocal interactions between fluid dynamics and drillstring vibrations under realistic drilling conditions.

The adoption of similitude principles in scaled experiments has significantly improved the applicability of laboratory results to field-scale operations. However, trade-offs involving model size, power requirements, and measurement sensitivity remain critical design considerations. Overall, the reviewed studies demonstrate that well-conceived experimental setups, supported by appropriate instrumentation, are essential for advancing understanding of drillstring vibrations in complex drilling environments.