A Methodology for Assessing the Impact of In Situ Fractures on the Intensity of Blast-Induced Damage
Abstract
1. Introduction
1.1. Mechanism of Rock Breakage by Blasting
1.2. Discrete Fracture Network (DFN)
1.3. Numerical Simulation of a Bench Blast
2. Blasting Pressure Boundary Formulations
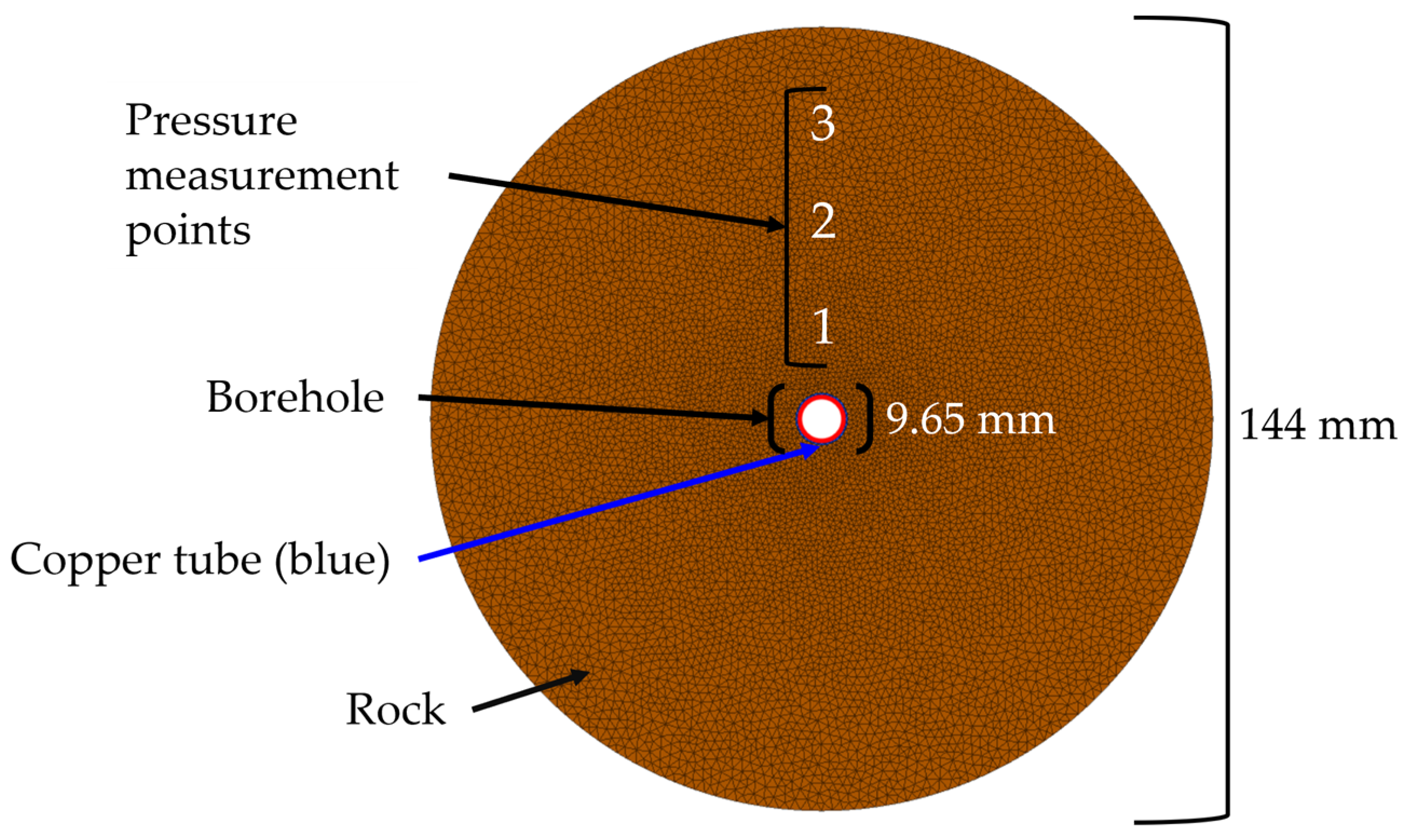
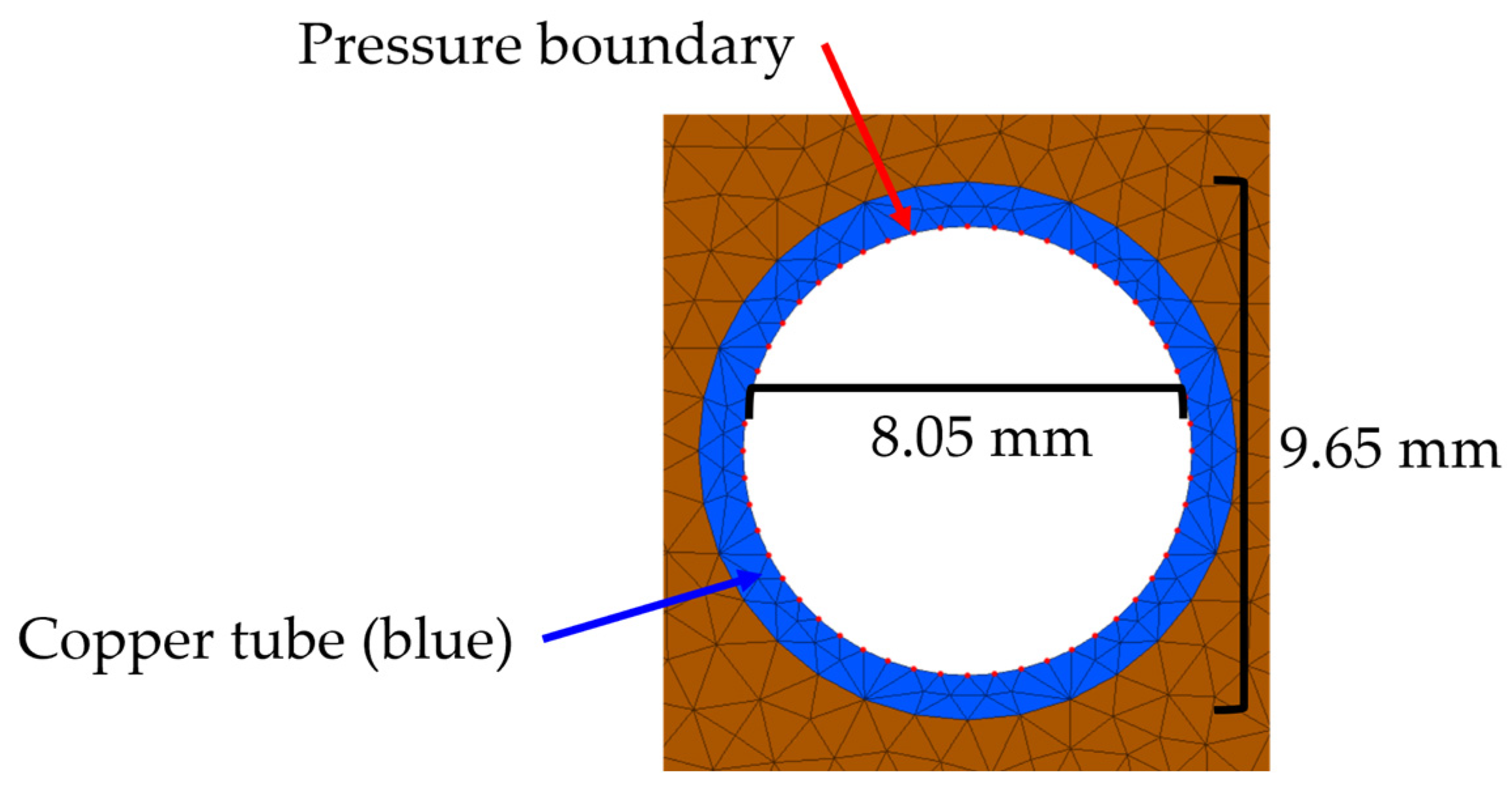
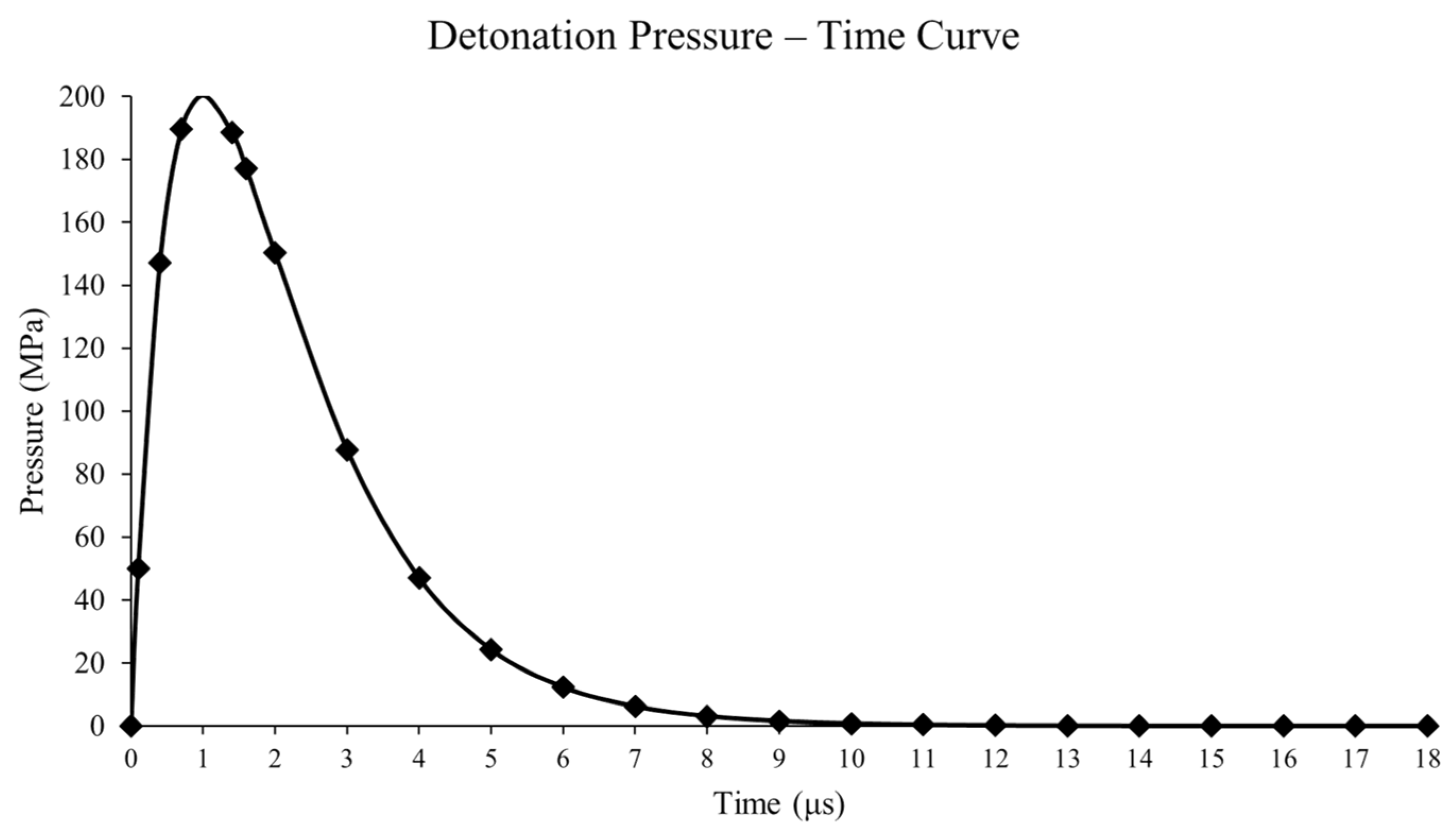
Laboratory-Scale Simulation for the Fractured Zone Around a Blasthole
3. Single-Hole Bench-Scale Blasting Scenarios
3.1. Discrete Fracture Network (DFN) Model
3.2. Numerical FDEM Bench Blast Model
3.3. Properties for FDEM Simulation
3.4. Blast-Damage Intensity Assessment
4. Bench Blast Simulation Results and Damage Assessment
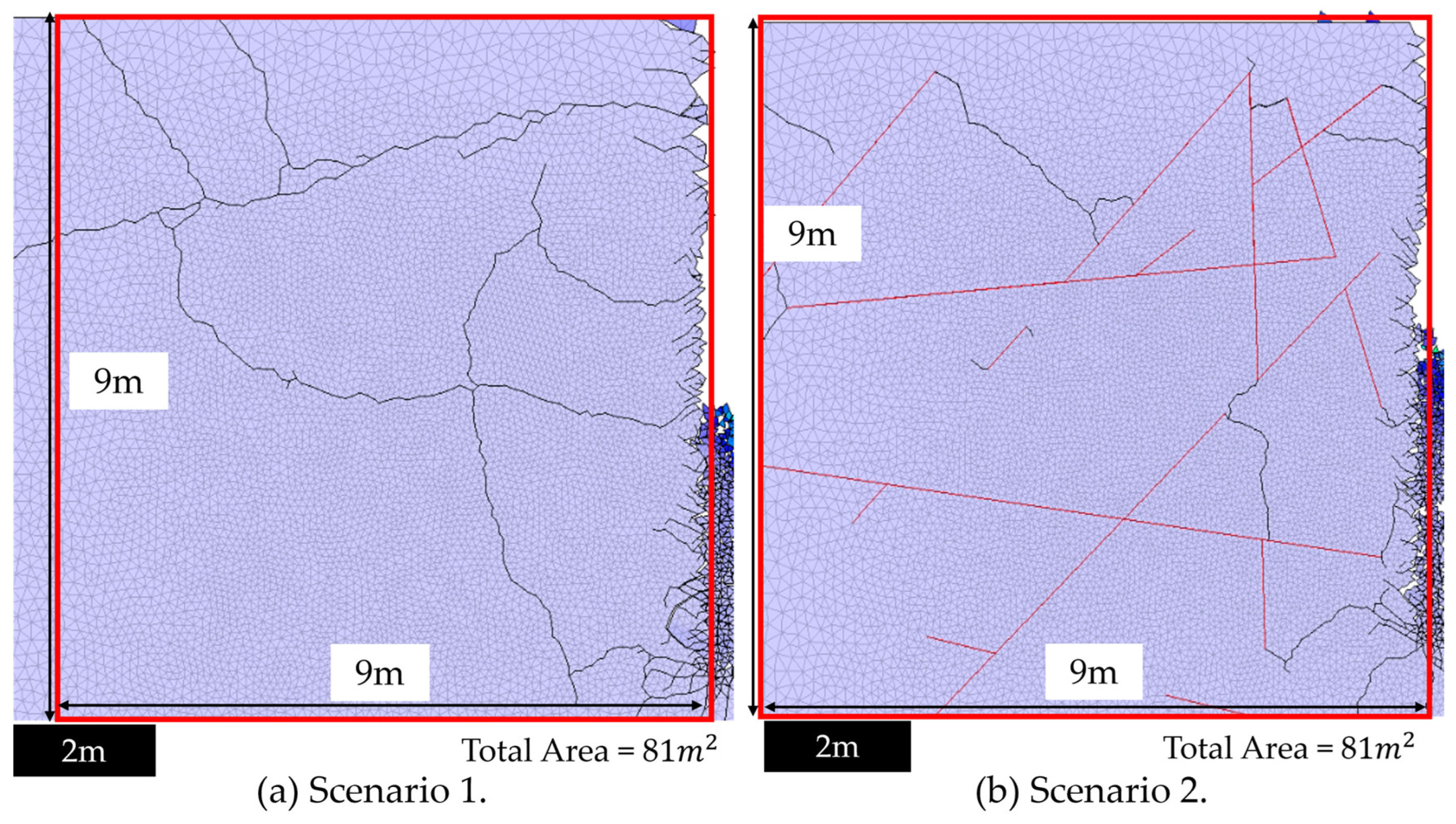
4.1. Scenario 1: Bench Blast Without DFN (Base Case)
4.2. Scenario 2: Bench Blast with DFN
4.3. Damage Intensity Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, A. Predicting Blast-Induced Damage for Open Pit Mines Using Numerical Modelling Software and Field Observations. Master’s Thesis, Laurentian University, Sudbury, ON, Canada, 2015. Available online: https://zone.biblio.laurentian.ca/handle/10219/2930 (accessed on 18 October 2021).
- International Society of Explosives Engineers. ISEE Blasters’ Handbook, 18th ed.; ISEE: Cleveland, OH, USA, 2011. [Google Scholar]
- Zhang, Z.-X. Rock Fracture and Blasting: Theory and Applications; Elsevier Inc.: Cambridge, MA, USA, 2016. [Google Scholar] [CrossRef]
- Silva, J.; Worsey, T.; Lusk, B. Practical assessment of rock damage due to blasting. Int. J. Min. Sci. Tech. 2019, 29, 379–385. [Google Scholar] [CrossRef]
- Kumar, S.; Mishra, A.K.; Choudhary, B.S. Prediction of back break in blasting using random decision trees. Eng. Comp. 2022, 38, 1185–1191. [Google Scholar] [CrossRef]
- Lu, Y.; Jin, C.; Wang, Q.; Han, T.; Zhang, J.; Chen, L. Numerical study on spatial distribution of blast-induced damage zone in open-pit slope. Int. J. Rock. Mech. Min. Sci. 2023, 163, 105328. [Google Scholar] [CrossRef]
- Dyno Nobel. Explosives Engineers’ Guide; Dyno Nobel Asia Pacific Pty Limited: Perth, Australia, 2020; Available online: https://www.dynonobel.com/apac/~/media/Files/Dyno/ResourceHub/Brochures/APAC/Explosives%20Engineers%20Guide.pdf (accessed on 11 March 2021).
- Mitelman, A.; Elmo, D. Modelling of blast-induced damage in tunnels using a hybrid finite-discrete numerical approach. J. Rock Mech. Geotech. Eng. 2014, 6, 565–573. [Google Scholar] [CrossRef]
- Dotto, M.S.; Pourrahimian, Y. The Influence of Explosive and Rock Mass Properties on Blast Damage in a Single-Hole Blasting. Mining 2024, 4, 168–188. [Google Scholar] [CrossRef]
- Han, H.; Fukuda, D.; Liu, H.; Salmi, E.; Sellers, E.; Liu, T.; Chan, A. Combined finite-discrete element modelling of rock fracture and fragmentation induced by contour blasting during tunnelling with high horizontal in-situ stress. Int. J. Rock. Mech. Min. Sci. 2020, 127, 104214. [Google Scholar] [CrossRef]
- Jimeno, C.L.; Jimeno, E.L.; Carcedo, F.J.A. Drilling and Blasting of Rocks; Taylor & Francis: New York, NY, USA, 1995. [Google Scholar]
- Himanshu, V.K.; Mishra, A.K.; Roy, M.P.; Shankar, R.; Priyadarshi, V.; Vishwakarma, A.K. Influence of Joint Orientation and Spacing on Induced Rock Mass Damage due to Blasting in Limestone Mines. Min. Met. Exp. 2023, 40, 2349–2359. [Google Scholar] [CrossRef]
- Zhang, P.; Bai, R.; Sun, X.; Wang, T. Investigation of Rock Joint and Fracture Influence on Delayed Blasting Performance. Appl. Sci. 2023, 13, 10275. [Google Scholar] [CrossRef]
- Elmo, D.; Rogers, S.; Stead, D.; Eberhardt, E. Discrete Fracture Network approach to characterise rock mass fragmentation and implications for geomechanical upscaling. Min. Technol. 2014, 123, 149–161. [Google Scholar] [CrossRef]
- Rogers, S.; Elmo, D.; Beddoes, R.; Dershowitz, W. Mine scale DFN modelling and rapid upscaling in geomechanical simulations of large open pits. In Proceedings of the International Symposium on ‘Rock Slope Stability in Open Pit Mining and Civil Engineering’, Santiago, Chile, 9–11 November 2009; 11p. [Google Scholar]
- Elmo, D.; Liu, Y.; Rogers, S. Principles of discrete fracture network modelling for geotechnical applications. In Proceedings of the First International DFNE Conference, Vancouver, BC, Canada, 19–23 October 2014. 8p. [Google Scholar]
- Dershowitz, W.; Herda, H. Interpretation of fracture spacing and intensity. In Proceedings of the 33rd U.S. Rock Mechanics Symposium, Santa Fe, New Mexico, 3–5 June 1992; pp. 757–766. [Google Scholar]
- Elmo, D.; Stead, D.; Eberhardt, E.; Vyazmensky, A. Applications of Finite/Discrete Element Modeling to Rock Engineering Problems. Int. J. Geomech. 2013, 13, 565–580. [Google Scholar] [CrossRef]
- Hamdi, P.; Stead, D.; Elmo, D. Damage characterization during laboratory strength testing: A 3D-finite-discrete element approach. Comp. Geotech. 2014, 60, 33–46. [Google Scholar] [CrossRef]
- Hazay, M.; Munjiza, A. Introduction to the Combined Finite-Discrete Element Method. In Computational Modeling of Masonry Structures Using the Discrete Element Method; Sarhosis, V., Bagi, K., Lemos, J., Milani, G., Eds.; IGI Global: Hershey, PA, USA, 2016; pp. 123–145. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock. Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Wang, B.; Li, H. Contribution of detonation gas to fracturing reach in rock blasting: Insights from the combined finite-discrete element method. Comput. Part Mech. 2024, 11, 657–673. [Google Scholar] [CrossRef]
- Jiang, X.; Xue, Y.; Kong, F.; Gong, H.; Fu, Y.; Zhang, W. Dynamic responses and damage mechanism of rock with discontinuity subjected to confining stresses and blasting loads. Int. J. Impact Eng. 2023, 172, 104404. [Google Scholar] [CrossRef]
- Sun, G.; Sui, T.; Korsunsky, A. Review of the hybrid finite-discrete element method (FDEM). In Proceedings of the World Congress on Engineering, London, UK, 29 June–1 July 2016. 5p. [Google Scholar]
- Munjiza, A.; Owen, D.R.J.; Bicanic, N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 1995, 12, 145–174. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons Ltd.: Chichester, UK, 2004. [Google Scholar] [CrossRef]
- Geomechanica Inc. Irazu 2D Geomechanical Simulation Software, Theory Manual; Computer Software; Geomechanica Inc.: Toronto, ON, Canada, 2022; 67p. [Google Scholar]
- Karimi, O.; Fillion, M.-H.; Dirige, P. Quantitative numerical assessment of blast-induced wall damage. In Proceedings of the IV Nordic Symposium on Rock Mechanics and Rock Engineering (NROCK2023), Reykjavik, Iceland, 24–26 May 2023. 10p. [Google Scholar] [CrossRef]
- Karimi, O.; Fillion, M.-H. Characterization of the extent of blast-induced damage in an open pit bench blast. In Proceedings of the 77th Canadian Geotechnical Conference (GeoMontreal 2024), Montréal, QC, Canada, 15–18 September 2024. 8p. [Google Scholar]
- Hajibagherpour, A.; Mansouri, H.; Bahaaddini, M. Numerical modeling of the fractured zones around a blasthole. Comp. Geotech. 2020, 123, 103535. [Google Scholar] [CrossRef]
- Zou, D. Theory and Technology of Rock Excavation for Civil Engineering; Springer: Singapore, 2017. [Google Scholar] [CrossRef]
- Yilmaz, O.; Unlu, T. Three-dimensional numerical rock damage analysis under blasting load. Tunn. Undergr. Space. Tech. 2013, 38, 266–278. [Google Scholar] [CrossRef]
- Jong, Y.; Lee, C.; Jeon, S.; Cho, Y.D.; Shim, D.S. Numerical modeling of the circular-cut using particle flow code. In Proceedings of the 31st Annular Conference of Explosives and Blasting Technique, Orlando, FL, USA, 6–9 February 2005. [Google Scholar]
- Ainalis, D.; Kaufmann, O.; Tshibangu, J.P.; Verlinden, O.; Kouroussis, G. Modelling the Source of Blasting for the Numerical Simulation of Blast-Induced Ground Vibrations: A Review. Rock. Mech. Rock. Eng. 2017, 50, 171–193. [Google Scholar] [CrossRef]
- Lu, W.; Yang, J.; Yan, P.; Chen, M.; Zhou, C.; Luo, Y.; Jin, L. Dynamic response of rock mass induced by the transient release of in-situ stress. Int. J. Rock. Mech. Min. Sci. 2012, 53, 129–141. [Google Scholar] [CrossRef]
- Oswald, C. An Improved Method to Calculate the Gas Pressure History from Partially Confined Detonations. In Proceedings of the International Explosives Safety Symposium & Exposition, San Diego, CA, USA, 6–9 August 2018. 18p. [Google Scholar]
- Banadaki, M.M.D. Stress-Wave Induced Fracture in Rock Due to Explosive Action. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2010. [Google Scholar]
- Wang, J.; Yin, Y.; Esmaieli, K. Numerical simulations of rock blasting damage based on laboratory-scale experiments. J. Geophys. Eng. 2018, 15, 2399–2417. [Google Scholar] [CrossRef]
- Liu, K.; Qiu, T.; Li, X.; Zhang, X.; Yang, J.; Song, R.; Li, X. Deep rock blasting using decoupled charge with different coupling mediums. Int. J. Geomech. 2023, 23, 04023112. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, Y.; Lopez, M.A.; Farbaniec, L.; Patsias, S.; Macdougall, D.; Reed, J.; Petrinic, N.; Eakins, D.; Siviour, C.; et al. The mechanical response of commercially pure copper under multiaxial loading at low and high strain rates. Int. J. Mech. Sci. 2022, 224, 107340. [Google Scholar] [CrossRef]
- ASM International. Metals Handbook Volume 2: Properties and Selection: Nonferrous Alloys and Special-Purpose Materials, 10th ed.; ASM International: Almere, The Netherlands, 1990; p. 1328. [Google Scholar]
- ASM International. Metals Handbook Volume 18: Friction, Lubrication, and Wear Technology, 10th ed.; ASM International: Almere, The Netherlands, 1990; p. 1108. [Google Scholar]
- WSP-Golder Associates. FracMan: DFN Software Suite, Computer Software; Golder Associates: Toronto, ON, Canada, 2020. Available online: http://www.golder.com/fracman/ (accessed on 12 April 2021).
- Rocscience Inc. DIPS Tutorial (version 8), Computer Software; Rocscience Inc.: Toronto, ON, Canada, 2021. Available online: https://www.rocscience.com/software/dips (accessed on 25 August 2022).
- Vlachopoulos, N.; Vazaios, I. The numerical simulation of hard rocks for tunnelling purposes at great depths: A comparison between the hybrid FDEM method and continuous techniques. Adv. Civil. Eng. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Lak, M.; Baghbanan, A.; Hashemolhoseini, H. Effect of seismic waves on the hydro-mechanical properties of fractured rock masses. Earthq. Eng. Eng. Vib. 2017, 16, 525–536. [Google Scholar] [CrossRef]
- Whittaker, B.N.; Singh, R.N.; Sun, G. Rock Fracture Mechanics: Principles, Design, and Applications; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Hoek, E. Practical Rock Engineering, 2023th ed.; Rocscience Inc.: Toronto, ON, Canada, 2023; Available online: https://www.rocscience.com/learning/hoeks-corner (accessed on 15 August 2023).
- Ning, Y.; Yang, J.; Ma, G.; Chen, P. Modelling Rock Blasting Considering Explosion Gas Penetration Using Discontinuous Deformation Analysis. Rock. Mech. Rock. Eng. 2011, 44, 483–490. [Google Scholar] [CrossRef]
- Lupogo, K.; Tuckey, Z.; Stead, D.; Elmo, D. Blast damage in rock slopes: Potential applications of discrete fracture network engineering. In Proceedings of the 1st International Discrete Fracture Network Engineering Conference, Vancouver, BC, Canada, 19–23 October 2014. 14p. [Google Scholar]
- Njock, M.C.; Meli’i, J.L.; Poufonne, Y.K.; Mbouombouo, I.N.; Well, T.H.L.; Arétouyap, Z.; Manguelle-Dicoum, E.; Nouck, P.N. Influence of natural discontinuities and mechanical properties on the fragmentation of marble by blasting in Central Africa. Environ. Earth. Sci. 2021, 80, 616. [Google Scholar] [CrossRef]
- Cho, S.H.; Kaneko, K. Influence of the applied pressure waveform on the dynamic fracture processes in rock. Int. J. Rock. Mech. Min. Sci. 2004, 41, 771–784. [Google Scholar] [CrossRef]
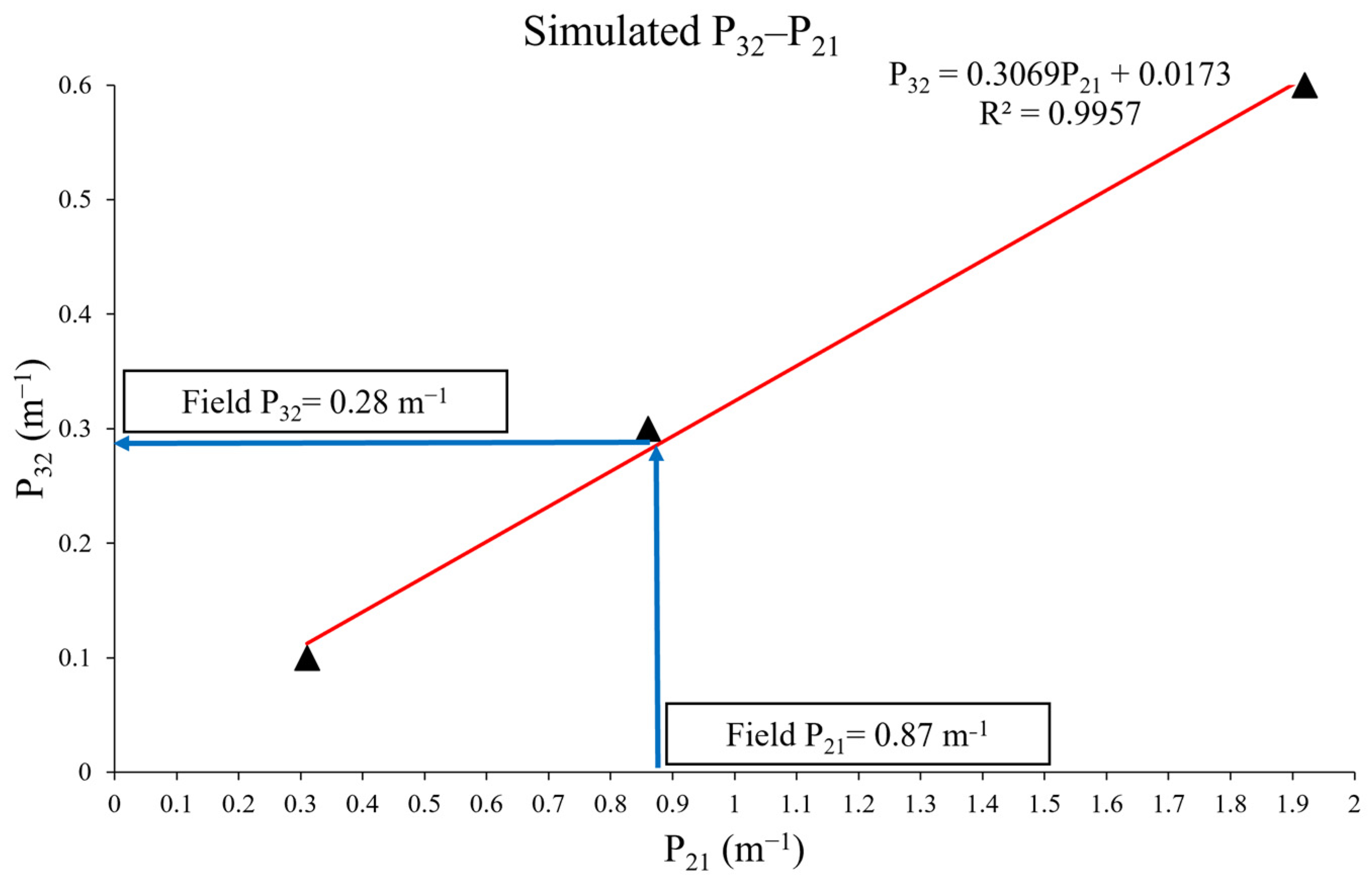
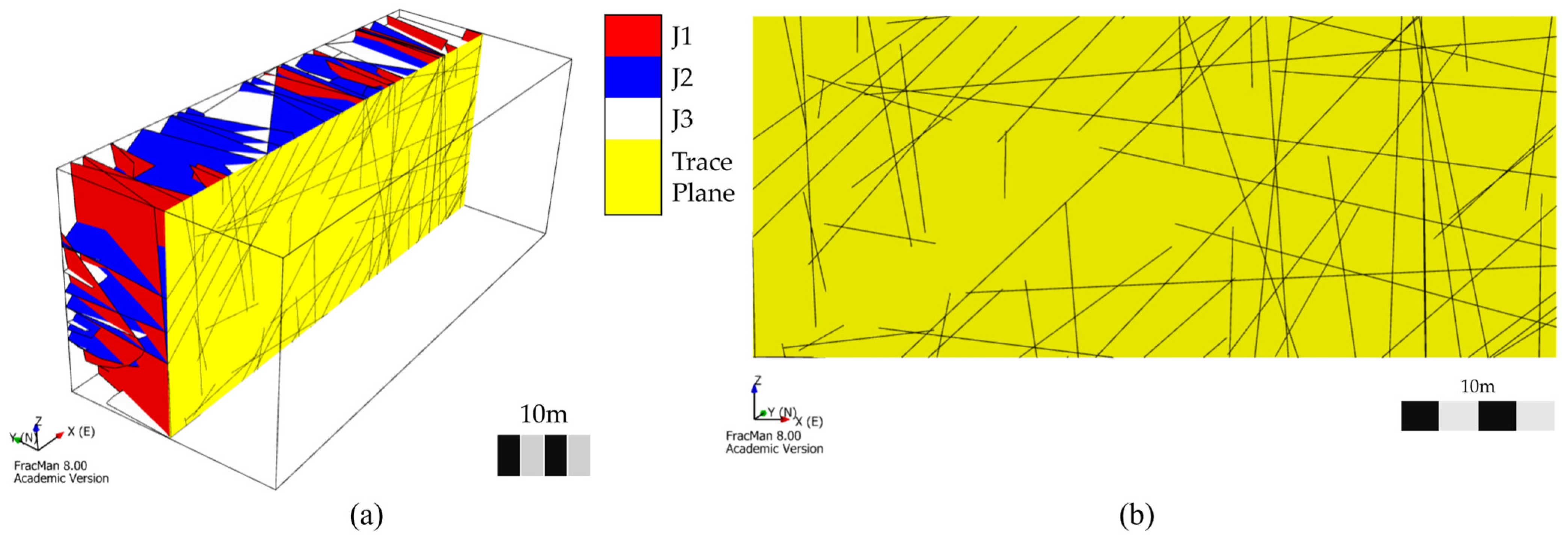

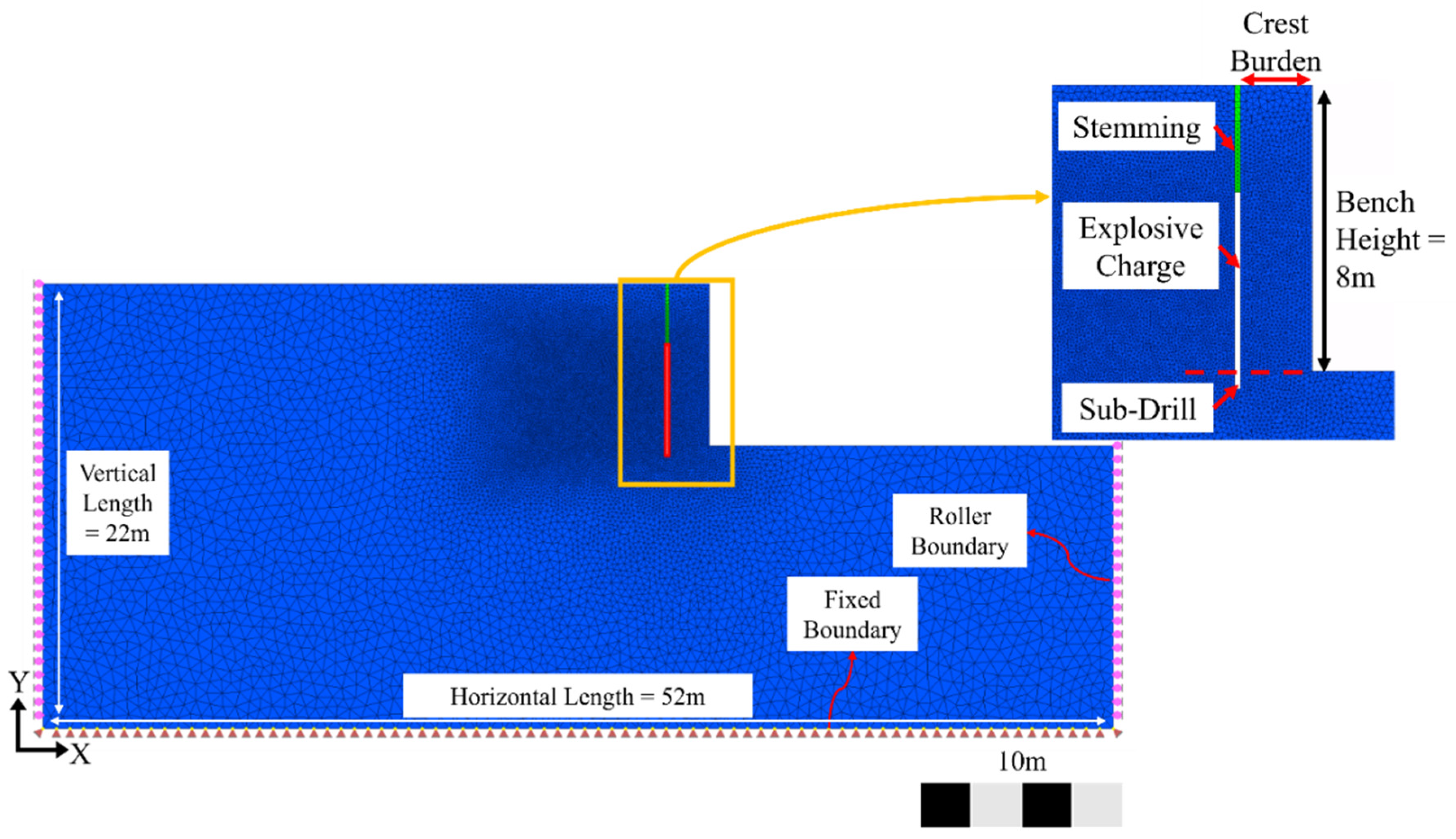

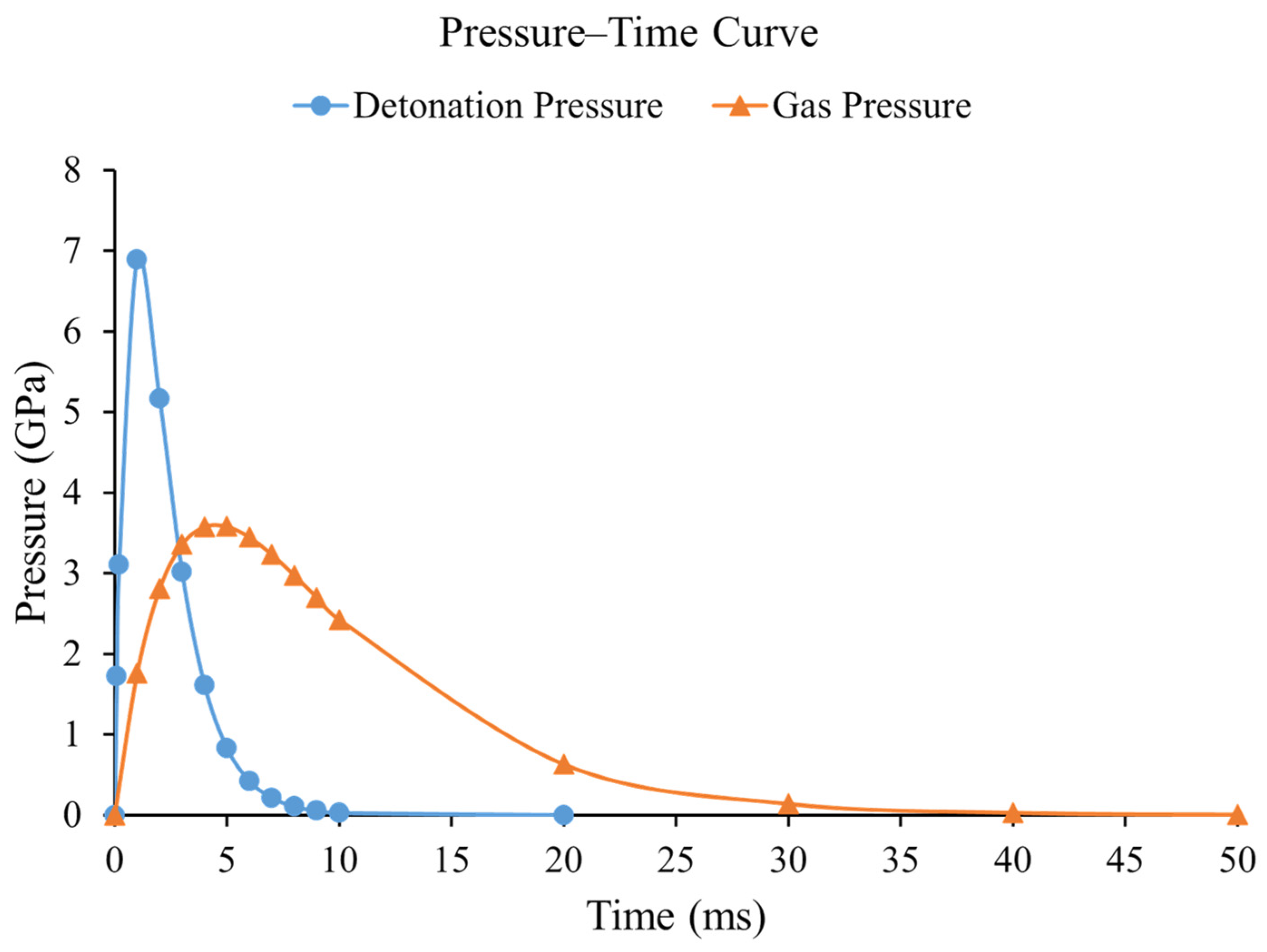



| Measurement Dimension | Measure Type | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |||
| Sample Dimension | 1 | P10 Quantity of fractures per unit length of borehole. | P11 Length of fractures per unit length. | Linear | ||
| 2 | P20 Quantity of fractures per unit area. | P21 Length of fractures per unit area. | P22 Area of fractures per area. | Areal | ||
| 3 | P30 Quantity of fractures per unit volume. | P32 Area of fractures per unit volume. | P33 Volume of fractures per unit volume. | Volumetric | ||
| Term | Density | Intensity | Porosity | |||
| Parameters | Value | Symbol |
|---|---|---|
| Density (kg/m3) | 2660 | |
| Young’s modulus (GPa) | 52 | E |
| Poisson’s ratio | 0.16 | υ |
| Cohesion (MPa) | 33 | C |
| Tensile strength (MPa) | 17 | ft |
| Friction coefficient | 1.26 | |
| Loading constraint | Plane strain |
| Parameters | Reference | Value | Symbol |
|---|---|---|---|
| Density (kg/m3) | [38,39] | 8330 | Cu |
| Young’s modulus (GPa) | [38,39] | 117 | ECu |
| Poisson’s ratio | [38,39] | 0.35 | υCu |
| Cohesion (MPa) | [40] 1 | 70 | CCu |
| Tensile strength (MPa) | [41] | 220 | ftCu |
| Friction coefficient | [42] | 0.55 | |
| Loading constraint | Plane strain |
| Monitoring Point | Distance from Blasthole (mm) | Experimental Peak Pressure (MPa) [30,37] | Numerical Peak Pressure (MPa) [30] | Numerical Peak Pressure (MPa) (This Paper) |
|---|---|---|---|---|
| 1 | 11.0 | 52.1 | 51.2 | 53.1 |
| 2 | 22.5 | 23.8 | 33.8 | 38.8 |
| 3 | 44.0 | 15.8 | 19.8 | 19.3 |
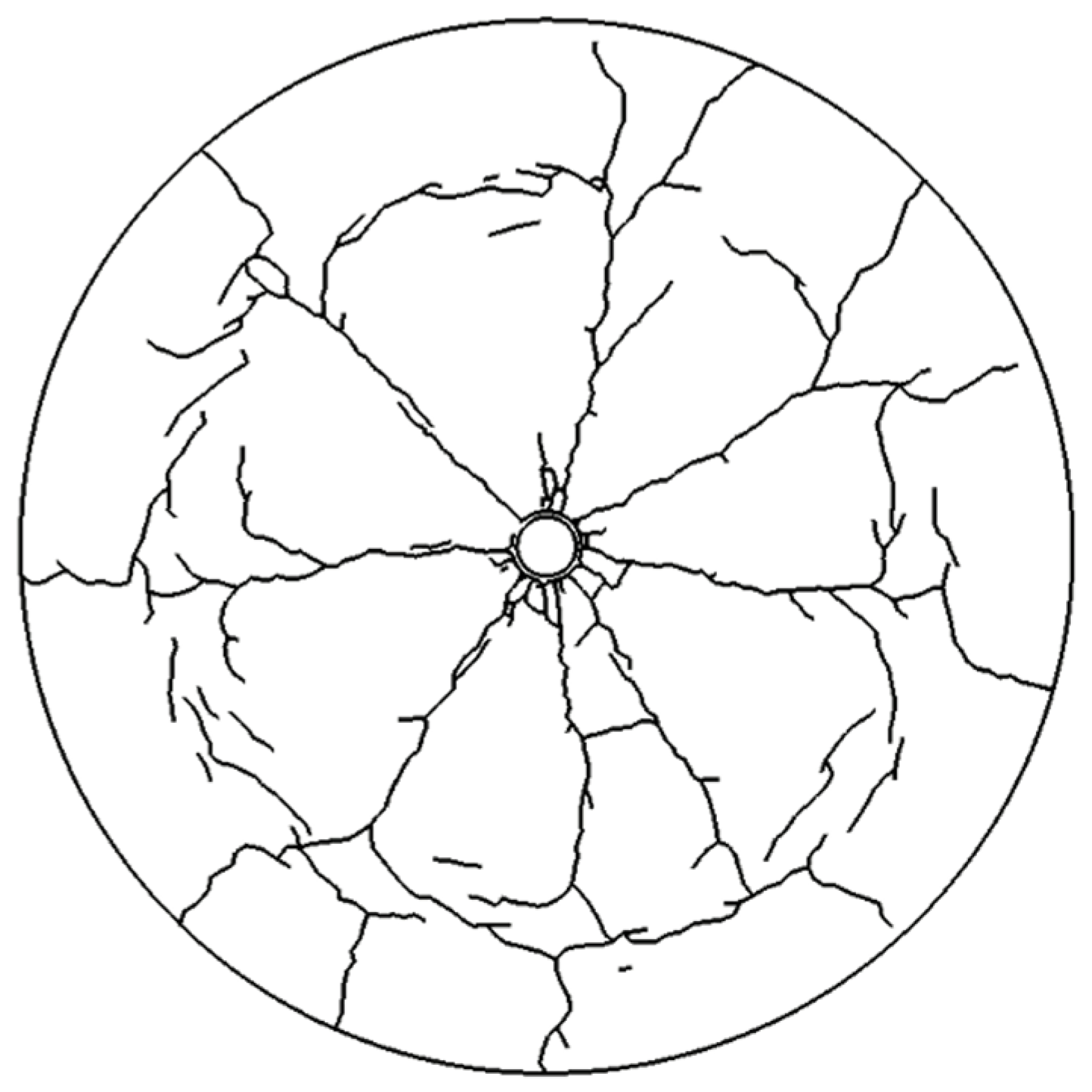
| Experimental [30,37] | Numerical [30] | Numerical (This Paper) |
|---|---|---|
| 9 | 8 | 8 |
| Parameters | Fracture Set | Value |
|---|---|---|
| Orientation (Dip/Dip Direction) (°) | J1 | 85/095 |
| J2 | 41/269 | |
| J3 | 04/096 | |
| Fisher’s K | J1/J2/J3 | 60 |
| P32 (1/m) | J1/J2/J3 | 0.28 |
| Input Orientation | DFN Generated Orientation | Variation (%) | ||||
|---|---|---|---|---|---|---|
| Fracture Sets | Dip (°) | Dip Direction (°) | Dip (°) | Dip Direction (°) | Dip | Dip Direction |
| J1 | 85 | 095 | 88 | 093 | 3.5 | 2.1 |
| J2 | 41 | 269 | 42 | 270 | 2.4 | 0.4 |
| J3 | 04 | 096 | 06 | 083 | 50.0 | 13.5 |
| Material | Parameters | Value | Units | Symbol |
|---|---|---|---|---|
| Rock | Density | 2700 | kg/m3 | |
| Young’s modulus | 60 | GPa | E | |
| Poisson’s ratio | 0.25 | υ | ||
| Uniaxial compressive strength | 110 | MPa | UCS | |
| Viscous damping | 1 | |||
| Cohesion 1 | 22 | MPa | C | |
| Tensile strength 2 | 11 | MPa | ft | |
| Friction coefficient | 0.47 | fr | ||
| Friction energy mode I | 31 | N/m | GI | |
| Friction energy mode II | 310 | N/m | GII | |
| Loading constraint | Plane strain | |||
| Explosive | Explosive type | Heavy ANFO | ||
| Density | 1200 | kg/m3 | e | |
| Velocity of detonation | 5000 | m/s | VOD | |
| DFN | Fracture type | Broken | ||
| Friction coefficient | 0.73 |
| Parameters | Value | Units |
|---|---|---|
| Crest burden | 2 | m |
| Stemming length | 3 | m |
| Charge length | 5 | m |
| Subdrill | 0.5 | m |
| Blasthole diameter | 165 | mm |
| Bench height 1 | 8 | m |
| Scenario | Damage Intensity (Di) |
|---|---|
| 1: Blast without DFN | 0.22 |
| 2: Blast with DFN | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi, O.; Fillion, M.-H.; Dirige, P. A Methodology for Assessing the Impact of In Situ Fractures on the Intensity of Blast-Induced Damage. Mining 2025, 5, 7. https://doi.org/10.3390/mining5010007
Karimi O, Fillion M-H, Dirige P. A Methodology for Assessing the Impact of In Situ Fractures on the Intensity of Blast-Induced Damage. Mining. 2025; 5(1):7. https://doi.org/10.3390/mining5010007
Chicago/Turabian StyleKarimi, Omid, Marie-Helene Fillion, and Philip Dirige. 2025. "A Methodology for Assessing the Impact of In Situ Fractures on the Intensity of Blast-Induced Damage" Mining 5, no. 1: 7. https://doi.org/10.3390/mining5010007
APA StyleKarimi, O., Fillion, M.-H., & Dirige, P. (2025). A Methodology for Assessing the Impact of In Situ Fractures on the Intensity of Blast-Induced Damage. Mining, 5(1), 7. https://doi.org/10.3390/mining5010007







