Featured Application
This research directly contributes to designing more sustainable and efficient milling processes within the mineral processing industry. It provides a detailed guide for converting ball mills from conventional overflow systems to more energy-efficient grate discharge systems by optimizing breakage rates and material transport. These enhancements deliver substantial benefits, such as increased throughput, reduced power consumption, and steeper particle size distribution.
Abstract
This study examines the conversion of an overflow ball mill into a new discharge system via Discrete Element Method (DEM) and Smoothed Particle Hydrodynamics (SPH) simulations, demonstrating significant performance improvements. The methodology integrates SPH to assess the effects of the slurry on energy dissipation, power loss, breakage rates, and material transport. The findings highlight significant operational inefficiencies in the overflow setup, extensive dead zones, and excessive charge volume that hinder milling efficiency by limiting grinding media interaction with the ore and reducing energy for comminution. Additionally, slurry pooling shifts the center of gravity, causing torque losses and direct material bypass to the discharge zone. Our simulations replicate these challenges and benchmark them against industrial-scale operations, identifying critical charge excesses that constrain throughput and elevate power consumption. The new proposed discharge system decouples the filling charge from the evacuation mechanism, releasing the effective volume in the mill, in addition to tackling common issues in the traditional grate discharge setups like backflow and carry-over. This arrangement substantially improved grinding efficiency, as demonstrated by enhanced breakage rates and diminished specific energy consumption. The results provide a robust framework for mill design and operational optimization, underscoring the value of integrated slurry behavior analysis in mill performance enhancement.
1. Introduction
1.1. Ball Mill
In mineral processing, ball mills are responsible for reducing the particle size of minerals and are critical for the successful liberation and recovery of valuable metals through processes such as flotation. As the mining industry contends with declining global ore grades and increasing mineral complexities and hardness, the efficiency of grinding operations has become central to the economic viability of the sector [1].
The operation of ball mills involves rotating a cylinder filled with grinding media at a speed that varies depending on the mill’s diameter. It is where the finer comminution of ores with diverse mineralogies takes place. Grate discharge mills, in particular, are designed to limit over-grinding and conserve energy by allowing only the finely ground product to pass through the grates. This selective retention and evacuation process significantly enhances the efficiency of the grinding process.
Traditionally, the industry has relied on overflow ball mills because of their simplicity and effectiveness across a variety of ore types. In an overflow mill, the material exits over the spillway, resulting in a very fine product size. However, with the evolving characteristics of mined ores, there is a growing need for more controlled milling operations to handle these changes effectively [1].
As an alternative, a new energy efficient pulp lifting system has been designed to offer a more selective grinding mechanism. Unlike the overflow type, the proposed design utilizes a diaphragm at the discharge end featuring a grate system that retains larger particles and grinding media, allowing only sufficiently ground particles to exit the equipment. This setup not only prevents unnecessary regrinding particles but also enhances operational efficiency by offering an option to remove undesired materials from the mill chamber in a continuous basis. The innovation relies on incorporating deflectors that prevent the slurry from returning to the mill chamber and curved vanes that effectively flush out material. This is coupled with adjustments to operating parameters, specifically the selection of grinding media and its filling load in the mill, which are tailored based on the new breakage rates required under these updated conditions.
In this context, adopting more energy and cost-efficient milling technologies becomes essential, where even marginal improvements in mill design and operation can result in substantial economic and environmental benefits.
Key Factors Affecting Grinding Efficiency in Ball Mills
Grinding efficiency in ball mills is governed by several key factors, including ore properties, grinding media dynamics, operational conditions, mill design, and circuit configuration. Each of these elements influences energy consumption, particle breakage efficiency, and overall mill performance.
- Ore Properties and Breakage Behavior: Hardness, grindability, and mineral composition all influence the breakage process, affecting energy transfer and grinding kinetics. Variability in ore properties necessitates operational adjustments to optimize charge motion and minimize inefficiencies. Studies have shown that ore-specific milling strategies can significantly improve breakage rates and energy efficiency, particularly when coupled with modern simulation techniques [2].
- Grinding Media Dynamics: The selection and arrangement of grinding media impact charge motion and breakage mechanisms. Factors such as ball size distribution, material composition, and media shape determine the energy transfer efficiency within the mill. A case study by Cleary et al. (2020) demonstrated how DEM simulations were used in an industrial SAG mill to optimize liner design, improving throughput by 20% [3].
- Operational Conditions: Mill speed, charge volume, and slurry density directly influence grinding efficiency. Recent advancements in AI-based mill control, such as real-time process adjustments and anomaly detection, have enabled mining operations to improve grinding efficiency while reducing energy consumption [4]. Implementing adaptive control strategies based on mill simulations has resulted in improved energy utilization and reduced variability in product size distribution.
- Mill Design and Liner Configuration: Liner profiles and lifter geometries dictate charge movement and impact energy distribution. Studies using DEM have shown that optimizing lifter configurations can reduce wear rates while maximizing energy transfer to the ore. Recent case applications in industrial mills have validated these findings, with modified liner designs achieving up to 20% improvement in throughput and lower maintenance costs [3].
- Circuit Configuration and Classification Efficiency: The choice between open and closed milling circuits, as well as the design of classification systems, affects how efficiently materials are processed. Hydrocyclone optimization and fine-screening integration have been successfully implemented to reduce over-grinding, enhance classification precision, and improve overall milling efficiency [1].
1.2. Simulation Tools
The efficiency of these operations and equipment hinges on understanding the behaviors of the fluid and granular solid particles during the grinding process, which are significantly impacted by the interaction dynamics within the mill [1,3].
Advanced simulation tools, such as Discrete Element Method (DEM) coupled with Computational Fluid Dynamics (CFD), are essential for accurately modeling these interactions. These tools allow for a comprehensive analysis of how changes in particle design—such as modifications to surface area, density, and shape—affect grinding. This level of detail is critical in ball mills, where the precise interactions between particles can significantly influence the efficiency of the mineral liberation process.
The necessity of these simulations is not only for understanding what happens inside the mill but also for optimizing operations and extending their applications to circuits processing increasingly complex and harder ores. The case study of application at an industrial scale presented in this research illustrates the practical benefits of implementing such advanced models.
By leveraging these simulation tools, engineers are equipped to design ball mills, mill linings, and discharge systems, select the appropriate ball top-up, and set the right operating parameters. This approach not only improves the operational efficiency of ball mills but also contributes to the broader goals of enhancing the sustainability and cost-effectiveness of mining operations.
1.3. Meshless Lagrangian Methods
Eulerian methods, commonly used in traditional CFD, involve discretizing the fluid domain into a fixed grid system where the fluid properties at each grid point are calculated over time. This approach provides a stable framework for analyzing fluid flow, especially in scenarios involving complex boundary interactions and steady-state flows. The primary advantage of Eulerian methods is their ability to handle problems where the geometry of the domain does not change significantly over time, making these methods highly effective for studying flow around solid objects or through channels [5].
However, Eulerian methods face significant challenges in capturing large deformations within the fluid, such as those occurring in free-surface flows or highly dynamic interfaces. These methods also struggle with the computational cost associated with refining the mesh to capture finer details, which becomes necessary in the presence of complex fluid behaviors.
In contrast, Lagrangian methods treat the fluid domain by tracking individual fluid particles as they move through space and time. This approach naturally accommodates large deformations and dynamic changes in the fluid’s topology, making it particularly suited for simulations involving complex interactions between fluids and moving boundaries. In the Lagrangian framework, the fluid is not constrained by a fixed spatial grid; instead, fluid particles carry their properties and interact based on their positions, which continuously update over time.
The material derivative formula integral to Lagrangian methods:
Directly captures the advection of fluid particles, facilitating a more natural and detailed simulation of fluid dynamics [6]. This method’s adaptability to changing fluid geometries offers a significant advantage in simulations where fluid structure interactions play a critical role.
Despite their flexibility, Lagrangian methods, particularly those implemented in meshless frameworks like Smoothed Particle Hydrodynamics (SPH), encounter difficulties with accuracy at boundaries and in regions of sparse particle distribution. These issues often result in numerical instabilities or require complex corrections to ensure the fidelity of the simulation. The misinterpretation of empty computational spaces as valid fluid areas is a notable challenge, often requiring enhancements in kernel functions or more sophisticated interpolation schemes to mitigate errors [6,7,8].
The SPH method has evolved significantly since its inception to address these challenges, incorporating improvements in particle weighting and distribution techniques to enhance simulation accuracy and stability. Recent advancements have also explored coupling SPH with traditional grid-based methods to leverage the strengths of both Eulerian and Lagrangian approaches, providing a hybrid solution that maximizes accuracy while maintaining computational efficiency [9].
Considering the inherent limitations of Eulerian methods, particularly in handling dynamic interactions and complex boundary conditions within our fluid–solid system, we have chosen to adopt the Meshless Lagrangian method for our simulations. The Smoothed Particle Hydrodynamics (SPH) technology, a subset of the Lagrangian approach, offers the flexibility and precision necessary to effectively model and predict the outcomes of modifications made to the discharge system in ball mills. The decision to utilize SPH was informed by its capability to accurately track and simulate the movements and interactions of individual particles within the fluid medium of the ball mill. This approach proved invaluable, as it allowed us to achieve results that closely align with the empirical data observed at an industrial level. The fidelity of SPH simulations to real-world phenomena, therefore, not only validates our methodological choice but also enhances our confidence in the predictive power of our computational models, ensuring that our design improvements are both scientifically grounded and practically viable.
1.4. Mass-Momentum Coupling of the Fluid Phase
The Navier–Stokes equations govern the evolution of a fluid, expressed in a Lagrangian framework as follows:
where is the fluid density, the fluid velocity, the pressure, the kinematic viscosity, and the body force. These equations are linked by a state equation that dictates how properties such as density and pressure interrelate, which is especially significant when considering fluid motion’s evolution. In the context of a compressed liquid, pressure directly relates to density.
In scenarios with negligible density variations, the system’s density remains relatively constant. To address this in fluid simulations, particularly when the fluid is nearly incompressible, a constraint is applied to ensure the flow is divergence-free:
To implement this, meshless methods like the moving semi-implicit (MPS) and Smoothed Particle Hydrodynamics (SPH) often use projection techniques to isolate and retain only the divergence-free velocity component. This truncation is essential for solving the pressure Poisson equation (PPE), expressed as:
where represents a source term derived from the mass density rate of change. Handling this linear system effectively is critical, especially in large-scale simulations where the incompressibility assumption must hold under variable flow conditions.
Furthermore, under extreme conditions where fluid velocities significantly exceed the sound speed, as in underwater explosions or very fast flows, it is possible to adopt a pressure-density relationship that adjusts dynamically:
with as the reference pressure, the reference density, and the adiabatic index. This formulation facilitates the simulation of incompressible flows by effectively coupling the fluid’s density and pressure [10].
Choosing a numerical sound speed much lower than the actual physical sound speed, yet considerably higher than the maximum fluid velocity, allows simulations to approximate incompressible fluid behavior more effectively, which is a method crucial for achieving stability and accuracy in fluid dynamics simulations.
1.5. Numerical Methods for Fluid-Particle Coupling
Coupling between a fluid and a solid phase is essential for accurately predicting the interactions within multiphase systems. One-way coupling focuses merely on the forces exerted by the fluid phase onto the solid phase. In contrast, two-way coupling enhances the model by redistributing these forces back onto the fluid phase, allowing an exchange of force information between solvers. This method only involves the transfer of information and necessitates independent frameworks for each solver to manage this data exchange, as depicted in Figure 1, which outlines the general structure of the coupling process.
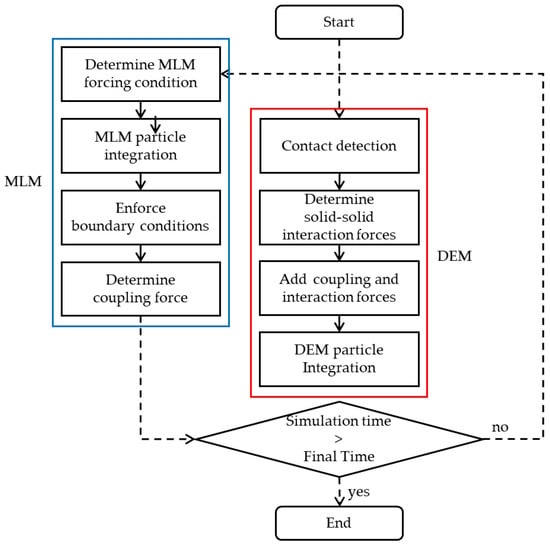
Figure 1.
Flow diagram of coupling scheme between DEM and MLMs.
Various strategies are employed to determine the coupling force, with the choice of strategy influencing the implementation’s complexity and accuracy. These can be broadly classified into two categories: direct-resolved and under-resolved approaches. Direct-resolved strategies require physically resolving the fluid flow around individual solid particles, thereby directly capturing the interactions between the fluid and solid phases. This method facilitates a reduction in the need for additional simplifications or empirical models and ensures that both the fluid and solid systems can be treated as independent entities, thereby streamlining the simulation process.
In contrast, under-resolved strategies involve determining a back-coupling force based on experimental correlations or analytical formulations, automatically managing boundary conditions during this process. The efficacy of direct-resolved versus under-resolved strategies is heavily dependent on the specific requirements of the simulation.
A notable example of a direct-resolved approach is the no-slip boundary conditions scheme, where the fluid is not allowed to penetrate the solid particle surface, a method meticulously detailed by Potapov et al. [11]. This ensures accurate adherence to the physical properties expected in such interactions, providing a high-fidelity model of fluid–solid dynamics.
Conversely, under-resolved methods offer a computational advantage by integrating a spatially averaged version of the fluid’s governing equations, which simplifies the computational load and allows for the inclusion of larger particle systems, including non-spherical shapes. This approach, as described by Potapov et al. [11], emphasizes efficiency and scalability, which is essential for large-scale simulations.
Figure 1 presents a flow diagram of the coupling scheme between Discrete Element Method (DEM) and Meshless Methods (M.L.M.), illustrating the sequence from initial condition settings through to the integration of interaction forces and the final time step of the simulation. This diagram highlights the procedural steps and decision points critical to the integration process, showing how each part of the system interacts and contributes to the overall simulation workflow.
Despite the flexibility offered by direct-resolved strategies, the high computational cost often makes under-resolved strategies more appealing for extensive or complex simulations. Future studies may focus on optimizing these methods, potentially integrating the strengths of both to enhance efficiency and applicability across various simulation scales and conditions.
2. Materials and Methods
2.1. Implementation of SPH Techniques in DualSPHysics
This section outlines the foundational equations and numerical techniques that underpin the application of the Smoothed Particle Hydrodynamics (SPH) method, as executed in the DualSPHysics framework [12], which is a Computational Fluid Dynamics tool that uses the Smoothed Particle Hydrodynamics (SPH) method for simulating the behavior of fluids and solids under various physical scenarios. It is an open-source framework designed to handle complex fluid dynamics simulations, including free surface flows, multiphase flows, and fluid–structure interactions.
The SPH method at the core of DualSPHysics is a mesh-free, Lagrangian approach where fluids are modeled as sets of discrete particles. These particles carry properties such as density, pressure, and velocity and interact with each other based on their proximity. This approach is particularly well-suited for problems involving complex geometries, dynamic interfaces, large deformations, and fragmentation.
DualSPHysics is developed collaboratively by researchers from multiple institutions, and it aims to provide a robust and efficient tool for academic and research purposes. It supports various features like GPU acceleration for faster computation, advanced boundary conditions, and coupling with other numerical methods and solvers to extend its application range further.
The method resolves the Navier–Stokes equations for fluid dynamics under assumptions of weak compressibility. The core equations—the continuity equation and the momentum equation—are delineated as follows:
In these formulations, i represents the particle of interest, while j denotes neighboring particles. The parameter δ, set at 0.1, moderates the density diffusion term , crucial for stabilizing the density fluctuations in scenarios of high-frequency oscillations.
where signifies the displacement vector between particles i and j, with “T” and “H” denoting total and hydrostatic components, respectively. The viscosity term is articulated to mitigate non-physical interpenetration of fluid particles:
To avoid the complexities of solving the Poisson pressure equation, the weakly compressible model employs the subsequent equation of state:
Here, is the reference density and , set to 7, indicates the polytropic index. The compressibility factor is governed by the speed of sound , calculated to limit relative density variations to less than 1%. is the maximum velocity and is the undisturbed depth of the fluid:
This setup, employing the Quintic Wendland kernel [13] with a smoothing length ℎ adjusted to 1.2 times the spacing of SPH particles (), results in a kernel interaction distance of 2.4 .
The Modified Dynamic Boundary Condition (MDBC) is deployed in this model to enhance stability in the pressure field near boundaries, effectively addressing potential discrepancies in the interactions between dynamic boundaries and fluid particles [13]. This method refines the handling of boundary particle arrangements, building upon the principles of the conventional Dynamic Boundary Condition (DBC). In the MDBC framework, boundary particles are typically organized in multiple layers, with the actual boundary interface positioned at half the distance to the innermost boundary layer, or .
In practical terms, the MDBC method involves the creation of a “ghost node” for each boundary particle located within the fluid domain. Directed by normal vectors that originate from the boundary particles and point toward the boundary interface, these ghost nodes dictate the interaction directions within the fluid. This configuration allows the normal vectors derived at the boundary to be projected onto these ghost nodes, thus enabling the simulation to handle complex boundary interactions more effectively.
Fluid properties at the boundary are then computed using a corrected SPH method at the ghost nodes, ensuring that these properties are accurately reflected onto the actual boundary particles. This technique allows for the precise simulation of fluid dynamics at interfaces, adapting seamlessly to various boundary geometries. The DualSPHysics framework supports this advanced boundary condition by efficiently mapping and managing ghost particles across different shapes and configurations, ensuring that the dynamic interactions are both accurate and computationally efficient. Detailed implementation procedures are elaborated in further studies [14].
In DualSPHysics, the accurate temporal integration of particle properties such as position, velocity, density, and pressure are facilitated by the use of a Symplectic integration algorithm [15]. This method is particularly chosen for its effectiveness in conserving the Hamiltonian properties of fluid dynamics, which is crucial for the accuracy and long-term stability of simulations involving complex fluid interactions. Additional specifics about this algorithm’s implementation in DualSPHysics are detailed in the literature [16].
To maintain numerical stability and ensure reliable simulation outcomes, DualSPHysics implements the Courant–Friedrichs–Lewy (CFL) condition, which governs the choice of a variable time step ) [17]. The CFL condition is fundamental in Computational Fluid Dynamics, as it ensures that the simulation time step is adequately small to capture the physics of the fast-moving flow phenomena, thus preventing numerical errors that could arise from overly large time steps.
Further elaborating on the force calculations within this framework, the force exerted on a boundary particle a by a fluid particle i is computed as follows:
where represents the force per unit mass exerted by the fluid particle on the boundary particle . Using these forces, the net force and the torque on any rigid body in the simulation can be derived from the SPH particles as shown below,
In these equations, is the position vector of the boundary particle , represents the center of mass of the rigid body , and, again, is the fluid force on boundary particle according to Equation (12).
This approach not only provides a mechanism for calculating the forces and torques exerted by the fluid on immersed or surrounding bodies but also encapsulates the interaction dynamics necessary for analyzing complex behaviors in fluid–structure interactions within the SPH framework.
2.2. Principles of Discrete Element Modeling
In Discrete Element Method (DEM) simulations, spherical particles are typically employed due to their simplicity in facilitating rapid contact detection and force calculations [18]. Yet, this approach often does not sufficiently mimic the complex behaviors of actual particulate materials, leading to significant limitations in the model’s realism [19]. To overcome these shortcomings, the DEM community has explored a variety of non-spherical particle shapes such as ellipsoids [20], hyperquadrics [21], multi-spheres [22], polyhedral [23], and other geometries. These shapes allow for a more accurate representation of the complex dynamics inherent in real-world materials, thereby enhancing the fidelity and applicability of the simulations.
In the context of fluid–structure interactions within DEM frameworks, accurately modeling irregularly shaped particles presents distinct challenges, especially at the interface with fluids. This research utilizes polyhedral particles within the Blaze-DEM solver to better address the influence of particle shape on dynamics. Polyhedral geometries are represented using a Standard Triangle List (STL) mesh. This process begins with the reading of the polyhedral geometry into the system, as illustrated in Figure 2a. Subsequent steps involve merging triangles that share similar orientations to form clearly defined feature edges and vertices, as shown in Figure 2b. The culmination of this process is the definition of unique polygonal faces, each characterized by a central point and a directional normal, which is depicted in Figure 2c for one such face, though similar treatment is applied to all faces.
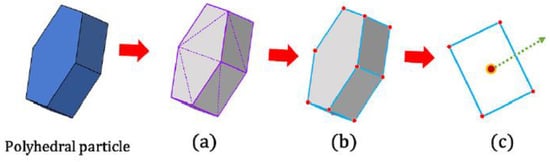
Figure 2.
Polyhedron modeling method in DEM; (a) triangles connected with similar orientation; (b) triangles connected and with same orientation are merged creating feature edges and vertex; (c) definition of a unique polygon faces including the center point and the normal direction.
This methodological approach enables each polyhedron to be effectively represented as a collection of planar faces, feature edges, and vertices, providing a detailed framework for accurately computing contact interactions between polyhedral particles. For those seeking a deeper insight into these techniques, additional details are available in the literature [24]. This enhanced representation not only improves the physical realism of the simulations but also significantly boosts the computational model’s ability to capture intricate particle dynamics within complex fluid–structure interaction scenarios.
Contact detection constitutes the most demanding aspect of Discrete Element Method (DEM) simulations, consuming approximately 90% of total computation time. To streamline this critical process, the model introduced in this study incorporates a three-tiered approach to efficiently pinpoint potential contacts among DEM particles. This method comprises a “broad phase”, an “intermediate phase”, and a “narrow phase”, each of which plays a strategic role in the detection sequence (as depicted in Figure 3).
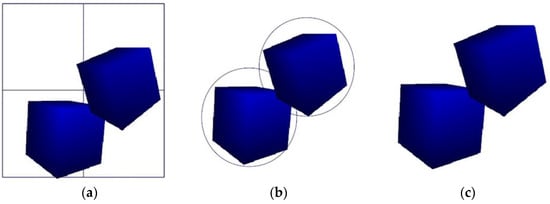
Figure 3.
Broad phase contact detection and detailed contact resolution for polyhedral particles: (a) broad phase—contact detection; (b) intermediate phase—contact resolution; (c) narrow phase—detail contact resolution.
During the “broad phase” (illustrated in Figure 3a), the model applies a grid-based spatial partitioning algorithm. This hashing strategy efficiently organizes potential particle neighbors, setting the stage for more focused inspection. Transitioning to the “intermediate phase” (shown in Figure 3b), the model utilizes boundary primitives to refine the search for proximate contacts among polyhedral particles. This step enhances accuracy by focusing on likely contact points without the computational overhead of a full pairwise check.
The process culminates in the “narrow phase” (Figure 3c), where the model finalizes contact pairings and calculates the necessary parameters to determine the forces’ directions and magnitudes. This sequential approach not only reduces the computational burden but also increases the accuracy and efficiency of modeling complex interactions within DEM simulations. Comprehensive explanations of these algorithms and their implementation specifics are detailed in the referenced literature [13,17,18], providing a deeper understanding of the advanced techniques used in this research.
In DEM simulations, accurately computing the contact forces between solid particles is essential for predicting their dynamic responses. This research incorporates a novel contact law [25] that utilizes overlap volume within the SPH-DEM coupling framework, specifically tailored for managing collisions among polyhedral particles. This enhanced method substantially boosts the robustness of particle interactions by integrating a Kelvin–Voigt linear viscoelastic model alongside a spring dashpot mechanism for rigid particles. This combination allows for the generation of an elastic force that conserves energy, complemented by a dissipative Coulomb force that accounts for energy loss during interactions.
These improvements significantly refine the precision and dependability of DEM simulations, especially beneficial for handling complex, irregularly shaped particles in fluid–structure interaction contexts. The normal force Fn exerted between contacting polyhedral particles is described by this refined spring dashpot model [24], which effectively models the nuanced physical behaviors observed in such interactions, ensuring a more accurate simulation of real-world phenomena.
where represents the volumetric spring stiffness (), which quantifies the resistance of the spring to compression or expansion per unit volume. denotes the overlap volume between particles during contact, which is a critical factor in calculating the interaction force, is the damping coefficient (), which moderates the velocity of the damping response to dynamic loads. signifies the relative velocity between the particles at the point of contact, and defines the normal vector at the contact surface, directing the force application. The expressions for and are formulated based on the physical properties of the materials and the specific interaction dynamics, as follows:
where is the effective mass of the Discrete Element Method (DEM) particles. ϵ, restitution coefficient, quantify the elasticity of collisions, affecting how kinetic energy is conserved or lost in collisions. The contact time, , critical for the temporal resolution of interactions, is based on the material properties and is adjusted to ensure that essential quantities, such as energy, are conserved throughout the simulation within the velocity range typically observed [26,27].
For all cases run in this research, we standardized a contact time equivalent to at least 10-DEM time steps, and the DEM time step is set to 1 s to maintain consistency in the simulation results across different scenarios.
The process of determining the overlap volume and the contact normal for interactions between two polyhedral-shaped particles is rigorously defined. As illustrated in Figure 4, the contact points between intersecting polyhedral particles (P1, P2) are used to construct a convex hull in Figure 4b. This geometric approach facilitates the accurate calculation of the contact volume. Simultaneously, the contact normal and the forces exerted on each particle are meticulously analyzed as depicted in Figure 4. These calculations provide a detailed understanding of the force distribution and dynamics at the contact points, ensuring that the model captures the physical behavior of the particles under stress accurately. For further in-depth explanations and the foundational theory behind these calculations, references [19,28] offer comprehensive insights.
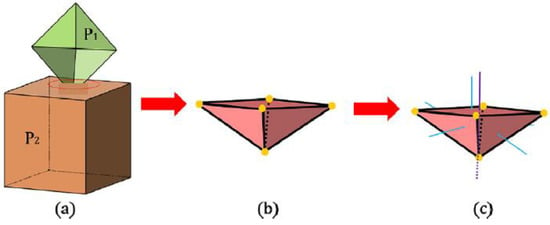
Figure 4.
The contact solution of two polyhedral particles (P1, P2) based on the overlap volume; (a) the convex hull is constructed to calculate the contact volume; (b) contact volume; (c) the corresponding contact normal and particle forces are analyzed for each particle.
The tangential force is determined by aggregating the tangential spring force along with a tangential viscous force. This combination effectively captures the directional forces acting parallel to the surface of contact, providing a comprehensive view of the forces in action during particle interactions:
where represents the volumetric spring stiffness, refers to overlap volume, is the damping coefficient, denotes the tangential spring stiffness (), r represents the relative tangential velocity, indicates the time step, signifies the tangential spring displacement from its equilibrium position. stands for the tangential damping coefficient. For a more detailed exploration of these parameters, references [24,28] provide additional context and foundational theories.
Finally, the resultant contact force and torque acting on this DEM particle is obtained:
where is the position of the contact point on a DEM particle, is the mass center of the current particle.
The equations governing the translational and rotational motion of the DEM particle k are solved with Newton’s second law:
where and represent the mass and moment of inertia matrix of DEM particle . Respectively, and are the translational and angular velocities. and denote the net force and torque acting on the particle , with the superscript and distinguishing the forces or torques originating from solid–solid and fluid–solid interactions, respectively. These dynamic equations are essential for simulating the realistic movement of particles under various forces and torques within the DEM framework.
2.3. Strategy for SPH-DEM Coupling
Figure 5 illustrates the processing of liquid and solid phases within our advanced coupling algorithm. In the SPH framework, fluids are modeled as discrete particles, allowing for precise simulation of fluid dynamics. Similarly, polyhedral structures are broken down into particles to facilitate the computation of fluid forces acting upon them. DualSPHysics is employed to dynamically update the fluid domain based on interactions among SPH particles, adhering strictly to the principles of fluid conservation.
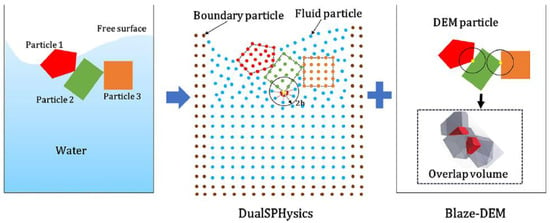
Figure 5.
Diagram of the free-surface flow interacting with polyhedral particles modeled in DualSPHysics and Blaze-DEM.
Simultaneously, the effect of fluid forces on rigid bodies is meticulously calculated, ensuring a realistic representation of fluid–structure interactions. In the DEM domain, polyhedral bodies are modeled as rigid entities characterized by defined points, lines, surfaces, and additional geometric properties. These entities adhere to contact laws which govern their interactions.
The accuracy of the simulation critically depends on the consistent management of all polyhedral data, ensuring that spatial and material property information is precisely synchronized between the SPH and DEM solvers. Blaze-DEM plays a vital role in this process by calculating the forces acting on these multi-body systems, considering both direct interactions and external fluid forces provided by the SPH framework.
The resultant motion data for these particles are then seamlessly integrated back into DualSPHysics, allowing for continuous updates to the representation of rigid bodies. This integrated approach not only enhances the realism of the simulation but also ensures the robustness of the interaction between fluid and solid phases, pivotal for analyzing complex dynamic systems.
Figure 6 presents a flow chart that outlines the fluid–solid coupling simulation process, which is structured around three core modules: the SPH (Smoothed Particle Hydrodynamics) module, the DEM (Discrete Element Method) module, and the coupling module. Within this simulation architecture, the SPH module serves as the primary control loop, orchestrating the overall progression of the simulation. It is responsible for relaying vital information, such as fluid forces and the current SPH timestep to the DEM solver through the coupling module.
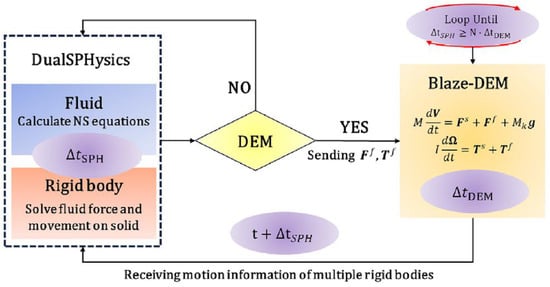
Figure 6.
Flowchart of the coupling of DualSPHysics and Blaze-DEM.
The DEM solver receives these inputs and processes them within its own computational loop, repeatedly iterating until a specific termination condition is met ().
Once this condition is satisfied, the updated particle motion data are sent back to the coupling module. This module then integrates these data into the SPH solver, updating the fluid domain and particle motion parameters accordingly.
Following the update, the SPH solver takes the new data to adjust the simulation environment for the ensuing computational cycle. This iterative process between the SPH and DEM modules, mediated by the coupling module, ensures a dynamic and continuous exchange of information, facilitating a seamless and synchronized simulation of fluid–solid interactions. The underlying numerical methods are meticulously crafted to support this complex interplay, enhancing the accuracy and efficiency of the simulation process.
The following steps outline the sequential process for conducting a fluid–solid coupling simulation, integrating both the Smoothed Particle Hydrodynamics (SPH) and Discrete Element Method (DEM) modules:
- Calculate the SPH Time Step (): Determine the appropriate time step for the SPH simulation to ensure stability and accuracy of the fluid dynamics calculations.
- Update the Neighbor List for SPH Particles: Refresh the list of neighboring particles for each SPH particle to account for movements and interactions that influence computational outcomes.
- Solve the SPH Governing Equations: Utilize Equations (6) and (7) to address particle interactions involving both fluid–rigid and fluid–fluid dynamics. This step is crucial for simulating the effects of fluid forces on various objects within the simulation environment.
- Calculate Fluid Force and Torque: Apply Equations (8) and (9) to compute the fluid force () and torque () exerted on rigid bodies. These results are then transmitted to the DEM module along with the updated SPH time step.
- DEM Particle Neighbor Search and Force Calculation: Within the DEM module, identify neighboring particles and calculate the contact forces and torques using Equations (14) and (15). This step is vital for understanding the mechanical interactions at the particle level.
- Apply External Forces and Calculate Particle Dynamics: Use the fluid force and torque calculated earlier as external forces to compute the acceleration and angular acceleration of DEM particles through Equations (16) and (17).
- Update DEM Particle Kinematics: Refresh the velocity, angular velocity, and position data for DEM particles based on the newly calculated dynamics, ensuring that the motion of each particle is accurately captured.
- Check DEM Loop Completion: Assess whether all necessary iterations within the DEM loop have been completed. If further processing is needed, return to step 5. Once complete, forward the updated DEM particle information to the coupling module.
- Update SPH Module with New Data: Integrate the updated DEM data back into the SPH module, refreshing the particle and rigid body information to prepare for the next computational cycle.
The Smoothed Particle Hydrodynamics (SPH) is applied in this research to model slurry transport in ball mills, replicating real-world conditions to enhance understanding of rheology in full, evacuation, power spectra, and other phenomena. Recent advancements in slurry transport and grinding dynamics modeling have further refined this approach. Cleary et al. (2006) introduced a coupled DEM-SPH framework for predicting slurry transport in SAG mills, which became a cornerstone for subsequent studies. Cleary and Morrison (2012) extended this work by developing 3D models of slurry flow and discharge behavior, capturing the intricate dynamics of grinding chambers. Further, Cleary et al. (2020) employed DEM-SPH to investigate interactions between grinding media, coarse rocks, and slurry, elucidating slurry grinding mechanisms. Cleary, Cummins, and Sinnott (2020) advanced these methods to focus on mill wear and slurry-phase grinding effects. Collectively, these studies underscore the transformative potential of particle-based simulations in optimizing mill operations and improving efficiency [2,3,29,30].
2.4. Industrial-Scale Implementation
To thoroughly examine the internal dynamics of the ball mill, the Discrete Element Method combined with the Smoothed Particle Hydrodynamics (DEM-SPH) approach was utilized. To substantiate the conclusions drawn from this method, a detailed industrial-scale conversion was conducted, involving the complete transformation of an overflow ball mill into a grate discharge configuration. This comprehensive modification not only involved changing the discharge system but also included a complete redesign of the mill liners. Specifically, the face angle of the lifters was adjusted to enhance the charge motion, optimizing energy utilization towards size reduction.
The industrial-scale implementation selected two distinct circuits, BM-5 and BM-6, both designed similarly. BM-5 was equipped with the traditional overflow discharge, while BM-6 incorporated a new discharge system featuring an advanced pulp lifting system. Both mills, although running in parallel configurations, were fed with the same material—ore that was blended and then split to ensure uniformity across both systems. This setup was crucial for a direct comparison of the two systems’ efficiency. Key performance indicators such as the particle size distribution (PSD), throughput (tph), and power consumption were measured and compared to evaluate the impact of the different discharge systems under identical feed conditions. This parallel approach not only facilitated an accurate assessment of the enhancements but also highlighted the potential benefits of the new discharge system in terms of operational efficiency and material handling.
The following procedural steps were undertaken using JKSimMet software with the provided data set:
- Mass Balancing: This step ensured the integrity and accuracy of material flow data by verifying that the total mass entering the system matched the total mass exiting it, accounting for feed, product, and recirculating loads. Accurate mass balancing not only validated the data set but also provided a solid foundation for subsequent model adjustments and simulations. This process identifies and rectifies any inconsistencies or errors in the data, ensuring that the analysis reflected true operating conditions.
- Model Fitting (Model Preparation for an Existing Overflow Ball Mill): The model was calibrated to accurately replicate the operation of the existing overflow ball mill configuration. Parameters such as grindability, size distribution, and power draw were adjusted to align with real-world performance. This step ensured that the baseline model provided a reliable reference point for evaluating the impact of the proposed modifications. The calibrated model acted as a benchmark, allowing direct comparison between the current and modified setups while minimizing uncertainties in performance predictions.
- Model Simulations (Grate Discharge): Simulating the modified grate discharge setup to evaluate performance changes and optimize the mill operations post-modifications.
3. Results
3.1. Baseline Scenario: Overflow Configuration
The base scenario describes the operational parameters of the primary ball mill, tagged as BM-5 configured with an overflow discharge arrangement. This mill has an internal diameter of 4.41 m, an internal length of 7.8 m, operates at 74% of the critical speed with a Bond Work Index (BWI) of 15.5 kWh/t, a hardness varying between 5.5 and 6.5 on the Mohs scale, and a specific gravity of 5.26 g/cm3. It carries a ball load of 29% with ball top sizes of 75 and 60 mm equally distributed. The accompanying hydro-cyclone classification system consists of two cyclones, each with a diameter of 0.50 m, inlet diameter of 0.20 m, vortex finder diameter of 0.19 m, spigot diameter of 0.13 m, cylinder length of 0.47 m, and operates at a cone angle of 20 degrees and a pressure of 90 kPa. The PSD of the mill’s discharge and the overflow from the hydrocyclone is detailed in Figure 7.
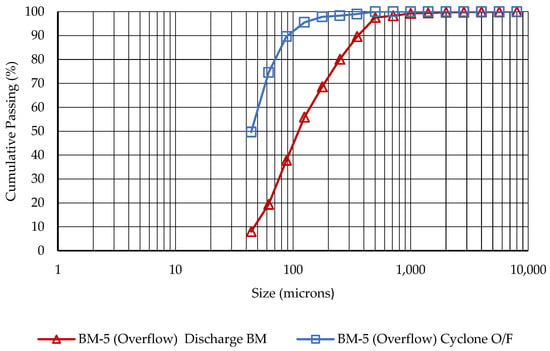
Figure 7.
Particle size distributions of mill discharge and hydrocyclone overflow in the baseline scenario: BM with overflow configuration.
For the circuit under discussion, which produces the specified particle size distribution, the throughput (tph) and the power draw are presented in Figure 8. These data serves as a reference point and they will be used as a baseline for comparison with the results of the proposed configuration, which includes modifications to both the discharge system and the operating conditions.
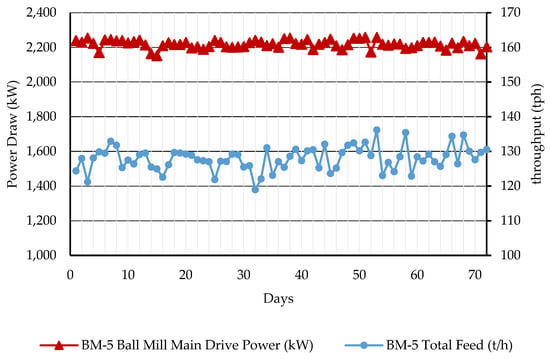
Figure 8.
Power output of BM-5 operating under standard conditions: data sourced from Plant Control Center.
Validation of the Mathematical Model and Numerical Methods
To validate the DEM-SPH model, we employed the baseline scenario mirroring the equipment at referred industrial setting. Moreover, the model was calibrated and tested against standard known cases. The validation procedure is fundamental to ensure that the numerical method accurately replicates the physical behaviors observed at the industrial scale.
For the DEM simulations, critical coefficients such as the restitution coefficient (ϵ), friction coefficient (μ), and the Poisson’s ratio () were finely adjusted. These parameters define the collision dynamics and energy dissipation within the mill, and they are all listed in Table 1.

Table 1.
Physical parameters used in the simulations.
For the SPH simulations, key parameters were configured to enhance the fidelity of fluid dynamics modeling. These include the smoothing length, which defines the interaction radius of particles, and the particle mass, crucial for accurate momentum exchanges. Fluid properties, such as viscosity, were adjusted to reflect real fluid behavior on both laminar and turbulent flows. The equation of state was applied to relate pressure and density, vital for modeling compressibility. Time step settings adhered to the Courant–Friedrichs–Lewy condition to balance simulation accuracy and computational feasibility. Finally, appropriate boundary conditions and Kernel functions were selected to ensure the simulated environment closely mirrored the physical conditions of the mill, aligning with the boundary constraints set in the DEM simulations.
Boundary conditions were defined to replicate the physical system constraints, including fixed walls and periodic boundaries where applicable. This setup ensured that the simulation space faithfully represented the mill’s operational environment.
Comparative analyses between the simulated results and the data extracted from the Distributed Control System (DCS) of the plant were conducted. The software predictions closely aligned with the recorded industrial data, confirming the reliability of the DEM-SPH approach under standardized conditions with a marginal difference of around 5%. This validation is shown in Figure 9, which illustrates the average power draw of the mill from DCS data, effectively showcasing the mill’s performance and the simulation’s precision in replicating these operational characteristics.
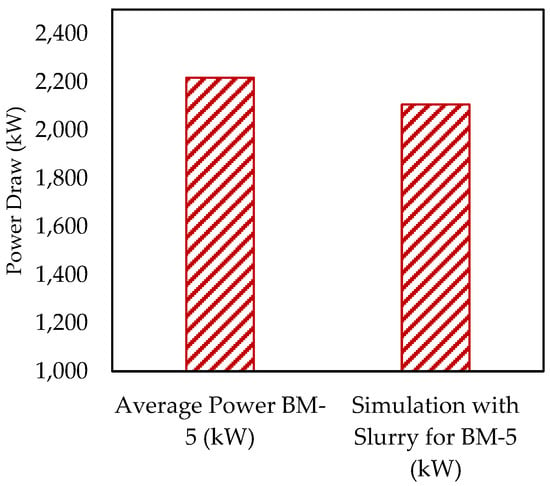
Figure 9.
Power output of BM-5 operating under standard conditions: real-time data from plant control center vs. model response.
In the calibration of the mathematical model for BM-5, emphasis was intentionally placed on power metrics rather than on predicting the product size distribution (PSD) through simulation. This choice was made to compare the PSD directly with that obtained from real-world trial rather than relying on a specific breakage model. Such an approach avoids the complexities and potential inaccuracies that can arise from overlapping multiple models and facilitates a clearer assessment of the PSD’s behavior under the proposed operational condition. The energy spectra analysis, which examined energy levels for each collision event inside the mill, including ball-to-ball, ball-to-slurry, and ball-to-surface (liners), supported the decision by showing that the energy required for ore competence remained approximately the same on both scenarios (overflow and grate discharge Figure 12a, discussed in the subsequent section on Energy Spectra, extends the analysis introduced here). Furthermore, throughput is inherently captured by the power draw, reflecting the torque generated by both the mill’s fixed and transient content—namely, the mass and its spatial distribution—at a constant speed, thereby serving as an indirect measure of throughput.
3.2. Trial Results
The trial undertaken involved modifications to the discharge system of the ball mill, transitioning to a non-conventional grate discharge arrangement. This novel system features a series of deflectors designed to prevent backflow, paired with crafted vanes that optimize slurry evacuation. Additionally, modifications were made to the liners profile to enhance the charge motion and fit to the new impact energy spectrum.
A significant change was made to the operating parameters, notably a reduction in the filling charge. The trial configuration saw the filling charge decreased by 50%, resulting in a new charge level of just 14% of the mill’s total effective volume. The top up balls size was also reduced from 75 and 60 mm to 50 mm. These adjustments were aimed at improving the breakage rates and overall milling efficiency.
The outcomes of these changes are detailed in Figure 10 and Figure 11. These figures provide a comparative analysis between the baseline setup and the trial configuration, highlighting the efficacy of the alterations in sustaining the particle size distribution under the new operating conditions, which involve a substantially reduced grinding media charge.
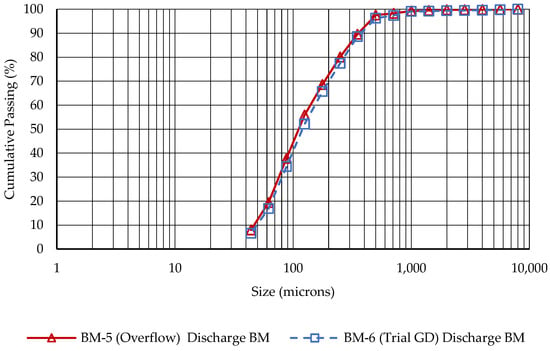
Figure 10.
Comparative particle size distributions of ball mill discharge: overflow vs. grate discharge arrangements.
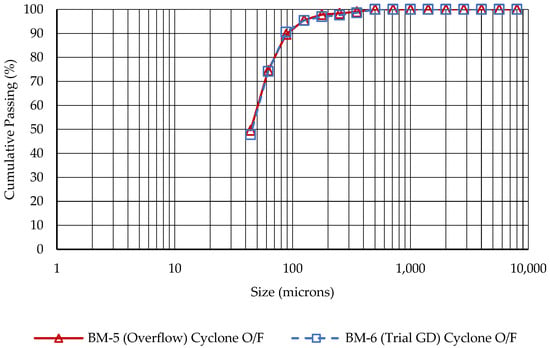
Figure 11.
Comparison of particle size distributions in hydrocyclone overflow: overflow vs. grate discharge arrangements.
To guarantee accuracy and consistency in the data collected, both the grate discharge and overflow mills were sampled simultaneously using the same standardized protocols. A total of 10 samples were taken from each stream, allowing for a comprehensive analysis of the conditions across both discharge types. The sampling intervals were set to capture both transient variations and steady-state conditions, ensuring that the results are representative of typical operational behaviors. The samples were taken at 30-min intervals, and the results, detailing the P80 of each stream for each sample, are presented in Table 2.

Table 2.
P80 values of mill discharge and cyclone overflow, under overflow, and grate discharge configurations.
3.3. Energy Spectra Analysis
When the mill is operational, the impact energy generated from interactions between particles and mill surfaces (such as liners) plays a crucial role in liberating fine powder. The quantity of fines produced is directly influenced by both the intensity and frequency of these impact energies. Typically, the energy from particle–particle collisions is less intense compared to particle–wall impacts. This is because the bulk of the particles are densely packed, restricting their relative movement and, consequently, the velocity at which they collide with each other.
In contrast, impacts between particles and the mill walls usually exhibit higher energies. This heightened impact energy is predominantly due to cataracting particles—those that are thrown from the rotating mill to fall onto the lower part of the mill, known as the toe region. These particles achieve greater velocities upon impact than those occurring at any other part of the mill, significantly contributing to the grinding process by generating higher energy collisions that are more effective at breaking down the material.
For each material ground in a mill, there is a critical impact energy level that depends on the particle size and material characteristics. Capece et al. [31] identified that the relevant impact energy threshold specific to particle size is 2.64 × 10−5 Joules, derived from a size-independent baseline. Consequently, in our analysis, we disregarded any impacts with energy below 2.5 × 10−5 Joules as they do not contribute effectively to the grinding process.
The energy required to operate a mill fluctuates based on various factors including the type of ore being processed, the characteristics of the grinding media, and operational conditions, such as mill speed and fill volume. This indicates that the input power is contingent upon these system-specific parameters. In our simulations, mill input power was determined by calculating the torque produced by the particles that collide with the mill drum.
At each time step, torques from all impacting particles were aggregated to derive the instantaneous torque exerted on the mill. Particles in free flight that are not in contact with the mill drum do not contribute to torque generation until they collide with the drum surface. Instantaneous power consumption, therefore, is calculated by multiplying the total torque by the mill’s angular speed (expressed in radians per second), which results in a characteristic impulsive pattern of power usage.
For this study, we computed the average power consumption over time to smooth out these impulsive fluctuations. This average was then benchmarked against power usage data from industrial-scale operations, as depicted in Figure 9. This comparison provides valuable insights into the efficiency and scaling of mill operations from laboratory-based models to real-world industrial applications.
Figure 12a illustrates a compelling finding in the comparative analysis of energy distribution between the two ball mill configurations: the overflow (SlurryOF) and grate discharge (SlurryGD), upon reaching steady state (Figure 12b). Notably, despite the grate discharge configuration operating with 50% fewer balls than the overflow configuration, the number of useful total impact energy events remains remarkably similar, leading to a more effective transfer of energy per event, i.e., collision among the several elements inside the mill.
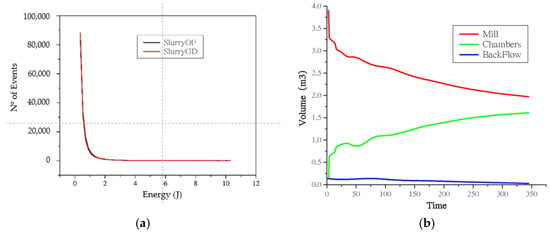
Figure 12.
(a) Energy spectra of standard (SlurryOF) and trial scenarios (SlurryGD). (b) Flow though the chambers till ready steady-state condition.
In addition to the consistent impact energy events, the operational efficiencies between the overflow and grate discharge configurations exhibit significant disparities. The power draw in the proposed setup was substantially reduced, dropping from 2214.5 kW in the overflow configuration to 1490 kW. This reduction in power was accompanied by an enhanced throughput of about 24.22%, where the mill with the new design processed 159 tph, a noticeable improvement over the 128 tph processed by the overflow mill, as illustrated in Figure 13. Consequently, these adjustments resulted in a reduction in specific energy consumption from 17.34 kWh/t to 9.38 kWh/t in the new discharge configuration, marking a decrease of approximately 45.93% in energy usage. These notable enhancements highlight the advantages of the new discharge system, particularly its superior energy efficiency and increased production capacity. These benefits yield a revenue increase while simultaneously reducing operational costs.
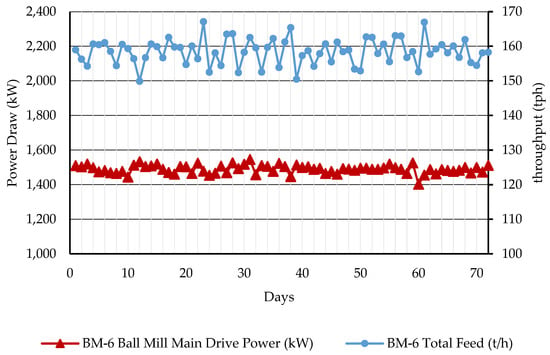
Figure 13.
Power output of BM-6 running with modified design: data sourced from Plant Control Center.
3.4. Slurry Pooling
In exploring the dynamics of mill operation, particularly regarding slurry pooling—defined as the excessive accumulation of slurry (a mixture of ore particles and water) inside the mill—its implications on power consumption are significant. This phenomenon is particularly prevalent in ball mills operating under overflow configurations, where the inherent presence of a slurry pool leads to a reduction in power draw.
Morrell’s work provides valuable insights into this effect, demonstrating through a continuum approach that slurry pooling alters charge dynamics, thereby reducing the effective torque and power required for mill operation [32]. This reduction in power draw is in stark contrast to grate discharge mills, which generally operate without a slurry pool and consequently exhibit higher power consumption. Predictive models, such as those discussed in Morrell’s studies and further explored in works like Napier-Munn et al. [1], show that transitioning a mill’s discharge mechanism from grate to overflow visibly decreases the power draw, which is directly attributable to the slurry pooling effect.
To further enhance understanding of the phenomena, we utilized the robust capabilities of the Discrete Element Method coupled with Smoothed Particle Hydrodynamics (DEM-SPH) properly calibrated to capture the nuanced effects of slurry pooling, particularly within overflow ball mill configurations. The simulations reveal that maintaining an ideal ore-ball ratio does not make possible the slurry evacuation, leading to excessive slurry within the mill on its standard running condition. This excess, in turn, hampers the ore-ball interaction, dissipates energy, and induces torque loss, culminating in diminished power draw and operational inefficiency. These findings not only corroborate the theoretical discussions presented earlier but also provide a visual framework to appreciate the operational challenges and potential adjustments needed for enhanced mill performance. Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, derived from our DEM-SPH simulations, vividly demonstrate these effects, offering a visual complement to the analytical discourse.
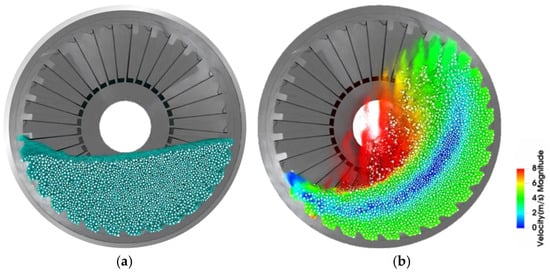
Figure 14.
Charge distribution within the mill chamber for an overflow discharge type. Showcasing the theoretical ideal ore–ball ratio: (a) standstill condition—slurry settled; (b) steady-state achieved following the fourth revolution in the simulation. Note: The velocity scale included in panel (b) uses a color spectrum, where blue indicates slower moving particles and red denotes the fastest, providing insights into the kinetic activity within the mill environment.

Figure 15.
Charge distribution within mill chamber for an overflow discharge type. Showcasing : (a) Standstill condition—slurry settled; (b) Steady-state achieved following the fourth revolution in the simulation.

Figure 16.
Charge distribution within mill chamber for an overflow discharge type. Showcasing : (a) standstill condition—slurry settled; (b) steady-state achieved following the fourth revolution in the simulation.

Figure 17.
Charge distribution within mill chamber for a non-conventional grate discharge arrangement. Showcasing : (a) Standstill condition—slurry settled—inside view; (b) Standstill condition—slurry settled—outside view.
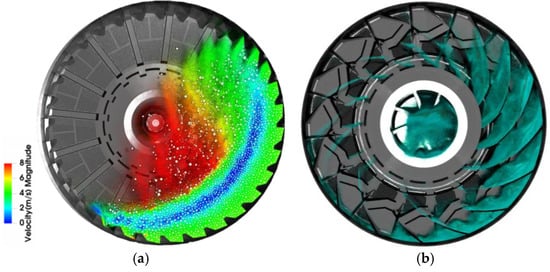
Figure 18.
Charge motion: (a) inside view; (b) outside view. Note: The color gradient in panel (a) represents velocity magnitudes, depicted on the scale from blue (minimum velocity) to red (maximum velocity), enabling precise visualization of particle speeds throughout the chamber.
Figure 14, Figure 15 and Figure 16 illustrate the impact of varying slurry levels on the operational dynamics of a ball mill, with changes in both the slurry–ball and ore–ball ratios.
Figure 14a,b presents a baseline scenario with both the slurry and the total charge (balls and slurry) at 34% of the mill’s volume ( and , respectively). In this configuration, the mass of balls totals 28.70 t within a volume of 3.69 m3. The slurry fills the void spaces, totaling 2.70 m3, approximating the simulation value of 2.90 m3. The ball-to-slurry volume ratio stands at approximately 84.9–15.1%, with the ball-to-ore volume ratio at 88.3–11.7%. In this scenario, the slurry is predominantly retained within the ball charge and fails to reach the discharge trunnion level for evacuation. This observation demonstrates that the theoretical ball-to-ore ratio does not accurately reflect the operational dynamics of a ball mill in an overflow application in real-world conditions.
Figure 15a,b depicts the increase in slurry level while maintaining a constant ball volume of 34% (), resulting in the total charge level escalating to 44.9% (). The ball mass and volume are consistent with the baseline configuration, but the slurry volume is elevated to 4.75 m3. This change modifies the ball-to-slurry ratio to 76.2–23.8% and the ball-to-ore ratio to 82.1–17.9%. The intention behind this adjustment was to determine whether the increased slurry level would suffice to reach the mill’s outlet zone, which it did not achieve. However, we observed a notable reduction in power consumption, with a 28% decrease, highlighting the impact of slurry levels on mill efficiency.
Figure 16a,b further elevates the slurry level to a total charge of 55% () while maintaining the ball volume at 34% (). The ball parameters remain the same as in Figure 14 and Figure 16, but the slurry volume increases to 6.65 m3, adjusting the ball-to-slurry ratio to 70–30% and the ball-to-ore ratio to 77.1–22.9%. The power reduction is consistent with the previous change, marking another 28% decrease.
These figures collectively underscore the role of slurry management in optimizing mill performance. The increase in slurry level is directly correlated with a decrease in power consumption, showcasing the substantial benefits of adjusting slurry levels to enhance mill operational efficiency. The slurry content during operation is over 250% more than in a standstill condition. Such excess slurry cannot be fully visualized during a crash-stop as it flushes out through the trunnion when the mill stops, leaving only the amount that can be retained at the trunnion level in the spaces among the balls.
Figure 17a,b and Figure 18a,b illustrate our experimental setup for a ball mill running in parallel to the overflow model. This configuration was specifically modified to assess how variations in slurry levels affect mill performance. In these figures, both the ball volume () and the total volume including slurry () are set at 20%. This configuration utilized 3.96 t of balls occupying a volume of 0.88 m3. The slurry fills the mill’s voids with a volume of 0.37 m3, while additional slurry was introduced to increase the total volume to 3 m3, filling both the mill and the discharge chambers.
This enhanced discharge arrangement approach allowed for the decoupling of the filling charge from the transport scheme (slurry evacuation), enabling an optimization of the ball ratio and leveraging the hydraulic gradient to enhance milling efficiency. By fine-tuning the operating parameters, higher breakage rates were achieved, which in turn allowed the equipment to maintain optimal throughput while preserving the desired particle size distribution at the mill’s discharge. This adjustment highlights the potential for substantial efficiency gains in mill operations through thoughtful control of slurry dynamics and filling strategies associated with a well-designed grate and pulp lifting system.
3.5. Particularities of the Pulp Lifting System
Extensive research into grinding circuits has revealed key challenges associated with conventional pulp lifter designs, such as Radial and Curved types, particularly when handling high slurry volumes in mills operating under closed-circuit conditions with cyclones or screens. In such scenarios, where circulating loads often reach as high as 400–500%, the structural design of these lifters causes continuous interaction between the slurry and the grate until discharge occurs. This interaction leads to the persistent issue of flow-back, as illustrated in Figure 19a.
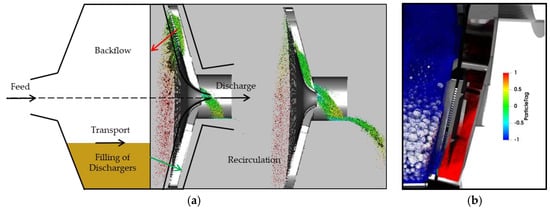
Figure 19.
(a) Flow-back process common to conventional discharge system. (b) Detail of the new discharger design which segregate materials and prevents recirculation inside the mill. Note for (b): particle location is marked by color; blue represents those inside the mill chamber, whereas red signifies particles successfully captured by the diaphragm system and positioned within the outer discharger.
Conventional designs often struggle with issues such as insufficient size, excessive carry-over, and, most critically, flow-back.
In grate discharge mills, flow-back can lead to slurry pooling and an increase in critical-sized particles—ore fragments too large to exit the grates but too small to be efficiently ground—particularly in AG and SAG mills. This phenomenon causes significant energy losses because particles that have already been sufficiently ground are unnecessarily recirculated and reprocessed. Industrial observations suggest that such inefficiencies can reduce mill throughput by as much as 10–40%, significantly impacting overall performance.
Additionally, in conventional pulp lifting systems, carry-over occurs due to the mill’s dynamic behavior during rotation. The material collected by the outer and middle dischargers has only a limited fraction of the revolution time—approximately 25%—to be fully evacuated. This issue is primarily influenced by the vane design, which, coupled with centrifugal forces generated by the mill’s rotation, delays the movement of material toward the outlet. For evacuation to begin, a stronger vertical component of the weight force is required to overcome the system’s balance and initiate the material’s fall. This dynamic reduces the effective time available for evacuation, often leaving some material behind in the dischargers. This residual material, known as carry-over, compromises the system’s efficiency in subsequent cycles by limiting the dischargers’ capacity to collect new material. As a result, recirculation occurs within the pulp lifting system, reducing throughput and overall operational efficiency.
To overcome these challenges, a novel discharge system was designed and implemented to address both flow-back and carry-over, conserving energy that would otherwise be wasted. The new system features carefully engineered deflectors to prevent slurry from directly contacting the grate apertures during evacuation, as shown in Figure 19b, thereby eliminating particle recirculation into the mill chamber. Additionally, the system incorporates highly curved vanes, which increase the timeframe for material discharge while reducing the required vertical component of the weight force needed to unbalance the system under centrifugal forces and initiate flushing. This improved design ensures more effective evacuation of material, preventing residual carry-over and maximizing the capacity for new material in each cycle. By directing all available energy toward breaking fresh particles, the system enhances milling efficiency, reduces energy consumption, and optimizes the overall process to achieve the desired product size distribution.
3.6. Dead Zone
Through numerical methods that merge methodologies presented in this research to mirror the real-world dynamics of a mill operating on an industrial scale, a critical relationship between increased filling charges and the formation of dead zones within the mill has been unveiled, as shown on Figure 20a–f. The formation of the dead zone, colored in blue, is clearly shown in Figure 20a,c,e. Meanwhile, Figure 20b,d,f illustrates a grate discharge system, where this zone appears in a lesser proportion. These dead zones are characterized by notably low relative velocity among the particles, rendering them incapable of generating the requisite energy to match the hardness of the minerals under processing. It has been found that these dead zones can constitute up to 32% of the mill’s charge by volume when the filling charges exceed 28%. In terms of weight, this proportion may escalate even further, as the central areas of the charge tend to accumulate deformed grinding balls and scats, resulting in a densely compacted core of material that is significantly heavier with a bulk density exceeding 6500 kg/m3.
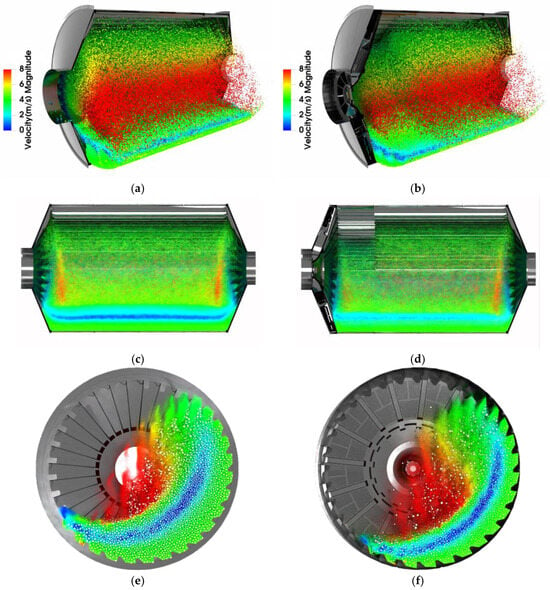
Figure 20.
Comparative visualization of dead zones in mill discharges systems: (a,c,e) show an overflow ball mill and (b,d,f) a grate discharge ball mill, respectively, with dead zones highlighted in various shades of blue. Panels (c,d) provide side views, while (e,f) cross-section interior view with the charge in steady-state, clearly illustrating the distribution and extent of low-activity regions within the mill chambers, indicating reduced grinding efficiency in these areas. Note: The color scale displayed in panel (a) applies to all panels, representing velocity magnitude across different sections of the mill.
This compacted central mass creates a scenario where slurry cannot permeate due to a lack of porosity, and despite its inactivity towards ore size reduction, it draws substantial power. The mill expends a massive amount of torque just to maintain this non-productive charge in such a position, significantly diminishing its performance. Addressing this inefficiency necessitates the removal of such non-useful material from the equipment, which is key for transitioning to an energy-efficient milling system. This process not only alleviates the unnecessary power draw but also enhances the overall operational efficacy of the mill generating effective volume and higher drop height for the balls.
In the industry, there is a prevailing belief that higher power draw is synonymous with increased throughput, suggesting a positive and even linear relationship between these two variables. However, extensive studies challenge this assumption, revealing that the relationship between power draw and throughput does not consistently maintain a positive relation across the entire operational spectrum. This research has identified a critical juncture where the rate of increase in specific input energy is higher than the rate of increase in specific impact energy, particularly as the mill size increases and is operated with excessive filling charge. This discrepancy becomes more pronounced in larger mills, indicating that the efficiency gains expected from merely increasing power are not realized.
The high inefficiencies in the tumbling mills, which are prevalent in mines worldwide, can largely be attributed to the excessive accumulation of materials within the mill chamber. This includes an excess of critical size balls, scats, and slurry. Such accumulation not only contributes to suboptimal milling conditions but also underscores a significant loss in energy efficiency. By decreasing the amount of non-contributive material in the mill, it becomes possible to enhance the milling process’s efficiency, pointing towards a more sustainable approach in mineral processing operations. This method represents a disruptive shift in optimizing mill performance, focusing on operational adjustments rather than simply increasing power input.
4. Discussion and Future Directions
Several key areas of inefficiency have been found in the conventional overflow setup, such as significant dead zones, excessive charge volume, and energy losses due to inadequate slurry interaction and pooling.
In the proposed configuration, a greater fall height is observed between the shoulder and the toe of the charge. This increased drop height amplifies the impact forces during collisions among the grinding media, thereby facilitating a more effective comminution per collision event. The energy spectra of the new setup mirrored the overflow one, despite containing nearly 50% less grinding media and consequently fewer collision events.
The efficacy of the proposed discharge system is underscored by its ability to facilitate a superior hydraulic gradient and its capacity to streamline the flow of materials through the mill. This system adeptly assists in the elimination of scats—coarser materials which, if accumulated, can severely impede the milling process. The efficient removal of these materials ensures the liberation of the mill’s internal volume for active grinding, thus preventing the occupation of this critical space by materials that do not contribute to the grinding process.
The discharge system modification also reduced the occurrence of ‘dead zones’—areas within the mill characterized by markedly reduced motion of the grinding media. These zones lead to considerable torque consumption with negligible impact on particle size reduction, diminishing the mill’s operational efficiency. It was found that the presence of dead zones escalates as the ball charge in the mill exceeds 25%, potentially constituting up to 32% of the mill’s charge volume in typical overflow mills, drastically impairing the mill’s efficiency. In stark contrast, the newly designed discharge minimized the extent of such non-contributive regions. It ensures that a larger proportion of the energy input is directly channeled towards effective particle size reduction, thereby optimizing the grinding process and enhancing overall mill performance.
In comparison with conventional grate discharge designs, the new system addressed both flow-back and carry-over. By incorporating carefully engineered deflectors, it prevents slurry from directly contacting the grate apertures during evacuation, thereby eliminating particle recirculation into the mill chamber, reducing it from an estimated 10–40% to zero. Additionally, the highly curved vanes extended the timeframe for material discharge from 25% to 45% of the revolution time while reducing the vertical component of the weight force required to unbalance the system under centrifugal forces. These modifications ensured more effective evacuation of material, prevented residual carry-over, and maximized the capacity for new material in each cycle, ultimately enhancing overall mill performance as demonstrated in the experiment.
The observed results highlight the transformative potential of the new system in achieving superior operational performance. By transitioning from the overflow setup to the new system, the power draw was notably reduced by approximately 32.7%, dropping from 2214.5 kW to 1490 kW. Simultaneously, throughput experienced a significant enhancement of 24.22%, with processing rates increasing from 128 tph to 159 tph. These improvements, achieved while maintaining the desired product size distribution, underscore the effectiveness of the modifications, culminating in a dramatic reduction in specific energy consumption by 45.93%, from 17.34 kWh/t to 9.38 kWh/t.
These improvements not only demonstrate the feasibility of reducing operational costs and enhancing revenue but also suggest a paradigm shift in milling technology, where energy efficiency and productivity can be maximized simultaneously. Furthermore, the compatibility of the new discharge configuration with reduced grinding media charge reinforces the system’s operational flexibility and adaptability to various milling conditions. This highlights the superiority of grate discharge mills in transcending conventional limitations and promoting innovative, energy-efficient milling methodologies.
Looking forward, the study opens several avenues for further research and development:
- Integration of Breakage Models: The suggestion to incorporate breakage models is directly tied to the observed effects of filling charge reduction and discharge mechanisms explored in this research. By integrating these models, future studies could directly predict product size at the mill’s discharge, based not only on the main operational parameters but also on the discharge mechanism.
- Advanced Monitoring and Control Systems: The simulation exposed a significant discrepancy in slurry pooling levels, with actual measurements at 65% contrasting sharply with the 30–35% estimated by mill operators. This finding underscores the challenge of detecting issues within encapsulated equipment like ball mills, where direct observation is not feasible. To address this, the implementation of exterior sensors on the mill is proposed. Such sensors could be developed to detect slurry pooling and critical impacts (direct collisions between balls and liners above the toe of the charge), providing real-time data to plant controllers, which would allow instantaneous corrective actions on charge motion and mill chamber content.
- Sustainability and Economic Impact Assessment: Reflecting the industry’s focus on both economic and environmental KPIs, and in light of the substantial energy reductions observed in this research, it is proposed to conduct a comprehensive evaluation of the broader impacts of deploying this mill discharge configuration. The investigation could include analyzing the life cycle costs of main components (like liners, dischargers, and grinding media), energy savings in large-scale operations, and reductions in carbon emissions, thereby providing a holistic view of the benefits.
Author Contributions
W.S.S.: conceptualization, data curation, formal analysis, investigation, methodology, software, writing—original draft. N.G.: data curation, investigation, software, writing—review. E.d.S.M.: supervision, writing—review. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Due to confidentiality agreements with the partner entity, specific details regarding the datasets used in this study cannot be publicly disclosed. For access to the datasets under controlled conditions, please contact the main author directly. This measure is in place to respect the privacy request of our collaborative partner.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DEM | Discrete Element Method |
| CFD | Computational Fluid Dynamics |
| SPH | Smooth particle hydrodynamics |
| BM | Ball mill |
| AG | Autogenous mill |
| SAG | Semi-autogenous mill |
| PSD | Particle size distribution |
| HC | Hydrocyclone |
| O/F | Overflow |
| U/F | Underflow |
| GD | Grate discharge |
| RPL | Radial pulp lifting system |
| CPL | Curved pulp lifting system |
| APSD | Particle size distribution |
| tph | Tonnage per hour |
| kW | Kilowatt |
| kWh | Kilowatt-hour |
| BWI | Bond Work Index |
| DCS | Distributed Control System |
| GPU | Graphics Processing Unit |
| CPU | Central Processing Unit |
References
- Napier-Munn, T.J.; Morrell, S.; Morrison, R.D.; Kojovic, T. Mineral Comminution Circuits: Their Operation and Optimization; Julius Kruttschnitt Mineral Research Centre: Indooroopilly, Australia; The University of Queensland: Brisbane, Australia, 1996. [Google Scholar]
- Cleary, P.W.; Morrison, R.D. Prediction of 3D slurry flow within the grinding chamber and discharge from a pilot 1082 scale SAG mill. Miner. Eng. 2012, 39, 184–198. [Google Scholar] [CrossRef]
- Cleary, P.W.; Morrinson, R.D.; Sinnott, M.D. Prediction of slurry grinding due to media and coarse rock interactions 1084 in a 3D pilot SAG mill using a coupled DEM+SPH model. Miner. Eng. 2020, 157, 106614. [Google Scholar] [CrossRef]
- Tavares, L.M.; King, R.P. Modeling breakage rates of coarse particles in ball mills. Minerals Engineering 1998, 11, 235–246. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Fatehi, R.; Manzari, M.T. Error estimation in smoothed particle hydrodynamics and a new scheme for second derivatives. Comput. Math. Appl. 2011, 61, 482–498. [Google Scholar] [CrossRef]
- Libersky, L.; Petschek, A. Smooth particle hydrodynamics with strength of materials. In Advances in the Free-Lagrange Method Including Contributions on Adaptive Gridding and the Smooth Particle Hydrodynamics Method; Springer: Berlin/Heidelberg, Germany, 1991; pp. 248–257. [Google Scholar]
- Kulasegaram, S.; Bonet, J.; Lewis, R.W.; Profit, M. A variational formulation based contact algorithm for rigid boundaries in two-dimensional SPH applications. Comput. Mech. 2004, 33, 316–325. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Cole, R.; Weller, I. Underwater explosions and their application in simulations. J. Fluid Dyn. 1977, 34, 214–227. [Google Scholar]
- Potapov, A.V.; Hunt, M.L.; Campbell, C.S. Liquid-solid flows using smoothed particle hydrodynamics and the discrete element method. Powder Technol. 2001, 116, 204–213. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Fourtakas, G.; Altomare, C.; Canelas, R.B.; Tafuni, A.; García-Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.J.C.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2022, 9, 867–895. [Google Scholar] [CrossRef]
- Crespo, A.; Gomez-Gesteira, M.; Dalrymple, R. Boundary conditions generated by dynamic particles in SPH methods. CMC Comp. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- English, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J.C.; Stansby, P.K.; Lind, S.J.; Chiapponi, L.; Gómez-Gesteira, M. Modified dynamic boundary conditions (mDBC) for general-purpose smoothed particle hydrodynamics (SPH): Application to tank sloshing, dam break and fish pass problems. Comput. Part. Mech. 2022, 9, 911–925. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C. (Eds.) Molecular Dynamics: With Deterministic and Stochastic Numerical Methods; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–51. [Google Scholar]
- Parshikov, A.; Medin, S.; Loukashenko, I.; Milekhin, V. Improvements in SPH method by means of interparticle contact algorithm and analysis of perforation tests at moderate projectile velocities. Int. J. Impact Eng. 2000, 24, 779–796. [Google Scholar] [CrossRef]
- Monaghan, J.; Kos, A. Solitary waves on a Cretan beach, J. Waterway Port Coast. Ocean Eng. Asce. 1999, 125, 145–154. [Google Scholar]
- Xie, F.; Zhao, W.; Wan, D. MPS-DEM coupling method for interaction between fluid and thin elastic structures. Ocean Eng. 2021, 236, 109449. [Google Scholar] [CrossRef]
- Govender, N. Study on the effect of grain morphology on shear strength in granular materials via GPU based discrete element method simulations. Powder Technol. 2021, 387, 336–347. [Google Scholar] [CrossRef]
- Kildashti, K.; Dong, K.; Samali, B.; Zheng, Q.; Yu, A. Evaluation of contact force models for discrete modelling of ellipsoidal particles, Chem. Eng. Sci. 2018, 177, 1–17. [Google Scholar] [CrossRef]
- Liu, L.; Wu, J.; Ji, S. DEM-SPH coupling method for the interaction between irregularly shaped granular materials and fluids. Powder Technol. 2022, 400, 117249. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, G.; Huang, D.; Jin, F. A resolved CFD-DEM coupling model for modeling two-phase fluids interaction with irregularly shaped particles. J. Comput. Phys. 2022, 448, 110695. [Google Scholar] [CrossRef]
- Govender, N.; Rajamani, R.; Kok, S.; Wilke, D. Discrete element simulation of mill charge in 3D using the BLAZE-DEM GPU framework. Miner. Eng. 2015, 79, 152–168. [Google Scholar] [CrossRef]
- Govender, N. A DEM study on the thermal conduction of granular material in a rotating drum using polyhedral particles on GPUs. Chem. Eng. Sci. 2022, 252, 117491. [Google Scholar] [CrossRef]
- Smeets, B.; Odenthal, T.; Vanmaercke, S.; Ramon, H. Polygon-based contact description for modeling arbitrary polyhedra in the discrete element method. Comput. Methods Appl. Mech. Eng. 2015, 290, 277–289. [Google Scholar] [CrossRef]
- Venugopal, R. 3D simulation of charge motion in tumbling mills by the discrete. Powder Technol. 2001, 115, 157–166. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.; Wu, C.-Y.; Rajamani, R.; Khinast, J.; Glasser, B. Large-scale GPU based DEM modeling of mixing using irregularly shaped particles. Adv. Powder Techol. 2018, 29, 2476–2490. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.; Pizette, P.; Abriak, N. A study of shape non-uniformity and poly-dispersity in hopper discharge of spherical and polyhedral particle systems using the Blaze-DEM GPU code. Appl. Math. Comput. 2018, 319, 318–336. [Google Scholar] [CrossRef]
- Cleary, P.W.; Cummins, S.J.; Sinnott, M.D. Advanced comminution modelling: Part 2-Mills. Appl. Math. Model. 2020, 89, 640–670. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.; Morrison, R. Prediction of slurry transport in SAG mills using SPH fluid flow in a dynamic DEM based porous media. Miner. Eng. 2006, 19, 1517–1527. [Google Scholar] [CrossRef]
- Capece, M.; Bilgili, E.; Dave, R. Insight into first-order breakage kinetics using a particle-scale breakage rate constant. Chem. Eng. Sci. 2014, 117, 318–330. [Google Scholar] [CrossRef]
- Morrell, S. Power draw of wet tumbling mills and its relationship to charge dynamics—Part 1: A continuum approach to mathematical modelling of mill power draw. Trans. Inst. Min. Metall. Sect. C Miner. Process. Extr. Metall. 1996, 105, A9–A14. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).