Insights on Prioritization Methods for Mining Exploration Areas: A Case Study of the Tiltil Mining District, Chile
Abstract
1. Introduction
2. Methodological Developments
2.1. Introduction to Multivariate Decision-Making Methods
2.2. Methodology for the Selection of MCDMs
2.3. AHP Method
2.4. PROMETHEE II Method
3. Methodology and Data
3.1. Characterization of the Study Area: The Tiltil Mining District
3.2. Inputs for the Selection of MCDMs
3.3. Inputs for the Prioritization of Mining Prospects
4. Results
4.1. Characterization of the Study Area and Database for the Prioritization Processes
4.2. Selection of MCDMs
4.3. Hierarchical Structure and Performance Matrix for the Prioritization of Exploration Projects
4.4. Prioritization Using AHP and PROMETHEE II
5. Discussion
5.1. Correlation between Results from Different MCDMs
5.2. Sensitivity Analysis for Expert Weights
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Fundamental Scale of Comparison between Pairs [32]
| Importance Index | |
| Value | Meaning |
| 1 | j and k are equally important |
| 3 | j is slightly more important than k |
| 5 | j is more important than k |
| 7 | j is considerably more important than k |
| 9 | j is much more important than k |
| 2,4,6,8 | Intermediate values |
Appendix A.2. Type Sheet Used to Collect Information
| New “Geomining” Strategies for the Development and Improvement of Skills of Small Mining |
| Information |
| Name: |
| Owner name: |
| Mines and/or mining property: |
| Phone: |
| Email: |
| Do you consider that you have relevant information for the project (indicate which ones): |
| Additional comments on exploitation and/or mining exploration of your mining property: |
Appendix A.3. Cadaster of Mines
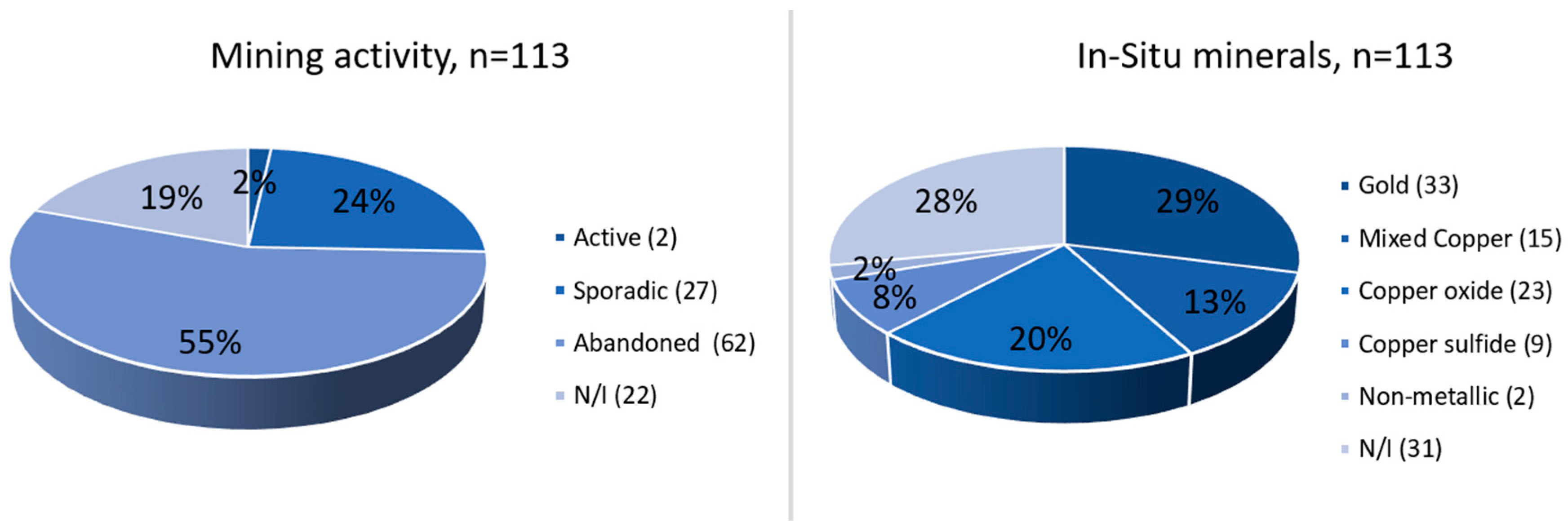
| Mine | San Aurelio | El Huracán | Lophan-Lujan | Condor | La Poza | La Despreciada | Valdi | San Jorge | Mogote | La Vaca | Los Guindos |
| WGS 284-East | 316,977 | 320,101 | 316,748 | 314,978 | 316,749 | 315,610 | 316,531 | 314,821 | 317,734 | 314,241 | 315,771 |
| WGS 284-North | 6,336,158 | 6,343,596 | 6,332,811 | 6,319,635 | 6,334,856 | 6,319,831 | 6,336,270 | 6,336,439 | 6,332,487 | 6,335,825 | 6,338,582 |
| WGS 284-AMSL | 784 | 653 | 857 | 1594 | 820 | 1211 | 860 | 963 | 925 | 1093 | 913 |
| Lithology | Amphibole Diorite to Quartzite Monzodiorite | Amphibole Granodiorite to Quartziferous Monzonite | Veta Negra Formation and dacitic porphyry dikes | Veta Negra Formation | Las Chilcas Formation | Veta Negra Formation and Amphibole Diorite to Quartzite Monzodiorite | Amphibole Diorite to Quartzite Monzodiorite | Amphibole Monzonite | Las Chilcas Formation | Veta Negra Formation | Las Chilcas Formation and Amphibole Diorite to Quartzite Monzodiorite |
| Mineralization | Cu Sulphides and Oxides | Au and Cu Sulphides and Oxides | Cu Sulphides and Oxides | Cu Sulphides and Oxides | Cu Sulphides and Oxides | Au and Cu Sulphides and Oxides | Cu Sulphides and Oxides | Au and Cu Sulphides and Oxides | Cu Sulphides and Oxides | Au and Cu Sulphides and Oxides | Au and Cu Sulphides and Oxides |
| Alteration | Potassic and Sericitic | Potassic and Sericitic | Potassic, Sericitic and Propylitic | Propylitic | Sericitic and Propylitic | Potassic and Propylitic | Sericitic and Propylitic | Sericitic and Propylitic | Propylitic | Sericitic and Propylitic | Sericitic and Propylitic |
| Activity | Sporadic | Sporadic | Sporadic | Sporadic | Sporadic | Sporadic | Inactive | Sporadic | Inactive | Inactive | Sporadic |
| Method | Open Pit-Underground | Underground | Open Pit | Underground | Open Pit-Underground | Underground | Open Pit-Underground | Underground | Underground | Underground | Underground |
| Main Ore | Cu Oxide and Sulphides | Gold | Cu Oxide and Sulphides | Cu Oxide | Cu Oxide and Sulphides | Cu Oxide and Sulphides | Cu Oxide | Gold | Cu Sulphides | Gold | Gold |
| Secondary Ore | Gold-Silver | Copper-Silver | - | - | - | Gold | - | Copper | - | Copper | Copper |
| Rock Element Anomalies | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization | With economic anomaly and without penalization |
| Element anomalies in sediment o others | No Sample | No Sample | No Sample | No Sample | No Sample | No Sample | No Sample | No Sample | No Sample | No Sample | No Sample |
| Resistivity Anomaly | Weak anomaly | Weak anomaly | No information | Weak anomaly | No information | No information | No information | No information | No information | No information | No information |
| Chargeability Anomaly | Weak anomaly | Weak anomaly | No information | Weak anomaly | No information | No information | No information | No information | No information | No information | No information |
| Magnetic Anomaly | Weak anomaly | No information | No information | No information | No information | No information | No information | No information | No information | No information | No information |
| Water resources | Underground water | Without Water | No information | Underground water | Without Water | Underground water | Without Water | Underground water | No information | No information | Underground water |
| Geography | Hillside | Hillside | Hillside | Hillside | Hillside | Hillside | Hillside | Hillside | Hillside | Hillside | Hillside |
| Weather | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean | Mediterranean |
| Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna | Unprotected Flora and Fauna |
| Land Use | Mining | Mining | Mining | Mining | Mining | Mining | Mining | Mining | Mining | Mining | Mining |
| Local Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities | Nearby Mixed Communities |
| Availability of Goods and Services (Water, Energy) | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services | Availability of Goods and Services |
| Access | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements | With Accesses and Easements |
| Resources | No information | 100 kTon–1 Mton | No information | No information | No information | No information | No information | No information | No information | No information | No information |
| Cu- Soluble Equivalent grade | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq | Less than 2.5% of Cu-eq | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq | Less than 2.5% of Cu-eq | 2.5–4.2% of Cu-eq | No information | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq |
| Cu-Insoluble Equivalent grade | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq | No information | No information | No information | 2.5–4.2% of Cu-eq | No information | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq | 2.5–4.2% of Cu-eq |
| Mining Property | Owner Company | Owner Company | Owner Company | Tenant Company | Tenant Company | Owner Company | Tenant Company | Tenant Company | Non-Owner Company | Tenant Company | Tenant Company |
Appendix A.4. Features of Endogenous Variables (from Guarini et al. [26,27,44])
| Type of Decision-Making Problems | Solution Approach | Implementation Procedure | Input Level | Output Typology | Decision Problem Solution | Tool |
| Sorting/Description | Outranking approach | Preference thresholds, indifference thresholds, veto thresholds | Medium | Partial ordering obtained by expressing pairwise preferences degrees | n categories of alternatives of equal score but different behavior | ELECTRE |
| Ranking/Choice | Full aggregation approach | Utility function | High | Full ordering obtained by considering the scores | Alternative with the higher global score | MAUT |
| Pairwise comparison on rational scale and interdependencies | High | Full ordering obtained by considering the scores | Alternative with the higher global score | ANP | ||
| Pairwise comparison on interval scale | High | Full ordering obtained by considering the scores | Alternative with the higher global score | MACBETH | ||
| Pairwise comparison on rational scale | Low | Full ordering obtained by considering the scores | Alternative with the higher global score | AHP | ||
| Goal, aspiration, or reference level approach | Ideal option and anti-ideal option | Low | Full ordering with score closest to the aim assumed | Alternative with the closest score to the ideal solution | TOPSIS | |
| Outranking approach | Preference thresholds, indifference thresholds, veto thresholds | Medium | Partial ordering obtained by expressing pairwise preference degrees | n categories of alternatives of equal score but different behavior | ELECTRE | |
| Preference thresholds, indifference thresholds, veto thresholds | Total ordering obtained by expressing pairwise preferences degrees | Alternative with the higher global score | ||||
| Preference thresholds, indifference thresholds | Medium | Partial ordering obtained by expressing pairwise preferences degrees | n categories of alternatives of equal score but different behavior | PROMETHEE | ||
| Preference thresholds, indifference thresholds | Total ordering obtained by expressing pairwise preferences degrees | Alternative with the higher global score |
Appendix A.5. Features of Exogenous Variables (from Guarini et al. [26,27,44])
| Technical Support of A Specialist | Number of Evaluation Elements | Typology of Indicators | Expected Solution | Stakeholders to Be Included in the Decision Process | Tool |
| Yes | Limited number of criteria and sub-criteria and a small number of alternatives | Quantitative | Definition of n alternatives valid in relation to the objectives | Participatory process not activated | ELECTRE |
| Limited number of criteria and sub-criteria and a large number of alternatives | Qualitative | A better overall alternative definition for the purpose. The ideal alternative definition closest to the lens | Participatory process activated with a limited and specialized number of stakeholders | MAUT | |
| No | Large number of criteria and sub-criteria and a small number of alternatives | Mixed | A better overall alternative definition for the purpose. The ideal alternative definition closest to the lens | Participatory process activated with a significant number of stakeholders, preferably organized in categories | AHP; ANP |
| Large number of criteria and sub-criteria and a large number of alternatives | MACBETH; PROMETHEE; TOPSIS |
Appendix A.6. Binary Matrix (Tn)
| Type of Variables | Variables | Qualification of Variables | Properties of MCDA Tools in Binary System (P) | ||||||
| ELECTRE | MAUT | ANP | MACBETH | AHP | TOPSIS | PROMETHEE II | |||
| Exogenous | Number of evaluation elements | Limited number of criteria and sub-criteria and a small number of alternatives | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Limited number of criteria and sub-criteria and a large number of alternatives | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| Large number of criteria and sub-criteria and a small number of alternatives | 0 | 0 | 1 | 0 | 1 | 0 | 0 | ||
| Large number of criteria and sub-criteria and a large number of alternatives | 0 | 0 | 0 | 1 | 0 | 1 | 1 | ||
| Typology of indicators | Quantitative | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Qualitative | 1 | 0 | 1 | 1 | 1 | 1 | 1 | ||
| Mixed | 1 | 0 | 1 | 1 | 1 | 1 | 1 | ||
| Stakeholders to be included in the decision process | Participatory process not activated | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Participatory process with a limited and specialized number of stakeholders | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Participatory process with a significant number of stakeholders preferably organized in categories | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Expected solution | Definition of n alternatives valid in relation to objectives | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |
| A better overall alternative definition for the purpose | 0 | 1 | 1 | 1 | 1 | 0 | 1 | ||
| The ideal alternative definition closest to the lens | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| Technical support of a decision aid specialist | Yes (advisable) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| No (not necessary) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| Endogenous | Type of decision-making problems | Sorting | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Description | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Ranking/Choice | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Solution approach | Outranking approach | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| Full aggregation approach | 0 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| Goal, aspiration, or reference level Approach | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| Implementation procedure | Preference thresholds, indifference thresholds, veto thresholds | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Preference thresholds, indifference thresholds | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| Utility function | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| Pairwise comparison on rational scale and interdependencies | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||
| Pairwise comparison on interval scale | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| Pairwise comparison on rational scale | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| Ideal option and anti-ideal option | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| Input level | High | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| Medium | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| Low | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| Output typology | Partial ordering obtained by expressing pairwise preferences degrees | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| Total ordering obtained by expressing pairwise preferences degrees | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| Full ordering obtained by considering the scores | 0 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| Full ordering with score closest to the aim assumed | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| Decision problem solution | n categories of alternatives of equal score but different behavior | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| Alternative with the higher global score | 0 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| Alternative with the closest score to the ideal solution | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
Appendix A.7. Assigning the Properties of the MCDMs
| Type ofVariable | Weight (Wn) | Variables (Vn) | Qualification of Variables (Qn) | Properties in Relation to Decision-Making Problem (Ep) | Properties of the MCDA Tool in Binary System (SRW = EP × Tn × Wn) | ||||||
| ELECTRE | MAUT | ANP | MACBETH | AHP | TOPSIS | PROMETHEE | |||||
| Exogenous | 1.00 | Number of evaluation elements | Limited number of criteria and sub-criteria and a small number of alternatives | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Limited number of criteria and sub-criteria and a large number of alternatives | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Large number of criteria and sub-criteria and a small number of alternatives | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Large number of criteria and sub-criteria and a large number of alternatives | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |||
| 1.00 | Typology of indicators | Quantitative | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Qualitative | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Mixed | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |||
| 1.00 | Stakeholders to be included in the decision process | Participatory process not activated | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Participatory process with a limited and specialized number of stakeholders | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| Participatory process with a significant number of stakeholders preferably organized in categories | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.00 | Expected solution | Definition of n alternatives valid in relation to objectives | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |
| A better overall alternative definition for the purpose | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |||
| The ideal alternative definition closest to the lens | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.00 | Technical support of a decision aid specialist | Yes (advisable) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| No (not necessary) | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||
| Endogenous | 1.00 | Type of decision-making problems | Sorting | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Description | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Ranking/Choice | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| 1.00 | Solution approach | Outranking approach | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| Full aggregation approach | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||
| Goal, aspiration, or reference level approach | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.00 | Implementation procedure | Preference thresholds, indifference thresholds, veto thresholds | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Preference thresholds, indifference thresholds | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| Utility function | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| Pairwise comparison on rational scale and interdependencies | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |||
| Pairwise comparison on interval scale | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |||
| Pairwise comparison on rational scale | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |||
| Ideal option and anti-ideal option | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.00 | Input level | High | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| Medium | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Low | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.00 | Output typology | Partial ordering obtained by expressing pairwise preferences degrees | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| Total ordering obtained by expressing pairwise preferences degrees | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| Full ordering obtained by considering the scores | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||
| Full ordering with score closest to the aim assumed | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.00 | Decision problem solution | n categories of alternatives of equal score but different behavior | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Alternative with the higher global score | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||
| Alternative with the closest score to the ideal solution | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
Appendix A.8. Ranges Assigned to Qualitative Variables
| Variable | Alternative 1 | Alternative 2 | Alternative 3 | Alternative 4 | Alternative 5 | Alternative 6 | Alternative 7 | Alternative 8 |
| Lithology | Covered Area (without outcrops) with Unknown Power | Covered Area (without outcrops) with less potential resource at critical depth | Covered Area (without outcrops) with higher potential resource at critical depth | Uncovered or partially uncovered area (with outcrops) with unfavorable main rock | Uncovered or partially uncovered area (with outcrops) with favorable main rock | Uncovered or partially uncovered area (with outcrops) with main rock and unfavorable intrusive | Uncovered or partially uncovered area (with outcrops) with favorable main rock and intrusive | |
| Alteration/Mineralization | No evidence of alteration or mineralization | No alteration or mineralization | Small to moderate areas with magmatic-hydrothermal alteration and without mineralization | Small to moderate zones with magmatic-hydrothermal and mineralized alteration | Large areas with magmatic-hydrothermal alteration and without mineralization | Large areas with magmatic-hydrothermal alteration and without mineralization | ||
| Structures | No evidence of structures | Without Structures | Small to moderate structures without alteration or mineralization | Small to moderate structure with alteration and without mineralization | Small to moderate structure with alteration and mineralization | Large structures without alteration or mineralization | Large structures with alteration and without mineralization | Large structures with alteration and mineralization |
| Rock elemental anomaly | No Sample | No anomaly | With economic anomaly | With economic and penalized anomaly | With main element anomaly | |||
| Anomaly of elements in sediment or others | No Sample | No anomaly | With economic anomaly | With economic and penalized anomaly | With main element anomaly | |||
| Resistivity anomaly | No information | Does not present anomaly | Weak anomaly | Strong anomaly | ||||
| Chargeability anomaly | No information | Does not present anomaly | Weak anomaly | Strong anomaly | ||||
| Magnetic anomaly | No information | Does not present anomaly | Weak anomaly | Strong anomaly | ||||
| Water resources | No Information | No Water | Groundwater | Surface and Groundwater | ||||
| Geography | Flat surface | River valley | Glacier valley | Hillside | Mountain hillside | Beach shore | ||
| Weather | Arid-semiarid | Mediterranean | Temperate-rainy cold | Steppe to tundra | Mountain | |||
| Flora and fauna | Unprotected flora and fauna | Flora protected | Fauna protected | Flora and fauna protected | ||||
| Land use | Mining | Agricultural-Livestock-Forestry | Fiscal land | Residential land | Protected area | |||
| Local communities | On-site communities | Nearby mining communities | Nearby mixed communities | Nearby non-mining communities | It has no nearby communities | |||
| Availability of goods/services (water, energy, roads, etc.) | Availability of goods and services | Availability of goods | Availability of services | Unavailable | ||||
| Access | Without access | With access | With access and easement | |||||
| Mining property | Owner company | Leasing company | Non-owner company | Not incorporated (free) |
Appendix A.9. Performance Matrix Valued for Exploration Projects
| cd | Sub Criteria | El Huracán Mine | Valdi Mine | San Aurelio Mine | Los Guindos Mine | San Jorge Mine | La Vaca Mine | La Poza Mine | Mogote Mine | Lophan-Lujan Mine | Cóndor Mine | La Despreciada Mine |
| Geology | Lithology | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 7 | 1 | 7 | 1 |
| Alteration/Mineralization | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| Structures | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 9 | |
| Geochemistry | Rock Element Anomalies | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| Element anomalies in sediment or others | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| Geophysics | Resistivity Anomaly | 5 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 4 |
| Chargeability Anomaly | 5 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 4 | |
| Magnetic Anomaly | 4 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| Environmental | Water Resources | 9 | 9 | 2 | 2 | 2 | 4 | 9 | 4 | 4 | 2 | 2 |
| Geography | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| Weather | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| Flora and Fauna | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| Social | Land Uses | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| Local communities | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| Availability of Goods and Services (Water, Energy, etc.) | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| Access | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| Economical | Resources | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Cu Soluble grades | 5 | 1 | 5 | 5 | 5 | 5 | 5 | 3 | 1 | 5 | 5 | |
| Cu-eq Insoluble grades | 5 | 3 | 5 | 5 | 5 | 5 | 3 | 5 | 3 | 3 | 5 | |
| Mining Property | 9 | 5 | 9 | 5 | 5 | 5 | 5 | 0 | 9 | 5 | 9 |
Appendix A.10. Weights of the Criteria and Sub-Criteria of the Tiltil Mining District Using AHP
| Criteria | Criteria Weight (%) | Sub Criteria | Global Weights (%) |
| Geology | 19.8% | Lithology | 2.5% |
| Alteration/Mineralization | 9.9% | ||
| Structures | 7.4% | ||
| Geochemistry | 12.4% | Rock Element Anomalies | 9.3% |
| Element anomalies in sediment or others | 3.1% | ||
| Geophysics | 5.8% | Resistivity Anomaly | 1.6% |
| Chargeability Anomaly | 2.7% | ||
| Magnetic Anomaly | 1.5% | ||
| Environmental | 18.6% | Water Resources | 6.9% |
| Geography | 3.1% | ||
| Weather | 2.1% | ||
| Flora and Fauna | 6.6% | ||
| Social | 19.4% | Land Uses | 4.4% |
| Local communities | 9.2% | ||
| Availability of Goods and Services (Water, Energy, etc.) | 3.3% | ||
| Access | 2.5% | ||
| Economical | 24.0% | Resources | 4.3% |
| Cu Soluble grades | 7.1% | ||
| Cu-Eq Insoluble grades | 4.4% | ||
| Mining property | 8.2% |
References
- Abedi, M.; Torabi, S.A.; Norouzi, G.H.; Hamzeh, M.; Elyasi, G. PROMETHEE II: A Knowledge-Driven Method for Copper Exploration. Comput. Geosci. 2012, 46, 255–263. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.; Hamzeh, M. Fuzzy Outranking Approach: A Knowledge-Driven Method for Mineral Prospectivity Mapping. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 556–567. [Google Scholar] [CrossRef]
- Abedi, M.; Torabi, S.A.; Norouzi, G.H. Application of Fuzzy AHP Method to Integrate Geophysical Data in a Prospect Scale, a Case Study: Seridune Copper Deposit. Boll. Geofis. Teor. Appl. 2012, 54, 145–164. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modeling with GIS; Pergamon Press: Oxford, UK, 1994. [Google Scholar]
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- McCuaig, T.C.; Hronsky, J.M. The Mineral System Concept: The Key to Exploration Targeting. Soc. Econ. Geol. Spec. Pub. 2014, 18, 153–175. [Google Scholar] [CrossRef]
- Wood, D.; Hedenquist, J. Mineral Exploration: Discovering and Defining Ore Deposits. SEG Discov. 2019, 116, 1–22. [Google Scholar] [CrossRef]
- Costa e Silva, E.; Silva, A.M.; Benfica Toledo, C.I.; Mol, A.G.; Otterman, D.W.; Cortez de Souza, S.R. Mineral Potential Mapping for Orogenic Gold Deposits in the Rio Maria Granite Greenstone Terrane, Southeastern Pará State, Brazil. Econ. Geol. 2012, 107, 1387–1402. [Google Scholar] [CrossRef]
- Hagag, A.M.; Yousef, L.S.; Abdelmaguid, T.F. Multi-Criteria Decision-Making for Machine Selection in Manufacturing and Construction: Recent Trends. Mathematics 2023, 11, 631. [Google Scholar] [CrossRef]
- Mergias, I.; Moustakas, K.; Papadopoulos, A.; Loizidou, M. Multi-Criteria Decision Aid Approach for the Selection of the Best Compromise Management Scheme for ELVs: The Case of Cyprus. J. Hazard. Mater. 2007, 147, 706–717. [Google Scholar] [CrossRef]
- Wu, J.; Huang, H.; Cao, Q. Research on AHP with Interval-Valued Intuitionistic Fuzzy Sets and Its Application in Multi-Criteria Decision-Making Problems. Appl. Math. Model. 2013, 37, 9898–9909. [Google Scholar] [CrossRef]
- Huang, I.B.; Keisler, J.; Linkov, I. Multi-Criteria Decision Analysis in Environmental Sciences: Ten Years of Applications and Trends. Sci. Total Environ. 2011, 409, 3578–3594. [Google Scholar] [CrossRef]
- Mendoza, G.A.; Martins, H. Multi-Criteria Decision Analysis in Natural Resource Management: A Critical Review of Methods and New Modelling Paradigms. For. Ecol. Manag. 2006, 230, 1–22. [Google Scholar] [CrossRef]
- Paraskevis, N.; Roumpos, C.; Stathopoulos, N.; Adam, A. Spatial Analysis and Evaluation of a Coal Deposit by Coupling AHP & GIS Techniques. Int. J. Min. Sci. Technol. 2019, 29, 943–953. [Google Scholar]
- Pirdashti, M.; Tavana, M.; Hassim, M.H.; Behzadian, M.; Karimi, I. A Taxonomy and Review of the Multiple Criteria Deci-sion-Making Literature in Chemical Engineering. Int. J. Multicrit. Decis. Mak. 2011, 1, 407–467. [Google Scholar]
- Rahimdel, M.J.; Ataei, M. Application of Analytical Hierarchy Process to Selection of Primary Crusher. Int. J. Min. Sci. Technol. 2014, 24, 519–523. [Google Scholar] [CrossRef]
- Rahimdel, M.J. Selection of the Most Proper Underground Mining Method for Kodakan Gold Mine in Iran. Rud.-Geol.-Naft. Zb. 2023, 38, 135–145. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antuchevičienė, J.; Kapliński, O. Multi-Criteria Decision Making in Civil Engineering: Part I—A State-of-the-Art Survey. Eng. Struct. Technol. 2015, 7, 103–113. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antuchevičienė, J.; Kapliński, O. Multi-Criteria Decision Making in Civil Engineering. Part II—Applications. Eng. Struct. Technol. 2015, 7, 151–167. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Sadeghi, M.; Billay, A. Predictive Mapping of Prospectivity for Orogenic Gold, Giyani Green-Stone Belt (South Africa). Ore Geol. Rev. 2015, 71, 703–718. [Google Scholar] [CrossRef]
- Jara, J.J.; Moreno, F.; Jara, R.; Dubournais, F.; Mata, R.; Peters, D.; Marquardt, C.; Lagos, G. Ranking of Placer Gold Prospects in Chile Trough Analytic Hierarchy Process. Nat. Resour. Res. 2018, 28, 813–832. [Google Scholar] [CrossRef]
- Oskouei, M.M.; Soltani, F. Mapping of Potential Cu and Au Mineralization Using EBF Method. Appl. Geomat. 2017, 9, 13–25. [Google Scholar] [CrossRef]
- Rakhmangulov, A.; Burmistrov, K.; Osintsev, N. Multi-Criteria System’s Design Methodology for Selecting Open Pits Dump Trucks. Sustainability 2024, 16, 863. [Google Scholar] [CrossRef]
- Sitorus, F.; Cilliers, J.J.; Brito-Parada, P.R. Multi-Criteria Decision Making for the Choice Problem in Mining and Mineral Pro-cessing: Applications and Trends. Expert Syst. Appl. 2019, 121, 393–417. [Google Scholar] [CrossRef]
- Yalcin, M.; Gul, F. A GIS-Based Multi-Criteria Decision Analysis Approach for Exploring Geothermal Resources: Akarcay Basin (Afyonkarahisar). Geothermics 2017, 67, 18–28. [Google Scholar] [CrossRef]
- Guarini, M.R.; D’Addabbo, N.; Morano, P.; Tajani, F. Multi-Criteria Analysis in Compound Decision Processes: The AHP and the Architectural Competition for the Chamber of Deputies in Rome (Italy). Buildings 2017, 7, 38. [Google Scholar] [CrossRef]
- Guarini, M.R.; Battisti, F.; Chiovitti, A. Public Initiatives of Settlement Transformation: A Theoretical-Methodological Approach to Selecting Toolsto Selecting Tools of Multi-Criteria Decision Analysis. Buildings 2017, 8, 1. [Google Scholar] [CrossRef]
- Guitouni, A.; Martel, J.M. Tentative Guidelines to Help Choosing an Appropriate MCDA Method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Haddad, M.; Sanders, D. Selection of Discrete Multiple Criteria Decision-Making Methods in the Presence of Risk and Un-certainty. Oper. Res. Perspect. 2018, 5, 357–370. [Google Scholar]
- Aquino, R.Q.; Zúñiga, F.F.G.; Malone, A. Soil and Urine Mercury Levels in Secocha: A Case Study of Artisanal and Small-Scale Gold Mining in Peru. Mining 2024, 4, 22. [Google Scholar] [CrossRef]
- Faúndez, P.I.; Marquardt, C.; Jara, J.J.; Guzmán, J.I. Valuation and Prioritization of Early-Stage Exploration Projects: A Case Study of Cu–Ag and Au-Mineralized Systems in the Tiltil Mining District, Chile. Nat. Resour. Res. 2020, 29, 2989–3014. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Processes; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Springer Science + Business Media, LLC: New York, NY, USA, 2001. [Google Scholar]
- Saaty, T.L. Fundamentals of the Analytic Network Process-Dependence and Feedback in Decision-Making with a Single Network. J. Syst. Sci. Syst. Eng. 2004, 13, 129–157. [Google Scholar] [CrossRef]
- Dyer, J.S. MAUT—Multiattribute Utility Theory. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer: New York, NY, USA, 2005; pp. 265–292. [Google Scholar]
- Bana e Costa, C.A.; Chagas, M.P. A Career Choice Problem: An Example of How to Use MACBETH to Build a Quantitative Value Model Based on Qualitative Value Judgments. Eur. J. Oper. Res. 2004, 153, 323–331. [Google Scholar] [CrossRef]
- Brans, J.P. L’Ingénierie de la Décision; Élaboration d’Instruments d’Aide à la Décision: La Méthode PROMETHEE. In L’Aide à la Décision: Nature, Instruments et Perspectives d’Avenir; Nadeau, R., Landry, M., Eds.; Presses de l’Université Laval: Québec, QC, Canada, 1982; pp. 183–214. [Google Scholar]
- Brans, J.P.; Vincke, P.; Mareschal, B. How to Select and How to Rank Projects: The PROMETHEE Method. Eur. J. Oper. Res. 1986, 24, 228–238. [Google Scholar] [CrossRef]
- Benayoun, R.; Roy, B.; Sussman, N. ELECTRE: Une Méthode Pour Guider le Choix en Présence de Points de Vue Multiples. Rep. SEMA-METRA. Int. Dir. Sci. 1966, 49, 2–120. [Google Scholar]
- Roy, B. Multicriteria Methodology for Decision Aiding; Springer Science + Business Media LLC: New York, NY, USA, 1996. [Google Scholar]
- Dias, L.C.; Morton, A.; Quigley, J. Elicitation—The Science and Art of Structuring Judgement; Springer: New York, NY, USA, 2018. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Opricovic, S.; Tzeng, G. Compromise Solution by MCDM Methods: A Comparative Analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Guarini, M.R.; Battisti, F.; Chiovitti, A. A Methodology for the Selection of Multi-Criteria Decision Analysis Methods in Real Estate and Land Management Processes. Sustainability 2018, 10, 507. [Google Scholar] [CrossRef]
- Ishizaka, A.; Siraj, S. Are Multi-Criteria Decision-Making Tools Useful? An Experimental Comparative Study of Three Methods. Eur. J. Oper. Res. 2018, 264, 462–471. [Google Scholar] [CrossRef]
- Kornyshova, E.; Salinesi, C. MCDM Techniques Selection Approaches: State of the Art. In Proceedings of the IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Honolulu, HI, USA, 1–5 April 2007; pp. 22–29. [Google Scholar]
- Ozernoy, V.M. Choosing the “Best” Multiple Criteria Decision-Making Method. INFOR 1992, 30, 159–171. [Google Scholar]
- Saaty, T.L.; Ergu, D. When is a Decision-Making Method Trustworthy? Criteria for Evaluating Multi-Criteria. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 1171–1187. [Google Scholar] [CrossRef]
- Pazand, K.; Hezarkhani, A.; Ataei, M.; Ghanbari, Y. Combining AHP with GIS for Predictive Cu Porphyry Potential Mapping: A Case Study in Ahar Area (NW, Iran). Nat. Resour. Res. 2011, 20, 251–262. [Google Scholar] [CrossRef]
- Partovi, F.Y.; Hopton, W.E. The Analytic Hierarchy Process as Applied to Two Types of Inventory Problems. Prod. Invent. Manag. J. 1994, 35, 13–19. [Google Scholar]
- Abedi, M.; Norouzi, G. Integration of various geophysical data with geological and geochemical data to determine additional drilling for copper exploration. J. Appl. Geophys. 2012, 83, 72–79. [Google Scholar] [CrossRef]
- Asadi, H.H.; Sansoleimani, A.; Fatehi, M.; Carranza, E.J.M. An AHP-TOPSIS Predictive Model for District-Scale Mapping of Porphyry Cu–Au Potential: A Case Study from Salafchegan Area (Central Iran). Nat. Resour. Res. 2016, 25, 417–429. [Google Scholar] [CrossRef]
- Sharma, A.; Gurjeet-Bansal, J. A Comparative Analysis of Promethee, AHP and Topsis Aiding in Financial Analysis of Firm Performance. Proc. First Int. Conf. Inf. Technol. Knowl. Manag. 2018, 14, 145–150. [Google Scholar]
- Brans, J.P.; Vincke, P. A Preference Ranking Organisation Method: (The PROMETHEE Method for Multiple Criteria Deci-sion-Making). Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Piquer, J.; Hermosilla, J.; Oyarzún, N.; Cuadra, P.; Floody, R.; Troncoso, L.; Pardo, R. Geology and Structural Evolution of the La Huifa Ore Deposit, Central Chile: A Newly Discovered Porphyry Cu-Mo System in the El Teniente District. Econ. Geol. 2023, 118, 371–390. [Google Scholar] [CrossRef]
- Cabello, J. Antecedentes Preliminares del Proyecto Tiltil-Rungue-Montenegro; Empresa Nacional de Minería: Santiago, Chile, 1977. [Google Scholar]
- Cuadra, W.; Arenas, M. De Margamarga a Colliguay: Minería Aurífera Colonial en Santiago de la Nueva Extremadura; Ediciones MSP-Consultores: Santiago, Chile, 2013. [Google Scholar]
- Guerrero, R. La Pequeña Minería en la Zona de la Cordillera de la Costa de la Provincia de Santiago. Unpublished Thesis, Universidad de Chile, Santiago, Chile, 1959. [Google Scholar]
- SERNAGEOMIN. Atlas de Faenas Mineras, Regiones de Valparaíso, del Libertador General Bernardo O’Higgins y Metropolitana de Santiago; Servicio Nacional de Geología y Minería: Santiago, Chile, 2012.
- Zeballos, J. Programa de Estudios Distritales: Informe Geológico Distrito Minero Tiltil; Empresa Nacional de Minería de Chile: Santiago, Chile, 2007. [Google Scholar]
- Boyce, D.; Charrier, R.; Farías, M. The First Andean Compressive Tectonic Phase: Sedimentologic and Structural Analysis of Mid-Cretaceous Deposits in the Coastal Cordillera, Central Chile (32°50′ S). Tectonics 2020, 39, e2019TC005825. [Google Scholar] [CrossRef]
- Thomas, H. Geología de la Cordillera de la Costa Entre el Valle de La Ligua y la Cuesta de Barriga; Instituto de Investigaciones Geológicas: Santiago, Chile, 1958.
- Wall, R.; Sellés, D.; Gana, P. Mapas Geológicos n°11 Área Tiltil, Santiago; Servicio Nacional de Geología y Minería: Santiago, Chile, 1999.
- Gana, P.; Zenttilli, M. Historia Termal y Exhumación de Intrusivos de la Cordillera de la Costa de Chile Central. In Congreso Geológico Chileno; Sociedad Geológica de Chile: Santiago, Chile, 2000; pp. 664–668. [Google Scholar]
- Bogdanovic, D.; Nikolic, D.; Ilic, I. Mining Method Selection by Integrated AHP and PROMETHEE Method. Anais Acad. Bras. Ciênc. 2012, 84, 219–233. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy and Analytic Network Processes for the Measurement of Intangible Criteria and for Deci-sion-Making. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer: New York, NY, USA, 2005; pp. 345–408. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy and Analytic Network Measurement Processes: Applications to Decisions under Risk. Eur. J. Pure Appl. Math. 2008, 1, 122–196. [Google Scholar] [CrossRef]
- Bahrami, Y.; Hassani, H.; Maghsoudi, A. BWM-ARAS: A New Hybrid MCDM Method for Cu Prospectivity Mapping in the Abhar Area, NW Iran. Spat. Stat. 2019, 33, 100382. [Google Scholar] [CrossRef]
- Dagdeviren, M. Decision Making in Equipment Selection: An Integrated Approach with AHP and PROMETHEE. J. Intell. Manuf. 2008, 19, 397–406. [Google Scholar] [CrossRef]
- Ballantyne, G.R.; Powell, M.S. Benchmarking Comminution Energy Consumption for the Processing of Copper and Gold Ores. Miner. Eng. 2014, 65, 109–114. [Google Scholar] [CrossRef]
- Kodihal, S.; Akhtar, M.P. GIS Based Multi-Criteria Decision Making to Identify Regional Groundwater Potential Zones: A Critical Review. Sustain. Water Resour. Manag. 2024, 10, 61. [Google Scholar] [CrossRef]
- Kader, Z.; Islam, M.R.; Aziz, M.T.; Hossain, M.M.; Islam, M.R.; Miah, M.; Jaafar, W.Z.W. GIS and AHP-Based Flood Suscep-tibility Mapping: A Case Study of Bangladesh. Sustain. Water Resour. Manag. 2024, 10, 170. [Google Scholar]
- Campos da Mata, J.F.; Nader, A.S.; Mazzinghy, D.B. A Case Study of Incorporating Variable Recovery and Specific Energy in Long-Term Open Pit Mining. Mining 2023, 3, 22. [Google Scholar] [CrossRef]
- Costa, F.R.; Carneiro, C.C.; Ulsen, C. Self-Organizing Maps Analysis of Chemical–Mineralogical Gold Ore Characterization in Support of Geometallurgy. Mining 2023, 3, 14. [Google Scholar] [CrossRef]
- Abedi, M.; Torabi, S.A.; Norouzi, G.H.; Hamzeh, M. ELECTRE III: A knowledge-driven method for integration of geophysical data with geological and geochemical data in mineral prospectivity mapping. J. Appl. Geophys. 2012, 87, 9–18. [Google Scholar] [CrossRef]
- Mayor, J.; Botero, S.; González-Ruiz, J.D. Modelo de Decisión Multicriterio Difuso para la Selección de Contratistas en Proyectos de Infraestructura: Caso Colombia. Obras Proy. 2016, 20, 56–74. [Google Scholar] [CrossRef][Green Version]




| Variables (Vn) | Qualification of Variables (Qn) | Binary Matrix (Tn) | ||||||
|---|---|---|---|---|---|---|---|---|
| ELECTRE | MAUT | ANP | MACBETH | AHP | TOPSIS | PROMETHEE II | ||
| Number of elements under evaluation | Limited number of criteria and sub-criteria and a small number of alternatives | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Limited number of criteria and sub-criteria and many alternatives. | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| Large number of criteria and sub-criteria and a small number of alternatives. | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| Large number of criteria and sub-criteria and many alternatives | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |
| Type of vs | Weight (Wn) | Variables (Vn) | Qualification of Variables (Qn) | Properties in Relation to Decision-Making Problem (Ep) | Properties of the MCDA Tool in Binary System (SRW = EP × T × Wn) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ELECTRE | MAUT | ANP | MACBETH | AHP | TOPSIS | PROMETHEE | |||||
| Endogenous | 1 | Type of decision-making problems | Sorting | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Description | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Ranking/Choice | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| MCDM | ISW | Ranking |
|---|---|---|
| AHP | 0.91 | 1 |
| PROMETHEE II | 0.91 | 1 |
| MACBETH | 0.91 | 1 |
| ANP | 0.82 | 4 |
| MAUT | 0.73 | 5 |
| ELECTRE | 0.64 | 6 |
| TOPSIS | 0.55 | 7 |
| Criteria | Extremely Important (9) | Very Important (7) | Important (5) | Moderately Important (3) | Equally Important (1) |
|---|---|---|---|---|---|
| Resources | More than 3 Mton | Between 1 and 3 Mton | Between 100 kton and 1 Mton | No information | Less than 100 kton |
| Cu soluble grades | More than 12% | 4.2–12% Cu | 2.5–4.2% of Cu | No information | Less than 2.5% Cu |
| Cu-eq grades | More than 12% | 4.2–12% Cu | 2.5–4.2% Cu | No information | Less than 2.5% Cu |
| Exploration Project | AHP Value | AHP Ranking |
|---|---|---|
| El Huracán mine | 0.97 | 1 |
| La Despreciada mine | 0.90 | 2 |
| San Aurelio mine | 0.90 | 2 |
| La Vaca mine | 0.89 | 4 |
| La Poza mine | 0.89 | 4 |
| Cóndor mine | 0.86 | 6 |
| San Jorge mine | 0.85 | 7 |
| Los Guindos mine | 0.85 | 7 |
| Valdi mine | 0.83 | 9 |
| Lophan-Lujan mine | 0.83 | 9 |
| Mogote mine | 0.81 | 11 |
| Exploration Project | Inflow + | Outflow - | PROMETHEE II Value | PROMETHEE II Ranking |
|---|---|---|---|---|
| El Huracán mine | 0.23 | 0.02 | 0.21 | 1 |
| La Despreciada mine | 0.17 | 0.07 | 0.10 | 2 |
| San Aurelio mine | 0.15 | 0.06 | 0.08 | 3 |
| La Vaca mine | 0.10 | 0.08 | 0.02 | 4 |
| La Poza mine | 0.08 | 0.10 | −0.01 | 5 |
| Cóndor mine | 0.08 | 0.12 | −0.03 | 6 |
| Lophan-Lujan mine | 0.09 | 0.15 | −0.06 | 7 |
| Los Guindos mine | 0.05 | 0.11 | −0.06 | 7 |
| San Jorge mine | 0.05 | 0.11 | −0.06 | 7 |
| Valdi mine | 0.06 | 0.16 | −0.10 | 10 |
| Mogote mine | 0.09 | 0.19 | −0.10 | 10 |
| Exploration Project | AHP Value | AHP Value | PROMETHEE II Ranking | PROMETHEE II Value |
|---|---|---|---|---|
| El Huracán mine | 1 | 0.97 | 1 | 0.21 |
| La Despreciada mine | 2 | 0.90 | 2 | 0.10 |
| San Aurelio mine | 2 | 0.90 | 3 | 0.08 |
| La Vaca mine | 4 | 0.89 | 4 | 0.02 |
| La Poza mine | 4 | 0.89 | 5 | −0.01 |
| Cóndor mine | 6 | 0.86 | 6 | −0.03 |
| San Jorge mine | 7 | 0.85 | 7 | −0.06 |
| Los Guindos mine | 7 | 0.85 | 7 | −0.06 |
| Lophan-Lujan mine | 9 | 0.83 | 7 | −0.06 |
| Valdi mine | 9 | 0.83 | 10 | −0.10 |
| Mogote mine | 11 | 0.81 | 10 | −0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina, C.S.; Marquardt, C.J.; Jara, J.J.; Faúndez, P.I. Insights on Prioritization Methods for Mining Exploration Areas: A Case Study of the Tiltil Mining District, Chile. Mining 2024, 4, 687-718. https://doi.org/10.3390/mining4030039
Molina CS, Marquardt CJ, Jara JJ, Faúndez PI. Insights on Prioritization Methods for Mining Exploration Areas: A Case Study of the Tiltil Mining District, Chile. Mining. 2024; 4(3):687-718. https://doi.org/10.3390/mining4030039
Chicago/Turabian StyleMolina, Claudio Sebastián, Carlos Jorge Marquardt, José Joaquín Jara, and Patricio Ignacio Faúndez. 2024. "Insights on Prioritization Methods for Mining Exploration Areas: A Case Study of the Tiltil Mining District, Chile" Mining 4, no. 3: 687-718. https://doi.org/10.3390/mining4030039
APA StyleMolina, C. S., Marquardt, C. J., Jara, J. J., & Faúndez, P. I. (2024). Insights on Prioritization Methods for Mining Exploration Areas: A Case Study of the Tiltil Mining District, Chile. Mining, 4(3), 687-718. https://doi.org/10.3390/mining4030039






