The Application of Geosynthetics in Tailings Storage Facilities: A General Review
Abstract
1. Introduction
2. Mechanical Properties of Tailings
2.1. Compressibility
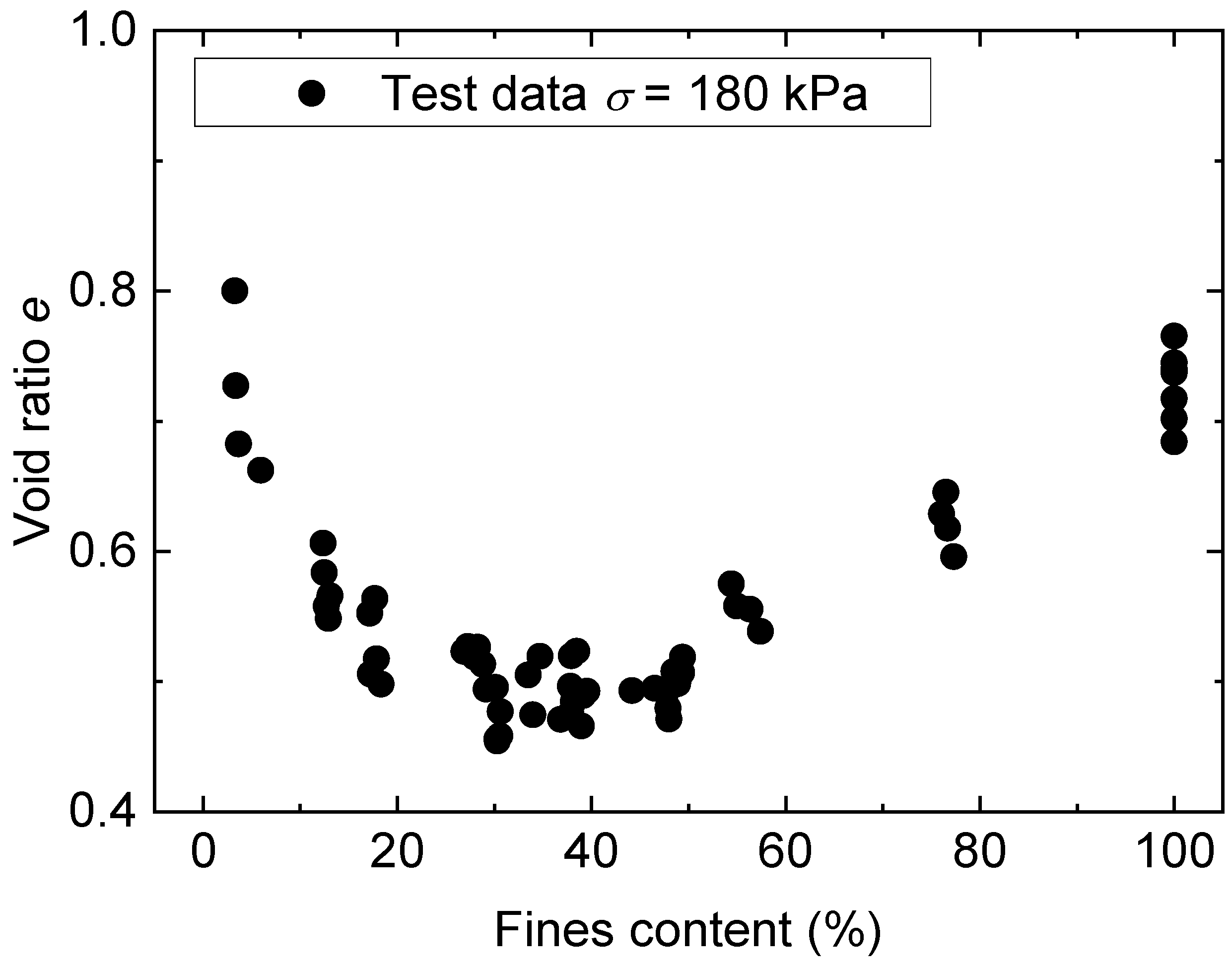
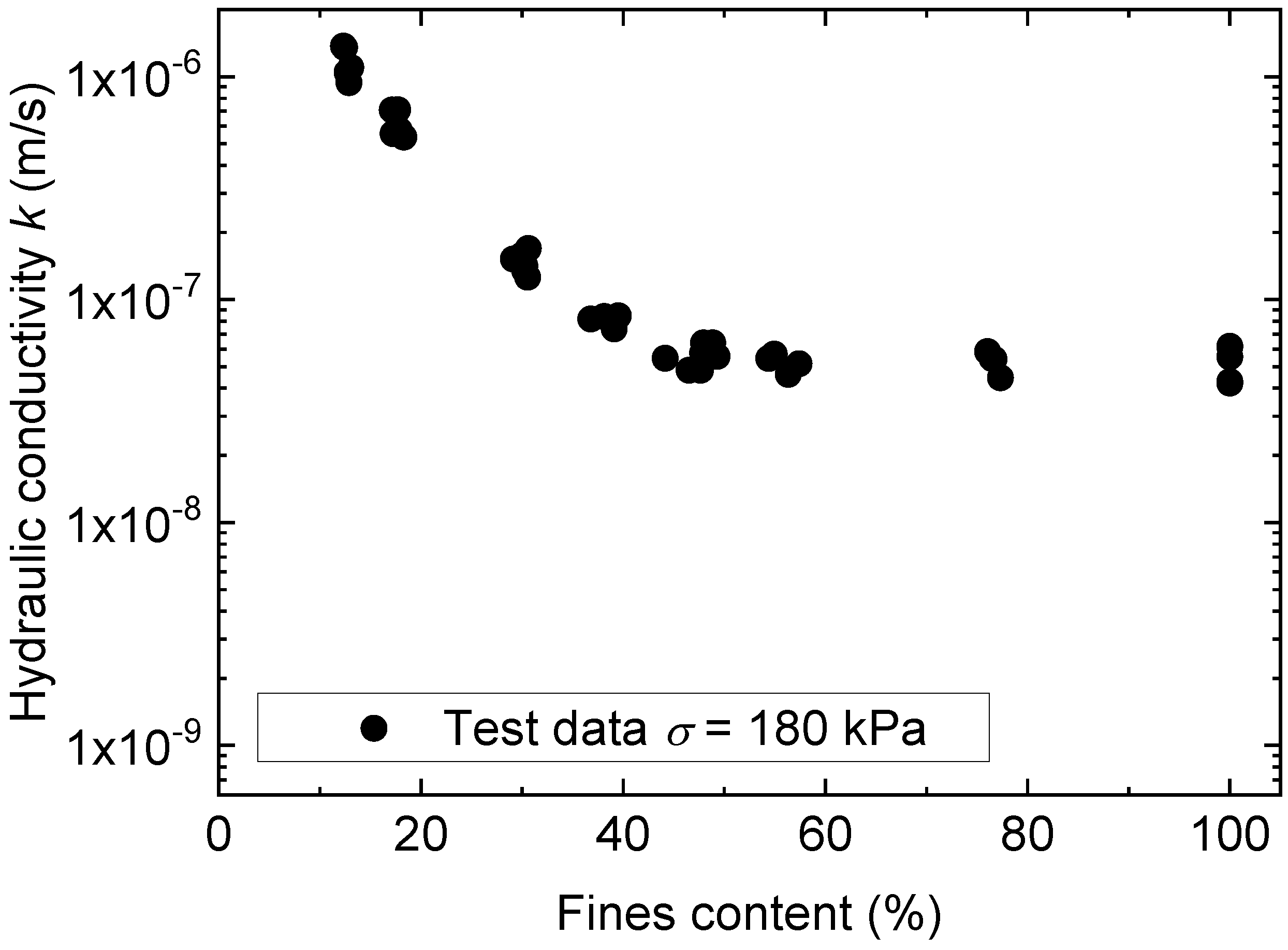
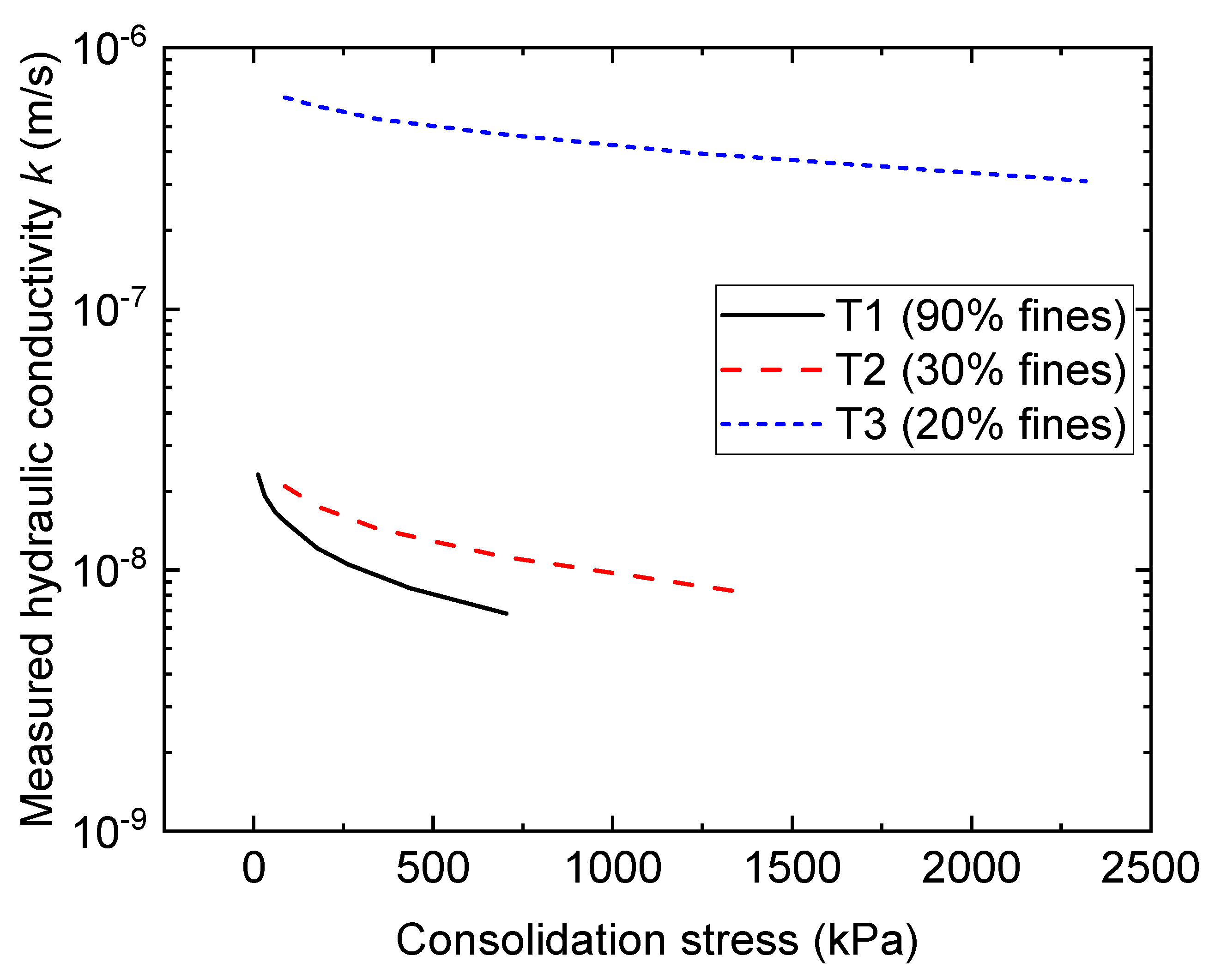
2.2. Permeability
3. Prediction of Leakage through Defective GMB Lines
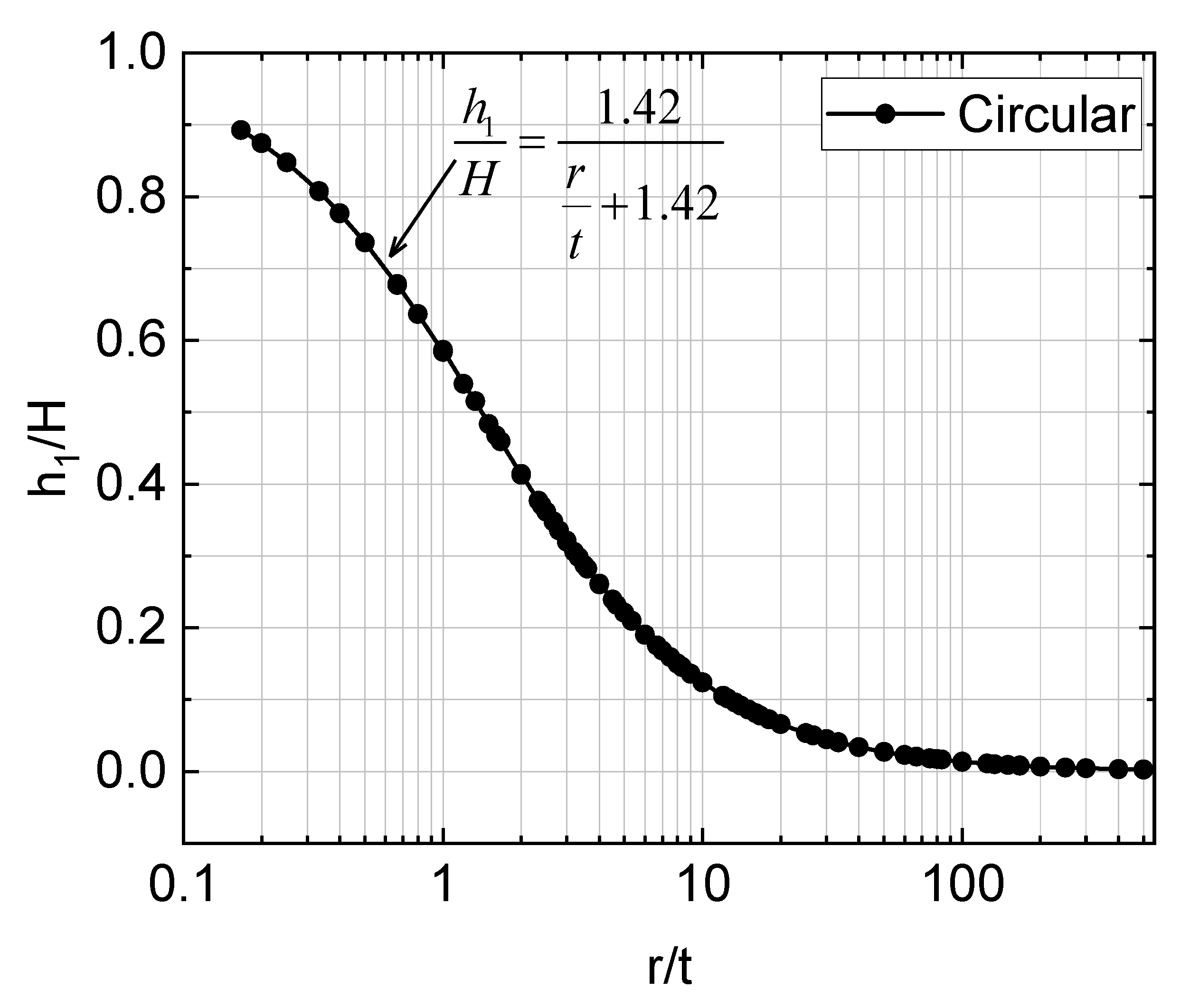
3.1. Circular GMB Defects
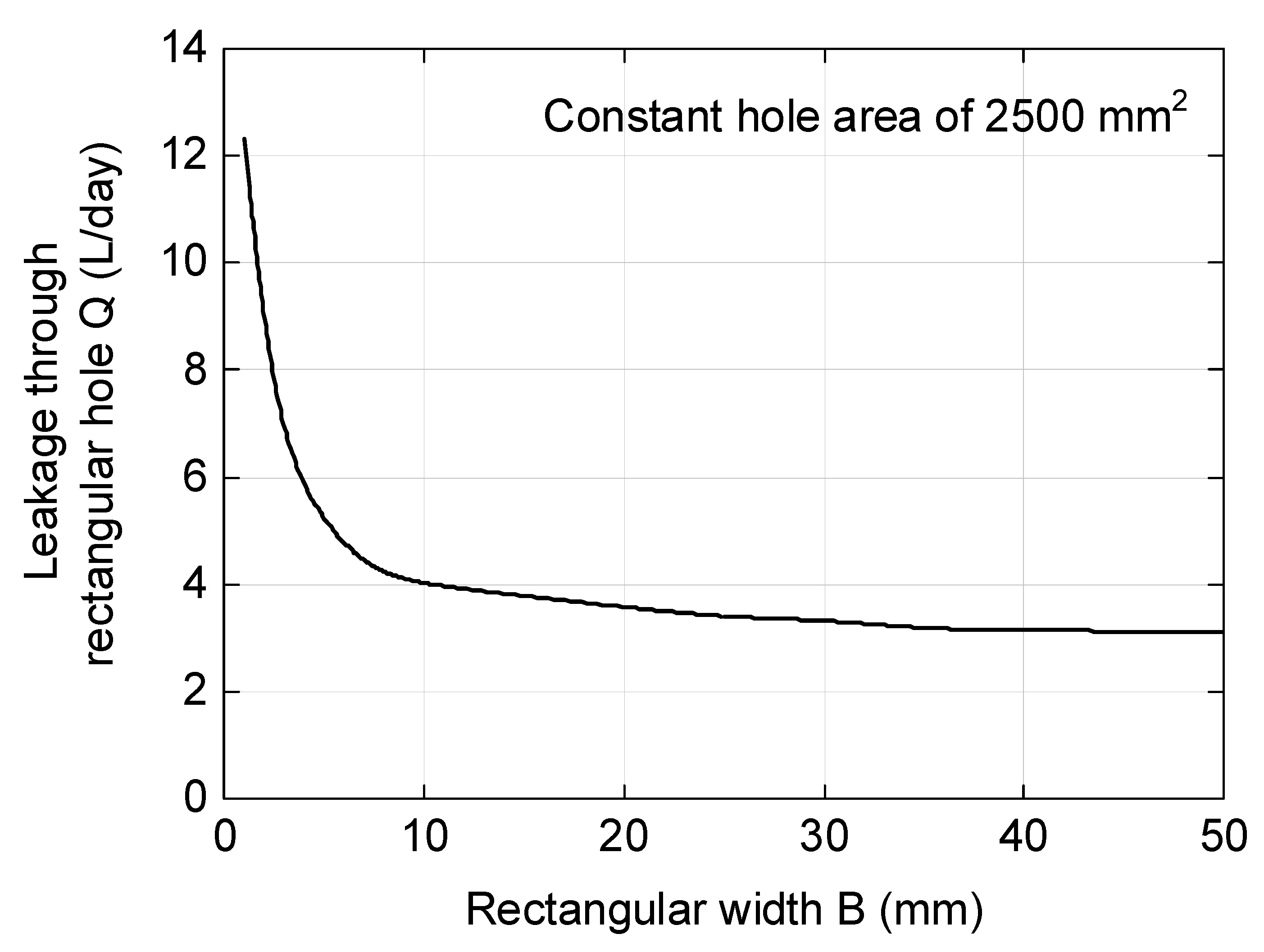
3.2. Non-Circular GMB Defects
3.3. Effect of Subgrade Permeability
3.4. Effect of a Lateral Drainage System
3.4.1. Case 3 Drainage Layer Is Not in Contact with GMB
3.4.2. Case 3 Drainage Layer Is in Contact with GMB
4. Application of Leakage Prediction Equations
4.1. Circular Hole: Piping and Internal Erosion
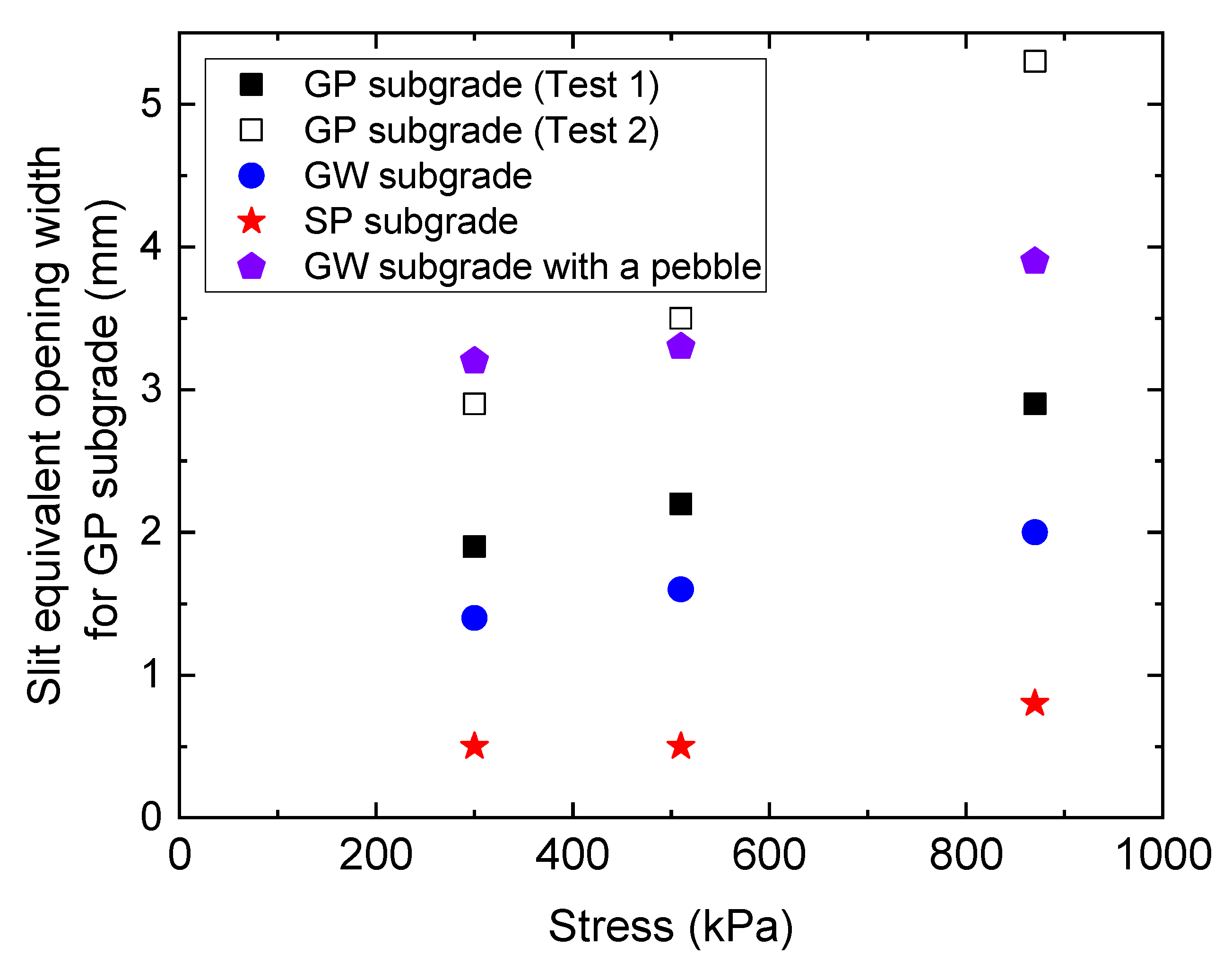
4.2. Non-Circular Hole: Opening Width of Defective GMB Seams
5. Issues Relating to Subgrade Imperfection
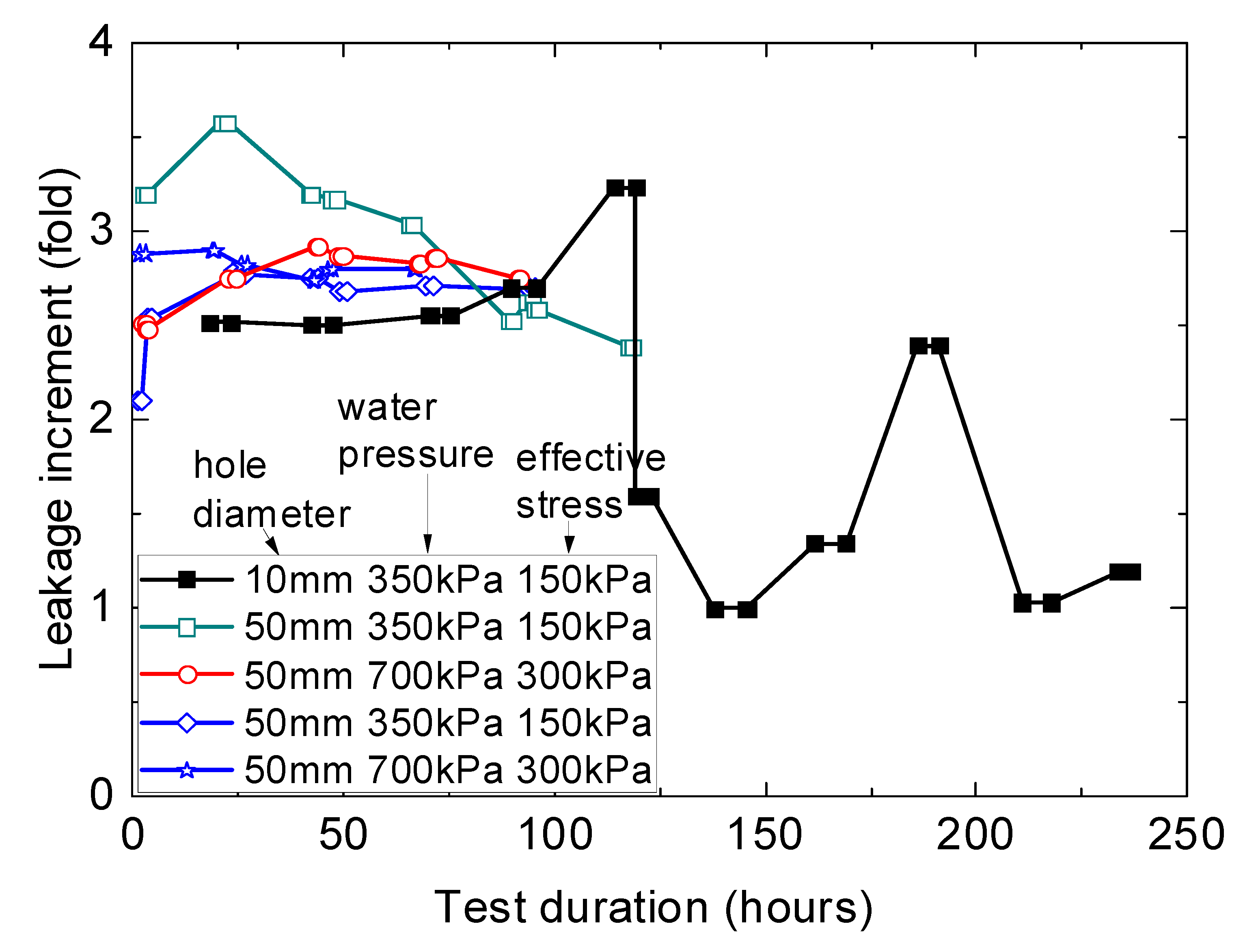
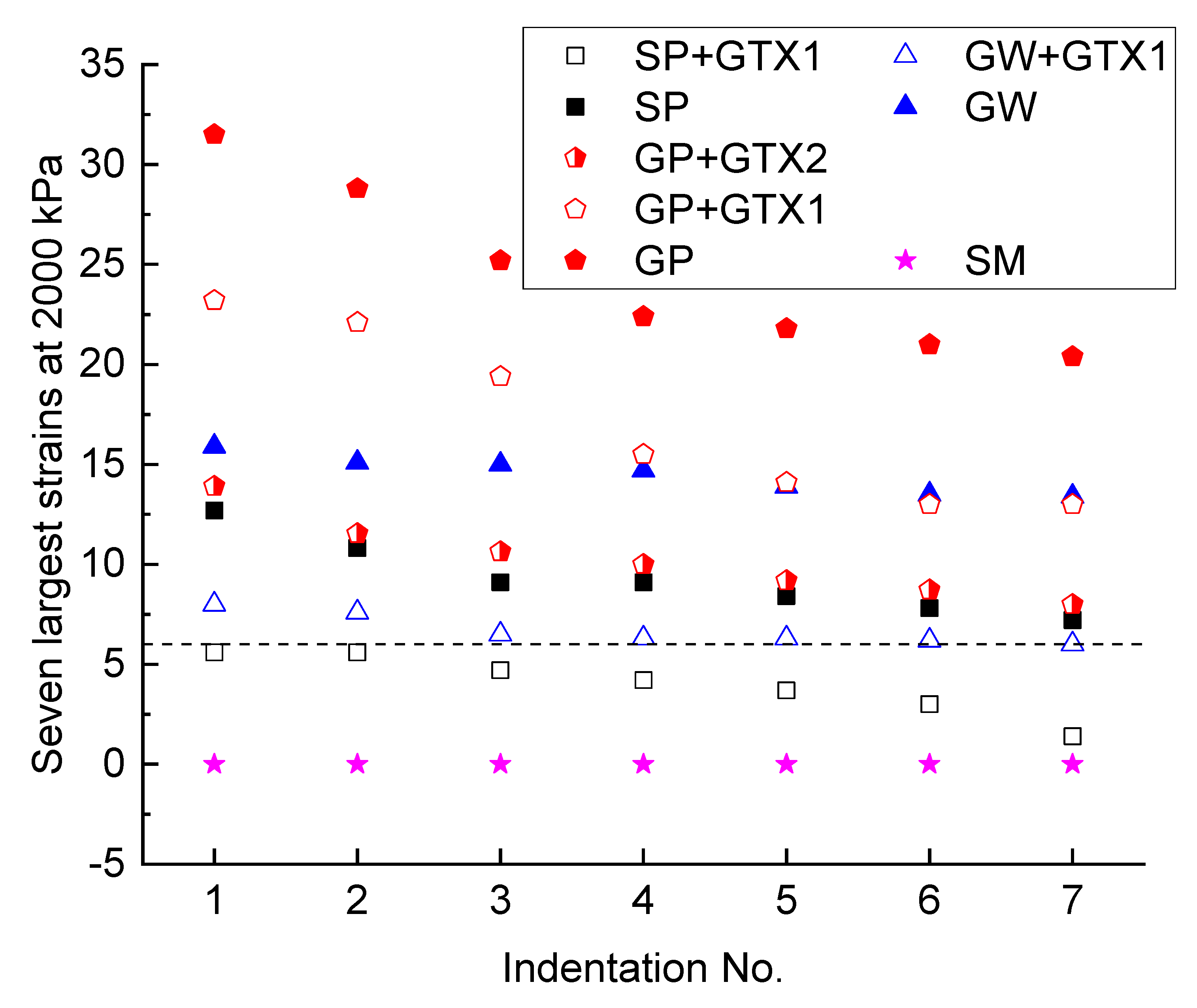
5.1. The Development of GMB Tensile Strains
5.2. Soluble Subgrade
6. Service Life of Geomembrane Liners
6.1. Polyethylene Geomembranes
6.2. Bituminous Geomembranes
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Cornwall, W. A dam big problem. Science 2020, 369, 906–909. [Google Scholar] [CrossRef] [PubMed]
- Roche, C.; Thygesen, K.; Baker, E. Mine tailings storage: Safety is no accident. In A UNEP Rapid Response Assessment; United Nations Environment Programme and GRID: Arendal, Norway; Nairobi, Kenya, 2017. [Google Scholar]
- Thiel, R.; Smith, M.E. State of the practice review of heap leach pad design issues. Geotext. Geomembr. 2004, 22, 555–568. [Google Scholar] [CrossRef]
- Lupo, J.F.; Morrison, K.F. Geosynthetic design and construction approaches in the mining industry. Geotext. Geomembr. 2007, 25, 96–108. [Google Scholar] [CrossRef]
- Touze-Foltz, N.; Lupo, J.; Barroso, M. Geoenvironmental applications of geosynthetics. Keynote Lecture. Proc. Eurogeo 2008, 4, 98. [Google Scholar]
- Scheirs, J. A Guide to Polymeric Geomembranes: A Practical Approach; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Rowe, R.K.; Hosney, M.S. Laboratory investigation of GCL performance for covering arsenic contaminated mine wastes. Geotext. Geomembr. 2013, 39, 63–77. [Google Scholar] [CrossRef]
- Rowe, R.K.; Brachman, R.W.I.; Irfan, H.; Smith, M.E.; Thiel, R. Effect of underliner on geomembrane strains in heap leach applications. Geotext. Geomembr. 2013, 40, 37–47. [Google Scholar] [CrossRef]
- Touze, N. Healing the world: A geosynthetics solution. Geosynth. Int. 2021, 28, 1–31. [Google Scholar] [CrossRef]
- Rowe, R.K. Protecting the Environment with Geosynthetics: 53rd Karl Terzaghi Lecture. J. Geotech. Geoenviron. Eng. 2020, 146, 04020081. [Google Scholar] [CrossRef]
- Rowe, R.K.; Jefferis, S. Protecting the environment from contamination with barrier systems: Advances and challenges, State-of-the-Art Lecture. In Proceedings of the 20th International Conference on Soil Mechanics and Geotechnical Engineering, Sydney, Australia, 1–5 May 2022; pp. 187–293. [Google Scholar]
- Giroud, J.P.; Bonaparte, R. Leakage through liners constructed with geomembranes—Part I. Geomembrane liners. Geotext. Geomembr. 1989, 8, 27–67. [Google Scholar] [CrossRef]
- Giroud, J.P.; Bonaparte, R. Leakage through liners constructed with geomembranes—Part II. Composite liners. Geotext. Geomembr. 1989, 8, 71–111. [Google Scholar] [CrossRef]
- Rowe, R.K. Geosynthetics and the minimization of contaminant migration through barrier systems beneath solid waste. In Proceedings of the 6th International Conference on Geosynthetics, Atlanta, GA, USA, 25–29 March 1998; Volume 1, pp. 27–103. [Google Scholar]
- Rowe, R.K. Long-term performance of contaminant barrier systems. Geotechnique 2005, 55, 631–678. [Google Scholar] [CrossRef]
- Rowe, R.K. Short and long-term leakage through composite liners. Can. Geotech. J. 2012, 49, 141–169. [Google Scholar] [CrossRef]
- Rowe, R.K. Geosynthetic clay liners: Perceptions and misconceptions. Geotext. Geomembr. 2020, 48, 137–156. [Google Scholar] [CrossRef]
- Zhan, L.T.; Chen, C.; Bouazza, A.; Chen, Y.M. Evaluating leakages through GMB/GCL composite liners considering random hole distributions in wrinkle networks. Geotext. Geomembr. 2018, 46, 131–145. [Google Scholar] [CrossRef]
- Pu, H.; Qiu, J.; Zhang, R.; Zheng, J. Assessment of consolidation-induced VOC transport for a GML/GCL/CCL composite liner system. Geotext. Geomembr. 2018, 46, 455–469. [Google Scholar] [CrossRef]
- Chang, J.Y.; Feng, S.J.; Zheng, Q.T.; Shen, Y. Cyclic shear behavior of GMB/GCL composite liner. Geotext. Geomembr. 2021, 49, 593–603. [Google Scholar] [CrossRef]
- Yan, H.; Wu, J.; Thomas, H.R.; Ding, H.; Zhan, L.; Xie, H. Analytical model for coupled consolidation and diffusion of organic contaminant transport in triple landfill liners. Geotext. Geomembr. 2021, 49, 489–499. [Google Scholar] [CrossRef]
- Tang, L.; Francey, W.; Zheng, J.; Wang, X.; Luo, X. Filtration behaviour of staple fibre geotextiles under unequal biaxial tensile strains. Geosynth. Int. 2023, 1–18. [Google Scholar] [CrossRef]
- Fu, X.L.; Jiang, Z.Y.; Reddy, K.R.; Ruan, K.L.; Du, Y.J. Hydraulic conductivity, microstructure and compositional changes of sand-bentonite backfill in cutoff walls exposed to organic acids. ASCE J. Geotech. Geoenviron. Eng. 2023, 149, 04023060. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Chen, H.; Guo, H.; Chen, R.; Xue, Q. Life cycle analysis of common landfill final cover systems focusing on carbon neutrality. Sci. Total Environ. 2024, 912, 168863. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.Y.; Rowe, R.K. Effect of a lateral drainage layer on leakage through a defect in a geomembrane overlain by saturated tailings. Geotext. Geomembr. 2024; in press. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. An empirical equation predicting the saturated hydraulic conductivity of tailings. Can. Geotech. J. 2024; in press. [Google Scholar] [CrossRef]
- Rowe, R.K.; Quigley, R.M.; Brachman, R.W.I.; Booker, J.R. Barrier Systems for Waste Disposal Facilities; Taylor & Francis (E & FN Spon): London, UK, 2004. [Google Scholar]
- Peggs, I.D.; Gassner, F.; Scheirs, J.; Tan, D.; Arango, A.M.N.; Burkard, B. Is there a resurgence of stress cracking in HDPE geomembranes. In Proceedings of the 10th International Geosynthetics Conference, Berlin, Germany, 21–25 September 2014; DGGT: Essen, Germany, 2014. CD-ROM. [Google Scholar]
- Ewais, A.M.R.; Rowe, R.K.; Brachman, R.W.I.; Arnepalli, D.N. Service life of a high-density polyethylene geomembrane under simulated landfill conditions at 85° C. J. Geotech. Geoenviron. Eng. 2014, 140, 04014060. [Google Scholar] [CrossRef]
- Rowe, R.K.; Shoaib, M. Long-term performance of high-density polyethylene (HDPE) geomembrane seams in municipal solid waste (MSW) leachate. Can. Geotech. J. 2017, 54, 1623–1636. [Google Scholar] [CrossRef]
- Rowe, R.K.; Shoaib, M. Durability of HDPE geomembrane seams immersed in brine for three years. J. Geotech. Geoenviron. Eng. 2018, 144, 04017114. [Google Scholar] [CrossRef]
- Badu-Tweneboah, K.; Giroud, J.P. Discussion of “Leakage through Holes in Geomembranes below Saturated Tailings” by R. Kerry Rowe, Prabeen Joshi, RWI Brachman, and H. McLeod. J. Geotech. Geoenviron. Eng. 2018, 144, 07018001. [Google Scholar] [CrossRef]
- Eldesouky, H.M.G.; Brachman, R.W.I. Calculating local geomembrane strains from a single gravel particle with thin plate theory. Geotext. Geomembr. 2018, 46, 101–110. [Google Scholar] [CrossRef]
- Brachman, R.W.I.; Joshi, P.; Rowe, R.K. A new laboratory apparatus for measuring leakage through geomembrane holes beneath mine tailings. Can. Geotech. J. 2017, 54, 147–157. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Effect of geosynthetic component characteristics on the potential for GCL internal erosion. Geotext. Geomembr. 2023, 51, 85–94. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K.; Brachman, R.W.I. Compressibility and permeability of sand-silt tailings mixtures. Can. Geotech. J. 2022, 59, 1348–1357. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Seepage through a circular geomembrane hole when covered by fine-grained tailings under filter incompatible conditions. Can. Geotech. J. 2022, 59, 410–423. [Google Scholar] [CrossRef]
- Rowe, R.K.; Fan, J.Y. Effect of geomembrane hole geometry on leakage overlain by saturated tailings. Geotext. Geomembr. 2021, 49, 1506–1518. [Google Scholar] [CrossRef]
- Rowe, R.K.; Fan, J.Y. A general solution for leakage through geomembrane defects overlain by saturated tailings and underlain by highly permeable subgrade. Geotext. Geomembr. 2022, 50, 694–707. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Leakage through a circular geomembrane hole overlain and underlain by silty sand tailings. Geosynth. Int. 2023, 1–12. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Piping of silty sand tailings through a circular geomembrane hole. Geotext. Geomembr. 2022, 50, 183–196. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Effect of subgrade on leakage through a defective geomembrane seam below saturated tailing. Geotext. Geomembr. 2023, 51, 360–369. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Effect of subgrade on tensile strains in a geomembrane for tailings storage applications. Can. Geotech. J. 2023, 60, 18–30. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Effect of a soluble subgrade on leakage through a geomembrane defect. Geosynth. Int. 2023, 1–13. [Google Scholar] [CrossRef]
- Kenney, T.C.; Lau, D. Internal stability of granular filters. Can. Geotech. J. 1985, 22, 215–225. [Google Scholar] [CrossRef]
- Rowe, R.K.; Joshi, P.; Brachman, R.W.I.; McLeod, H. Leakage through holes in geomembranes below saturated tailings. J. Geotech. Geoenviron. Eng. 2017, 143, 04016099. [Google Scholar] [CrossRef]
- Fan, J.Y.; Rowe, R.K. Effect of tailings fines content on leakage though circular geomembrane holes overlain by saturated tailings. In Geosynthetics: Leading the Way to a Resilient Planet; CRC Press: Boca Raton, FL, USA, 2023; pp. 1643–1649. [Google Scholar]
- Taylor, D. Fundamentals of Soil Mechanics; Chapman and Hall, Limited: New York, NY, USA, 1948. [Google Scholar]
- Chou, Y.C.; Brachman, R.W.; Rowe, R.K. Leakage through a hole in a geomembrane beneath a fine-grained tailings. Can. Geotech. J. 2022, 59, 372–383. [Google Scholar] [CrossRef]
- Sherard, J.L.; Dunnigan, L.P.; Talbot, J.R. Basic properties of sand and gravel filters. J. Geotech. Eng. 1984, 110, 684–700. [Google Scholar] [CrossRef]
- Foster, M.; Fell, R. Assessing embankment dam filters that do not satisfy design criteria. J. Geotech. Geoenviron. Eng. 2001, 127, 398–407. [Google Scholar] [CrossRef]
- Wong, R.C.; Mills, B.N.; Liu, Y.B. Mechanistic model for one-dimensional consolidation behavior of nonsegregating oil sands tailings. J. Geotech. Geoenviron. Eng. 2008, 134, 195–202. [Google Scholar] [CrossRef]
- Fell, R.; Wan, C.F.; Cyganiewicz, J.; Foster, M. Time for development of internal erosion and piping in embankment dams. J. Geotech. Geoenviron. Eng. 2003, 129, 307–314. [Google Scholar] [CrossRef]
- Rollin, A.L.; Marcotte, M.; Jacqueline, T.; Chaput, L. Leak location in exposed geomembrane liners using an electrical leak detection technique. In Proceedings of the Geosynthetic’99, Industrial Fabrics Association International, Boston, MA, USA, 28–30 April 1999; IFAI: Roseville, MI, USA, 1999; Volume 2, pp. 615–626. [Google Scholar]
- Gilson-Beck, A. Controlling leakage through installed geomembranes using electrical leak location. Geotext. Geomembr. 2019, 47, 697–710. [Google Scholar] [CrossRef]
- Gilson-Beck, A.; Giroud, J.P. A quantification of the short-term reliability of HDPE geomembrane seaming methods. Geosynth. Int. 2022, 29, 337–341. [Google Scholar] [CrossRef]
- Zhang, L.; Bouazza, A.; Rowe, R.K.; Scheirs, J. Effect of welding parameters on properties of HDPE geomembrane seams. Geosynth. Int. 2017, 24, 408–418. [Google Scholar] [CrossRef]
- Rowe, R.K.; Ali, M.M. Effect of welding parameters on properties of HDPE geomembrane extrusion welds. Geotext. Geomembr. 2024, 52, 355–367. [Google Scholar] [CrossRef]
- Ali, M.; Rowe, R.K. Long-term performance of HDPE extrusion Welds aged at 85 °C in synthetic leachate. Geosynth. Int. 2024, 1–37. [Google Scholar] [CrossRef]
- Giroud, J.; Tisseau, B.; Soderman, K.; Beech, J. Analysis of strain concentration next to geomembrane seams. Geosynth. Int. 1995, 2, 1049–1097. [Google Scholar] [CrossRef]
- Kavazanjian, E.; Andresen, J.; Gutierrez, A. Experimental evaluation of HDPE geomembrane seam strain concentrations. Geosynth. Int. 2017, 24, 333–342. [Google Scholar] [CrossRef]
- Cheng, Q.; Tang, C.S.; Zeng, H.; Zhu, C.; An, N.; Shi, B. Effects of microstructure on desiccation cracking of a compacted soil. Eng. Geol. 2020, 265, 105418. [Google Scholar] [CrossRef]
- Tang, C.S.; Zhu, C.; Cheng, Q.; Zeng, H.; Xu, J.J.; Tian, B.G.; Shi, B. Desiccation cracking of soils: A review of investigation approaches, underlying mechanisms, and influencing factors. Earth-Sci. Rev. 2021, 216, 103586. [Google Scholar] [CrossRef]
- Tognon, A.R.; Rowe, R.K.; Moore, I.D. Geomembrane strain observed in large-scale testing of protection layers. J. Geotech. Geoenviron. Eng. 2000, 126, 1194–1208. [Google Scholar] [CrossRef]
- Marcotte, B.A.; Fleming, I.R. The role of undrained clay soil subgrade properties in controlling deformations in geomembranes. Geotext. Geomembr. 2019, 47, 327–335. [Google Scholar] [CrossRef]
- Rowe, R.K.; Yu, Y. Magnitude and significance of tensile strains in geomembrane landfill liners. Geotext. Geomembr. 2019, 47, 439–458. [Google Scholar] [CrossRef]
- Rowe, R.K.; Abdelaal, F.B. Antioxidant depletion in HDPE Geomembrane with HALS in low pH heap leach environment. Can. Geotech. J. 2016, 53, 1612–1627. [Google Scholar] [CrossRef]
- Abdelaal, F.B.; Kerry Rowe, R. Effect of high pH found in low-level radioactive waste leachates on the antioxidant depletion of a HDPE geomembrane. J. Hazard. Toxic Radioact. Waste 2017, 21, D4015001. [Google Scholar] [CrossRef]
- Abdelaal, F.B.; Samea, A. Chemical durability of elastomeric bituminous geomembranes (BGMs) in heap leach pad applications. Geosynth. Int. 2023, 1–18. [Google Scholar] [CrossRef]
- Abdelaal, F.B.; Samea, A. The long-term performance of an elastomeric bituminous geomembrane (BGM) under single-sided conditions. Can. Geotech. J. 2023; in press. [Google Scholar] [CrossRef]
- Abdelaal, F.B.; Rowe, R.K.; Morsy, M.S.; e Silva, R.A. Degradation of HDPE, LLDPE, and blended polyethylene geomembranes in extremely low and high pH mining solutions at 85 °C. Geotext. Geomembr. 2023, 51, 27–38. [Google Scholar] [CrossRef]
- Rowe, R.K.; Abdelaal, F.B.; Zafari, M.; Morsy, M.S.; Priyanto, D.G. An approach to high-density polyethylene (HDPE) geomembrane selection for challenging design requirements. Can. Geotech. J. 2020, 57, 1550–1565. [Google Scholar] [CrossRef]
- Francey, W.; Rowe, R.K. Factors affecting the tensile strength of bituminous geomembrane seams. Geosynth. Int. 2024, 1–25. [Google Scholar] [CrossRef]
- Rowe, R.K.; Morsy, M.S.; Ewais, A.M.R. Representative stress crack resistance of polyolefin geomembranes used in waste management. Waste Manag. 2019, 100, 18–27. [Google Scholar] [CrossRef]
- Touze-Foltz, N.; Farcas, F. Long-term performance and binder chemical structure evolution of elastomeric bituminous geomembranes. Geotext. Geomembr. 2017, 45, 121–130. [Google Scholar] [CrossRef]
- Samea, A.; Abdelaal, F.B. Effect of elevated temperatures on the degradation behaviour of elastomeric bituminous geomembranes. Geotext. Geomembr. 2023, 51, 219–232. [Google Scholar] [CrossRef]
- Samea, A.; Abdelaal, F.B. Durability of two bituminous geomembranes (BGMs) with different thicknesses in MSW synthetic leachate. Waste Manag. 2023, 165, 179–188. [Google Scholar] [CrossRef] [PubMed]
- Addis, P.; Andruchow, B.; Wislesky, I. Bituminous Geomembrane Failure at a Co-Disposal Tailings Storage Facility. In Proceedings of the Tailings and Mine Waste, Banff, AB, Canada, 2–5 October 2016. [Google Scholar]
- Bremner, H.; Belanger, J.-F.; Charpentier, C.; Jacquelin, T. Case study on quality control and leak location performed on a bituminous liner mine closure project near the arctic circle in NWT, Canada. In Proceedings of the GeoAmericas—Pan-American Conference on Geosynthetics, Miami Beach, FL, USA, 10–13 April 2016. [Google Scholar]








| Tailings | Grain Size (mm) | Cu | Cc | Fines Content a | Specific Gravity | ||
|---|---|---|---|---|---|---|---|
| d85 | d50 | d15 | |||||
| T1 | 0.07 | 0.01 | 0.002 | 14.3 | 0.9 | 90% | 3.65 |
| T2 | 0.4 | 0.14 | 0.02 | 23.5 | 3.4 | 30% | 2.65 |
| T3 | 0.4 | 0.18 | 0.06 | 6.2 | 1.4 | 20% | 2.65 |
| Subgrade | Grain Size (mm) | Cu | Cc | k a (m/s) | Erosion Category b for T3 Tailings | ||||
|---|---|---|---|---|---|---|---|---|---|
| d10 | d15 | d30 | d60 | d85 | |||||
| GP | 4.7 | 5.5 | 8.3 | 18.8 | 37.7 | 4.0 | 0.8 | 0.1 | Excessive erosion |
| GW | 2.1 | 3.5 | 8.3 | 18.8 | 37.7 | 8.8 | 1.7 | 0.04 | Some erosion |
| SP | 0.75 | 0.85 | 1.3 | 3.0 | 6.0 | 4.0 | 0.8 | 0.003 | No erosion |
| Time to Nominal Failure, tNF (Years), Based on Immersion Tests | ||||||||
|---|---|---|---|---|---|---|---|---|
| pH | 0.5 | 6.5 | 9.5 | 11.5 | Air | MSW | ||
| Temp. | Water | B1 | B2 | |||||
| 20 °C | 100 | 60 | 55 | 45 | 70 | 40 | 31 | |
| 30 °C | 45 | 28 | 25 | 20 | 30 | 18 | 14 | |
| 40 °C | 20 | 15 | 11 | 10 | 14 | 8 | 7 | |
| 55 °C | 7 | 5 | 4 | 3 | 5 | 3 | 2 | |
| Ref. | #2 | #1 | #2 | #2 | #1 | #3 | #3 | |
| Time to Nominal Failure, tNF (Years), Based on Immersion Tests | |||||||
|---|---|---|---|---|---|---|---|
| BGM | HDPE | BGM | HDPE | BGM | HDPE | ||
| pH | 0.5 | 0.5 * | 9.5 | 9.5 * | 11.5 | 11.5 * | |
| Temp. | |||||||
| 20 °C | 100 | >100 | 55 | >80 | 45 | >75 | |
| 30 °C | 45 | >54 | 25 | >43 | 20 | >39 | |
| 40 °C | 20 | >28 | 11 | >24 | 10 | >21 | |
| 55 °C | 7 | >11 | 4 | >10 | 3 | >9 | |
| Ref. | #2 | #4 | #2 | #5 | #2 | #5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rowe, R.K.; Fan, J. The Application of Geosynthetics in Tailings Storage Facilities: A General Review. Mining 2024, 4, 447-468. https://doi.org/10.3390/mining4020026
Rowe RK, Fan J. The Application of Geosynthetics in Tailings Storage Facilities: A General Review. Mining. 2024; 4(2):447-468. https://doi.org/10.3390/mining4020026
Chicago/Turabian StyleRowe, Ronald Kerry, and Jiying Fan. 2024. "The Application of Geosynthetics in Tailings Storage Facilities: A General Review" Mining 4, no. 2: 447-468. https://doi.org/10.3390/mining4020026
APA StyleRowe, R. K., & Fan, J. (2024). The Application of Geosynthetics in Tailings Storage Facilities: A General Review. Mining, 4(2), 447-468. https://doi.org/10.3390/mining4020026







