Evaluation and Prediction of Blast-Induced Ground Vibrations: A Gaussian Process Regression (GPR) Approach
Abstract
1. Introduction
Research Significance
2. Materials and Methods
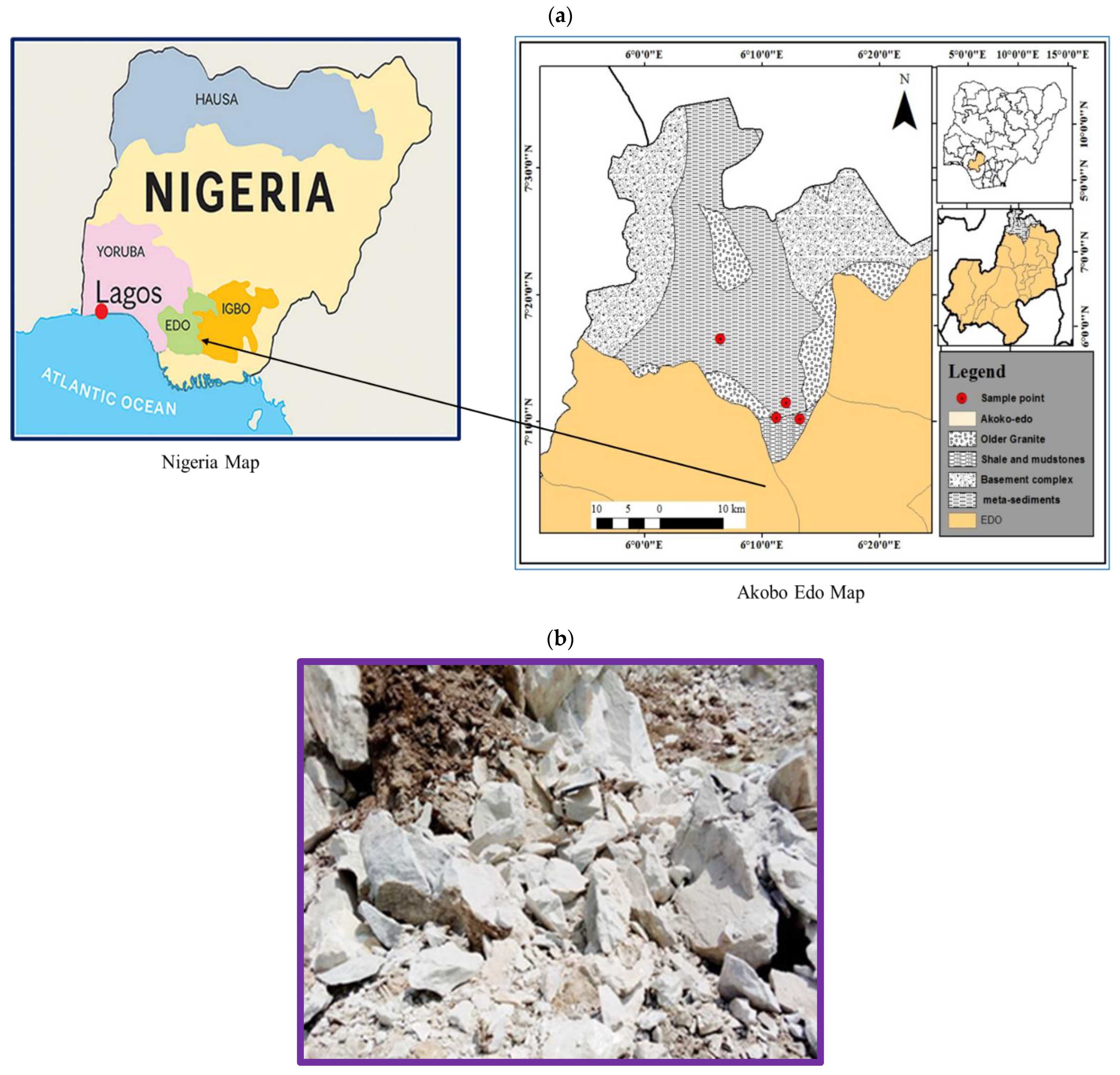
2.1. Study Area
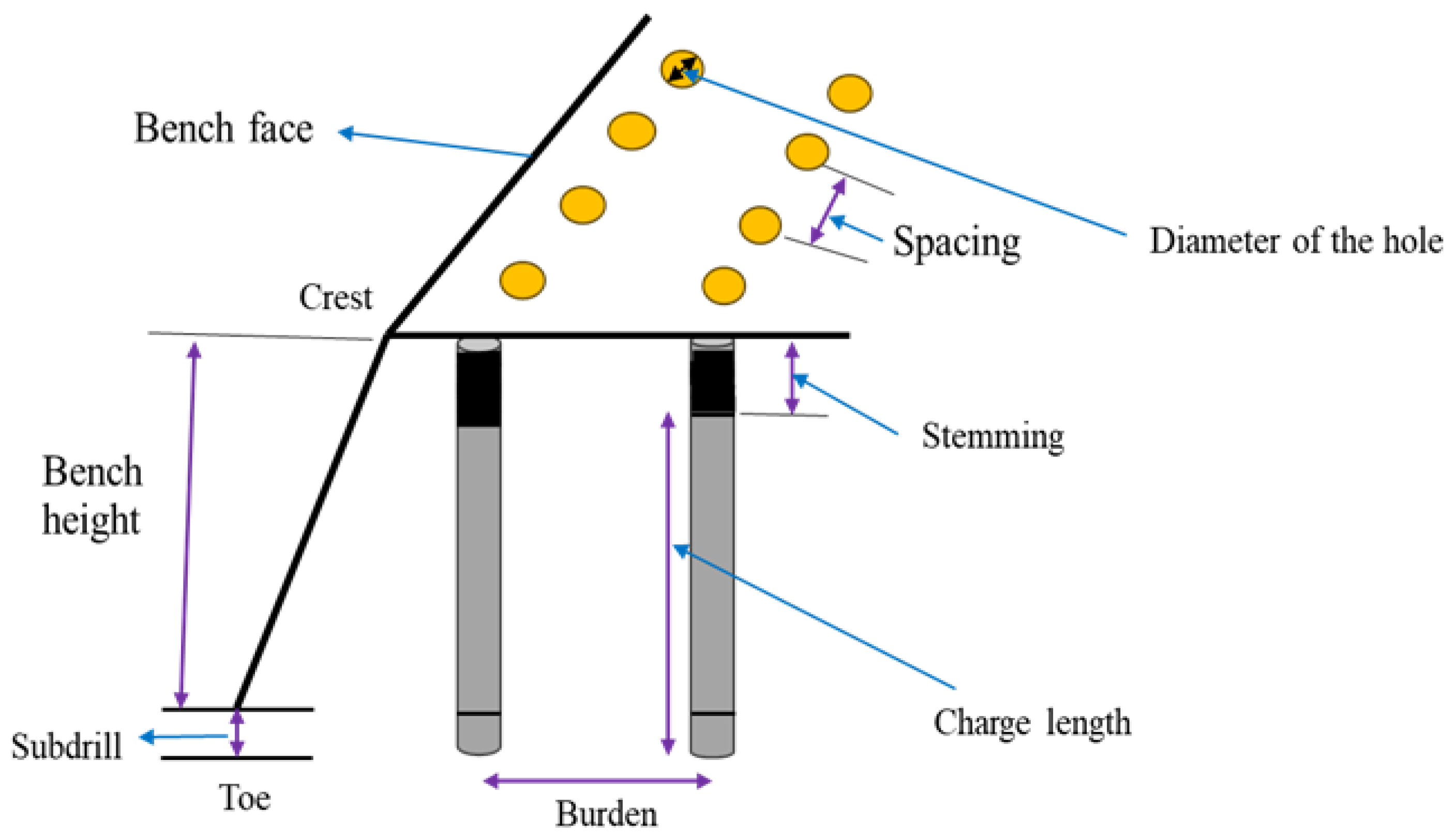
2.2. Blasting Vibration Monitoring Procedures at the Quarry Site
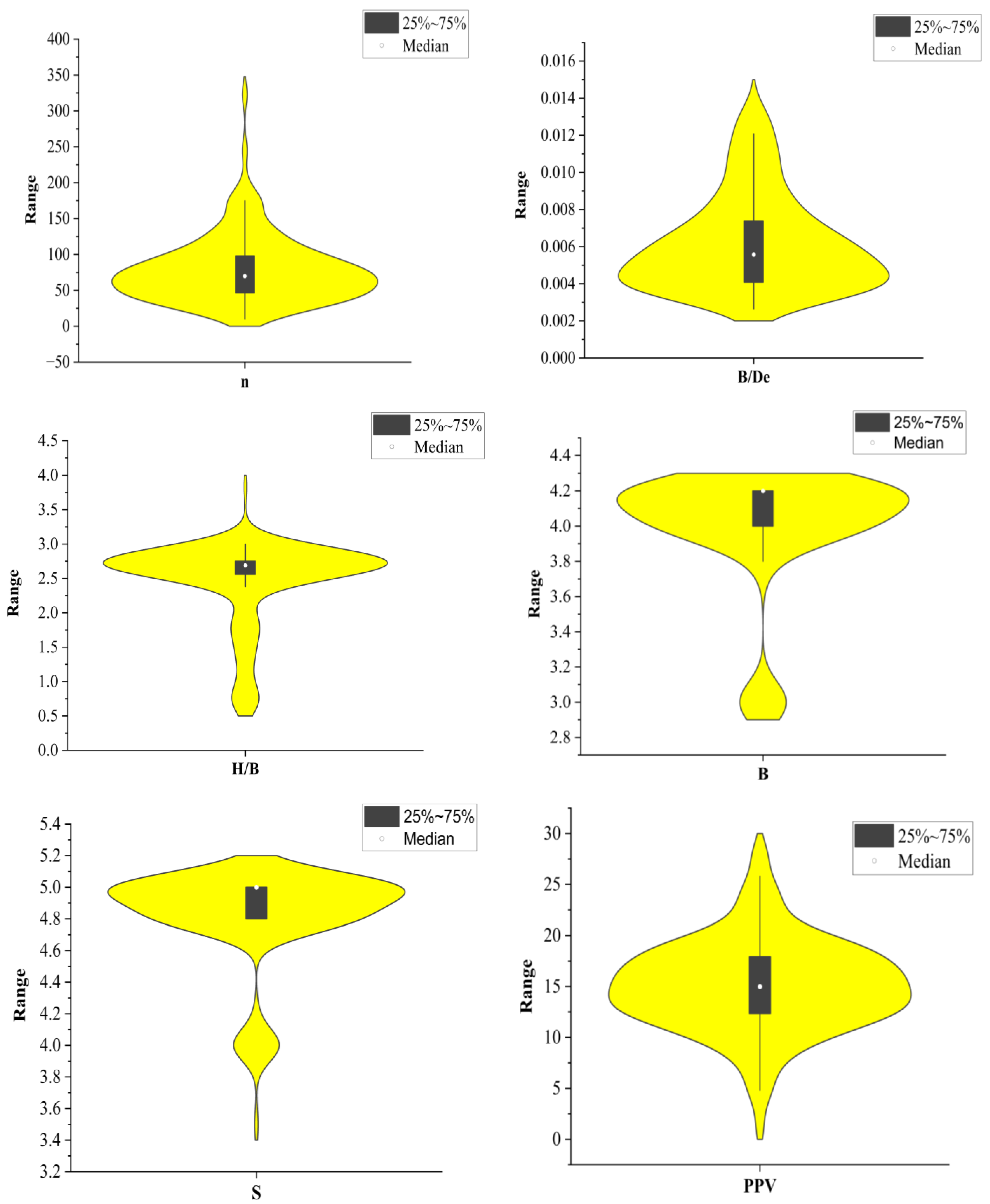
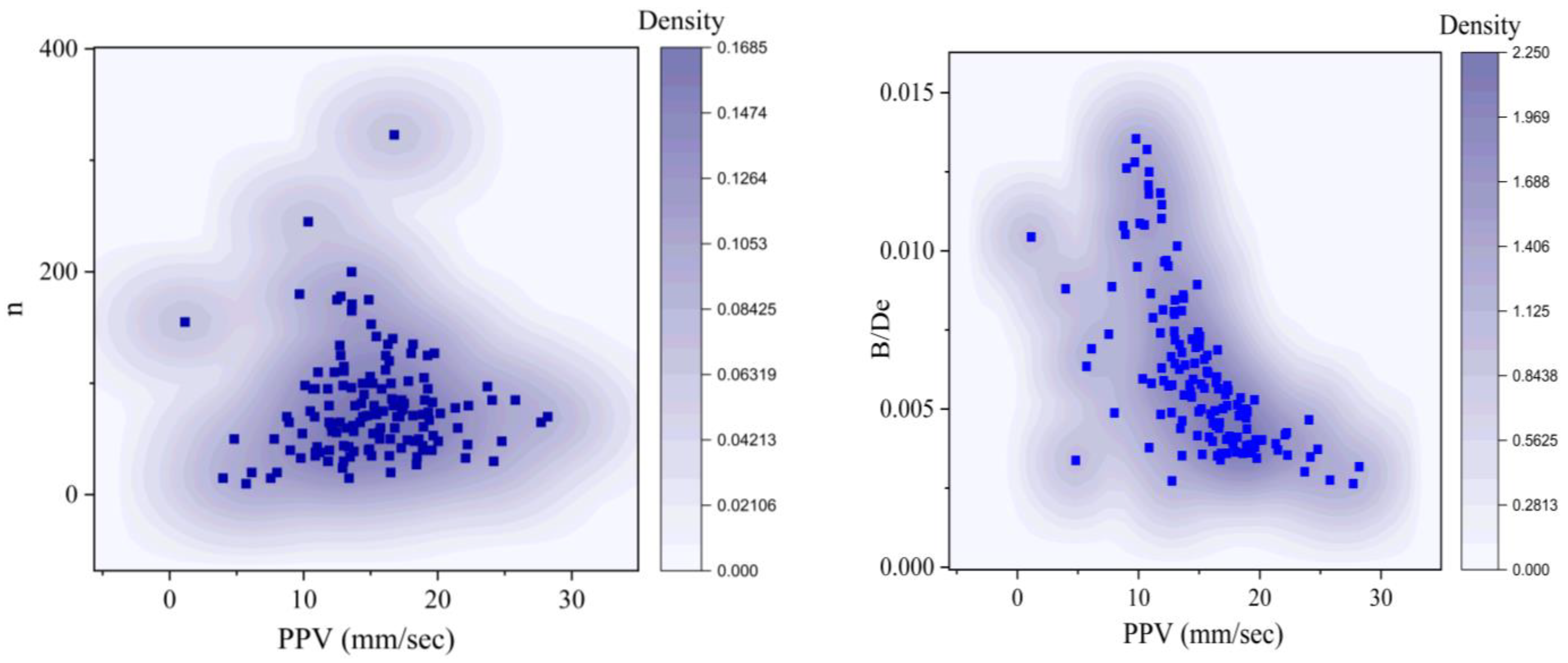
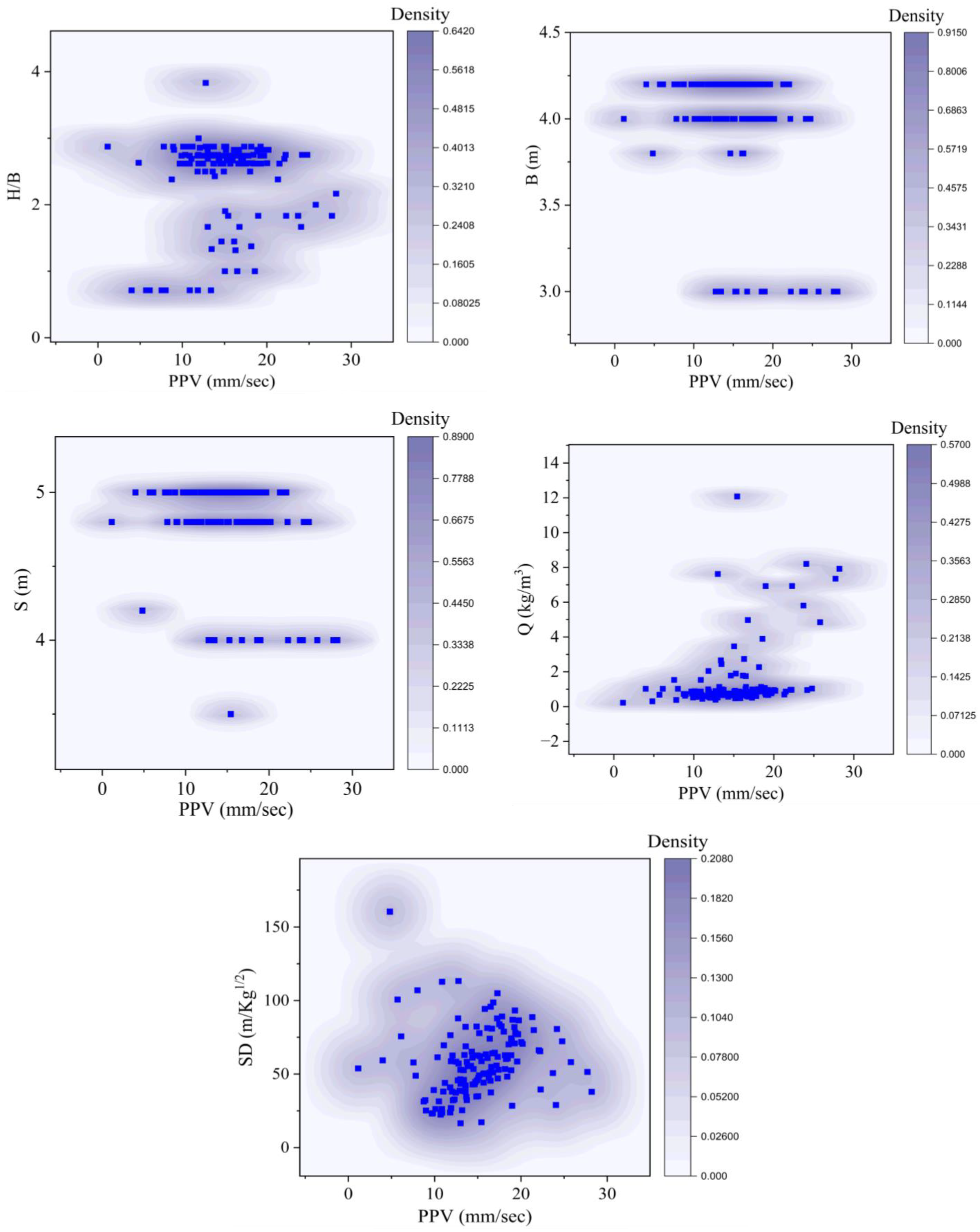
2.3. Data Analysis
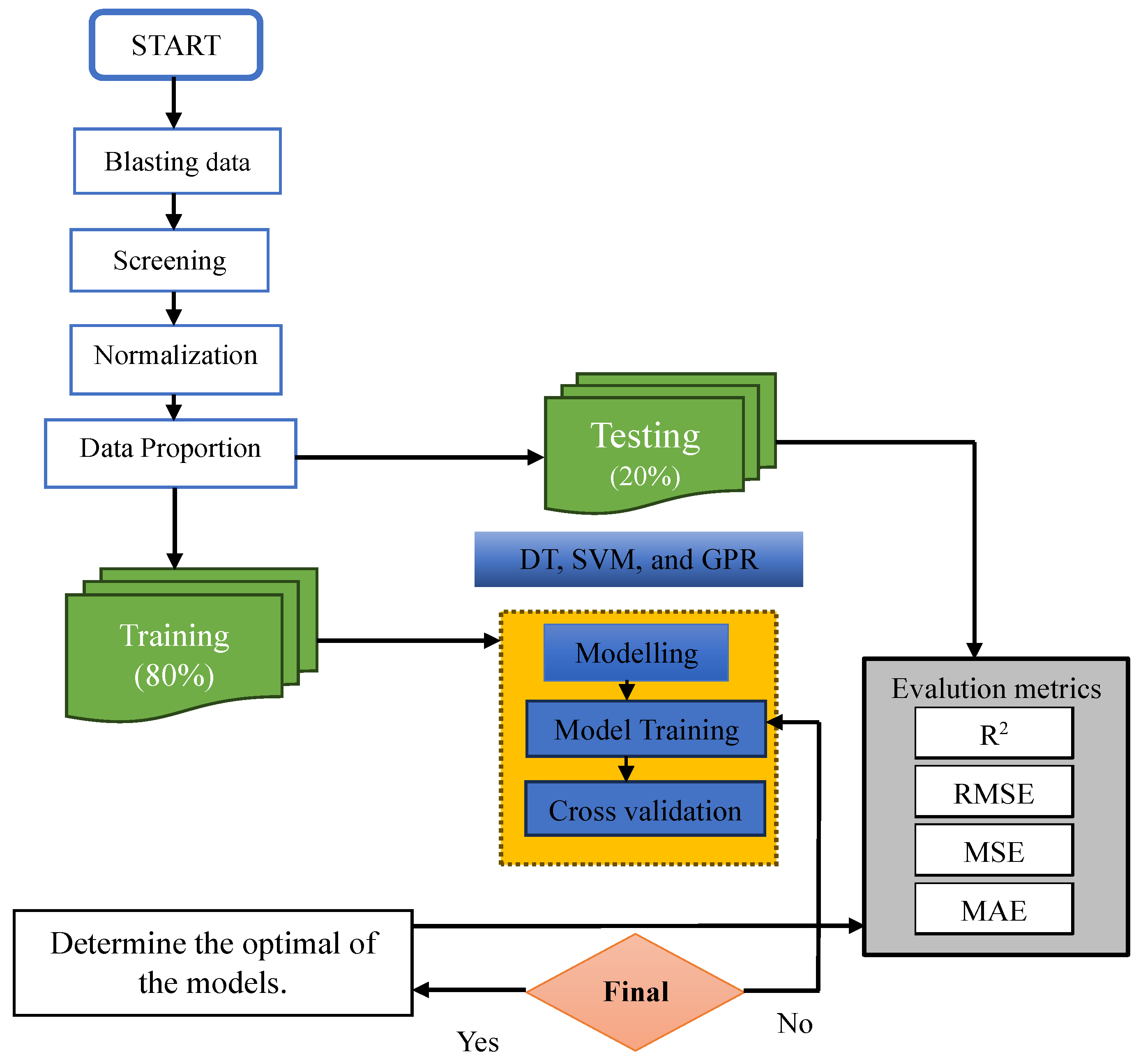
2.4. Machine Learning (ML) Techniques
2.4.1. Decision Tree (DT)
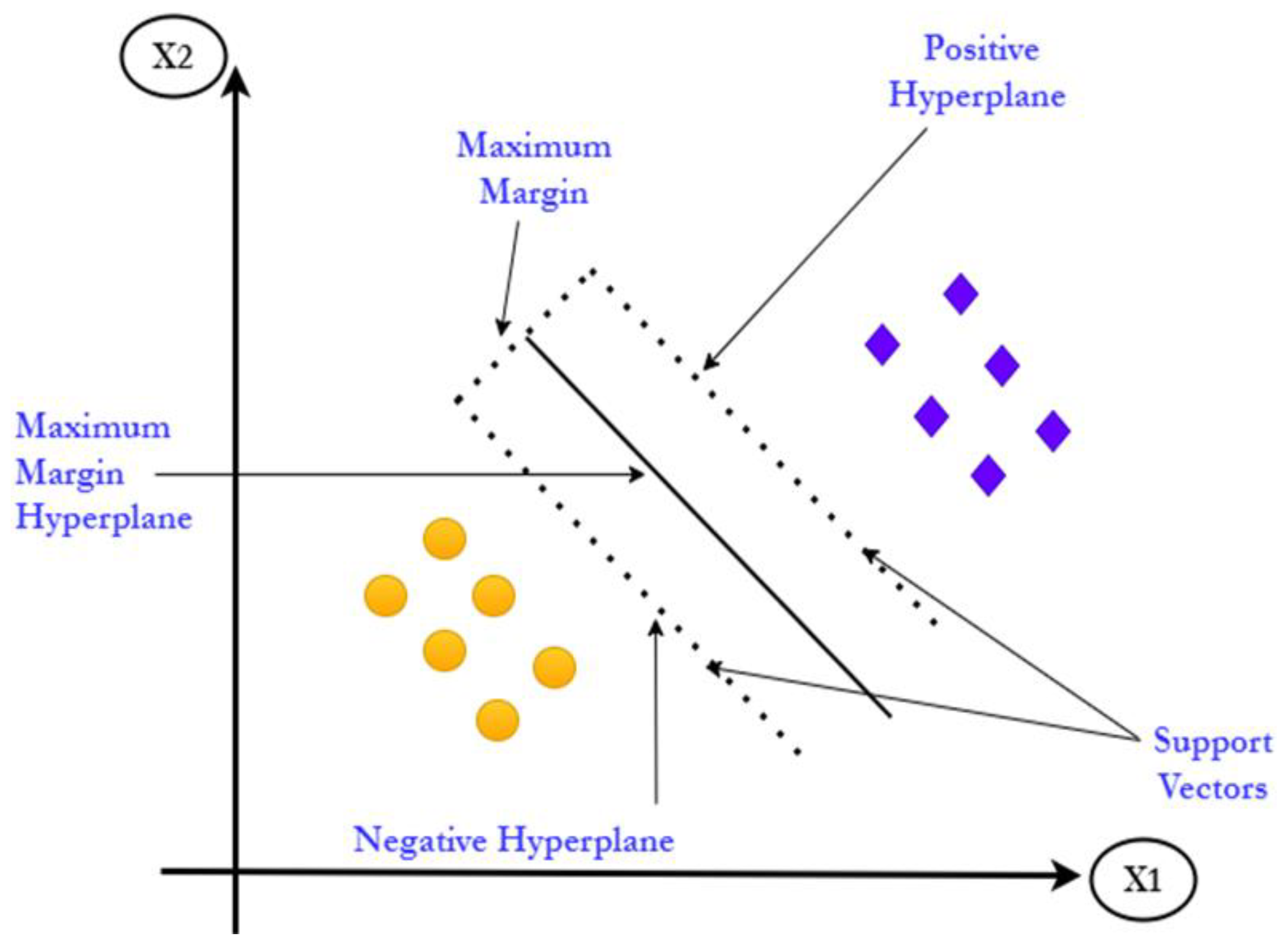
2.4.2. Support Vector Machine (SVM)
2.4.3. Gaussian Process Regression (GPR)
3. Result and Discussion
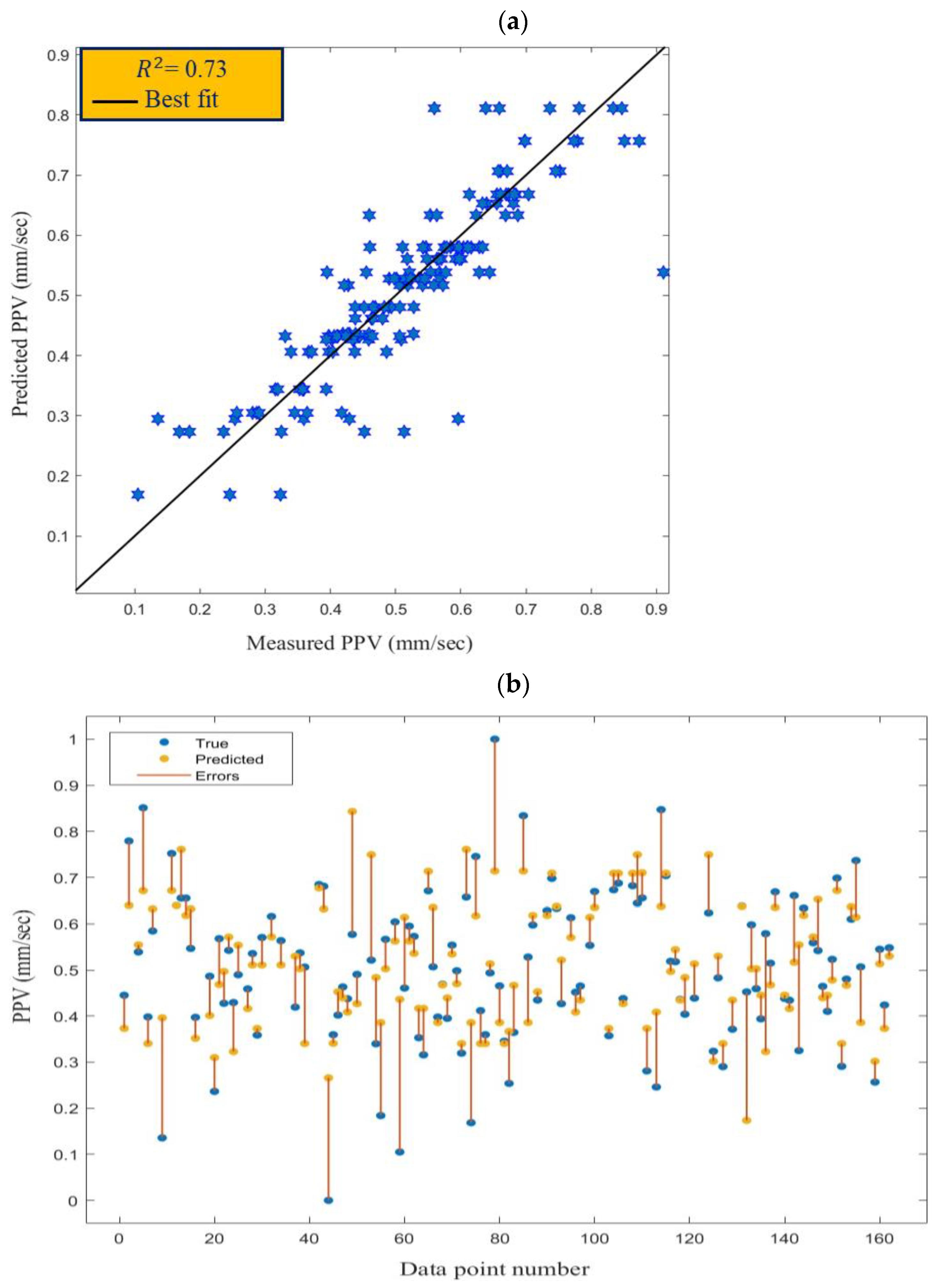
3.1. DT Model
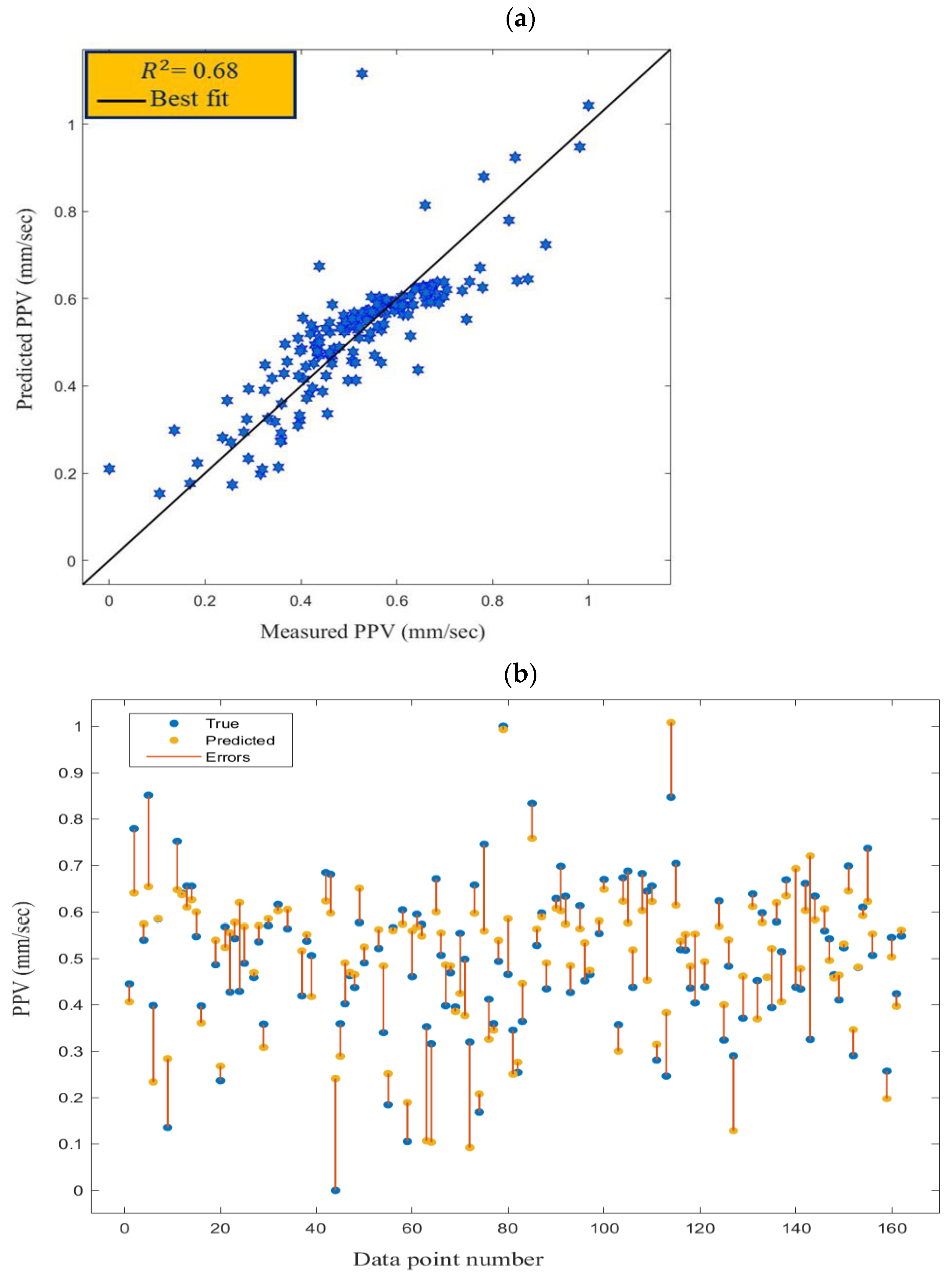
3.2. SVM Model
3.3. GPR Model

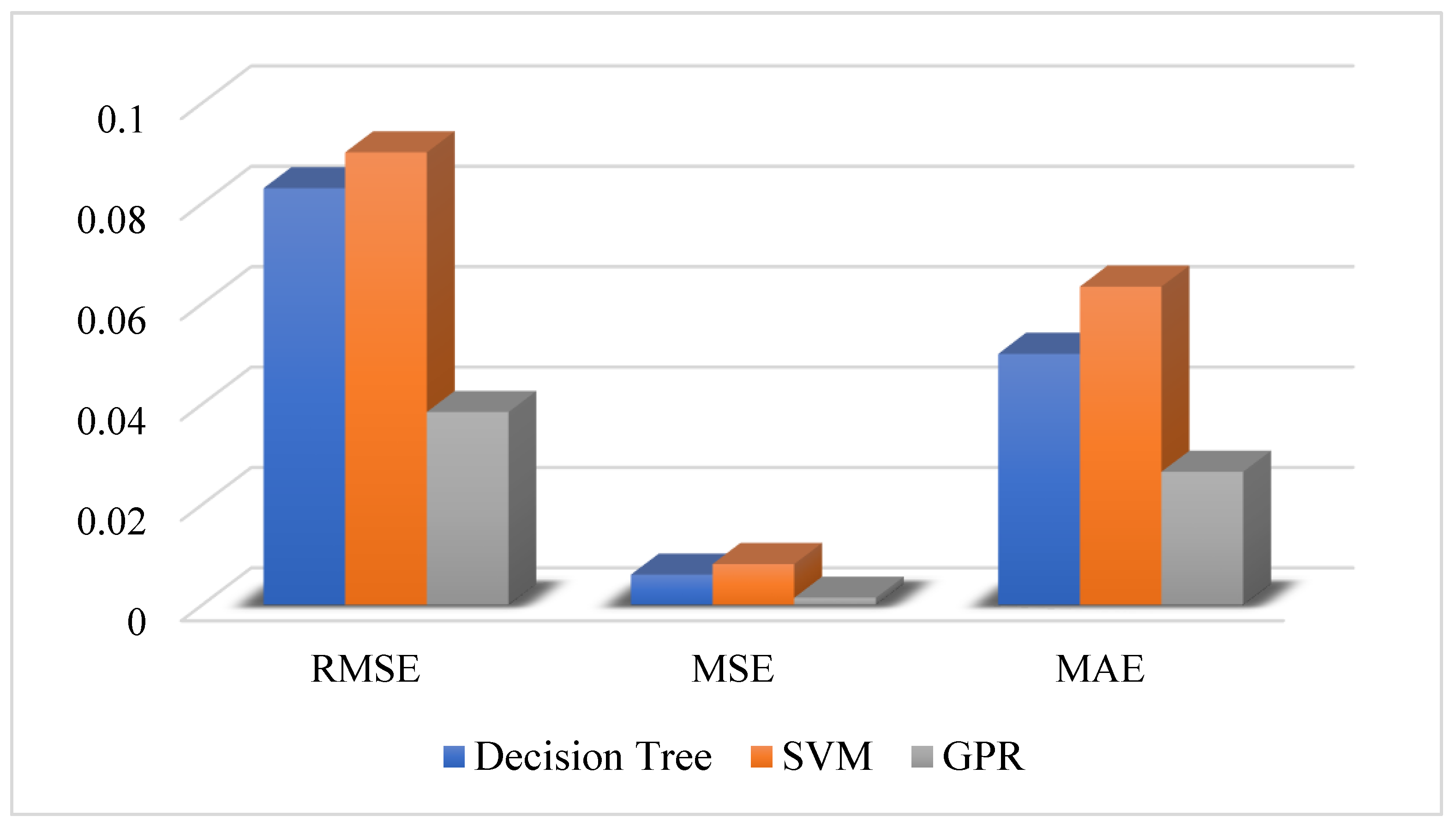
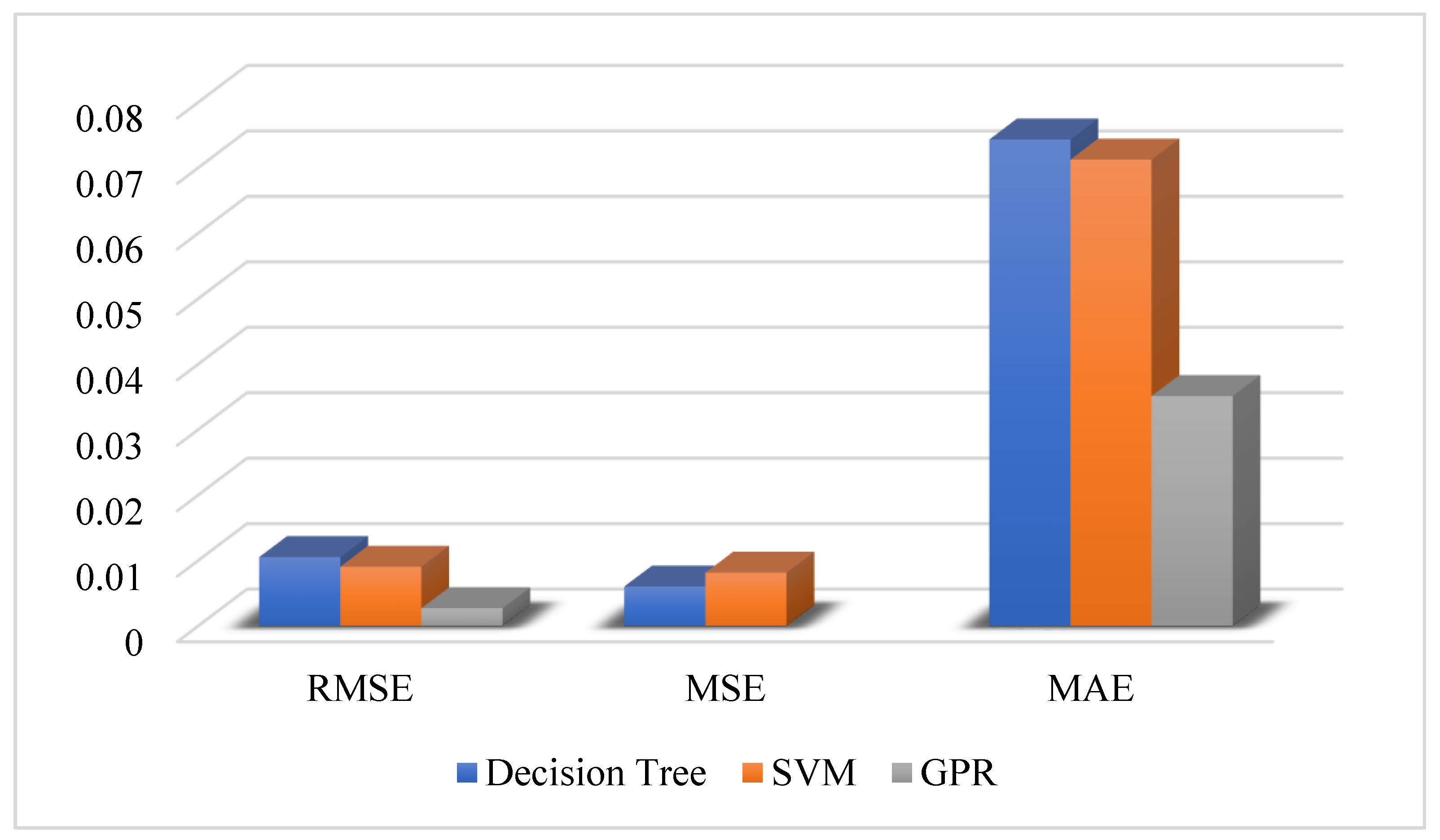
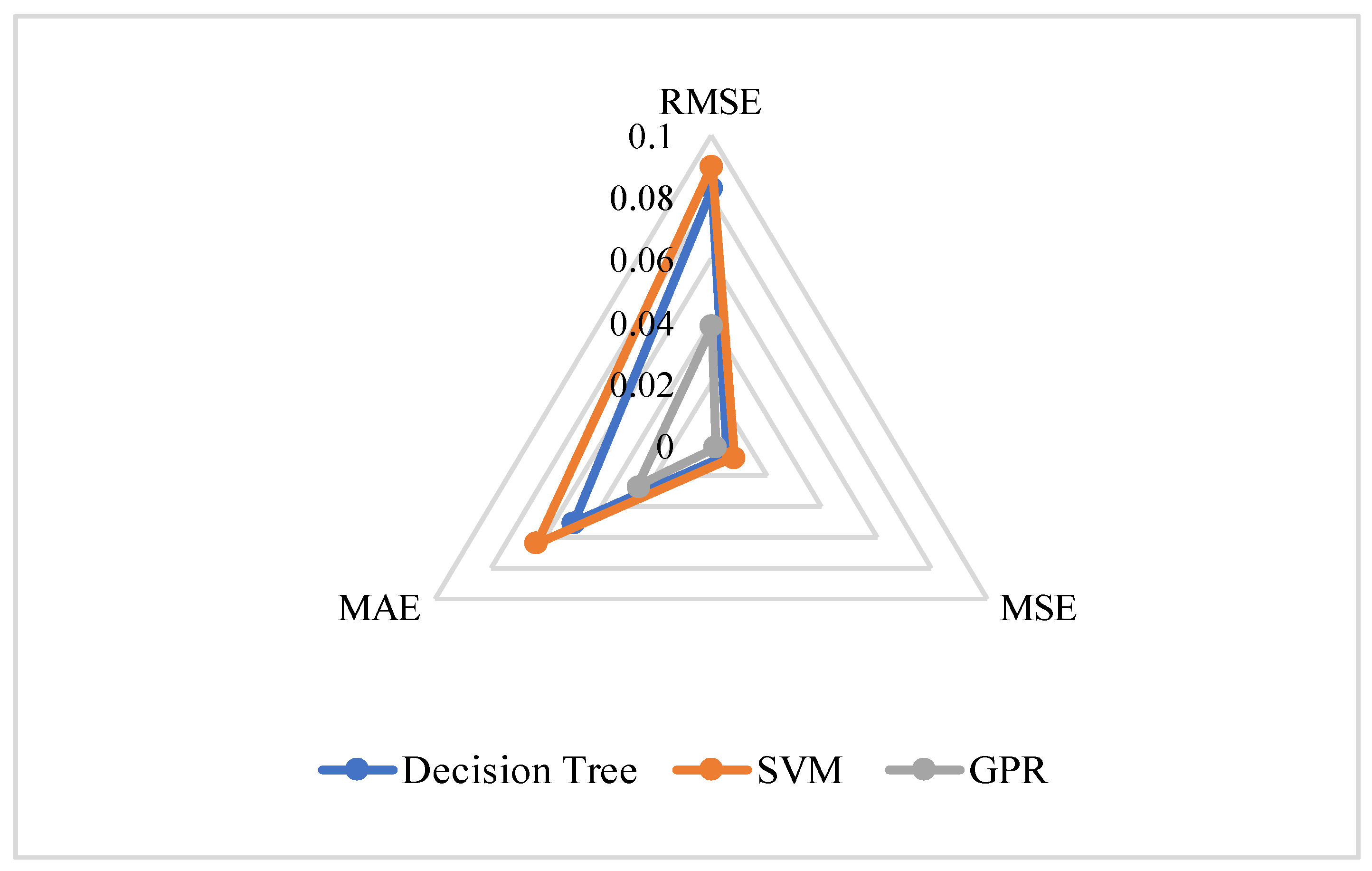
3.4. Validation of the Models
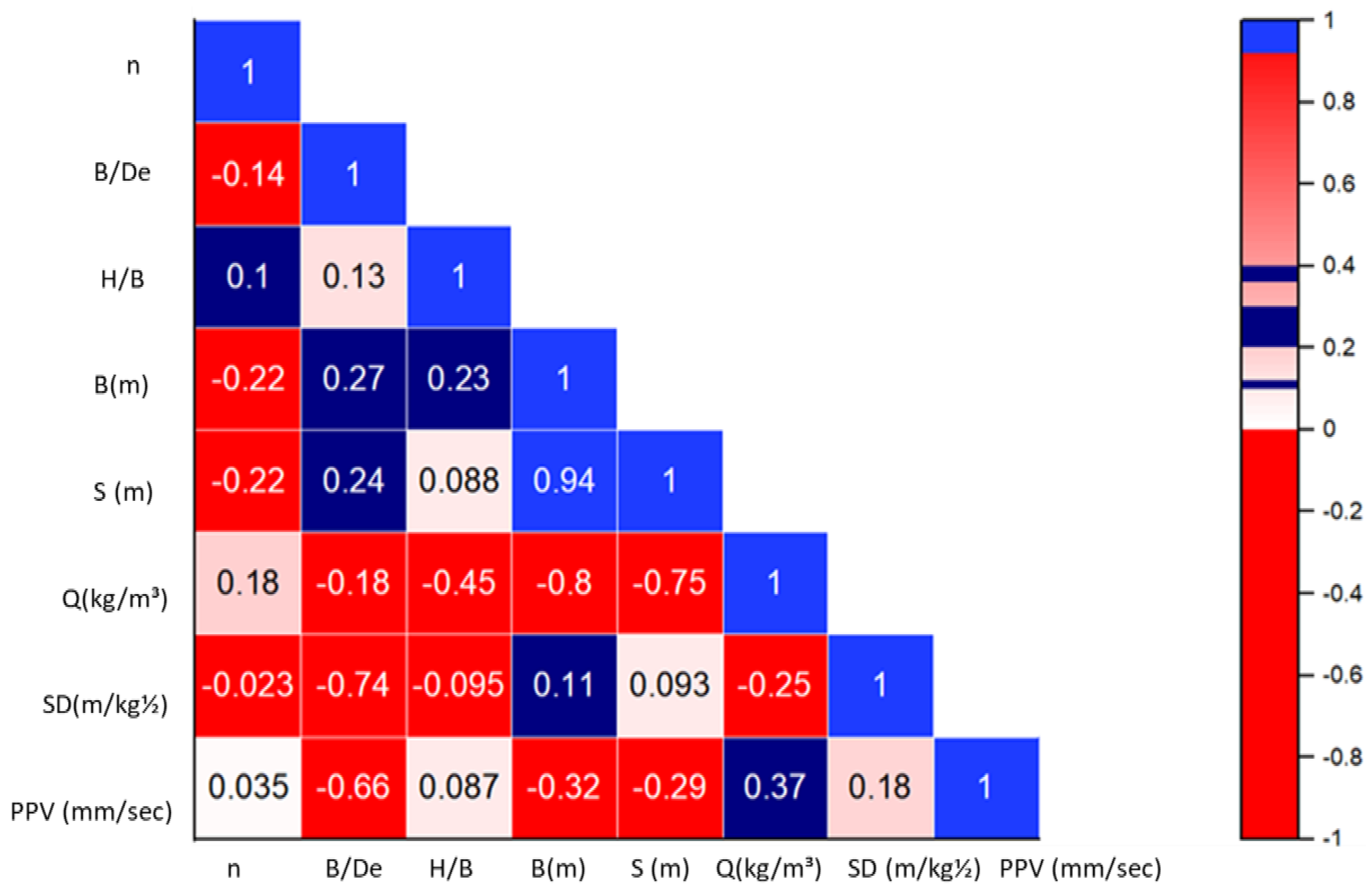
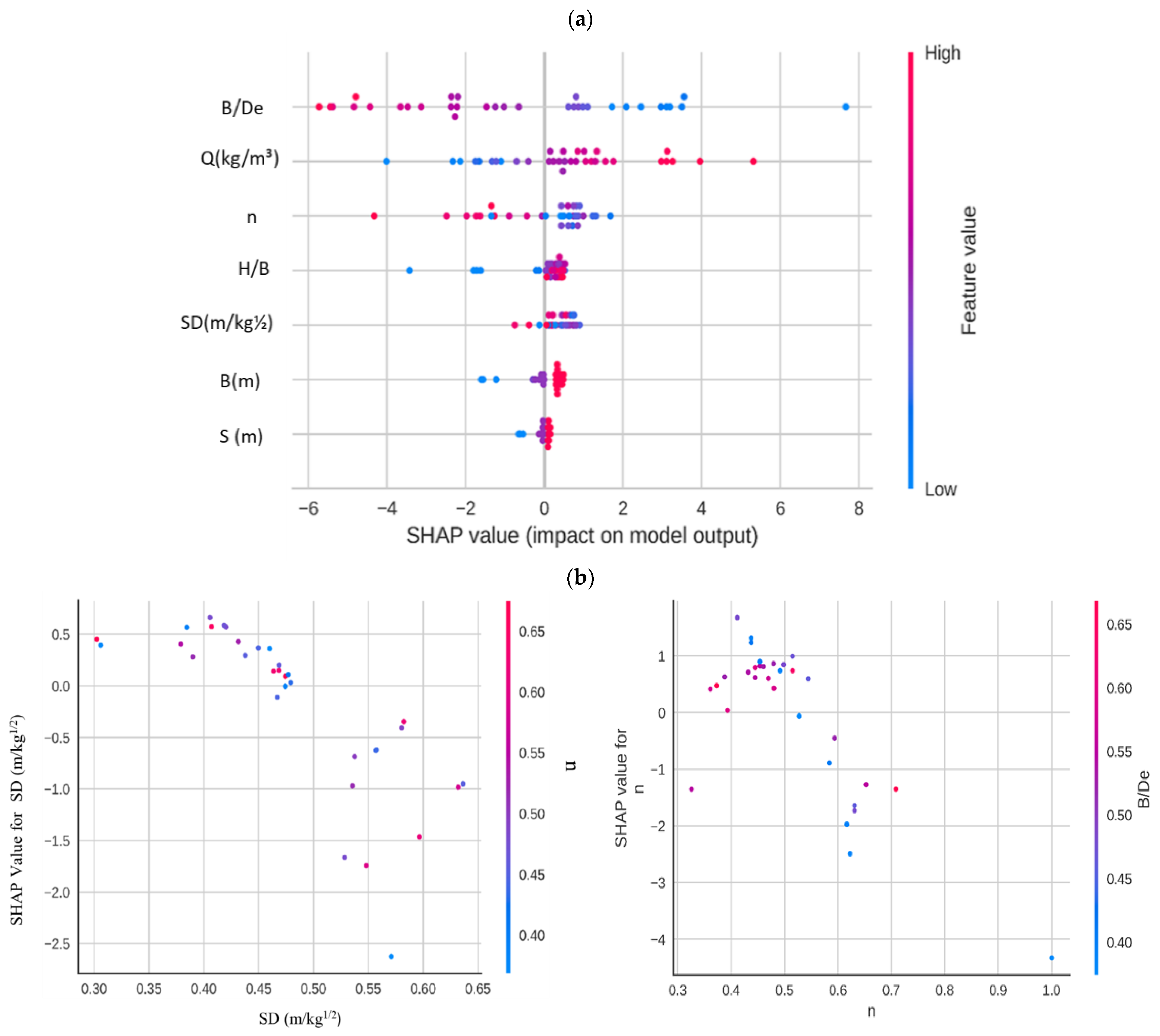
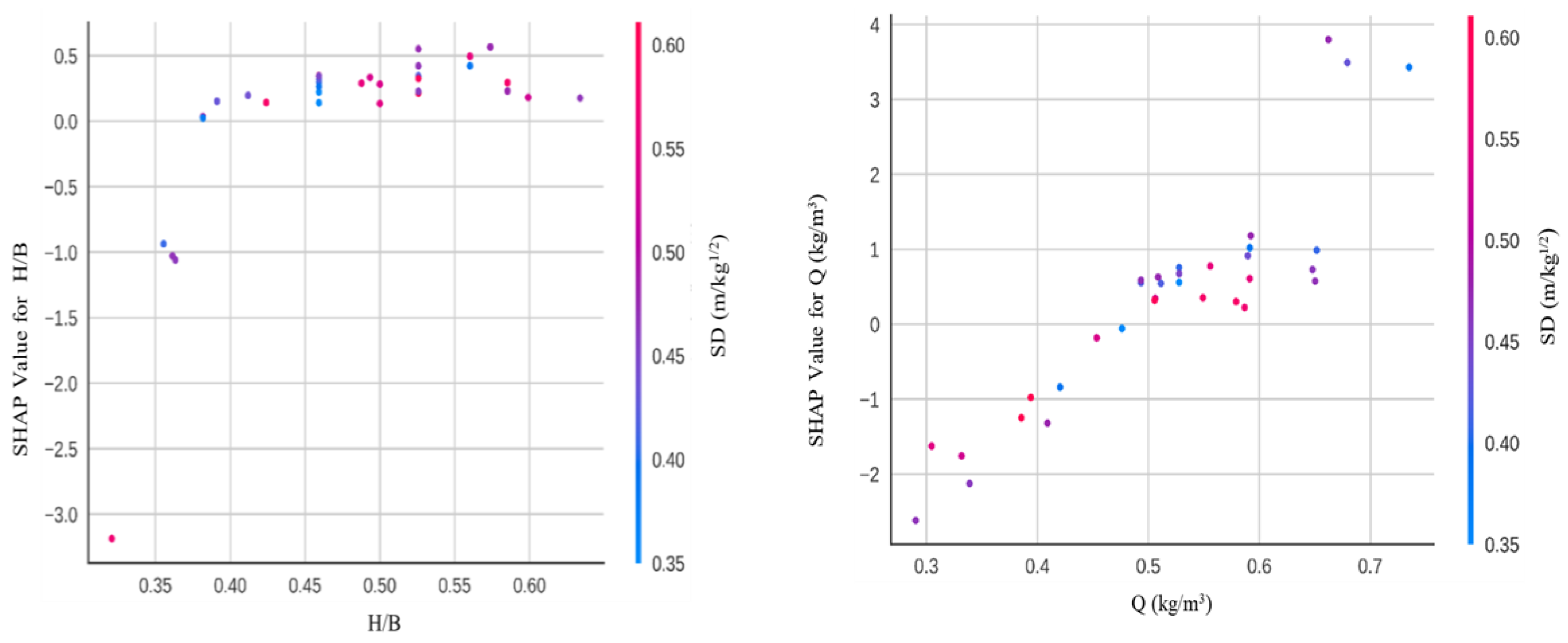
3.5. Sensitivity Analysis
- ⮚
- B/De: The ratio of the blast charge weight to the effective distance. A higher B/De ratio means that more energy is released closer to the target, which can lead to a higher PPV.
- ⮚
- H/B: The ratio of the hole depth to the blast charge diameter. A higher H/B ratio means that the blast charge is more deeply confined, which can also lead to a higher PPV.
- ⮚
- B (m): The blast charge diameter. A more significant blast charge diameter will generally result in a higher PPV.
- ⮚
- S (m): The spacing between blast holes. A smaller spacing will generally result in a higher PPV, but it is essential to consider other factors, such as safety and ground vibration, when selecting the spacing.
- ⮚
- Q (kg/m3): The rock density. A higher rock density will generally result in a higher PPV.
- ⮚
- SD (m/kg1/2): The specific drill energy. This measures the energy required to drill a unit volume of rock. A higher specific drill energy will generally result in a lower PPV.
3.6. Shapley Additive Explanation (SHAP)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| ANFS | Adaptive neuro fuzzy model |
| B | Burden |
| B/De | Burden-to-diameter ratio |
| B/S | Burden-to-spacing ratio |
| CPH | Charge per hole |
| D | Distance |
| Dh | Horizontal distance |
| E | Young’s modulus |
| ED | Elevation difference |
| GA | Genetic algorithm |
| GEP | Gene expression programming |
| GPR | Gaussian process regression |
| HD | Hole depth |
| HDM | Hole diameter |
| H/B | Stiffness ratio |
| HD/B | Hole depth-to-burden ratio |
| IC | Integrity coefficient |
| ICA | Imperialist competitive algorithm |
| MAE | Mean absolute error |
| MAPE | Mean absolute error percentage |
| MARS | Multivariate adaptive regression splines |
| MCPD | Maximum charge per delay |
| MLR | Multiple linear regression |
| MSE | Mean-squared error |
| MVRA | Multivariate regression analysis |
| N | Number of holes |
| NLMR | Nonlinear multiple regression |
| PF | Powder factor |
| Pv | P-wave |
| PPR | Presplit penetration ratio |
| PPV | Peak particle velocity |
| PSO | Particle swarm optimization |
| Qmax | Maximum charge per delay |
| Qtoat | Total amount of charge |
| R2 | Coefficient of determination |
| RMSE | Root-mean-square error |
| RQD | Rock quality designation |
| S | Spacing |
| SHAP | Shapley additive explanation |
| SL | Stemming length |
| SVR | Support vector regression |
| T | Stemming |
| TC | Total charge |
| TS | Tunnel cross section |
| VAF | Variance accounted for |
| VoD | Velocity of detonator |
| XGBoost | Extreme gradient-boosting |
| Ve | Volume of extracted block |
References
- Fissha, Y.; Ikeda, H.; Toriya, H.; Adachi, T.; Kawamura, Y. Application of Bayesian Neural Network (BNN) for the Prediction of Blast-Induced Ground Vibration. Appl. Sci. 2023, 13, 3128. [Google Scholar] [CrossRef]
- Fissha, Y. Mining for a Sustainable World: The Adoption of Sustainable Blasting Techniques. Asp. Min. Miner. Sci. 2023, 10, 1175–1176. [Google Scholar] [CrossRef]
- Yewuhalashet, B.O.T.F. Quarry Slope Stability Assessment Methods with Blast Induced Effect Monitoring in Akoko Edo, Nigeria. Geotech. Geol. Eng. 2023, 41, 2553–2571. [Google Scholar] [CrossRef]
- Taiwo, B.O.; Yewuhalashet, F.; Adamolekun, L.B.; Bidemi, O.O.; Famobuwa, O.V.; Victoria, A.O. Development of Artificial Neural Network Based Mathematical Models for Predicting Small Scale Quarry Powder Factor for Efficient Fragmentation Coupled with Uniformity Index Model. Artif. Intell. Rev. 2023, 56, 14535–14556. [Google Scholar] [CrossRef]
- Olamide Taiwo, B. Improvement of Small-Scale Dolomite Blasting Productivity: Comparison of Existing Empirical Models with Image Analysis Software and Artificial Neural Network Models. J. Min. Environ. 2022, 13, 627–641. [Google Scholar] [CrossRef]
- Kweku, C.; Victor, A.; Temeng, A.; Yevenyo, Y. Novel Approach to Predicting Blast-Induced Ground Vibration Using Gaussian Process Regression. Eng. Comput. 2020, 36, 29–42. [Google Scholar] [CrossRef]
- Onederra, I.A.; Furtney, J.K.; Sellers, E.; Iverson, S. International Journal of Rock Mechanics & Mining Sciences Modelling Blast Induced Damage from a Fully Coupled Explosive Charge. Int. J. Rock Mech. Min. Sci. 2013, 58, 73–84. [Google Scholar] [CrossRef]
- Ragam, P.; Komalla, A.R.; Kanne, N. Estimation of Blast-Induced Peak Particle Velocity Using Ensemble Machine Estimation of Blast-Induced Peak Particle Velocity Using Ensemble Machine Learning Algorithms: A Case Study. Noise Vib. Worldw. 2022, 53, 404–413. [Google Scholar] [CrossRef]
- Khandelwal, M.; Jahed, D.; Roohollah, A.; Faradonbeh, S. Classification and Regression Tree Technique in Estimating Peak Particle Velocity Caused by Blasting. Eng. Comput. 2017, 33, 45–53. [Google Scholar] [CrossRef]
- Khandelwal, M.; Kankar, P.K. Prediction of Blast-Induced Air Overpressure Using Support Vector Machine. Arab. J. Geosci. 2011, 4, 427–433. [Google Scholar] [CrossRef]
- Zhou, J.; Li, C.; Koopialipoor, M.; Armaghani, D.J.; Pham, B.T. Development of a New Methodology for Estimating the Amount of PPV in Surface Mines Based on Prediction and Probabilistic Models (GEP-MC). Int. J. Min. Reclam. Environ. 2020, 35, 48–68. [Google Scholar] [CrossRef]
- Khandelwal, M.; Kumar, D.L.; Yellishetty, M. Application of Soft Computing to Predict Blast-Induced Ground Vibration. Eng. Comput. 2011, 27, 117–125. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, P.; Sharma, S.K.; Kishore, N.; Singh, C.S. Quantitative Assessment of BIGV and Structural Response Based on Velocity and Frequency around an Opencast Mine. Curr. Sci. 2021, 121, 275–285. [Google Scholar] [CrossRef]
- Kekeç, B.; Ghiloufi, D. Propagation characteristics of surface and in-depth vibrations in sand grounds: A comparative analysis. Konya J. Eng. Sci. 2022, 10, 1–17. [Google Scholar] [CrossRef]
- Paurush, P.; Rai, P.; Sharma, S.K. Selection of Blasting Design Parameters Affecting Peak Particle Velocity—A Case Study. Min. Metall. Explor. 2021, 38, 1435–1447. [Google Scholar] [CrossRef]
- Görgülü, K.; Arpaz, E.; Demirci, A.; Koçaslan, A.; Dilmaç, M.K.; Yüksek, A.G. Investigation of Blast-Induced Ground Vibrations in the Tülü Boron Open Pit Mine. Bull. Eng. Geol. Environ. 2013, 72, 555–564. [Google Scholar] [CrossRef]
- Saadat, M.; Khandelwal, M.; Monjezi, M. An ANN-Based Approach to Predict Blast-Induced Ground Vibration of Gol-E-Gohar Iron Ore Mine, Iran. J. Rock Mech. Geotech. Eng. 2014, 6, 67–76. [Google Scholar] [CrossRef]
- Lawal, A.I.; Idris, M.A. An Artificial Neural Network-Based Mathematical Model for the Prediction of Blast-Induced Ground Vibrations. Int. J. Environ. Stud. 2020, 77, 318–334. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Hajihassani, M.; Monjezi, M.; Mohamad, E.T.; Marto, A.; Moghaddam, M.R. Application of Two Intelligent Systems in Predicting Environmental Impacts of Quarry Blasting. Arab. J. Geosci. 2015, 8, 9647–9665. [Google Scholar] [CrossRef]
- Vasović, D.; Kostić, S.; Ravilić, M.; Trajković, S. Environmental Impact of Blasting at Drenovac Limestone Quarry (Serbia). Environ. Earth Sci. 2014, 72, 3915–3928. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Evaluation of Blast-Induced Ground Vibration Predictors. Soil Dyn. Earthq. Eng. 2007, 27, 116–125. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Bui, H.-B.; Cuong, D.T. Developing an XGBoost model to predict blast-induced peak particle velocity in an open-pit mine: A case study. Acta Geophys. 2019, 67, 477–490. [Google Scholar] [CrossRef]
- Lawal, A.I. An Artificial Neural Network-Based Mathematical Model for the Prediction of Blast-Induced Ground Vibration in Granite Quarries in Ibadan, Oyo State, Nigeria. Sci. Afr. 2020, 8, e00413. [Google Scholar] [CrossRef]
- Zhang, Y. Study on Attenuation Law of Open-Pit Bench Blasting Vibration. Procedia Eng. 2014, 84, 868–872. [Google Scholar] [CrossRef][Green Version]
- Rana, A.; Bhagat, N.K.; Jadaun, G.P.; Rukhaiyar, S.; Pain, A.; Singh, P.K. Predicting Blast-Induced Ground Vibrations in Some Indian Tunnels: A Comparison of Decision Tree, Artificial Neural Network and Multivariate Regression Methods. Min. Metall. Explor. 2020, 37, 1039–1053. [Google Scholar] [CrossRef]
- Verma, A.K.; Singh, T.N. Intelligent Systems for Ground Vibration Measurement: A Comparative Study. Eng. Comput. 2011, 27, 225–233. [Google Scholar] [CrossRef]
- Ghasemi, E.; Ataei, M. Development of a Fuzzy Model for Predicting Ground Vibration Caused by Rock Blasting in Surface Mining. J. Vib. Control 2012, 19, 755–770. [Google Scholar] [CrossRef]
- Iphar, M.; Yavuz, M.; Ak, H. Prediction of Ground Vibrations Resulting from the Blasting Operations in an Open-Pit Mine by Adaptive Neuro-Fuzzy Inference System. Environ. Geol. 2008, 56, 97–107. [Google Scholar] [CrossRef]
- Xi, B.; Li, E.; Fissha, Y.; Zhou, J.; Segarra, P. LGBM-Based Modeling Scenarios to Compressive Strength of Recycled Aggregate Concrete with SHAP Analysis. Mech. Adv. Mater. Struct. 2023. [Google Scholar] [CrossRef]
- Hauke, J.; Kossowski, T. Comparison of Values of Pearson’s and Spearman’s Correlation Coefficients on the Same Sets of Data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Khatti, J.; Grover, K.S. Determination of the Optimum Performance Ai Model and Methodology To Predict the Compaction Parameters of Soils. ICTACT J. Soft Comput. 2022, 12, 2640–2650. [Google Scholar]
- Kingsford, C.; Salzberg, S.L. What Are Decision Trees? Nat. Biotechnol. 2008, 26, 1011–1012. [Google Scholar] [CrossRef] [PubMed]
- Kamiński, B.; Jakubczyk, M.; Szufel, P. A Framework for Sensitivity Analysis of Decision Trees. Cent. Eur. J. Oper. Res. 2018, 26, 135–159. [Google Scholar] [CrossRef] [PubMed]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar] [CrossRef] [PubMed]






| Authors | Total Datasets | Input Parameters | AI Models | Evaluation Metrics |
|---|---|---|---|---|
| Armaghani et al. [19] | 109 | BS, MC, HD, ST, SD, DI, PF, RQD | ANFIS | R2 = 0.97 |
| Vasovic et al. [20] | 32 | D, TC, MCPD | Empirical predictor, ANN | R2 = 0.9 RMSE = 0.018 |
| Khandelwal and Singh [21] | 150 | B, S, MCPD, HD, D V, E, Pv, BI, VoD | ANN, MVRA, empirical model | MAE = 0.24 |
| Nguyen et al. [22] | 136 | DI, MC | HKM-CA | R2 = 0.99 |
| Saadat et al. [17] | 69 | D, MCPD, HD | ANN, MLR, empirical model | R2 = 0.95 MSE = 0.00072 |
| Lawal [23] | 100 | D, MCPD | ANN, MLR | R2 = 0.988, RMSE = 2.90, VAF = 98.74 MAPE = 7.14 |
| Zhang [24] | 175 | PF, T, B, S H, D, MCPD | PSO-XG Boost, empirical models | R2 = 0.96 RMSE = 0.58, MAE = 0.34 VAF = 96.08 |
| Rana et al. [25] | 137 | MCPD, HDM, CPH, HD, TC, D, NH, TS | ANN, MVRA, CART, empirical predictor | RMSE = 1.56 R2 = 0.95 |
| Verma and Singh [26] | 127 | MCPD, TC HD, B, S, T, | GA, ANN, MVRA, empirical predictor | R2 = 0.99 MAPE = 0.088 |
| Ghasemi et al. [27] | 120 | B, S, T, NH, MCPD, D | ANFIS-PSO, SVR | R2 = 0.96 RMSE = 1.83 |
| Iphar et al. [28] | 44 | MCPD, D | ANFIS, MLR | R2 = 0.98 RMSE = 0.80 |
| Variables | N | Missing | Mean | Median | SD | Variance | Range | Minimum | Maximum |
|---|---|---|---|---|---|---|---|---|---|
| n | 140 | 0 | 78.729 | 70.00 | 46.746 | 2185.178 | 313 | 10 | 323 |
| B/De | 140 | 0 | 0.000 | 0.00 | 0.000 | 0.000 | 0 | 0 | 0 |
| H/B | 140 | 0 | 1.779 | 2.00 | 0.563 | 0.318 | 3.00 | 0.00 | 3.00 |
| B | 140 | 0 | 3.871 | 4.00 | 0.336 | 0.113 | 1 | 3 | 4 |
| S | 140 | 0 | 4.536 | 5.00 | 0.515 | 0.265 | 2 | 3 | 5 |
| Q | 140 | 0 | 0.707 | 0.00 | 1.837 | 3.374 | 12 | 0 | 12 |
| SD | 140 | 0 | 57.257 | 55.00 | 23.277 | 541.833 | 144 | 16 | 160 |
| PPV | 140 | 0 | 14.571 | 14.50 | 4.560 | 20.793 | 27 | 1 | 28 |
| Main Parameters | Condition |
|---|---|
| Iteration | 30 |
| Maximum time for training | 300 s |
| Number of grid division | 10 |
| Optimizer | Bayesian Optimisation |
| Acquisition function | Expected improved per second plus |
| Main Parameters | Condition/Value |
|---|---|
| Kernel scale | Auto |
| Kernel function | Auto |
| Basic function | Auto |
| Sigma | Auto |
| Signal standard deviation | 3.55 |
| Optimizer numeric parameters | Enable |
| Standardize | Enable |
| Models | RMSE | MSE | MAE | R2 |
|---|---|---|---|---|
| DT | 0.083 | 0.006 | 0.050 | 0.73 |
| SVM | 0.090 | 0.008 | 0.063 | 0.68 |
| GPR | 0.038 | 0.001 | 0.026 | 0.94 |
| Models | RMSE | MSE | MAE | R2 |
|---|---|---|---|---|
| DT | 0.010 | 0.006 | 0.074 | 0.58 |
| SVM | 0.009 | 0.008 | 0.071 | 0.64 |
| GPR | 0.002 | 0 | 0.035 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fissha, Y.; Ikeda, H.; Toriya, H.; Owada, N.; Adachi, T.; Kawamura, Y. Evaluation and Prediction of Blast-Induced Ground Vibrations: A Gaussian Process Regression (GPR) Approach. Mining 2023, 3, 659-682. https://doi.org/10.3390/mining3040036
Fissha Y, Ikeda H, Toriya H, Owada N, Adachi T, Kawamura Y. Evaluation and Prediction of Blast-Induced Ground Vibrations: A Gaussian Process Regression (GPR) Approach. Mining. 2023; 3(4):659-682. https://doi.org/10.3390/mining3040036
Chicago/Turabian StyleFissha, Yewuhalashet, Hajime Ikeda, Hisatoshi Toriya, Narihiro Owada, Tsuyoshi Adachi, and Youhei Kawamura. 2023. "Evaluation and Prediction of Blast-Induced Ground Vibrations: A Gaussian Process Regression (GPR) Approach" Mining 3, no. 4: 659-682. https://doi.org/10.3390/mining3040036
APA StyleFissha, Y., Ikeda, H., Toriya, H., Owada, N., Adachi, T., & Kawamura, Y. (2023). Evaluation and Prediction of Blast-Induced Ground Vibrations: A Gaussian Process Regression (GPR) Approach. Mining, 3(4), 659-682. https://doi.org/10.3390/mining3040036







