A Comprehensive Review of Large Strain Consolidation Testing for Application in Oil Sands Mine Tailings
Abstract
1. Introduction
1.1. Theoretical Background
1.2. Constitutive Relationships
2. Large Strain Consolidation Tests
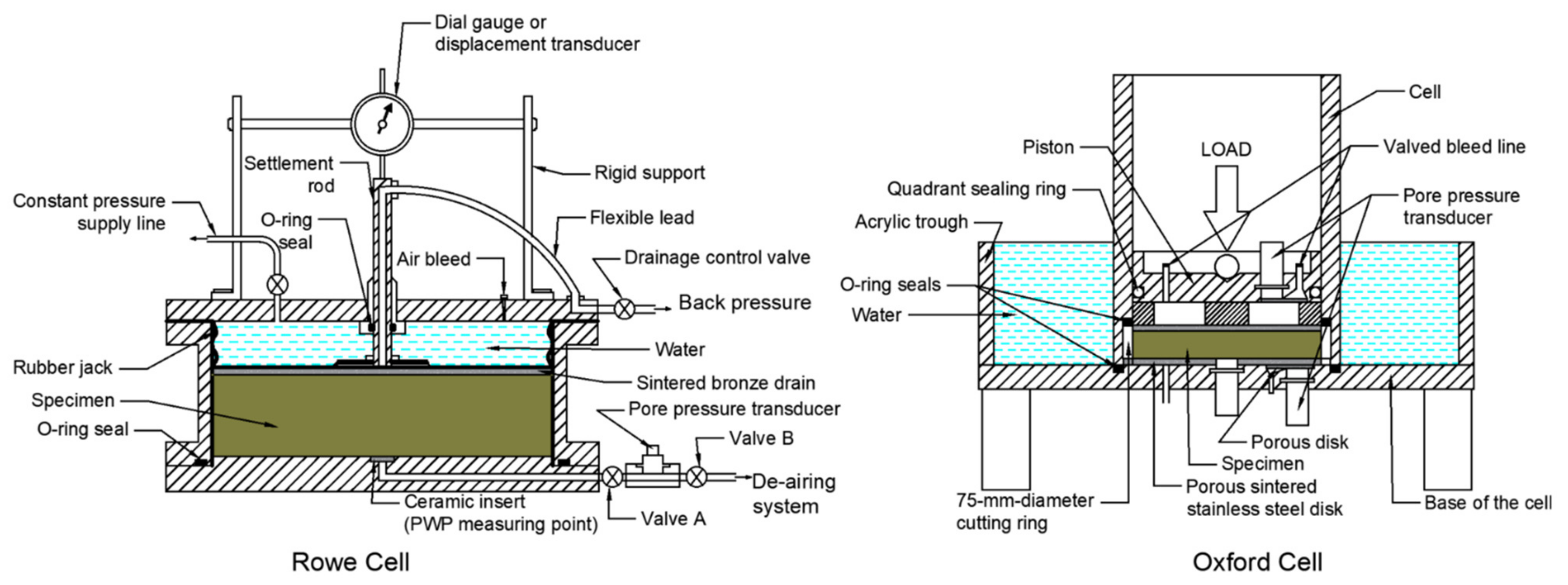
2.1. Modified Conventional Oedometer Consolidation Test
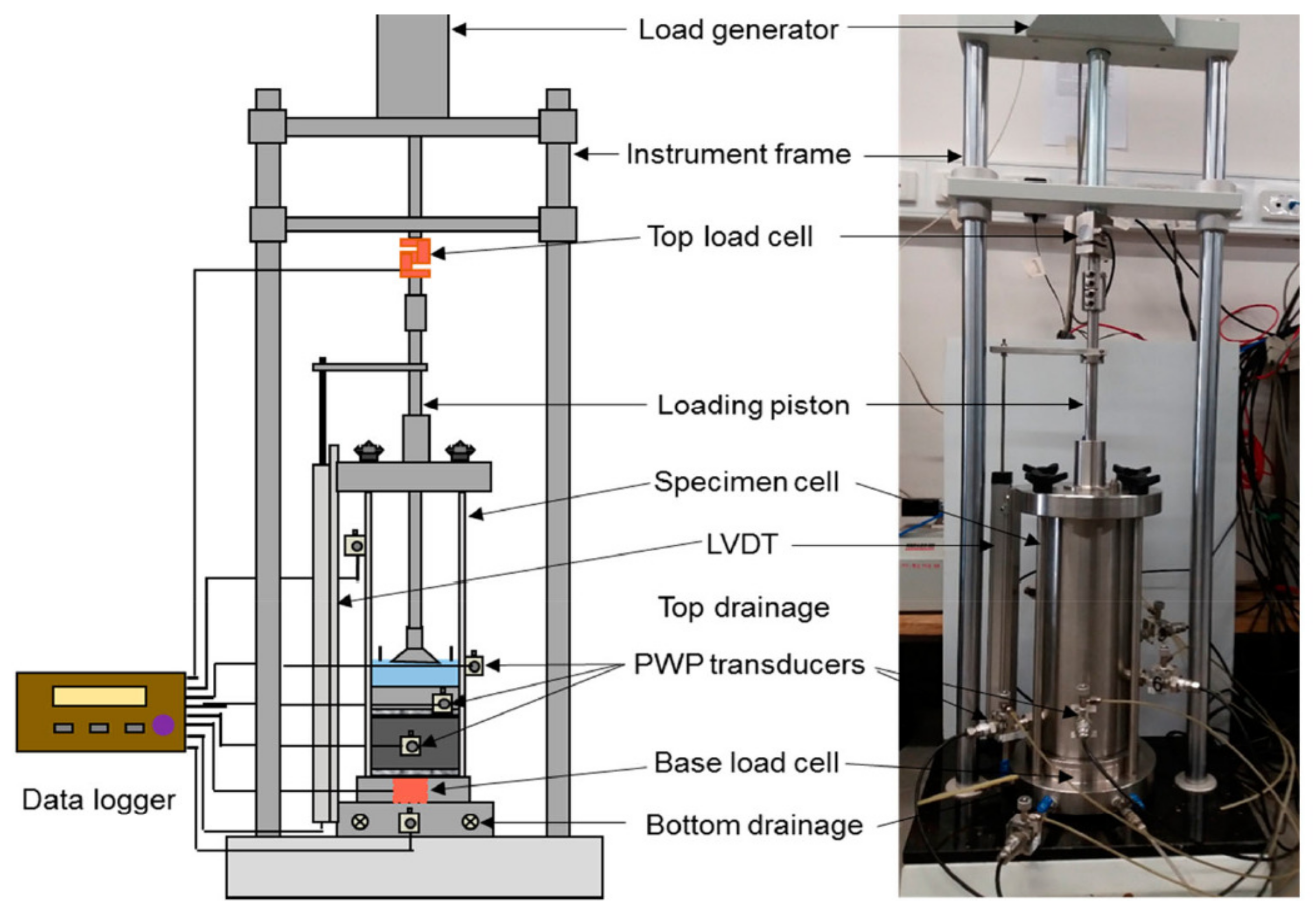
2.2. Multi-Step Loading Large Strain Consolidation Test
2.3. Constant Rate of Deformation (CRD) Test
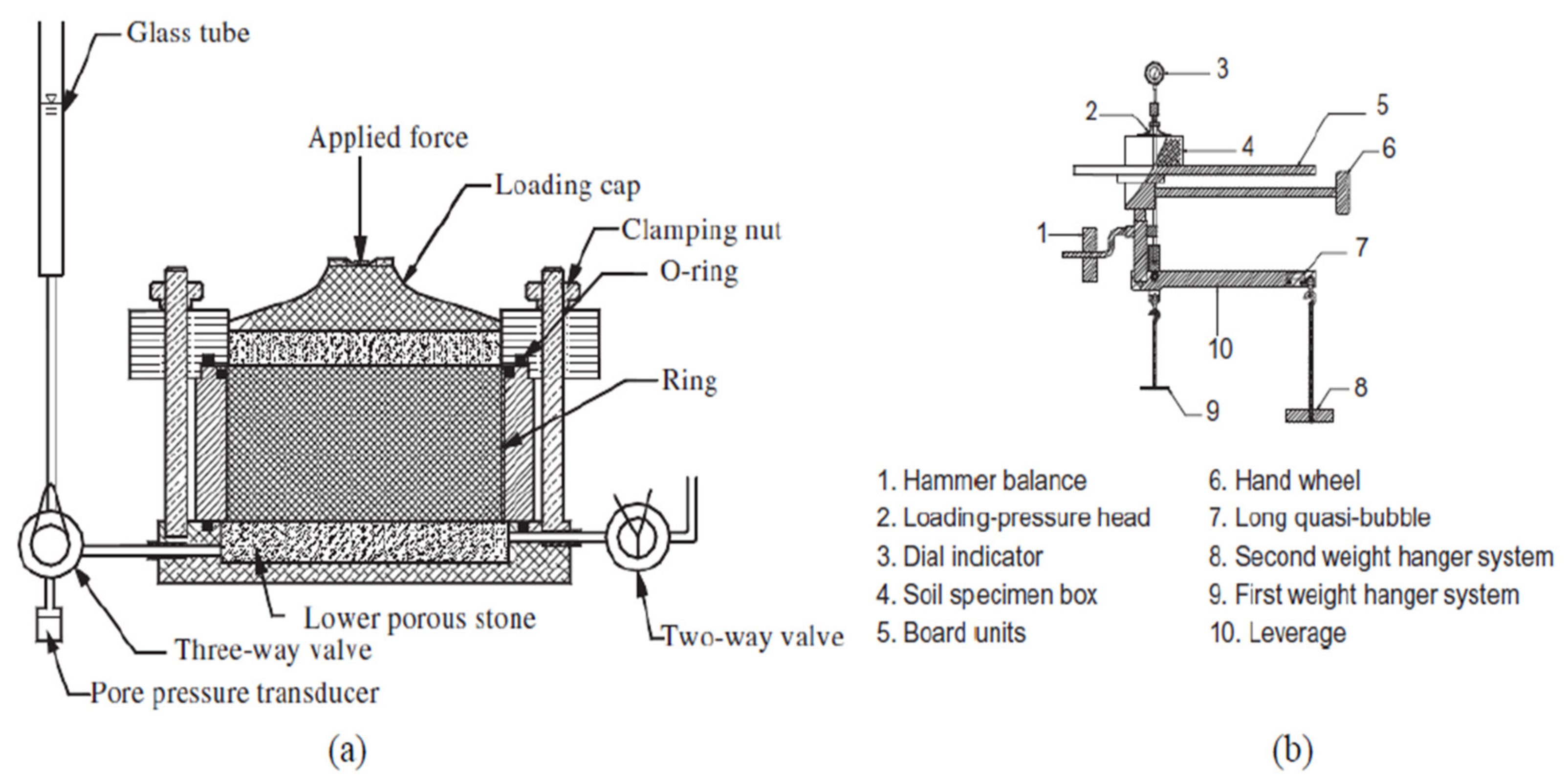
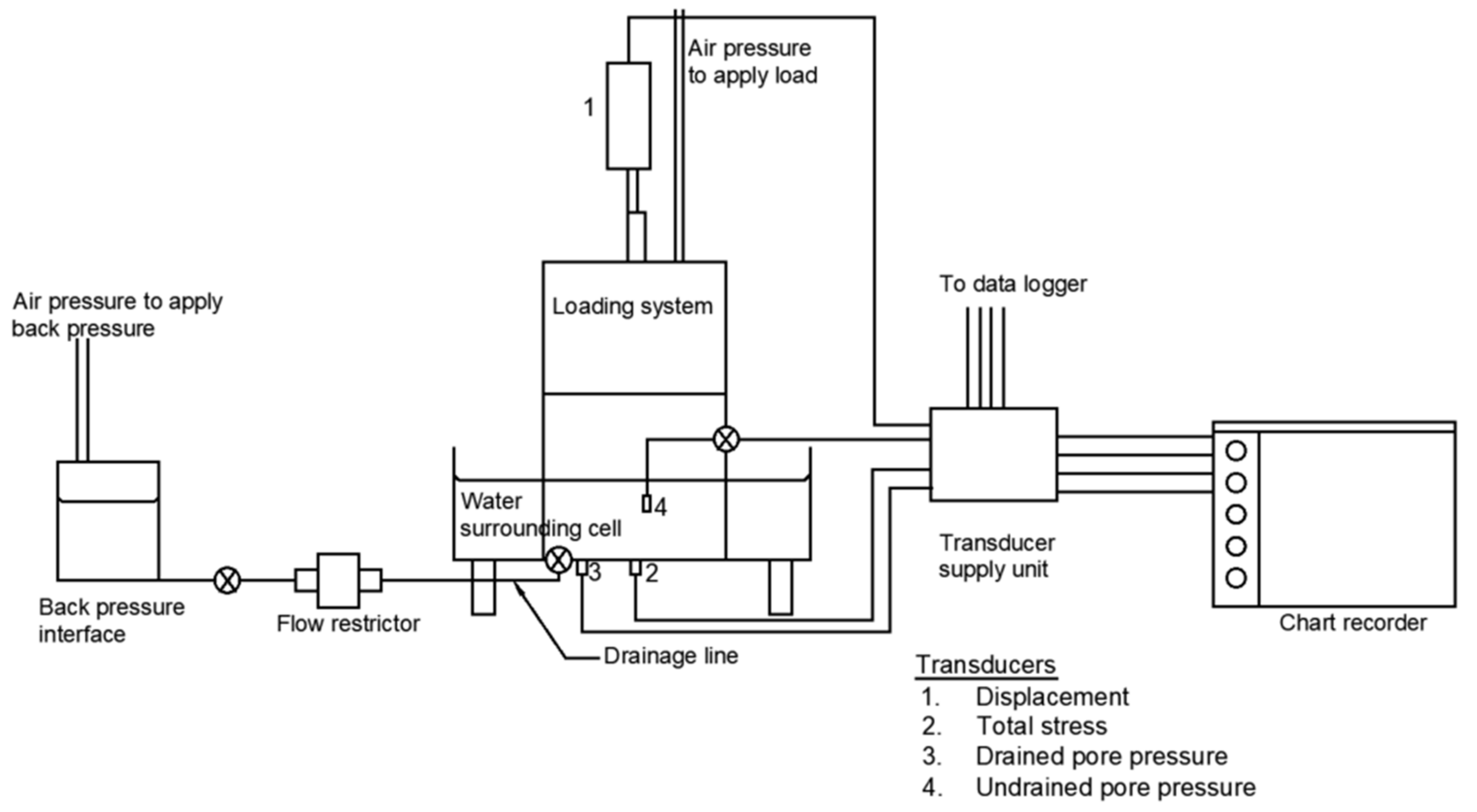
2.4. Controlled Hydraulic Gradient (CHG) Test

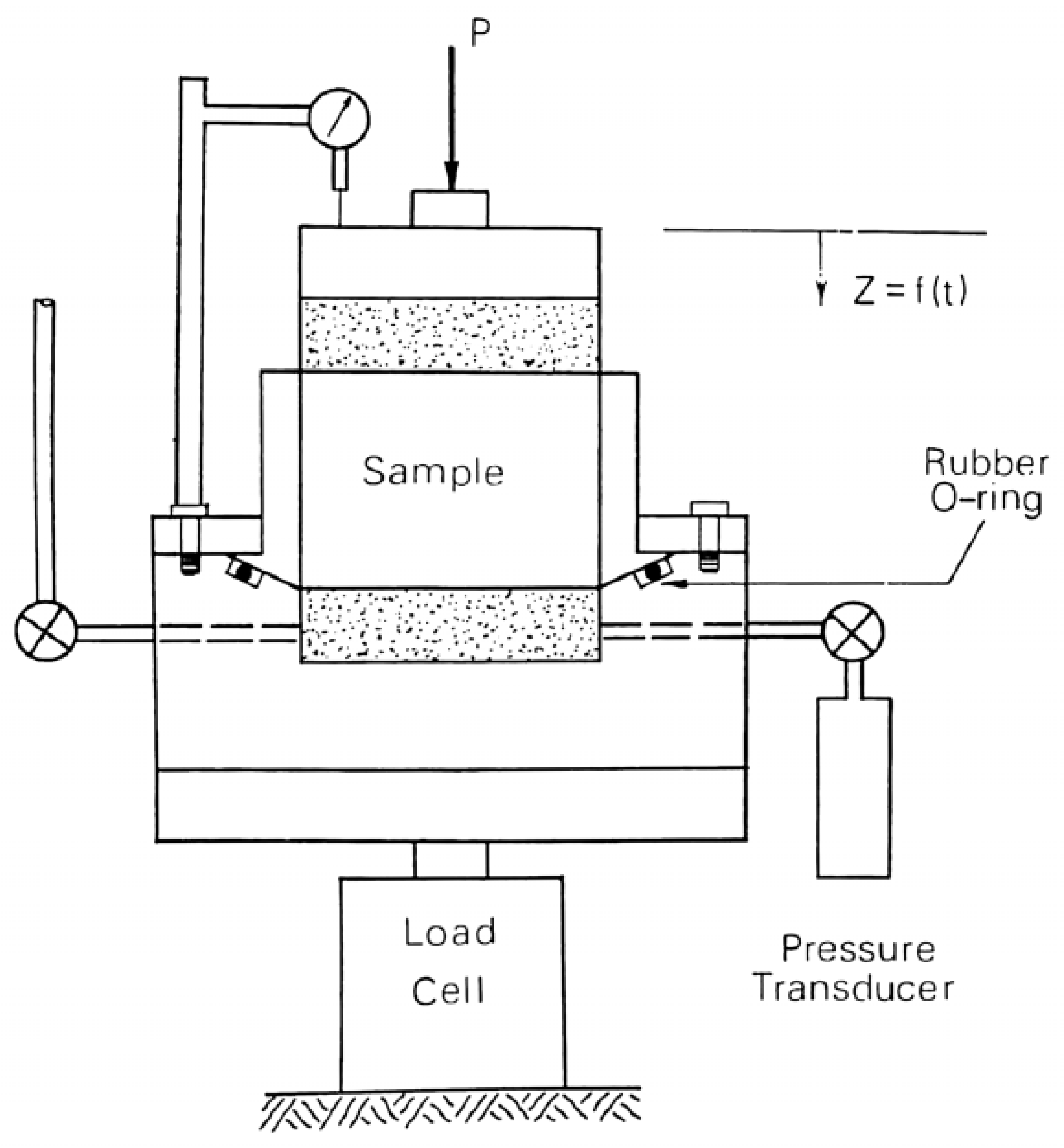
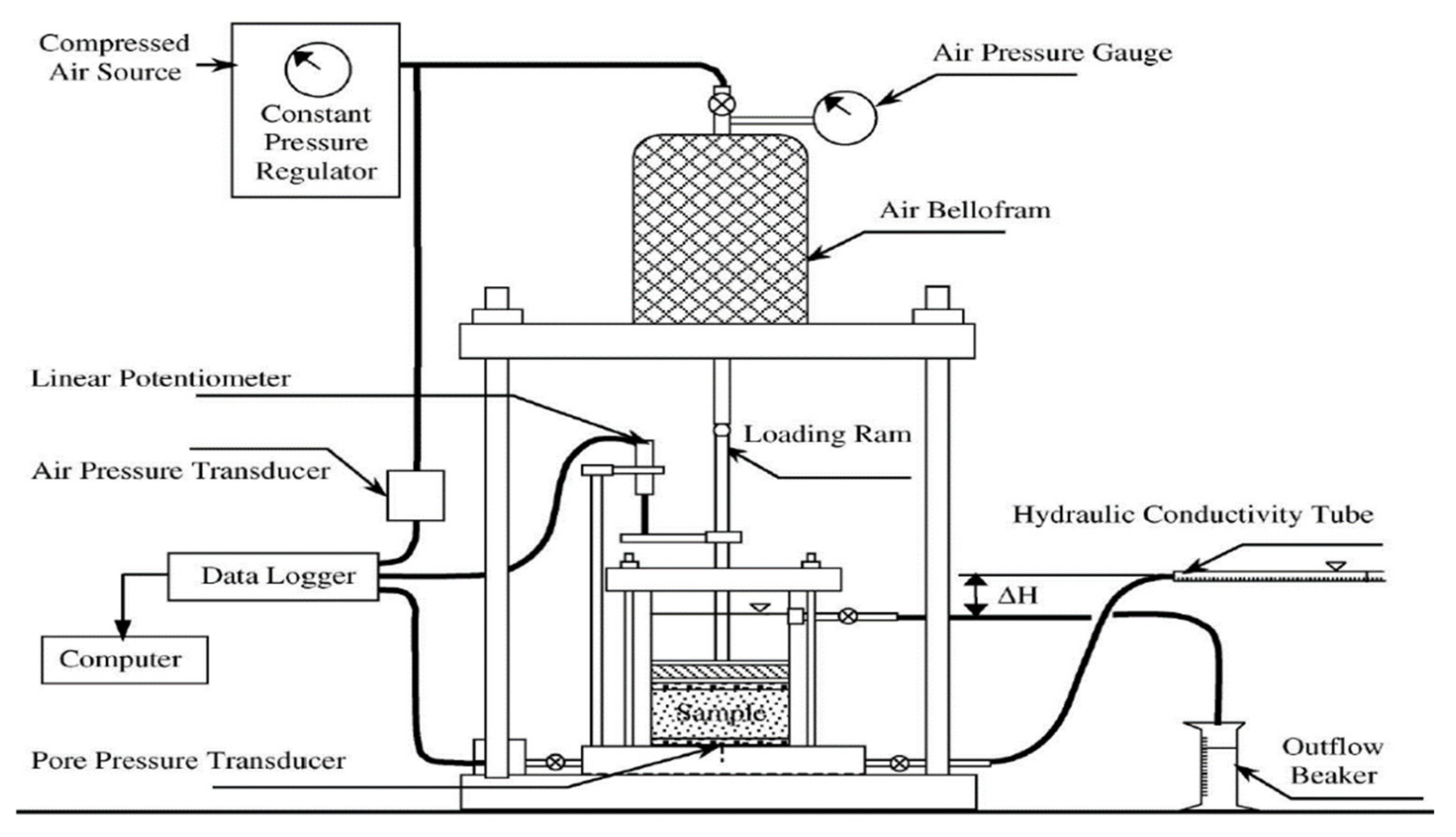
2.5. Seepage Induced Consolidation Test (SICT)
2.6. Compressibility Standpipe Test
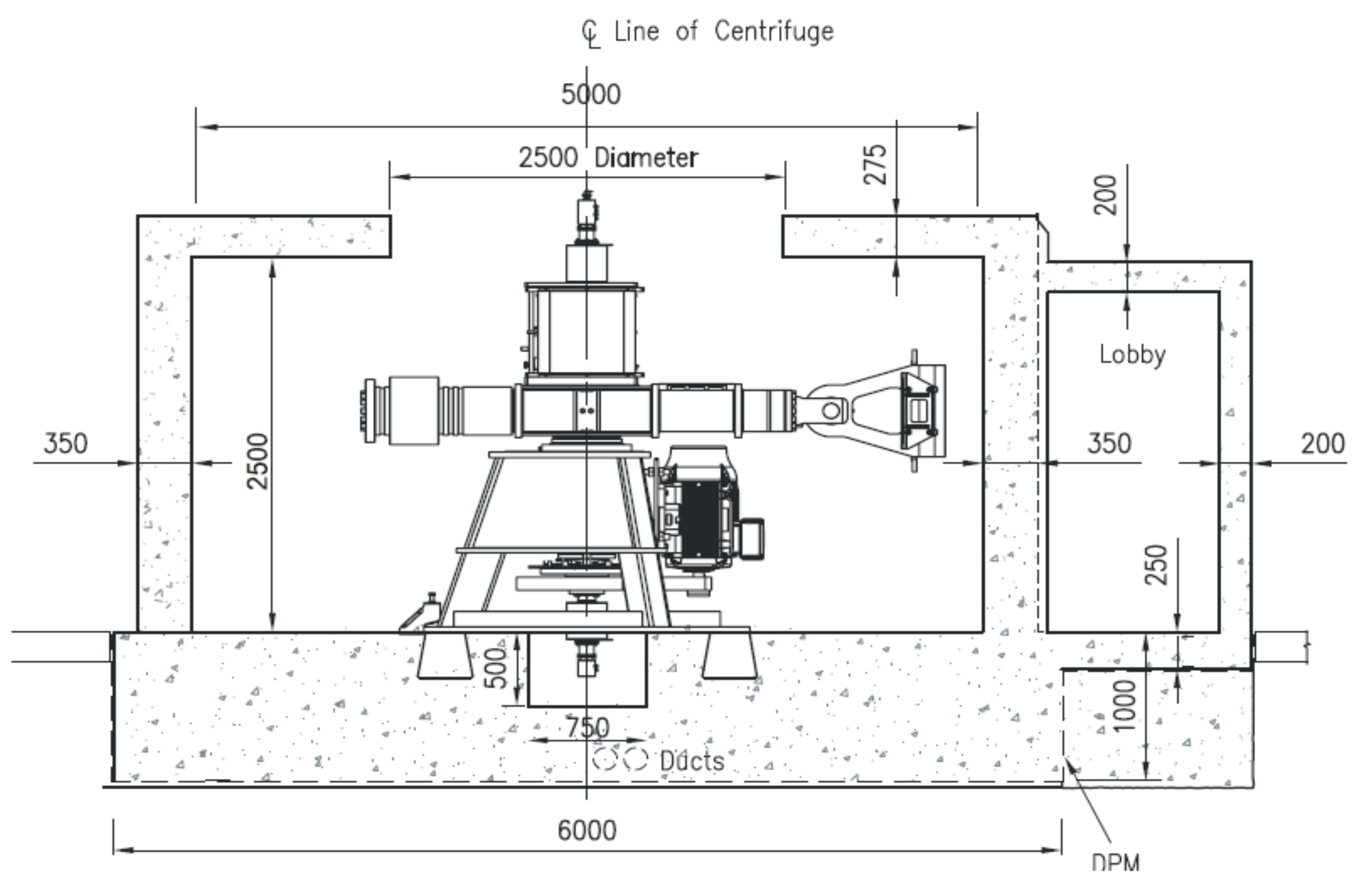
2.7. Geotechnical Beam Centrifuge Test
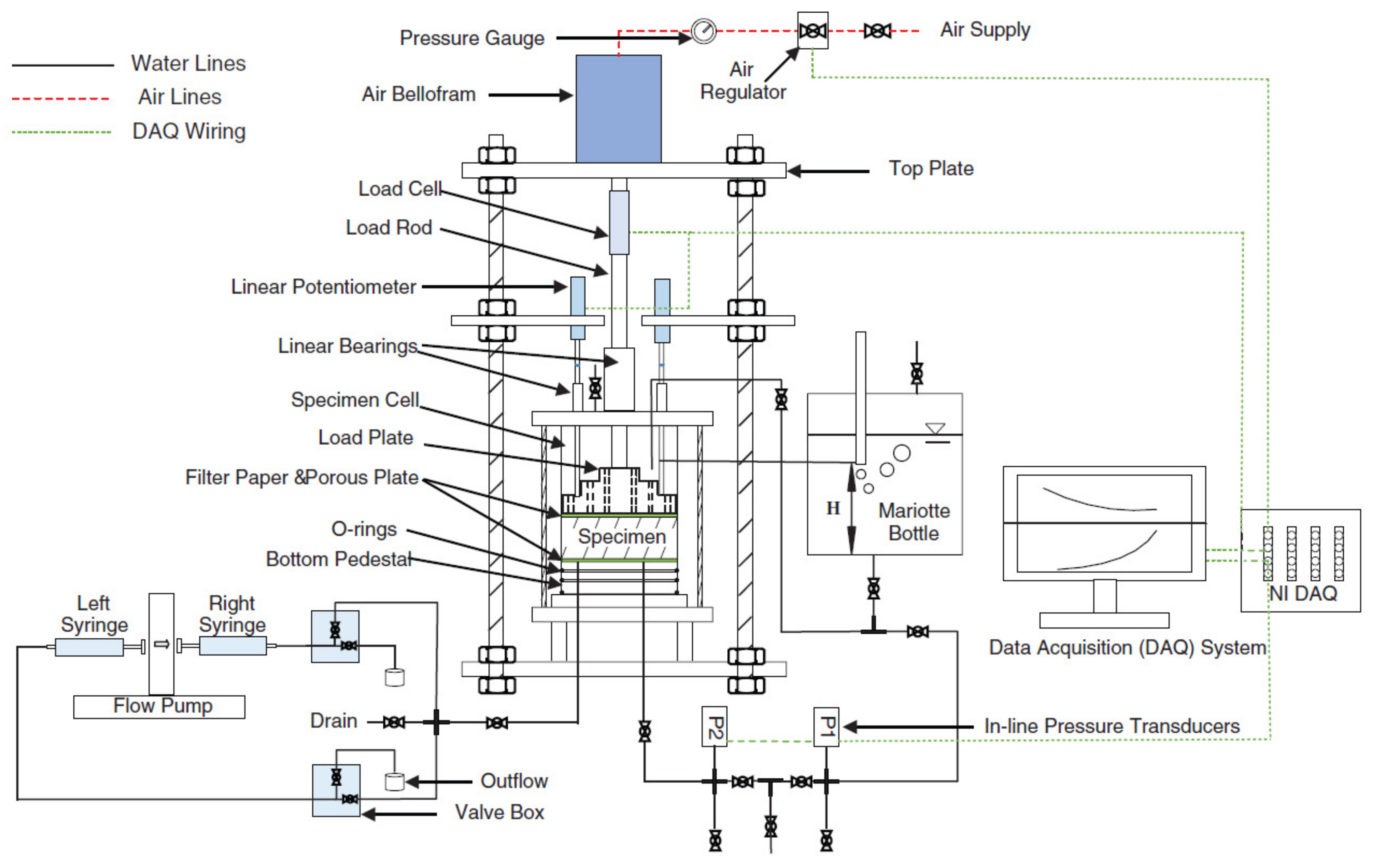
2.8. Bench-Top Centrifuge Test

2.9. Restricted Flow Consolidation (RFC) Test
3. Discussion
| Type of Consolidation Test | Test Procedure, Specimen Dimensions and Theory Used for Data Analysis | Limitations |
|---|---|---|
| Modified Conventional Oedometer Test [53,54,55,56,57] |
|
|
| Multi-step Loading Large Strain Consolidation Test [34,64,71,142,143] |
|
|
| Constant Rate of Deformation Test [73,75,78,79,80,87,144] |
|
|
| Controlled Hydraulic Gradient Test [75,83,87,144] |
|
|
| Seepage Induced Consolidation Test [96,145,146] |
|
|
| Compressibility Standpipe Test [34,90,101,102,107,147,148] |
|
|
| Geotechnical Beam Centrifuge Test [49,125,126,127,136,149,150,151] |
|
|
| Bench-top Centrifuge Test [50,131,132,133,135,152,153] |
|
|
| Restricted Flow Consolidation Test [14,138,154] |
|
|
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Government of Alberta. Oil Sands: Facts and Stats. 2021. Available online: https://www.alberta.ca/oil-sands-facts-and-statistics.aspx (accessed on 1 August 2022).
- Chalaturnyk, R.J.; Scott, J.D.; Özüm, B. Management of oil sands tailings. Pet. Sci. Technol. 2002, 20, 1025–1046. [Google Scholar] [CrossRef]
- Government of Alberta. Alberta’s Energy Resources Heritage: Oil Sands—The Hot Water Separation Process. 2022. Available online: http://www.history.alberta.ca/energyheritage/sands/unlocking-the-potential/the-scientific-and-industrial-research-council-of-alberta/the-hot-water-separation-process.aspx (accessed on 29 May 2022).
- Kasperski, K.L.; Mikula, R.J. Waste streams of mined oil sands: Characteristics and remediation. Elements 2011, 7, 387–392. [Google Scholar] [CrossRef]
- Alberta Energy Regulator. State of Fluid Tailings Management for Mineable Oil Sands, 2020; Alberta Energy Regulator: Calgary, AB, Canada, 2021; p. 124. [Google Scholar]
- COSIA. Deep Deposit Design Guide for Oil Sands Tailings; Canada’s Oil Sands Innovation Alliance—Deep Deposit Working Group: Calgary, AB, Canada, 2022; p. 260. Available online: https://cosia.ca/research/tailings (accessed on 13 December 2022).
- McKenna, G. Landscape Engineering and Sustainable Mine Reclamation. Ph.D. Thesis, University of Alberta, Department of Civil and Environmental, Edmonton, AB, Canada, 2002. [Google Scholar]
- OSTC; COSIA. Technical Guide for Fluid Fine Tailings Management; Oil Sands Tailings Consortium (OSTC) and Canada’s Oil Sands Innovation Alliance (COSIA): Calgary, AB, Canada, 2012; Available online: https://cosia.ca/node/57 (accessed on 13 December 2022).
- Alberta Energy Regulator. Directive 085: Fluid Tailings Management for Oil Sands Mining Projects. 2022, pp. 1–59. Available online: https://static.aer.ca/prd/documents/directives/Directive085.pdf (accessed on 13 December 2022).
- Hyndman, A.; Sawatsky, L.; McKenna, G.; Vandenberg, J. Fluid fine tailings processes: Disposal, capping, and closure alternatives. In Proceedings of the 6th International Oil Sands Tailings Conference, Edmonton, AB, Canada, 9–12 December 2018. [Google Scholar]
- McKenna, G.; Mooder, B.; Burton, B.; Jamieson, A. Shear strength and density of oil sands fine tailings for reclamation to a boreal forest landscape. In Proceedings of the Fifth International Oil Sands Tailings Conference (IOSTC), Lake Louis, AB, Canada, 4–7 December 2016. [Google Scholar]
- Carrier, D.; Bromwell, L.; Somogyi, F. Design capacity of slurried mineral waste ponds. J. Geotech. Eng. 1983, 109, 699–716. [Google Scholar] [CrossRef]
- Agapito, L.A.; Bareither, C.A. Application of a one-dimensional large-strain consolidation model to a full-scale tailings storage facility. Miner. Eng. 2018, 119, 38–48. [Google Scholar] [CrossRef]
- Abu-Hejleh, A.N.; Znidarčić, D.; Barnes, B.L. Consolidation characteristics of phosphatic clays. J. Geotech. Eng. 1996, 122, 295–301. [Google Scholar] [CrossRef]
- Cossey, H.L.; Batycky, A.E.; Kaminsky, H.; Ulrich, A.C. Geochemical Stability of Oil Sands Tailings in Mine Closure Landforms. Minerals 2021, 11, 830. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Vick, S.G.; van Zyl, D. Independent Expert Engineering Investigation and Review Panel Report on Mount Polley Tailings Storage Facility Breach; Government of British Columbia: Victoria, BC, Canada, 2015.
- Schafer, H.L.; Beier, N.A.; Macciotta, R. A Failure Modes and Effects Analysis Framework for Assessing Geotechnical Risks of Tailings Dam Closure. Minerals 2021, 11, 1234. [Google Scholar] [CrossRef]
- Arulrajah, A.; Choa, V. Large deformation of slurry-like soil. In Deformation and Progressive Failure in Geomechanics; Elsevier Science: Nagoya, Japan, 1997; p. 437. [Google Scholar]
- Schiffman, R.L. Finite and infinitesimal strain consolidation. J. Geotech. Eng. Div. 1980, 106, 203–207. [Google Scholar] [CrossRef]
- Terzaghi, K. Theory of Consolidation, in Theoretical Soil Mechanics. 1943, pp. 265–296. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/9780470172766.ch13 (accessed on 2 September 2022).
- ASTM Committee D-18 on Soil and Rock. Standard Test Methods for One-Dimensional Consolidation Properties of Soils Using Incremental Loading; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior; John Wiley & Sons: New York, NY, USA, 2005; Volume 3. [Google Scholar]
- Crawford, C.B. State of the art: Evaluation and interpretation of soil consolidation tests. Consol. Soils Test. Eval. 1986, 892, 71–103. [Google Scholar]
- Cryer, C. A comparison of the three-dimensional consolidation theories of Biot and Terzaghi. Q. J. Mech. Appl. Math. 1963, 16, 401–412. [Google Scholar] [CrossRef]
- Znidarcic, D.; Schiffman, R. On Terzaghi’s concept of consolidation. Geotechnique 1982, 32, 387–389. [Google Scholar] [CrossRef]
- Clayton, C.R.I.; Steinhagen, H.M.; Powrie, W. Terzaghi’s theory of consolidation, and the discovery of effective stress. (Compiled from the work of K. Terzaghi and A.W. Skempton). Proc. Inst. Civ. Eng.-Geotech. Eng. 1995, 113, 191–205. [Google Scholar] [CrossRef]
- Koppula, S.D. The Consolidation of Soil in Two Dimensions and with Moving Boundaries; National Library: Ottawa, ON, Canada, 1970. [Google Scholar]
- Caldwell, J.A.; Ferguson, K.; Schiffman, R.L.; Van Zyl, D. Application of finite strain consolidation theory for engineering design and environmental planning of mine tailings impoundments. In Sedimentation Consolidation Models—Predictions and Validation; ASCE: Reston, VA, USA, 1984. [Google Scholar]
- Gibson, R.; England, G.; Hussey, M. The Theory of one-dimensional consolidation of saturated clays: 1. finite non-Linear consolidation of thin homogeneous layers. Geotechnique 1967, 17, 261–273. [Google Scholar] [CrossRef]
- Ito, M.; Azam, S. Large-strain consolidation modeling of mine waste tailings. Environ. Syst. Res. 2013, 2, 7. [Google Scholar] [CrossRef]
- Somogyi, F. Large strain consolidation of fine grained slurries. In Proceedings of the Canadian Society for Civil Engineering, Winnipeg, Manitoba, 29 May 1980; pp. 29–30. [Google Scholar]
- Gibson, R.E.; Schiffman, R.L.; Cargill, K.W. The theory of one-dimensional consolidation of saturated clays. II. Finite nonlinear consolidation of thick homogeneous layers. Can. Geotech. J. 1981, 18, 280–293. [Google Scholar] [CrossRef]
- Lee, K. An Analytical and Experimental Study of Large Strain Soil Consolidation; University of Oxford: Oxford, UK, 1979. [Google Scholar]
- Jeeravipoolvarn, S. Geotechnical Behavior of In-Line Thickened Oil Sands Tailings. Master’s Thesis, University of Alberta, Department of Civil and Environmental, Edmonton, AB, Canada, 2010. [Google Scholar]
- Koppula, S.; Morgenstern, N. On the consolidation of sedimenting clays. Can. Geotech. J. 1982, 19, 260–268. [Google Scholar] [CrossRef]
- Schiffman, R.; Cargill, K. Finite strain consolidation of sedimenting clay deposits. In Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering, Stockholm, UK, 15–19 June 1981; Volume 1, pp. 239–242. [Google Scholar]
- Krizek, R.J.; Somogyi, F. Perspectives on modelling consolidation of dredged materials. In Unknown Host Publication Title; ASCE: Reston, VA, USA, 1984; pp. 296–332. [Google Scholar]
- Bromwell, L.G. Consolidation of mining wastes. In Sedimentation Consolidation Models—Predictions and Validation; ASCE: Reston, VA, USA, 1984. [Google Scholar]
- Bartholomeeusen, G.; Sills, G.C.; Znidarčić, D.; Van Kesteren, W.; Merckelbach, L.M.; Pyke, R.; Carrier, W.D., III; Lin, H.; Penumadu, D.; Winterwerp, H.; et al. Sidere: Numerical prediction of large-strain consolidation. Géotechnique 2002, 52, 639–648. [Google Scholar] [CrossRef]
- Cargill, K.W. Consolidation of Soft Layers by Finite Strain Analysis; U.S. Army Engineer Research and Development Center (ERDC): Vicksburg, MI, USA, 1982; Available online: https://hdl.handle.net/11681/10139 (accessed on 15 October 2022).
- Jeeravipoolvarn, S.; Chalaturnyk, R.; Scott, J. Consolidation modeling of oil sands fine tailings: History matching. In Proceedings of the GeoEdmonton’08, Edmonton, AB, Canada, 21–24 September 2008; pp. 190–197. [Google Scholar]
- Liu, J.-C.; Znidarčić, D. Modeling one-dimensional compression characteristics of soils. J. Geotech. Eng. 1991, 117, 162–169. [Google Scholar] [CrossRef]
- Townsend, F.; McVay, M. SOA: Large strain consolidation predictions. J. Geotech. Eng. 1990, 116, 222–243. [Google Scholar] [CrossRef]
- Morris, P.; Lockington, D.; Apelt, C. Correlations for mine tailings consolidation parameters. Int. J. Surf. Min. Reclam. Environ. 2000, 14, 171–182. [Google Scholar] [CrossRef]
- Carrier, W.; Beckman, J. Correlations between index tests and the properties of remoulded clays. Geotechnique 1984, 34, 211–228. [Google Scholar] [CrossRef]
- Morris, P.H.; Lockington, D.A. Geotechnical Compressibility and Consolidation Parameters and Correlations for Remoulded Fine-Grained Marine and Riverine Sediments; CRC for Sustainable Tourism: Boca Raton, FL, USA, 2002. [Google Scholar]
- Morris, P. Compressibility and permeability correlations for fine-grained dredged materials. J. Waterw. Port Coast. Ocean. Eng. 2003, 129, 188–191. [Google Scholar] [CrossRef]
- Morris, P. Correlations for zero effective stress void ratio of fine-grained marine and riverine sediments. J. Waterw. Port Coast. Ocean. Eng. 2007, 133, 305–308. [Google Scholar] [CrossRef]
- Robinson, R.; Tan, T.; Lee, F. A comparative study of suction-induced seepage consolidation versus centrifuge consolidation. Geotech. Test. J. 2003, 26, 92–101. [Google Scholar]
- Khan, F.S.; Azam, S. Determination of consolidation behavior of clay slurries. Int. J. Min. Sci. Technol. 2016, 26, 277–283. [Google Scholar] [CrossRef]
- Proskin, S.; Sego, D.; Alostaz, M. Freeze–thaw and consolidation tests on Suncor mature fine tailings (MFT). Cold Reg. Sci. Technol. 2010, 63, 110–120. [Google Scholar] [CrossRef]
- Schiffman, R.L. The consolidation of soft marine sediments. Geo-Mar. Lett. 1982, 2, 199–203. [Google Scholar] [CrossRef]
- Hong, Z.-S.; Yin, J.; Cui, Y.-J. Compression behavior of reconstituted soils at high initial water contents. Géotechnique 2010, 60, 691–700. [Google Scholar] [CrossRef]
- Xu, G.; Gao, Y.; Yin, J.; Yang, R.; Ni, J. Compression behavior of dredged slurries at high water contents. Mar. Georesour. Geotechnol. 2015, 33, 99–108. [Google Scholar] [CrossRef]
- Xu, G.; Gao, Y.-F.; Xu, C. Permeability behavior of high-moisture content dredged slurries. Mar. Georesour. Geotechnol. 2015, 33, 348–355. [Google Scholar] [CrossRef]
- Tavenas, F.; Jean, P.; Leblond, P.; Leroueil, S. The permeability of natural soft clays. Part II: Permeability characteristics. Can. Geotech. J. 1983, 20, 645–660. [Google Scholar] [CrossRef]
- Tavenas, F.; Leblond, P.; Jean, P.; Leroueil, S. The permeability of natural soft clays. Part I: Methods of laboratory measurement. Can. Geotech. J. 1983, 20, 629–644. [Google Scholar] [CrossRef]
- Zeng, L.L.; Hong, Z.S.; Cai, Y.Q.; Han, J. Change of hydraulic conductivity during compression of undisturbed and remolded clays. Appl. Clay Sci. 2011, 51, 86–93. [Google Scholar] [CrossRef]
- Pane, V.; Croce, P.; Znidarčić, D.; Ko, H.Y.; Olsen, H.W.; Schiffman, R.L. Effects of consolidation on permeability measurements for soft clay. Geotechnique 1983, 33, 67–72. [Google Scholar] [CrossRef]
- Sheeran, D.; Krizek, R. Preparation of homogeneous soil samples by slurry consolidation. J. Mater. 1971, 6, 356–373. [Google Scholar]
- Monte, J.L.; Krizek, R. One-dimensional mathematical model for large-strain consolidation. Geotechnique 1976, 26, 495–510. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Permeability of Granular Soils (Constant Head); ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- Caughill, D.L. Geotechnics of Nonsegregating Oil Sand Tailings. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 1992. [Google Scholar] [CrossRef]
- Azam, S. Large strain settling behavior of polymer-amended laterite slurries. Int. J. Geomech. 2011, 11, 105–112. [Google Scholar] [CrossRef]
- Pollock, G.W. Large Strain Consolidation of Oil Sand Tailings Sludge. Ph.D. Thesis, University of Alberta, Department of Civil and Environmental, Edmonton, AB, Canada, 1988. [Google Scholar]
- Suthaker, N. Geotechnics of Oil sand Tailings. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1995. [Google Scholar]
- Shokouhi, A.; Williams, D.J. Volume change behavior of mixtures of coarse coal reject and tailings. Min. Technol. 2017, 126, 163–176. [Google Scholar] [CrossRef]
- Shokouhi, A.; Zhang, C.; Williams, D.J. Settling, consolidation and desiccation behavior of coal tailings slurry. Min. Technol. 2018, 127, 1–11. [Google Scholar] [CrossRef]
- Islam, S.; Williams, D.J.; Bhuyan, M.H. Consolidation testing of tailings in a slurry consolidometer using constant rate and accelerated loading. Proc. Inst. Civ. Eng. Geotech. Eng. 2021. ahead of print. [Google Scholar] [CrossRef]
- Islam, S.; Williams, D.J.; Zhang, C.; Llano-Serna, M. Geotechnical characterisation of coal tailings down the beach and constant rate of loading consolidation in a slurry consolidometer. Min. Technol. 2021, 130, 67–80. [Google Scholar] [CrossRef]
- He, W.; Williams, D.; Shokouhi, A. Numerical study of slurry consolidometer tests taking into account the influence of wall friction. Comput. Geotech. 2017, 91, 39–47. [Google Scholar] [CrossRef]
- Hamilton, J.J.; Crawford, C.B. Improved Determination of Preconsolidation Pressure of a Sensitive Clay; ASTM International: West Conshohocken, PA, USA, 1959; pp. 254–271. [Google Scholar]
- Znidarcic, D.; Croce, P.; Pane, V.; Olsen, H.W.; Schiffman, R.L. The theory of one-dimensional consolidation of saturated clays: III. existing testing procedures and analyses. Geotech. Test. J. 1984, 7, 123–134. [Google Scholar]
- Crawford, C.B. Interpretation of the consolidation test. J. Soil Mech. Found. Div. 1964, 90, 87–102. [Google Scholar] [CrossRef]
- Gorman, C.T.; Hopkins, T.C.; Deen, R.C.; Drnevich, V.P. Constant-rate-of-strain and controlled-gradient consolidation testing. Geotech. Test. J. 1978, 1, 3–15. [Google Scholar]
- Smith, R.E.; Wahls, H.E. Consolidation under constant rates of strain. J. Soil Mech. Found. Div. 1969, 95, 519–539. [Google Scholar] [CrossRef]
- Wissa, A.E.; Christian, J.T.; Davis, E.H.; Heiberg, S. Consolidation at constant rate of strain. J. Soil Mech. Found. Div. 1971, 97, 1393–1413. [Google Scholar] [CrossRef]
- Znidarčić, D.; Schiffman, R.L.; Pane, V.; Croce, P.; Ko, H.Y.; Olsen, H.W. The theory of one-dimensional consolidation of saturated clays: Part V, constant rate of deformation testing and analysis. Géotechnique 1986, 36, 227–237. [Google Scholar] [CrossRef]
- Umehara, Y.; Zen, K. Constant rate of strain consolidation for very soft clayey soils. Soils Found. 1980, 20, 79–95. [Google Scholar] [CrossRef]
- Lee, K. Consolidation with constant rate of deformation. Geotechnique 1981, 31, 215–229. [Google Scholar] [CrossRef]
- González, J.H. Experimental and Theoretical Investigation of Constant Rate of Strain Consolidation; Massachusetts Institute of Technology: Singapore, 2000. [Google Scholar]
- Crawford, C. The Influence of Rate of Strain on Effective Stresses in Sensitive Clay; ASTM International: West Conshohocken, PA, USA, 1960; pp. 36–61. [Google Scholar] [CrossRef]
- Lowe, J.; Jonas, E.; Obrcian, V. Controlled gradient consolidation test. J. Soil Mech. Found. Div. 1969, 95, 77–97. [Google Scholar] [CrossRef]
- Crawford, C.B. Closure to “Interpretation of the Consolidation Test”. J. Soil Mech. Found. Div. 1965, 91, 104–108. [Google Scholar] [CrossRef]
- Leroueil, S.; Samson, L.; Bozozuk, M. Laboratory and field determination of preconsolidation pressures at Gloucester. Can. Geotech. J. 1983, 20, 477–490. [Google Scholar] [CrossRef]
- Leroueil, S.; Tavenas, F.; Samson, L.; Morin, P. Preconsolidation pressure of Champlain clays. Part II. Laboratory determination. Can. Geotech. J. 1983, 20, 803–816. [Google Scholar] [CrossRef]
- Silvestri, V.; Yong, R.N.; Soulié, M.; Gabriel, F. Controlled-strain, controlled-gradient, and standard consolidation testing of sensitive clays. In Consolidation of Soils: Testing and Evaluation; ASTM International: West Conshohocken, PA, USA, 1986. [Google Scholar]
- Imai, G. Development of a new consolidation test procedure using seepage force. Soils Found. 1979, 19, 45–60. [Google Scholar] [CrossRef]
- Fox, P.J.; Baxter, C.D. Consolidation properties of soil slurries from hydraulic consolidation test. J. Geotech. Geoenviron. Eng. 1997, 123, 770–776. [Google Scholar] [CrossRef]
- Been, K.; Sills, G. Self-weight consolidation of soft soils: An experimental and theoretical study. Geotechnique 1981, 31, 519–535. [Google Scholar] [CrossRef]
- Znidarcic, D. Laboratory Determination of Consolidation Properties of Cohesive Soil; University of Colorado at Boulder: Boulder, CO, USA, 1982. [Google Scholar]
- Huerta, A.; Kriegsmann, G.A.; Krizek, R.J. Permeability and compressibility of slurries from seepage-induced consolidation. J. Geotech. Eng. 1988, 114, 614–627. [Google Scholar] [CrossRef]
- Znidarcic, D.; Liu, J. Consolidation characteristics determination for dredged materials. Proc 1989, 22, 45–65. [Google Scholar]
- Abu-Hejleh, A.N.; Znidarcic, D. Estimation of the consolidation constitutive relations. In International Conference on Computer Methods and Advances in Geomechanics; A.A. Balkema: Rotterdam, The Netherlands, 1994. [Google Scholar]
- Znidarcic, D.; Abu-Hejleh, A.N.; Fairbanks, T.; Roberson, A. Seepage Induced Consolidation Test, Equipment Description and User’s Manual; Report prepared for FIPR; Department of Civil Engineering, University of Colorado: Boulder, CO, USA, 1992. [Google Scholar]
- Tian, Z.; Bareither, C.A.; Scalia, J. Development and assessment of a seepage-induced consolidation test apparatus. Geotech. Test. J. 2019, 43, 894–917. [Google Scholar] [CrossRef]
- Imai, G. Experimental studies on sedimentation mechanism and sediment formation of clay materials. Soils Found. 1981, 21, 7–20. [Google Scholar] [CrossRef]
- Aubertin, M.; Bussiere, B.; Chapuis, R.P. Hydraulic conductivity of homogenized tailings from hard rock mines. Can. Geotech. J. 1996, 33, 470–482. [Google Scholar] [CrossRef]
- Ou, X.D.; Yang, J.W.; Yin, X.T.; Liao, Y.F. Experimental study on mechanism for self-weight consolidation of the red mud tailings placed in the karsts. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2011. [Google Scholar]
- Vick, S.G. Planning, Design, and Analysis of Tailings Dams; BiTech Publishers Ltd.: Richmond, BC, Canada, 1990. [Google Scholar]
- Wickland, B.E.; Wilson, G.W. Self-weight consolidation of mixtures of mine waste rock and tailings. Can. Geotech. J. 2005, 42, 327–339. [Google Scholar] [CrossRef]
- Scott, J.D.; Dusseault, M.B.; Carrier, W.D. Large-scale self-weight consolidation testing. In Consolidation of Soils: Testing and Evaluation; ASTM International: West Conshohocken, PA, USA, 1986. [Google Scholar]
- Sills, G. Time dependent process in soil consolidation. Compress. Consol. Clayey Soils 1995, 2, 875–890. [Google Scholar]
- Sills, G. Development of structure in sedimenting soils. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Eng. Sci. 1998, 356, 2515–2534. [Google Scholar] [CrossRef]
- Jeeravipoolvarn, S.; Scott, J.; Chalaturnyk, R. 10 m standpipe tests on oil sands tailings: Long-term experimental results and prediction. Can. Geotech. J. 2009, 46, 875–888. [Google Scholar] [CrossRef]
- Li, L.; Alvarez, I.; Aubertin, J. Self-weight consolidation of slurried deposition: Tests and interpretation. Int. J. Geotech. Eng. 2013, 7, 205–213. [Google Scholar] [CrossRef]
- Babaoglu, Y.; Simms, P. A Rapid Measurement Method to Determine Hydraulic Conductivity of Tailings Under Self-Weight Consolidation. In Proceedings of the 24th International Conference on Tailings and Mine Waste ‘20, Fort Collins, CO, USA, 15–18 November 2020. [Google Scholar]
- Watson, K. An instantaneous profile method for determining the hydraulic conductivity of unsaturated porous materials. Water Resour. Res. 1966, 2, 709–715. [Google Scholar] [CrossRef]
- Schofield, A.N. Cambridge geotechnical centrifuge operations. Geotechnique 1980, 30, 227–268. [Google Scholar] [CrossRef]
- Beasley, D.; James, R. Use of a hopper to simulate embankment construction in a centrifugal model. Geotechnique 1976, 26, 220–226. [Google Scholar] [CrossRef]
- King, G.; McLoughlin, J. Centrifuge model studies of a cantilever retaining wall in sand. In Retaining Structures; Thomas Telford Publishing: London, UK, 1993; pp. 711–720. [Google Scholar]
- Lyndon, A.; Pearson, R. Pressure Distribution on a Rigid Retaining Wall in Cohesionless Material.; A.A. Balkema: Rotterdam, The Netherlands, 1985. [Google Scholar]
- Antonaki, N.; Sasanakul, I.; Abdoun, T.; Sanin, M.V.; Puebla, H.; Ubilla, J. Centrifuge modeling of deposition and consolidation of fine-grained mine tailings. In Proceedings of the Geo-Congress 2014: Geo-characterization and Modeling for Sustainability, Atlanta, Georgia, USA, 23–26 February 2014. [Google Scholar]
- Antonaki, N.; Abdoun, T.; Sasanakul, I. Centrifuge tests on comixing of mine tailings and waste rock. J. Geotech. Geoenvironmental Eng. 2018, 144, 04017099. [Google Scholar] [CrossRef]
- Bassett, R. Centrifugal model tests of embankments on soft alluvial foundations. In Proceedings of the 8th International Conference on Soil Mechanics and Foundation Engineering, Moscow, Russia, 6–11 August 1973. [Google Scholar]
- Ko, H.-Y. Summary of the state-of-the-art in centrifuge model testing. In Centrifuges in Soil Mechanics; CRC Press: Boca Raton, FL, USA, 1988; pp. 11–18. [Google Scholar]
- Bloomquist, D. Centrifuge Modeling of Large Strain Consolidation Phenomena in Phosphatic Clay Retention Ponds (Florida); University of Florida: Gainesville, FL, USA, 1982. [Google Scholar]
- Lawver, J.; Carrier, W. Mathematical and centrifuge modeling of phosphatic clay disposal systems. In Proceedings of the SME-AIME Annual Meeting, Atlanta, GA, USA, 6–10 March 1983. [Google Scholar]
- Townsend, F.; Hernandez, J. Predictions of phosphatic clay consolidation by numerical and centrifugal models. In Flocculation, Sedimentation and Consolidation; Moudgil, B.M., Somasundaran, P., Eds.; American Institute of Chemical Engineers: Sea Island, GA, USA, 1986; pp. 449–455. [Google Scholar]
- Weiland, R.; Bunnaul, P.; Hogg, R. Centrifugal dewatering of flocculated clays. Min. Metall. Explor. 1994, 11, 37–40. [Google Scholar] [CrossRef]
- Mikasa, M.; Takada, N. Selfweight consolidation of very soft clay by centrifuge. In Sedimentation Consolidation Models—Predictions and Validation; ASCE: Reston, VA, USA, 1984. [Google Scholar]
- McVay, M.; Townsend, F.; Bloomquist, D. Quiescent consolidation of phosphatic waste clays. J. Geotech. Eng. 1986, 112, 1033–1049. [Google Scholar] [CrossRef]
- Croce, P.; Pane, V.; Znidarčić, D.; Ko, H.Y.; Olsen, H.W.; Schiffman, R.L. Evaluation of Consolidation Theories by Centrifuge Modelling; CRC Press: Boca Raton, FL, USA, 1985. [Google Scholar]
- Takada, N.; Mikasa, M. Determination of consolidation parameters by selfweight consolidation test in centrifuge. In Consolidation of Soils: Testing and Evaluation; ASTM International: West Conshohocken, PA, USA, 1986. [Google Scholar]
- McVay, M.C.; Townsend, F.C.; Bloomquist, D.G.; Martinez, R.E. Reclamation of Phosphatic Clay Waste Ponds by Capping Volume 6: Consolidation Properties of Phosphatic Clays from Automated Slurry Consolidometer and Centrifugal Model Tests; FIPR Publication; Florida Institute of Phosphate Research: Bartow, FL, USA, 1987. [Google Scholar]
- Sorta, A.R. Centrifugal Modelling of Oil Sands Tailings Consolidation. Ph.D. Thesis, University of Alberta, Department of Civil and Environmental, Edmonton, AB, Canada, 2015. [Google Scholar]
- Taylor, R. Centrifuges in modelling: Principles and scale effects (Chapter 2). In Geotechnical Centrifuge Technology; Taylor, R.N., Ed.; Blackie Academic & Professional: London, UK, 1995; pp. 20–34. [Google Scholar]
- Black, J.A.; Baker, N.; Ainsworth, A. Establishing a 50g-ton geotechnical centrifuge at the University of Sheffield. In Physical Modelling in Geotechnics-Gaudin & White; Taylor & Francis Group: London, UK, 2014; pp. 181–186. [Google Scholar]
- Madabhushi, G. Centrifuge Modelling for Civil Engineers; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Muir Wood, D. Geotechnical Modelling; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- McDermott, I.; King, A. Use of a bench-top centrifuge to assess consolidation parameters. In Tailings and Mine Waste’98; Routledge: London, UK, 1998. [Google Scholar]
- El-Shall, H.; Moudgil, B.; Bogan, M. Centrifugal modeling of the consolidation of solid suspensions. Min. Metall. Explor. 1996, 13, 98–102. [Google Scholar] [CrossRef]
- Reid, D.; Fourie, A.; Watson, S. Accelerated consolidation of soft clays and mine tailings using a desktop centrifuge. In Proceedings of the 15th International Seminar on Paste and Thickened Tailings, Sun City, South Africa, 17–19 April 2012; Australian Centre for Geomechanics: Crawley, WA, Australia. [Google Scholar]
- Lehane, B.M.; O’loughlin, C.D.; Gaudin, C.; Randolph, M.F. Rate effects on penetrometer resistance in kaolin. Géotechnique 2009, 59, 41–52. [Google Scholar] [CrossRef]
- Anderson, C.; Sivakumar, V.; Black, J. Measurement of permeability using a bench-top centrifuge. Géotechnique 2015, 65, 12–22. [Google Scholar] [CrossRef]
- Black, J.A. Development of a small scale teaching centrifuge. In Physical Modelling in Geotechnics-Gaudin & White; Taylor & Francis Group: London, UK, 2014; pp. 187–192. [Google Scholar]
- Fox, P.J.; Lee, J.; Qiu, T. Model for large strain consolidation by centrifuge. Int. J. Geomech. 2005, 5, 267–275. [Google Scholar] [CrossRef]
- Sills, G.; Hoare, S.; Baker, N. An experimental assessment of the restricted flow consolidation test. In Consolidation of Soils: Testing and Evaluation; ASTM International: West Conshohocken, PA, USA, 1986. [Google Scholar]
- Rowe, P.W.; Barden, L. A new consolidation cell. Geotechnique 1966, 16, 162–170. [Google Scholar] [CrossRef]
- Premchitt, J.; Ho, K.; Evans, N. Conventional and CRS Rowe cell consolidation test on some Hong Kong clays; Geotechnical Engineering Office, Civil Engineering Department: Hong Kong, China, 1996. [Google Scholar]
- Suthaker, N.N.; Scott, J.D. Measurement of hydraulic conductivity in oil sand tailings slurries. Can. Geotech. J. 1996, 33, 642–653. [Google Scholar] [CrossRef]
- Jeeravipoolvarn, S. Compression Behavior of Thixotropic Oil Sands Tailings; University of Alberta: Edmonton, AB, Canada, 2005. [Google Scholar]
- Jeeravipoolvarn, S.; Masala, S.; Zhang, C.; Moore, T. Revisiting the large strain consolidation test for oil sands. In Proceedings of the Tailings and Mine Waste 2015, Vancouver, BC, Canada, 26–28 October 2015. [Google Scholar]
- Gorman, C.T. Constant-Rate-of-Strain and Controlled-Gradient Consolidation Testing; Kentucky Transportation Center Research Report, Research Report No. 448. 1976. Available online: https://uknowledge.uky.edu/ktc_researchreports/866 (accessed on 15 October 2022).
- Znidarcic, D.; Abu-Hejleh, A.N.; Fairbanks, T.; Robertson, A. Consolidation Characteristics Determination for Phosphatic Clays, Volume 1: Seepage Induced Consolidation Test Equipment Description and Users Manual; Technical Report; Florida Institute of Phosphate Research: Bartow, FL, USA, 1994. [Google Scholar]
- Estepho, M. Seepage Induced Consolidation Test: Characterization of Mature Fine Tailings; University of British Columbia: Vancouver, BC, Canada, 2014. [Google Scholar]
- Dromer, J.B.; Aubertin, M.; Kennedy, G.; Pedroni, L.; Bussière, B. A new testing system to investigate the sedimentation and consolidation of sludge and slurry. In Proceedings of the 57th Canadian Geotechnical Conference, Québec, QC, Canada, 24–26 October 2004. [Google Scholar]
- Miller, W.G. Comparison of geoenvironmental properties of caustic and noncaustic oil sand fine tailings. Ph.D. Thesis, University of Alberta, Department of Civil and Environmental, Edmonton, AB, Canada, 2010. [Google Scholar]
- Dunmola, A.; Wang, N.; Lorentz, J.; Chalaturnyk, R.; Zambrano, G.; Song, J. Comparison of geotechnical beam centrifuge predictions to field data from 10m deep FFT centrifuge cake columns. In Proceedings of the 6th International Oil Sands Tailings Conference, Edmonton, AB, Canada, 3 June 2018; pp. 290–298. [Google Scholar]
- Znidarčić, D.; Miller, R.; Van Zyl, D.; Fredlund, M.; Wells, S. Consolidation testing of oil sand fine tailings. In Proceedings of the Tailings and Mine Waste, Vancouver, BC, Canada, 6–9 November 2011. [Google Scholar]
- McNamara, A.; Divall, S.; Goodey, R.; Taylor, N.; Stallebrass, S.; Panchal, J. Physical Modelling in Geotechnics. In Proceedings of the 9th International Conference on Physical Modelling in Geotechnics (ICPMG 2018), London, UK, 17–20 July 2018; CRC Press: Boca Raton, FL, USA, 2018; Volume 1. [Google Scholar]
- Gaudin, C.; White, D. Physical Modelling in Geotechnics. In Proceedings of the 8th International Conference on Physical Modelling in Geotechnics 2014 (ICPMG 2014), Perth, Australia, 14–17 January 2014. [Google Scholar]
- Sharma, J.S. Consolidation characteristics of tailings using a high-g bench-top centrifuge. In Proceedings of the 8th International Conference on Physical Modelling in Geotechnics, Perth, Australia, 14–17 January 2014. [Google Scholar]
- Nash, D.; Sills, G.; Davison, L. One-dimensional consolidation testing of soft clay from Bothkennar. Géotechnique 1992, 42, 241–256. [Google Scholar] [CrossRef]
- Dunmola, A.; Werneiwski, R.A.; McGowan, D.; Shaw, B.; Carrier, D. Geotechnical performance of fine tailings in an oil sands pit lake. Can. Geotech. J. 2022. [Google Scholar] [CrossRef]

| Physical Property | Scale Factor (Prototype/Model) |
|---|---|
| Length (m) | N |
| Settlement (Deformation) (m) | N |
| Cross-sectional Area (m2) | N2 |
| Weight Force (N) | N2 |
| Time (Consolidation) (s) | N2 |
| Mass (kg) | N3 |
| Mass Density (kg/m3) | 1 |
| Stress (N/m2) | 1 |
| Hydraulic Gradient | 1 |
| Acceleration (m/s2) | 1/N |
| Fluid Velocity (m/s) | 1/N |
| Hydraulic Conductivity (m/s) | 1/N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.; Beier, N.A.; Kaminsky, H. A Comprehensive Review of Large Strain Consolidation Testing for Application in Oil Sands Mine Tailings. Mining 2023, 3, 121-150. https://doi.org/10.3390/mining3010008
Ahmed M, Beier NA, Kaminsky H. A Comprehensive Review of Large Strain Consolidation Testing for Application in Oil Sands Mine Tailings. Mining. 2023; 3(1):121-150. https://doi.org/10.3390/mining3010008
Chicago/Turabian StyleAhmed, Mahmoud, Nicholas A. Beier, and Heather Kaminsky. 2023. "A Comprehensive Review of Large Strain Consolidation Testing for Application in Oil Sands Mine Tailings" Mining 3, no. 1: 121-150. https://doi.org/10.3390/mining3010008
APA StyleAhmed, M., Beier, N. A., & Kaminsky, H. (2023). A Comprehensive Review of Large Strain Consolidation Testing for Application in Oil Sands Mine Tailings. Mining, 3(1), 121-150. https://doi.org/10.3390/mining3010008