Modeling Productivity Reduction and Fuel Consumption in Open-Pit Mining Trucks by Considering the Temporary Deterioration of Mining Roads through Discrete-Event Simulation

Abstract

Open pit mining is based on dynamic operations within the open pit, with the haulage operation being the most decisive in terms of the cost and the overall productivity of the operation. A vital aspect for the success of the haulage operation are the conditions of the roads, which change over time due to wear and tear. The present work aims to model and to evaluate the effect of temporal deterioration affecting mining roads in an open pit mining operation through rolling resistance, using the discrete event simulation (SED) tool to evaluate two key aspects of the operation: productivity and fuel consumption. Additionally, to reverse road deterioration, the assignment of a grader with a variable frequency of use will be modeled through a parallel model. The case study is a 5 km road with a slope of 9.5%, a fleet of 10 trucks, and their capacities of 300 tons, loaded in a 24 h simulation model. The results show that not considering road deterioration can mean an overestimation of productivity of up to 600 Ton/hr, and an overconsumption of 78%. The application of a motor grader could decrease the negative effects of roads deterioration, which depends on the frequency of its assignment. The results show that for the rate of productivity and fuel consumption for every hour of frequency that the motor grader does not do road maintenance, the production loss is 600 tons, and the fuel consumption increases by approximately 1800 L in a day.

1. Introduction

Improving the efficiency of open pit mining operations is a constant challenge that involves various factors of the operation under evaluation, such as economic, environmental, and social aspects. In this framework, one of the critical steps in mine operations is the hauling, which concentrates 50% of the total extraction costs [1], and whose performance is determined, among other reasons, by the quality of the mine haul road on which the trucks travel. Unfortunately, the roads are deteriorated because of the passage of the trucks, and the action of atmospheric agents such as rain, wind, and poor operational practices [1]; all these elements affect the speed of the trucks, which is critical for achieving the goal of production.

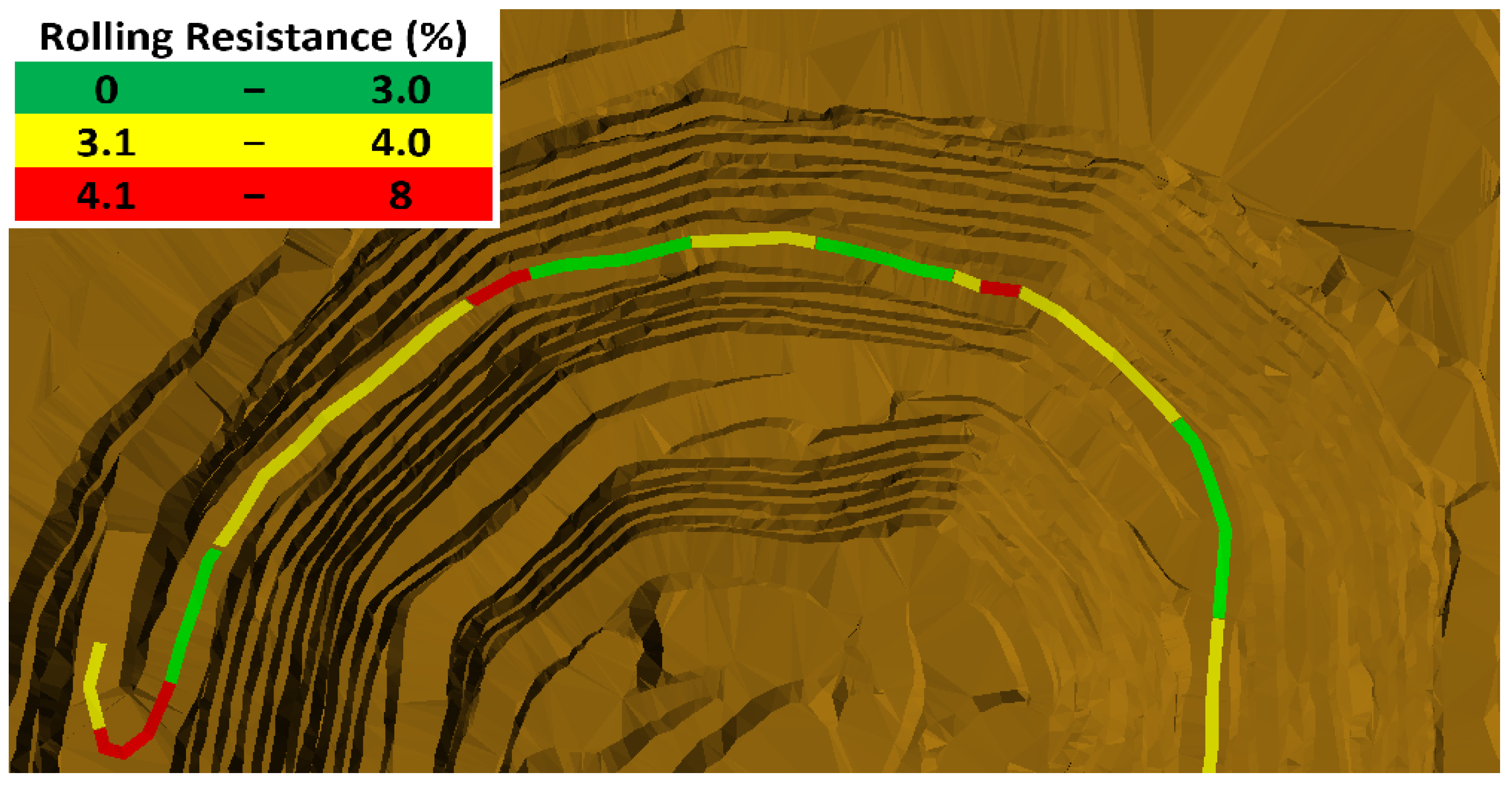
For the modeling of the temporary deterioration of the road, it can be represented through the rolling resistance (RR) [1,2], where it establishes that the deterioration rate is not uniform along the road [3], as shown in Figure 1, and it is dependent on the time of the operation. Additionally, the RR has a well-established behavioral stage through time. The RR can be expressed in units of inclination degree, and it can be added to the ramp slope; it could generate a significant increase in the total slope of a road, which ultimately causes a reduction in truck speed.

Truck manufacturers have generated several methods to determine the truck speed [2,4], and this parameter is decisive, since it allows us to meet the mine plan, generating a high degree of productivity. However, if the speed of the trucks is lower than expected, it will cause the cycle time of the trucks to increase, impacting on low productivity. On the other hand, the truck speed is dependent on road deterioration; furthermore, it is one of the most common factors that are connected to technical and economic indicators such as: fuel consumption, higher particulate matter pollution, higher greenhouse gas emissions, tire wear, spare parts, and the repairs of transport equipment [1,5].

Despite mine road maintenance management being studied in considerable detail in the literature [1,6,7], and often within the mining operation context, it has been seen as a second-order factor, but it has ignored that many of the gaps in meeting goals could be achieved when better road maintenance management is included.

In order to contribute toward the study/solution of these problems, different simulation techniques are used that have been applied in various fields with aims to model, understand, and experiment with a system under controlled conditions. In the case of road deterioration, Monte Carlo Simulation (SM) [8] has been used with some limitations regarding the flexibility of modeling and the inability to represent the dynamism of more complex mining operations. Another type of simulation technique is the Simulation of Discrete Elements (SED), where this technique allows for the evolution of the simulation in events that happen at specific times over a period of time, and where the state variables of a system can change [9]; therefore, it is a more complex and versatile technique than the SM, and it can reflect the complexity of mining operations, being widely applied in different areas of engineering [9] and mining [10,11]. This technique has been successfully applied in the determination of the fuel consumption of mining trucks, considering RR without temporary variation [12].

The present work advances the study of the maintenance management of roads, considering two relevant elements: the first one is an evolution of the temporary deterioration of the road, and the second one is the sectorization of the truck’s path, where it presents different conditions. In order to solve these two conditions, the SED allows for the understanding of the relationship between the effect of deterioration in the mine haul road, and some of the most important key performance indicators, fleet truck productivity and fuel consumption. Finally, the simulation can measure the effectiveness of maintenance through the frequency of the motor grader in the mine haul road.

2. Materials and Methods

To model and to simulate the process associated with the transport of the material, four phases of the simulation are defined, which are: (a) the definition and characterization of the source material; in this case, it is associated with the shovels. (b) The material transport process by means of trucks that interact with the roads. (c) The definition and characterization of the destination point, which closes the first path. (d) The transport process without material, by means of trucks that interact with the road. In its development, a single circuit or route is used, along which a fleet of trucks will complete a cycle that goes from the shovel at the production front, to the crusher, through a ramp with a fixed slope, and then back to the shovel, as shown in Figure 2.

To implement the model computationally, the simulation software for general use SIMIO [13] will be used, and both the shovel and the crusher will be modeled as SERVERS [11,12], since they are static elements within the simulation, having both in common a time of attention to the trucks and the capacity to generate a queue. The trucks will be modeled as entities [14] because they are the dynamic elements of the system; their particularity is that their gross weight machine ($T_t$) and payload ($w$) changes when the truck is loaded with rock (ore or waste). The crusher has a variable that stores the tonnage ($T$), and when the truck arrives at the crusher, this variable increases its value to $T=T+w$; this represents the tonnage where the truck unloads in the crusher. Once the truck leaves the crusher $w=0$, this represents that the truck returns empty to the shovel.

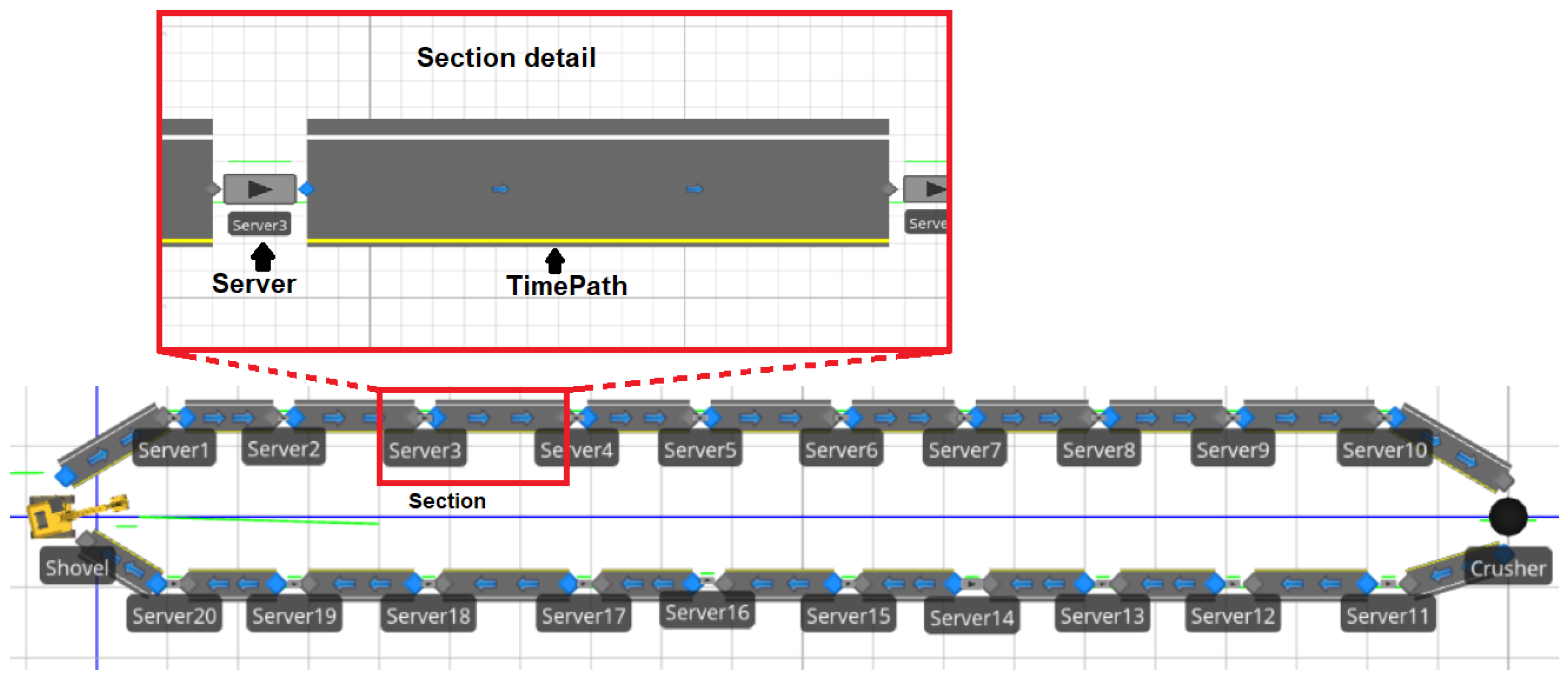
The modeling of the road will be equally important compared to the modeling of the mining system, since it will represent the temporary deterioration of the road and all the characteristics that derive from it [1]. For this purpose, the road will be separated into two independent tracks according to the direction of the truck, and each track will be separated into sections of constant length. A section will be represented in the simulation model, using two elements: Server and TimePath. The Server element of each section will help us to represent the processes that are associated with the decomposition of road quality and road repair when it is visited by the motor grader. Furthermore, the TimePath element represents the time that it takes for the truck to cross a given section of the road. Hence, this will help us to appreciate the effects of road deterioration on the speed of the trucks, mainly when they go up the ramp to the crusher. In Figure 3, we can see a general scheme of the simulation model, where the main elements can be appreciated.

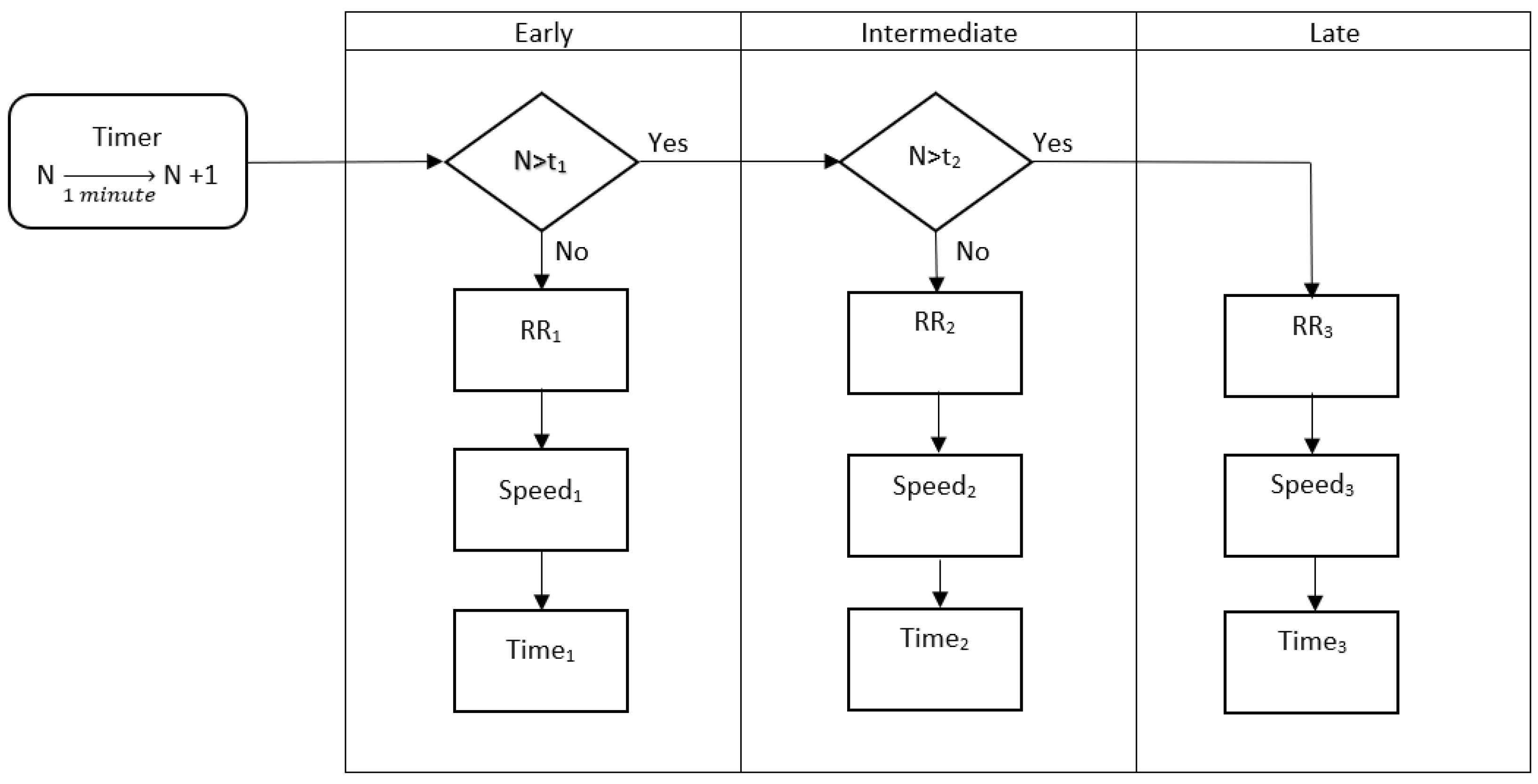
For the representation of the path deterioration within the simulation, a process or algorithm will be established for each section of the path. Each process associated with a section is identical and independent of the processes of the other sections, and its operation is detailed in Figure 4. The process consists of a Timer and a recursive execution element where every minute adds one unit to the variable $N$; this variable represents how the time increases every minute; that is, it counts the minutes within the process. The process considers that deterioration evolves in stages; in Figure 4, three stages of deterioration are established: early, intermediate, and late. To differentiate which stage is being used, there are conditionals that decide what degree of deterioration the section is in; for example, if $N$ is less than $t_1$, then the process is in an early stage of deterioration. Each stage calculates three variables: RR, speed, and time.

As a control parameter, the fluctuation in fuel consumption is evaluated based on the work of Soofastaei [15], who establishes a fuel consumption factor ($CF$), which depends on the slope of the road, and the weight ($T_t$) and speed (expressed in time used $t$) of the truck, with the following mathematical expression (Equation (1)):

$$Consumption\left[lts\right]=CF\left[\raisebox{1ex}{$lts$}\!\left/ \!\raisebox{-1ex}{$ton hr$}\right.\right]\ast T_t\left[ton\right]\ast t\left[hr\right]$$

(1)

In addition, the simulation model will use a variable that captures the $CF$ on each section of the road, ($i$) when the truck passes through that section in one of the travel cycles ($N$), it must accomplish as determined using the following variable, which can be represented in Equation (2):

$$C{F}_{i,j,N}=the CF in the section i for the truck j in the cicle N$$

(2)

To maintain the road and to stop the deterioration of the road conditions, a motor grader travels through each of the road sections, reversing the deterioration of the road by returning the variable that counts the minutes to zero ($N=0$), in the process of Figure 3, for each of the sections. For this purpose, a parallel process or algorithm is constructed that represents the action of the motor grader, which is detailed in Algorithm 1.

The motor grader is assigned to the road with a frequency ($Frec$) that must be greater than the truck’s cycle time of the travel ($T_{cl}$) over the entire road, and that is less than the total simulation time ($T_t$), so that $T_{cl}<Frec<T_t$. In order for the motor grader to start its path, there must be a timer that is executed according to the assignment frequency and that triggers the grader process; this means that the timer is triggered in a time sequence belonging to the $\mathrm{Starting} \mathrm{Set}=\left\{0, 1\ast Frec, 2\ast Frec, \dots \right\}$.

The motor grader process consists of an iterative work, traversing each section of the road; for this purpose, sections are defined as a set of all road sections from 1 to n, in a sequence that can be traversed by the motor grader. $Sections=\left\{sectio{n}_1, sectio{n}_2, \dots , sectio{n}_n\right\}$; the motor grader must spend time $t_{mov}$ moving from one section to another until it finishes its traversal of the entire road, as presented in Algorithm 1.

Algorithm 1: Pseudo Code.
Motor grader process
1:	$\mathbf{\hspace{1em}\hspace{1em}\hspace{1em}\; If} {\mathit{T}}_{\mathit{c}\mathit{l}}<\mathit{F}\mathit{r}\mathit{e}\mathit{c}<{\mathit{T}}_{\mathit{t}}$then:
2:		For    i in Starting set:
3:			Execute Timer(Starting Set[i]):
4:				For j in Sections:
5:					${\mathit{N}}_{\mathit{j}}=\mathbf{0}$
6:					$\mathbf{Wait} {\mathit{t}}_{\mathit{m}\mathit{o}\mathit{v}}$
7:				End For
8:		End For
9:	End if

3. Results

The case study reported below is based on an open pit road, Figure 5, of 5 km length and a slope of 9.5%, which is divided into 12 total sections, corresponding to 6 sections in each direction, respectively.

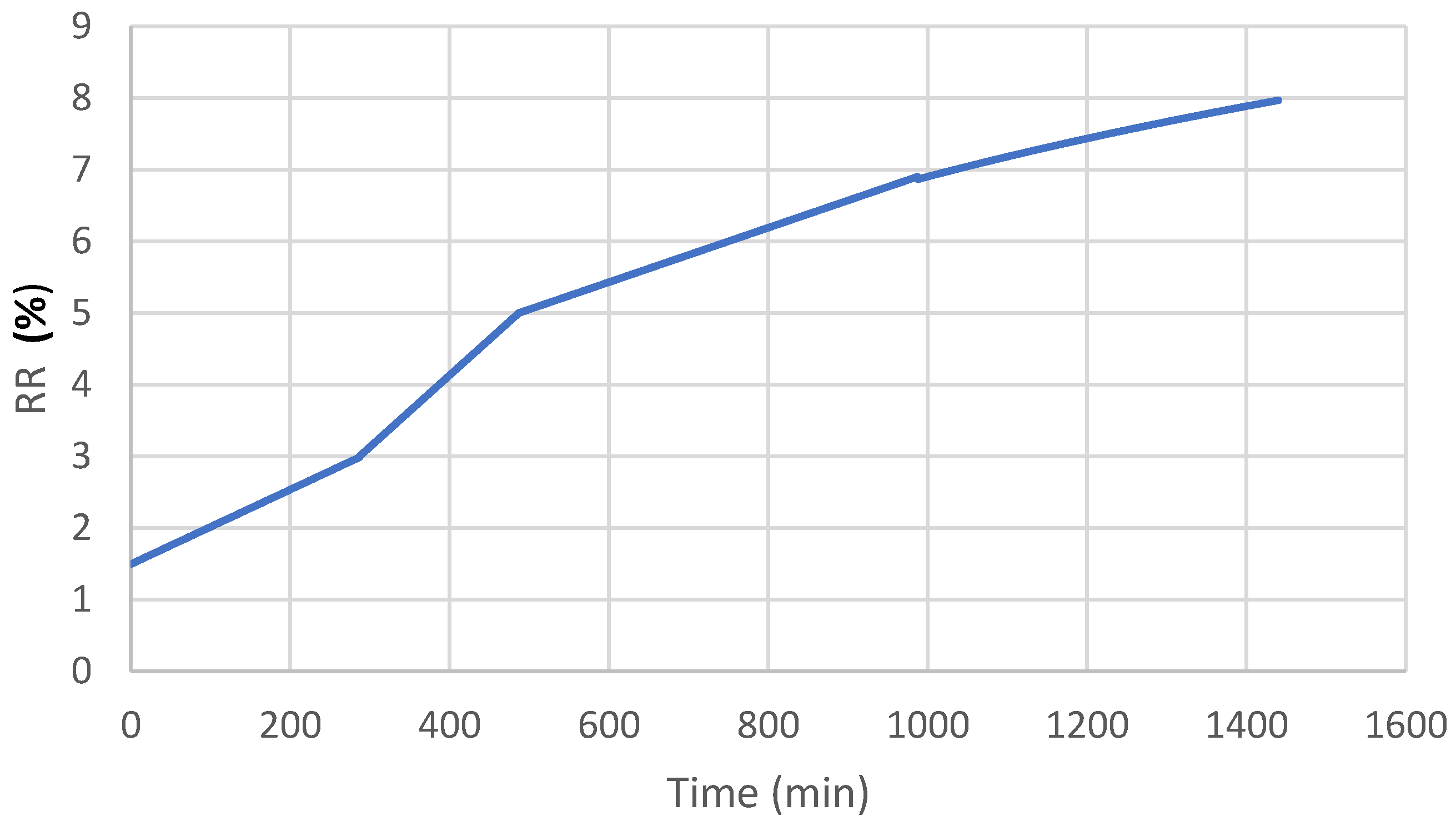
A fleet of 10 trucks is used, where each truck has a weight of 150 Ton, and a transport capacity of 150 ton, so that the total gross weight of a loaded truck is 300 ton. With these characteristics, the temporal wear model expressed in rolling resistance for 24 h (1440 min), is shown in Figure 6, and this function is the one used in this simulation.

The speed of the trucks ($v_c$) will be established according to the direction that the respective trucks follow. When the truck is going to the crusher, it is loaded, while when the truck is going down towards the shovel, it is unloaded; therefore, mathematically, the speed of a truck could be represented using Equation (3):

$$v_c\left[\raisebox{1ex}{$Km$}\!\left/ \!\raisebox{-1ex}{$Hr$}\right.\right]=\{\begin{array}{c}0.0348\ast R{R}^2-1.3239\ast RR+17.696;when the truck is going up\\ 40;when the truck coming down\end{array}$$

(3)

All these elements will be evaluated by the simulation through the loss of productivity that would eventually be caused by the uncontrolled deterioration of the road mine haul.

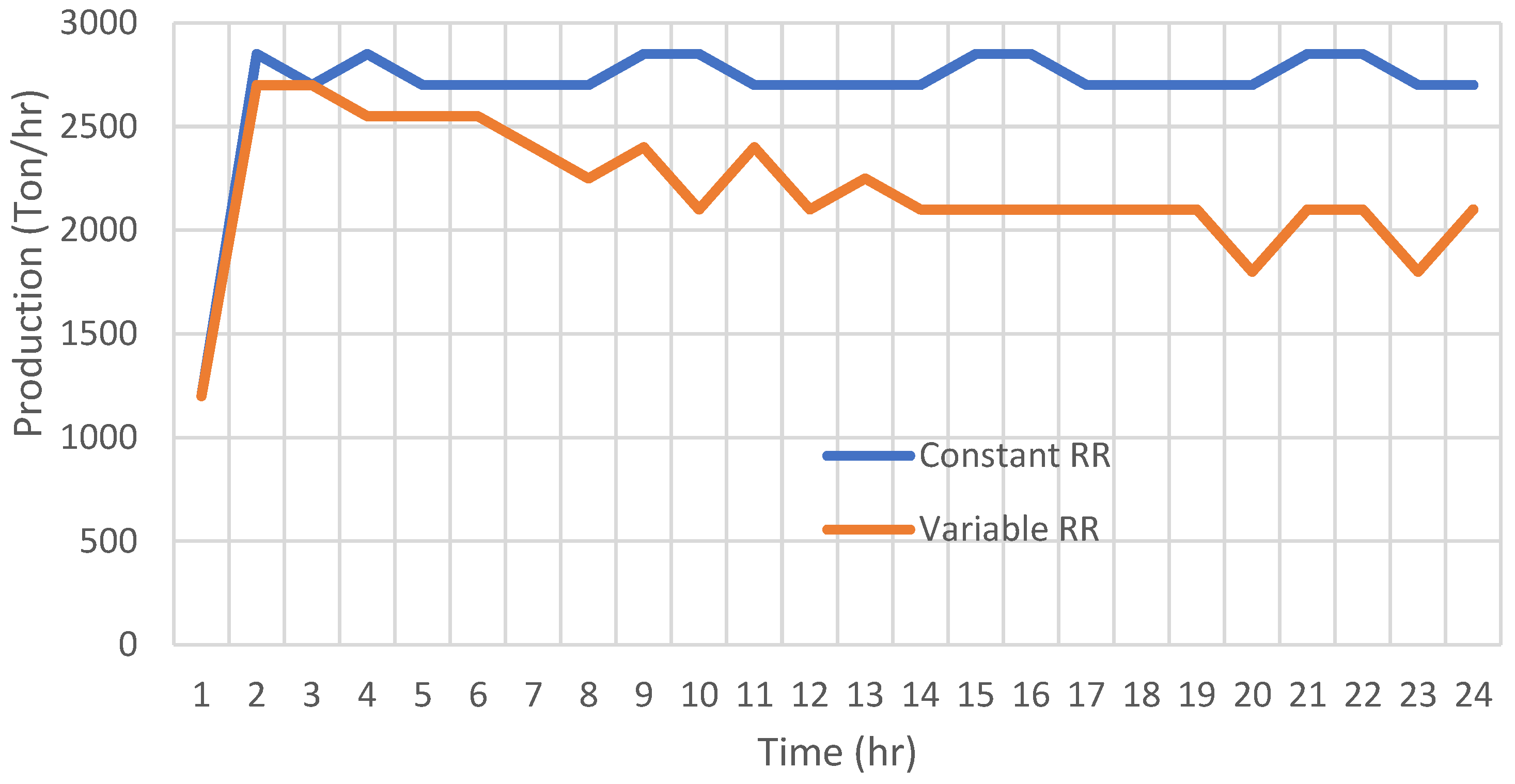
The first case study (Figure 7) that we are reporting is when comparing the productivity of trucks, to over hour along a simulation time of 24 h, between a model simulation with an RR constant value of 1.5%, and a second model simulation, where RR presents a temporal deterioration (variable RR); in both cases, the slope of mine haul road used is 9.5%. Their results show the differences between both models in terms of productivity Ton/Hr, where it is clearly seen that if we do not consider the temporary deterioration of the road through RR, we are overestimating the productivity of the mining system.

For fuel consumption modeling, the CF model is used, which is in units of Lt/(ton h), and is represented in Equation (4):

$$CF\left[\frac{lt}{ton hr}\right]=0.04375\ast slope-0.00201 \ast T_t+0.007\ast v_c+1.43$$

(4)

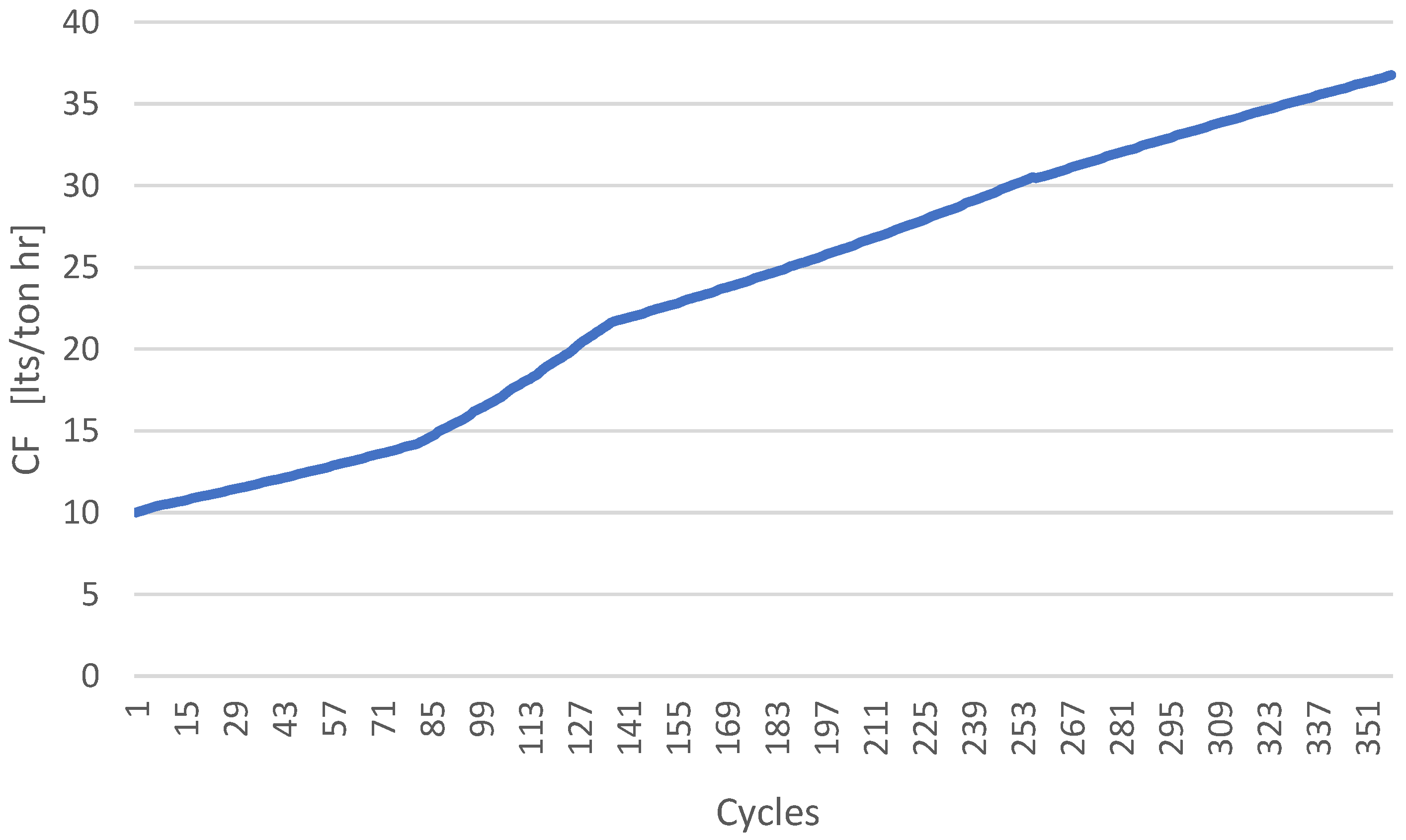
Figure 8 shows the result for a specific section of the road. As the CF increases, the truck complete cycles of hauling along the route, considering that the road deteriorates temporally, i.e., as the RR increases as a function of time, and this time effect is observed as the truck completes its respective transport cycles over the simulation time.

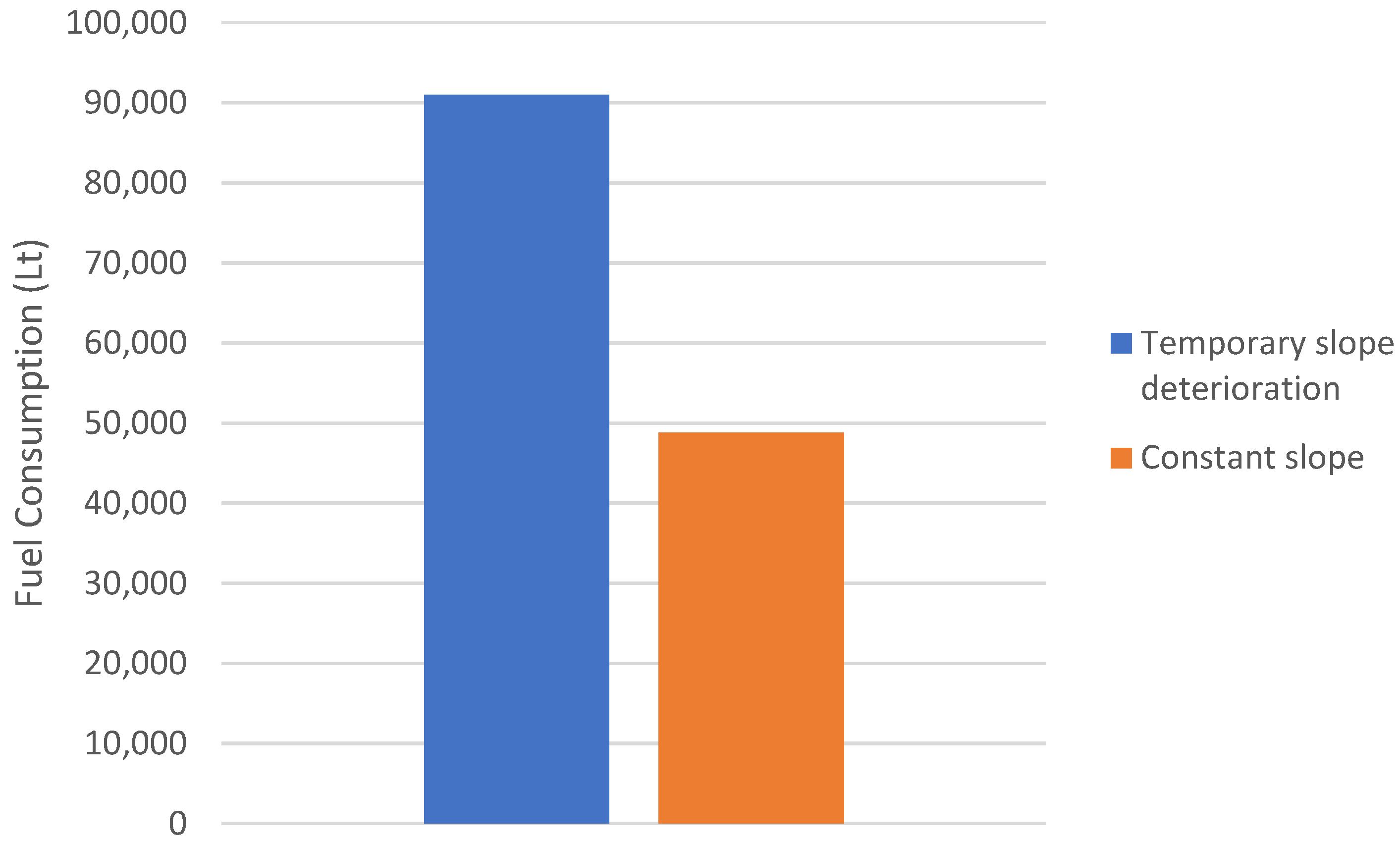
Now, the 24 h fuel consumption of the trucks is different when they are loaded up the ramp at a constant slope, compared to the consumption of the same trucks subjected to temporary road deterioration, so we can observe this effect as an overconsumption of 87%, as shown in Figure 9.

The application of the motor grader for mine haul road maintenance, has assigned a constant movement speed of 40 km/h; therefore, the time of each cycle is 15 min. In addition, different frequencies, which means different intervals of time between cycles of the motor grader, were analyzed in a range from 1 h to 15 h, being compared under two aspects: production and fuel consumption for each frequency.

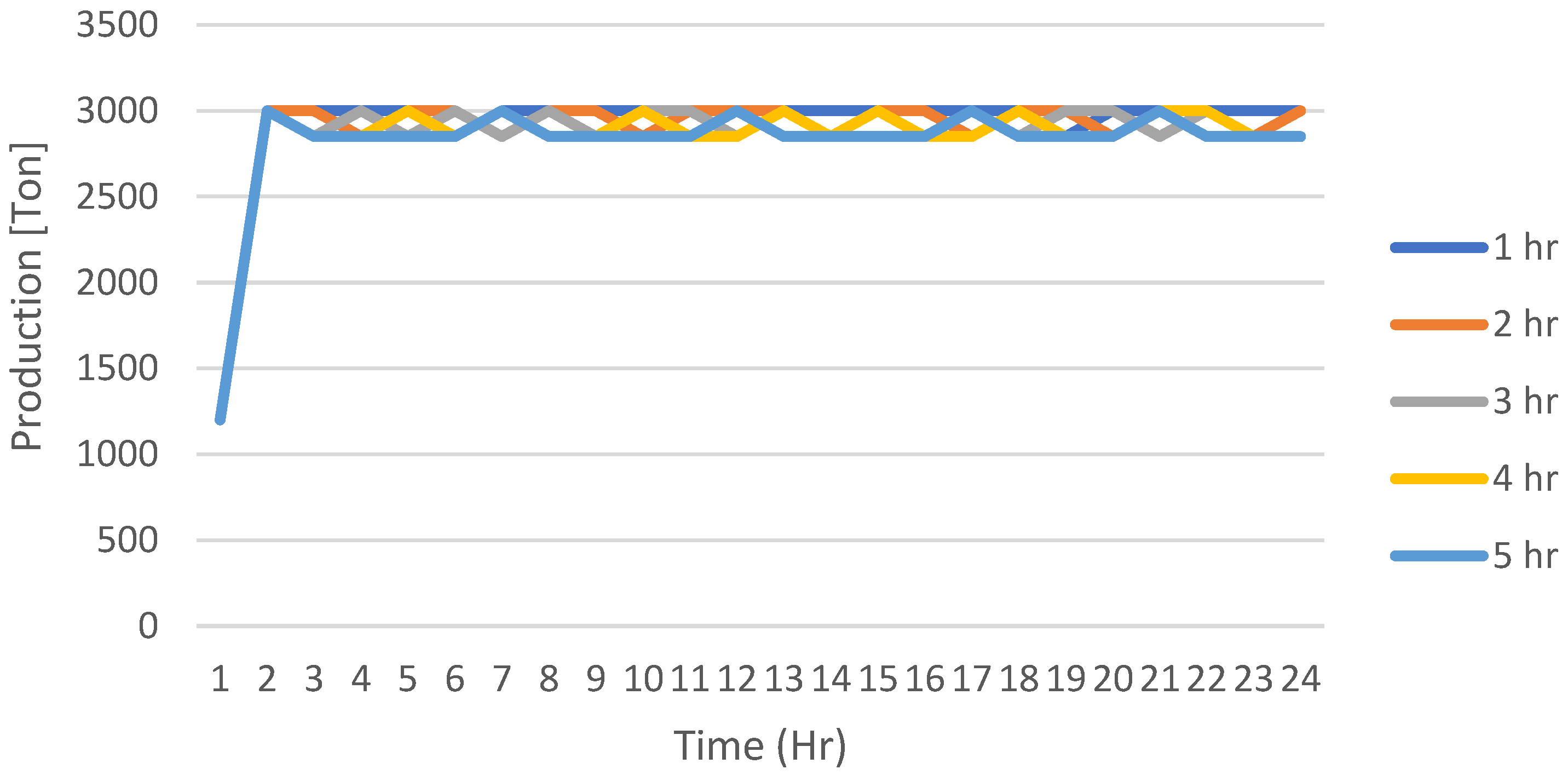
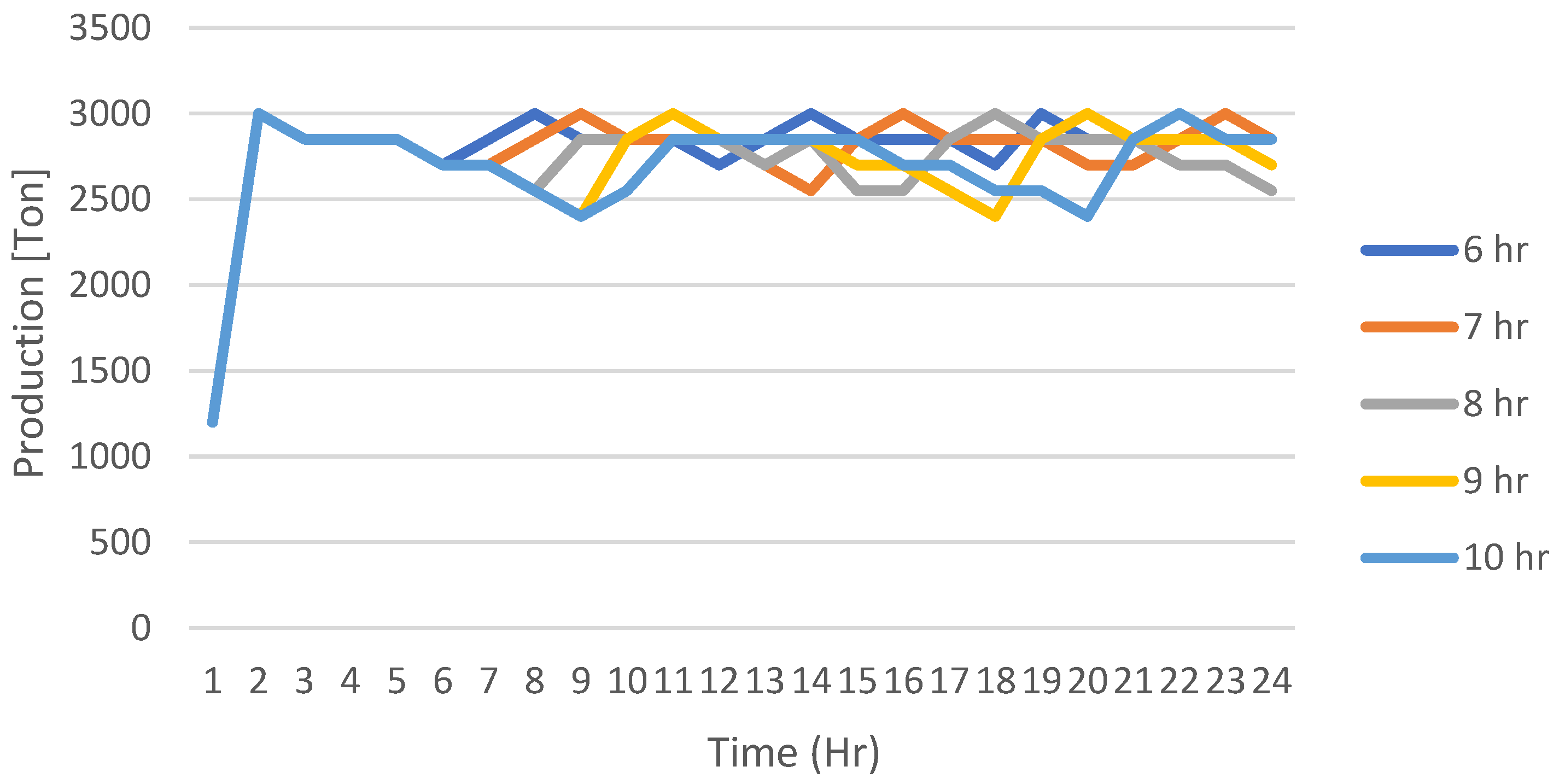
The results obtained show that the productivity (Appendix A) of the trucks, considering a horizon of 24 h, has established a directly proportional relationship between the productivity (ton/h) and the frequency of the motor grader. In the first place, the high frequency of the maintenance of the haul road in Figure A1 have shown a performance that is close to the productivity with an RR constant (see Figure 6), which is equivalent to 3000 ton/h, approximately. On the other hand, the medium frequency in Figure A2 has a productivity of between 2500 and 3000 ton/h, and finally, the low frequency in Figure A3 produces a more variable performance, even under 2500 ton/h in some hours of the simulation.

An interesting relationship has been found between the productivity and the fuel consumption under time intervals of maintenance of the haul road, as shown in Figure 10. Although the frequency and the productivity are directly related, fuel consumption and frequency have the opposite relationship, and this means that while we decrease the frequency of the motor grader application, the production decreases from almost 70 thousand ton/day if we apply the grader every hour, to 62 thousand ton/day if we apply the grader every 15 h; on the other hand, the fuel consumption increases if we do not apply the grader regularly, increasing from approximately 50 thousand (Lt of fuel)/day, with graders being applied to the road every 1 h, to 72 thousand Lt of fuel/day if we apply the grader every 15 h. Furthermore, an analysis of the rate of productivity and fuel consumption shows that for every hour where the motor grader does not do road maintenance, the production loss is 600 tons and the fuel consumption increases by approximately 1800 L in a day.

4. Conclusions

The present work has demonstrated that road deterioration has important negative effects on the performance of a mining operation, which has been observed empirically in field work [3,7,16,17], and the results of this work corroborate through two variables: production and fuel consumption. One of the most interesting aspects of this work is the degree of precision that can be achieved in the representation of both the phenomenon of the deteriorating conditions, and the consequences on production and fuel consumption. Also noteworthy is the flexibility of DES in being able to change not only the parameter models that feed the simulation, but also the simulation itself, by having the ability to modify even the process or algorithms that are present in the simulation model.

Undoubtedly, DES can help us to better understand the complexity of mining systems and to find new ways to improve performance, by considering constraints such as road deterioration, which was the objective of this work.