An Overview of Slope Failure in Mining Operations
Abstract
:1. Introduction
Instability and Rock Mass Failure in Slopes
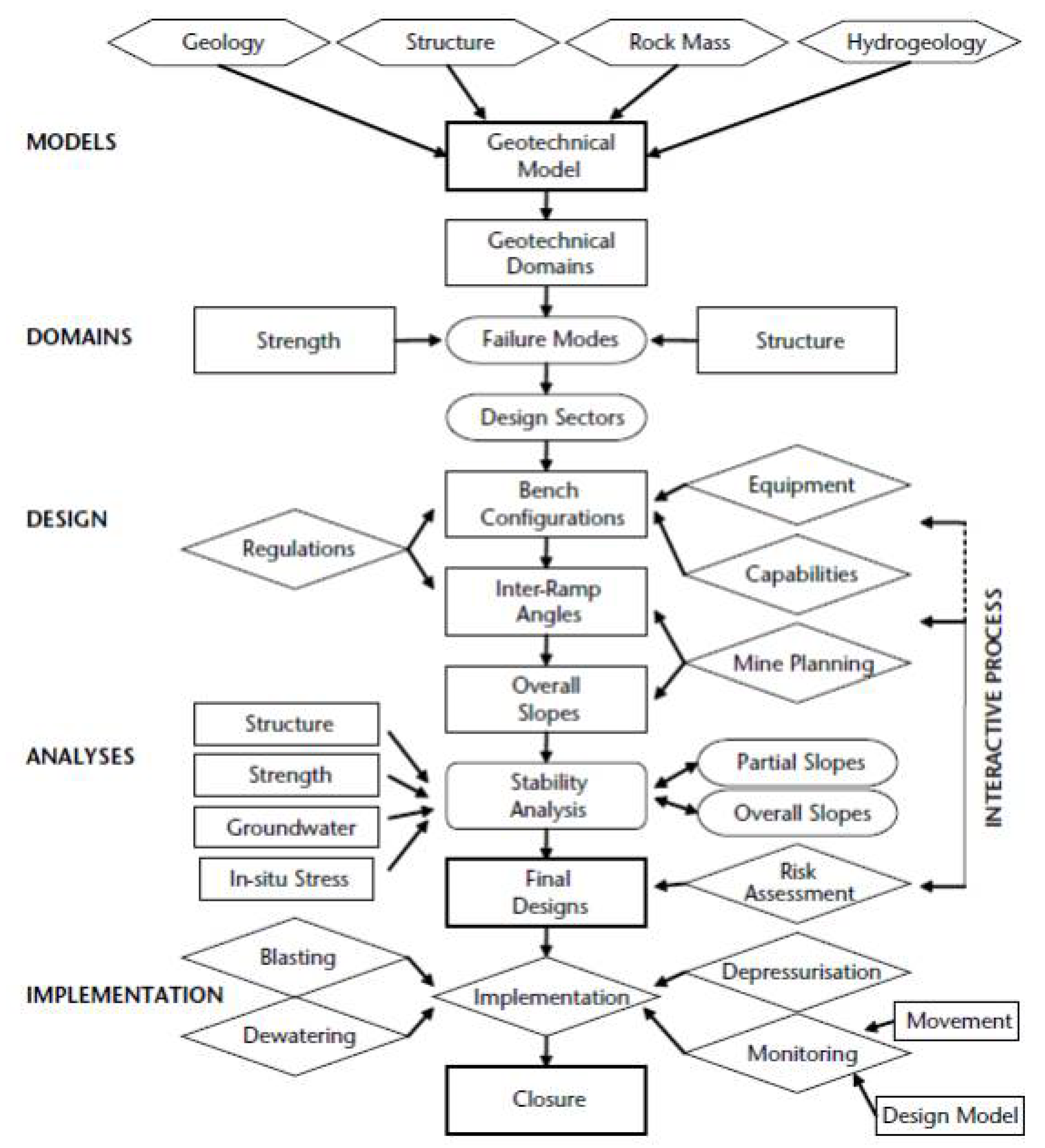
2. Evaluation of Slope Stability in Mining
2.1. Limit Equilibrium Method (LEM)
- (a)
- In estimating the stability of slopes, if the movement of rock mass is detected, the LEM approach cannot estimate the impact of such movement on the overall stability [27];
- (b)
- LEM is restricted to the evaluation of slope stability with simple problems, such as providing little insight into the slope failure mechanism [12];
- (c)
- LEM can only identify the onset of slope failure. Complex rock slope stability problems associated with in situ stresses, such as the geometry of the slope, pre-pressure and seismic loading, require a continuum-mechanics-based numerical modeling approach [28].
2.2. Numerical and Mathematical Modeling Method of Slope Stability Analysis
3. Process and Mechanisms of Slope Failure
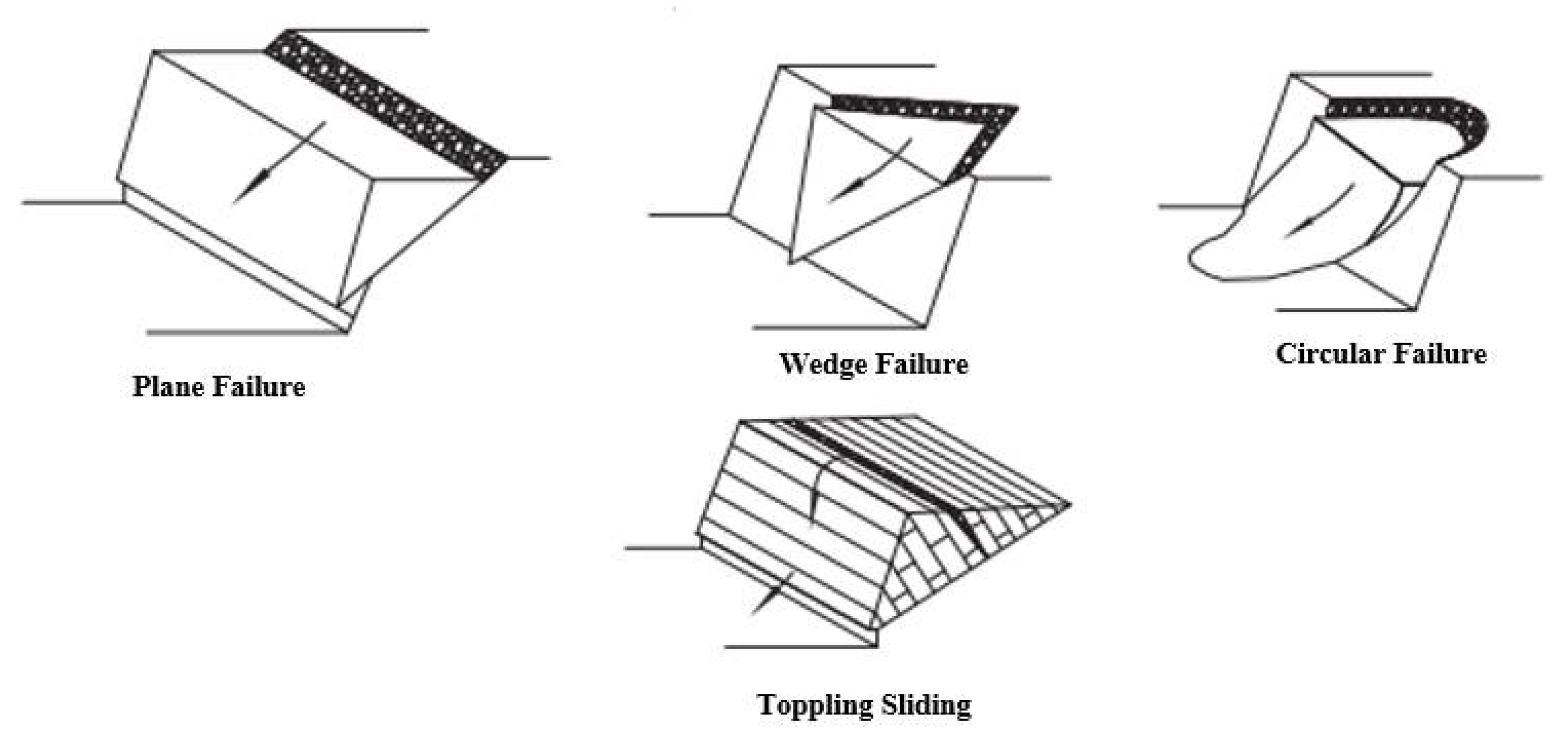
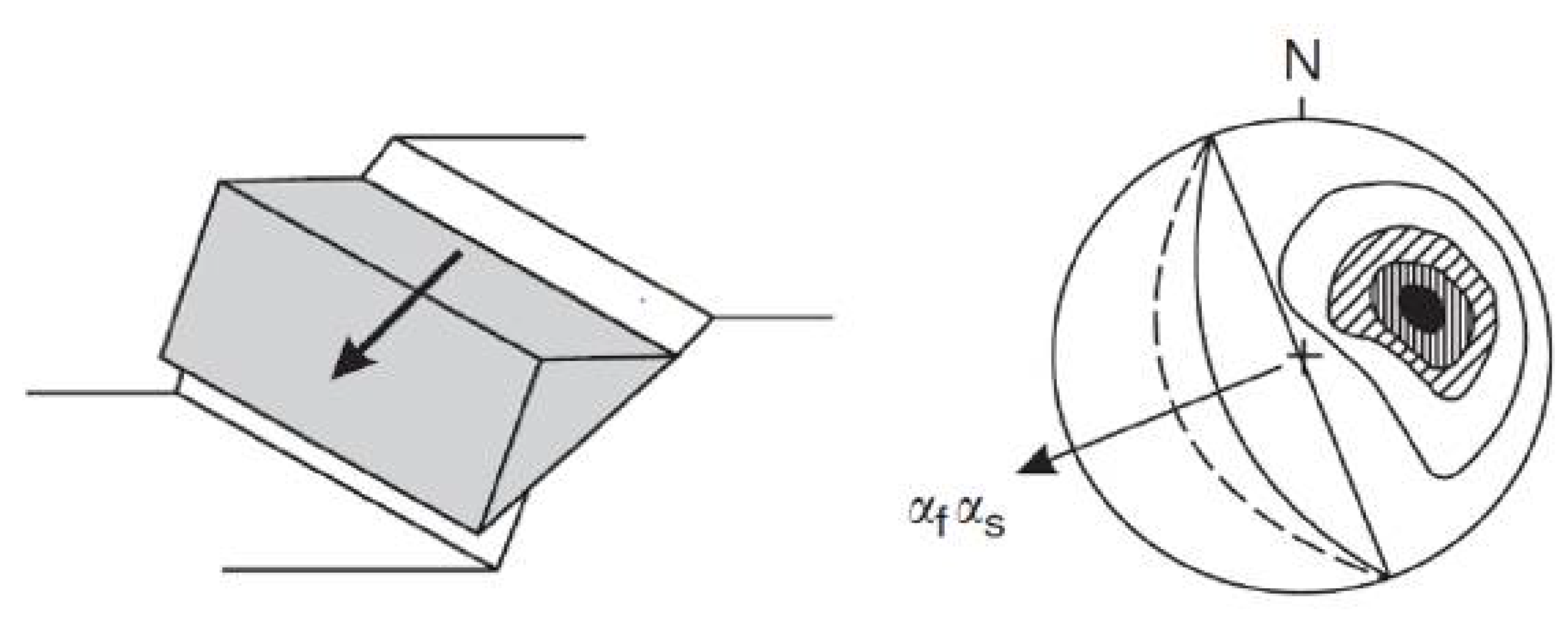
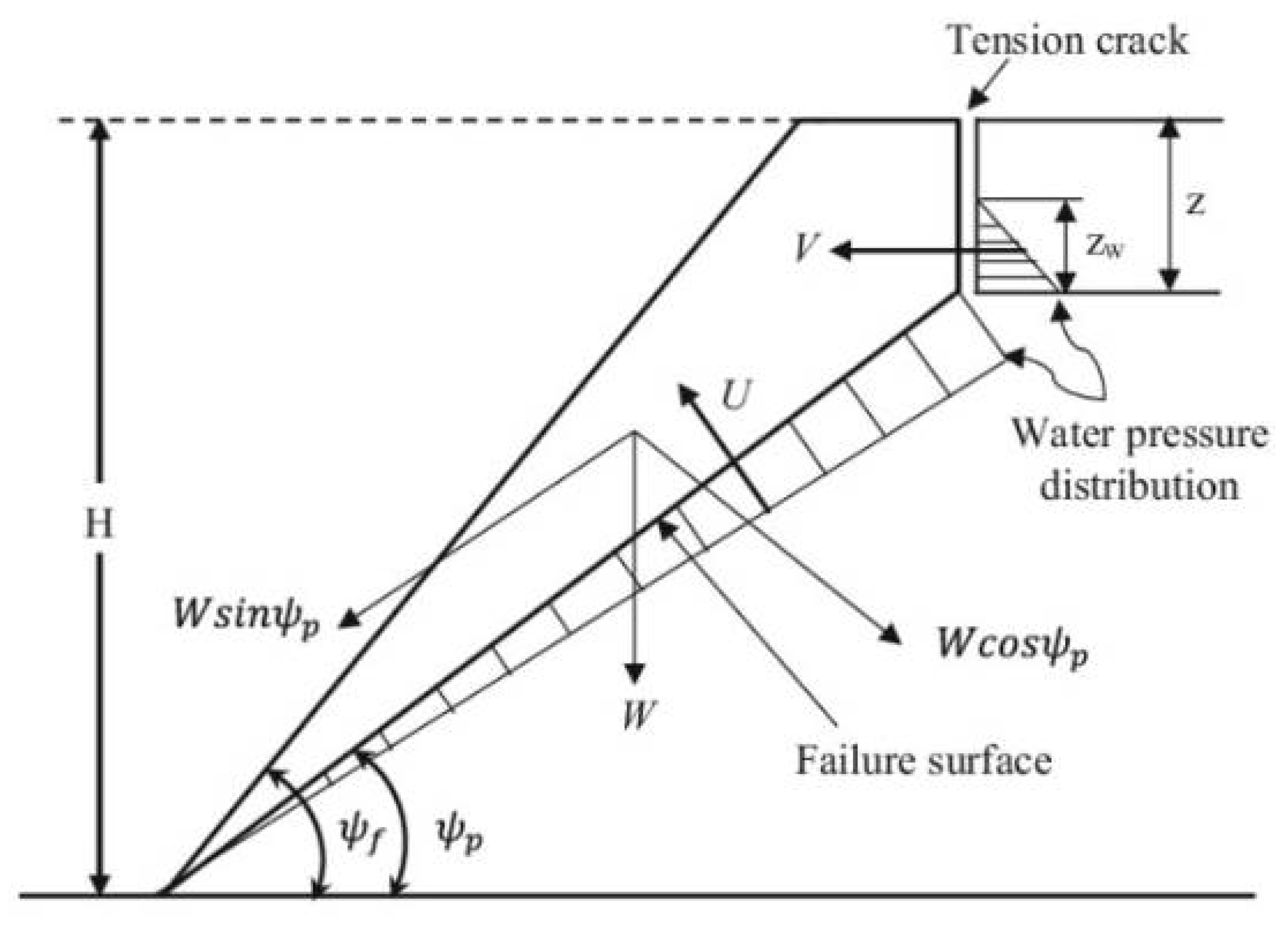
3.1. Plane Failure
- (a)
- The strike of the plane of weakness must be within +/−20° of the crest of the slope;
- (b)
- The toe of the failure plane must daylight between the toe and the crest of the slope;
- (c)
- The dip of the failure plane must be less than the dip of the slope face and greater than the angle of internal friction of the failure plane;
- (d)
- The upper end of the sliding surface either intersects the upper slope or terminate in tension cracks;
- (e)
- Release surfaces that provide negligible resistance to sliding must be present in the rock mass to define the lateral boundaries of the slide.
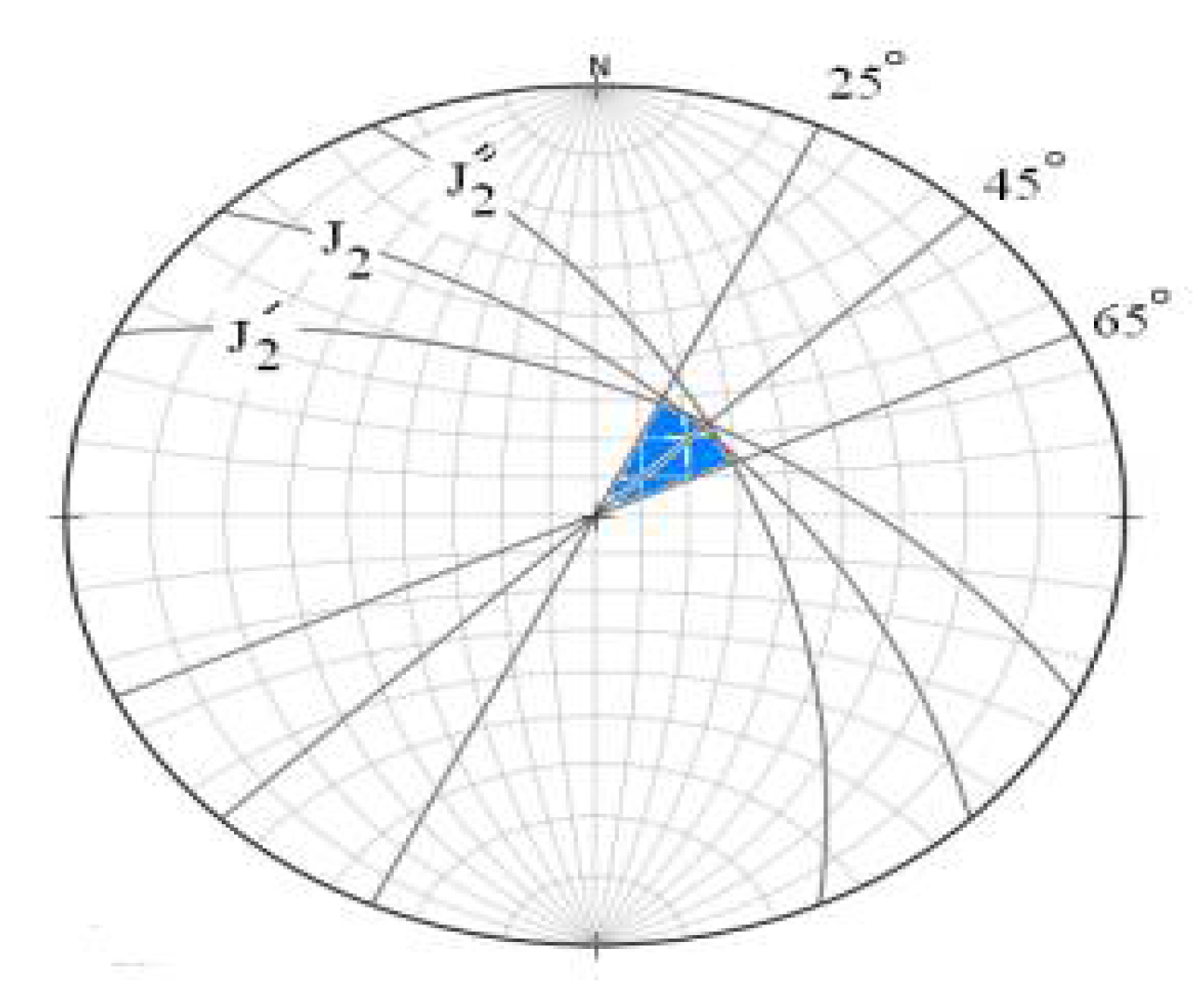
3.2. Wedge Failure
- (a)
- When the line of intersection of two discontinuity planes associated with the potentially unstable wedge is daylighting on the slope plane;
- (b)
- When the dip of the slope exceeds the dip of the line of intersection of the two discontinuity planes associated with the potentially unstable;
- (c)
- When the line of intersection of the two discontinuity planes associated with the potentially unstable wedge must be such that the strengths of the two planes are reached.
- (a)
- Sliding along the line of intersection of both planes forming the block;
- (b)
- Sliding along plane A only;
- (c)
- Sliding along plane B only;
- (d)
- A floating type of failure.
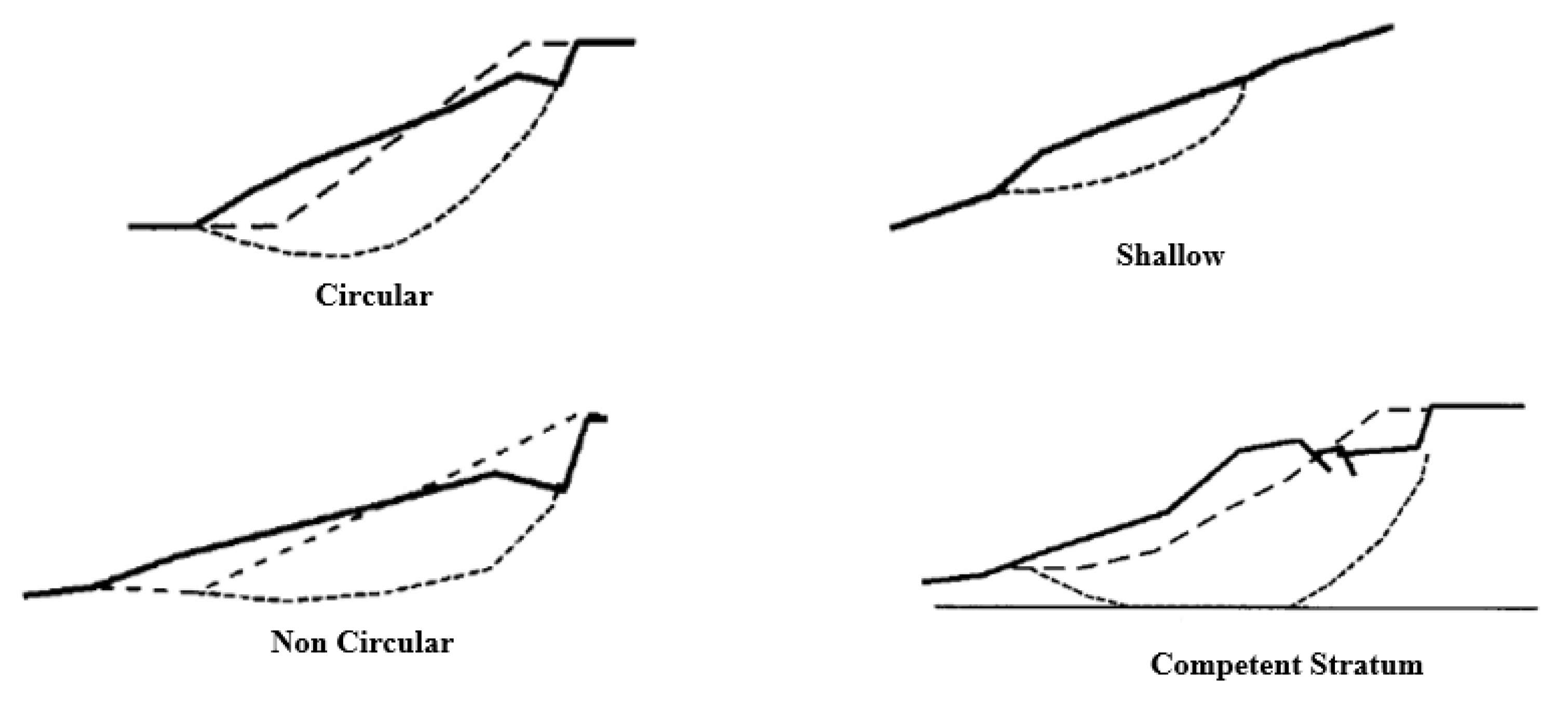
3.3. Circular Failure
- (a)
- Elastic displacement is caused by the removal of rock material during mining activities;
- (b)
- Yielding commences at the toe and spreads upwards as more material is removed or as a result of mining to a new and critical slope height;
- (c)
- Accumulation of shear strain at the toe of the slope will progress upward;
- (d)
- When failure surface is developed, the slope will start showing some displacements, which can be tracked if there is a good monitoring system in place;
- (e)
- Slope fails with time with larger displacement starting from the toe;
- (f)
- When failure occurs, the failing mass can slide away from the slope.
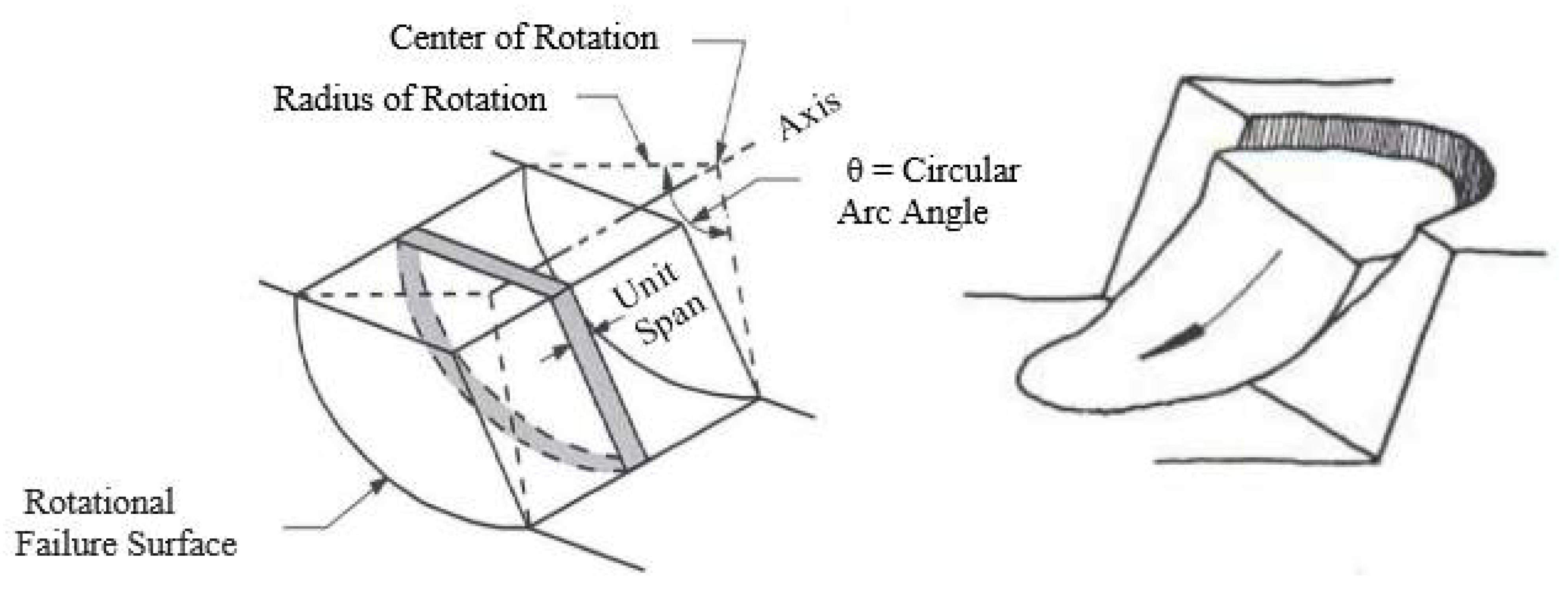
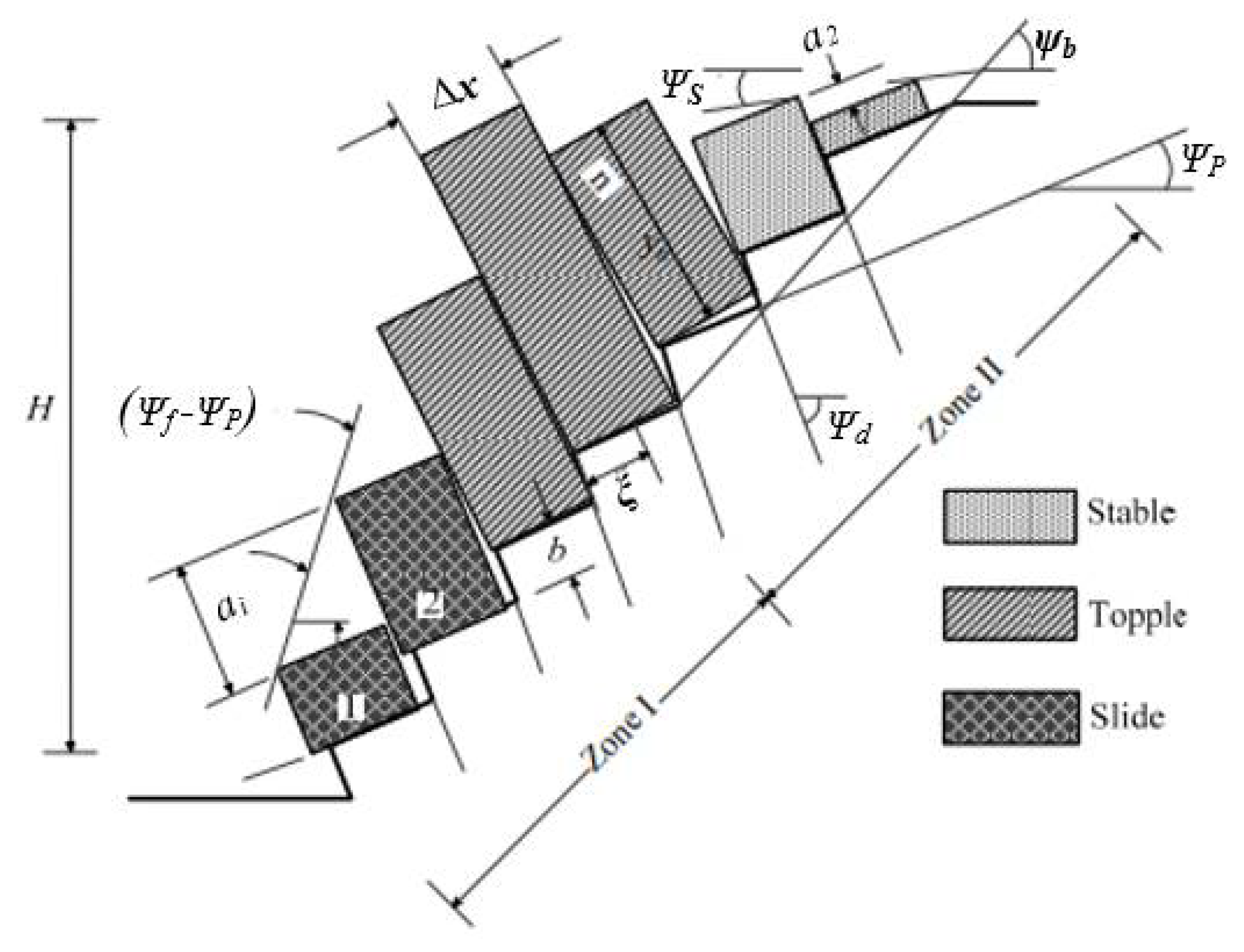
3.4. Toppling Failure
- (1)
- The joint sets must dip relatively steeply into the slope and must be able to slip relative to each other;
- (2)
- The rock mass must be able to deform substantially for toppling to have room to develop;
- (3)
- The tensile strength of the rock mass must be low to allow a tensile bending failure at the base of the toppling columns.
4. Factors Affecting Rock Slope Stability
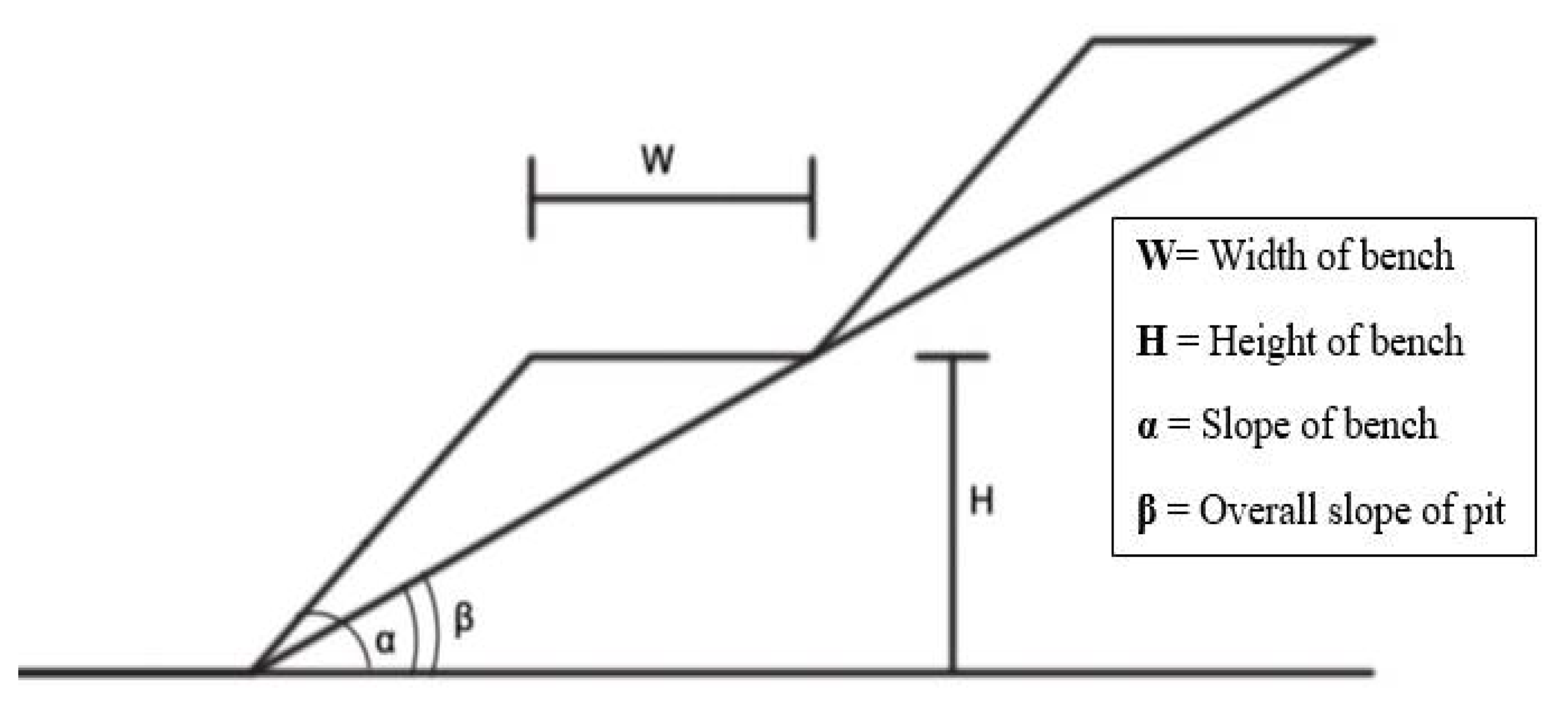
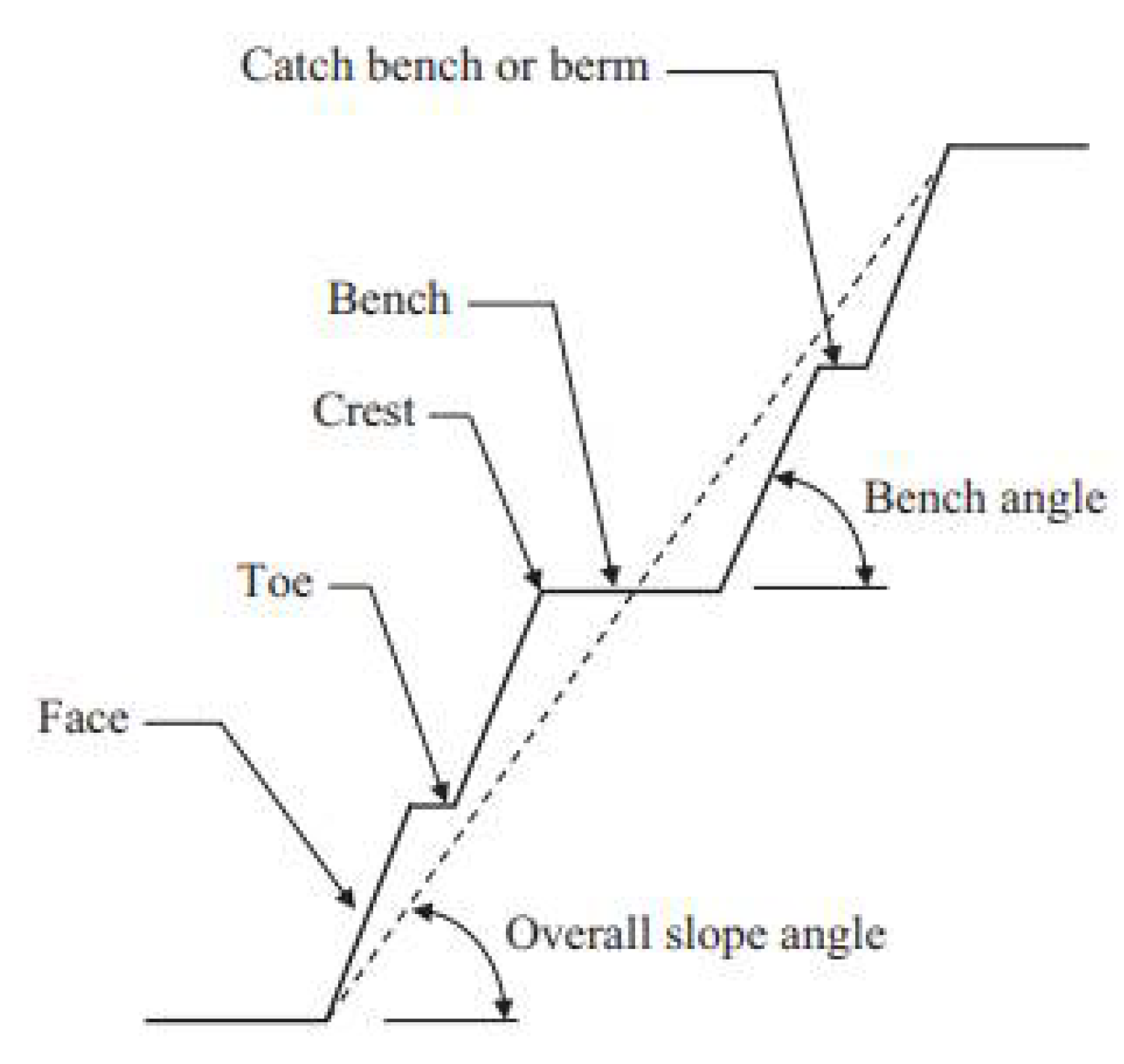
4.1. Slope Geometry
4.2. Geological Structure
4.3. Groundwater
4.4. Lithology
4.5. Cohesion and Angle of Internal Friction
4.6. Blasting
4.7. Mining Method and Equipment Usage
4.8. Stresses on Slope
5. Slope Failure in Mining Operations
6. Factors Required in the Design of a Stable Slope
6.1. Methods to Improve Slope Stability
6.1.1. Drainage Construction
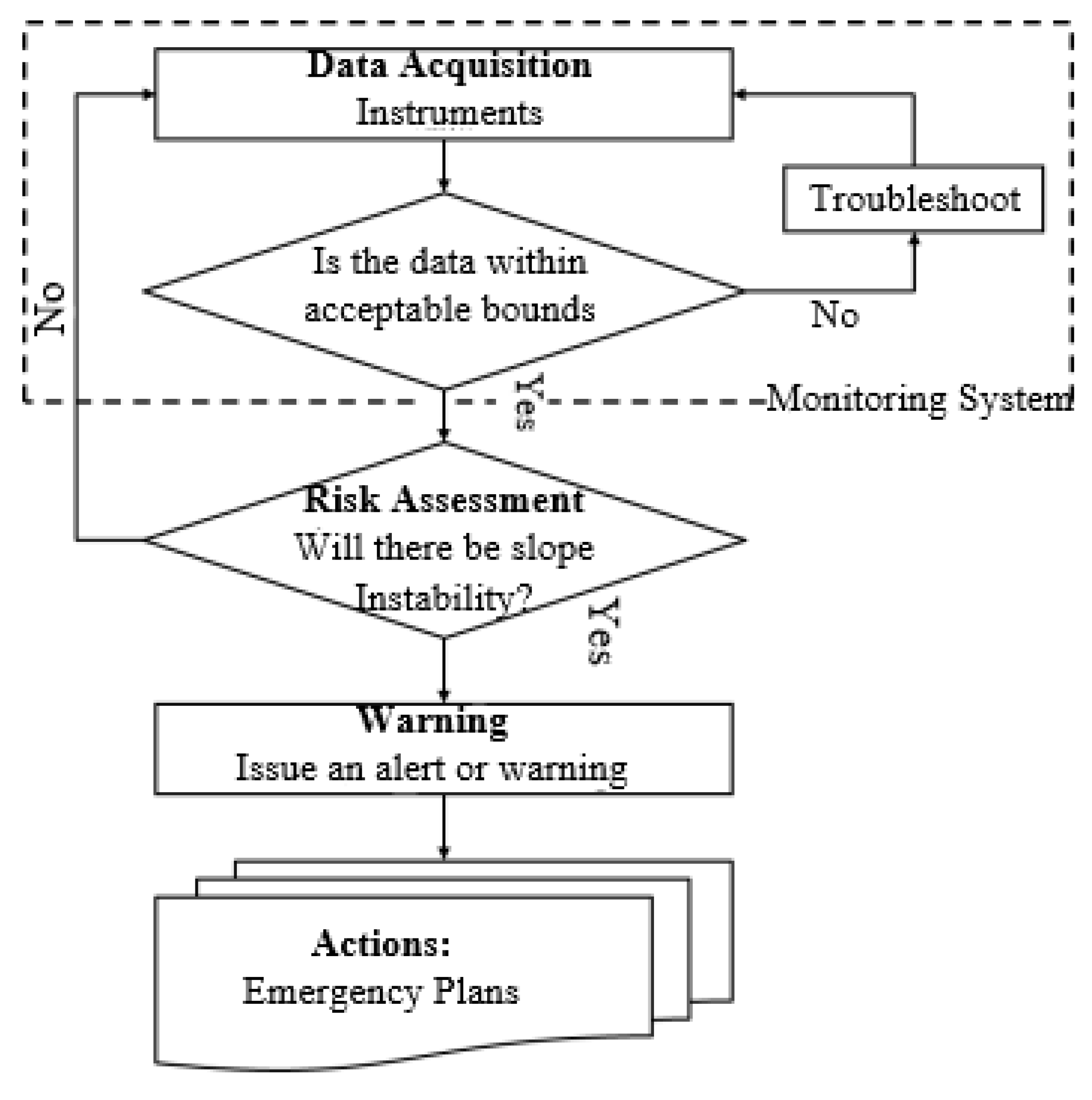
6.1.2. Slope Monitoring
6.1.3. Ground Improvement with Enhancement of Geological Structures
6.1.4. Installation of Reinforcement Units
6.2. Role of Artificial Intelligence in the Management of Slope Failure As a Reflection on the Current State of the Art
7. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Naghadehi, M.; Jimenez, R.; Khalokakaie, R.; Jalali, S.-M. A probabilistic systems methodology to analyze the importance of factors affecting the stability of rock slopes. Eng. Geol. 2011, 118, 82–92. [Google Scholar] [CrossRef]
- Ghobadi, M. Engineering Geological Factors Influencing the Stability of Slope in the Illawarra Region. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 1994; p. 1. [Google Scholar]
- Gao, W.; Dai, S.; Xiao, T.; He, T. Failure process of rock slopes with cracks based on the fracture mechanics. Eng. Geol. 2017, 231, 190–199. [Google Scholar] [CrossRef]
- Sha, L. Analysis of slope instability factors and protection. Int. J. Multidiscip. Res. Dev. 2016, 3, 181–182. [Google Scholar]
- Simataa, E. Investigating Slope Stability in Open Pit Mine—A Case Study of the Phyllites Wall at Sentinel Pit; The University of Witwatersrand: Johannesburg, South Africa, 2019. [Google Scholar]
- Raghuvanshi, T. Plane failure in rock slopes—A review on stability analysis techniques. J. King Saud Univ. Sci. 2019, 31, 101–109. [Google Scholar] [CrossRef]
- Wang, X.; Niu, R. Spatial forecast of landslides in three gorges based on spatial. Sensors 2009, 9, 2035–2061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiwaye, H. A Comparison of the Limit Equilibrium and Numerical Modelling Approaches to Risk Analysis for Open Pit Mine Slopes. Ph.D. Thesis, Faculty of Engineering and the Built Environment, University of the Witwatersrand, Johannesburg, South Africa, 2010. [Google Scholar]
- Nicholas, D.E.; Sims, D.B. Collecting and Using Geological Structure Data for Slope Design; Hustrulid, W.A., McCarter, M.K., Van Zyl, D.J.A., Eds.; Society for Mining, Metallurgy, and Exploration: Golden, CO, USA, 2000. [Google Scholar]
- Hustrulid, W.A.; McCarter, M.K.; Van Zyl, D.J.A. Slope Stability in Surface Mining; Society for Mining, Metallurgy, and Exploration: Littleton, CO, USA, 2000; pp. 81–88. [Google Scholar]
- Read, J.; Stacey, P. Guidelines for Open Pit Slope Design, 1st ed.; CSIRO: Canberra, Australia, 2009. [Google Scholar]
- Eberhardt, E. Rock Slope Stability Analysis—Utilization of Advanced Numerical Techniques; Earth and Ocean Sciences at UBC Report; University of British Columbia (UBC): Vancouver, BC, Canada, 2003. [Google Scholar]
- Stacey, T.R.; Swart, A.H. Booklet Practical Rock Engineering Practice for Shallow and Opencast Mines; The Safety in Mines Research Advisory Committee (SIMRAC): Johannesburg, South Africa, 2001. [Google Scholar]
- Suman, S. Slope Stability Analysis Using Numerical Modelling; B.Tech Report; National Institute of Technology: Rourkela, India, 2015. [Google Scholar]
- Abramson, L. Slope Stability and Stabilization Methods, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Eberhardt, E.; Stead, D.; Coggan, J.S. Numerical analysis of initiation and progressive failure in natural rock slopes. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Johansson, J. Impact of Water-Level Variations on Slope Stability; Luleå University of Technology: Luleå, Sweden, 2014. [Google Scholar]
- Zhu, J.; Xue, Y.; Tao, Y.; Zhang, K.; Li, Z.; Zhang, X.; Yang, Y. The Numerical Simulation on the Stability of Steep Rock Slope by DDA. Bydgoszcz, Poland. AIP Conf. Proc. 2017, 1839, 020134. [Google Scholar]
- Hoek, E.; Read, J.; Karzulovic, A.; Chen, Z.Y. Rock slopes in Civil and Mining Engineering. In Proceedings of the International Conference on Geotechnical and Geological Engineering, GeoEng, Melbourne, Australia, 19–24 November 2000. [Google Scholar]
- Li, A.J.; Cassidy, M.J.; Wanga, Y.; Merifield, R.S.; Lyamin, A.V. Parametric Monte Carlo studies of rock slopes based on the Hoek–Brown failure criterion. Comput. Geotech. 2012, 45, 11–18. [Google Scholar] [CrossRef]
- Duncan, J.; Wright, S.; Brandon, T. Soil Strength and Slope Stability, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Fleurisson, J.-A.; Cojean, R. Error Reduction in Slope Stability Assessment; MINES ParisTech: Paris, France, 2014. [Google Scholar]
- Stacey, T.R. Mechanics and Design of Major Rock Slopes, Lecture Note; The University of Witwatersrand: Johannesburg, South Africa, 2018; unpublished. [Google Scholar]
- Gundewar, C. Application of Rock Mechanics In surface and Underground Mining; Indian Bureau of Mines: Nagpur, Maharashtra, India, 2014; pp. 62–66. [Google Scholar]
- Valdivia, C.; Lorig, L. Slope stability at Escondida mine. In Slope Stability in Surface Mining; Hustrulid, M., Zyl, V., Eds.; SME: Golden, CO, USA, 2000; pp. 153–162. [Google Scholar]
- Ceryan, N.; Kesimal, A.; Ceryan, S. Probabilistic Analysis Applied to Rock Slope Stability: A Case Study from Northeast Turkey. In Integrating Disaster Science and Management; Samui, P., Kim, D., Ghosh, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 221–261. [Google Scholar]
- Corkum, A.; Martin, C. Analysis of a rockslide stabilized with a toe-berm: A case study in British Columbia, Canada. Int. J. Rock Mech. Min. Sci. 2004, 41, 1109–1121. [Google Scholar] [CrossRef]
- Chiwaye, H.; Stacey, T. A comparison of limit equilibrium and numerical modelling approaches to risk analysis for open pit mining. S. Afr. Inst. Min. Metall. 2010, 110, 571–580. [Google Scholar]
- Stead, D.; Eberhardt, E.; Coggan, J. Developments in the characterization of complex rock slope deformation and failure using numerical modelling techniques. Eng. Geol. 2006, 83, 217–235. [Google Scholar] [CrossRef]
- Fredj, M.; Hafsaoui, A.; Boukarm, R.; Nakache, R.; Saardoum, A. Numerical Modelling of Slope Stability in Open Pit Phosphate. Prague, Czech, World Multidisciplinary Earth Sciences Symposium (WMESS). IOP Conf. Ser. Earth Environ. Sci. 2018, 221, 012020. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.; Lane, P. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Hammah, R.; Yacoub, T.; Corkum, B. The Shear Strength Reduction Method for the Generalized Hoek-Brown Criterion; American Rock Mechanics Association (ARMA): Anchorage, AK, USA, 2005. [Google Scholar]
- Alzo’ubi, A. Rock slopes processes and recommended methods for analysis. Int. J. Geomate 2016, 11, 2520–2527. [Google Scholar] [CrossRef]
- Tang, X.-T.; Li, D.-Q.; Rong, G.; Phoon, K.-K. Zhou Impact of copula selection on geotechnical reliability under incomplete probability information. Comput. Geotech. 2013, 49, 264–278. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.-P.; Tsang, C.-F. The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks. Comput. Geotech. 2017, 85, 151–176. [Google Scholar] [CrossRef]
- Ahmad, F.; Tang, X.-W.-N.; Wróblewski, P.; Ahmad, M. Prediction of slope stability using Tree ugmented Naive-Bayes classifier: Modeling and performance evaluation. Math. Biosci. Eng. 2022, 19, 4526–4546. [Google Scholar] [CrossRef]
- Haghshenas, S.S.; Haghshenas, S.S.; Geem, Z.W.; Kim, T.H.; Mikaeil, R.; Pugliese, L.; Troncone, A. Application of Harmony Search Algorithm to Slope Stability Analysis. Land 2021, 10, 1250. [Google Scholar] [CrossRef]
- Huang, L.; Liu, F.; Dong, V. Geotechnical Slope Protection Model Based on Genetic Algorithm. Nat. Environ. Pollut. Technol. 2019, 18, 1509–1513. [Google Scholar]
- Figueiredo, L.; Barros, M.; Hammah, R.; Santos, Y.; Souza, T.; Nogueira, C. Case Study: Open Pit Three-Dimensional Slope Stability Back-Analysis for an Anisotropic Iron Ore Rock Mass; Australian Centre for Geomechanics: Perth, Australia, 2021. [Google Scholar]
- Tugelbayeva, G.K. Mathematical models for numerical solution of nonstationary problems of geomechanics. AIP Conf. Proc. 2020, 2312, 050024. [Google Scholar]
- Nemirovisky, Y.V.; Tyrymov, A.A. Mathematical modeling in problems of geomechanics of layered rock massifs. AIP Conf. Proc. 2021, 2448, 020025. [Google Scholar]
- Pirklbauer, A. The influence of land use on the stability of slopes with examples from the European Alps. Mitt. Naturwiss. Ver. Steiermark 2002, 132, 43–62. [Google Scholar]
- Wyllie, D.C.; Mah, C.W. Rock Slope Engineering: Civil and Mining, 4th ed.; Spon Press: New York, NY, USA, 2004. [Google Scholar]
- Babikar, A.; Smith, C.; Gilbert, M.; Ashbly, J. Non-associative limit analysis of the toppling-sliding failure. Int. J. Rock Mech. Min. Sci. 2014, 71, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Kliche, C. Rock Slope Stability; Society for Mining, Metallurgy and Exploration: Littleton, CO, USA, 1999. [Google Scholar]
- Hoek, E.; Bray, J. Rock Slope Engineering, 3rd ed.; CRC: Boca Raton, FL, USA, 1981. [Google Scholar]
- Alabideen, K.; Helal, M. Determination of the Safe Orientation and Dip of a Rock Slope in an Open Pit Mine in Syria Using Kinematic Analysis. Al-Nahrain Univ. Coll. Eng. J. (NUCEJ) 2016, 19, 33–45. [Google Scholar]
- Goodman, R.E.; Kieffer, D.S. Behaviour of rock in slopes. J. Geotech. Geoenviron. Eng. 2000, 126, 675–684. [Google Scholar] [CrossRef]
- Hudson, J.A.; Harrison, J.P. Engineering Rock Mechanics; Elsevier: Oxford, UK, 1997; p. 444. [Google Scholar]
- Low, B.K. Reliability analysis of rock wedges. J. Geotech. Geoenviron. Eng. 1997, 123, 498–505. [Google Scholar] [CrossRef]
- Coates, D.F. Rock Mechanics Principles; Canadian Centre for Mineral and Energy Technology (CANMET): Energy, Mines, and Resources Canada in Ottawa: Ottawa, ON, Canada, 1981; p. 410. [Google Scholar]
- Dahner-Lindqvist, C. Liggvagga Stabiliteten I Kiirunavaara. In Proceedings of the Bergmekanikdagen, Papers presented at Rock Mechanics Meeting, Stockholm, Sweden, 19 March 1992; pp. 37–52. [Google Scholar]
- Prakash, B. Design of Stable Slope for Open Cast Mines; B.Tech Report; National Institute of Technology: Rourkela, India, 2009. [Google Scholar]
- Sjöberg, J. Analysis of Large-Scale Rock Slopes. Ph.D. Thesis, University of Technology, Luleå, Sweden, 1999. [Google Scholar]
- Sjöberg, J. Failure Mechanisms for High Slopes in Hard Rock. Colorado, Denver, USA, Slope Stability in Surface Mining; Hustrulid, M., Zyl, V., Eds.; Society for Mining, Metallurgy & Exploration: Englewood, CO, USA, 2000. [Google Scholar]
- Adeyeri, J. Technology and Practice in Geotechnical Engineering: Stability of Earth Masses and Slopes; IGI Global: Pennsylvania, PA, USA, 2014; pp. 528–588. [Google Scholar]
- Guo, S.; Qi, S.; Yang, G.; Zhang, S.; Saroglou, C. An Analytical Solution for Block Toppling Failure of Rock Slopes during an Earthquake. Appl. Sci. 2017, 7, 1008. [Google Scholar] [CrossRef]
- Chaulya, S.; Prasad, G. Slope Failure Mechanism and Monitoring Techniques. In Sensing and Monitoring Technologies for Mines and Hazardous Areas: Monitoring and Prediction Technologies; Elsevier: Amsterdam, The Netherlands, 2016; pp. 1–86. [Google Scholar]
- Chakraborty, A.; Goswami, D. State of the art: Three-Dimensional (3D) Slope-Stability Analysis. Int. J. Geotech. Eng. 2016, 10, 493–498. [Google Scholar] [CrossRef]
- Wines, D. A comparison of slope stability analyses in two and three dimensions. J. South. Afr. Inst. Min. Metall. 2016, 116, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Totonchi, A.; Askari, F.; Farzaneh, O. 3D stability analysis of concave slopes in plan view using linear finite element and lower bound method. Iran. J. Sci. Technol. Trans. Civ. Eng. 2012, 36, 181–194. [Google Scholar]
- Cala, M. Convex and concave slope stability analyses with numerical methods. Arch. Min. Sci. 2007, 52, 75–89. [Google Scholar]
- Zhang, Y.; Chen, G.; Zheng, L.; Li, Y.; Zhuang, X. Effects of geometries on three-dimensional slope stability. Can. Geotech. J. 2013, 50, 233–249. [Google Scholar] [CrossRef]
- Dana, H.; Kakaie, R.; Rafiee, R.; Bafghi, A. Effects of geometrical and geomechanical properties on slope stability of open-pit mines using 2D and 3D finite difference methods. J. Min. Environ. 2018, 9, 941–957. [Google Scholar]
- Keykha, H.; Huat, B.; Asadi, A.; Moayedi, H. The effect of discontinuities on stability of rock blocks in tunnel. Int. J. Phys. Sci. 2011, 6, 7132–7138. [Google Scholar]
- Liu, S.; Huang, X.; Zhou, X.; Hu, J.; Wang, W. Soil-Rock Slope Stability Analysis by Considering the Nonuniformity of Rocks. Math. Probl. Eng. 2018, 2018, 3121604. [Google Scholar] [CrossRef]
- Kolapo, P.; Munemo, P. Investigating the correlations between point load strength index, uniaxial compressive strength and Brazilian tensile strength of sandstones. A case study of QwaQwa sandstone deposit. Int. J. Min. Miner. Eng. 2021, 12, 67–83. [Google Scholar] [CrossRef]
- Brian, D.; Greg, M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 2016, 9, 395–400. [Google Scholar]
- Cravero, M.; Labichino, G. Analysis of the flexural failure of an overhanging rock slab. Int. J. Rock Mechanics Min. Sci. 2004, 41 (Suppl. S1), 605–610. [Google Scholar] [CrossRef]
- Borrelli, L.; Greco, R.; Gulla, G. Weathering grade of rock masses as a predisposing factor to slope instabilities: Reconnaissance and control procedures. Geomorphology 2007, 87, 158–175. [Google Scholar] [CrossRef]
- Wieczorek, G.; Jager, S. Triggering mechanisms and depositional rates of postglacial slope-movement processes in the Yosemite Valley, California. Geomorphology 1996, 15, 17–31. [Google Scholar] [CrossRef]
- Shang, J.; West, L.J.; Hencher, S.R.; Zhao, Z. Geological discontinuity persistence: Implication and quantification. Eng. Geol. 2018, 241, 41–54. [Google Scholar] [CrossRef]
- Shang, J.; Zhao, Z.; Hu, J.; Handley, K. 3D particle-based DEM investigation into the shear behaviour of incipient rock joints with various geometries of rock bridges. Rock Mech. Rock Eng. 2018, 51, 3563–3584. [Google Scholar] [CrossRef]
- Kalenchuk, K.; Diederichs, M.; Mckinnon, S. Characterizing block geometry in jointed rock masses. Int. J. Rock Mechanics Min. Sci. 2006, 43, 1212–1225. [Google Scholar] [CrossRef]
- Higuchi, K.; Fujisawa, K.; Asai, K.; Pasuto, A.; Marcato, G. Development of slope failure displacement detection sensor using optical fiber in the OTDR method. In Proceedings of the 44th Colloquium of Japan Slope Failure Society, Sasebo, Japan, 2015; pp. 315–318. [Google Scholar]
- Ganapathy, G.; Mahendran, K.; Sekar, S. Need and urgency of slope failure risk planning for Nilgiris district, Tamil Nadu State, India. Intern. J. Geosci. 2012, 1, 29–40. [Google Scholar]
- Central Geological Survey. Taiwan Geoscience Portal. 2014. Available online: https://twgeoref.moeacgs.gov.tw/GipOpenWeb/wSite/mp (accessed on 10 June 2021).
- Tiwari, B.; Beena, A.; Mohammed, K.; Samin, D.; Rosalie, C. Developments in Earth Retention, Support Systems, and Tunneling. In Proceedings of the International Foundations Congress & Equipment Expo, Orlando, FL, USA, 5–6 March 2018. [Google Scholar]
- Tiwari, B.; Caballero, S. Experimental Model of Rainfall Induced Slope Failure in Compacted Clays. Geotech. Spec. Publ. 2015, 256, 1217–1226. [Google Scholar]
- Aladejare, A.; Akeju, V. Design and Sensitivity Analysis of Rock Slope Using Monte Carlo Simulation. Geotech. Geol. Eng. 2020, 38, 573–585. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Li, J. Effects of Water Seepage on the Stability of Soil-Slopes; Procedia IUTAM: Beijing, China, 2015. [Google Scholar]
- Zhu, Y.; Xiao, Y. Slope Stability from a Hydrological Perspective: Taking Typical Soil Slope as an Example. Adv. Civ. Eng. 2020, 17, 2020. [Google Scholar] [CrossRef]
- Tandon, R.; Gupta, V. The control of mineral constituents and textural characteristics on the petrophysical & mechanical (PM) properties of different rocks of the Himalaya. Eng. Geol. 2013, 153, 125–143. [Google Scholar]
- McNeilly, M.; Funkhouser, M.; Lupo, J. Design and Evaluation of Ground Support for the Exchange Place Station Improvements Project. In Proceedings of the North American Tunneling Conference, Atlanta, GA, USA, 17–22 April 2004. [Google Scholar]
- Yasir, S.; Awang, H.; Ayub, M. The Relationship of Sandstone’s Strength with Mineral Content and Petrographic Characteristics in Sungai Tekai, Jerantut, Pahang. In Proceedings of the AIP Conference Proceedings, Depok, Indonesia, 6–8 November 2021. [Google Scholar]
- Villeneuve, M.; Heap, M. Calculating the cohesion and internal friction angle of volcanic rocks and rock masses. Volcanica 2022, 4, 279–293. [Google Scholar] [CrossRef]
- Sullivan, R.; Anderson, R.; Biesiadecki, J.; Bond Stewart, H. Cohesions, friction angles, and other physical properties of Martian regolith from Mars Exploration Rover wheel trenches and wheel scuffs. J. Geophys. Res. 2011, 116, 1–38. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Shi, C.; Xu, F.-G. Geotechnical Characteristics and Stability Analysis of Rock-Soil Aggregate Slope at the Gushui Hydropower Station, Southwest China. Sci. World J. 2013, 2013, 540636. [Google Scholar] [CrossRef] [PubMed]
- Harabinová, S.; Panulinová, E. Impact of Shear Strength Parameters on Slope Stability. In Proceedings of the MATEC Web of Conferences, Tleń/Osie, Poland, 8–11 September 2020. [Google Scholar]
- Yin, Z.-Q.; Hu, Z.-X.; Wei, Z.-D.; Zhao, G.-M.; Hai-Feng, M.; Zhang, Z.; Feng, R.-M. Assessment of Blasting-Induced Ground Vibration in an Open-Pit Mine under Different Rock Properties. Adv. Civ. Eng. 2018, 2018, 4603687. [Google Scholar] [CrossRef]
- Sutejo, Y.; Gofar, N. Effect of Area Development on the stability of cut slopes. In Proceedings of the 5th International Conference of Euro Asia Civil Engineering Forum (EACEF-5), Surabaya, East Java, Indonesia, 15–18 September 2015. [Google Scholar]
- Zou, D.; Kaiser, P.K. Determination of in situ stresses from excavation-induced stress changes. Rock Mech. Rock Eng. 1990, 23, 167–218. [Google Scholar] [CrossRef]
- Stacey, T.; Ndlovu, X.; Ortlepp, W. Dynamic Rock Failures Due to “High” Stress at Shallow Depth; Deep Mining: Australia Centre for Geomechnaics: Perth, Australia, 2007. [Google Scholar]
- Stacey, T.; Wesseloo, J. In situ stresses in mining areas in South Africa. J. South Afr. Inst. Min. Metall. 1998, 98, 365–368. [Google Scholar]
- Vazaios, I.; Farahmand, K.; Vlachopoulos, N.; Dederichs, M. Effects of confinement on rock mass modulus: A synthetic rock mass modelling (SRM) study. J. Rock Mech. Geotech. Eng. 2018, 10, 436–456. [Google Scholar] [CrossRef]
- Peng, C.; Guo, Q.; Yan, Z.; Wang, M.; Pan, J. Investigating the Failure Mechanism of Jointed Rock Slopes Based on Discrete Element Method. Adv. Civ. Eng. 2020, 2020, 8820158. [Google Scholar]
- Ryan, T. Shear Strength of Closely Jointed Porphyry Rock Masses. In Proceedings of the 40th U.S. Symposium on Rock Mechanics (USRMS): Rock Mechanics for Energy, Mineral and Infrastructure Development in the Northern Regions, Anchorage, AK, USA, 25–29 June 2005. [Google Scholar]
- Pariseau, W.; Puri, S.; Schmelter, S. A new model for effects of impersistent joint sets on rock slope stability. Int. J. Rock Mech. Min. Sci. 2008, 45, 122–131. [Google Scholar] [CrossRef]
- Cundall, P.; Damjanac, B. Considerations on Slope Stability in a Jointed Rock Mass. In 50th U.S. Rock Mechanics/Geomechanics Symposium; America Rock Mechanics Association: Houston, TX, USA, 2016. [Google Scholar]
- Carlàab, T.; Farinab, P.; Intrieri, E.; Botsialas, K.; Casaglib, N. On the monitoring and early-warning of brittle slope failures in hard rock masses: Examples from an open-pit mine. Eng. Geol. 2017, 228, 71–81. [Google Scholar] [CrossRef]
- Simmons, J.; Simpson, P. Composite failure mechanisms in coal measures rock masses-myths and reality. Journal South. Afr. Inst. Min. Metall. 2006, 106, 459–469. [Google Scholar]
- Wesseloo, J.; Dight, P. Rock mass damage in hard rock open pit mine slopes. In Proceedings of the 2009 International Symposium on Rock Slope Stability in Open Pit and Civil Engineering, Santiago, Chile, 10 September 2009; Read, J.R., Ed.; University de Los Andes: Los Andes, Chile, 2009; Volume CD ROM, p. 7. [Google Scholar]
- Hoek, E. Fundamentals of slope design. In Proceedings of the Keynote address at Slope Stability 2009, Santiago, Chile, 9–11 November 2009. [Google Scholar]
- Hu, Y.; Ren, F.; Ding, H.; Fu, Y.; Tan, B. Study on the Process and Mechanism of Slope Failure Induced by Mining under Open Pit Slope: A Case Study from Yanqianshan Iron Mine, China. Adv. Civ. Eng. 2019, 1–27. [Google Scholar] [CrossRef]
- Zevgolis, I.; Deliveris, A.; Koukouzas, N. Slope failure incidents and other stability concerns in surface lignite mines in Greece. J. Sustain. Min. 2019, 18, 182–197. [Google Scholar] [CrossRef]
- DTE. Down to Earth (DTE). Available online: https://www.downtoearth-indonesia.org/story/protests-over-fatal-collapse-freeportrio-tinto-west-papua-mine (accessed on 19 July 2021).
- Graham, R. The Northern Miner: Slippage Causes Deaths at Grasberg. 2003. Available online: https://www.northernminer.com/news/slippage-causes-deaths-at-grasberg/1000143698 (accessed on 25 July 2021).
- Reuters. Reuters: Vedanta Zinc suspends mining at South Africa’s Gamsberg mine after accident. 2020. Available online: https://www.reuters.com/article/us-vedanta-zinc-accident-idINKBN27Y0VO (accessed on 4 April 2021).
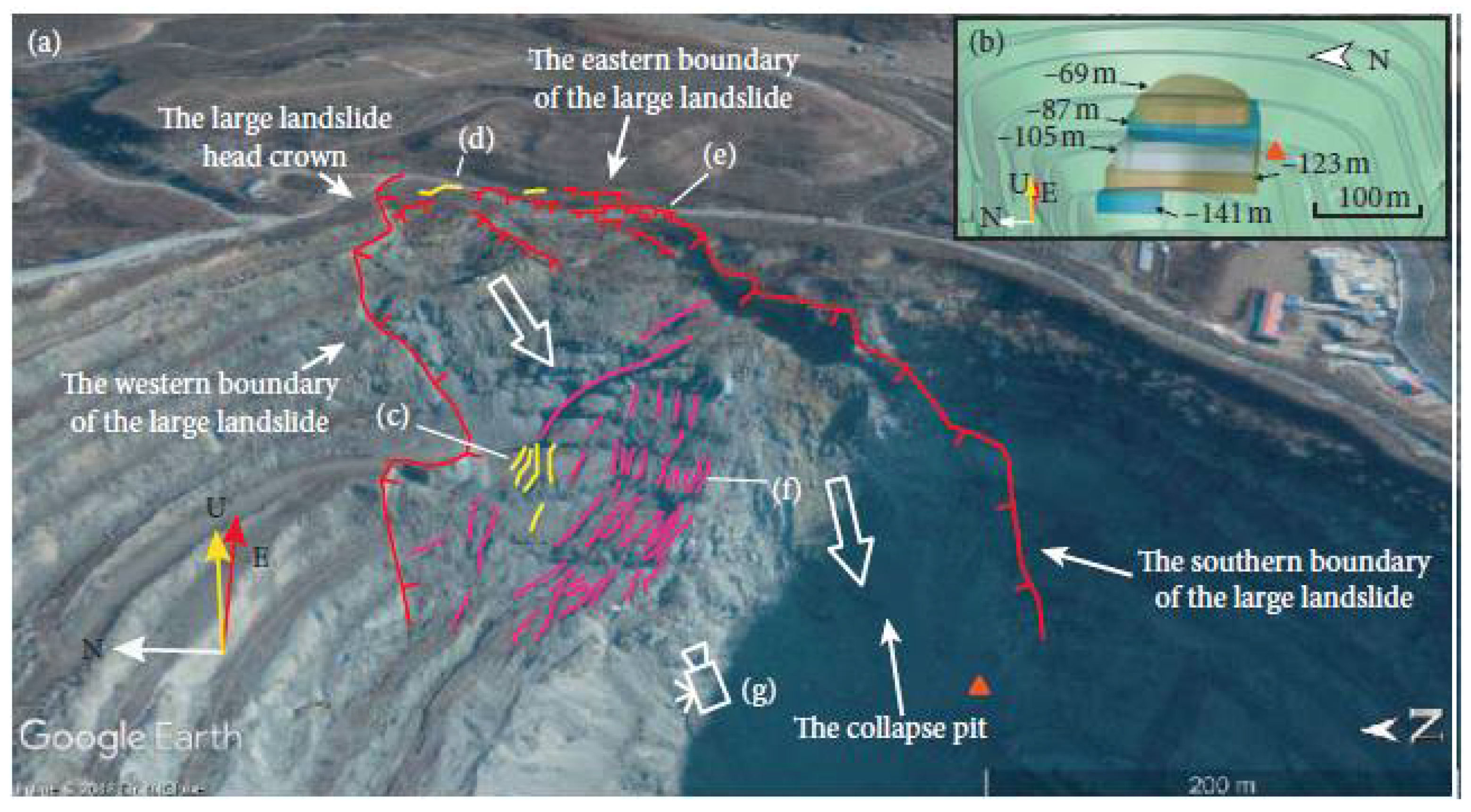
- Petley, D. Advance Earth Science. 2020. Available online: https://blogs.agu.org/landslideblog/2020/12/15/the-large-landslide-at-gamsberg-mine-high-resolution-satellite-images/#:~:text=used%20with%20permission.-,The%20large%20landslide%20at%20Gamsberg%20mine%3A%20high%20resolution%20satellite%20images,been%20anti (accessed on 9 April 2021).
- Voight, B.; Kennedy, B.A. Slope failure of 1967–1969, Chiquicamata Mine Chile. In Rockslides & Avalanches; Voight, B., Ed.; Developments in Geotechnical Engineering, 14b; Elsevier: Amsterdam, The Netherlands, 1979; pp. 595–632. [Google Scholar]
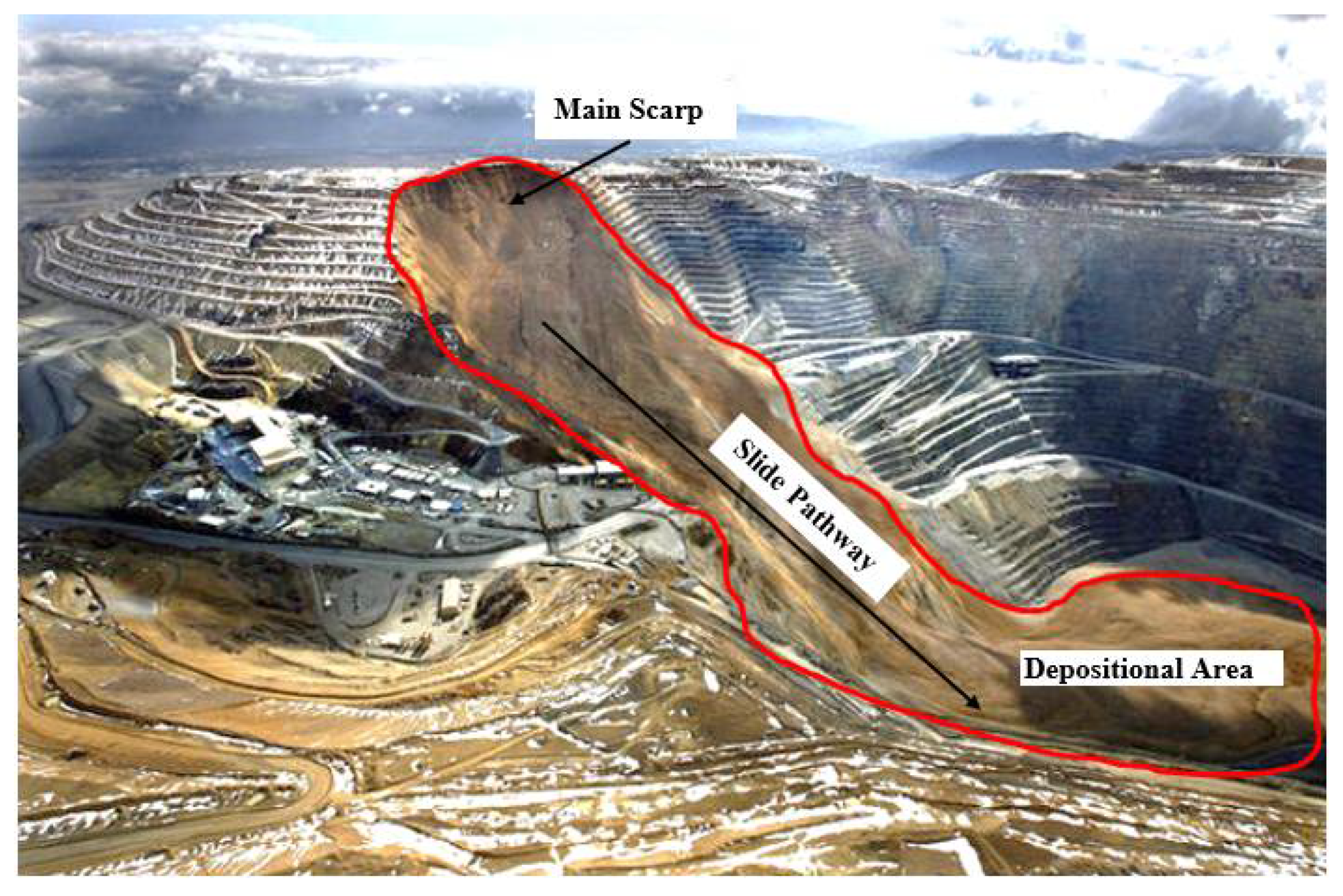
- Serna, M.; Williams, D.; Ruest, M. Analysis of Kennecott Utah copper’s Bingham Canyon mine pit wall slides. In Proceedings of the Tailing and Mine Waste, Denver, CO, USA, 2–5 October 2016. [Google Scholar]
- Pankow, K.L.; Moore, J.R.; Hale, J.M.; Koper, K.D.; Kubacki, T.; Whidden, K.M.; McCarter, M.K. Massive landslide at Utah copper mine generates wealth of geophysical data. Geol. Soc. Am. 2014, 24, 4–9. [Google Scholar] [CrossRef] [Green Version]
- Hibert, C.; Ekström, G.; Stark, C. Dynamics of the Bingham Canyon Mine landslides from seismic signal analysis. Geophys. Res. Lett. 2014, 41, 4535–4541. [Google Scholar] [CrossRef]
- Blackwell, G.H.; Calder, P.N. Practical aspects of wall stability at Brenda Mines Ltd., Peachland, B.C. In Proceedings of the Third International Conference on Stability in Surface Mining, Vancouver, BC, Canada, 1–3 June 1981; Brawner, C.O., Ed.; Society of Mining Engineers, AIME: New York, NY, USA, 1982; pp. 573–605. [Google Scholar]
- Blake, W. Finite Element Model Study of Slope Modification at the Kimbley Pit. Trans. Soc. Min. Eng. 1968, 241, 525–532. [Google Scholar]
- Brawner, C.O. Chapter 1, Introduction. In Proceedings of the First International Conference on Stability in Open Pit Mining, Vancouver, BC, Canada, 23–25 November 1971; Brawner, C.O., Milligan, V., Eds.; Society of Mining Engineering: New York, NY, USA, 1971; pp. 1–3. [Google Scholar]
- Brummer, R.; Li, H.; Moss, A. The transition from open pit to underground mining: An unusual slope failure mechanism at Palabora. In Proceedings of the International Conference S44 Stability of Rock Slopes in Open Pit Mining and Civil Engineering, Cape Town, South Africa, 3–6 April 2006. [Google Scholar]
- Bye, A. Stability assessment and slope design at Sandsloot open pit, South Africa. Int. J. Rock Mech. Min. Sci. 2001, 38, 449–466. [Google Scholar] [CrossRef]
- Call, R.; Ryan, T.; Barkely, R. Geotechnical analysis for open pit mining in areas of large-scale slope instability. In Proceedings of the Innovative Mine Design for the 21st Century, Kingston, ON, Canada, 23–26 August 1993; A.A. Balkema: Rotterdam, The Netherlands; pp. 45–56. [Google Scholar]
- Golder Associate (UK) Ltd. Slope Stability Review East Football, Aznalcollar Mine; Draft report to Boliden Aspira: Seville, Spain, 1995. [Google Scholar]
- Jian, W.X.; Xu, Q.; Yang, H.F.; Wang, F.W. Mechanism and failure process of Qianjiang Ping landslide in the Three Gorges Reservoir, China. Environ. Earth Sci. 2014, 72, 2999–3013. [Google Scholar] [CrossRef]
- Kayesa, G. Prediction of Slope Failure at Letlhakane Mine with the Geomos Slope Monitoring System. In International Symposium on Stability of Rock Slopes in Open Pit Mining and Civil Engineering; The South African Institute of Mining and Metallurgy: Cape Town, South Africa, 2006. [Google Scholar]
- Martin, D.C. Deformation of Open Pit Mines Slopes by Deep Seated Toppling. Int. J. Surf. Min. Reclam. 1990, 4, 153–164. [Google Scholar] [CrossRef]
- Martin, D.C.; Mehr, E.F. Assesment of Slope Deformation and Deep Seated Instability in the CAssiar Open Pit. CIM Bull. 1993, 86, 58–67. [Google Scholar]
- Marthis, J.I.; Robertson, A.M.; Robertson, R.B. Mining Below Sea Level: Design and Performance of the South Slope Expansion at Island Copper. In Proceedings of the Innovative Mine for the 21st Century, Kingston, ON, Canada, 23–26 August 1993; Balkema: Rotterdam, The Netherlands, 1993; pp. 57–65. [Google Scholar]
- Miller, V. The northeast tripp slide—A 11.7 million cubic Meter Wedge Failure at Kennecott’s Nevada Mine Division. In Proceedings of the 3rd International Conference on Stability in Surface Mining, Vancouver, BC, Canada, 1 December 1982; Society of Mining Engineers, A.I.M.E.: New York, NY, USA; pp. 743–752. [Google Scholar]
- Nilsen, B.; Hagen, R. Stabilitwtsproblemer og forslag till ukonvensjonell Sikring ved Tellness dagbrudd. Fjellsprengningsteknikk Bergmek./Geotek. 1990, 23, 1–20. (In Norwegian) [Google Scholar]
- Newcomen, H.; Martin, D. Geotechnical Assessment of the Southeast wall slope failre at Highmont Mine, British Columbia. CIM Bull. 1988, 81, 71–76. [Google Scholar]
- Rapiman, M. Slope stability and rock mechanics analyses Chiquicamata mine, Codelco, Chile. In Proceedings of the Innovative Mine Design for the 21st Century, Kingston, ON, Canada, 23–26 August 1993; A.A. Balkema: Rotterdam, The Netherlands, 1993; pp. 35–44. [Google Scholar]
- Pritchard, M.; Savigny, K. Numerical mobility of toppling. Can. Geotech. J. 1990, 27, 823–834. [Google Scholar] [CrossRef]
- Reid, G.; Stewart, D. A large-Scale Toppling Failure at Afton. In Proceedings of the International Symposium on Geotechnical Stability in Surface Mining, Calgary, AL, Canada, 6–7 November 1986; A.A Balkema: Rotterdam, The Netherlands, 1996; pp. 215–223. [Google Scholar]
- Ren, S.-L.; He, M.-C.; Pang, S.-H.; Li, M.-N.; Xu, H.-T. Stability analysis of open-pit gold mine slopes and optimization of mining scheme in Inner Mongolia, China. J. Mt. Sci. 2020, 17, 2997–3011. [Google Scholar] [CrossRef]
- Stacey, P.F. Pit Slope Designs for the 21st Century. In Proceedings of the Innovative Mine Design for the 21st Century, Kingston, ON, Canada, 23–26 August 1993; A.A. Balkema: Rotterdam, The Netherlands, 1993; pp. 3–11. [Google Scholar]
- Zavodni, Z.M.; McCarter, M.K. Main Hill Slide Zone, Utah Copper Division. In The 17th US Symposium on Rock Mechanics (USRMS); Monograph on Rock Mechanics Applications in Mining, AIME: New York, NY, USA, 1977; pp. 84–92. [Google Scholar]
- Niroumand, H.; Kassim, K.A.; Ghafooripour, A.; Nazir, R.; Far, S.Y.Z. Investigation of Slope Failures in Soil Mechanics. Electron. J. Geotech. Eng. 2012, 17, 2703–2719. [Google Scholar]
- Roux, M.; Terbrugge, M.; Badenhorst, M. Slope management at Navachab Gold Mine, Namibia. In Proceedings of the South Africa Institute of Mining and Metallurgy: International Symposium on Stability of Rock Slopes in Open Pit Mining and Civil Engineering, Cape Town, South Africa, 12–14 October 2015. [Google Scholar]
- Singh, P.; Kainthola, A.; Prasad, S.; Singh, T. Protection Measures on the Failed Cut-slope along the Free Expressway, Chembur, Mumbai, India. J. Geol. Soc. India 2015, 86, 687–695. [Google Scholar] [CrossRef]
- Normaniza, O.; Faisal, H.; Barakbah, S. Engineering properties of Leucaena leucocephala for prevention of slope failure. Ecol. Eng. 2008, 31, 215–221. [Google Scholar] [CrossRef]
- Karam, K.; He, M.; Sousa, L. Slope stability risk management in open pit mines. In Proceedings of the 7th GiT4NDM and 5th EOGL International Conference, Abu Dhabi, United Arab Emirates, 14–16 March 2015; UAE University: Al-Ain, United Arab Emirates, 2015. [Google Scholar]
- Brawner, C. Control of groundwater in surface mining. Int. J. Mine Water 1982, 1, 1–16. [Google Scholar] [CrossRef]
- Kecojevic, V.; Mrugala, M.; Simic, R.; Stankovic, R. A computer-aided system for design of drainage facilities in surface mining. Mine Water Environ. 2003, 22, 149–154. [Google Scholar] [CrossRef]
- Cawood, F.; Stacey, T. Survey and geotechnical slope monitoring considerations. J. S. Afr. Inst. Min. Metall. 2006, 106, 495–502. [Google Scholar]
- Simonetta, C.; Alberto, B.; Corrado, P.; Stefano, F.; Giovanni, S.; Giulia, T. Reinforcement works for the slope stabilization: Standard and new approaches for the use of micropiles and anchors. In Proceedings of the 11th International Workshop on Micropiles, ISM, Milano, Italy, 3–6 October 2012. [Google Scholar]
- Hua, Z.; Yang, L.; Qiang, C. Numerical Simulation of Reinforcement for Rock Slope with Rock Bolt (Anchor Cable) Frame Beam. J. Highw. Transp. Res. Dev. 2008, 3, 65–71. [Google Scholar]
- Sazzad, M.; Hie, A.; Hossain, M.S. Stability analysis of reinforcement slope using FEM. Int. J. Adv. Struct. Geotech. Eng. 2016, 5, 83–88. [Google Scholar]
- Bui, X.-N.; Nguyen, H.; Choi, Y.; Nguyen-Thoi, T.; Zhou, J.; Dou, J. Prediction of slope failure in open-pit mines using a novel hybrid artificial intelligence model based on decision tree and evolution algorithm. Sci. Rep. 2020, 10, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Bui, X.N.; Nguyen, H. A novel artificial intelligence technique for analyzing slope stability using PSO-CA model. Eng. Comput. 2021, 37, 533–544. [Google Scholar] [CrossRef]
- Kothari, U.C.; Momayez, M. Machine Learning: A Novel Approach to Predicting Slope Instabilities. Int. J. Geophys. 2018, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Chebrolu, A.; Sasmal, S.K.; Behera, R.N.; Das, S.K. Prediction of Factor of Safety for Slope Stability Using Advanced Artificial Intelligence Techniques. In Advances in Intelligent Systems and Computing; Springer: Singapore, 2019; pp. 173–181. [Google Scholar]
- Du, S.; Feng, G.; Wang, J.; Feng, S.; Malekian, R.; Li, Z. A New Machine-Learning Prediction Model for Slope Deformation of an Open-Pit Mine: An Evaluation of Field Data. Energies 2019, 12, 1288. [Google Scholar] [CrossRef] [Green Version]
- Ferentinou, M.; Fakir, M. Integrating rock engineering systems device and artificial neural networks to predict stability conditions in an open pit. Eng. Geol. 2018, 246, 293–309. [Google Scholar] [CrossRef]




| Calculated FOS | Stability Condition | Recommended Action |
|---|---|---|
| FOS > 2.0 | Stable | None |
| 1.0 < FOS < 2.0 | Marginal | Analyse stability rigorously |
| FOS < 1.0 | Unstable | Revise design or stabilise |
| Slope Aspect | Sources of Uncertainty |
|---|---|
| Topography | |
| Geometry | Geology/Structures |
| Groundwater surface | |
| Strength | |
| Rock mass Properties | Deformation |
| Hydraulic conductivity | |
| In situ stresses | |
| Loading | Blasting |
| Earthquakes | |
| Failure Prediction | Model reliability |
| Country | Location | Names of Mining Company | Mode of Failure | Causes of Failure | Sources |
|---|---|---|---|---|---|
| Botswana | Central District | Letlhakane mine | Toppling | Presence of tension crack formation, crack widening and extension | i |
| Canada | British Columbia | Afton Mine | Wedge, Toppling and circular failure | Multiple failures occurred as a result of intersection of discontinuities | j, r, a |
| British Columbia | Brenda Mine | Toppling | Intersection of joint sets | q, a, j | |
| British Columbia | Cassiar Mine | Toppling | Presence of shear zones, faults and sets of discontinuities | j, k | |
| British Columbia | Highland Valley Copper | Toppling | Steeply dipping joints, increase in groundwater pressure and melting of snow | t | |
| British Columbia | Lonex Pit at Highland valley | Toppling | Groundwater condition, Steeply dipping faults | o | |
| British Columbia | Highmont | Planar | Structural discontinuities, precipitation, run off, poor quality and low strength rock mass | o | |
| Vancouver | Island Copper | Wedge and Toppling | Large fault zone passing through a weaker rock mass | l | |
| Quebec | Jeffrey Mine, Asbestos | Wedge and Planar | Intersection of several thick shear zones and smaller scale discontinuities | t, c | |
| British Columbia | Nickel Plate Mine | Wedge | Steeply dipping joint sets and faults | t | |
| China | Mongolia | Changshanhao open-pit | Wedge and Toppling | Presence of faults and joints | s |
| Shazhenxi | Qianjiangping | Planar | Increase in water level, poor geological structure and continuous rainfall | h | |
| Norway | Hange i Dalane | Tellness Dagbrudd | Wedge | Heavy rainfall | n |
| Mexico | Calama, Antofagasta | Chiquicamata | Toppling | Presence of fault zones | f, p |
| Spain | Seville | Aznacollar Mine | Complex | Presence of tension cracks, Heavy rainfall, groundwater pressure | g |
| Sweden | Kiruna | Kirunavaara | Rotational | Presence of tension cracks | u |
| United States of America | Utah | Bingham Canyon Mine | Rotational, Planar | Rise in water table, fractured rock mass with minor joints and larger fault structure | t, v |
| Nevada | Carlin Trend | NA | Presence of wider fault zones and clay infillings | v | |
| Arizona | Cyprus Bagdad and Sierrita | Toppling | Presence of steeply joint sets | j | |
| Nevada | Liberty Pit | Wedge | Intersection of joint sets | c | |
| Nevada | Veteran—Tripp Pit | Wedge | Intersection of faults, presence of clay gouge in fault zones | m | |
| Nevada | Kimbley pit | Wedge | Presence of flat sipping fault, High water pressure | b | |
| Arizona | Twin Butes | Toppling | Numerous faults and several joints | c | |
| South Africa | Limpopo | Palabora Mine | Wedge | Presence of faults and set of joints | t, d |
| Mokopane | Sandsloot open pit | Planar and Wedge | Presence of set of joints | e | |
| Zambia | Chingola | Nchanga Open Pit | Wedge | Intersection of joint sets, abnormally rainfall, weathering | u |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolapo, P.; Oniyide, G.O.; Said, K.O.; Lawal, A.I.; Onifade, M.; Munemo, P. An Overview of Slope Failure in Mining Operations. Mining 2022, 2, 350-384. https://doi.org/10.3390/mining2020019
Kolapo P, Oniyide GO, Said KO, Lawal AI, Onifade M, Munemo P. An Overview of Slope Failure in Mining Operations. Mining. 2022; 2(2):350-384. https://doi.org/10.3390/mining2020019
Chicago/Turabian StyleKolapo, Peter, Gafar Omotayo Oniyide, Khadija Omar Said, Abiodun Ismail Lawal, Moshood Onifade, and Prosper Munemo. 2022. "An Overview of Slope Failure in Mining Operations" Mining 2, no. 2: 350-384. https://doi.org/10.3390/mining2020019
APA StyleKolapo, P., Oniyide, G. O., Said, K. O., Lawal, A. I., Onifade, M., & Munemo, P. (2022). An Overview of Slope Failure in Mining Operations. Mining, 2(2), 350-384. https://doi.org/10.3390/mining2020019






