Cemented Paste Backfill (CPB) Material Properties for Undercut Analysis

Abstract

A longstanding mine backfill design challenge is determining the strength required if the (partially) cured backfill is subsequently undercut. Mitchell (1991) called the undercut backfill a sill mat and proposed an analytical solution that is still often used, at least for preliminary design, and has motivated subsequent empirical design methods. However, fully employing the Mitchell sill mat solution requires knowledge of the backfill material’s Unconfined Compressive Strength ($UCS$), tangent Young’s modulus ($E_t$), tensile strength (${\sigma }_t$), as well as estimates of stope wall closure. Conducting a high-quality $UCS$ test poses challenges but relating the test result to the remaining material parameters is more difficult. Some new material testing data is presented and compared to available published results. Using the parameter $m_i=UCS/{\sigma }_t$ the range of available testing data is found to be $m_i=$ 3 to 22, however, the most compelling data is obtained when the Mohr’s failure circle in tension is tangential to the corresponding Mohr–Coulomb failure envelope determined from other strength tests. In these cases, the value $m_i=$ 4 is found for the materials tested, which is much lower than the value $m_i=$ 10 commonly assumed and implies a limiting $UCS$ 60% lower compared to the conventional assumption. It is also found that the relationship between $E_t$ and $UCS$ is described by a power function that is close to linear, but the values for the constant and exponent in the power function depend on the material tested. However, for given tailings the power function is found to be independent of void ratio, binder type or concentration, curing time, and water salinity, within the ranges these parameters were investigated. Therefore, when $E_t$ is used in the Mitchell sill mat solution it should be correlated with the $UCS$ using the appropriate power function. These correlations are then used with the Mitchell sill mat solution and published measurements of backfill closure strains to estimate the Mitchell solution’s range of applicability based on its underlying assumptions, and a similar analysis is extended to an “empirical design method” motivated by the Mitchell sill mat solution. It is demonstrated that these existing approaches have limited applicability, and more generally a full analysis in support of rational design will require numerical modeling that incorporates the effect of confining stress on the material’s stiffness and mobilized strength.

1. Introduction

Optimizing mining methods and stope sequences can result in a decision to mine underneath previously placed backfill, as shown in Figure 1. One of the design questions to then address is: what backfill strength is required to keep the undercut span stable? Mitchell [1] considered the case shown in Figure 1a and called the lowest portion of backfill, adjacent to the fill barricade, the sill mat. However, this zone is also called a plug when the contained backfill has higher binder content than the overlying main backfill or is allowed to cure before starting to pour the main backfill. The cross-sectional stope dimensions in Figure 1a can be tens of meters in span and height in the case of long hole mining methods, or only a few meters span and up to 200 m high for Alimak mining methods. The elapsed time between pouring the plug (or sill mat) and the next mining stage when the backfill is undercut will depend on the mine’s stope sequencing plans, but the backfill plug (or sill mat) must have sufficient strength by this time to maintain a self-supporting condition, including the stress imposed on it by the main backfill. The same considerations apply to Underhand Cut and Fill (UC&F) mining methods (Figure 1b), although the overall dimensions are modest by comparison and usually the hangingwall to footwall span is smaller than for long hole stopes. Additionally, in this case, there will be no overlying backfill stress if an air gap is left between successive pours.

In 1991, Mitchell [1] proposed an analysis approach for the sill mat design problem based on four different failure mechanisms: flexural failure, tensile detachment (leading to caving), block sliding, and block rotation. The flexural failure mode is the one most often considered critical by mines reporting using Mitchell’s approach for sub-vertical backfilled stopes [2,3]. Mitchell presented the limiting solution for this failure mode as Equation (1),

$${\left(\frac{L}{d}\right)}^2=2\left({\sigma }_t+{\sigma }_c\right)/w$$

(1)

where $L$ is the undercut span, $d$ is the sill mat height, ${\sigma }_t$ is the backfill’s tensile strength, ${\sigma }_c$ is a “clamping stress” due to sidewall closure, and $w$ is the vertical stress. Equation (1) will be referred to in the present work as the “Mitchell sill mat solution”.

The Mitchell sill mat solution assumes a fully encastered (fixed-ended) beam-column, for which the critical stress concentrations are at the encastered ends. Assuming that the clamping stress is small or is ignored, and that the material strength in tension is less than in compression as is the case for cemented backfill, then the tensile failure mode dominates which is why the Mitchell sill mat solution is expressed in terms of tensile strength. The clamping stress term is modeled in the Mitchell solution as an average column compressive stress due to backfill compression caused by hangingwall to footwall closure, and this clamping stress reduces the tensile stress concentration. The clamping stress can be estimated by assuming the backfill behaves in unconfined compression, using Equation (2),

$${\sigma }_c=E_t{\epsilon }_c=E_t\frac{\mathsf{\Delta }}{L}$$

(2)

where $E_t$ is the backfill’s tangent Young’s modulus, ${\epsilon }_c$ is the sidewall-to-sidewall closure strain, and $\mathsf{\Delta }$ is the sidewall-to-sidewall closure displacement.

There are two main challenges to using the Mitchell sill mat solution in practice, and both challenges arise from the fact that the $UCS$ is the most commonly cited strength parameter used in parametric studies and for routine Quality Assurance and Quality Control (QA/QC) programs at mines. First, measuring the tensile strength of backfill presents testing challenges and few tensile strength test results are currently available. Second, in conducting individual unconfined compression tests, most studies and QA/QC programs focus on peak stress (the $UCS$) and not the elastic modulus. The first challenge is typically addressed by assuming the tensile strength is an order of magnitude less than the $UCS$ (i.e., ${\sigma }_t=UCS/10$) [3,4], which is a heuristic arising from testing intact rock, even though it does not apply to all rock types. This assumption has important implications because backfill strength is approximately proportional to binder content in the strength ranges of interest to backfill design. Hence, using laboratory tests to validate that ${\sigma }_t>UCS/10$ has proportionate savings implications for binder cost. The second challenge is more problematic. The closure strains measured and reported from various mines range from several percent [5,6,7,8,9,10,11,12,13] up to 15% at Lucky Friday mine [2,14], and so closure can be significantly influential when using the Mitchell sill mat solution. In principle, a relationship should exist between $E_t$ and $UCS$ as appears in many concrete design codes (usually incorporating $\sqrt{UCS}$), but this has not been investigated thoroughly for mine backfills.

Given the practical challenges identified above, the current work has two objectives. First, to present recent backfill testing data and compare the results to similarly published data, thereby establishing correlations between ${\sigma }_t$ and $UCS$, and between $E_t$ and $UCS$. Second, to use these correlations to assess potential limitations of using Mitchell’s sill mat solution for undercut backfill stability assessments, as well as other empirical design methods motivated by the original Mitchell sill mat solution.

The Mitchell sill mat solution has been used to design sill mats made of cemented rock fill, hydraulic fill, and Cemented Paste Backfill (CPB). The emphasis in this work is on CPB owing to its increasing popularity in underground mining. Because the UCS is critically important to applying the Mitchell sill mat solution, some issues with obtaining quality $UCS$ test data are first identified.

2. Obtaining Quality $UCS$ Test Data

A set of standardized laboratory test methods for CPB does not yet exist, but [15] review several equivalent standards meant for (cemented) soils, rock, and concrete, and [16] reviews how these should be used in backfill quality control (QC) programs at operating mines. The testing issues considered by [15] include specimen geometry (cylinders versus cubes, dimensions, and aspect ratios), curing conditions, edge preparation and tolerances, loading rates, results interpretation, and the number of tests and statistical evaluation of multiple test results. All the tests reviewed or reported in the current work fall within the scope of guidelines presented by [15].

It is now well established that reducing void space (as quantified by void ratio or porosity) for a given binder content results in stronger and stiffer backfill, as is the case for conventional concrete, because the hydration products generated by the available binder have smaller distances to span between solid particles (sand and silt) and form a denser network. This is shown at the microstructure level in Figure 2 where diamond-polished sections of a conventional mortar and a CPB are imaged using a Hitachi 2460N Scanning Electron Microscope fitted with a Backscattered Electron (BSE) imager and an Oxford Energy-dispersive X-Ray analyser (located in the Department of Civil & Mineral Engineering, University of Toronto, Toronto, ON, Canada): compared to the mortar, the CPB hydration products are diffuse and amorphous.

It was also demonstrated in $UCS$ tests by [17] and co-workers, where different samples were consolidated at different times and the resulting strengths were invariably greater than a control sample’s strength. For example, initial consolidation using a 100 kPa surcharge increased the density from 1.64 to 1.77 t/m³ and the resulting 7-day $UCS$ approximately doubled. Importantly, they demonstrated that the applied stress had no intrinsic strengthening effect: two samples were rapidly consolidated just after mixing, with the load removed from one and remaining on the other (but with no further consolidation occurring) and the resulting strengths were essentially identical. The void-ratio strength dependency was also demonstrated in [18] where specimens were mixed at different water contents and comparing 78% with 74% solids content the 28-day $UCS$ approximately doubled. Much more general load paths are considered by [19,20]. For example, ramping the vertical stress to 400 kPa over a 10 h period decreased the void ratio from about 0.9⁺ to 0.7 and approximately doubled the 7-day $UCS$. It is therefore imperative in laboratory test work to carefully determine the bulk properties and achieve consistency in $UCS$ results for multiple samples.

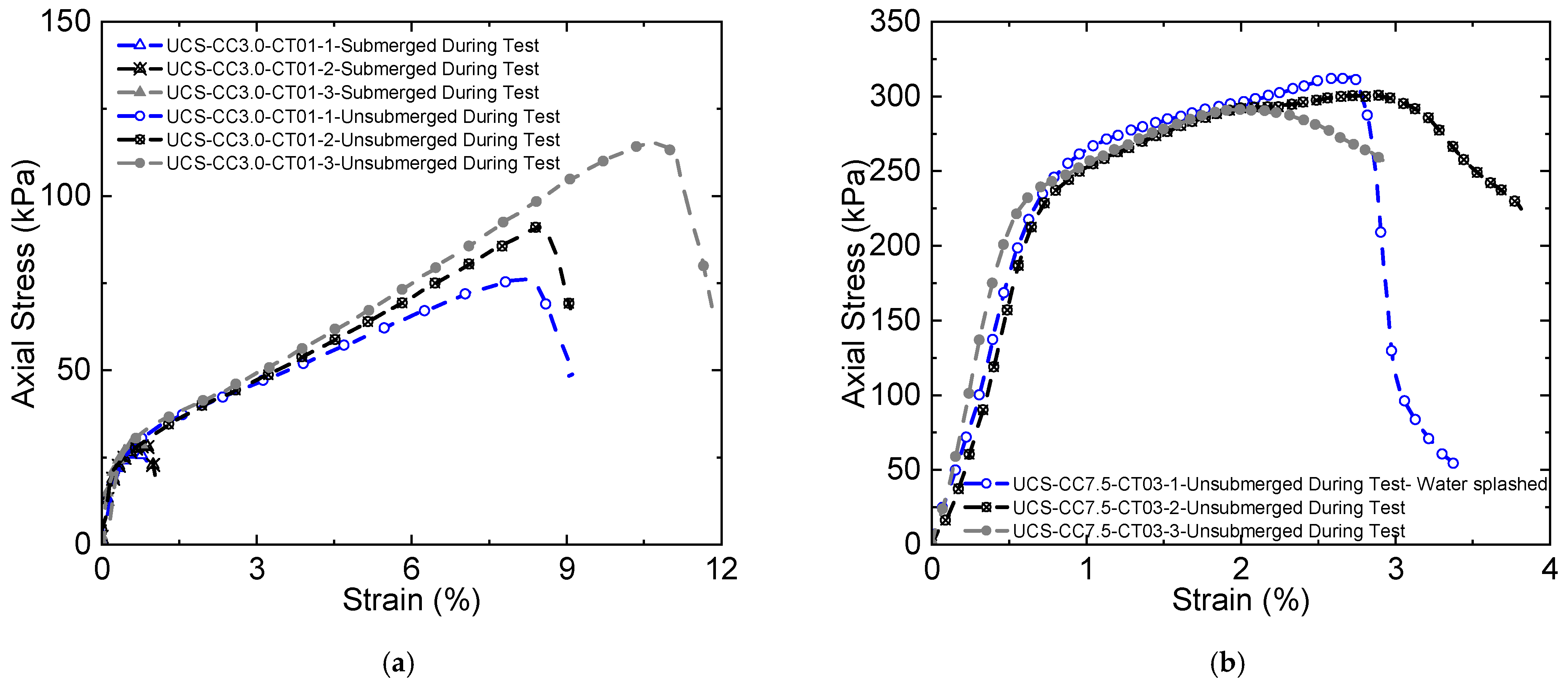
A testing issue not covered by the quoted standards is mitigating suction development during the dilation phase of the sample response. Figure 3a shows results for a relatively weak and soft CPB tested in two ways. First, three samples are tested underwater (submerged) at an axial strain rate of 0.03 %/min so that the samples can absorb water during their dilation phase to mitigate suction development. These three samples give consistent peak stress, $UCS\approx 30$ kPa. Second, three samples are tested in the usual way and at an axial strain rate of 1%/min to exaggerate the suction development effect. These samples exhibit a distinct bilinear response and achieve a peak stress at least double the true $UCS$. The second demonstration of this effect is shown in Figure 3b, with stronger and stiffer CPB. All tests are conducted following the second method but this time the sample indicated with open blue circle markers is sprayed with water from a misting bottle close to the artificial peak stress, and the suction within the sample is quickly suppressed and the sample fails under the applied load in the displacement-controlled load frame. The characteristic bilinear response can be seen in some of the published CPB literature, and those works were not included in the present analysis if it was deemed that their results could be affected by suction development during material testing.

In contrast to obtaining the peak strength ($UCS$), assessing the elastic response is an even greater challenge. It is now established that determining the axial strain based on end-to-end platen displacement is inappropriate at small strain levels [21], however, most of the tests reviewed or reported in the current work rely on determining the tangential Young’s modulus, $E_t$, from strains at about ½$UCS$ calculated based on end-to-end platen displacement. Only [14] compare a variety of strain determination methods, including strain gauges glued on the sample at mid-height, but they do not provide strains calculated in the usual way for comparison. The use of Particle Velocity Imaging, PVI, to determine radial strain and therefore estimate Poisson’s ratio is described in [22], but those results were assessed as unreliable, and more research and development is required before this method might become generally practical and reliable.

Finally, the tangential modulus $E_t$ is an apparent instantaneous quantity and even if it is linear it cannot necessarily be taken as elastic. This is demonstrated in Figure 4 using load–unload–reload cycles on Macassa backfill (considered in detail subsequently). Similar results are shown in [3] for Stillwater CPB. Nevertheless, it is arguably $E_t$ that should be used in the Mitchell sill mat solution if the backfill’s closure response is believed to be essentially one-dimensional and unconfined. The issue is revisited at the end of this work. Another complicating factor in determining a suitable modulus to be used in the Mitchell sill mat solution is that, similar to other geomaterials, a CPB’s Young’s modulus is pressure-dependent and increasing confining stress increases the elastic modulus. This effect is quantified using consolidated drained triaxial test data in [23] where increasing the confining stress from 50 to 200 kPa increased the CPB’s $E_t$ from about 25% for 5% binder content at 28-day cure time, to 100% for 2% binder content at 3-day cure time. Similar effects are shown in the consolidated drained triaxial test results for Williams CPB in [24].

3. Correlating ${\sigma }_t$ and $UCS$

A meta-analysis of tensile and other strength testing data for intact rock is provided by [25]. The test methods covered include direct tensile tests (DTSs) using four different arrangements (split grips, glued end caps, biaxial extension in a Hoek cell, and compression-to-tension load conversion), and indirect tests based on 3-point and 4-point beam bending, Brazilian Tensile Strength (BTS), Ring Test, Disc Bending, and hydraulic fracture. They conclude that the DTS is the truest measure of tensile strength, however, it is impractical for large-scale test programs and therefore corrected BTS test results are suggested, which can then be correlated to $UCS$. A similar meta-analysis will be carried out next for CPB materials, however, there is significantly less data available than is the case for rocks. For the current analysis it will be convenient to use the parameter $m_i$ from the Hoek–Brown failure criterion, where $m_i=UCS/{\sigma }_t$. In [26], the author gives tabulated values of $m_i$ by rock type, showing trends of decreasing $m_i$ going from igneous to metamorphic to sedimentary rocks, and decreasing $m_i$ going from coarse to very fine-grained texture. The common assumption for CPB, $m_i=10$ is representative of fine-grained clastic materials and is similar to the value assumed for normal strength concrete in North American reinforced concrete design codes. However, the authors of [26] indicate a value as low as $m_i=4 \pm$ 2 is appropriate for very fine-grained clastic rocks (e.g., claystone), and $m_i=7 \pm$ 2 is appropriate for fine-grained clastic rocks (e.g., siltstone), therefore, it is possible that values of $m_i$ as low as 3 or 4 might be found for CPB. Given the significance this parameter has on the assessed required $UCS$ when determining ${\sigma }_t$ using the Mitchell sill mat solution, direct measurements using the mine’s CPB are clearly desirable.

Table 1. Summary of $m_i=UCS/{\sigma }_t$ for various mines. n is the number of datapoints in the dataset.

Mine	n	Test Type	${\mathit{m}}_{\mathit{i}}$
Lucky Friday	14	Brazilian	8.8 avg
	5	Splitting	7.3 avg
	3	Direct Tension	16 avg
	14	In Situ Direct Tension	22 avg
Cannington	8 *	Direct Tension	7–10
Stillwater	4	Brazilian	4.5–7
Raleigh	2	3-Point Bending	3
	3	Brazilian	8
Brunswick	4	3-Point Bending	11
Williams	18	Direct Tension	4
Macassa (new)	6	Direct Tension	3–5
Uncemented	32	4-Point Bending	4

* 7- and 14-day subsets.

summarizes CPB tensile test data found in the literature, and the details of these are described next.

Lucky Friday CPB (i.e., the CPB produced at Lucky Friday mine) tensile strength was tested by [27] using Brazilian tests, splitting tests (loading along the long axis of cylindrical core samples), direct tension with glued end caps, and pull tests on samples partially cored (i.e., not end detached) from large block samples (which the authors call an “in situ test”). These resulted in $m_i$ values in the range of about 7–22, but the photograph of a failed sample from a direct tension test showed a failure plane inclined to the tensile loading axis, suggesting that these test results may not be reliable.

Cannington CPB tensile strength was tested by [22] using direct tension with glued end caps, with reported values equivalent to $m_i$ of about 7–10, however the tensile strength was relatively invariant between 7 and 56 days which does not seem reasonable given that compressive strength continued to increase after 28 days. It was noted that samples dried out (indicated by decreasing degrees of saturation) during the test period, but it is unclear if the samples were re-saturated prior to tensile testing.

Stillwater CPB tensile strength was tested by [3] using Brazilian tests conducted on samples obtained from mass pours at the mine, and although only four tests were conducted the range of corresponding $m_i$ was 4.5–7.

Raleigh CPB tensile strength test results are reported in [28] using three Brazilian tests and two 3-point beam bending tests, and these are compared with Cannington direct results [22], and Brunswick CPB using four 3-point beam bending test results [29]. Significant scatter is observed, with equivalent values for $m_i$ ranging from about 3 (Rayleigh 3-point beam bending) to 11 (Brunswick 3-point beam bending), but the authors conclude that the most credible results are from Brazilian tests with an upper bound $m_i$ about 8.

More recently, Pan et al. [30,31] developed a direct tension test based on a compression-to-tension load conversion method, and compared the measured Williams CPB tensile strengths to the $UCS$ and also to direct shear test results from samples with corresponding mix designs. Importantly, all tested samples were cured in virtually saturated conditions and the $UCS$ and direct shear tests were carried out with the samples submerged to prevent suction development associated with sample dilation. The tensile tests could not be carried out submerged, but water was sprayed on the sample during testing as discussed for the test results shown in Figure 3. An example of the combined results is shown in Figure 5, which shows the Mohr’s failure circles for three $UCS$ tests, three direct tension tests, and seven direct shear tests at varying normal stress from 0 to about ¼$UCS$. The consistency between the three independent test methods adds confidence to the reliability of the combined results, and the conclusion is that $m_i=K_p$, the passive earth pressure coefficient which for the material tested is about 4. This combination of tests is now recommended for high-quality CPB strength determination at low confining stress levels. For comparison, Williams tensile strengths were also determined using the Brazilian test method [32], with resulting strengths much lower than from direct tension tests. This is contrary to the trends for rock reported in [25] where the Brazilian strength results are typically higher than direct strength results. The differences may be due to the relatively soft nature of CPB as opposed to intact rock.

Macassa CPB was tested using the same direct tension device as [30,31]. For 10% binder content and testing at 3, 7, and 14 days the strength ratios varied from $m_i=$ 5 to 3. However, it was found that a maximum tensile strength of about 1 MPa could be reliably determined, beyond which the samples did not fail in the expected fashion (meaning, a fracture surface normal to the tension loading axis and in the middle third specimen length) and so the test frame and specimen casting mold are being modified to overcome this limitation.

An interesting contrast to cohesion created by hydraulic binders is presented in [33] where matric suction in uncemented samples creates an apparent cohesion, and the unsaturated tensile strength was determined using carefully measured 4-point beam bending tests. The unsaturated backfill samples were assumed to retain the effective stress friction angle (35°) determined from triaxial test results on the same backfill, and the measured tensile strength and failure envelope results were consistent with the findings of [30,31] shown in Figure 5.

Based on the reviewed and presented new results, it is recommended that wider consideration is given to carrying out the direct tension, direct shear, and $UCS$ test methods following the procedures discussed in [30,31] and shown in Figure 5. For the Williams and Macassa CPB, it was reliably determined that the tensile strength is much higher than the conventional assumption ${\sigma }_t=UCS/10$, as may well be the case for many other CPBs.

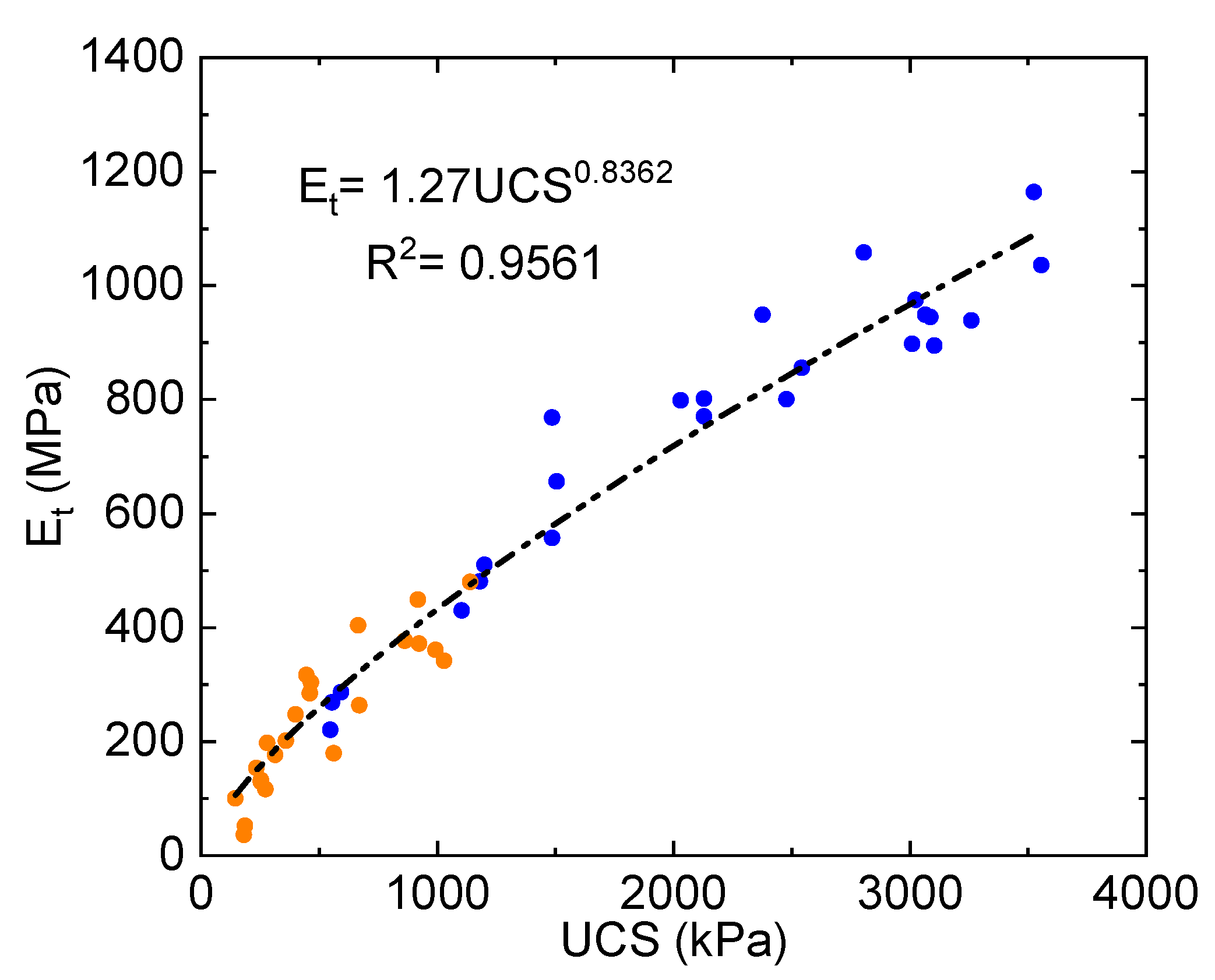
4. Correlating $E_t$ and $UCS$

The Williams and Macassa datasets mentioned previously contain a relatively large number of $UCS$ tests (25 and 45, respectively) which are useful for evaluating the functional relationship between the tangential Young’s modulus, $E_t$, and the $UCS$. The Williams dataset is in two test series: the first considers binder contents of 4.2%, 6.9%, and 9.7% tested at 3, 7, 14, and 28 days (12 tests total), all mixed at the same water content resulting in a void ratio $e\approx 1.0$; and the second considers binder contents 3%, 5%, 7%, and 10% all tested at 56 days but mixed at lower water contents resulting in void ratios as low as $e\approx 0.7$. Recall that mixing at lower water contents to achieve lower void ratios is like the approach used in [18]. The Macassa dataset uses binder contents of 5%, 7%, and 10% tested at 1, 3, 7, 14, and 28 days, and at water contents of 19.0%, 20.5%, and 22.0%. The Macassa CPB contains sand, and its void ratio is lower than the Williams samples, generally $e\approx 0.65$. 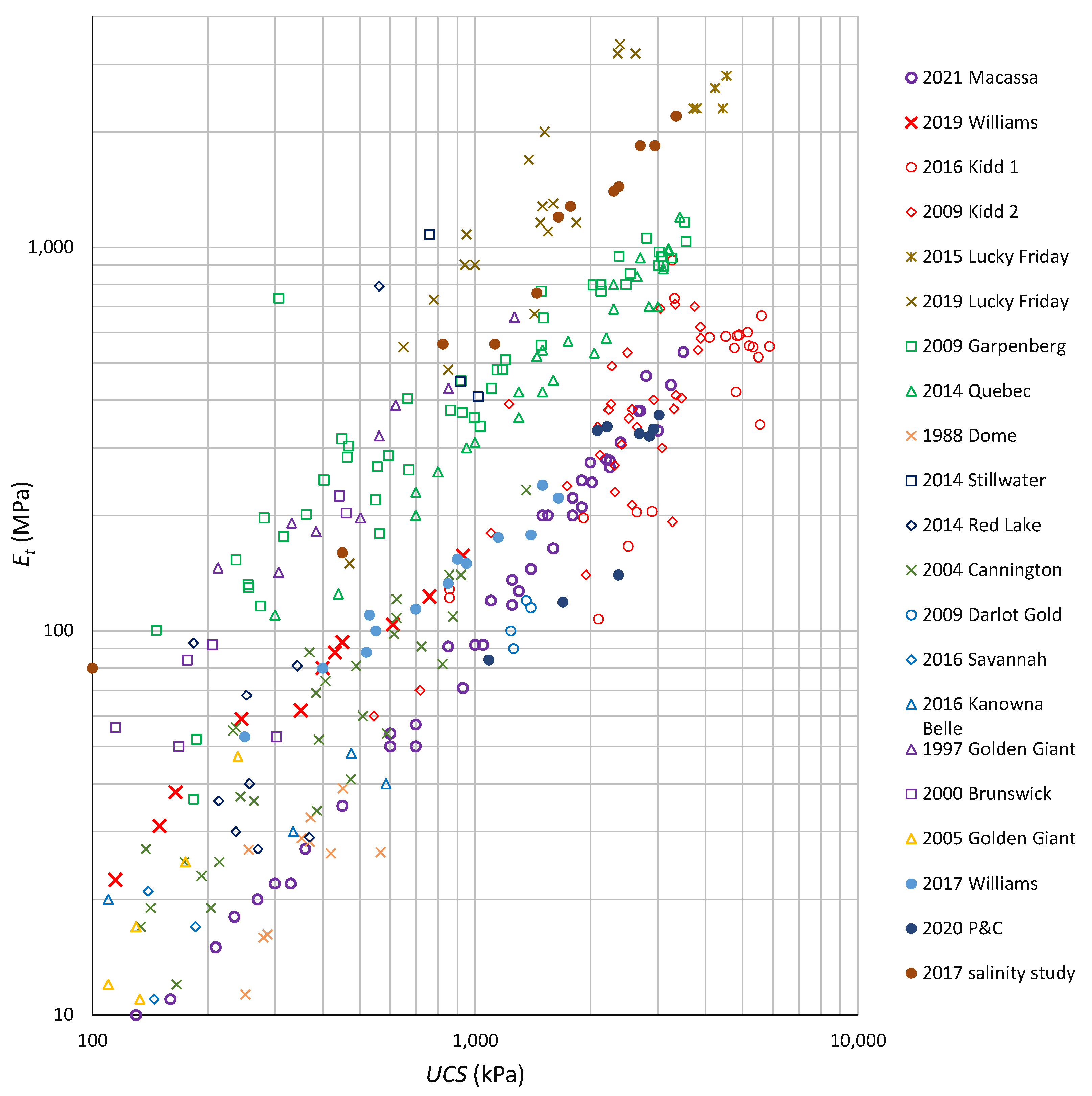The relationship between $E_t$ and $UCS$ for the combined Williams datasets and the Macassa dataset are shown in Figure 6.

Both datasets are fit with power functions and show good statistical significance (i.e., coefficients of determination close to unity). For these datasets, it is important to note that the trends are independent of cure time and void ratio. For example, a sample prepared at 4.2% binder content and tested at 28-day cure time has about the same strength as a sample prepared at 6.9% binder content and tested at 3-day cure time (although this is not shown), and correspondingly similar tangent Young’s moduli. Similarly, for the Williams results the combined datasets are shown to overlap in the range 250–935 kPa $UCS$, although the void ratios are significantly different between the two preparation methods. However, the statistical fits for the Williams and Macassa datasets are demonstrably different, with the exponent in the power function being < 1 for Williams and > 1 for Macassa. Given that consistent preparation and testing procedures were used, it must be concluded that the relationship between $E_t$ and $UCS$ is material dependent.

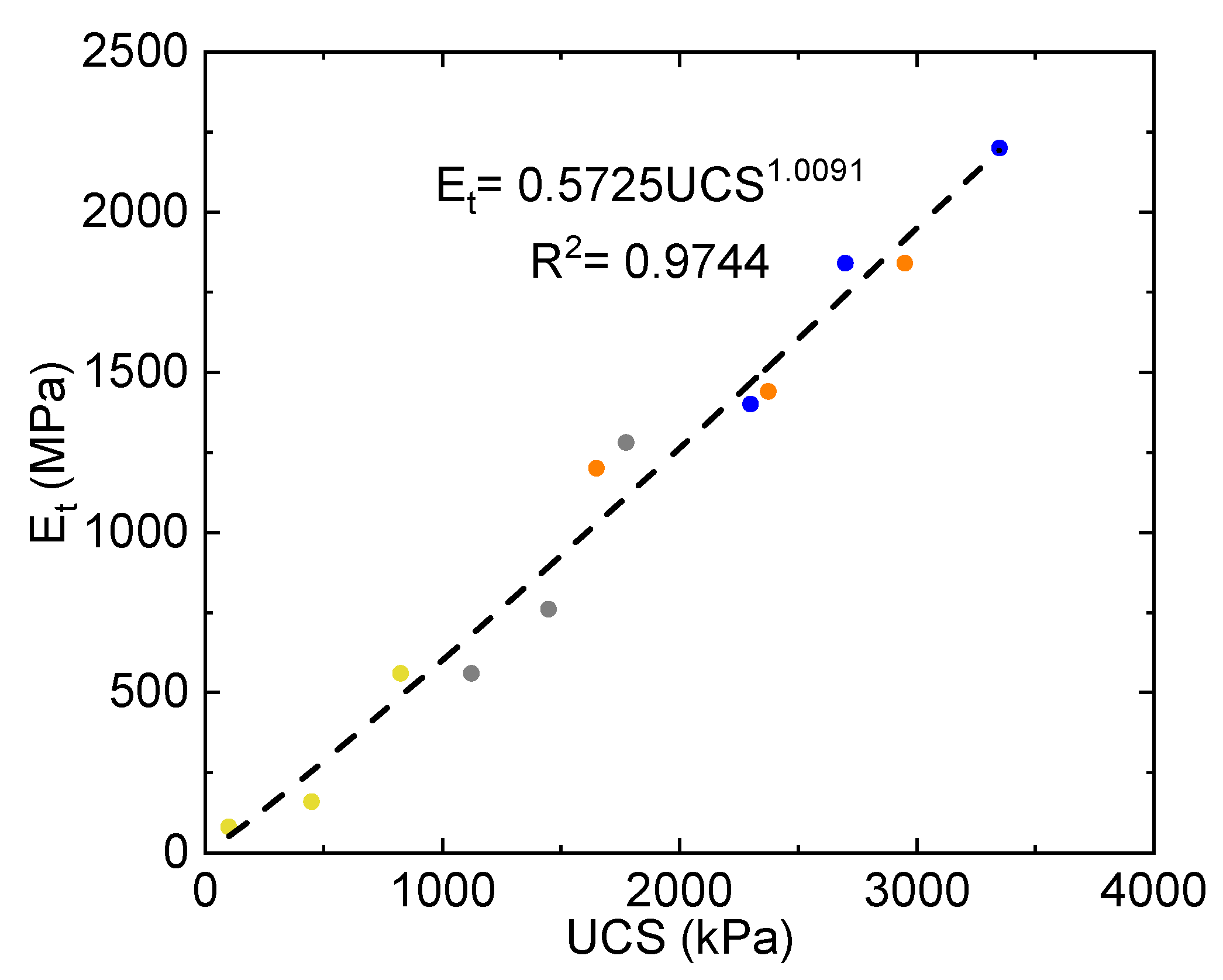
Another high-quality dataset is provided for Garpenberg by [19], where two types of binder were trialed: unblended Portland cement, and a blend of 20% Portland cement to 80% ground blast furnace slag. In each case, 3, 5, 7, and 10% binder contents were tested, and a range of water contents and corresponding void ratios were achieved through different rates of load application resulting in $e\approx 0.7-0.9$ for the Portland-only series and $e\approx 0.6-0.9$ for the Portland/slag blend series. The corresponding 28-day strength results are shown in Figure 7. Although the Portland/slag blend is more effective in achieving higher strengths for equivalent mix design and cure time, the trend between $E_t$ and $UCS$ appears to be consistent suggesting the different binder type is not significant to this trend for the range of parameters considered. Additionally, note that the exponent in the power function is similar to the Williams CPB, however, the constant is about 2.7 times higher.

A similar dataset is generated by the same authors for an unidentified mine in Quebec [20], this time using only the Portland/slag blend but with a range of curing times between 7 and 28 days. The best-fit power function to this dataset has a constant of 0.4328 and exponent of 0.9526, with a coefficient of determination of 0.9267. Presumably the authors’ testing procedures were consistent for the Garpenberg and Quebec datasets, indicating that the same binder was less effective at strength and stiffness gains for the Quebec mine. This also supports the hypothesis that the $E_t$ versus $UCS$ relationship is unique to each CPB.

A further previously unpublished dataset comes from Kidd mine. Kidd uses blended aggregates from an esker deposit, which can make sample preparation and testing difficult especially if the samples come from field coring (Figure 8b). The results shown in Figure 8a show considerable scatter (and a correspondingly low coefficient of determination) but its significance is that the data is combined from three different organizations (the University of Toronto and two industry laboratories) tested at three different times, yet similar results were obtained in terms of both trend and variability.

The effect of the mixing water’s salinity on hydration at cold temperatures (−6 °C) was considered in [34] using a synthetic tailing (ground silica), 4.5% Portland cement, water:cement ratio 7.35, and water salinities of 0, 5, 35, and 100 g/L. Results are shown in Figure 9 for testing times of 7, 28, and 90 days, and indicate that the range of studied salinities profoundly influences hydration effectiveness in the studied timeframes, however, the salinity concentration does not seem to influence the functional relationship between $E_t$ and $UCS$ in any statistically significant way.

Additional data was found in the literature and is summarized in

Table 2. Summary of $E_t$ and $UCS$ datasets, and fitting parameters for $E_t=\mathrm{const} UC{S}^{\exp }$ where the modulus is in MPa and the strength is in kPa; n is the number of datapoints in the dataset; the strength range is $UC{S}_{min}$ to $UC{S}_{max}$; $R^2$ is the coefficient of determination; $e$ is void ratio; $G_s$ is specific gravity of tailings; % sand is the fraction of tailings (and any blended aggregates) greater than 0.075 mm; values may be approximated from the original publications and the reader should refer to the original if detailed information is required. Regression analysis is performed using MS Excel for power functions. The abbreviations used for binder type are Portland Cement (PC), fly ash (FA), and ground granulated blast furnace slag (Slag) and their relative proportions when blended. The regression analysis parameters and other mix design information are not reported for small datasets nor datasets with poor coefficients of determination. For the remaining datasets, mix design parameters unavailable from the original article are indicated using n/a.

Mine	n	$\mathit{U}\mathit{C}{\mathit{S}}_{\mathit{m}\mathit{i}\mathit{n}}$ (kPa)	$\mathit{U}\mathit{C}{\mathit{S}}_{\mathit{m}\mathit{a}\mathit{x}}$ (kPa)	const	exp	${\mathit{R}}^2$	$\mathit{e}$	Binder Type	Binder %’s	Curing Days	${\mathit{G}}_{\mathit{s}}$	% Sand
Williams(a) [31]	12	95	935	0.427	0.858	0.995	1.0	PC	4, 7, 10	3, 7, 14, 28	2.85	10
Williams(b) (new)	13	250	1650	0.838	0.756	0.971	>0.7	PC	3, 5, 7,10	56	2.85	10
combined (new)	25	95	1650	0.471	0.845	0.971
Macassa (new)	45	70	3500	0.019	1.241	0.975	0.65	10PC:90Slag	5, 7, 10	1, 3, 7, 14, 28	2.76	67
Garpenberg(a) [19]	23	147	1140	0.687	0.939	0.760	0.7–0.9	PC	3, 5, 7, 10	28	2.96	49
Garpenberg(b) [19]	24	549	3558	2.154	0.765	0.949	0.6–0.9	20PC:80Slag	3, 5, 7, 10	28	2.96	49
combined	48	147	3558	1.270	0.836	0.956
Quebec [20]	27	300	3425	0.433	0.953	0.927	0.6–0.9	20PC:80Slag	3, 4.5, 7	7, 14, 28	3.70	20
Lucky Friday(a) [27]	5	3720	4540
Lucky Friday(b) [2]	18	470	2625	0.032	1.458	0.808	0.55–0.67	25PC:75Slag	8–10	>28	n/a	29
combined	23	470	4540	0.784	1.000	0.741
Cannington [22]	36	58	1361	0.048	1.178	0.818	4 wc	PC	2, 4, 6	7, 14, 28	3.20	35
Kidd (new)	54	544	5880	0.014	1.270	0.450	0.7	10PC:90Slag	2–3, 4.5	>28	2.74	55
Salinity study * [34]	12	100	3550	0.573	1.009	0.974	n/a	PC	4.5	7, 28, 90	2.7	n/a
Golden Giant [35]	9	213	1267	0.801	0.933	0.905	1.0	50PC:50FA	3, 5, 7	28, 56, 112	2.86	40
Red Lake [3]	13	54	562
Dome [36]	12	246	566
P&C [37]	9	1085	3025
Brunswick [28,29]	7	115	461
Golden Giant [38]	6	90	240
Darlot [17]	4	1240	1400
Kenowna Bell [39]	4	110	585
Savannah Nickel [39]	3	140	186
Stillwater [3]	3	760	1018

* There appears to be an inconsistency between the reported $E_t$ values and the corresponding stress–strain curves in the original publication, and it is possible that the $E_t$ values used here are an order of magnitude too large. The authors [34] were asked to clarify this issue, but a response was not obtained by the publication date.

and plotted in Figure 10 and Figure 11. The entries in Table 2 are approximately ordered so that the strongest datasets (those with the most datapoints, n, and strongest statistical fit, $R^2$) are first. Some of these datasets have been parsed or combined, indicated by the highlighted cells. Fitting parameters are not provided for datasets that have low numbers of datapoints and/or very poor statistical fits, but these data are used in the figures.

All datapoints from the literature review and the new data are plotted in Figure 10 to provide an indication of the variability within individual datasets and the ranges of $E_t$, $UCS$, and the ratio of these for all available data. Note that the ratio of upper-bound to lower-bound $E_t$ values for a given $UCS$ is approximately an order of magnitude. Where a given organization produces multiple datasets (e.g., the Williams vs. Macassa datasets, and the Garpenberg vs. Quebec datasets) the differences between those datasets should be considered “statistically significant”. However, the Kidd dataset notwithstanding, it is plausible that differences in testing procedures between organizations (e.g., sample preparation, machine stiffness, loading rates, transducer types and locations of testing equipment, data reduction and interpretation of raw test results, etc.) may be responsible for some of the variability observed. Regardless, it is useful to understand the range of results obtained by different organizations testing different CPB materials, so that new test results can be interpreted in the context of this combined data. Furthermore, the wealth of available evidence compellingly indicates that the $\sqrt{UCS}$ type functional relationships commonly accepted for normal strength concrete are inappropriate for CPBs.

Taking the data in Table 2 at face value, it is not clear that the functional relationship between $E_t$ and $UCS$ can be related to any of the indicated parameters, such as % sand content, void ratio (or porosity), binder type, or specific gravity of the solids. Therefore, when a new CPB is being considered, high-quality laboratory test results will remain necessary to establish that material’s $E_t$ versus $UCS$ functional relationship.

A clearer comparison between the different datasets is provided in Figure 11 where those datasets with fitted power functions are plotted as straight lines in log-log space, and the remaining datasets are shown as individually plotted datapoints. For the sake of comparison with other geomaterials, it is useful to define the Modulus Ratio $MR=E_t/UCS$. From Figure 10 and Figure 11, reasonable limits for the reviewed CPB materials are $100<MR<1000$. The upper bound is like normal strength concrete, while the lower bound compares well with very-fine grained clastics, and the mid-range is consistent with many of the rock types reported in [26].

Finally, direct tension tests of the type described by [30,31] allow comparing $E_t$ in uniaxial tension and compression. For the nine cases considered by [30,31], with 6.9% and 9.7% binder content tested at 7, 14, and 28 days, the modulus in tension was approximately half of that in compression. However, this is a limited dataset using only one material, and much more testing using other materials is required to determine if the heuristic is generally applicable to other CPBs.

5. Implications for Mine Backfill Design Using Mitchell’s Sill Mat Solution

The Mitchell sill mat solution assumes a fully fixed-ended (encastered) ideal beam for which the critical tensile stress concentrations are located at the top corners, which for sill mats (or plugs) correspond to the contacts at the sidewalls. If the side wall closure effect is ignored (i.e., ${\sigma }_c=0$) then the Mitchell sill mat solution can be rewritten to determine the limiting $UCS$ (strength factor = 1) as Equation (3),

$$UCS=m_i\frac{1}{2}w{\left(\frac{L}{d}\right)}^2$$

(3)

making it immediately apparent that the required strength is directly proportional to $m_i$, commonly assumed to be 10. However, the values summarized in Table 1 show many CPBs having $m_i$ values less than $m_i=10$. More important, the results obtained by [30,31] which are substantiated by consistency with direct shear and $UCS$ test results indicate $m_i=K_p$, or about 4 for the material tested. This result is consistent with the observations of suction-induced tensile strengths in unsaturated beam tests conducted by [33]. It should be noted that $K_p=4$ corresponds to an effective stress friction angle ${\varphi }^{\prime }=$ 37° which is a commonly reported value for CPBs composed of non-plastic silt (ML) tailings. Furthermore, $m_i=4$ is consistent with the Hoek–Brown recommendations for very fine-grained clastic materials. It is therefore plausible that many CPBs have greater tensile strength than is currently thought to be the case, and future direct tensile strength testing of the type described in [30,31] is therefore encouraged.

If the fixed-ended beam analogy is strictly accepted, then it is necessary to question if the backfill tensile strength is relevant or if it is instead the backfill-to-host rock contact tensile strength that should be used, which will likely be generally much smaller and perhaps negligible. If the contact tensile strength is taken as zero, then the assumed failure mechanism is no longer relevant and the underlying mechanism must account for the progressive failure of a fixed-ended beam. However, this additional complexity is not warranted if sidewall closure is considered, described next.

If the Mitchell sill mat solution is used and reasonable values of $E_t$ are determined based on laboratory studies (or the trends shown in Figure 11, if considered in a parametric study) then one finds the results are very sensitive to the assumed closure displacements and therefore closure strain, ${\epsilon }_c=E_t\frac{\mathsf{\Delta }}{L}$. This is because the $UCS$ is typically reached at less than 2% axial strain for the lower-bound trends shown in Figure 10 and Figure 11 and milli-strain for the upper-bound trends, and proportionately less for the tensile strength. The literature reviewed in Section 1 indicated that many mines have measured several percent closure strains, and up to 15% closure strain at Lucky Friday mine. Even if the effects of confinement on the elastic modulus and mobilized strength are accounted for, such strains must drive the CPB into its post-peak response. For example, drained triaxial tests were conducted by [23] with confinement 50–200 kPa on Shandong CPB, and by [24] with confinement 25–350 kPa on Williams CPB, and for the strongest materials tested by each, the axial strains to failure ranged from about 4% at the lowest confinement levels to 12% at the highest. Similarly, the authors of [40] interpreted 1-dimensional consolidation results in the context of ground reaction curves between CPB and the host rock during stope closure and concluded that the strains can essentially be ignored until the induced stress in the CPB reaches 2$UCS$, beyond which the stiffness increases exponentially and so too does the reaction. Considering the likelihood that many undercut CPB sill mats or plugs will be forced into the post-peak regime of their stress–strain response, design based on elastic beam analysis is tenuous. This interpretation is consistent with recent numerical modeling simulations considered in [41,42,43,44], where a reasonable expanse of rock mass was included surrounding the modeled stope to better capture the closure strains induced by excavation. In [43] a parametric study considered sill mats in (sub-) vertical orebodies at depths from 300 to 800 m, corresponding to horizontal stresses of 16–43 MPa. The CPB’s cohesion and Young’s modulus were not varied in a consistent way, but instead the modulus was varied from 0.6 to 1.8 GPa and the limiting cohesion for stability was determined. For Young’s modulus of 0.6 GPa the corresponding $UCS$ based on the assessed cohesion was about 1–2 MPa; and for Young’s modulus 1.8 GPa it was 3–7 MPa. Note that these ranges lie within the composite data presented in Figure 11 and are therefore plausible, but do not consistently represent a single CPB. (The authors acknowledge that strength and stiffness should increase in some systematic fashion.) They found that the hypothesized fixed-ended beam type response failed to materialize, and the resulting closure displacements drove the backfill to crushing failure for undercut spans up to 7 m. This finding is only applicable to the range of parameters studied but does indicate that the Mitchell sill mat solution cannot be applied indiscriminately.

6. Implications for Empirical Mine Design Motivated by Mitchell’s Sill Mat Solution

Simplified design charts “based on” or “motivated by” Mitchell’s sill mat solution have been proposed [45,46,47,48], but their development has never been fully explained. Pakalnis’s “empirical” design chart [46,48] is particularly interesting because it compares the design chart strength recommendations with case histories. The presentation of the chart does not, however, clarify if each plotted case study obtains the intended Factor of Safety FS = 2, or if the design has a higher or lower FS. It can be shown that the design chart has the underlying formula, for strength in MPa and lengths in meters, given in Equation (4),

$$UC{S}_{FS=2}=0.15L{\left(\frac{L}{d}\right)}^{1.5}$$

(4)

The motivation for Equation (4) as compared to the modified Mitchell sill mat solution (Equation (3)) can be assessed as follows: the factor $0.15L$ in Equation (4) can be explained using reasonable assumptions (e.g., $w={\sigma }_{v,max}=\frac{\gamma L}{2K\tan {\varphi }^{\prime }}$, unit weight $\gamma =$ 0.02 MN/m³, stress ratio $K=$ 1.0, $\tan {\varphi }^{\prime }=\frac{2}{3}$, $m_i=10$, ignore clamping stress); but the reduction of the exponent from 2 to 1.5 must be considered empirical, as indicated by the authors. If the results are instead presented in terms of required strength for a given span and depth of sill mat or plug, then the strength factor for each case history can be computed and compared to the modified Pakalnis empirical design chart shown in Figure 12. Many of the case histories included in the database use strengths considerably larger than recommended by the design chart, especially the cases with narrow spans. This may be because the underlying basis for the design chart is not too dissimilar from Mitchell’s fixed beam analogy, and so also does not account for backfill stresses induced by large (several percent) closure strains.

7. Conclusions

Two fundamental contributions are arising from this work. First, understanding backfill material behavior under the range of loading conditions relevant to undercut CPB requires careful laboratory testing using a variety of test methods. The advantage of the direct tensile test is that the failure geometry can be observed to confirm whether the failure mode is consistent with expectations of a brittle fracture surface normal to the tensile loading direction; and the pre-fracture response can be assessed to determine a tangent Young’s modulus in tension. More importantly, the tensile strength test results can be directly compared with direct shear test results and $UCS$ test results to confirm a consistent interpretation of the CPB’s strength envelope. The tangent Young’s modulus, $E_t$, can be correlated to $UCS$ using a power function, but this functional relationship appears to be unique for each CPB. The $E_t$ to $UCS$ relationship was found to be independent of binder type (Portland cement only versus a Portland/Slag blend) for Garpenberg CPB; and independent of void ratio for Garpenberg, Quebec, Williams, and Macassa CPBs; and independent of water salinity (for synthetic tailings) over the range of parameters studied in each case, however, these findings should not be automatically assumed for all CPBs. While the combination of direct tension, direct shear, and $UCS$ tests is useful to characterize the material strength and stiffness under low confining stresses, undercut CPB analysis is generally more complicated and needs to consider material response under higher ranges of confinement and strain. This may require drained triaxial testing, one-dimensional (oedometer) consolidation testing, and isotropic consolidation testing for massive orebodies where the deformation may occur in multiple directions.

The second contribution is to a better understanding of the design scenarios to which the original Mitchell sill mat solution and the Pakalnis empirical design chart may apply. If the rock mass is very stiff and field stresses are low, the closure displacements and strains may be low enough (i.e., less than 1% for the lower-bound trends reviewed) to prevent crushing stresses in the CPB. In this case, the Mitchell sill mat solution can be used but care must be taken when evaluating the clamping stress. Similarly, the trends in the (modified) Pakalnis empirical design chart, which presumably ignores clamping stress, may be useful for parametric studies during preliminary design. In either case, laboratory test results are recommended in support of final design. Where larger closure displacements and strains can be anticipated, such as deep and high stress mining, additional consideration must be given to the CPB’s strength and stiffness dependency on confining stress levels, in which case drained triaxial and consolidation test results are required, and numerical modeling is generally needed to fully understand the mechanisms by which the CPB remains stable and transmits stress across the undercut span.

Finally, it is imperative to remember that any analysis of undercut stability inherently assumes that the CPB’s material properties in the sill mat or plug are homogeneous and isotropic. In contrast, the authors of [27] described an incident at Lucky Friday mine where a large backfill roof failure occurred which was attributed to, in part, the presence of flat-lying cold joints. Therefore, quality assurance and control procedures are needed to ensure the as-placed CPB properties are consistent with design expectations, and in particular any incidents of inconstant or irregular backfill pouring are noted and accounted for.