Abstract
Crash-tolerant systems rely on total order protocols to ensure consistent request execution across replicated servers. The Logical Clock and Ring (LCR) protocol employs a ring-based, leaderless design that provides a high throughput but suffers latency inefficiencies under a high message concurrency due to its use of vector clocks and a fixed last-process rule for ordering concurrent messages. This paper presents the Daisy Chain Total Order Protocol (DCTOP), an enhanced version of LCR that integrates Lamport logical clocks for message sequencing and introduces dynamic last-process identification based on sender activity to accelerate message stabilisation and delivery. A modified fairness-control mechanism further balances message distribution among processes. The simulation results show that the DCTOP achieves an over 40% latency reduction compared to LCR while maintaining the same fairness and throughput across various cluster configurations.
Keywords:
LCR; total order; fairness control; latency; throughput; performance comparison; simulation 1. Introduction
A crash-tolerant system is designed to continue functioning despite a threshold number of crashes occurring and is crucial to maintaining a high availability of systems [1,2,3,4]. Replication techniques have made it possible to create crash-tolerant distributed systems. Through replication, redundant service instances are created on multiple servers, and a given service request is executed on all servers so that, even if some servers crash, the rest will ensure that the client receives the response. The set of replicated servers hosting service instances may also be referred to as a replicated group and simply as a group. A group is a collection of distributed processes in which a member process communicates with other members only by sending messages to the full membership of the group [5]. Typically, a client can send its service to any one of the redundant servers in the group and the server that receives a client request, in turn, disseminates it within the group so all can execute. Thus, different servers can receive client requests in a different order, but, despite this, all servers must process client requests in the same order [6,7]. To accomplish this, a total order mechanism that employs logical clock is utilised to guarantee that replicated servers process client requests or simply messages in the same order [8]. A logical clock is a mechanism used in distributed systems to assign timestamps to events, enabling processes to establish a consistent order of events occurring. Thus, a total order protocol is a procedure used within distributed systems to achieve agreement on the order in which messages are delivered to all process replicas in the group. This protocol ensures that all replicas receive and process the messages in the same order, irrespective of the order in which they were initially received by individual replicas. While total order protocols play a critical role in maintaining consistency and system reliability, achieving crash tolerance requires the implementation of additional mechanisms. One such mechanism, as defined in our work, is the crashproofness policy. Specifically, this policy dictates that a message is deemed crashproof and safe for delivery once it has successfully reached at least f+1 operative processes, where f is the maximum tolerated failures in a group.
Research into total-order broadcast and distributed consensus has evolved significantly beyond the traditional ring and token-passing systems, exemplified by the LCR algorithm [9] and the Fixed Sequence Ring (FSR) protocol [10] which employ neighbour-to-neighbour communication to maintain the same fairness and message order under asynchronous conditions. Contemporary consensus frameworks, including Apache Zookeeper [11,12], Chubby [13,14], Paxos [15], View-stamp replication [16], and Raft [17,18,19], rely on leader-based coordination to achieve strong consistency guarantees. However, this approach often introduces coordination overhead, which can hinder scalability. To address these limitations, protocols such as Fast Paxos [20], S-Paxos [21], and EPaxos [22] have been proposed to reduce decision latency by minimising or eliminating the reliance on a centralised leader, enabling a more decentralised or leaderless consensus execution. In the Byzantine fault-tolerant (BFT) domain, protocols like HotStuff [23] utilise multi-phase authenticated voting schemes, typically incurring a communication complexity in the worst case to maintain agreement in the presence of multiple leader failures. Mir-BFT [24] enhances the throughput by parallelising the leader role, while Dumbo [25] and Dumbo-NG [26] optimise asynchronous consensus to reduce latency and communication overhead. Flutter [27] further improves responsiveness and throughput through pipelined and leaderless message dissemination. Emerging efforts such as Antipaxos [28] and BBCA-Ledger [29] explore new directions in high-throughput consensus: while Antipaxos achieves leaderless parallel agreement through k-Interactive Consistency (k-IC), BBCA-Ledger combines a low-latency broadcast path with a DAG-based fallback mechanism to sustain the throughput under network faults. Ring-based broadcast schemes, including Ring Paxos [30] which still internally elects a leader and chain replication [31], achieve message ordering with linear communication overhead by sequentially relaying messages across nodes. BPaxos [32] adopts a modular state machine replication design that scales consensus components independently to remove the leader bottleneck in traditional protocols. While this improves the throughput, it introduces a higher latency and greater implementation complexity. In contrast, the DCTOP achieves a low-latency concurrency through a simpler ring-based, leaderless structure using Lamport timestamping for efficient total order delivery. Building on the foundation established by ring-based broadcast [33] such as LCR, the DCTOP introduces dynamic last-process identification and a Lamport logical clock mechanism to enhance the ordering latency and determinism. Compared to consensus-based frameworks, the DCTOP offers a lightweight, topology-aware ordering service that minimises coordination costs. This makes it particularly well-suited for deployment in cloud and edge environments, where the overhead of full consensus protocols may be prohibitive. As such, the DCTOP represents a complementary alternative that prioritises ordered message dissemination with reduced synchronisation requirements. The aim of this research is to design and evaluate an efficient ring-based total order protocol that improves the message ordering latency and fairness in asynchronous distributed environments. Specifically, the study seeks to enhance the classical LCR protocol. Despite the progress made by LCR, certain design choices may lead to increased latency. The LCR protocol utilises vector clock where each process, denoted as , maintains its own clock as . A vector clock is a tool used to establish the order of events within a distributed system which can be likened to an array of integers, with each integer corresponding to a unique process in the ring. In the LCR protocol, processes are arranged in a logical ring, and the flow of messages is unidirectional as earlier described. However, LCRs’ design may lead to performance problems, particularly when multiple messages are sent concurrently within the cluster: firstly, it uses a vector timestamp for sequencing messages within replica buffers or queues [34], and, secondly, it uses a fixed idea of the “last” process to order concurrent messages. Thus, in the LCR protocol, the use of a vector timestamp takes up more space in a message, increasing its size.
Consequently, the globally fixed last process will struggle to rapidly sequence multiple concurrent messages, potentially extending the message-to-delivery average maximum latency. The size of a vector timestamp is directly proportional to the number of process replicas in a distributed cluster. Hence, if there are N processes within a cluster, each vector timestamp will consist of N counters or bits. As the number of processes increases, larger vector timestamps must be transmitted with each message, leading to a higher information overhead. Additionally, maintaining these timestamps across all processes requires greater memory resources. These potential drawbacks can become significant in large-scale distributed systems, where both the network bandwidth and storage efficiency are critical. Thirdly, in the LCR protocol, the assumption implies that , where f represents the maximum number of failures the system can tolerate. This configuration results in a relatively high f, which can delay the determination of a message as crashproof. While the assumption is practically valid, it is not necessary for f to be set at a high value. Reducing f can enhance performance by lowering the number of processes required to determine the crashproofness of a message.
Prompted by the above potential drawbacks in LCR, a new total order protocol was design with , , processes arranged in a unidirectional logical ring where is the number of processes within the server clusters. Messages are assumed to pass among processes in a clockwise direction as shown in Figure 1. If a message originates from , it moves to until it gets to which is the last process for . The study aims to achieve the following objectives: (i) Optimise message timestamping with Lamport logical clocks, which uses a single integer to represent message timestamps. This approach is independent of N, unlike the vector timestamping used in LCR, which is dependent on N.
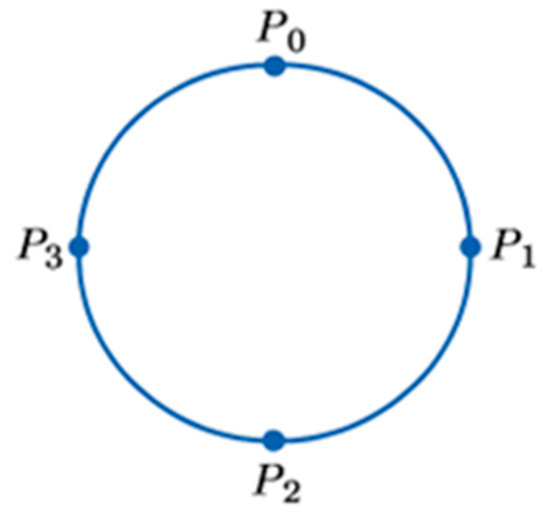
Figure 1.
Last process concept.
(ii) Dynamically determine the “Last” Process for ordering concurrent messages. Instead of relying on a globally fixed last process for ordering concurrent messages, as in LCR, this study proposes a dynamically determined last process based on proximity to the sender in the opposite direction of message flow. This adaptive mechanism improves ordering flexibility and enhances system responsiveness under high workloads. (iii) Reduce message delivery latency. This study proposes reducing the value of f to (N − 1)/2 to minimise the overall message delivery latency and enhance system efficiency. This contrasts with the LCR approach, where f is set to N − 1. Specifically, when a message must be received by every process in the cluster before it can be delivered. Under high workloads or in the presence of network delays, this requirement introduces significant delays, increasing the message delivery latency and impacting system performance. The goal of this study was accomplished using three methods: First, we considered a set of restricted crash assumptions: each process crashes independently of others and, at most, processes involved in group communication can crash. Hence, the number of crashes that can occur in an N process cluster is bounded by , where denotes the largest integer . The parameter is known as the degree of fault tolerance as described in Raft [17]. As a result, at least two processes are always operational and connected. Thus, an Eventually Perfect Failure Detector (♦P) was assumed in this study’s system model, operating under the assumption that N = 2f + 1 nodes are required to tolerate up to f crash failures. This approach enables the new protocol to manage temporary inaccuracies, such as false suspicions, by waiting for a quorum of at least f + 1 nodes before making decisions. This ensures that the system does not advance based on incorrect failure detections. Secondly, the last process of each sender is designated to determine the stability of messages. It then communicates this stability by sending an acknowledgement message to other processes. When the last process of the sender receives the message, it knows that all the logical clocks within the system have exceeded the timestamp of the message (stable property). Then, all the received messages whose timestamp is less than the last process logical clock can then be totally ordered. In addition, a new concept of “deliverability requirements” was introduced to guarantee the delivery of crashproof and stable messages in total order. A message is crashproof if the number of messages ; that is, a message must make at least number of hops before it is termed crashproof. Thus, the delivery of a message is subject to meeting both deliverability and order requirements. As a result of enhancements made in this regard, a new leaderless ring-based total order protocol was designed, known as the Daisy Chain Total Order Protocol (DCTOP). Thirdly, fairness is defined as the condition where every process has an equal chance of having its sent messages eventually delivered by all processes within the cluster. Every process ensures messages from the predecessor are forwarded in the order they were received before sending their own message. Therefore, no process has priority over another during the sending of messages.
1.1. Contributions
The contributions of this paper can be summarised as follows:
- (i)
- Protocol-Level Innovations Within a Ring-Based Framework: This study introduces the DCTOP, a novel improvement to the classical LCR protocol while retaining its ring-based design. It introduces the following:
- a
- A Logical Clock is used for message timestamping which achieves efficient concurrent message ordering, reducing latency and improving fairness.
- b
- Dynamic Last-Process Identification is used to replace LCR’s globally fixed last process assumption, accelerating message stabilisation and delivery.
- (ii)
- Relaxed Failure Assumption: The DCTOP reduces N = f + 1 to N = 2f + 1, enabling faster message delivery with fewer failures. Importantly, this relaxation remains consistent with the theoretical lower bounds for consensus fault tolerance, which require at least N ≥ 2f + 1 replicas to guarantee safety in asynchronous distributed systems [35,36]. Thus, the DCTOP improves latency performance without violating the fundamental resilience limits established by the classical consensus theory.
- (iii)
- Foundation for Real-World Deployment: While simulations excluded failures and large-scale setups, ongoing work involves a cloud-based, fault-tolerant implementation to validate the DCTOP under practical conditions.
1.2. Practical Integration and Application Scenarios of DCTOP
The DCTOP can be practically deployed as a lightweight ordering layer within modern distributed infrastructures. In a cloud or edge cluster, each process Pi in the DCTOP model corresponds to an individual service instance or virtual node, connected through asynchronous communication channels such as message-oriented middleware. The daisy-chain configuration forms a logical ring that can be established dynamically at runtime, allowing the DCTOP to operate independently of any centralised coordinator. Because each process communicates only with its immediate neighbours, the communication overhead is linear O(N) rather than quadratic, making the DCTOP suitable for large-scale, latency-sensitive environments. The DCTOP’s logical clock mechanism ensures global ordering under varying network delays, providing consistent message sequencing even in the presence of asynchronous message arrivals. The DCTOP attains total order through deterministic topological progression and local timestamp stabilisation. This property makes it particularly useful as a complementary component in distributed logging, event streaming, and replicated state machine frameworks where high-frequency, ordered message dissemination is required without full consensus overhead. As a use case, the DCTOP can be integrated into a cloud-based logging replication service where each node in the ring represents a log replica [37,38]. Incoming events are timestamped, propagated clockwise, and stabilised through the ring, ensuring a consistent total order across all replicas. This approach offers an improved throughput and reduced coordination delay compared to leader-based ordering schemes, demonstrating the DCTOP’s applicability to real-world, fault-tolerant distributed systems.
This paper is structured as follows: Section 2 presents the system model, while Section 3 outlines the design objectives and rationale for the DCTOP. Section 4 details the fairness control primitives. Section 5 provides performance comparisons of the DCTOP, LCR, and Raft in terms of the latency and throughput under crash-free and high-workload conditions. Finally, Section 6 presents the paper’s conclusion.
2. DCTOP System Model
The system is modelled as a group of N processes, denoted by organised in a circular (ring-based) structure under an asynchronous communication framework. The message transmission intervals follow an exponential distribution, with no constraints on communication delays. The model assumes FIFO message delivery, ensuring that messages are received in the order sent. Each process can transmit messages only to its clockwise neighbour and receive from its anticlockwise neighbour Formally,
- .
Messages, therefore, propagate exclusively in the clockwise direction. Each process maintains a stability clock representing the largest stable timestamp known to . When a message m becomes stable, is updated as .
The number of hops between any two processes from to is denoted as
- (i)
- (ii)
- (iii)
3. DCTOP—Daisy Chain Total Order Protocol
The DCTOP system employs a group of interconnected process replicas, with a group size of , where is an odd integer, and, at most, 9, to provide replicated services. The main goals of the system design are threefold:
- (a)
- First, to improve the latency of LCR by utilising Lamport logical clocks for sequencing concurrent messages;
- (b)
- Second, to employ a novel concept of the dynamically determined “last” process for ordering concurrent messages, while ensuring optimal achievable throughput;
- (c)
- Third, the relaxation of the crash failure assumption in LCR.
3.1. Data Structures
The data structures associated with each process , message m, and the µ message are discussed in this section as used in the DCTOP system design and simulation experiment:
Each process has the following data structures:
- 1.
- Logical clock : This is an integer object initialised to zero and used to timestamp messages.
- 2.
- Stability clock : As specified in Section 2. is initially set to zero.
- 3.
- Message Buffer (): This field holds the sent or received messages by
- 4.
- Delivery Queue ( This queue holds messages pending delivery.
- 5.
- Garbage Collection Queue (: Once a message has been delivered by , it is subsequently transferred to for garbage collection.
M is used to denote all types of messages used by the protocol. Usually, there are two types of M: the data message denoted by m, and an announcement or ack message that is bound to a specific data message. The latter is denoted as µ(m) when it is bound to m. µ(m) is used to announce that m has been received by all processes in the group. The relationship between m and its counterpart µ(m) is shown in Figure 2.
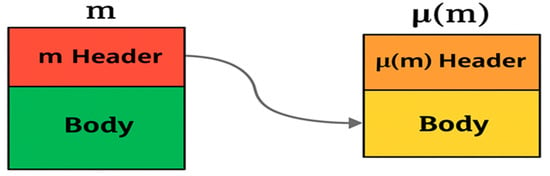
Figure 2.
Relationship between m and µ.
A message, m, consists of a header and a body, with the body containing the data application information. Every m has a corresponding µ, denoted as µ, which contains the information from m’s header. This is why we refer to µ instead of just µ. µ has m header information as its main information and does not contain its own data; therefore, the body of µ is essentially m’s header (see Figure 2).
A message M has at least the following data structures:
- 1.
- The message origin field shows the id of the process in that initiated the message multicast.
- 2.
- The message timestamp field holds the timestamp given to M by M_origin.
- 3.
- The message destination field holds the destination of M which is the CN of the process that sends/forwards M.
- 4.
- The message flag (M_flag) is a Boolean field that can be either true or false and is initially set to false when M is created.
3.2. DCTOP Principles
The protocol comprises three design aspects: (i) message handling (sending, receiving, and forwarding), (ii) timestamp stability, and (iii) crashproofing, which was introduced in Section 1. This subsection focuses on the first two.
- 1.
- Message Sending, Receiving, and Forwarding: The Lamport logical clock is used to timestamp a message m within the ring network before m is sent. Therefore, denotes the timestamp for message
The system as shown in Figure 3 uses two main threads in any process Pi to handle message transmission and reception in a distributed ring network. The send(m) thread operates by dequeuing a message m from the non-empty SendingQueuei when allowed by the transmission control policy (see Section 4). It timestamps the message with the current value of the LCi as , increments LCi by one afterwards, and then places the timestamped message into the OutgoingQueuei for transmission as shown in Figure 3. A copy of the message is also stored in mBufferi for the local record. On the receiving side, the receive(m) thread dequeues a message m from the IncomingQueuei when permitted by the transmission control policy, updates the as , and delivers the message to process Pi for further handling. Typically, m is entered in and may be forwarded if required to by entering a copy of m with the destination set to into the . A message is forwarded to only if it has not completed a full cycle in the ring; once it does, forwarding stops. However, once the message completes a full cycle in the ring network, it is no longer forwarded, and the process stops. When two messages are received in succession, they are transmitted in the same sequence; however, their delivery may not be immediate or consecutive, as determined by the transmission control policy. As shown in Figure 3, received messages enter , and are logged in and forwarded copies are placed in in receive order.
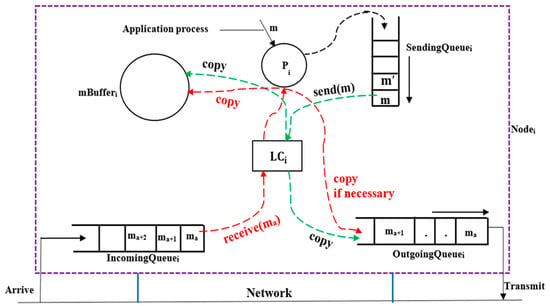
Figure 3.
Message sending, receiving, and forwarding.
- 2.
- Timestamp Stability: A message timestamp TS, is said to be stable in a given process if and only if the process is guaranteed not to receive any , any longer.Observations:
- (1)
- A timestamp is also stable in when TS becomes stable in
- (2)
- The term “stable” is used to refer to the fact that, once TS becomes stable in , it remains stable forever. This usage corresponds to that of the “stable” property used by Chandy and Lamport [39].
- (3)
- When TS becomes stable in , the process can potentially total order (TO) deliver all previously received but undelivered , because the stability of TS eliminates the possibility of ever receiving any , in the future.
Building on the message-handling and stability mechanisms discussed above, the DCTOP algorithm integrates these principles into a unified procedure for ensuring total-order delivery across all processes. The key operational steps are summarised in Section 3.3.
3.3. DCTOP Algorithm Main Points
The DCTOP algorithm’s main points are outlined as follows:
- 1.
- When forms and sends m, it sets m_flag = false before it deposits m in its .
- 2.
- When receives m and = m_origin, it carries out the following:
- It checks if ≥ f. If this condition holds, then m is considered crashproofed and is not delivered immediately. Additionally, m_flag is set to true, and m is deposited accordingly. If m is not crashproofed, m_flag remains false.
- It then checks if ≠ . If so, it sets m destination, m_destn = and deposits m in its .
- Otherwise, m is stable, and then it updates as = max { , m_ts}, and transfer all received m, m_ts ≤ to . Then, it forms µ(m), sets µ(m)_origin= and µ(m)_destn=, and deposits µ(m) in
- 3.
- When receives µ(m), it knows that every process has received m:
- If m in µ(m) does not indicate a higher stabilisation in , that is, m_ts ≤ and ≥ f, then ignores µ(m); otherwise, if < f, sets m_flag= true and µ(m)_destn = , and deposits µ(m) in
- However, if m in µ(m) indicates a higher stabilisation in , i.e., m_ts > , updates as = max { , m_ts}, and transfers all m, m_ts ≤ to
- If = , ignores µ(m); otherwise, it sets µ(m)_destn = and deposits µ(m) in
- 4.
- Whenever is non-empty, deques m from the head of and delivers to the application process. then enters a copy of into to represent a successful TO delivery. This action is repeated until becomes empty (see Figure 4).
 Figure 4. Algorithm for handling uniform total order delivery in DCTOP.
Figure 4. Algorithm for handling uniform total order delivery in DCTOP.
It is important to note that the DCTOP maintains total order. Thus, if forms and sends and then , (i) every process receives and then ; (ii) µ() will be formed and sent before µ(); and (iii) any process that receives both µ() and µ() will receive µ() and then µ(). The message-handling logic discussed above ensures that all processes consistently propagate, stabilise, and acknowledge messages. To complete the protocol description, the following delivery requirements formally define when a message may be safely delivered to the application layer while preserving total order: A message m is deliverable to the high-level application process by once it is both stable and crashproof. Two such messages m and m′ are delivered in total order; m precedes m′ if and only if m_ts < m′_ts or, when timestamps are equal, m_origin > m’_origin.
In summary, the pseudocode representations for total order message delivery, message communication, and membership changes are presented in Figure 4, Figure 5 and Figure 6, respectively.

Figure 5.
Algorithm for handling message multicasting in DCTOP.

Figure 6.
Algorithm for handling membership changes in DCTOP.
Figure 4, Figure 5 and Figure 6 collectively illustrate the operational flow of the DCTOP protocol. Figure 5 presents the main steps for message multicast and processing, covering initialisation, timestamping, forwarding, and crashproof handling among processes. Figure 6 extends this by showing how the protocol manages group membership changes, ensuring message recovery, queue stabilisation, and consistent delivery when nodes join or leave the system. Finally, Figure 4 demonstrates the uniform total order delivery (utoDelivery) and garbage collection mechanism, where stable messages are delivered to the application layer and archived to preserve correctness and efficiency.
For clarity, Table 1 provides a summary of the main notations used in the membership change procedure as illustrated in Figure 6. These notations correspond to the elements referenced in Steps 1–9 of the algorithm, supporting the reproducibility and interpretation of the DCTOP reconfiguration logic.

Table 1.
Notations used in DCTOP membership change algorithm.
3.4. Group Membership Changes
The DCTOP protocol is built on top of a group communication system [40,41]. Membership of the group of processes executing the DCTOP can change due to (i) a crashed member being removed from the ring and/or (ii) a former member recovering and being included in the ring. Let G represent the group of DCTOP processes executing the protocol at any given time. G is initially and G is always true. The membership change procedure is detailed in Figure 6 and all the notations used are described in Table 1. Note that the local membership is assumed to send an interrupt to the local DCTOP process, say, , when a membership change is imminent. On receiving the interrupt, completes the processing of any message it has already started processing and then suspends all DCTOP activities and waits for the new G’ to be formed: the sending of m or µ(m) (by enqueueing into ), receiving of m or µ(m) (from ), and delivering of m (from ) are all suspended. The group membership change works as follows: Each process Pi in the set of Survivors(G) (i.e., survivors of the current group G) exchanges information about the last message they TO-delivered. Once this exchange is complete, additional useful information is derived among all Survivors, which helps identify the Lead Survivor. Subsequently, each Survivor sends all messages from its respective SendingQueue to the other Survivors. If Pi has any missing messages, they are sent to another Survivor, Ps, where Ps represents any Survivor process other than Pi. After sending, Pi transmits a Finishedi message to all Ps processes, signalling that it has completed its sending. Upon receiving messages, Pi stores all non-duplicate messages in its buffer, mBufferi. The receipt of Finisheds messages from all Ps processes confirms that Pi has received all expected messages, with duplicates discarded. Pi then waits to receive Readys from every other Ps, ensuring that every Survivor Ps, has received the messages sent by Pi. At this point, all messages in mBufferi are stable and can be totally ordered. If there are Joiners (defined as incoming members of G’ that were not part of the previous group (Gprev) but joined G’ after recovering from an earlier crash), the Lead Survivor sends its checkpoint state and TO_Queue to each Pj in the set of NewComer(G’), allowing them to catch up with the Survivors(G). Following this, all Survivors(G) resume TO delivery in Gprev. Pi then sends a completedi message to every process in G, indicating that it has finished TO-delivering in Gprev. Each Survivor waits to receive a completedk message from every other Pk in G before resuming DCTOP operations in the new G’. The Joiners, after replicating the Lead Survivor’s checkpoint state, also performed the TO delivery of messages in Gprev and then resumed operations in the new G’ of the DCTOP. Hence, at the conclusion of the membership change procedure, all buffers and queues are emptied, ensuring that all messages from Gprev have been fully processed.
3.5. Proof of Correctness
Lemma 1 (VALIDITY).
If any correct process uniformly total order Multicasts (utoMulticasts) a message m, then it will eventually uniformly total order Deliver m. For brevity, the term “uto” is used as a prefix in all related procedures, e.g., utoMulticast and utoDeliver.
Proof.
Let be a correct process and let mi be a message sent by . This message is added to mBufferi (Line 15 of Figure 5). There are two cases to consider:
Case 1:
Presence of membership change. If there is a membership change, will be in Survivor(G) since is a correct process. Consequently, the membership changes ensure that will deliver all messages stored in its mBufferi, TO_Queuei, or GCQi, including mi (Line 32 to 44 of Figure 5). Thus, utoDelivers message mi that it sent.
Case 2: No membership changes.
When there is no membership change, all the processes within the DCTOP system including the mi_origin will eventually deliver mi after setting mi to be stable (Line 28 of Figure 5). This happens because, when the timestamp sets mi_flag=false and sends mi to its CNi, it deposits a copy of mi to its mBufferi and sets LCi > mi_ts afterwards. The message is forwarded along the ring network until the ACNi receives mi. Any process that receives mi deposits a copy of it into their mBuffer and sets LC > mi_ts. It also checks if Hopsi,j ≥ f; if so, then mi is crashproof and it sets mi_flag=true. The ACNi sets mi to be stable (Line 28 of Figure 5) and crashproof (Line 20 of Figure 5) at ACNi, transfers mi to DQ, and then it attempts to utoDeliver mi (Lines 1 to 8 of Figure 4) if mi is at the head of DQ. ACNi generates timestamp µ(mi) using its LC, and then sends it to its CN. Similarly, µ(mi) is forwarded along the ring (Line 31 of Figure 5) until the ACN of µ(mi)_origin receives µ(mi). When any process receives µ(mi) and Hopsi,j < f, it knows that mi is crashproof and stable, but, if Hopsi,j ≥ f, then mi is only stable because mi is already known to be crashproof since at least f+1 processes had already received mi. Any process that receives µ(mi) transfers mi from mBuffer to DQ and then attempts to utoDeliver mi if mi is at the head of DQ. Suppose Pk sends mk before receiving mi, . Consequently, ACNi will receive mk before it receives mi and, thus, before sending µ(mi) for mi. As each process forwards messages in the order in which it receives them, we know that will necessarily receive mk before receiving µ(mi) for message mi.
- (a)
- If mi_ts = mk_ts, then orders mk before mi in mBufferi since (this study assumed that, when messages have an equal timestamp, the message from a higher origin is ordered before the message from a lower origin.). When receives µ(mi) for message mi, it transfers both messages to DQ and can utoDeliver both messages, mk before mi, because TS is already known to be stable because of TS equality.
- (b)
- If mi_ts < mk_ts, then orders mi before mk in mBufferi. When receives µ(mi) for message mi, it transfers both messages to DQ and can utoDeliver mi only since it is stable and is at the head of DQ. will eventually utoDeliver mk when it receives µ(mk) for mk since it is now at the head of DQ after mi delivery.
- (c)
- Option (a) or (b) is applicable in any other processes within the DCTOP system since there are no membership changes. Thus, if any correct process sends a message m, then it eventually delivers m.
Note that, if f + 1 processes receive a message m, then m is crashproof, and, during the concurrent multicast, TS can become stable quickly, making m to be delivered even before the ACN of the m_origin receives m. □
Lemma 2 (INTEGRITY).
For any message m, any process Pk utoDelivers m at most once, and only if m was previously utoMulticast by some process
.
Proof.
The crash failure assumption in this study ensures that no false message is ever utoDelivered by a process. Thus, only messages that have been utoMulticast are utoDelivered. Moreover, each process maintains an LC, which is updated to ensure that every message is delivered only once. The sending rule ensures that messages are sent with an increasing timestamp by any process , and the receive rule ensures that the LC of the receiving process is updated after receiving a message. This means that no process can send any two messages with equal timestamps. Hence, if there is no membership change, Lines 16 and 19 of Figure 5 guarantee that no message is processed twice by process Pk. In the case of a membership change, Line 3a(ii) of Figure 6 ensures that process Pk does not deliver messages twice. Additionally, Lines 7(i–iv) of Figure 6 ensure that Pk’s variables such as the logical and stability clock are set to zero, and the buffer and queues are emptied after a membership change. This is carried out because the processes had already delivered all the messages of the old group, discarding message duplicates (Line 3a(ii) of Figure 6) to the application process, and no messages in the old group will be delivered in the new group. Thus, after a membership change, the new group is started as a new DCTOP operation. The new group might contain messages with the same timestamp as those in the old group, but these messages are distinct from those in the old group. Since timestamps are primarily used to maintain message order and delivery, they do not hold significant meaning for the application process itself. This strict condition ensures that messages already delivered during the membership change procedure are not delivered again in the future. □
Lemma 3 (UNIFORM AGREEMENT).
If any process utoDelivers any message m in the current G, then every correct process in the current G eventually utoDelivers m.
Proof.
Let mi be a message sent by process and let be a process that delivered mi in the current G.
Case 1:
delivered mi in the presence of a membership change.
delivered mi during a membership change. This means that had mi in its mBufferi, TO_Queuei, or GCQi before executing Line 6a(ii) of Figure 6. Since all correct processes exchange their mBufferi, TO_Queuei, and GCQi during the membership change procedure, we are sure that all correct processes that did not deliver mi before the membership change will have it in their mBufferi, TO_Queuei, or GCQi before executing Line 1 to 9 of Figure 6. Consequently, all correct processes in the new G’ will deliver mi.
Case 2:
delivered mi in the absence of a membership change.
The protocol ensures that mi does a complete cycle around the ring before being delivered by : indeed, can only deliver mi after it knows that mi is crashproof and stable, which either happens when it is the ACNi in the ring or when it receives µ(mi) for message mi. Remember that processes transfer messages from their mBuffer to DQ when the messages become stable. Consequently, all processes stored mi in their DQ before delivered it. If a membership change occurs after delivered mi and before all other correct processes delivered it, the protocol ensures that all Survivor(G) that did not yet deliver mi will do it (Line 6a(ii) of Figure 6). If there is no membership change after delivered mi and before all other processes delivered it, the protocol ensures that µ(mi) for mi will be forwarded around the ring, which will cause all processes to set mi to be crashproof and stable. Remember, when any process receives µ(mi) and Hopsi,j < f, it knows that mi is crashproof and stable, but, if Hopsi,j ≥ f, then mi is only stable because mi is already known to be crashproof since at least f+1 processes had already received mi. Each correct process will thus be able to deliver mi as soon as mi is at the head of DQ (Line 3 of Figure 4). The protocol ensures that mi will become first eventually. The reasons are the following: (1) the number of messages that are before mi in DQ of every process Pk is strictly decreasing, and (2) all messages that are before mi in DQ of a correct process Pk will become crashproof and stable eventually. The first reason is a consequence of the fact that, once a process Pk sets message mi to be crashproof and stable, it can no longer receive any message m such that m ≺ mi. Indeed, a process Pc can only produce a message mc ≺ mi before receiving mi. As each process forwards messages in the order in which it received them, we are sure that the process that will produce an µ(mi) for mi will have first received mc. Consequently, every process setting mi to be crashproof and stable will have first received mc. The second reason is a consequence of the fact that, for every message m that is utoMulticast in the system, the protocol ensures that m and µ(m) will be forwarded around the ring (Lines 25 and 31 of Figure 5), implying that all correct processes will mark the message as crashproof and stable. Consequently, all correct processes will eventually deliver mi. □
Lemma 4 (TOTAL ORDER).
For any two messages m and , if any process utoDelivers m without having delivered , then no process utoDelivers before m.
Suppose that deduces the stability of TS, , for the first time by (i) above at, say, time t, that is, by receiving m, and , at time t. cannot have any , in its at time t nor will it ever have at any time after t.
Proof (By Contradiction).
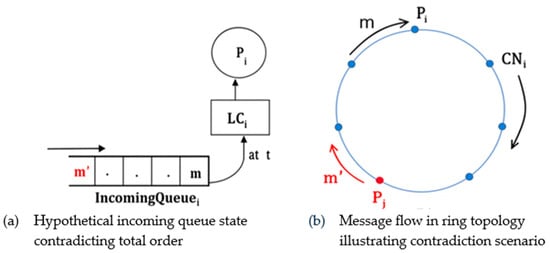
Assume, contrary to Lemma, that is to receive , , after t as shown in Figure 7a.

Figure 7.
Example contradicting Lemma 1.
Case 1:
Let . Therefore, imagine that is the same as ,
, as shown in Figure 7b. Given that , must be true when . Therefore, must have sent first and then .
Note the following:
- (a)
- The link between any pair of consecutive processes in the ring maintains FIFO;
- (b)
- Processes forward messages in the order they received those messages.
Therefore, it is not possible for to receive after it received m, that is, after t. Therefore, case 1 cannot exist.
Case 2:
Imagine that is from and is from , , as shown in Figure 7b. Since is the last process to receive m in the system, must have received m before t; since , could not have sent after receiving m. Therefore, the only possibility for to hold is as follows: must form and send before it is received and forwarded m. For the cases of (a) and (b) in case 1, must receive before m. Therefore, the assumption made contrary to Lemma 1 cannot be true. Thus, Lemma 1 is proven. □
4. Fairness Control Environment
In this section, the DCTOP fairness mechanism was discussed: for a given round k, any process either sends its own message to the or forwards messages from its to the . A round is defined as follows: for any round k, every process sends at most one message, m, to its and also receives at most one message, m, from its in the same round. Every process has an which contains the list of all messages received from the which was sent by other processes, and a . The consists of the messages generated by the process waiting to be transmitted to other processes. When the is empty, the process forwards every message in its but, whenever the is not empty, a rule is required to coordinate the sending and forwarding of messages to achieve fairness. Suppose that process has one or more message(s) to send stored in its , it follows these rules before sending each message in its to the : process sends exactly one message in to the if
- (1)
- the is empty, or
- (2)
- the is not empty and either:
- (2.1)
- had forwarded exactly one message originating from every other process, or
- (2.2)
- the message at the head of the originates from a process whose message the process had already forwarded.
To implement these rules and verify rules 2.1 and 2.2, a data structure called forwardlist was introduced. The at any time consists of the list of the origins of the messages that process forwarded ever since it last sent its own message. Obviously, by definition, as soon as the process sends a message, the is empty. Therefore, if forwards a message that originates from the process ,, which was initially in its , then process will contain the process in its forward list, and, whenever it sends a message, the process will be deleted from the .
5. Experiments and Performance Comparison
This section presents a performance comparison of the DCTOP protocol against the LCR [9] protocol and Raft [17,18], a widely implemented, leader-based ordering protocol, by evaluating the latency and throughput across varying numbers of messages transmitted within the cluster environment. A Java (OpenJDK-17, Java version 17.02) framework was used to run a discrete event simulation for the protocols with at most nine processes,. Every simulation method made use of a common PC with a 3.00 GHz 11th Gen Intel(R) Core (TM) i7-1185G7 Processor and 16 GB of RAM. A request is received from the client by each process, which then sends the request as a message to its neighbour on the ring-based network. When one process receives a message, it forwards the message to another process, continuing this pattern until all processes have received the message. When the ACN of the message origin receives the message, then it knows that it is stable and tries to deliver it, a process known as uniform total order delivery [42]. The process then uses an acknowledgement called a µ-message to notify all other processes of the message’s stability, which they were previously unaware of. Other processes that receive this acknowledgement recognise the message’s stability and endeavour to ensure its delivery in total order. For a Raft cluster, when a client sends a request to the leader, the leader adds the command to its local log, then sends a message to follower processes to replicate the entry. Once a majority (including the leader) confirms replication, the entry is committed. The leader then applies the command to its state machine for execution, notifies followers to do the same, and responds to the client with the output of execution.
The time between successive message transmissions is modelled as an exponential distribution with a mean of 30 milliseconds, reflecting the memoryless property of this distribution, which is well-suited for representing independent transmission events. The delay between the end of one message transmission and the start of the next is also assumed to follow an exponential distribution, with a mean of 3 milliseconds, to realistically capture the stochastic nature of network delays. For the simulation, process replicas are assumed to have 100% uptime, as crash failure scenarios were not considered. Additionally, no message loss is assumed, meaning every message sent between processes is successfully delivered without failure. The simulations were conducted with a varying number of process replicas, such as four, five, seven, and nine processes. The arrival rate of messages follows a Poisson distribution with an average of 40 messages per second, modelling the randomness and variability commonly observed in real-world systems. The simulation duration ranges from 40,000 to 1,000,000 s. This extended period is chosen to ensure the system reaches a steady state and to collect sufficient data for a 95% confidence interval analysis. The long duration also guarantees that each process sends and delivers between one million (1 Mega (×106)) and twenty-five million (25 Mega (×106)) messages.
Latency: These order protocols calculate latency as the time difference between a process’s initial transmission of a message m and the point at which all m destinations deliver m in total order to the applications process. For illustration, let t0 represent the time when process P0 sends a message to its CN0, and let t1 denote the time when the final process in the cluster (e.g., P2 in a four-node setup) delivers that same message. The latency for that message is, therefore, defined as (t1 − t0), representing the maximum delivery time observed. The average of such maximum latencies, computed across 1 to 25 million messages, was then calculated and repeated 10 times to obtain a 95% confidence interval. The average maximum latency was plotted against the number of messages sent by each process.
Throughput: The throughput is calculated as the average number of total order messages delivered (aNoMD) by any process during the simulation time calculated, like latencies, with a 95% confidence interval. Similarly, to the latency, we also determined a 95% confidence interval for the average maximum throughput. Additionally, we presented the latency enhancements offered by the proposed protocol in comparison to LCR, as well as the throughput similarities. Nevertheless, all experiments were carried out independently to prevent any inadvertent consequences of running multiple experiments simultaneously. All processes were configured to send and receive an equal number of messages at uniform transmission intervals, ensuring a balanced message distribution and adherence to the fairness control mechanism during simulation. For this preliminary validation, failure and fault models are left out to focus on verifying the DCTOP’s key features and order consistency during controlled asynchronous communication. The Discrete Event Simulation framework monitors the flow of messages, their timestamps, and when stability is reached, all without external disruptions. Once the protocol’s correctness is validated, future evaluations in cloud environments will explore how it handles failures, message loss, and scalability. In Figure 8 and Figure 9, the Y axis indicates latency measured in seconds, and the X axis is rescaled to mega (×106) for clarity.
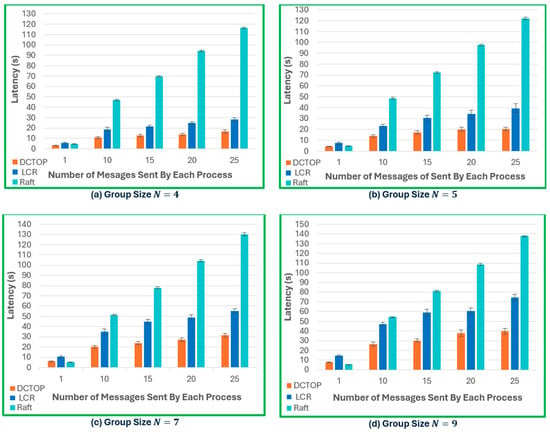
Figure 8.
Latency comparison of Raft, LCR and DCTOP protocols under varying message load and group sizes (N = 4, 5, 7, and 9).
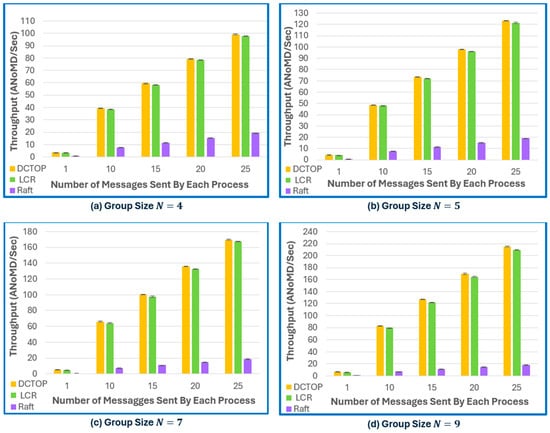
Figure 9.
Throughput comparison of Raft, LCR, and DCTOP protocols under varying message load and group sizes (N = 4, 5, 7, and 9).
Results and Discussion
As shown in Figure 8a–d, the latency trends for the DCTOP, LCR, and Raft across increasing group sizes (N = 4, 5, 7, and 9) and message volumes reveal distinct performance characteristics. The DCTOP consistently exhibits the lowest latency across all configurations. This efficiency stems from its use of Lamport logical clocks for the lightweight sequencing of concurrent messages, the dynamic assignment of a unique last process for each message originator, and a relaxed crash-failure assumption that enables faster message stabilisation and delivery. LCR shows a moderately higher latency, which increases with both the group size and message load. This behaviour can be attributed to its reliance on the vector timestamp, whose dimensionality scales with the number of processes, and the use of a globally fixed last process for concurrent message ordering. Together, these design choices introduce larger message headers and a higher coordination overhead, particularly in larger groups. Raft, as a leader-based protocol, consistently incurs the highest latency, especially under heavier loads. The centralisation of log replication and client handling at the leader creates a sequential processing bottleneck, which limits the responsiveness as the system load grows. However, under lower traffic conditions (e.g., 1 million messages per process), Raft performs competitively and, in configurations with N = 7 (see Figure 8c) and N = 9 (see Figure 8d), even outperforms the DCTOP and LCR. This suggests that Raft may remain suitable in low-load or moderately scaled environments.
In terms of the throughput as illustrated in Figure 9a–d, the DCTOP and LCR outperform Raft across all group sizes and message volumes. The DCTOP and LCR are leaderless ring-based order protocols that benefit from a decentralised execution, enabling all processes to concurrently receive and process client requests. This distributed handling results in a cumulative throughput that almost scales linearly with group size. In contrast, Raft centralises all client communication and log replication at a single leader. This architectural bottleneck constrains the throughput to the leader’s processing capacity, causing performance to saturate under higher loads. Among the leaderless protocols, the DCTOP achieves the highest throughput, followed closely by LCR, which incurs a small overhead due to its vector timestamp management and centralised ordering logic. Raft consistently exhibits the lowest throughput, and its performance plateaus with increasing load, reinforcing the inherent scalability limitations of leader-based protocols in high-throughput environments. Notably, all three protocols—Raft, LCR, and the DCTOP—were implemented from a unified code base, differing only in protocol-specific logic. The experiments were conducted under identical evaluation setups and hardware configurations, ensuring a fair and unbiased comparison. In summary, these findings indicate that decentralised, leaderless architectures such as the DCTOP and LCR achieve a higher scalability and throughput efficiency relative to leader-based consensus protocols like Raft.
6. Conclusions
In this study, we introduced the DCTOP, a novel ring-based and leaderless total order protocol that extends the classical LCR approach through three innovations: the integration of Lamport logical clocks for concurrent message sequencing, a dynamic last-process identification mechanism, and a relaxed crash failure assumption. Together, these mechanisms significantly reduced the message latency and improved fairness in distributed message ordering. The simulation results across group sizes (N = 4, 5, 7, and 9) demonstrated that the DCTOP achieves an over 43% latency improvement compared to LCR under concurrent message loads, confirming the effectiveness of its design. The inclusion of Raft as a benchmark further emphasised the DCTOP’s scalability advantage in decentralised coordination settings.
Overall, this work establishes the DCTOP as a viable foundation for efficient and fair total order delivery in distributed systems. Future work will extend this study to large-scale, fault-tolerant cloud environments to evaluate the performance under realistic failure conditions and dynamic workloads.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/digital5040064/s1.
Author Contributions
Conceptualization, A.E.; methodology, A.E.; software, A.E.; validation, A.E. and C.I.N.; formal analysis, A.E.; investigation, A.E., J.N.O.; resources, A.E.; data curation, A.E.; writing—original draft preparation, A.E.; writing—review and editing, C.I.N., E.A.E., J.N.O.; visualization, A.E.; supervision, C.I.N.; project administration, E.A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LCR | Logical Ring and Ring Protocol |
| DCTOP | Daisy Chain Total Order Protocol |
| VC | Vector Clock |
| LC | Logical Clock |
| TO | Total Order |
| TS | Timestamp Stability |
| The set of processes in a ring | |
| CN | Clockwise Neighbour |
| ACN | Anti-Clockwise Neighbour |
| SC | Stability Clock |
| DQ | Delivery Queue |
| GCQ | Garbage Collection Queue |
| FIFO | First In First Out |
| BFT | Byzantine Fault Tolerance |
| FSR | Fixed Sequence Ring |
References
- Choudhury, A.; Garimella, G.; Patra, A.; Ravi, D.; Sarkar, P. Crash-tolerant consensus in directed graph revisited. In International Colloquium on Structural Information and Communication Complexity; Springer International Publishing: Cham, Switzerland, 2018; pp. 55–71. [Google Scholar] [CrossRef]
- Pease, M.; Shostak, R.; Lamport, L. Reaching agreement in the presence of faults. J. ACM (JACM) 1980, 27, 228–234. [Google Scholar] [CrossRef]
- Vollset, E.W.; Ezhilchelvan, P.D. Design and performance-study of crash-tolerant protocols for broadcasting and reaching consensus in manets. In Proceedings of the 24th IEEE Symposium on Reliable Distributed Systems, Orlando, FL, USA, 26–28 October 2005; pp. 166–175. [Google Scholar]
- Correia, M.; Ferro, D.G.; Junqueira, F.P.; Serafini, M. Practical hardening of crash-tolerant systems. In Proceedings of the 2012 USENIX Conference on Annual Technical Conference, Boston, MA, USA, 13–15 June 2012; pp. 453–466. [Google Scholar]
- Ezhilchelvan, P.D.; Macedo, R.A.; Shrivastava, S.K. Newtop: A fault-tolerant group communication protocol. In Proceedings of the 15th International Conference on Distributed Computing Systems, Vancouver, BC, Canada, 30 May–2 June 1995; pp. 296–306. [Google Scholar] [CrossRef]
- Wiesmann, M.; Pedone, F.; Schiper, A.; Kemme, B.; Alonso, G. Understanding replication in databases and distributed systems. In Proceedings of the 20th IEEE International Conference on Distributed Computing Systems, Taipei, Taiwan, 10–13 April 2000; pp. 464–474. [Google Scholar] [CrossRef]
- Helal, A.A.; Heddaya, A.A.; Bhargava, B.B. Replication Techniques in Distributed Systems; Springer Science & Business Media: Boston, MA, USA, 2006. [Google Scholar]
- Défago, X.; Schiper, A.; Urbán, P. Total order broadcast and multicast algorithms: Taxonomy and survey. ACM Comput. Surv. (CSUR) 2004, 36, 372–421. [Google Scholar] [CrossRef]
- Guerraoui, R.; Levy, R.R.; Pochon, B.; Quéma, V. Throughput optimal total order broadcast for cluster environments. ACM Trans. Comput. Syst. (TOCS) 2010, 28, 1–32. [Google Scholar] [CrossRef]
- Guerraoui, R.; Levy, R.R.; Pochon, B.; Quema, V. High Throughput Total Order Broadcast for Cluster Environments. In Proceedings of the International Conference on Dependable Systems and Networks (DNS’06), Philadelphia, PA, USA, 25–28 June 2006; pp. 549–557. [Google Scholar] [CrossRef]
- Junqueira, F.; Reed, B. ZooKeeper: Distributed Process Coordination; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2013. [Google Scholar]
- Hunt, P.; Konar, M.; Junqueira, F.P.; Reed, B. ZooKeeper: Wait-free Coordination for Internet-scale Systems. In Proceedings of the 2010 USENIX Conference on USENIX Annual Technical Conference (USENIXATC’10), Boston, MA, USA, 23–25 June 2010. [Google Scholar]
- Burrows, M. The Chubby lock service for loosely-coupled distributed systems. In Proceedings of the 7th Symposium on Operating Systems Design and Implementation (OSDI ‘06), Seattle, WA, USA, 6–8 November 2006; pp. 335–350. [Google Scholar]
- Pu, J.; Gao, M.; Qu, H. SimpleChubby: A Simple Distributed Lock Service. Available online: https://www.scs.stanford.edu/14au-cs244b/labs/projects/pu_gao_qu.pdf (accessed on 31 May 2024).
- Lamport, L. Paxos made simple. In ACM SIGACT News (Distributed Computing Column) 32, 4 (Whole Number 121, December 2001); ACM: New York, NY, USA, 2001; pp. 51–58. [Google Scholar]
- Liskov, B.; Cowling, J. Viewstamped Replication Revisited. MIT Technical Report MIT-CSAIL-TR-2012-021. 2012. Available online: https://dspace.mit.edu/handle/1721.1/71763 (accessed on 7 April 2024).
- Ongaro, D.; Ousterhout, J. In Search of an Understandable Consensus Algorithm (Extended Version). Tech Report. May 2014. Available online: https://raft.github.io/raft.pdf (accessed on 6 June 2024).
- Ongaro, D.; Ousterhout, J. In search of an understandable consensus algorithm. In Proceedings of the 2014 USENIX Conference on USENIX Annual Technical Conference (USENIX ATC’14), Philadelphia, PA, USA, 19–20 June 2014; pp. 305–319. [Google Scholar]
- Ejem, A.; Ezhilchevan, P. Design and performance evaluation of raft variations. In Proceedings of the 39th Annual UK Performance Engineering Workshop (2023), Birmingham, UK, 7–8 September 2023. [Google Scholar]
- Lamport, L. Fast Paxos. Distrib. Comput. 2006, 19, 79–103. [Google Scholar] [CrossRef]
- Biely, M.; Milosevic, Z.; Santos, N.; Schiper, A. S-paxos: Offloading the leader for high throughput state machine replication. In Proceedings of the 2012 IEEE 31st Symposium on Reliable Distributed Systems, Irvine, CA, USA, 8–11 October 2012; pp. 111–120. [Google Scholar] [CrossRef]
- Moraru, I.; Andersen, D.G.; Kaminsky, M. There is more consensus in Egalitarian parliaments. In Proceedings of the 24th ACM Symposium on Operating Systems Principles, Farminton, PA, USA, 3–6 November 2013; pp. 358–372. [Google Scholar] [CrossRef]
- Yin, M.; Malkhi, D.; Reiter, M.K.; Gueta, G.G.; Abraham, I. HotStuff: BFT consensus with linearity and responsiveness. In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing (PODC ’19), Toronto, ON, Canada, 29 July–2 August 2019; pp. 347–356. [Google Scholar] [CrossRef]
- Stathakopoulou, C.; David, T.; Pavlovic, M.; Vukolić, M. Mir-BFT: Scalable and Robust BFT for Decentralized Networks. J. Syst. Res. 2022, 2, 1–34. [Google Scholar] [CrossRef]
- Guo, B.; Lu, Z.; Tang, Q.; Xu, J.; Zhang, Z. Dumbo: Faster asynchronous BFT protocols. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security (CCS ’20), Virtual Event, USA, 9–13 November 2020; pp. 803–818. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, Y.; Lu, Z.; Tang, Q.; Xu, J.; Zhang, Z. Dumbo-NG: Fast asynchronous BFT consensus with throughput-obliv ious latency. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security (CCS ’22), Los Angeles, CA, USA, 7–11 November 2022; pp. 1187–1201. [Google Scholar] [CrossRef]
- Monti, M.; Camaioni, M.; Roman, P.-L. Fast Leaderless Byzantine Total Order Broadcast. arXiv 2024, arXiv:2412.14061. Available online: https://arxiv.org/abs/2412.14061 (accessed on 17 October 2025). [CrossRef]
- Mao, C.; Golab, W.; Wong, B. Antipaxos: Taking interactive consistency to the next level. J. Parallel Distrib. Comput. 2024, 187, 104839. [Google Scholar] [CrossRef]
- Stathakopoulou, C.; Wei, M.; Yin, M.; Zhang, H.; Malkhi, D. BBCA-LEDGER: High throughput consensus meets low latency. arXiv 2023, arXiv:2306.14757. Available online: https://arxiv.org/abs/2306.14757 (accessed on 17 October 2025). [CrossRef]
- Marandi, P.J.; Primi, M.; Schiper, N.; Pedone, F. Ring Paxos: A high-throughput atomic broadcast protocol. In Proceedings of the 2010 IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Chicago, IL, USA, 28 June–1 July 2010; pp. 527–536. [Google Scholar] [CrossRef]
- van Renesse, R.; Schneider, F.B. Chain replication for supporting high throughput and availability. In Proceedings of the 6th USENIX Symposium on Operating Systems Design and Implementation (OSDI’04), San Francisco, CA, USA, 6–8 December 2004; p. 7. [Google Scholar]
- Whittaker, M.; Giridharan, N.; Szekeres, A.; Hellerstein, J.M.; Stoica, I. Bipartisan Paxos: A Modular State Machine Replication Protocol. arXiv 2020, arXiv:2003.00331. Available online: https://arxiv.org/abs/2003.00331 (accessed on 19 October 2025). [CrossRef]
- Bianco, A.; Cuda, D.; Finochietto, J.M. Short-Term Fairness in Slotted WDM rings. Comput. Netw. 2015, 83, 235–248. [Google Scholar] [CrossRef]
- Ejem, A.; Njoku, C.N.; Uzoh, O.F.; Odii, J.N. Queue Control Model in a Clustered Computer Network using M/M/m Approach. Int. J. Comput. Trends Technol. (IJCTT) 2016, 35, 12–20. [Google Scholar] [CrossRef]
- Fischer, M.J.; Lynch, N.A.; Paterson, M.S. Impossibility of distributed consensus with one faulty process. J. ACM 1985, 32, 374–382. [Google Scholar] [CrossRef]
- Lamport, L. The Part-Time Parliament. ACM Trans. Comput. Syst. 1998, 16, 133–169. [Google Scholar] [CrossRef]
- Kreps, J.; Narkhede, N.; Jun, R. Kafka: A Distributed Messaging System for Log Processing. In Proceedings of the NetDB 2011, Athens, Greece, 12 June 2011; Volume 11, pp. 1–7. Available online: https://classpages.cselabs.umn.edu/Spring-2018/csci8980/Papers/PublishSubscribe/Kafka.pdf (accessed on 6 November 2025).
- Zhang, I.; Sharma, N.K.; Szekeres, A.; Krishnamurthy, A.; Ports, D.R.K. Building Consistent Transactions witInconsistent Replication. ACM Trans. Comput. Syst. (TOCS) 2018, 35, 1–37. [Google Scholar] [CrossRef]
- Chandy, K.M.; Lamport, L. Distributed snapshots: Determining global states of distributed systems. ACM Trans. Comput. Syst. (TOCS) 1985, 3, 63–75. [Google Scholar] [CrossRef]
- Birman, K.; Joseph, T. Exploiting virtual synchrony in distributed systems. In Proceedings of the Eleventh ACM Symposium on Operating Systems Principles, Austin, TX, USA, 8–11 November 1987; pp. 123–138. [Google Scholar] [CrossRef]
- Amir, Y.; Stanton, J. The Spread Wide Area Group Communication System; Technical Report: CNDS 98-4; Johns Hopkins University, Center for Networking and Distributed Systems: Baltimore, MD, USA, 1998. [Google Scholar]
- Vicente, P.; Rodrigues, L. An indulgent uniform total order algorithm with optimistic delivery. In Proceedings of the 21st IEEE Symposium on Reliable Distributed Systems, 2002. Proceedings, Suita, Japan, 13–16 October 2002; pp. 92–101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).