Abstract
Optimizing tourist routes is a critical challenge in smart tourism, which aims to enhance the visitor experience while optimizing practical parameters. However, traditional routing algorithms often fail to provide personalized and efficient itineraries in complex real-world environments. This study aims to develop a hybrid framework that integrates Simulated Annealing for global route optimization with the A algorithm* for accurate local pathfinding, leveraging geographic data from OpenStreetMap. The proposed method computes the shortest paths between all Points of Interest using A*, constructing a comprehensive distance matrix, and applying Simulated Annealing to determine the most efficient visiting sequence. The framework was evaluated in the Old Medina of Fez, Morocco, demonstrating its effectiveness in generating realistic and efficient itineraries. Compared to alternative strategies such as Genetic Algorithms, the hybrid approach achieves superior computational efficiency and produces better routes in terms of travel distance. These findings highlight the practical applicability of the framework as a modular service for smart tourism applications, offering tourists and tourism platform developers a scalable solution for personalized and sustainable itinerary planning.
1. Introduction
Tourism, a pillar of worldwide cultural exchange and economic development, is expanding at an exponential rate. As tourists seek new and immersive experiences, the need for efficient and customized tourism routes continues to increase [1]. It is a complicated problem to create itineraries that combine attraction discovery, minimize travel time, and conform to practical constraints. To address this complexity, this study introduces an innovative framework that integrates metaheuristic and heuristic optimization methods with accurate spatial data.
The importance of optimizing tourist routes extends beyond basic convenience; it includes enriching tourists’ experiences, mitigating environmental impacts, and fueling local economies. Traditional tourism itinerary planning approaches often fall short of delivering routes that mix exploration and efficiency. Therefore, this work aims to close this gap by offering a hybrid method that investigates the various permutations of tourism routes and fine-tunes them to provide optimal travel solutions.
The optimization of tourist routes has attracted significant attention in recent years because of its potential to enhance visitor experiences while addressing constraints such as limited time, accessibility, and environmental impact. Various approaches have been proposed, ranging from classical heuristics to advanced metaheuristic algorithms including genetic algorithms (GAs), ant colony optimization, and simulated annealing (SA) [2,3,4,5]. However, these methods often struggle to accommodate the complexity of real-world urban environments and multicriteria decision making.
More recently, hybrid methods that combine heuristic search algorithms such as A* with metaheuristics have shown promising results in generating more practical and adaptable itineraries [6]. The integration of geographic information systems (GIS) and open-source spatial data, such as OpenStreetMap (OSM), further enriches the applicability of these models by grounding optimization in accurate, context-aware maps [7,8,9].
The goal of this study is not only to propose an abstract optimization algorithm but also to develop a practical framework that can be integrated into existing digital tourism systems to enhance their itinerary planning services. The hypothesis is that combining Simulated Annealing with A* pathfinding, supported by accurate OSM spatial data, will produce itineraries that are more efficient, realistic, and user-oriented than those generated by standalone methods. The object of this research is tourist route optimization, while the subject focuses specifically on designing and testing a hybrid algorithm that integrates metaheuristics, heuristic search, and GIS data.
This framework is designed as a modular service for integration into mobile applications or smart tourism platforms. The stakeholders benefiting from this work include tourism application developers, smart city tourism departments, and tourists, who will gain access to practical, personalized, and efficient itineraries. Beyond its practical significance, its theoretical contribution lies in demonstrating the effective integration of these optimization approaches with spatial data to solve complex real-world problems.
To evaluate this approach, we developed a dedicated experimental environment and compared its performance against alternative optimization strategies, such as Genetic Algorithms, focusing on both the computational efficiency and the quality of the resulting routes, particularly in terms of minimizing the total travel distance. The empirical results validate the relevance of our method, demonstrating its ability to minimize travel time and logistical complexity while maximizing site coverage and the user experience. Furthermore, this work contributes to broader goals in sustainable tourism by promoting intelligent planning and environmentally responsible decision making.
In the following sections, we deconstruct the logic that underpins this approach, analyze the mechanisms of Simulated Annealing and the A* algorithm in the context of tourism route optimization, present experimental findings demonstrating the efficacy of our technique, and explore opportunities for further breakthroughs in this field.
2. Literature Review
Tourist route optimization is a central theme in smart tourism, with the goals of improving travel efficiency, enriching the visitor experience, and supporting sustainable urban planning [1]. In recent years, various heuristic and metaheuristic algorithms have been explored to address this challenge, often relying on well-established combinatorial optimization paradigms. This section reviews the key computational approaches, with particular emphasis on how they have been applied in real-world smart tourism systems and research.
2.1. Travelling Salesman Problem and Smart Tourism
The Travelling Salesman Problem (TSP) remains a foundational model for route optimization [10,11]. Its relevance in tourism is clear; given a list of points of interest (POIs), how can one construct a route that visits each site once with minimal travel cost? In the context of tourism, this problem is enriched by constraints such as opening hours, user preferences, and transportation modes.
In smart tourism systems, the TSP is rarely solved exactly; instead, researchers have proposed various approximations using heuristic and metaheuristic approaches to accommodate real-time and spatial complexities. For example, Gavalas et al. analyzed TSP variants for tour planning by integrating semantic information into points of interest to better reflect user preferences [12]. More recent studies have focused on real-time and context-aware adaptations of the TSP using hybrid metaheuristic algorithms and dynamic data sources to improve itinerary personalization and responsiveness [13,14].
2.2. Genetic Algorithms in Tourism Applications
Genetic Algorithms are widely employed in tourism route optimization because of their ability to explore large search spaces and handle complex constraints [15,16,17]. Several studies have demonstrated their effectiveness in constructing optimal or near-optimal tourist itineraries.
For example, Cao (2022) proposed an improved Genetic Algorithm for optimal round-trip tourism route planning, taking into account factors such as travel time, attraction preferences, and route length [18]. The study demonstrated that the enhanced GA significantly improved route quality and convergence speed compared to traditional methods, making it suitable for generating personalized and efficient tourist itineraries. Gavalas et al. also proposed a mobile recommender system based on GAs to assist tourists in planning visits according to their preferences, accessibility, and real-time location [19].
These applications highlight the flexibility of GAs in smart tourism, particularly when they are combined with spatial databases and context-aware services.
2.3. Simulated Annealing for Urban and Tourism Optimization
Simulated Annealing, known for its robustness in avoiding local optima, has been increasingly applied in tourist route optimization [20]. Its probabilistic nature allows it to explore complex solution spaces, making it particularly useful for cities with intricate pedestrian networks.
Ma et al. (2023) have applied a simulated annealing algorithm to optimize travel routes for tourists in Mudanjiang, China [21]. By modeling the problem as a Traveling Salesman Problem (TSP) with 15 attractions, they aimed to maximize the number of sites visited while minimizing travel distance. Their results demonstrated that simulated annealing effectively solved the TSP, providing tourists with efficient and satisfactory itineraries. Similarly, Qiu et al. (2023) integrated simulated annealing with genetic algorithms to optimize urban travel routes by intelligently selecting destinations and sequencing visits on the basis of user preferences and geographic constraints [22]. These studies highlight the potential of simulated annealing and hybrid metaheuristics for adaptive and efficient tourist itinerary planning in smart cities.
2.4. Pathfinding with A* Algorithm in Tourism Services
The A* algorithm is extensively used in geographic information systems and tourism-related applications because of its efficiency in finding optimal paths between POIs [23,24]. Its deterministic search strategy makes it particularly suitable for integration into real-time navigation systems.
Stefanov et al. (2023) developed a mobile application prototype for cultural tourism that incorporates the A* algorithm for route calculation, along with features such as opening hours, intuitive design, and easy access to tourist and cultural sites [25]. Their approach aimed to meet the needs and preferences of contemporary users, enhancing the user experience in heritage areas. In a related study, Yudha et al. (2022) applied the A* algorithm to optimize routes to tourist destinations in West Java, demonstrating effective pathfinding capabilities tailored for tourism routing problems [26].
2.5. Hybrid and Real-World Implementations
Several studies have explored hybrid approaches that combine heuristics with metaheuristics. Our own previous work tested two combinations: one integrating genetic algorithms with the Bing Maps API and another with the A* algorithm [8,27]. While the first offered good distance optimization, the execution time was limited by API calls. The second improved performance but still fell short in scalability.
Building on these limitations, our current hybrid framework, which combines simulated annealing and A* with OpenStreetMap data, addresses both route quality and computational efficiency. This approach reflects recent trends in the field, where hybrid methods increasingly integrate heuristic algorithms such as A* with metaheuristic strategies to develop adaptive and efficient travel planning systems. These combinations aim to improve route optimization by leveraging the strengths of both precise pathfinding and global search methods within modular and flexible platforms for tourism decision support.
3. Methods
3.1. Data Sources
With the aim of crafting efficient and personalized tourist circuits, we introduce an approach founded on three key components: the GIS platform OpenStreetMap, the A* algorithm, and the simulated annealing method.
In the first step of our suggested methodology, we import data from OSM, which serves as an enormous repository of geographic data. This information contains specifics about various points of interest, road networks, and landmarks. We build a full knowledge graph from this dataset, enabling us to identify connections and relationships between the various geographical components.
We may encounter a problem with intersections after obtaining data from OSM, which has the ability to distort results and misrepresent reality. For example, we find cases in which a path and a bridge look to cross one another, resulting in a false intersection point on the map. In these situations, advising people to turn left or right while remaining on the bridge would be misleading because it does not represent an actual route. We put in place a data management system to address this and similar scenarios involving bridges or underground routes. To do this, the itinerary must be divided and segmented into two or more pathways, resulting in unique nodes (vertices) at the ends of each track. These nodes accurately identify each path between a given starting and destination point.
3.2. Algorithms and Methodologies
We use the A* algorithm to find the shortest and most efficient paths between two points of interest using our knowledge graph as input data. This algorithm offers a flexible method for route calculation, as it may consider many factors, including distance, trip duration, and associated costs. However, in this paper, we focus primarily on considering distance only. We will consider additional constraints and variables in future works.
To demonstrate this procedure in our context, we begin with a departure point and N points of interest that we aim to visit, as well as data for pathways and vertices (nodes). Connecting the POIs that are not immediately on pathways to the nearest path on the map is the first step. This is accomplished by locating the nearest node (vertex) to the POI, creating a straight link, and integrating it into the map to guarantee a fully connected graph. We use the A* algorithm once the graph is closed. This algorithm calculates potential paths between point A and point B through spatial intersection and subsequently identifies the most critical pathway.
After completing the first two steps of our approach, we obtain a distance matrix among all the points of interest. The relationship between each pair of POIs can be determined by this distance matrix, which is a vital representation for providing an overview of spatial connectivity within a study area.
Finally, we use the simulated annealing method to quickly and efficiently generate better routes by minimizing the cumulative travel distance across all selected points of interest. We have the ability to test various route combinations and make adjustments to improve the overall visitor experience via simulated annealing. It uses a starting route and an objective function that takes distance into account. The method creates neighboring routes by permuting destinations during iterations and ranks the quality of each route. On the basis of a probability criterion, it accepts better routes and, occasionally, even bad routes. As it advances, the algorithm increasingly reduces the probability of accepting mediocre routes. This iterative process produces a tourist route that offers the best-found solution, continuing until a predetermined stopping condition is satisfied.
We examine each component and their interactions using an architecture graphic to provide a more comprehensive understanding of the architectural framework of our proposed approach; see Figure 1. This graphical illustration shows how our method effectively generates better and competitive tourist routes by combining the power of a knowledge graph from OpenStreetMap, the A* algorithm, and simulated annealing.
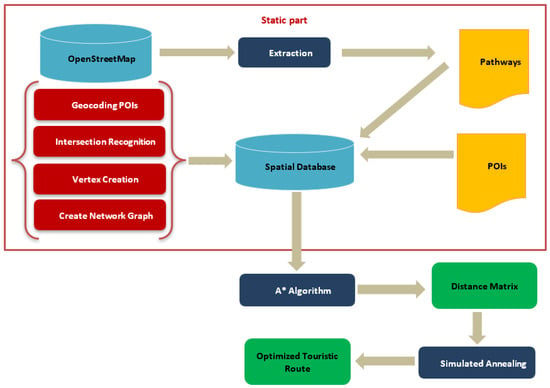
Figure 1.
Architectural framework of the proposed approach.
This visual illustration provides an overview of our approach and how it transforms unprocessed data into customized travel routes.
Furthermore, in this work, we provide a detailed explanation of each step of our algorithm, focusing on the data flow, key decision points, and the calculations involved in route optimization. The proposed method integrates the A* algorithm, a distance matrix, and Simulated Annealing to determine the optimal tourist route. Below, we present an overview of the algorithm’s main steps:
- Step 1: Calculate the shortest path between two Points of Interest using A*
The A* algorithm finds the most efficient path between two locations by exploring different possible routes and choosing the one with the lowest total cost. It calculates the actual cost reaching a point plus an estimate of how far it is from the destination. This helps quickly find the shortest way while avoiding unnecessary detours. In this work, we apply the Algorithm 1 to spatial datasets derived from OpenStreetMap and the selected Points of Interest, enabling realistic and context-aware route planning. In our implementation, the cost used by the A* algorithm corresponds to the geographical distance between nodes, ensuring that the computed paths are the shortest in terms of travel distance.
| Algorithm 1 A* Algorithm used in this work |
|
- Step 2: Build the distance matrix for all Points of Interest
This Algorithm 2 creates a matrix showing the shortest distances between every pair of points. Each pair uses the A* algorithm to find the shortest route. The resulting matrix is then used to evaluate the total travel cost (in terms of distance) of different possible routes.
| Algorithm 2 Function to create the distance matrix |
|
- Step 3: Optimize the tourist route using Simulated Annealing
The Simulated Annealing algorithm (Algorithm 3), which makes use of Algorithm 4, uses different route combinations to find the best overall itinerary. Initially, it accepts suboptimal routes to avoid getting trapped in local optima. Gradually, it becomes more selective and only keeps better routes, resulting in a final best-found route.
| Algorithm 3 Simulated Annealing algorithm |
|
| Algorithm 4 Helper functions for simulated annealing |
|
- Step 4: Generate the best tourist circuit using all the components
This final Algorithm 5 combines the distance matrix and the Simulated Annealing algorithm to generate the best possible route that visits all tourist points efficiently and returns the best-found cost and path for the itinerary.
| Algorithm 5 Generate the best tourist circuit using A* and simulated annealing |
|
3.3. Tools and Implementation Environment
The methodology was implemented using Python 3.9, with custom Python functions for pathfinding and optimization algorithms. PostgreSQL with the PostGIS extension was used for spatial data storage, manipulation, and querying. Tests were conducted on an Intel Core i7 laptop with 8 GB of RAM running Windows 10.
4. Results
To validate our approach, we chose the ancient Medina of Fez, a place rich in historical significance and cultural legacies, to test our method. Nevertheless, the geographical and agglomeration criteria are very complex (see Figure 2). Medina is home to more than 70 points of interest, each of which provides a different window into the history and allure of the city. Additionally, Medina boasts a complex network of pathways consisting of more than 9400 alleyways. This presents a challenging and dynamic environment in which to showcase the capabilities of our tourist route optimization method. By focusing our research on a place with such a diverse and complicated culture, we hope to show how flexible and reliable our method is in a variety of tourist locations.
We carefully selected a group of 15 points of interest from the old Medina of Fez for our next tests, as shown in Table 1. These choices were made with the help of local guides, using information from different applications and surveys, as well as suggestions from reliable websites such as TripAdvisor. Our aim was to cover some of the most captivating and enduring attractions within Medina. These specific POIs are the ones most warmly recalled by tourists following their visit to Fez, making them ideal candidates for our evaluations.

Table 1.
Test POIs.
The latitude and longitude coordinates of the POIs enable us to convert these attribute data into geographical information through geocoding. We subsequently incorporate them into a spatial database.
After this stage, we retrieve the pedestrian pathways within the old Medina of Fez from OpenStreetMap, comprising approximately 3500 nodes and over 5000 alleyway segments. These data are integrated into our spatial database and processed to construct a graph model, where each segment is represented as an edge weighted by real-world distances. Non-pedestrian routes are excluded to accurately reflect actual walking conditions in the Medina.
To ensure data reliability and consistency, we performed a thorough validation and cleaning process before running the optimization algorithms. This included the removal of duplicate or erroneous nodes and verification that all the POIs were properly connected to the pedestrian network. Topological errors such as floating nodes or disconnected pathways were corrected to maintain the integrity of the graph structure.
To guarantee full connectivity between the POIs and the pathway network, an automatic correction process was implemented. Specifically, for POIs not directly located on a pathway, we detected the nearest node within a buffer zone of 1 meter and connected it automatically, which allowed approximately 90% of the POIs to be seamlessly integrated. For POIs located farther than 1 meter from any pathway, we perform manual verification and integration after automatic detection to ensure accurate connections without introducing errors. Regarding the completeness of the pathway data, we relied on the comprehensive pedestrian coverage provided by OpenStreetMap for the Medina of Fez, which benefits from detailed mapping by the community, and focused on validating topological consistency using PostGIS spatial queries. As a final step, we conducted sanity checks and cross-verifications to ensure data integrity and readiness for analysis. After the queries were executed, no discrepancies were found, confirming that the dataset was ready for use.
By building this topologically consistent and detailed pedestrian graph and combining it with accurately geocoded POIs, we created a realistic and navigable spatial model. This comprehensive dataset serves as a robust foundation for validating our hybrid route optimization approach within a complex, culturally rich urban environment.
Below is the map displaying the pathways of the old Medina of Fez, including our points of interest.
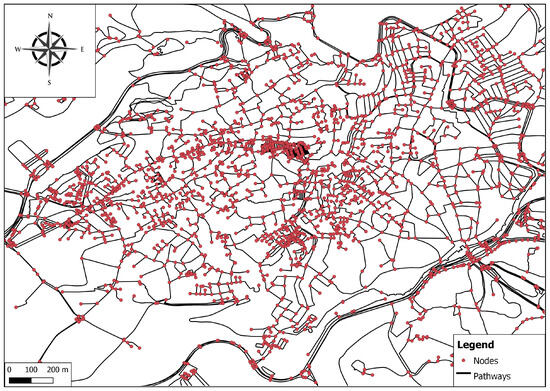
Figure 2.
Graph structures of the Old Medina of Fez.
We started the process by giving the A* algorithm the input data, including the POIs and pathways, and then we performed multiple iterations to find the most efficient path. The chosen heuristic function is the Manhattan distance, given by the following equation:
where and are the coordinates of two POIs.
The simulated annealing method was applied to achieve this. The parameters used to conduct the SA algorithm are listed in Table 2.

Table 2.
The parameters of the simulated annealing algorithm.
These parameter values were defined on the basis of a combination of previous literature and multiple preliminary trials [28,29]. The initial temperature and cooling factor were tested with different values to find a good balance between the solution quality and computational time. A lower cooling factor caused premature convergence, whereas a higher cooling factor extended the runtime unnecessarily. The other parameters were set to commonly accepted ranges for similar route optimization problems [30]. Although a full parameter sensitivity analysis is not included in this paper, the current configuration provided stable and satisfactory results for the tested scenarios.
This method presented satisfying results, with an execution time of less than one second, approximately 0.3 seconds for the longest circuit of 15 POIs and 8.72 km. The results are presented in Table 3.

Table 3.
Results of simulated annealing and A* algorithm.
Snapshots of different suggested circuits are mapped below. In the following Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, each segment of the generated tourist route is displayed in a different color. These colors are used solely for visual differentiation between the segments of the itinerary and do not carry any semantic meaning.
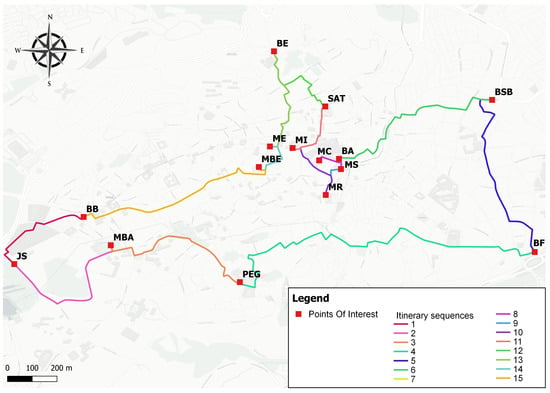
Figure 3.
Itinerary for 15 POIs.
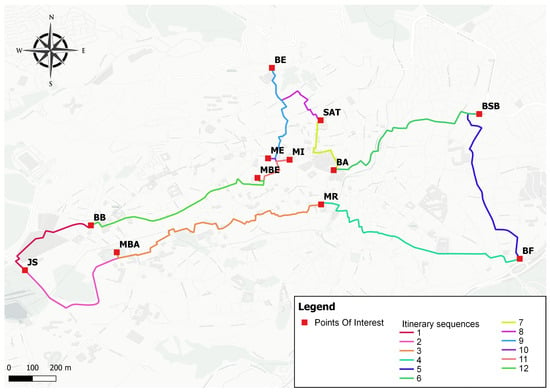
Figure 4.
Itinerary for 12 POIs.
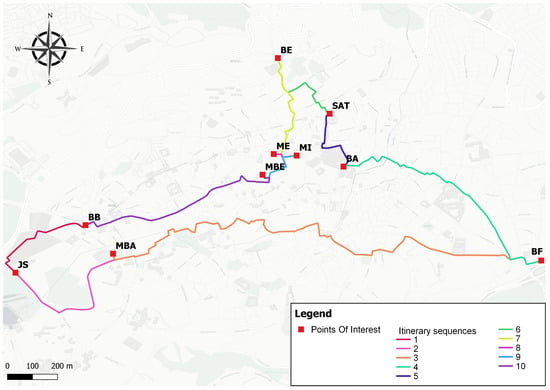
Figure 5.
Itinerary for 10 POIs.
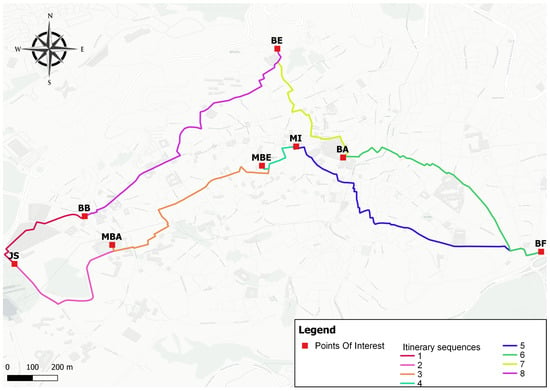
Figure 6.
Itinerary for 8 POIs.
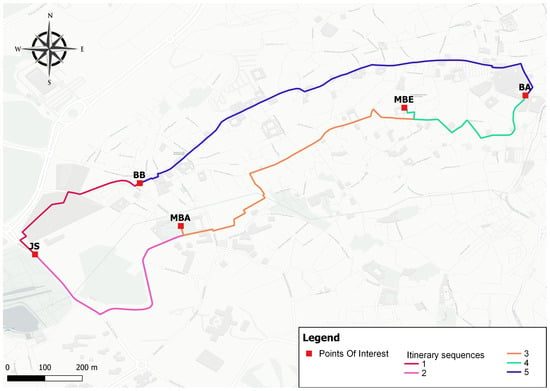
Figure 7.
Itinerary for 5 POIs.
5. Comparison and Discussion
These results are in line with previous work by Qiu et al. (2023) and Pasandi et al. (2021), who also highlighted the effectiveness of hybrid optimization methods for complex problems [22,24]. These studies emphasized that combining metaheuristic strategies can significantly enhance the performance of routing algorithms by balancing exploration and exploitation in complex urban travel scenarios.
However, the results differ from those of other studies that have explored alternative hybrid approaches tailored to route optimization problems in tourism contexts. For example, combinations of traditional shortest path algorithms such as Dijkstra with metaheuristics such as Genetic Algorithms or Ant Colony Optimization have been proposed to enhance route planning under various constraints [31]. While these methods have improved itinerary optimization by integrating spatial data and intelligent search strategies, they often face challenges related to computational scalability and execution time, especially when applied to large-scale or dynamic datasets. Additionally, the majority of these methods do not explicitly consider the computation of cost matrices (such as distance matrices in our case), which can lead to less accurate or suboptimal routing solutions.
This approach also outperforms previous combinatory attempts; we previously combined the Bing Maps API with genetic algorithms in our initial study [27]. Although the initial investigation yielded positive outcomes concerning distance optimization, the overall execution was restricted because of the Bing Maps API execution duration. After that, we improved upon the first attempt by combining the A* algorithm with genetic algorithms in our second contribution [8]. However, the computational time continues to be a major obstacle. Our present work, based on the combination of the A* algorithm and the simulated annealing approach, improves the efficacy and quality of tourist routes by simultaneously addressing execution time and route planning requirements.
To ensure a meaningful and objective comparison, the algorithms selected for evaluation in this study are those we have fully implemented and tested under identical conditions in our previous works. This choice allows for a fair assessment on the basis of consistent datasets and spatial contexts. The aim is not to present an exhaustive benchmark of all available optimization techniques but rather to compare practical solutions using real pedestrian networks and OSM data. Importantly, our comparison includes the total execution time, covering both the distance matrix construction and the optimization itself, an aspect frequently omitted in other studies. This comprehensive comparison allows us to better understand the trade-offs between solution quality and computational efficiency in real-world scenarios.
To further assess the effectiveness of the proposed hybrid approach, we compared its performance with that of two methods from our previous studies: Genetic Algorithms combined with A* and Genetic Algorithms using the Bing Maps API. The results presented correspond to the best execution times observed over 500 generations. The evaluation focuses on two key metrics: the total execution time (in seconds), which already includes the distance matrix computation, and the distance of the resulting route (in kilometers). Table 4 presents the outcomes for different numbers of Points of Interest.

Table 4.
Comparison of execution time and route distance for the three approaches.
The results highlight a significant reduction in execution time achieved by the hybrid SA and A* algorithm, as illustrated in Figure 8. For example, when optimizing a route with 15 POIs, the proposed method completes the task in just 0.270 s, compared to 5.03 s for GA and A* and 31.42 s for the GA and Bing Maps API. This improvement is consistent across all the scenarios, reflecting the scalability and computational efficiency of the proposed method.
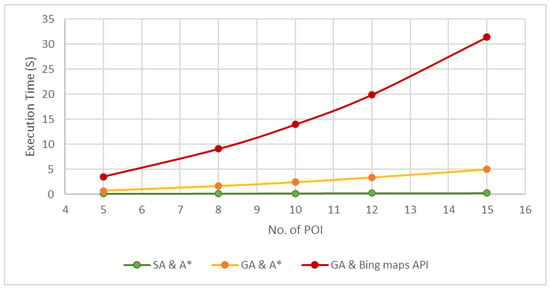
Figure 8.
Execution time comparison of the three approaches.
Regarding route distance, as shown in Figure 9, the proposed approach remains highly performant. While the GA and A* algorithm occasionally achieves marginally shorter routes—such as 8.48 km versus 8.72 km for 15 POIs—the difference is negligible and does not outweigh the considerable gains in computational time. Moreover, the hybrid SA and A* approach consistently outperforms the GA and Bing Maps API in terms of both distance and execution time, confirming its utility for practical applications.
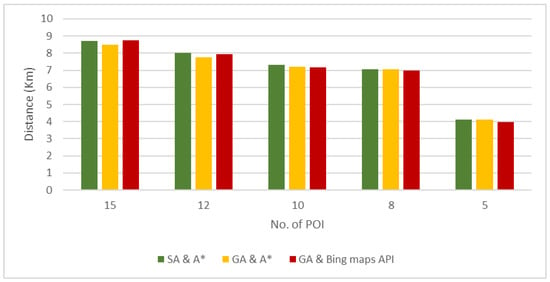
Figure 9.
Route distance comparison of the three approaches.
These findings underscore the performance, scalability, and robustness of the hybrid SA and A* algorithm as the proposed approach for addressing the dual challenges of computational efficiency and route quality. By overcoming the limitations of previous methods, this approach proves to be a powerful tool for real-world tourist route optimization scenarios, offering a compelling balance between speed and accuracy.
While the proposed hybrid optimization method has shown positive results and significant advancements in terms of execution time and other optimization parameters, we still foresee certain areas for improvement. One such opportunity lies in addressing computational complexity, particularly when the method is applied to large-scale problems involving complex geographical constraints. Although the integration of Simulated Annealing and the A* algorithm contributes to generating efficient routes, the method’s performance remains sensitive to initial parameters and configurations. Moreover, the optimization process heavily depends on the quality and completeness of the geographical data, such as those provided by OpenStreetMap.
Another key direction for improvement involves enhancing the system’s adaptability to dynamic conditions, such as real-time pedestrian traffic, sudden pathway closures, or temporary access restrictions. To address this, future research will focus on integrating real-time data sources, such as updated pedestrian access information or crowd density data, enabling the framework to dynamically adjust itineraries during execution. Additionally, combining the current model with incremental optimization techniques or reactive replanning modules could significantly enhance its adaptability and robustness in rapidly changing scenarios. These enhancements evolve the approach from a static planning tool into a dynamic, context-aware pedestrian routing system that is well suited for real-time smart tourism applications.
6. Conclusions
To conclude, the present article introduces a novel method that combines the power of simulated annealing and the accuracy of the A* algorithm to improve tourist experiences and optimize the planning of touristic routes. The results obtained from this integrated methodology underscore its potential to significantly reshape tourist route planning, delivering efficient, tailored, and memorable travel itineraries within the context of Smart Tourism.
This study makes a significant contribution to the field of route optimization and broadly to the field of smart tourism by highlighting the effectiveness of a hybrid optimization model that combines simulated annealing and the A* algorithm. The results could be used to optimize routes and broadly contribute to the development of smart city infrastructures, which could improve the tourist experience. The core of the document examines the balance between computational performance and solution quality. This study paves the way for further advancements in smart tourism tools and itinerary generation, promoting more sustainable and enjoyable travel experiences.
Our experiments and findings show that the approach successfully balances exploration and efficiency, resulting in tourist routes that minimize travel time while covering a set of important points of interest. This accomplishment not only enhances the tourist experience but also has broader implications for sustainable tourism, reducing environmental impacts through efficient routes and supporting local economies by encouraging visitors to explore various attractions.
The potential for further advancements in this field is promising. The incorporation of OpenStreetMap geographic data, combined with the adaptability of simulated annealing and the precision of the A* algorithm, provides a solid foundation for future research and innovation.
Finally, future research may investigate additional constraints and factors to accommodate a broader range of traveller preferences and needs, while further optimizing the algorithm to more effectively reduce tourism costs.
Author Contributions
Conceptualization, Y.B. and K.H.; methodology, Y.B.; software, Y.B.; validation, Y.B. and K.E.M.; formal analysis, Y.B.; investigation, Y.B.; resources, H.S.; data curation, H.S.; writing—original draft preparation, Y.B.; writing—review and editing, K.E.M. and K.H.; visualization, Y.B.; supervision, K.H.; project administration, K.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Scientific and Technical Research Center of Morocco (CNRST), project number 28/2020 under the Khawarizmi program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy or institutional restrictions.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kontogianni, A.; Alepis, E. Smart tourism: State of the art and literature review for the last six years. Array 2020, 6, 100020. [Google Scholar] [CrossRef]
- Morais, R.; Batista, A.; Tavares, E. A systematic literature review for the tourist trip design problem: Extensions, solution techniques and future research lines. Oper. Res. Perspect. 2022, 9, 100228. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A Consolidated Review of Path Planning and Optimization Techniques: Technical Perspectives and Future Directions. Electronics 2021, 10, 2250. [Google Scholar] [CrossRef]
- Liang, S.; Jiao, T.; Du, W.; Qu, S. An improved ant colony optimization algorithm based on context for tourism route planning. PLoS ONE 2021, 16, e0257317. [Google Scholar] [CrossRef]
- Beed, R.; Roy, A.; Sarkar, S.; Bhattacharya, D. A hybrid multi-objective tour route optimization algorithm based on particle swarm optimization and artificial bee colony optimization. Comput. Intell. 2020, 36, 884–909. [Google Scholar] [CrossRef]
- Gavalas, D.; Katris, C.; Kenteris, M. Hybrid metaheuristics for personalized tourist trip planning: A comparative study. Expert Syst. Appl. 2023, 213, 119026. [Google Scholar]
- Handling OpenStreetMap georeferenced data for route planning. Transp. Res. Procedia 2022, 62, 189–196. [CrossRef]
- Benchekroun, Y.; Senba, H.; Haddouch, K.; El Moutaouakil, K. Tourist route optimization with a combined A* algorithm and genetic algorithm. Math. Model. Comput. 2024, 11, 966–977. [Google Scholar] [CrossRef]
- Cohen, A.; Dalyot, S. Route planning for blind pedestrians using OpenStreetMap. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 1511–1526. [Google Scholar] [CrossRef]
- Sui, J.; Ding, S.; Huang, X.; Yu, Y.; Liu, R.; Xia, B.; Ding, Z.; Xu, L.; Zhang, H.; Yu, C. A survey on deep learning-based algorithms for the traveling salesman problem. Front. Comput. Sci. 2025, 19, 196322. [Google Scholar] [CrossRef]
- Adamo, T.; Colizzi, L.; Dimauro, G.; Ghiani, G.; Guerriero, E. A multi-modal tourist trip planner integrating road and pedestrian networks. Expert Syst. Appl. 2024, 237, 121457. [Google Scholar] [CrossRef]
- Gavalas, D.; Konstantopoulos, C.; Mastakas, K.; Pantziou, G. A survey on algorithmic approaches for solving tourist trip design problems. J. Heuristics 2014, 20, 291–328. [Google Scholar] [CrossRef]
- Esper, J.P.; Fraga, L.d.S.; Viana, A.C.; Cardoso, K.V.; Correa, S.L. +Tour: Recommending personalized itineraries for smart tourism. arXiv 2025, arXiv:2502.17345. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z.; Qu, A.; Zhao, Y.; Li, C.; Zhang, L. ITINERA: Integrating spatial optimization with large language models for open-domain urban itinerary planning. arXiv 2024, arXiv:2402.07204. [Google Scholar]
- Damos, M.A.; Zhu, J.; Li, W.; Hassan, A.; Khalifa, E. A novel urban tourism path planning approach based on a multiobjective genetic algorithm. ISPRS Int. J. Geo-Inf. 2021, 10, 530. [Google Scholar] [CrossRef]
- Choi, K.C.; Li, S.; Lam, C.T.; Wong, A.; Lei, P.; Ng, B.; Siu, K.M. Genetic algorithm for tourism route planning considering time constraints. Int. J. Eng. Trends Technol. 2022, 70, 170–178. [Google Scholar] [CrossRef]
- Bolotbekova, A.; Hakli, H.; Beskirli, A. Trip route optimization based on bus transit using genetic algorithm with different crossover techniques: A case study in Konya/Türkiye. Sci. Rep. 2025, 15, 2491. [Google Scholar] [CrossRef] [PubMed]
- Cao, S. An Optimal Round-Trip Route Planning Method for Tourism Based on Improved Genetic Algorithm. Comput. Intell. Neurosci. 2022, 2022, 7665874. [Google Scholar] [CrossRef]
- Gavalas, D.; Konstantopoulos, C.; Pantziou, G.; Vathis, N. The eCOMPASS multimodal tourist tour planner. Expert Syst. Appl. 2015, 42, 7303–7316. [Google Scholar] [CrossRef]
- Pan, Q.; Wang, X. Independent travel recommendation algorithm based on analytical hierarchy process and simulated annealing for professional tourist. Appl. Intell. 2018, 48, 1565–1581. [Google Scholar] [CrossRef]
- Ma, Y.; Li, W.; Li, S.; Zu, P. Mudanjiang travel routing problem by simulated annealing approach. In Proceedings of the 2023 3rd International Conference on Public Management and Intelligent Society (PMIS 2023), Wuhan, China, 24–26 March 2023; Atlantis Press: Zhengzhou, China, 2023; pp. 493–499. [Google Scholar]
- Qiu, P.; Wang, J.; Gu, S.; Wu, D.; Xi, Q. Optimization of urban travel routes based on simulated annealing and genetic algorithm. SPIE Conf. Ser. 2023, 12941, 1294116. [Google Scholar]
- Muslim, R.; Hidayatullah, B.A.; Imran, B.; Yani, A.; Salman, S. Mapping Locations and Shortest Route of Tourism Objects in Central Lombok Using GIS-Based A-STAR Algorithm. J. Pilar Nusa Mandiri 2022, 18, 193–202. [Google Scholar] [CrossRef]
- Pasandi, L.; Hooshmand, M.; Rahbar, M. Modified A* Algorithm integrated with ant colony optimization for multi-objective route-finding; case study: Yazd. Appl. Soft Comput. 2021, 113, 107877. [Google Scholar] [CrossRef]
- Stefanov, T.; Varbanova, S.; Stefanova, M.; Tsenkova, Y. Mobile Applications for Cultural Tourism – Past, Present, and Future. Criteria for a Successful Mobile App. Int. J. Interact. Mob. Technol. (IJIM) 2023, 17, 54–78. [Google Scholar] [CrossRef]
- Yudha, M.H.P.; Supian, S.; Napitupulu, H. Optimalization Route to Tourism Places in West Java Using A-STAR Algorithm. CAUCHY J. Mat. Murni Apl. 2022, 7, 464–473. [Google Scholar] [CrossRef]
- Benchekroun, Y.; Senba, H.; Haddouch, K. A novel approach to intelligent touristic visits using bing maps and genetic algorithms. In Proceedings of the International Conference on Digital Technologies and Applications (ICDTA), Fez, Morocco, 27–28 January 2023. [Google Scholar]
- Vargas-Martínez, M.; Rangel-Valdez, N.; Fernández, E.; Gómez-Santillán, C.; Morales-Rodríguez, M.L. Performance analysis of multi-objective simulated annealing based on decomposition. Math. Comput. Appl. 2023, 28, 38. [Google Scholar] [CrossRef]
- Karabin, M.; Stuart, S.J. Simulated annealing with adaptive cooling rates. J. Chem. Phys. 2020, 153, 114112. [Google Scholar] [CrossRef]
- Shah, G.A.; Polette, A.; Pernot, J.P.; Giannini, F.; Monti, M. Case-based tuning of a metaheuristic algorithm exploiting sensitivity analysis and design of experiments for reverse engineering applications. Eng. Comput. 2023, 39, 2699–2715. [Google Scholar] [CrossRef]
- Zhu, D.-D.; Sun, J.-Q. A new algorithm based on Dijkstra for vehicle path planning considering intersection attribute. IEEE Access 2021, 9, 19761–19775. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).