Abstract
(1) Background: to propose a new approach for crown veneers, with the use of an aesthetic porcelain coating, only in part of the zirconia infrastructure, and to analyze its biomechanical behavior to minimize chipping failures. (2) Methods: a maxillary molar was modeled using CAD software, preparing for traditional crowns and veneer crowns with various lengths. Five groups were formed: M—control group (monolithic crown of ultra-translucent zirconia); B—conventional (bilayer crown of ultra-translucent zirconia and ceramic covering); V—veneer (ultra-translucent zirconia crown with reduction only in the buccal and application of covering ceramics); V1—ultra-translucent zirconia crown with buccal reduction and 1 mm occlusal extension for covering ceramic application); V1.5—ultra-translucent zirconia crown with buccal reduction and 1.5 mm occlusal extension for application of covering ceramics. A load of 600 N was performed axially to a fossa bottom to simulate parafunction, and 300 N to the cusp tip to obtain the maximum principal stress results. (3) Results: group B showed a higher stress concentration in the occlusal region of the restorations, while the other groups absorbed the stress and dissipated it throughout the crown, presenting a higher stress concentration in the interface region with the tooth. (4) Conclusion: the highly translucent zirconia ceramic only associated with buccal covering ceramic could add aesthetic gain and rigidity to the system and could be a good option to restore maxillary molars in patients who do not have parafunction.
1. Introduction
There is a close relationship amongst the effectiveness of facial muscles, occlusion, and mouth opening, when evaluating the masticatory loads in the natural dentition during chewing [1]. Stress distribution is different, according to the type and location of the tooth in the arch. The first molar is the area that receives the greatest effort when in function [2], making it a challenge in oral rehabilitation.
With the development of metal-free restorations, the demand for aesthetic and resistant materials has increased [3,4,5]. In addition, some flaws (delamination, chipping, catastrophic fracture) are still found, despite the diversity of indirect restorative materials currently available on the market. This is because “aesthetics” and “resistance” are antagonistic, meaning that the more components that are associated with providing resistance to the material, the less aesthetics are achieved [6]. One practical example is zirconia ceramic, which has the highest biaxial flexural strength (800–1200 MPa) [6,7,8] in relation to other materials, such as lithium disilicate (400–450 MPa), zirconia-reinforced lithium disilicate (510 MPa) [9], hybrid ceramic (174 MPa) [9], or feldspar (97–200 MPa) [9,10]. However, because it is an extremely opaque material, it is mainly used as infrastructure in restorations covered by aesthetic ceramics. Thus, bilayer crowns composed of zirconia coping and feldspar or leucite cover ceramics [10,11,12,13,14]. The different characteristics between infrastructure ceramics and cover ceramics generate residual stress, which in turn could cause delamination or chipping. An alternative to minimize these issues is the use of monolithic crowns; however, the optical aspects are not fully satisfactory when there is a greater aesthetic requirement [15].
In view of these setbacks, other types of zirconia have been developed, which have greater translucency, ranging from whitest to yellowish tones [10,16]. In terms of composition, Y2O3 generally stabilizes ZrO2 in the tetragonal phase; however, Al2O3 reduces by about 20% in relation to conventional zirconia and there is an increase in Fe2O3 to obtain more yellowish tones [10]. Thus, it is possible to maintain high flexural strength, respecting the minimum thickness of 1.5 mm for monolithic crowns, but with the benefit of presenting less opacity [15,16].
Zirconia partially coated with porcelain showed superior performance in a fatigue test when compared to traditional restoration completely coated with porcelain. On the other hand, it is not known whether the occlusal extension of porcelain could be promising from a biomechanical point of view [17]. This fact is still unclear in the literature. It is believed that the difference between the two types of ceramics may return to previous flaws in chipping or delamination.
In terms of manufacturing, CAD/CAM technology (computer-aided design/ computer-aided manufacturing) makes it possible to “machine” high-strength ceramics quickly and effectively [18]. Using CAD software makes it feasible to make crowns with diverse designs [19,20] and to associate it with more favorable biomechanical concepts, according to the complexity of each case, enabling adequate individualization for treatments.
In the case of masticatory functioning, the upper molars are quite apparent when the patient’s smile is more extensive. The buccal face is not directly subjected to stress during habitual chewing; thus, favoring the use of the covering ceramic, which is responsible for optimizing the optical characteristics. The objective of this study was to propose new models for crown veneers with zirconia infrastructure and evaluate the biomechanical behavior with finite element analysis. The null hypothesis was that the stress dissipation would not be altered with the extension of the aesthetic restorative material to the occlusal material in habitual chewing and parafunction simulations.
2. Materials and Methods
The first molar upper models were prepared in five different groups of crowns. The crowns were prepared with 5.5 mm of height and 12° of occlusal convergence in the axial walls (Figure 1). Control group (M: monolithic crown of ultra-translucent zirconia); conventional (B: bilayer crown of ultra-translucent zirconia and ceramic covering); veneer (V: ultra-translucent zirconia crown with reduction of 1.5 mm only in the buccal and application of covering ceramics); veneer 1 (V1: ultra-translucent zirconia crown with buccal reduction and 1 mm occlusal extension for covering ceramic application); Veneer 1.5 (V1.5: ultra-translucent zirconia crown with buccal reduction and 1.5 mm occlusal extension for application of covering ceramics).
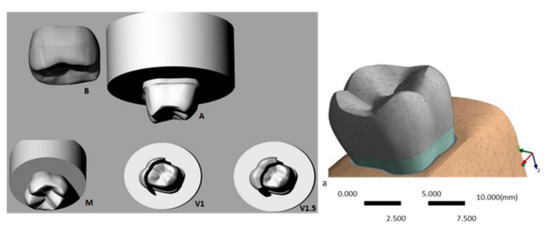
Figure 1.
A. Three-dimensional models of the upper molar peripheral preparation. B. Conventional crown group; M. monolithic crown group. V1. Zirconia crown group with buccal reduction and 1 mm occlusal extension. V1.5. Zirconia crown with buccal reduction and 1.5 mm occlusal extension; a. 3D model with volumetric solids.
The models acquired from the database of Biomaterials and Bioengineering Laboratory (Institute of Science and Technology São Paulo State University) were exported to CAE Software (Computer Aided Engineering-Ansys version 15.0) in step format. The generated mesh was controlled with 50% contact relevance, obtaining 159,061 nodes and 91,759 tetrahedral elements. In the calculations, sufficient accuracy of the results was guaranteed by the large numbers of elements and the corresponding degrees of freedom (dofs) at the nodes. The contemporary alternative could have been an adaptive approach, where the error could be controlled element-wise and the number of dofs could be optimized. See [21,22] for the general rules of this approach and [23,24] for its exemplary application in mechanics.
In our analysis, the solids were considered isotropic, linearly elastic, and homogeneous. The fixation occurred at the cylinder base. For the structural static analysis, 600 N stress loading was performed axially to a fossa bottom representing habitual chewing, touching only the zirconia ceramic, while 300 N stress onto the cusp tips represented an exaggerated masticatory action suggestive of parafunction, touching both the zirconia ceramic and porcelain [25]. The mechanical properties required for analysis are shown in Table 1. During the mathematical simulation, the interface replicating the layer of dental preparations contacting the crown was reduced. The maximum principal stress results were then solicited for tensile strength.

Table 1.
Elastic modulus and Poisson ratio of the restorative system components.
3. Results
Stress Concentration
Figure 2 and Table 2 show the stress concentration results in the crowns and in the restoration interface with the tooth after application of the usual load and during parafunction.
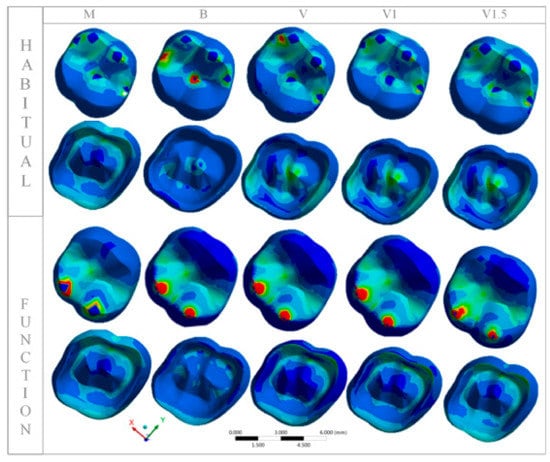
Figure 2.
Distribution of the maximum principal stress in each group with habitual loading and simulating function with loading in the central fossa.

Table 2.
Maximum principal stress (MPa) in each group with habitual loading and simulating function with loading in the central fossa.
The maximum principal stress was higher in all groups in which the parafunction was simulated compared to the groups with usual load applications. Group B had a higher stress concentration in the occlusal region of the restorations, while the other groups absorbed the stress and dissipated it throughout the crown, presenting a higher stress concentration in the interface region with the tooth, with similar peaks among V, V1, and V1.5, but with less intensity for M.
The same behavior in the interface region occurred during parafunctional chewing, in which group B also presented less stress concentration. However, the stress distribution on the occlusal surface was similar in all groups.
The occlusal extension of the covering ceramic did not change the stress distribution pattern in V, V1, and V1.5. The covering ceramic had adequate stiffness for habitual chewing on maxillary molars, and the three crown models modified by veneers could be used.
Figure 3 and Table 3 show the stress results only in the aesthetic aspect of groups V, V1, and V1.5 in the buccal view and at the interface with high translucency zirconia.
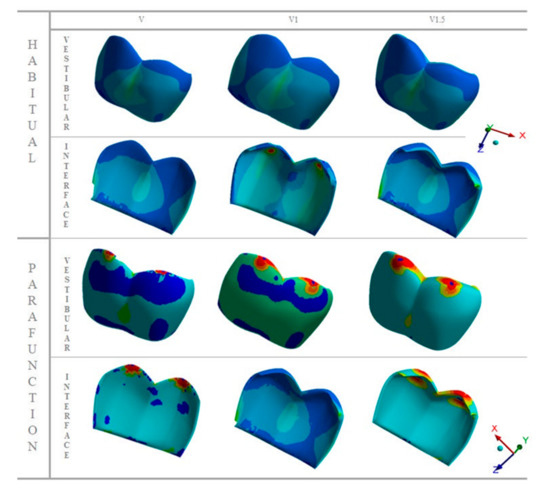
Figure 3.
Distribution of the maximum principal stress in the occlusal, middle, and cervical thirds of the aesthetic facets, with buccal view and their interfaces in each group, with usual loading and simulated chewing.

Table 3.
Maximum principal stress (MPa) in modification crowns groups with habitual loading and simulating function with loading in the central fossa.
In the habitual chewing simulation, it is observed that the stress distribution is homogeneous in the three groups on both the buccal surface and at the interface, but the representative images of parafunctional chewing show that the greater facet extension (V1.5) provided lower stress peak. The load incidence on the buccal face stresses this region, so that the ceramic covering absorbs the stress and dissipates little energy to the interface.
It can be seen in Figure 4 that the stress distribution is similar when the restoration is subjected to loads during the usual masticatory function, but the extension of the ceramic covering, limited to the buccal area, contributed to greater homogeneity of the stress distribution. On the other hand, the stress concentration during the parafunction in restorations with occlusal extension was higher and more concentrated.
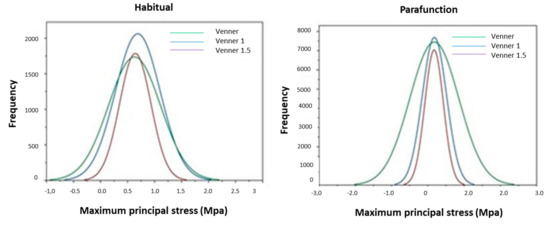
Figure 4.
Representative graph of stress peaks in modified restorations during habitual function (left) and parafunction (right). The stress peaks at veneer and veneer with 1.5 extension is similar during habitual function, but for parafunction the stress peaks are higher for modification veneers.
In Figure 4, the Gaussian curves were fit in the histogram of the stress frequencies, depending on the occlusal condition and type of restoration. The negative and positive numbers regard compressive and tensile stresses, respectively.
4. Discussion
The present study aimed to propose new applicability for the concept of crown veneers through ceramic materials currently available on the market, and to analyze the biomechanical behavior of these models. The null hypothesis was rejected, as there was a difference in the stress distribution according to the occlusal extension in the groups simulating habitual chewing.
Clinical studies show that conventional crowns that suffer from the fatigue process have cohesive porcelain flaws, resulting in chipping and delamination [27,28,29,30,31,32]; however, modifying the anatomy of the crowns is one way to improve porcelain support and minimize failures over time [17,31,32].
Starting from the concept that the first molar is the area that receives the greatest effort when solicited during functioning [2], with the upper one being approximately 400 to 600 N [33], according to age, gender, and race [34], it is believed that the greatest challenge in oral rehabilitation is exactly in these teeth, as they demand resistance and a certain aesthetic, according to the smile extent. The occlusal anatomy of a restoration is also an important aspect for the occlusion principles to contribute to the stomatognathic system functioning [19,35]. One can consider the occlusal extension of the coverage ceramic as a limiting aspect of the modified crowns proposed in this study, because, depending on the size of the porcelain extension to the occlusal surface, the zirconia/porcelain interface can be located exactly at the contact point with the antagonist. When following principles of prosthetic preparations, it is recommended that this interface region be spared in terms of direct stress application. It is conceptually more favorable that the region that suffers greater stress during habitual chewing is located on zirconia ceramic instead of porcelain or interface, because zirconia presents greater rigidity and is able to absorb greater stress, minimizing the stress values for porcelain.
The three extension proposals do not reach the triploid region of direct load application in habitual chewing in order to avoid stress at the interface between the two ceramics (when thinking about a patient with Angel class I). In this respect, Figure 3 shows that the porcelain extension did not, in fact, interfere in the locations of stress peaks, but in the distribution homogeneity of these stresses during habitual chewing (Figure 4). However, groups V and V1 showed similar behaviors during the parafunction simulation, but different from V1.5, in which the greater extension of the aesthetic facet to the occlusal region generated less stress concentration in the porcelain. The image shows that the stress is distributed over the entire length of the aesthetic facet, so the greater volume of the material can avoid stress in the middle and cervical thirds of the restoration.
From the occlusal perspective, groups V, V1, and V1.5 show very similar behaviors to group M. The stress distribution in this region is homogeneously distributed, corroborating the findings of Ramos (2015) [17] on fatigue analysis. This characteristic possibly prevents chipping, which is an aspect that the literature points to as a favorable point for monolithic crowns [29,36]. However, the stress concentration becomes greater in the inner region of the crown. The failure type that could occur is a catastrophic fracture [15]. Thus, with the results of this study, it is suggested that crowns modified with aesthetic facets do not suffer catastrophic failures when subjected to habitual chewing; however, they may have this type of failure when in parafunction.
Although the study by finite element analysis does not simulate the cumulative effect of the fatigue process, it is possible to recognize the regions with the highest stress concentrations through colorimetric graphs of stress isolines, where the first failures may occur. It is observed that group B presents a higher stress concentration at the load application site in the occlusal region compared to group M, corroborating with Ramos (2015) [17], who proved the same origin of bilayer crown failures through scanning electron microscopy images after a fatigue test, which could be justified by the fact that the greater quantity of porcelain generates greater residual stress between it and the infrastructure [12,37,38,39]. These findings drive the idealization of new anatomical modifications of crowns, which minimize the use of porcelain.
The combination of zirconia and ceramic covering in groups V, V1, and V1.5 in this study demonstrated that there would be no chipping problems during the usual chewing, regardless of the porcelain extension to the occlusal region, since the load application occurs directly onto zirconia and not to the interface. Although translucent zirconia (210 GPa Ivoclar Vivadent) presents an inferior elastic modulus to traditional zirconia (Lava Plus: 299.6 GPa) [40], it is still considered high in relation to other types of ceramics, which enables stress absorption and prevents its transmission to the covering ceramic. This favorable stress distribution behavior cannot be extrapolated for parafunction cases, as they receive loads with greater intensity and frequency, exactly at the interface between the two ceramics, generating failures, regardless of the porcelain extension to the occlusal region.
The results show that the porcelain extension to the occlusal region up to 1.5 mm is safe for creating veneer-type restorations, associating high translucency zirconia and porcelain, but the smaller the extension to the occlusal region, the greater stress homogeneity distributed by the aesthetic facet. Despite the unfavorable results for the simulated parafunction groups, they all presented similar stress distribution at the modified crown interface with the tooth, demonstrating that a fracture of the dental remnant is not a problem for these cases, but catastrophic failure of the ceramic, when in parafunction, could be. Another aspect to consider is the residual stress due to the thermal differences between zirconia and porcelain, which could not be estimated in our analysis. It is known that the stresses in restorations coated entirely with porcelain resulted in thermal gradients throughout the porcelain length and could contribute to an early fracture. On the other hand, with porcelain only in the buccal region, the distribution of these stresses could be altered and future studies need to be conducted in this sense.
In view of the findings in the literature, and with the present finding, it is believed that zirconia partially coated with porcelain up to 1.5 mm towards the central fossa, is able to provide better aesthetic conditions and resistance to restoration.
5. Conclusions
Through finite element analysis, it is possible to conclude that:
- (1)
- Crowns with veneer modifications exhibit similar biomechanical behavior to monolithic crowns and could be used in patients without parafunction.
- (2)
- The highly translucent zirconia ceramic only associated with buccal covering ceramic is a rigid system.
Author Contributions
C.F.L.M.: resources and data curation; G.F.R.: investigation and resources; A.L.S.B.: methodology and software; G.d.S.F.A.S.: conceptualization and methodology; R.O.S.: conceptualization and validation; R.M.d.M.M.: supervision and writing review; M.M.P.: data curation, writing—original draft preparation, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Bioengineering of materials Laboratory, Institute of Science and Technology Unesp, São José dos Campos, São Paulo, Brazil.
Acknowledgments
The authors are grateful to the Institute of Science and Technology Unesp and UFPB for the support technique.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Braun, S.; Hnat, W.P.; Freudenthaler, J.W.; Marcotte, M.R.; Hönigle, K.; Johnson, B.E. A study of maximum bite force during growth and development. Angle Orthod. 1996, 66, 261–264. [Google Scholar]
- Tortopidis, D.; Lyons, M.F.; Baxendale, R.H.; Gilmour, W.H. The variability of bite force measurement between sessions, in different positions within the dental arch. J. Oral Rehabil. 1998, 25, 681–686. [Google Scholar] [CrossRef] [PubMed]
- Lawn, B.R.; Pajares, A.; Zhang, Y.; Deng, Y.; Polack, M.A.; Lloyd, I.K.; Rekow, E.D.; Thompson, V.P. Materials design in the performance of all-ceramiccrowns. Biomaterials 2004, 25, 2885–2892. [Google Scholar] [CrossRef] [PubMed]
- Raptis, N.V.; Michalakis, K.X.; Hirayama, H. Optical behavior of current ceramic systems. Int. J. Perio. Restor. Dent. 2006, 26, 31–41. [Google Scholar]
- Zhang, Y. Making yttria-stabilized tetragonal zirconiatranslucent. Dent. Mater. 2014, 30, 1195–1203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holand, W.; Apel, E.; Hoen, C.; Rheinberger, V. Studies of Crystal phase formations in high-strength lithium disilicate glass-ceramics. J. Non Cryst. Solids 2006, 352, 4041–4050. [Google Scholar] [CrossRef]
- Komine, F.; Blatz, M.B.; Matsumura, H. Current status of zirconia-based fixed restorations. J. Oral Sci. 2010, 52, 531–539. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.H.; Chang, J.; Son, H.H. Flexural strength and microstructure of two lithium disilicate glass ceramics for CAD/CAM restoration in the dental clinic. Restor. Dent. Endod. 2013, 38, 134–140. [Google Scholar] [CrossRef]
- Sen, N. Mechanical and optical properties of monolithic CAD-CAM restorative materials. J. Prosthet. Dent. 2018, 119, 593–599. [Google Scholar] [CrossRef]
- Matsuzaki, F.; Sekine, H.; Honma, S.; Takanashi, T.; Furuya, K.; Yajimara, Y.; Youshinari, M. Translucency and flexural strength of monolithic translucent zirconia and porcelain-layered zirconia. Dent. Mater. 2015, 34, 910–917. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chai, H.W.; Lee, J.J.; Lawn, B.R. Chipping Resistance of Graded Zirconia Ceramics for Dental Crowns. J. Dent. Res. 2012, 91, 311–315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benetti, P.; Kelly, J.R.; Sanchez, M.; Della Bona, A. Influence of thermal gradients on stress state of veneered restorations. Dent. Mater. 2014, 30, 554–563. [Google Scholar] [CrossRef]
- Lee, Y.K. Translucency of human teeth and dental restorative materials and its clinical relevance. J. Biomed. Opt. 2015, 20, 045002. [Google Scholar] [CrossRef]
- D’Arcangelo, C.; Vanini, L.; Rondoni, G.D.; De Angelis, F. Wear properties of dental ceramics and porcelains compared with human enamel. J. Prosthet. Dent. 2016, 115, 350–355. [Google Scholar] [CrossRef] [PubMed]
- Schwindling, F.S.; Rues, S.; Schmitter, M. Fracture resistance of glazed, full-contour ZLC incisor crowns. J. Prosthet. Dent. 2017, 61, 344–349. [Google Scholar]
- Harada, K.; Raigroski, A.J.; Chung, K.; Flinn, B.D.; Dogan, S.; Mancl, L.A. A comparative evaluation of the translucency of zirconias and lithium disilicate for monolithic restorations. J. Prosthet. Dent. 2016, 116, 257–263. [Google Scholar] [CrossRef] [PubMed]
- Ramos, G.F.; Monteiro, E.B.C.; Bottino, M.A.; Zhang, Y.; Melo, R.M.M. Failure probability of three designs of zirconia crowns. Int. J. Periodontics Restor. Dent. 2015, 35, 843–849. [Google Scholar] [CrossRef] [Green Version]
- Santos, G.C., Jr.; Boksman, L.L.; Santos, M.J. CAD/CAM technology and esthetic dentistry: A case report. Compend. Contin. Educ. Dent. 2013, 34, 764–768. [Google Scholar]
- Ender, A.; Mörmann, W.H.; Mehl, A. Efficiency of a mathematical model in generating CAD/CAM-partial crowns with natural tooth morphology. Clin. Oral Investig. 2011, 15, 283–289. [Google Scholar] [CrossRef] [Green Version]
- Arslan, Y.; Nemli, S.L.; Güngör, M.B.; Tamam, E.; Yilmaz, H. Evaluation of biogeneric design techniques with CEREC CAD/CAM system. J. Adv. Prosthodont. 2015, 7, 431–436. [Google Scholar] [CrossRef]
- Demkowicz, L. Computing with hp-adaptive finite elements. In One and Two Dimensional Elliptic and Maxwell Problems; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; Volume 1. [Google Scholar]
- Demkowicz, L.; Kurtz, J.; Pardo, D.; Paszyński, M.; Rachowicz, W.; Zdunek, A. Computing with hp adaptive finite elements. In Three-Dimensional Elliptic and Maxwell Problems with Applications; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; Volume 2. [Google Scholar]
- Zboiński, G. Adaptive hpq finite element methods for the analysis of 3D-based models of complex structures. Part 1. Hierarchical modeling and approximation. Comput. Methods Appl. Mech. Engrg. 2010, 199, 2913–2940. [Google Scholar] [CrossRef]
- Zboiński, G. Adaptive hpq finite element methods for the analysis of 3D-based models of complex structures. Part 2. A posteriori error estimation. Comput. Methods Appl. Mech. Eng. 2013, 267, 531–565. [Google Scholar] [CrossRef]
- Tribst, J.P.M.; Dal Piva, A.M.O.; Madruga, C.F.L.; Valera, M.C.; Borges, A.L.S.; Bresciani, E.; de Melo, R.M. Endocrown restorations: Influence of dental remnant and restorative material on stress distribution. Dent. Mater. 2018, 34, 1466–1473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Versluis, A.; Tantbirojn, D.; Pintado, M.R.; DeLong, R.; Douglas, W.H. Residual shrinkage stress distributions in molars after composite restoration. Dent. Mater. 2004, 20, 554–564. [Google Scholar] [CrossRef] [PubMed]
- Dal Piva, A.M.O.; Tribst, J.P.M.; Souza, R.O.A.; Borges, A.L.S. Influence of Alveolar Bone Loss and Cement Layer Thickness on the Biomechanical Behavior of Endodontically Treated Maxillary Incisors: A 3-dimensional Finite Element Analysis. J. Endod. 2017, 43, 791–795. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Jager, N.; Pallav, P.; Feilzer, A.J. The influence of design parameters on the FEA-determined stress distribution in CAD-CAM produced all-ceramic dental crowns. Dent. Mater. 2005, 21, 242–251. [Google Scholar] [CrossRef]
- Sailer, I.; Feher, A.; Filser, F.; Gauckler, L.J.; Lüthy, H.; Hämmerle, C.H. Five-year clinical results of zirconia frameworks for posterior fixed partial dentures. Int. J. Prosthod. 2007, 20, 383–388. [Google Scholar]
- Silva, N.R.; Bonfante, E.A.; Zavanelli, R.A.; Thompson, V.P.; Ferencz, J.L.; Coelho, P.G. Reliability of metalloceramic and zirconia-based ceramic crowns. J. Dent. Res. 2010, 89, 1051–1056. [Google Scholar] [CrossRef] [PubMed]
- Christensen, R.P.; Ploeger, B.J. A clinical comparison of zirconia, metal and alumina fixed-prosthesis frameworks veneered with layered or pressed ceramic: A three-year report. J. Am. Dent Assoc. 2010, 141, 1317–1329. [Google Scholar] [CrossRef]
- Zhang, Y.; Sailer, I.; Lawn, B.R. Fatigue of dental ceramics. J. Dent. 2013, 41, 1135–1147. [Google Scholar] [CrossRef] [Green Version]
- Corazza, P.H.; Feitosa, A.S.; Borges, A.L.; Della Bona, A. Influence of convergence angle of tooth preparation on the fracture resistance of Y-TZP-based all-ceramic restorations. Dent. Mater. 2013, 29, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Van Ejjden, T.M. Three-dimensional analyses of human bite-force magnitude and moment. Arch. Oral Biol. 1991, 36, 535–539. [Google Scholar] [CrossRef]
- Varga, S.; Spalj, S.; Varga, M.L.; Milosevic, A.S.; Mestrovic, S.; Slaj, M. Maximum voluntary molar bite force in subjects with normal occlusion. Eur. J. Orthod. 2011, 33, 427–433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kollmuss, M.; Jakob, F.M.; Kirchner, H.G.; Ilie, N.; Hickel, R.; Huth, K.C. Comparison of biogenerically reconstructed and waxedup complete occlusal surfaces with respect to the original tooth morphology. Clin. Oral Investig. 2013, 17, 851–857. [Google Scholar] [CrossRef]
- Bonfante, E.A.; Rafferty, B.; Zavanelli, R.A.; Silva, N.R.F.A.; Rekow, E.D.; Thompson, V.P.; Coelho, P.G. Thermal/mechanical simulation and laboratory fatigue testing of an alternative yttria tetragonal zirconia polycrystal core-veneer all-ceramic layered crown design. Eur. J. Oral Sci. 2010, 118, 202–209. [Google Scholar] [CrossRef]
- Baldassarri, M.; Stappert, C.F.; Wolff, M.S.; Thompson, V.P.; Zhang, Y. Residual stresses in porcelain-veneered zirconia prostheses. Dent. Mater. 2012, 28, 873–879. [Google Scholar] [CrossRef] [Green Version]
- Lucas, T.J.; Lawsona, N.C.; Janowski, G.M.; Burgess, J.O. Effect of grain size on the monoclinic transformation, hardness, roughness, and modulus of aged partially stabilized zirconia. Dent. Mater. 2015, 31, 1487–1492. [Google Scholar] [CrossRef]
- Campo Silva, E.; Leonec, R.; Gremillarda, L.; Sorrentinoc, R.; Zaronec, F.; Ferrarid, M.; Chevaliera, J. Aging resistance, mechanical properties and translucency of different yttria-stabilized zirconia ceramics for monolithic dental crown applications. Dent. Mater. 2018, 34, 879–890. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).