Simulation of Radiation-Induced DNA Damage and Protection by Histones Using the Code RITRACKS
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Setup
2.2. DNA Models
2.3. Irradiation of a Volume
2.3.1. Monte Carlo Simulation of Radiation Tracks
2.3.2. Calculation of the Number of Tracks
2.3.3. Periodic Boundary Conditions
2.4. Overview of Radiation Interactions with Biomolecules
2.4.1. DNA Damage by Direct Effect
2.4.2. DNA Damage by Indirect Effect
2.4.3. Histone Damage
2.4.4. Histone Protection
2.5. Simulation of DNA Damage
2.5.1. Simulation of the Direct Effect
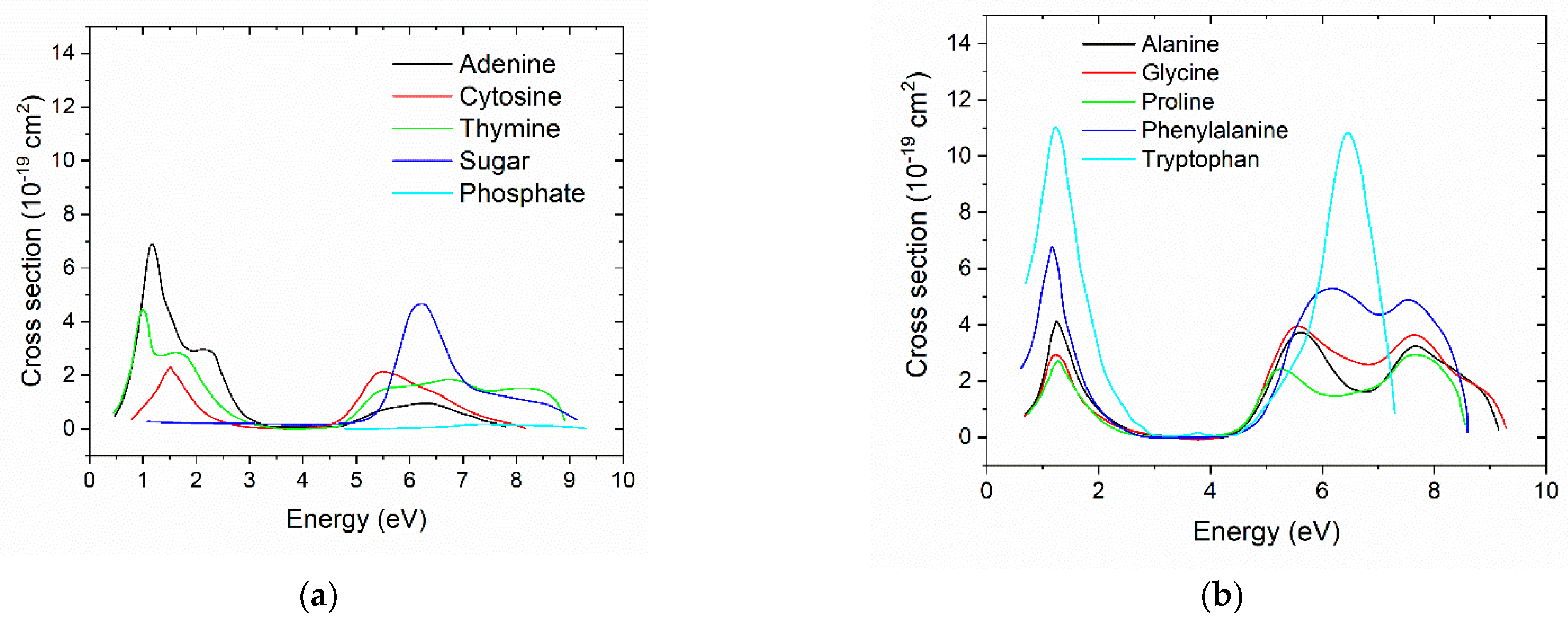
Ionization cross Sections
Dissociative Electron Attachment cross Section
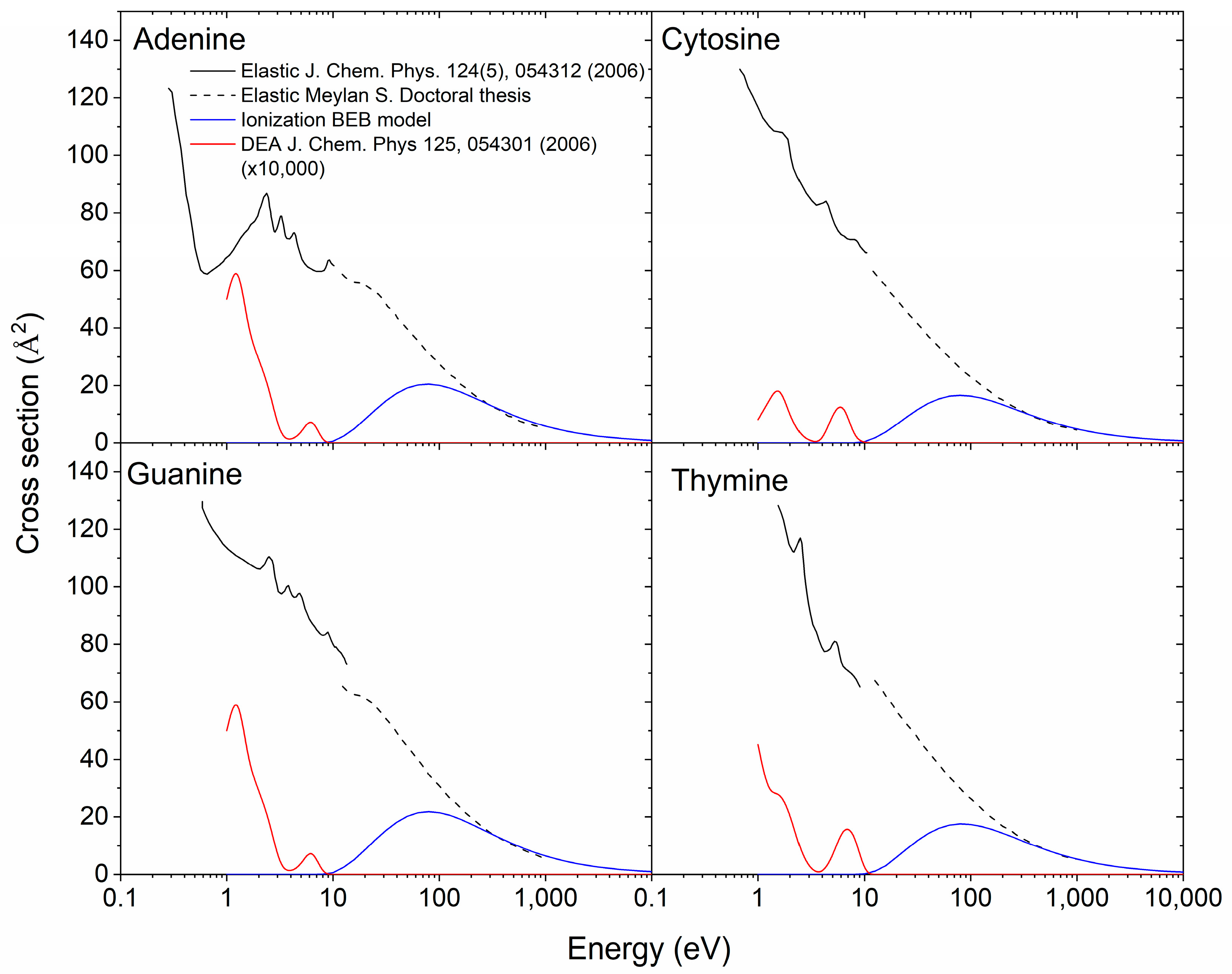
Elastic cross Sections
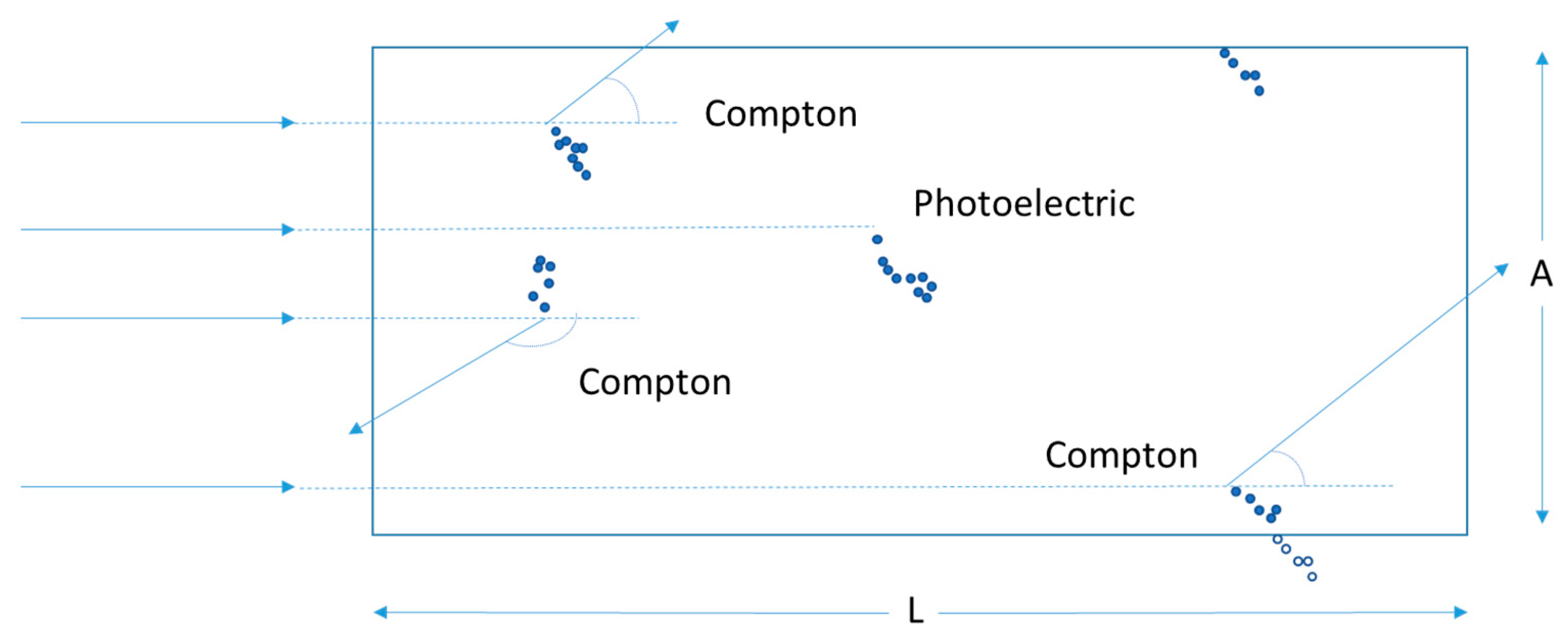
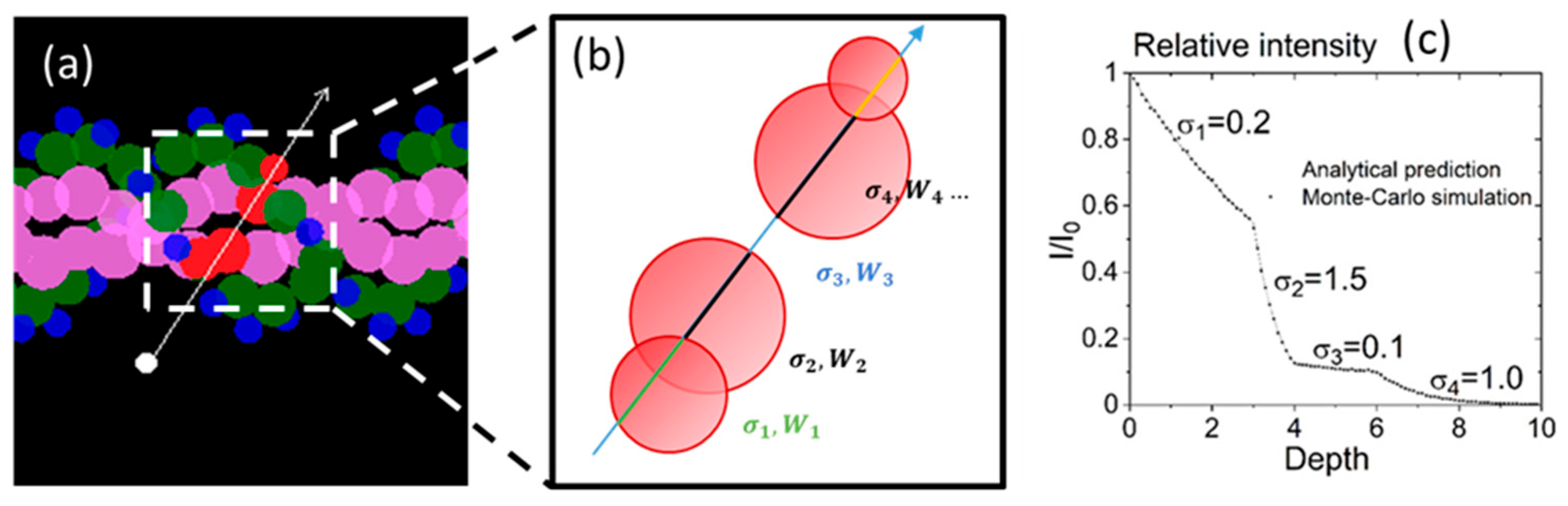
Particle Transport in Media of Different cross Sections
2.5.2. Simulation of the Indirect Effect
- (1)
- Go to during and then during ; or
- (2)
- React during or go to during and then react during .
2.5.3. Classification of DNA Damage
2.6. Simulation of Histone Damage
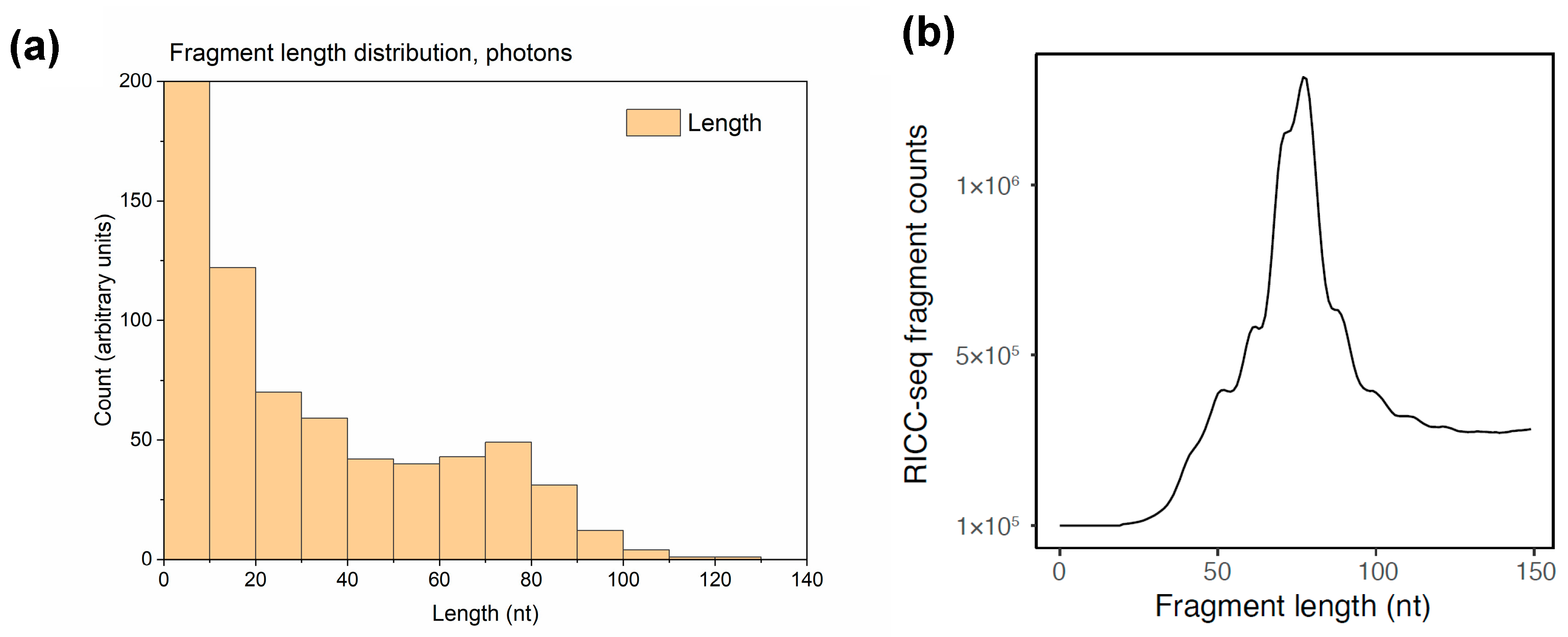
2.7. Fragment Length Distribution
2.8. Damage Location
2.9. Error Bars
3. Results
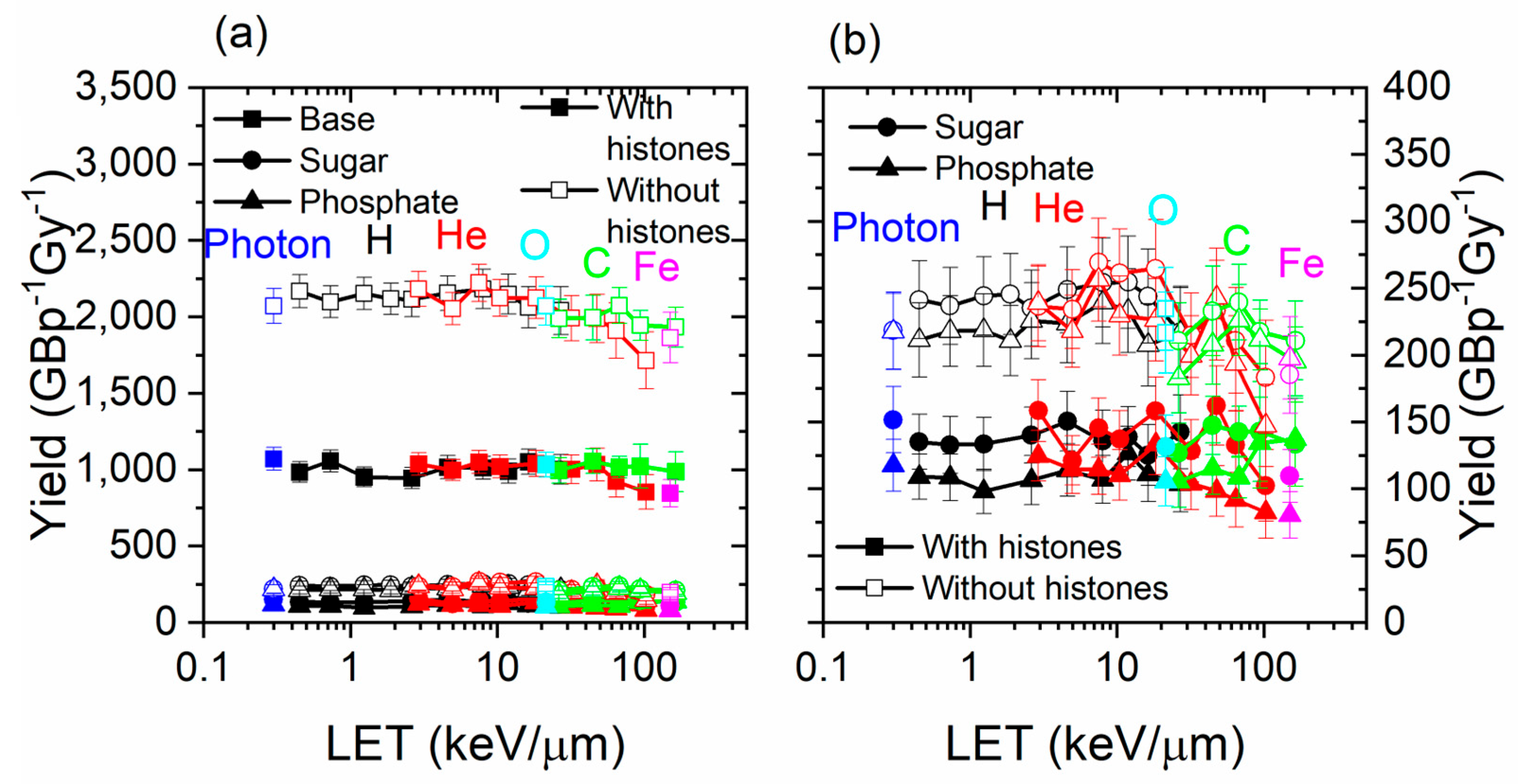
3.1. Damage by Structure Type and by Contribution
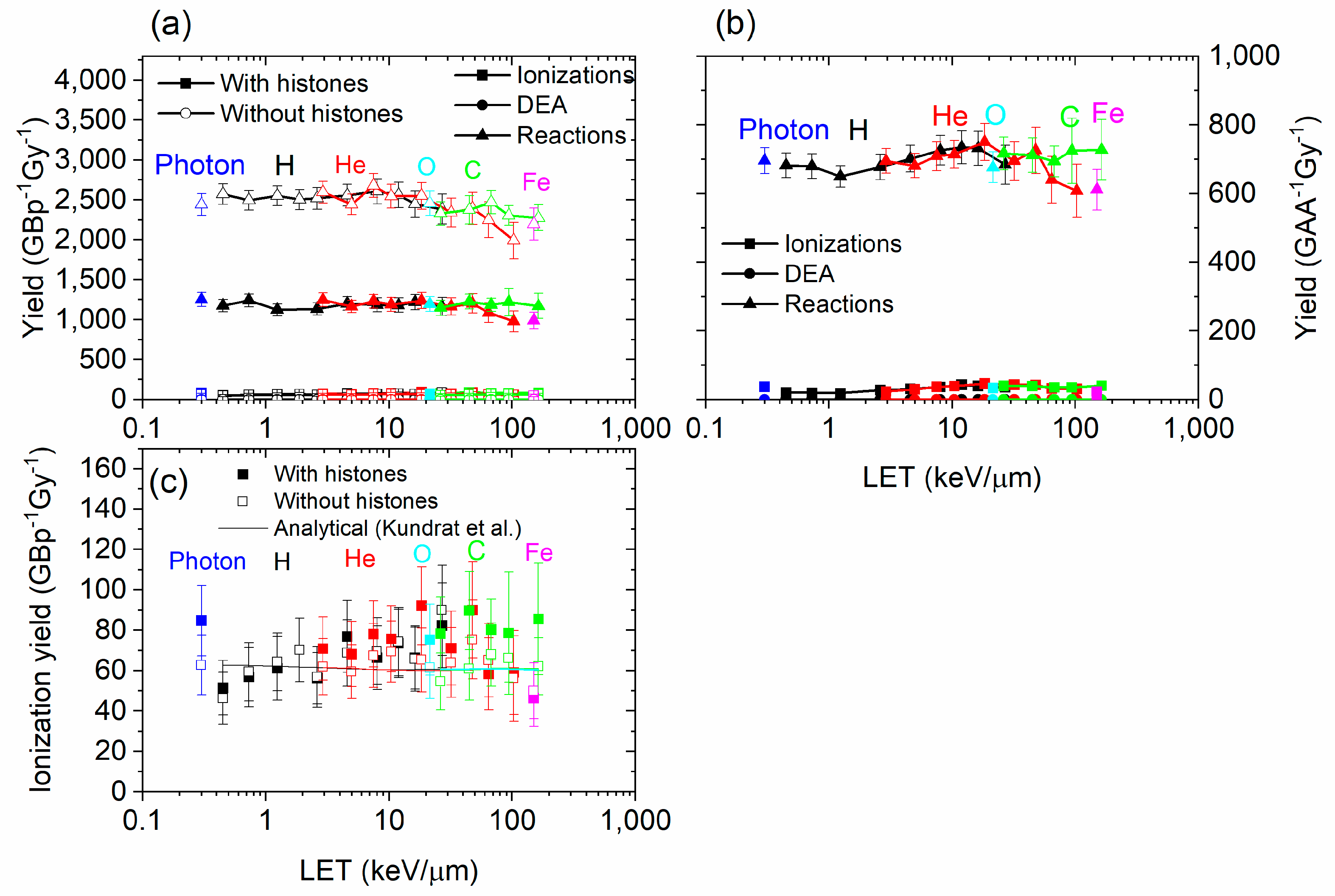
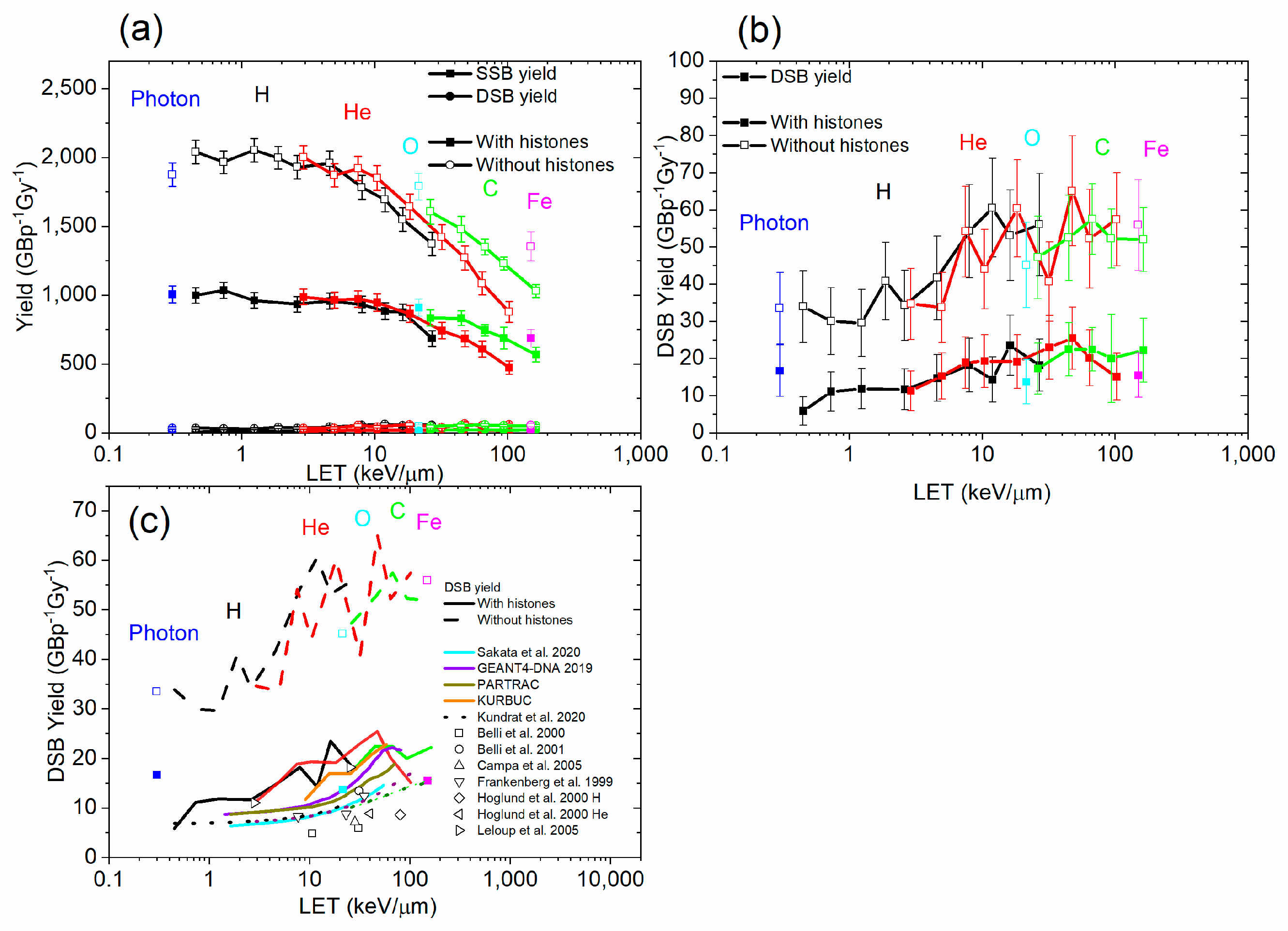
3.2. Damage Types
3.3. Histone Protection
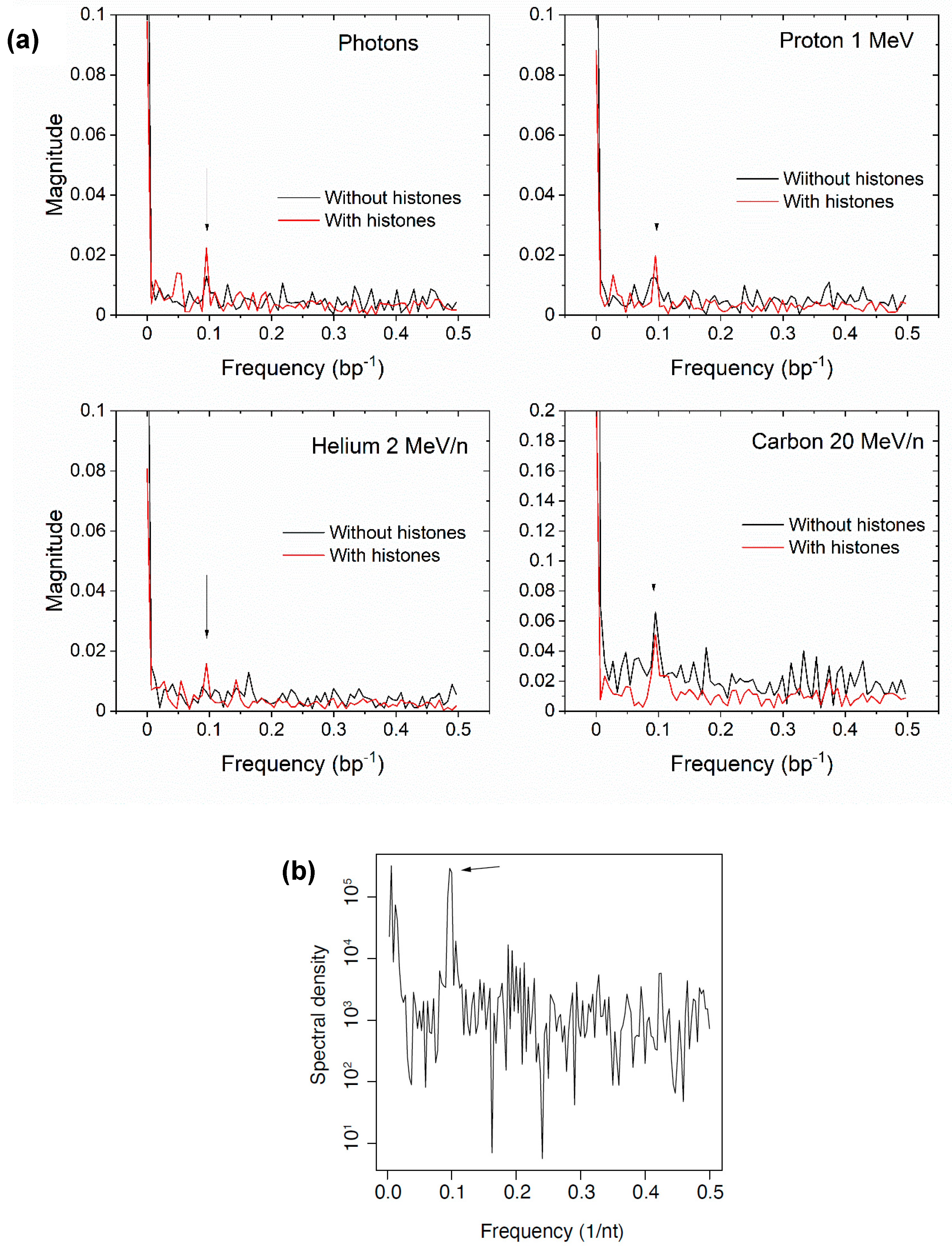
3.4. Fragment Length Distribution
4. Discussion
5. Conclusions
6. New Technology
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Energy (keV) | (cm2/g) | (cm2/g) | (%) | |||
|---|---|---|---|---|---|---|
| 1 | 4020 | 4020 | 360.85 | 48.35 | 312.5 | 86.6 |
| 2 | 566 | 566 | 633.93 | 477.68 | 156.25 | 24.6 |
| 3 | 179 | 179 | 1216.73 | 1112.56 | 104.17 | 8.56 |
| 5 | 39.6 | 39.5 | 3195.99 | 3133.33 | 62.66 | 1.96 |
| 10 | 4.87 | 4.72 | 13,257.65 | 13,225.40 | 32.25 | 0.24 |
| 20 | 0.676 | 0.505 | 61,891.64 | 61,870.72 | 20.92 | 0.0338 |
| 30 | 0.314 | 0.140 | 148,821.20 | 148,797.84 | 23.36 | 0.0157 |
| 50 | 0.204 | 0.0383 | 326,387.40 | 326,354.11 | 33.29 | 0.0102 |
| 100 | 0.165 | 0.0248 | 252,026.52 | 252,005.73 | 20.79 | 8.25 × 10−3 |
| 200 | 0.135 | 0.0295 | 105,935.77 | 105,928.62 | 7.15 | 6.74 × 10−3 |
| 300 | 0.118 | 0.0319 | 65,310.181 | 65,306.328 | 3.853 | 5.90 × 10−3 |
| 500 | 0.0966 | 0.0331 | 37,765.262 | 37,763.438 | 1.824 | 4.82 × 10−3 |
| 1000 | 0.0707 | 0.0310 | 20,161.646 | 20,160.933 | 0.713 | 3.53 × 10−3 |
References
- Watanabe, R.; Rahmanian, S.; Nikjoo, H. Spectrum of Radiation-Induced Clustered Non-DSB Damage—A Monte Carlo Track Structure Modeling and Calculations. Radiat. Res. 2015, 183, 525–540. [Google Scholar] [CrossRef]
- Jenner, T.J.; Fulford, J.; O’Neill, P. Contribution of base lesions to radiation-induced clustered DNA damage: Implication for models of radiation response. Radiat. Res. 2001, 156, 590–593. [Google Scholar] [CrossRef]
- Friedland, W.; Schmitt, E.; Kundrát, P.; Dingfelder, M.; Baiocco, G.; Barbieri, S.; Ottolenghi, A. Comprehensive track-structure based evaluation of DNA damage by light ions from radiotherapy-relevant energies down to stopping. Sci. Rep. 2017, 7, 45161. [Google Scholar] [CrossRef]
- Frankenberg-Schwager, M.; Frankenberg, D. DNA double-strand breaks: Their repair and relationship to cell killing in yeast. Int. J. Radiat. Biol. 1990, 58, 569–575. [Google Scholar] [CrossRef]
- Ward, J.F. The Complexity of DNA Damage Relevance to Biological Consequences. Int. J. Radiat. Biol. 1994, 66, 427–432. [Google Scholar] [CrossRef]
- Höglund, H.; Stenerlöw, B. Induction and rejoining of DNA double strand breaks in normal human skin fibroblasts after exposure to radiation of different linear energy transfer: Possible roles of track structure and chromatin organization. Radiat. Res. 2001, 155, 818–825. [Google Scholar] [CrossRef]
- Asaithamby, A.; Uematsu, N.; Chatterjee, A.; Story, M.D.; Burma, S.; Chen, D.J. Repair of HZE-particle-induced DNA double-strand breaks in normal human fibroblasts. Radiat. Res. 2008, 169, 437–446. [Google Scholar] [CrossRef]
- Ritter, M.A.; Cleaver, J.E.; Tobias, C.A. High-LET radiations induce a large proportion of non-rejoining DNA breaks. Nature 1977, 266, 653–655. [Google Scholar] [CrossRef]
- Blanpain, C.; Mohrin, M.; Sotiropoulou, P.A.; Passegue, E. DNA-damage response in tissue-specific and cancer stem cells. Cell Stem Cell 2011, 8, 16–29. [Google Scholar] [CrossRef]
- Goodhead, D.T.; Leenhouts, H.P.; Paretzke, H.G.; Terrisol, M.; Nikjoo, H.; Blaauboer, R. Track structure approaches to the interpretation of radiation effects on DNA. Radiat. Prot. Dosim. 1994, 52, 217–223. [Google Scholar] [CrossRef]
- Baiocco, G.; Bartzsch, S.; Conte, V.; Friedrich, T.; Jakob, B.; Tartas, A.; Villagrasa, C.; Prise, K.M. A matter of space: How the spatial heterogeneity in energy deposition determines the biological outcome of radiation exposure. Radiat. Environ. Biophys. 2022, 61, 545–559. [Google Scholar] [CrossRef]
- Magee, J.L.; Chatterjee, A. Track reactions of radiation chemistry. In Kinetics of Nonhomogenous Processes; Freeman, G.R., Ed.; Wiley: New York, NY, USA, 1987; pp. 171–214. [Google Scholar]
- Davisson, C.M.; Evans, R.D. Gamma-Rays absorption coefficients. Rev. Mod. Phys. 1952, 24, 70–107. [Google Scholar] [CrossRef]
- Burton, M. Radiation chemistry: A godfatherly look at its history and its relation to liquids. Chem. Eng. News 1969, 47, 86–96. [Google Scholar] [CrossRef]
- Hamm, R.N.; Turner, J.E.; Ritchie, R.H.; Wright, H.A. Calculation of heavy-ion tracks in liquid water. Radiat. Res. 1985, 104, S20–S26. [Google Scholar] [CrossRef][Green Version]
- Roots, R.; Okada, S. Estimation of life times and diffusion distances of radicals involved in X-ray-induced DNA strand breaks or killing of mammalian cells. Radiat. Res. 1975, 64, 306–320. [Google Scholar] [CrossRef]
- Sakata, D.; Belov, O.; Bordage, M.C.; Emfietzoglou, D.; Guatelli, S.; Inaniwa, T.; Ivanchenko, V.; Karamitros, M.; Kyriakou, I.; Lampe, N.; et al. Fully integrated Monte Carlo simulation for evaluating radiation induced DNA damage and subsequent repair using Geant4-DNA. Sci. Rep. 2020, 10, 20788. [Google Scholar] [CrossRef]
- Nikjoo, H.; Taleei, R.; Liamsuwan, T.; Liljequist, D.; Emfietzoglou, D. Perspectives in radiation biophysics: From radiation track structure simulation to mechanistic models of DNA damage and repair. Radiat. Phys. Chem. 2016, 128, 3–10. [Google Scholar] [CrossRef]
- Tang, N.; Bueno, M.; Meylan, S.; Incerti, S.; Tran, H.N.; Vaurijoux, A.; Gruel, G.; Villagrasa, C. Influence of chromatin compaction on simulated early radiation-induced DNA damage using Geant4-DNA. Med. Phys. 2019, 46, 1501–1511. [Google Scholar] [CrossRef]
- Kyriakou, I.; Sakata, D.; Tran, H.N.; Perrot, Y.; Shin, W.G.; Lampe, N.; Zein, S.; Bordage, M.C.; Guatelli, S.; Villagrasa, C.; et al. Review of the Geant4-DNA simulation toolkit for radiobiological applications at the cellular and DNA level. Cancers 2021, 14, 35. [Google Scholar] [CrossRef]
- Schuemann, J.; McNamara, A.L.; Ramos-Méndez, J.; Perl, J.; Held, K.D.; Paganetti, H.; Incerti, S.; Faddegon, B. TOPAS-nBio: An extension to the TOPAS simulation toolkit for cellular and sub-cellular radiobiology. Radiat. Res. 2019, 191, 125–138. [Google Scholar] [CrossRef]
- Roadmap Epigenomics Consortium. Integrative analysis of 111 reference human epigenomes. Nature 2015, 518, 317–330. [Google Scholar] [CrossRef]
- Chen, P.; Li, W.; Li, G. Structures and Functions of Chromatin Fibers. Annu. Rev. Biophys. 2021, 50, 95–116. [Google Scholar] [CrossRef]
- Mansisidor, A.R.; Risca, V.L. Chromatin accessibility: Methods, mechanisms, and biological insights. Nucleus 2022, 13, 236–276. [Google Scholar] [CrossRef]
- Misteli, T. The Self-Organizing Genome: Principles of Genome Architecture and Function. Cell 2020, 183, 28–45. [Google Scholar] [CrossRef]
- Luger, K.; Dechassa, M.L.; Tremethick, D.J. New insights into nucleosome and chromatin structure: An ordered state or a disordered affair? Nat. Rev. Mol. Cell Biol. 2012, 13, 436–447. [Google Scholar] [CrossRef]
- Goodarzi, A.A.; Noon, A.T.; Jeggo, P.A. The impact of heterochromatin on DSB repair. Biochem. Soc. Trans. 2009, 37, 569–576. [Google Scholar] [CrossRef]
- Ortega, P.; Gómez-González, B.; Aguilera, A. Heterogeneity of DNA damage incidence and repair in different chromatin contexts. DNA Repair. 2021, 107, 103210. [Google Scholar] [CrossRef]
- ENCODE Project Consortium. An integrated encyclopedia of DNA elements in the human genome. Nature 2012, 489, 57–74. [Google Scholar] [CrossRef]
- Risca, V.L.; Denny, S.K.; Straight, A.F.; Greenleaf, W.J. Variable chromatin structure revealed by in situ spatially correlated DNA cleavage mapping. Nature 2017, 541, 237–241. [Google Scholar] [CrossRef]
- Rydberg, B. Radiation-induced DNA damage and chromatin structure. Acta Oncol. 2001, 40, 682–685. [Google Scholar] [CrossRef]
- Rydberg, B.; Holley, W.R.; Mian, I.S.; Chatterjee, A. 1998 Chromatin conformation in living cells: Support for a zig-zag model of the 30 nm chromatin fiber. J. Mol. Biol. 1998, 284, 71–84. [Google Scholar] [CrossRef]
- Brambilla, F.; Garcia-Manteiga, J.M.; Monteleone, E.; Hoelzen, L.; Zocchi, A.; Agresti, A.; Bianchi, M.E. Nucleosomes effectively shield DNA from radiation damage in living cells. Nucleic Acids Res. 2020, 48, 8993–9006. [Google Scholar] [CrossRef]
- Thibaut, Y.; Tang, N.; Tran, H.N.; Vaurijoux, A.; Villagrasa, C.; Incerti, S.; Perrot, Y. Nanodosimetric calculations of radiation-induced DNA damage in a new nucleus geometrical model based on the isochore theory. Int. J. Mol. Sci. 2022, 23, 3770. [Google Scholar] [CrossRef]
- Plante, I.; Cucinotta, F.A. Monte-Carlo simulation of ionizing radiation tracks. In Applications of Monte Carlo Methods in Biology, Medicine and Other Fields of Science; Mode, C.B., Ed.; InTech: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef]
- Davey, C.A.; Sargent, D.F.; Luger, K.; Maeder, A.W.; Richmond, T.J. X-ray Structure of the Nucleosome Core Particle, NCP147, at 1.9 A Resolution. J. Mol. Biol. 2002, 319, 1097–1113. [Google Scholar] [CrossRef]
- Baba, K.; Kusumoto, T.; Okada, S.; Ishikawa, M. A simulation-based study on water radiolysis species for 1H+, 4He2+, and 12C6+ ion beams with multiple ionization using Geant4-DNA. J. Appl. Phys. 2021, 129, 244702. [Google Scholar] [CrossRef]
- Schmollack, J.U.; Klaumuenzer, S.L.; Kiefer, J. Stochastic radial dose distributions and track structure theory. Radiat. Res. 2000, 153, 469–478. [Google Scholar] [CrossRef]
- Plante, I.; Cucinotta, F.A. Energy deposition and relative frequency of hits of cylindrical nanovolume in medium irradiated by ions: Monte Carlo simulation of tracks structure. Radiat. Environ. Biophys. 2010, 49, 5–13. [Google Scholar] [CrossRef]
- Plante, I.; Poignant, F.; Slaba, T. 2021 Track structure components: Characterizing energy deposited in spherical cells from direct and peripheral HZE ion hits. Life 2021, 11, 1112. [Google Scholar] [CrossRef]
- Turner, J. Atoms, Radiation and Radiation Protection, 3rd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Becker, D.; Sevilla, M.D. The chemical consequences of radiation-damage to DNA. Adv. Radiat. Biol. 1993, 17, 121–180. [Google Scholar] [CrossRef]
- La Vere, T.; Becker, D.; Sevilla, M.D. 1996 Yields of •OH in gamma-irradiated DNA as a function of DNA hydration: Hole transfer in competition with •OH formation. Radiat. Res. 1996, 145, 673–680. [Google Scholar] [CrossRef]
- O’Neill, P. Radiation-induced damage in DNA. In Radiation Chemistry: Present Status and Future Trends; Jonah, C.D., Rao, B.S.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 585–622. [Google Scholar]
- von Sonntag, C. Free-Radical-Induced DNA Damage and Its Repair. A Chemical Perspective; Springer: Berlin, Germany, 2006. [Google Scholar]
- Lee, B.; Richards, F.M. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 1971, 55, 379–400. [Google Scholar] [CrossRef]
- Plante, I.; Cucinotta, F.A. A Binary-Encounter-Bethe approach to simulate DNA damage by the direct effect of ionizing radiation. Radiat. Prot. Dosim. 2015, 166, 19–23. [Google Scholar] [CrossRef]
- Edel, S. Modélisation du Transport des Photons et des Électrons dans l’ADN Plasmide. Ph.D. Thesis, University of Toulouse, Toulouse, France, 2006. [Google Scholar]
- Rudek, B.; Bennett, D.; Bug, M.U.; Wang, M.; Baek, W.Y.; Buhr, T.; Hilgers, G.; Champion, C.; Rabus, H. Double differential cross sections for proton induced electron emission from molecular analogues of DNA constituents for energies in the Bragg peak region. J. Chem. Phys. 2016, 145, 104301. [Google Scholar] [CrossRef]
- Barkas, W.H. Nuclear Research Emulsions. Vol. 1: Techniques and Theory. Pure and Applied Physics; Academic Press: London, UK, 1963; Chapter 9; p. 371. [Google Scholar]
- Boudaïffa, B.; Cloutier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant formation of DNA strand breaks by low-energy (3–20 eV) electrons. Science 2000, 287, 1658–1660. [Google Scholar] [CrossRef]
- Aflatooni, K.; Sheer, A.M.; Burrow, P. Total dissociative electron attachment cross sections for molecular constituents of DNA. J. Chem. Phys. 2006, 125, 054301. [Google Scholar] [CrossRef]
- Scheer, A.M.; Możejko, P.; Gallup, G.; Burrow, P. Total dissociative electron attachment cross sections of selected amino acids. J. Chem. Phys. 2007, 126, 174301. [Google Scholar] [CrossRef]
- Liu, W.; Tan, Z.; Zhang, L.; Champion, C. Calculation on spectrum of direct DNA damage induced by low-energy electrons including dissociative electron attachment. Radiat. Environ. Biophys. 2017, 56, 99–110. [Google Scholar] [CrossRef]
- Możejko, P.; Sanche, L. Cross section calculations for electron scattering from DNA and RNA bases. Radiat. Environ. Biophys. 2003, 42, 201–211. [Google Scholar] [CrossRef]
- Tonzani, S.; Greene, C.H. Low-energy electron scattering from DNA and RNA bases: Shape resonances and radiation damage. J. Chem. Phys. 2006, 124, 054312. [Google Scholar] [CrossRef]
- Meylan, S. Développement d’un Outil de Simulation Multi-Échelle Adapté au Calcul des Dommages Radio-Induits Précoces Dans des Cellules Exposées à des Irradiations D’ions Légers (Proton et Alpha). Ph.D. Thesis, Université de Bordeaux, Bordeaux, France, 2016. [Google Scholar]
- Zhu, H.; McNamara, A.L.; McMahon, S.J.; Ramos-Mendez, J.; Henthorn, N.T.; Faddegon, B.; Held, K.D.; Perl, J.; Li, J.; Paganetti, H.; et al. Cellular response to proton irradiation: A simulation study with TOPAS-nBio. Radiat. Res. 2020, 194, 9–21. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Wilson, W.E.; Goodhead, D.T. Computational approach for determining the spectrum of DNA damage induced by ionizing radiation. Radiat. Res. 2001, 156, 577–583. [Google Scholar] [CrossRef]
- Friedland, W.; Jacob, P.; Paretzke, H.G.; Stork, T. Monte Carlo simulation of the production of short DNA fragments by low-linear energy transfer radiation using higher-order DNA models. Radiat. Res. 1998, 150, 170–182. [Google Scholar] [CrossRef]
- Friedland, W.; Jacob, P.; Bernhardt, P.; Paretzke, H.G.; Dingfelder, M. Simulation of DNA damage after proton irradiation. Radiat. Res. 2003, 159, 401–410. [Google Scholar] [CrossRef]
- Sakata, D.; Lampe, N.; Karamitros, M.; Kyriakou, I.; Belov, O.; Bernal, M.A.; Bolst, D.; Bordage, M.C.; Breton, V.; Brown, J.M.C.; et al. Evaluation of early radiation DNA damage in a fractal cell nucleus model using Geant4-DNA. Phys. Med. 2019, 62, 152–157. [Google Scholar] [CrossRef]
- Chatzipapas, K.P.; Tran, N.H.; Dordevic, M.; Zivkovic, S.; Zein, S.; Shin, W.G.; Sakata, D.; Lampe, N.; Brown, J.M.C.; Ristic-Fira, A.; et al. Simulation of DNA damage using Geant4-DNA: An overview of the “molecularDNA” example application. Precis. Radiat. Oncol. 2023, 7, 4–14. [Google Scholar] [CrossRef]
- Kreipl, M.S.; Friedland, W.; Paretzke, H.G. Time and space-resolved Monte Carlo study of water radiolysis for photon, electron and ion irradiation. Radiat. Environ. Biophys. 2009, 48, 11–20. [Google Scholar] [CrossRef]
- Park, S.; Agmon, N. Theory and simulation of diffusion-controlled Michaelis-Menten kinetics for a static enzyme in solution. J. Phys. Chem. B. 2008, 112, 5977–5987. [Google Scholar] [CrossRef]
- Gopich, I.; Agmon, N. Excited-state reversible geminate reaction. III. Exact solution for noninteracting partners. J. Chem. Phys. 1999, 110, 10433–10444. [Google Scholar] [CrossRef]
- Agmon, N.; Gopich, I. Exact long-time asymptotics for reversible binding in three dimensions. J. Chem. Phys. 2000, 112, 2863–2869. [Google Scholar] [CrossRef][Green Version]
- van Zon, J.S.; ten Wolde, P.R. Green’s-function reaction dynamics: A particle-based approach for simulating biochemical networks in time and space. J. Chem. Phys. 2005, 123, 234910. [Google Scholar] [CrossRef]
- Plante, I.; Devroye, L.; Cucinotta, F.A. Random sampling of the Green’s functions for reversible reactions with an intermediate state. J. Comput. Phys. 2013, 242, 531–543. [Google Scholar] [CrossRef]
- Plante, I. A review of simulation codes and approaches for radiation chemistry. Phys. Med. Biol. 2021, 66, 03TR02. [Google Scholar] [CrossRef]
- Plante, I.; Cucinotta, F.A. Simulation of the radiolysis of water using Green’s functions of the diffusion equation. Radiat. Prot. Dosim. 2015, 166, 24–28. [Google Scholar] [CrossRef]
- Plante, I.; Devroye, L. On the Green’s function of the partially diffusion-controlled reversible ABCD reaction for radiation chemistry codes. J. Chem. Phys. 2015, 297, 515–529. [Google Scholar] [CrossRef]
- Meylan, S.; Incerti, S.; Karamitros, M.; Tang, N.; Bueno, M.; Clairand, I.; Villagrasa, C. Simulation of early DNA damage after the irradiation of a fibroblast cell nucleus using Geant4-DNA. Sci. Rep. 2017, 7, 11923. [Google Scholar] [CrossRef]
- Cobut, V.; Frongillo, Y.; Patau, J.P.; Goulet, T.; Fraser, M.J.; Jay-Gerin, J.P. Monte Carlo simulation of fast electron and proton tracks in liquid water-I. Physical and physicochemical aspects. Radiat. Phys. Chem. 1998, 51, 229–244. [Google Scholar] [CrossRef]
- Karamitros, M.; Luan, S.; Bernal, M.A.; Allison, J.; Baldacchino, G.; Davidkova, M.; Francis, Z.; Friedland, W.; Ivantchenko, V.; Ivantchenko, A.; et al. Diffusion-controlled reactions modeling in Geant4-DNA. J. Comput. Phys. 2014, 274, 841–882. [Google Scholar] [CrossRef]
- Kundrát, P.; Friedland, W.; Becker, J.; Eidemüller, M.; Ottolenghi, A.; Baiocco, G. Analytical formulas representing track-structure simulations on DNA damage induced by protons and light ions at radiotherapy-relevant energies. Sci. Rep. 2020, 10, 15775. [Google Scholar] [CrossRef]
- Margis, S.; Magouni, M.; Kyriakou, I.; Georgakilas, A.G.; Incerti, S.; Emfietzoglou, D. Microdosimetric calculations of the direct DNA damage induced by low energy electrons using the Geant4-DNA Monte Carlo code. Phys. Med. Biol. 2020, 65, 045007. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D. Proton-Coupled Electron Transfer in DNA on Formation of Radiation-Produced Ion Radicals. Chem. Rev. 2010, 110, 7002–7023. [Google Scholar] [CrossRef]
- Belli, M.; Cherubini, R.; Dalla Vecchia, M.; Dini, V.; Moschini, G.; Signoretti, C.; Simone, G.; Tabocchini, P.; Tiveron, M. DNA DSB induction and rejoining in V79 cells irradiated with light ions: A constant field gel electrophoresis study. Int. J. Radiat. Biol. 2000, 76, 1095–1104. [Google Scholar] [CrossRef]
- Belli, M.; Cherubini, R.; Dalla Vecchia, M.A.; Dini, V.; Esposito, G.; Moschini, G.; Sapora, O.; Signoretti, C.; Simone, G.; Sorrentino, E.; et al. DNA Fragmentation in mammalian cells exposed to various light ions. Adv. Space Res. 2001, 27, 393–399. [Google Scholar] [CrossRef]
- Campa, A.; Ballarini, F.; Belli, M.; Cherubini, R.; Dini, V.; Esposito, G.; Friedland, W.; Gerardi, S.; Molinelli, S.; Ottolenghi, A.; et al. DNA DSB induced in human cells by charged particles and gamma rays: Experimental results and theoretical approaches. Int. J. Radiat. Biol. 2005, 81, 841–854. [Google Scholar] [CrossRef]
- Frankenberg, D.; Brede, H.J.; Schrewe, U.J.; Steinmetz, C.; Frankenberg-Schwager, M.; Kasten, G.; Pralle, E. Induction of DNA Double-Strand Breaks by 1H and 4He Ions in Primary Human Skin Fibroblasts in the LET Range of 8 to 124 keV/µm. Radiat. Res. 1999, 151, 540–549. [Google Scholar] [CrossRef]
- Höglund, E.; Blomquist, E.; Carlsson, J.; Stenerlöw, B. DNA damage induced by radiation of different linear energy transfer: Initial fragmentation. Int. J. Radiat. Biol. 2000, 76, 539–547. [Google Scholar] [CrossRef]
- Leloup, C.; Garty, G.; Assaf, G.; Cristovao, A.; Breskin, A.; Chechik, R.; Shchemelinin, S.; Paz-Elizur, T.; Livneh, Z.; Schulte, R.W.; et al. Evaluation of lesion clustering in irradiated plasmid DNA. Int. J. Radiat. Biol. 2005, 81, 41–54. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plante, I.; West, D.W.; Weeks, J.; Risca, V.I. Simulation of Radiation-Induced DNA Damage and Protection by Histones Using the Code RITRACKS. BioTech 2024, 13, 17. https://doi.org/10.3390/biotech13020017
Plante I, West DW, Weeks J, Risca VI. Simulation of Radiation-Induced DNA Damage and Protection by Histones Using the Code RITRACKS. BioTech. 2024; 13(2):17. https://doi.org/10.3390/biotech13020017
Chicago/Turabian StylePlante, Ianik, Devany W. West, Jason Weeks, and Viviana I. Risca. 2024. "Simulation of Radiation-Induced DNA Damage and Protection by Histones Using the Code RITRACKS" BioTech 13, no. 2: 17. https://doi.org/10.3390/biotech13020017
APA StylePlante, I., West, D. W., Weeks, J., & Risca, V. I. (2024). Simulation of Radiation-Induced DNA Damage and Protection by Histones Using the Code RITRACKS. BioTech, 13(2), 17. https://doi.org/10.3390/biotech13020017








