1. Introduction
The bystander effect is one of the non-targeted (indirect) effects of ionizing radiation’s interaction with cells. As a result of its occurrence, various types of damage (including mutations) appear not only in the directly irradiated cell, but also among its non-irradiated neighbors. One of the first experiments to confirm the presence of the bystander effect took place in the early 1990s. It consisted in irradiating 1% of Chinese hamster ovary cells with a low dose of ionizing radiation. As a result of this irradiation, as much as 30% of cells were damaged [
1,
2]. Moreover, by increasing the dose from 0.3 to 2.5 mGy, the number of lesions increased, while for higher doses, their number remained constant. These results were the first observations of the bystander effect, although its mechanism was initially not fully understood. Generally speaking, this phenomenon consists of the appearance of various types of irradiation effects, such as reduced survival, carcinogenesis or apoptosis, in cells that have not been directly exposed to ionizing radiation. In irradiated cells, apart from specific ionization of macromolecules, long-lived radicals (atoms or molecules containing unpaired electrons) may appear with a half-life of approximately 20 h. Thus, mainly they can induce DNA damage in bystander (neighboring) cells. Moreover, studies [
2] have shown that nitric oxide also had a significant influence on the irradiation of cells, causing cell damage. Being a free radical, this molecule plays an important role in many biological processes, e.g., it stimulates apoptosis.
It is important to clarify, at this point, that the indirectness of the bystander effect (the use of term “indirect”) means something different than the direct/indirect ionization of the DNA molecule. In this case, the ionizing radiation interacts with the cell which is not the bystander one.
With regard to the mechanism of the propagation of signals of the bystander effect to other cells, some theoretical models [
3] have distinguished two ways in which it occurs, as follows:
The process of signals propagation from the irradiated cell to the bystander cell can be described by the diffusion equation, which is the process of the spontaneous spreading and permeation of molecules in the medium, which is a consequence of chaotic collisions of diffusing particles.
The probability of this effect increases quasi-linearly as the dose increases in the low dose area, and then becomes saturated and constant for the higher doses. The effect is observed when the cells are irradiated both by low and high linear energy transfer (LET) radiation [
1,
6].
The bystander effect can have both positive and negative effects. If healthy cells are damaged, the effect is negative. It can lead to secondary cancers and other radiation-related detrimental effects. However, if a bystander cell is a neoplastic one, it will be the most desirable result. Moreover, the bystander effect may, under certain conditions, lead to an adaptive response [
7,
8,
9], commonly regarded as a positive effect.
Interestingly, the bystander effect is observed not only between cells, within one organism, but also between different organisms. This is evidenced by an experiment in which a certain proportion of the fish population was exposed to X-rays at a dose of 0.5 Gy. In the next step, the above group was brought into contact with non-irradiated individuals. After some time, some radiation effects were noticed among the fish which were not exposed directly to radiation. This is one of the first indications that the bystander effect can also occur between different organisms and not, as previously thought, only between cells within single organism. In this particular case, it is important that the environment was water, which allowed for the propagation of physicochemical signals to surrounding organisms, analogically to the signals in the subcellular environment [
10].
2. Review of Existing Models
Although the bystander effect is studied primarily by radiobiologists, due to the specific propagation processes of physicochemical signals that can be expressed mathematically, physicists also began to deal with this subject. In particular, in recent years, many biophysical models (see subsections below) have been developed, which, by implementing biological data and physical mechanisms into computational code, successfully generate results that help to better understand this relatively recently discovered effect.
The most important models describing the radiation bystander effect are described below. The method of models’ selection was based on the Google Scholar database, with the search term “bystander effect”—only the papers that addressed the biophysical or biomathematical modeling with computational application were taken into consideration. Additionally, the last item describes our own Monte Carlo model of the bystander effect.
2.1. Chinese Model Xia–Liu–Xue–Wang–Wu
This is one of the first models simulating the response of cells to ionizing radiation, taking into account the bystander effect using the Monte Carlo technique [
11]. It assumes that a cell that is directly irradiated can send signals to its neighbors, causing them indirect damage. The authors call these bystander signals. Their distribution is strictly defined and described using the simplified Einstein diffusion equation, as follows:
where D is a translational mobility,
is a time interval and
corresponds to the distance traveled by the signal after the time interval.
Translational mobility related to signal propagation depends, among other things, on the mass of the signal-carrying molecule. In the case of the bystander effect, these may be cytokines [
12] with a mass of about 10 kDa [
13]. Hence, the translational mobility of D approximately equals
.
After the time, , passes, one assumes that the signal travels a certain distance in any direction. The signal at the distance, a, from the cell can cause reactions between them. The model assumes that the distance, a, is equal to the cell size, i.e., approximately 10 µm. In this case, two possibilities were assumed, as follows:
the signal hitting a cell (that is already damaged) will disappear from the simulation due to being absorbed by the cell;
as soon as a signal hits a cell that is not damaged, it will continue to move in any direction.
In addition, each cell that comes into contact with the bystander effect signals can send another signal with the probability . Next, the damage occurs with the probability denoted as . The lifetime of a signal (after which it disappears from the simulation) is also strictly defined. However, from a biological point of view, it has nothing to do with the lifetime of the cytokine, but is merely a phenomenological assumption of the model.
In the described Chinese model, apart from the damage related to direct irradiation and as a result of the reaction with the bystander effect signals, the natural damage described by the Gaussian distribution was also taken into account.
In order to estimate individual parameters, the authors of the model performed simulations in which the number of generated signals was strictly defined. For each of them, the probability and lifetime values were adjusted so that their results were consistent with the experimental data. The values of individual parameters are presented in
Table 1.
The simulation results show that damages occur not only among bystander cells, but also in those distant from each other, which is consistent with the assumptions and experimental data.
2.2. BSDM Model
The BSDM (Bystander Diffusion Model) is another biophysical model simulating the appearance of the bystander effect among non-irradiated cells [
14,
15,
16,
17]
. It assumes that only cells killed by a direct hit of ionizing radiation send molecules called bystander signals to their neighbors. The way of their propagation is related to diffusion and can be described by an equation analogous to Equation (1).
The value of mobility is closely related to the mass and size of proteins, as in the Chinese model. The authors assumed that the mass was from 400 Da to 40 kDa, and the radius was 0.67–6.7 nm, assuming a spherical shape. Therefore, the value of D has been estimated between . This is a value similar to the one described in the previous section. For a typical exposure time, i.e., about 10–15 min, the average distance traveled by the signal is from 120 to 1000 μm.
Moreover, the model assumes the following:
that the lifetime of the signals is greater than the expected diffusion time;
that the reaction between the signal and the cell occurs when the distance between them is less than half the size of the cell (R);
that a cell can emit two kinds of bystander effect signals: S-type signals—causing cell death; T signals—transforming into a cancer cell;
that bystander effect signals do not react with each other;
that diffuse cell movements are ignored;
that neighborhood signals do not react with the cells that emit them.
For the calculation of the fraction of cells that survived irradiation, not only the direct interaction with radiation, but also the contact with the signals of the bystander effect is taken into account. This relationship is described by the following equation:
where
is the fraction of survived cells,
is the fraction of cells that have survived direct irradiation with ionizing radiation, i.e., the relative number of recipients of the signals of the bystander effect, and
corresponds to the fraction of cells that received bystander effect signals and died as a result.
An analytical solution of Equation (2) is rather impossible; however, authors of the model created a simple algorithm that allows calculation of the values of
Sd and
BS. By definition, Formula (2) can be written as follows:
where
is the initial number of cells,
is the number of dead cells killed by direct irradiation and
is the number of cells which received the bystander signal.
Knowing the irradiation conditions, the total number of surviving cells and the exact pattern of signal propagation, it is possible to estimate the function
B(
x), as follows:
with
c1 and
c2 as so-called expansion coefficients. Assuming that
and using the appropriate substitution, the following equations can be obtained, enabling the calculation of individual fractions:
It follows from the above equations that the fraction of cells that survived both direct and bystander interaction with radiation is dependent on the fraction of cells hit by the radiation beam. Therefore, having appropriate data, it is possible to experimentally estimate the values of the numerical constants c1 and c2.
Referring to the fraction of cells transformed into neoplastic cells, the model assumed that their density can be given as follows:
where
c and
b are constants given by the experiment and
D is the dose to cell.
Applying the algorithms presented above, the authors of the model performed simulations enabling the calculation of the number of cells that received the bystander effect signals and the values of
B(
x). The results are presented in
Table 2.
Comparison with existing experimental data shows that this model works better for the dose described by the Poisson distribution than for homogeneous cell irradiation. It is worth adding that the assumption about the Poisson nature of the dose dependence as a function of the distance from the beam axis is also reflected in other independent studies on the bystander effect [
18,
19].
2.3. BaD Model
The BaD model [
20] (Bystander and Direct) is a quantitative model investigating the bystander and direct effects of ionizing radiation on cells. It places particular emphasis on the bystander effect and assumes that:
in the case of neoplastic transformation, the “all or nothing” principle prevails, according to which the radiation dose increase does not cause the increase in the observed neoplastic effects, but only the transformation process itself;
in the case of a cell hit directly by radiation, the bystander effect is negligible.
The signal propagation mechanism in the BaD model is not described in detail, so it can be used both for cells which are in contact with, or are distant from each other. The assumptions of this model were based on the results of three different experiments, as follows:
in the first one, a whole group of cells was exposed to ionizing radiation;
in the second, only 10% of the total cell population was irradiated;
in the last one, the cells were irradiated, where the dose is described by the Poisson distribution from the beam axis (irradiated cell).
On this basis, three different methods of calculating both the irradiated cell fraction and the cell fraction associated with neoplastic transformation were determined. In the first case, where all cells have been irradiated, the calculation of the fraction of surviving cells is described by the following:
where
q is a probability of cell survival after a single hit by an ionizing particle, and
N is the number of alpha particles which irradiated the cell. Based on experimental data, the value of
q was assessed as
. Thus, the fraction of survived cells will decrease when the number of alpha particles increases.
Next, the fraction of cells which are mutated after irradiation is given by the following:
where
v is a slope of linear response to the dose. Thus, the ratio of transformed cells to survived cells equals the following:
which is proportional to the number of α particles interacting with the cell.
In the second case, where 10% of cells were irradiated, the fraction of survived cells is given by the following:
where
F(N) is a fraction of cells which survived after bystander signal interaction.
As one can see, the first part of Equation (12) is identical to Equation (9), multiplied by 0.1. This is closely related to the fact that only 10% of all cells were irradiated. The second part is related to the bystander effect. Next, having determined the value of the parameter,
q, knowing the number of particles (
N) with which the cell has been irradiated, the value of
F(N) can be determined empirically using Equation (12) which gives the following:
The above function confirms that in the case of cell death caused by signals of the bystander effect, the aforementioned “all or nothing” rule does not apply, which means that as the radiation dose increases, the number of dead cells also increases. The fraction of cells which reacted with both ionizing radiation and bystander effect signals, and survived, can be described by the following relationship:
where
is a scaling constant for number of cancer transformation for low doses. Similarly to before, the first term of Equation (14) was multiplied by 0.1, as only 10% of cells were irradiated. The second term applies to the remaining 90% of cells that can be reached by the bystander effect signals, which is the reason for the value of 0.9.
The fraction of cells that underwent neoplastic transformation is finally presented as follows:
In the case of the last experiment, where the cells were irradiated with the radiation dose determined by the Poisson distribution, the fraction of surviving cells is presented as follows:
where
is the fraction of cells surviving after bystander effect signal interaction. As described in the case of the cell fraction, knowing
q, it was possible to determine
F(N). Here, on the basis of experimental data, the value
was estimated (where
it is the average number of particles with which the cell has been irradiated) and equals the following:
The fraction of cells which survived transformation (and assuming the dose given by Poisson distribution) is given by the following:
Thanks to Equations (17) and (19), with the assumption of
G = 1, the frequency of cancer transformation per living cell equals the following:
For large
, the second term in Equation (19) can be neglected; therefore, a simple linear relationship can be used instead, as follows:
In the opposite situation, when is small, the mentioned second term is significant and larger than the term connected with direct irradiation.
Equations (14) and (18) show the main assumptions of the presented model, namely the fact that those cells that are hypersensitive (susceptible) to neoplastic transformations related to bystander signals are also hypersensitive to death associated with direct radiation.
In order to test the model, the authors of the original paper [
20] conducted appropriate simulations, and their results were compared with the experimental data. The obtained results show good compliance of the model with real data.
2.4. The Ebert–Suchowerska–Jackson–McKenzie Model
This is a biomathematical model in which it is assumed that the responses of a group of cells to direct irradiation and to bystander effect signals (resulting from earlier irradiation) are independent of each other [
21].
When a cell is hit (it interacts directly with ionizing radiation), it can send bystander effect signals. They propagate by diffusion (similar to the previously described models) and end up in bystander cells that have not been directly irradiated.
According to the information mentioned earlier, as a result of interaction with radiation, a cell can produce various types of signals. However, this model assumes that this is the sole type of signal that can cause cell death, cell damages (that can be repaired), and might not cause any changes. The response to the bystander effect signals is related to the radiation dose and the number of bystander signals accumulated in the cell, which is described by the following equation:
where
W is a probability of signal diffusion from point
r to point
r’, and
is a local density of bystander signals.
The complete response of cells to radiation is related to both direct irradiation and bystander effect signals, and is given by the following:
where
is a fraction of survived cells,
is a fraction of cells survived direct irradiation and
is a fraction of cells that survived bystander signals interaction. The first, right hand term of Equation (22) can be described by saturated linear–quadratic function of dose per cell (
dlocal), as follows:
where
and
are linear–quadratic parameters.
With regard to the fraction of cells that survived the interaction with the bystander signals, three different methods of its calculation are considered in the described model. Before they are presented, first the µ parameter should be defined, which determines the number of signals of the bystander effect, thanks to which it is possible to calculate the strength of the produced signals, , which is proportional to their density.
Method 1:
In the first case, the signal strength is proportional to the fraction of cells which died after direct irradiation, as follows:
Method 2:
In the second case, the signal strength is proportional to the number of cells which were hit (irrespective of their death), as follows:
where
is a probability of radiation interaction of the cell (proportional to the physical cross section [
22]).
Method 3:
In the last case, the signal strength is proportional to the number of cells which survived direct irradiation, as follows:
For each method of calculation of the signal strength, individual parameters were adjusted so that the simulation results agree with the experimental data. Moreover, in time-dependent or diffusion-limited experiments, the propagation pattern was the same as that used in the BSDM model. In this case, the spatially averaged signal density is considered and can be calculated using the following equation:
Finally, the fraction of cells which survived the interaction with bystander signals, can be described as follows:
In both Method 1 and Method 2, the signal strength increases to a certain point and saturates. However, in Method 3, the maximum value is reached for a particular dose value. This is because as the number of surviving cells decreases, so does the number of cells that can receive these signals.
In order to test the model, its authors conducted a series of simulations, during which they adjusted all parameters so that the results were consistent with the experimental data.
Table 3 and
Table 4 show the values of individual parameters for NCI-H460 (non-small-cell lung cancer cells) and MM576 (melanoma cells).
All three approaches in the model give results that are consistent with the experimental data. Additionally,
Table 3 and
Table 4 present the results of the chi square test [
23]. It shows that the best compatibility with experimental data was obtained with Method 1, and the least satisfactory fit is observed using Method 3. However, as mentioned earlier, all simulation results agree with the experiment within the limits of uncertainty.
2.5. Japanese Hattori–Yokoya–Watanabe Model
It is another model [
3] that simulates the response of cells to ionizing radiation, taking into account the bystander effect. It is based on a two-dimensional cellular automaton in which three main components (states) can be distinguished, as follows:
cells;
medium (e.g., empty space, water);
wall (walls of a vessel containing a group of cells or other tissue, e.g., bone).
In practice, each field labeled as a cell can be filled with a culture liquid where the cell is directly located. However, only the culture liquid is present in the medium state, and the wall may represent, for example, a container in which the cell culture is located.
The entire simulation algorithm consists of four main components, as follows:
cell irradiation;
generating bystander effect signals;
DNA damage induced by direct irradiation and by bystander signals;
cell response to induced DNA damage.
The dose absorbed by the irradiated cell can be calculated using the following equation:
where
is a dose per cel which is a result of single particle track irradiation, and
is the number of ionizing radiation tracks in the cell labelled as (
i,
j) in the moment of time,
t.
It should be mentioned here that the number of radiation tracks in bystander cells is described by the Poisson distribution, as follows:
where
is a probability of
n tracks appearance in the cell (
i,
j) in the time,
t, and
a is the average number of ionizing radiation tracks in the cell (
i,
j) in the time,
t.
Both values
and
are different for various types of radiation. For example, for cells irradiated by gamma radiation of
, both values equal
= 1 mGy and
a = 1000 tracks/min, respectively, which was calculated by microdosimetric methods [
3].
The irradiated cell can send bystander signal to nearby cells by two ways, as follows:
Moreover, the model assumes that the signals cannot interact with each other, and their number is proportional to the dose. The propagation of signals is also strictly defined and described by the following equation:
where the following are true:
is a bystander signal concentration in the position (i,j) in the time, t;
is a time interval (time step);
is a cell’s two dimensional surface;
is a diffusion constant;
are coordinates of cells which are located linearly close to the irradiated cell (i,j) in positions: (i + 1, j), (i − 1, j), (i, j + 1) and (i, j − 1);
are analogical coordinates but diagonal: (i + 1, j + 1), (i − 1, j − 1), (i − 1, j + 1) and (i + 1, j − 1);
Due to the fact that the model takes into account two signal propagation paths, two variables related to the direction of signal diffusion should be defined— (related to MDP) and (related to GJP)—the value of which is related to whether the position (k,l) is a cell, wall or medium. Therefore, we have the following:
, when the position (k,l) is a cell;
, when the position (k,l) is a medium;
, when the position (k,l) is a wall;
, when the position (k,l) is a cell;
, when the position (k,l) is a medium;
, when the position (k,l) is a wall.
The values of the diffusion constants are directly related to the way the signals propagate in two ways, as mentioned. Therefore, if the signal propagates on an MDP path, then it can appear in the cell and medium; therefore, if the position (k,l) has this status, then the coefficient . In the case of GJP, the signal can appear only in the cell, so if the position (k,l) has the status of a cell, then . In both cases, the signal cannot appear in the wall. In addition, with the GJP, the signal does not propagate to the medium. In this case, the diffusion constant is 0, which is equivalent to stopping the signal.
Regarding the number of bystander effect signals produced by MDP and GJP, it can be calculated using the following equations:
where the following are true:
and are constants related to creation of signals;
and are constants related to reduction (decay) of signals;
is a radiation dose to cell.
Knowing the number of signals of the bystander effect produced by the irradiated cells, it is possible to analyze the induced damage. It was assumed that direct irradiation and signals of the bystander effect can cause DSBs (double strand breaks), which in turn can cause, inter alia, cell cycle arrest or cell death. Moreover, the damage caused by direct radiation and by the bystander effect signals are produced independently, and the number of DSBs are proportional to the number of bystander effect signals.
The total number of damages is calculated by the following equation:
where the following are true:
are damages created by direct irraditation;
are damages created by MDP signals;
are damages created by GJP signals;
are damages created by some other external events;
are damages already repaired.
All mentioned terms of Equation (34) can be described by Poisson distribution with: , , and where , , and are average values of , and , respectively. The coefficient is constant for each parameter.
The last term of Equation (34), which is related to the probability of DSBs repair, was simplified and constant for all types of damages, and equals .
2.6. Monte Carlo Model
Another model simulating the bystander effect is the Monte Carlo model, based on a probability tree [
24,
25], developed at the National Center for Nuclear Research (NCBJ) in Poland, as part of a larger model describing the behavior of a irradiated group of cells. In this model, only the negative effects of the bystander effect, consisting in the appearance of additional damage in the cell, were taken into account.
The aforementioned Monte Carlo model is completely stochastic and describes comprehensively, but on a general level, possibly all biophysical phenomena concerning the irradiated cell, taking into account various factors—e.g., cell death, transformation into a cancer cell, spontaneous formation of damage, and repair of damage, etc.—which, as mentioned, uses the Monte Carlo processes and the probability tree in its algorithm.
The model assumes that the probability of the bystander effect appearance is given by the probability function [
24], as follows:
This is a quasi-linear function related to the dose (
D) with scaling constants
and
, which saturates for high doses. This is fully consistent with many experimental findings [
1,
6].
The described model treats time as a discrete one, where the i-th cell, in which the bystander effect may occur, is taken into account in each time step, according to Equation (35). In other words, Equation (35) describes whether or not the bystander effect will be initiated by the i-th cell at a given time step.
Then, if the
i-th cell is able to initiate the bystander effect (the probability
Pb is met), it sends signals to the bystander cells that can damage them with a probability expressed as a distribution of [
24] the following:
where
r is the distance between the
i-th cell, i.e., the cell that initiates the bystander effect, and the
j-th cell, where the bystander effect can occur. The factor 1/
r! comes from the Poisson distribution, which has already been discussed many times in other models. The block diagram of the described bystander effect algorithm is shown in
Figure 1.
In order to test the bystander effect, simulations were performed in which 700 healthy cells were irradiated with a constant radiation dose rate of 1 UAD/step, where the UAD (unit of absorbed dose) is the uncalibrated unit of the absorbed dose. Its precise determination can only take place after the model has been calibrated on the experimental data. The values of the parameters used in the simulations were = 0.001 and = 300, respectively. In each simulation, the number of cells damaged during a single bystander effect was counted. Then, on the basis of all the results, the mean was calculated, which was 5 ± 4. This result is in line with the expectations, as it shows that the bystander effect occurs mainly for cells closest to the cell initiating the effect.
2.7. Models Comparison
The review of some computational models presented in previous sections shows that there are many possibilities for a detailed description of this interesting radiobiological phenomenon—the radiation bystander effect. Most models have some common features (e.g., the use of the diffusion equation to describe the propagation of the bystander signal, or the Poisson dose distribution from the irradiated cell), but there are also fundamental differences between them. Of course, each of these models were intended to be applied to a specific situation, and the exact mathematical formalism was selected by the authors as the most optimal in the dedicated scope. The presented review does not decide which model is the best one. Generally, all the presented models describe the effect in a proper way, but with different approaches. A short comparison of the reviewed models is presented in
Table 5.
Due to the fact that the bystander effect is still investigated and some of its elements are not fully understood, there is no one universal model of its description. Therefore, the approach assuming the creation of a dedicated model for a specific application seems to be the only possible solution, although it essentially narrows the possibilities of using such a specific solution in a more general aspect.
3. Methodology
The review of the existing models presented in the previous section shows that there are many possibilities for a biomathematical description of the radiation bystander effect. Biophysical research on the bystander effect, and specifically its computer simulations, was also carried out in Poland, including the National Center for Nuclear Research and the Faculty of Physics of the Warsaw University of Technology. The simulations of the effect were an element of wider simulations of the influence of ionizing radiation on a group of cells, in particular the neoplastic processes [
27].
3.1. Description of the Algorithm
The aforementioned model of the bystander effect, developed by the authors of the presented paper, is based on the combination of the last two models described in the previous section, namely the Monte Carlo model and the Japanese Hattori–Yokoya–Watanabe model with some modifications. This approach takes into account the most important features of the bystander effect, namely the following:
diffusion signal propagation;
saturation of its probability distribution for a certain dose;
Poisson shape of the dependence of the number of damages on the distance from the hit cell.
The Monte Carlo model is based on the dedicated numerical code created by the authors. This code uses the iterative loops over the probability tree to simulate the behavior of irradiated cells which are arranged in three-dimensional geometry with appropriate states up to the Japanese approach. The detailed explanation of the adapted algorithm is presented below.
In the first stage of the simulation, the individual elements of the three-dimensional array imitating a group of cells are assigned appropriate statuses (such as medium, i.e., the intercellular area identical to the lack of a cell, or the cell, which in turn may be healthy, damaged, mutated or cancerous). Then, at each time step, the number of bystander effect signals, both MDP and GJP propagating, is calculated using Equations (32) and (33) (see Japanese model).
The next step is to calculate with the modified formula the total number of damages occurring in individual cells caused by GJP and MDP signals using the modified Equation (34):
where
and
. Wherein,
and
are constants, while
and
correspond to number of damages created in the MDP and GJP paths, respectively. The total number of damages, after appropriate rescaling, is treated as a contribution to the probability of the bystander effect appearance, which is described in detail according to the diagram in
Figure 1. The remaining processes are described according to the aforementioned Monte Carlo model: each cell has its age, number of lesions and a status table, in which information about the doses with which it was irradiated in a given time step (history of cell irradiation) is stored. Cells with healthy status have a damage index of 0, and above this value the status changes to damaged. Unrepaired (or incorrectly repaired) damage becomes mutation. If a mutation occurs in a cell, it automatically changes its status to mutated. The accumulation of mutations in the cell leads to the transformation into a neoplastic cell according to the sigmoid probability distribution [
27].
The whole algorithm consists of two iterative instructions (loops). The first one is a loop through time steps, and the second one follows all the elements of the three-dimensional array, that is, after all the cells. At each time step, the cell may or may not be irradiated, which may consequently cause various phenomena, in particular the bystander effect, described herein.
3.2. Exemplary Results of Simulation
The exemplary input parameters, which can be applied to the bystander effect simulation, are presented in
Table 6.
One of the basic elements that can be relatively easily tested by the simulation is the calculation of the fraction of all damages caused by the bystander signals. For this purpose, the irradiation of 512 healthy cells with the same radiation dose per one step (i.e., constant dose rate) for 500 time steps was simulated. Each simulation was repeated 100 times, and the presented results are the arithmetic mean of the values obtained for three different variants:
Option 1:
Option 2:
Option 3:
It follows from the above that the major part of damages are those caused by direct irradiation. The damages originating from the bystander signals, regardless of the value of the dose used, account for about 20% of all damages. The result is therefore in line with expectations [
2].
In the next simulation, the cells were irradiated only in the 5th and 15th time steps with the dose equal to 0.001 Gy; in the remaining time steps the dose was equal to zero. Duration of the simulation and the initial number of healthy cells did not change. As a result, the number of all damages was 0.15 ± 0.05, of which those resulting from the bystander effect signals were 0.03 ± 0.02.
Another simulation checked the propagation of signals of the bystander effect. For this purpose, a constant radiation dose rate was used, the value of which was 1 mGy/step, to irradiate the cell with the coordinates x = 5, y = 5, z = 5. For the remaining cells, the dose was zero. After the 1st time step, damage occurs only in the directly irradiated cell with a frequency of 6.52 × 10−6. After the 2nd time step, damage occurred in 7 cells, 1 of them being that which was directly irradiated. The remaining 6 cells were located in the nearest neighborhood to the directly irradiated cells: most damages occurred in a cell with coordinates (x, y, z) = (5,5,5) with the frequency 1.94 × 10−5, and in the other cells 1.78 × 10−8. After the third time step, damage appeared in 25 cells. The number of damages obtained as a result of the simulation was calculated using Equation (37), but in a more general approach, these values after scaling will be the probability of the appearance of the bystander effect in a particular cell at a given time step.
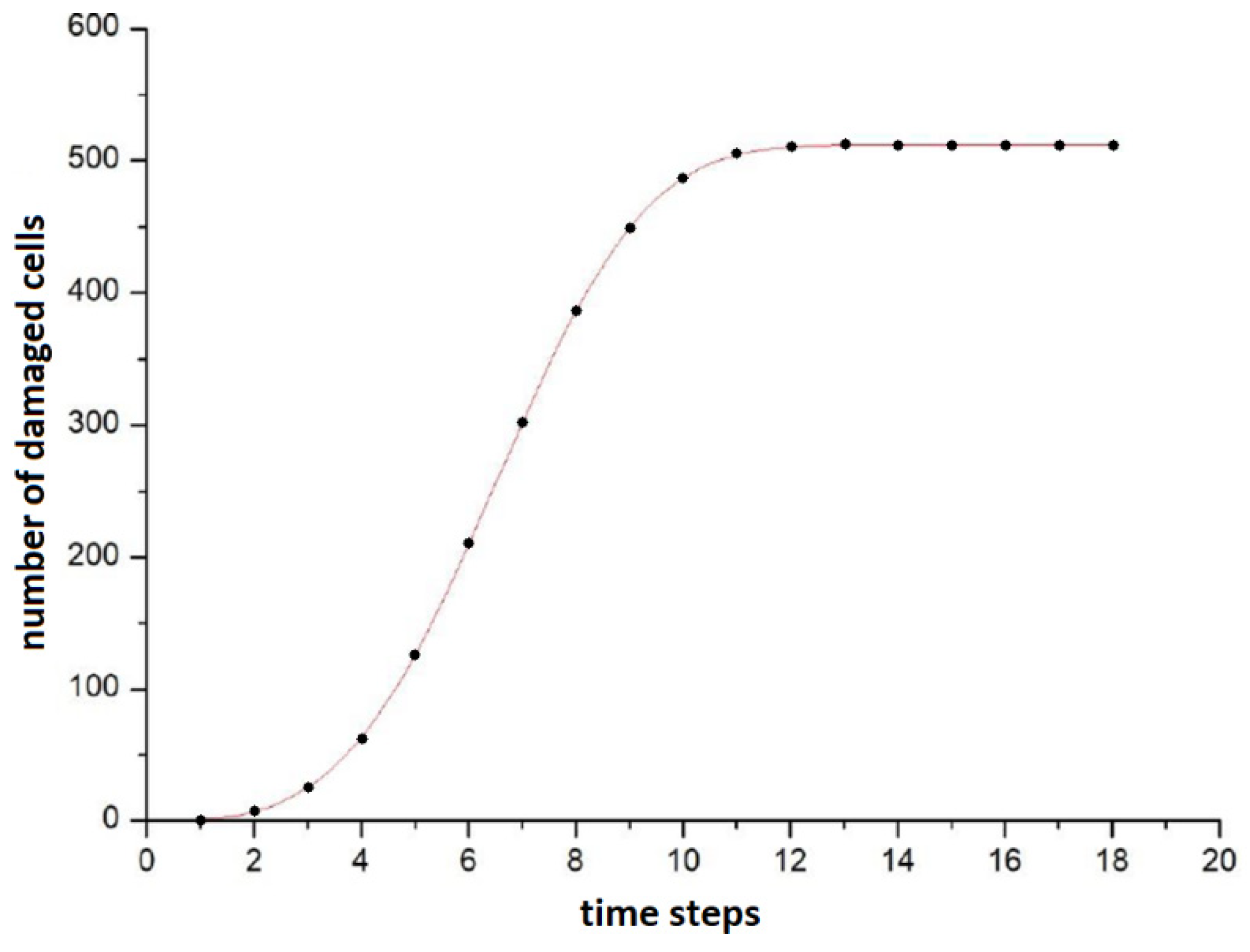
In subsequent time steps, the damage appeared to more and more distant cells. After 13 steps, all cells participating in the simulation had a failure frequency different from 0, which means that with a sufficiently long irradiation, the signals of the bystander effect can spread even to very distant cells from the irradiation site. The plot of the number of damaged cells against time is sigmoidal, as shown in
Figure 2. It shows that the number of cells between 4 and 9 times increases quasi-linearly, before the saturation. The best fit curve turned out to be the Avrami curve of the form
a − b·exp (−
c·xd) (which was originally derived from the theory of nucleation and crystal growth [
27]); however, this does not mean that after saturation the frequency of damage in all cells is the same—it follows a distribution similar to the Poisson one.
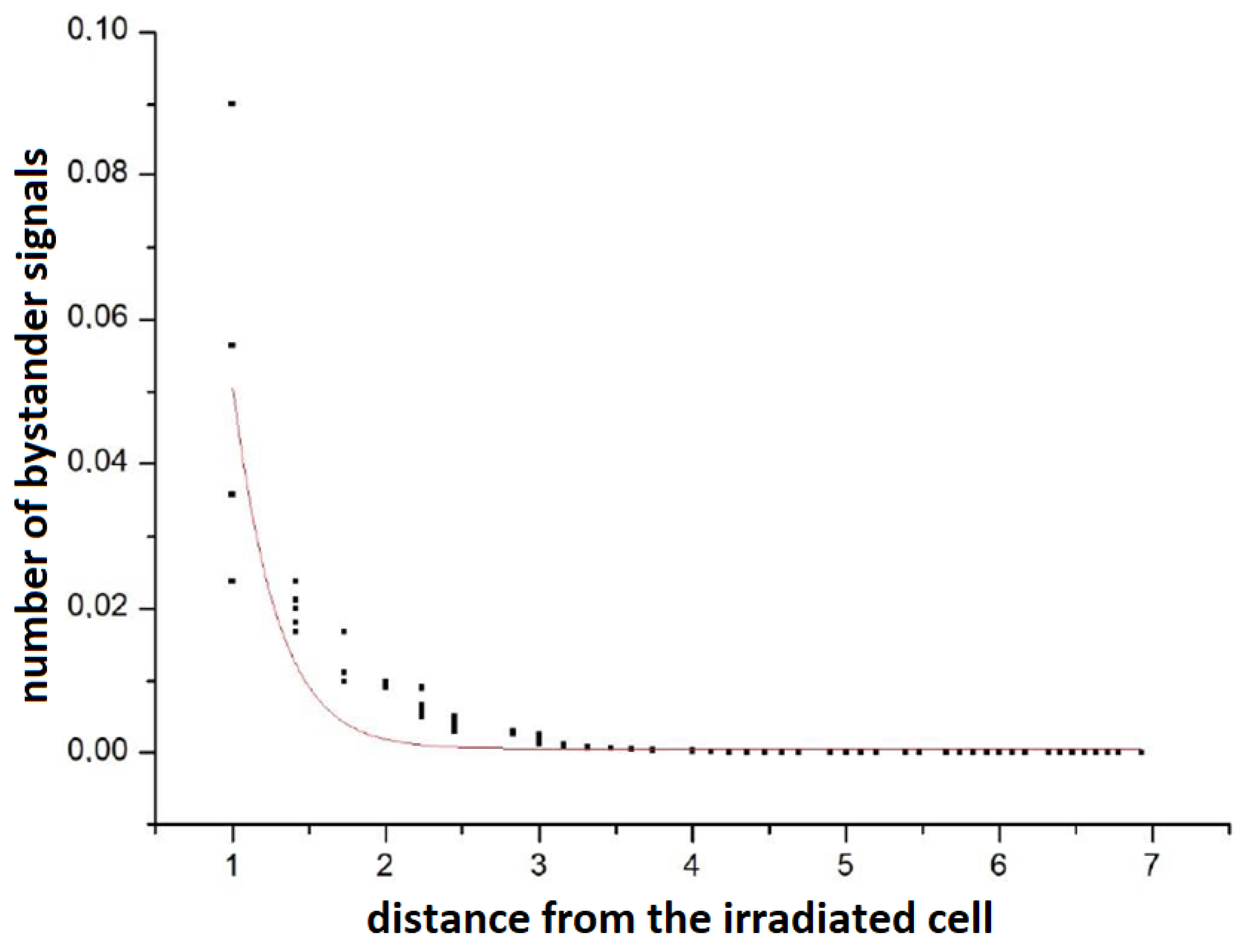
At this point, it is worth mentioning that the Poisson nature of the propagation of signals was checked: simulations were performed when one cell was irradiated with a dose of 2 UAD in the 1st time step. In the remaining time steps and for the remaining cells, the dose was 0. Then, the number of signals in all cells was checked after 500 steps.
Figure 3 shows the number of bystander signals in a cell versus the distance from the directly irradiated cell. It can be seen that the shape is slightly different from the Poisson curve. This is due to the influence of other cells (including changes in their status) and the complexity of the full model in relation to the ideally Poisson single cell description [
26].
The above simulation results confirm the thesis that damage occurs not only among directly irradiated cells, but also among their neighbors. In addition, the number of damages from bystander effect signals is only a part of total damages produced in cells, which also qualitatively proves the correct operation of the model.