Abstract
Phased injection of natural gas into internal combustion marine engines is a promising solution for optimizing performance and reducing harmful emissions, particularly unburned methane, a potent greenhouse gas. This innovative practice distinguishes itself from continuous injection because it allows for more precise control of the combustion process with only a slight increase in system complexity. By synchronizing the injection of natural gas with the intake and exhaust valve opening and closing times while also considering the gas path in the manifolds, methane release into the atmosphere is significantly reduced, making a substantial contribution to efforts to address climate change. Moreover, phased injection improves the efficiency of marine engines, resulting in reduced overall fuel consumption, lower fuel costs, and increased ship autonomy. This technology was tested on a single-cylinder, large-bore, four-stroke research engine designed for marine applications, operating in dual-fuel mode with diesel and natural gas. Performance was compared with that of the conventional continuous feeding method. Evaluation of the effect on equivalent CO2 emissions indicates a potential reduction of up to approximately 20%. This reduction effectively brings greenhouse gas emissions below those of the diesel baseline case, especially when injection control is combined with supercharging control to optimize the air–fuel ratio. In this context, the boost pressure in DF was reduced from 3 to 1.5 bar compared with the FD case.
1. Introduction
The use of phased natural gas injection in dual-fuel marine engines is an increasingly researched topic in the naval sector. In a context where emissions are at the forefront of global environmental concerns, the adoption of dual-fuel systems offers a promising solution to reduce the environmental impact of maritime operations by using high fractions of natural gas [1,2]. As highlighted by numerous studies available in the literature, the use of dual-fuel propulsion in the marine sector has long been a research interest, given its potential to reduce emissions in a sector where heavy fuels still predominate. The interest is further heightened when considering the possibility of using fuels produced from biomass and waste or derived from renewable energy sources combined with synthesis systems, further reducing the environmental impact of naval operations.
Many researchers have examined the application of dual-fuel engines for marine use, primarily experimenting with the injection of non-phased primary fuel into the intake manifold. A large portion of these studies evaluated various fuel combinations and operational strategies. Zhao et al. performed numerical simulations and experimental tests to evaluate the effects of different hydrogen ratios on combustion and emissions from maritime shipping engines with hydrogen–natural gas–diesel tri-fuel [3]. Zhang et al. used biodiesel–diesel blends to ignite natural gas and found that the best configuration was 80% energy of natural gas (NG) as the main fuel and 25% biodiesel by volume in the pilot fuel [4]. In [5], methanol–water blends were used as the primary fuel, and the authors analyzed benefits on thermal efficiency and other issues like methanol knock resulting in lower maximum diesel substitution limits. A joint experimental and computational investigation was conducted in [6] for a comparative assessment between ammonia/diesel fueling and a baseline natural gas/diesel, highlighting the potential for better performance of ammonia on total CO2-equivalent greenhouse gas (GHG) emissions. Other studies have focused mainly on optimizing the diesel pilot injection timing while maintaining continuous primary fueling admission or fixed injection phasing in the manifold. Valladolid et al. conducted activities in a single-cylinder engine configuration with compressed NG injection timing fixed at 330 CAD BTDC (crank angle degree, before top dead center), changing the pilot timing and highlighting the importance of combustion phasing control on pilot-ignited lean natural gas combustion under strict NOx emissions targets [7]. In [8], the NG injection timing was fixed at 300 CA BTDC for a throttled NG/diesel dual-fuel engine. The control of air intake and pilot injection timing led to performance benefits accompanied by a dramatic increase in specific NOx emissions for early combustion and high diesel substitution rates. Wang et al. investigated a pilot pre-injection strategy in a large marine four-stroke dual-fuel (DF) engine with eight cylinders placed in line [9]. The NG injection system was modeled as a timed multipoint. The authors found that different combustion modes can be achieved by advancing the pre-injection time and increasing the pre-injection mass ratio. Conversely, Yousefi et al. experimentally and numerically investigated the pilot post-injection benefits in a DF single-cylinder, four-stroke engine [10]. A fixed optimal natural gas injection timing was adopted. Results were compared with single and pre-main diesel injection strategies, showing the advanced start of combustion only in the second case. In [11], an extensive numerical analysis of several parameters was conducted. The pilot fuel injection timing and pressure, exhaust gas recirculation rate, nozzle number, and NG substitution ratio were swept, while NG was injected through the intake port with a fixed timing before the intake valve closed.
Another area of research focuses on the direct injection of diesel and natural gas in dual-fuel engines. In this context, the greater complexity of the system makes gaseous injection timing inherently linked to the adopted technology. For this type of engine, more parameters can be controlled for combustion optimization. For instance, in [12], the potential for achieving peak efficiency above 48% was reported, whereas in [13], direct low-pressure post-injection of NG was modeled to evaluate a more reasonable distribution of NG and increase stratification and combustion completeness at low load, where DF suffers from excessive air and poor combustion propagation. In [14], a numerical study was presented to evaluate the effect on combustion propagation by varying both the gas and diesel injection timing. These studies have contributed to improving the understanding of combustion dynamics and energy efficiency of dual-fuel engines. In addition, experimental investigations confirmed the benefits of pilot-ignited high-pressure direct injection DF technologies [15,16].
The focus of this study is to further explore the topic of gas injection timing. Several studies in the literature also address this aspect. Yang et al. experimentally investigated the effects of natural gas injection timing in a four-cylinder heavy-duty engine under a constant split pilot injection strategy. Their results indicated that certain stratification of natural gas occurred and was capable of enhancing the ignition kernel formation and flame propagation inside the chamber [17]. In [18], three variation pulse widths as the injection timing of natural gas were investigated on a single-cylinder diesel engine at a constant speed of 2000 rpm, and it was found that backing the injection time toward the closing of the intake valve with the right injection duration could reduce the value of methane slip. In [19], a double NG port fuel phased injection strategy was modeled to increase stratification, while experimental activities were conducted on a single-cylinder diesel engine [20] or a six-cylinder [21], highlighting the possibility of timing optimization. In general, advanced natural gas injection timing can improve mixture uniformity, but too early injection timing will involve a part of natural gas scavenging. However, only a limited number of studies have specifically addressed the issue of primary fuel injection timing. In this context, the present study aims to fill this gap in the literature by examining in detail the effects of primary fuel injection timing in dual-fuel marine engines. Through an in-depth experimental analysis and the use of an interpretative simple model, this study aims to provide a more comprehensive understanding of combustion dynamics in dual-fuel marine engines, thus contributing to the future development of more efficient and environmentally friendly technologies for the maritime sector. The novelty of this study lies in the experimental data collection using a dedicated system for the phased injection of NG and the interpretation of results using a numerical model. The aim is not only to determine the optimal injection timing but also to understand the reasons behind the experimental trends observed. Therefore, the main objectives are to define the optimal angle of NG injection, highlighting its benefits on efficiency and emissions. Additionally, this study aims to evaluate the performance of the DF system with phased injection, including insights into the phenomenological reasons for deviations from optimal conditions.
2. Materials and Methods
2.1. Experimental Setup
The experiments were carried out on a single-cylinder, large-bore, four-stroke research engine for marine applications, the main characteristics of which are reported in Table 1.

Table 1.
Engine parameters.
The experimental apparatus is shown in Figure 1. An external supercharging system provides air intake, with a throttling globe valve controlling the boost pressure. The pilot liquid fuel is injected directly into the combustion chamber at controlled pressure and injection law, while the main gaseous fuel is injected into the intake manifold. An eddy current brake is set to fix the speed of the motor regardless of the torque delivered. In addition to the torque measured by the brake, a pressure sensor in the combustion chamber coupled to an angle encoder with an accuracy of 0.5 CAD is used to acquire the indicated cycle and evaluate the indicated mean effective pressure (IMEP) delivered by the engine.
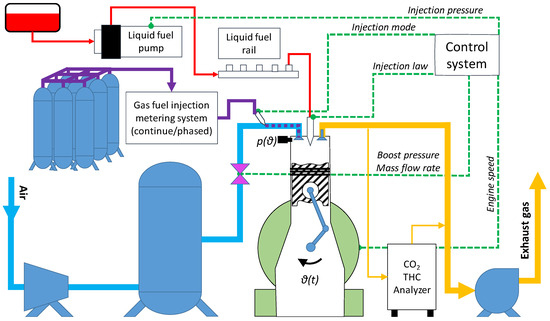
Figure 1.
Schematic diagram of the experimental apparatus and the system for controlling the test conditions.
Experiments were performed using a retrofit dual-fuel NG fuel system. Two injection systems were used to introduce the gas into the intake port immediately upstream of the inlet valves. In the first system, for the continuous admission of natural gas into the intake manifold, a pressure regulator was used, keeping the injection pressure 3.5 bar higher than the intake pressure, and a mass flow controller (range 0–150 slm N2 equivalent) was used to adjust the gas flow rate. The other system, for phased injection, is made up of a control unit, a dedicated phase sensor, and control software to set the injection valve in a completely independent manner from the liquid pilot fuel control system. The control system software provides maximum customization of injection parameters such as duration and angular phase shift with respect to a pre-established position identified by the phase sensor. The injector is current controlled with a signal characterized by a high initial current peak, which remains fairly constant for a relatively limited time, compared with the overall duration of the injection phase, and then drops to a significantly lower value in the maintenance phase, in which the gas continues to flow through the injector. The reduction in injection times is mainly achieved by decreasing the signal maintenance time. The NG injection signal is measured by an amperometric ring coupled to the shaft encoder. For both systems, a Coriolis natural gas mass flow rate was used.
The diesel fuel injection is controlled by an open engine control unit, allowing the setting of injection pressure and multiple injection intervals and timings.
The properties of the fuels used are in Table 2.

Table 2.
Test fuel properties.
According to a lambda sensor placed at the engine exhaust, the fuel injection rate is finely adjusted to reach the set air/fuel ratio.
THC exhaust gaseous emissions and CO2 were measured using a flame ionization detector (accuracy ± 1%) and a cold extractive IR gas analyzer (accuracy ± 2%).
2.2. Engine Test Conditions
Tests were conducted under steady-state conditions at 1500 rpm and a load level of almost 8 bar BMEP (brake mean effective pressure), corresponding to medium/low load conditions. Various types of tests were performed. Some were swept-type tests, with predefined operating conditions obtained by varying only certain control parameters with a constant step, whereas others were optimal search-type tests, with operating conditions modified by adjusting all available control parameters but only around some optimal points identified in the initial analysis. During the tests, the diesel injection pressure was varied from 800 to 1200 bar, and the pilot diesel injection timing was adjusted to ignite the DF combustion. The number and angular distance (dwell) between injections and the quantity of diesel in each injection were also varied. An NG/diesel mass ratio of almost 4 was set as it was the maximum compatible with stable combustion at the tested load conditions, keeping the diesel flow rates to a minimum. Tests were conducted with both continuous NG supply and phased injection.
The tests were conducted with boost air pressure at approximately 3 bar absolute for the full diesel (FD) conditions and 1.5 bar for most of the DF tests. DF tests were then conducted at higher boost pressures. As mentioned earlier, the boost pressure is achieved by an external supercharging system. The exhaust back pressure was left at ambient value to avoid complicating the experimental phase and to not have to account for significant differences in the concentration of residual gasses in the combustion chamber, thus obtaining more easily comparable results. However, the comparison between FD and DF was made by referring the quantities to a net power value to account for the external work performed by the supercharging air. That is, the gross power measured at the brake was reduced by the work performed by the supercharging air, which is greater in FD than in DF. Considering the energy supplied by the external supercharging system, it is possible to evaluate the additional IMEP beyond that related solely to combustion and thus evaluate the net BMEP using the following equations [22]:
where IMEPcor represents an estimate of the work per unit volume provided by combustion. It would coincide with the measured IMEP if the exhaust backpressure was set approximately equal to the boost pressure. The actual BMEP, measured at the brake of a single-cylinder engine, is provided by the sum of the following two contributions: the work performed by the gasses on the piston due to combustion and external supercharging. BMEPcor is an estimated value that takes into account only the contribution of combustion.
From the net BMEP, one can derive the net torque and the net efficiency, which is less influenced by the additional energy supplied by the supercharging system because it is the ratio of multiple quantities. It should be noted that the real case might lie somewhere between the performance in terms of gross BMEP and net BMEP, depending on the actual supercharging system configuration. It could be a mechanically driven compressor, which can be considered an additional load applied to the engine, similar to any other auxiliary load. In this case, the reference performance will be very close to that considering the net power output. However, more commonly, supercharging is achieved using a turbocharger. In this scenario, the real BMEP value might be intermediate between the gross and net quantities.
Indeed, the higher exhaust backpressure in the FD case compared with the DF case results in greater pumping work and thus an additional load equivalent to increased work absorption, which would reduce BMEP [23]. On the other hand, it must be considered that part of the energy supplied by the turbine is derived from the exhaust gas heat, which would otherwise be lost. In this way, an additional form of energy recovery is obtained, partially mitigating the negative effect of increased pumping work. Therefore, with equal supercharging pressure, the balance between passive and active work improves.
2.3. NG Phased Injection Interpretative Model
Phased injection, unlike continuous injection, requires optimizing the timing of the gas valve opening, considering the opening and closing times of the engine valves (intake and exhaust). The main purpose of this system, which is more complex than continuous fueling, is to reduce the loss of fresh mixture during valve overlap and, consequently, the emissions of THC, which mainly consist of NG and have a global warming potential (GWP) of about 30 times larger than CO2 [24] over a 100-year time scale. This goal is achieved by injecting the gas at a specific angular position, considering the time it takes for the gas to enter the cylinder under certain conditions. The most influential operational factors on this metric, in addition to the characteristics of the intake ducts, are engine speed and airflow rate. Paradoxically, unburned methane emissions could even increase compared with continuous injection if phased injection occurs such that the fresh mixture enters the cylinder mostly during valve overlap. In this case, a significant amount of gas would be lost through the exhaust valve during overlap without participating in combustion. This can never happen with continuous injection because the gas is always mixed (more or less uniformly) with the air trapped in the cylinder when the exhaust valve closes.
Therefore, an initial test campaign was conducted at 1500 rpm and 1.5 bar MAP (corresponding to about 270 kg/h of air) to identify the best injection timing. During the tests, the injection duration was kept constant, varying only the start of injection (SOI) angle relative to the top dead center (TDC) of the active cycle (compression–combustion–expansion).
The correct timing for NG injection is strongly influenced by the geometry of the intake ducts (diameters and lengths) and the airflow rates, which affect the velocities of the air/gas mixture and thus the time (expressed in CAD at a fixed engine speed) it takes to reach the cylinder. This avoids the major drawback of continuous gas injection systems, which is the loss of fresh mixture through the exhaust valve during overlap.
A reasonably accurate estimate of the time needed to travel the distance from the NG injection point to the cylinder was performed using a simplified model of the intake manifold geometry, as shown in Figure 2.
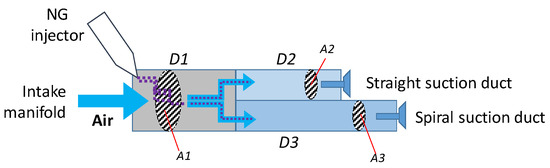
Figure 2.
Simplified scheme of the air and gaseous fuel supply system from the gas injection point into the intake manifold to the two intake valves at the end of the ducts. Ai and Di indicate duct section and diameter respectively while the purple squares represent the NG injected.
Table 3 presents the values used to calculate the angular durations of the natural gas injection through the injector and the interval that the air/gas mixture takes to reach the intake valves. This interval will differ for the two ducts of the single-cylinder head because of their different shapes and lengths. The length of manifold D1 includes the section where the gas injector is mounted and the short section of the duct in the cylinder head up to the beginning of the bifurcation into the two ducts leading to the two intake valves. Of the two ducts, one is straight and shorter than the spiral one, which in turn induces swirl motion. In these approximate calculations, the higher pressure losses induced by the swirl motion were not considered; therefore, the difference in CAD travel of the mixture in the two ducts is solely due to the difference in length.

Table 3.
Geometries and characteristic dimensions of the elements in the simplified diagram of the air and fuel supply system with phased injection.
In the table, the operating conditions of the tests are also reported. In this regard, it should be noted that when calculating the air velocity entering the cylinder, it was considered that the flow occurs only when the valves are open, and the intake phase coincides solely with the intake stroke from TDC to BDC (bottom dead center), with an angular duration equal to a quarter of the entire cycle. Therefore, a multiplicative factor of four was included in the calculation of the air velocity in the ducts to account for the fact that the air flow entering the cylinder during the entire cycle has only a quarter of its angular duration available. In the calculation approximations, the advanced opening and delayed closing of the intake valve were not considered. However, it should be considered that in the early opening and final closing phases of the valves, the air passage sections are very small, despite having a non-negligible angular duration, to allow for a gradual ramp for the opening and closing command that is not too abrupt, to reduce the impact and thus the wear and noise of the valve train. Another assumption is that the overall airflow is divided equally into each of the two ducts, whose sections are approximately half that of the intake manifold. Therefore, the velocity in all three ducts will be roughly the same, and the travel time, converted in CAD at the selected engine speed, of the mixture in the two ducts will be minimal in the straight duct (shorter) and maximum in the swirl duct (longer). From the travel times of the mixture in the individual ducts, the total travel times are derived by summing the travel in intake manifold D1 with those of the two ducts D2 and D3, respectively. In the case of the average value, segment D1 and the average between the travel in ducts D2 and D3 are considered, resulting in an angular interval of 141.5 CAD. This value represents the time taken for the gas injected at the SOI moment to reach the two intake valves on average. Therefore, in identifying the optimal conditions for gas injection timing, these travel times must be considered from when the gas starts entering following the activation command from the control system to when the mixture effectively passes through the intake valves. As previously highlighted, the injected gas travel time is not a fixed value but depends primarily on engine speed boost pressures. The load could also affect the optimal conditions if long injection times are required.
3. Results
3.1. NG Phased Injection Optimization
The results of the tests with variable NG injection timing are shown in Figure 3, where the TDC at the end of the compression stroke corresponds to the zero point on the abscissa. The THC values are plotted in correspondence with the CAD at which the electrical impulse for injector activation is initiated. The air/gas mixture formed in the intake manifold enters the cylinder only after several rotation angles from this impulse. The values of this lag due to the physics of the process and the characteristics of the experimental system will be discussed later. In the figure, a section with small variations can be observed starting from approximately 60 CAD BTDC to approximately 180 CAD ATDC (after top dead center), and then reaching optimal values, approximately one-third of the values measured with continuous admission, around TDC in the exhaust phase. It is also important to note that the maximum THC value (about 45 g/kWh at 255 CAD) can be up to approximately three times higher than the emissions recorded with continuous manifold feeding.
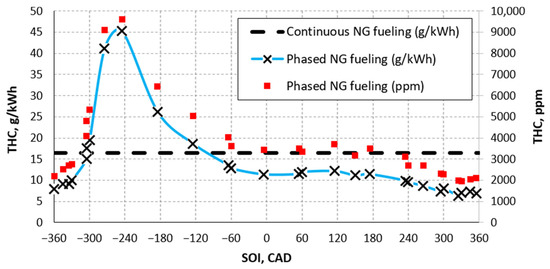
Figure 3.
THC in continuous NG fueling and with phased injection at varying gas SOI at 1500 rpm and a boost pressure of 1.5 bar.
The tests were conducted with the same injection duration, resulting in nearly identical fuel flow rates. Therefore, higher THC values correspond to lower BMEP values delivered by the engine because of the reduced fraction of fuel trapped in the combustion chamber. In the specific value expressed in g/kWh, BMEP is considered the denominator for power evaluation, thus impacting the calculated value. However, the maximum THC value is not significantly influenced by the lower BMEP value. To support this statement, the THC concentrations (ppm) measured at the exhaust are also considered, as shown in the figure. Both the raw concentration and the specific value relative to power follow the same trend. Consequently, the effect of methane slip due to non-optimal timing is significantly greater than the negative impact of a lower BMEP on the evaluation of specific emission data.
3.2. Performance Comparison between Continuous and Phased NG Fueling
To characterize the engine’s behavior, all different types of tests conducted at a net BMEP of approximately 8 bar were considered. During the tests, there was some data dispersion, mainly caused by varying environmental conditions, in addition to the usual variation due to random phenomena and control system inaccuracies. The data were then analyzed to derive the minimum and maximum values for the different parameters and operational trade-offs. Table 4 shows the values of some parameters of interest under different engine fueling conditions while keeping the net power output of the engine constant.

Table 4.
Comparison of the best performances in FD and DF, considering specific emissions, evaluated with respect to net power.
The best-measured values refer to different test conditions; therefore, they represent potential values but are not actually achievable together. The combustion efficiency in the dual-fuel mode is influenced by the complexity of the phenomenon, involving dual combustion modes (diesel ignition and flame front propagation); the difficulty of maintaining the mixture at optimal lambda conditions as the engine lacks a throttle valve for air flow regulation; and the losses of the unburned mixture during valve overlap. Although phased gas injection does not affect the first two factors, it significantly reduces the losses of the unburned mixture at the exhaust compared with continuous feeding, thereby indirectly increasing combustion efficiency. However, the degradation in combustion efficiency that still occurs in the DF mode leads to higher THC emissions compared with the FD mode, where THC emissions are always very low and often close to zero. Nonetheless, eliminating the losses due to valve overlap with phased injection contributed to a reduction of approximately 60% in THC emissions compared with the DF mode with continuous feeding.
In the case of the FD mode, the CO2 related to net power is significantly higher than the values calculated with brake power, as it accounts for the additional diesel consumption required to achieve increased supercharging compared with the DF mode with an external compressor, thus considering a lower available power (net power). For the DF mode, given the lower boost pressure, there is less difference between the two power values, but it is necessary to consider equivalent CO2 to account for the GWP of methane at the exhaust, which is about 30 times higher than that of CO2. For the total measured THC, 10% non-methane hydrocarbons and 90% methane hydrocarbons were considered. Changing the gas supply mode to phased injection allows for an approximately 20% reduction in equivalent CO2 emissions into the atmosphere. This result achieves substantial parity in equivalent CO2 emissions between the FD mode and the DF mode with phased injection.
As previously highlighted, to achieve optimal operating conditions through the correct setting of various control parameters, both for gas injection and pilot diesel injection, it is necessary to consider certain trade-offs among the parameters listed in Table 4. A significant trade-off exists between efficiency and equivalent CO2 emissions, as shown in Figure 4. Switching to phased injection allows DF performance to approach that of FD, provided the pilot diesel injection settings are optimized. The data cloud was obtained using different control parameter settings. With the phased injection, DF operation can achieve slightly higher net efficiency values than those measured in FD (by about 5%), with equivalent CO2 emissions similar to those recorded in FD. Moreover, considering that the optimal equivalent CO2 results in FD generally correspond to conditions of higher NOx emissions, a trade-off in the FD scenario might lead to selecting conditions with higher equivalent CO2 emissions. Therefore, DF fueling could ensure similar equivalent CO2 emissions while maintaining the same NOx levels. As a consequence, choosing operating conditions in FD with optimal efficiency may require the use of selective catalysts to mitigate NOx emissions. Once again, the DF supply could be optimized with greater flexibility. Indeed, in the DF mode, higher exhaust temperatures are expected because of the lower air index used, thereby favoring NOx conversion into the catalysts.
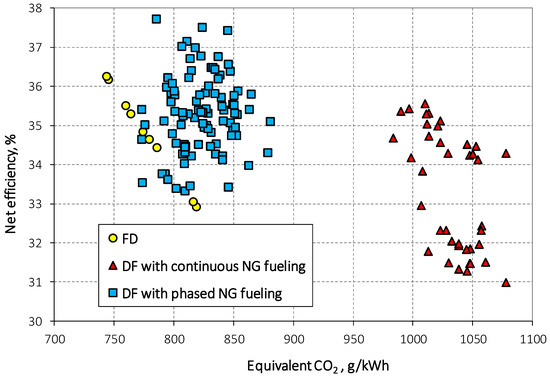
Figure 4.
Trade-off between efficiency and equivalent CO2 emissions.
4. Discussion
4.1. Analysis of the Optimal Phased Injection Conditions
Figure 5 displays the THC trend in the DF as previously discussed, alongside the intake and exhaust valve operation diagrams. The figure highlights the optimal conditions for phased injection, with the start at 330 CAD and the end at 360 CAD (light blue segment), aimed at minimizing THC emissions. This occurs when the mixture approaches the open intake valves while the exhaust valves remain closed at approximately 250 ATDC CAD (green segment). The length of the green segment represents the average angular period that the air/gas mixture takes to reach the intake valves. In practice, since the engine features two intake valves with distinct ducts—one straight and shorter and the other helical and longer—the mixture initiates entry through the straight duct at 270 CAD ATDC (orange asterisks) and completes intake at around 200 CAD ATDC through the swirl duct (red asterisks). Segments with asterisks can be considered as the angular injection from two hypothetical injectors positioned near the two intake valves.
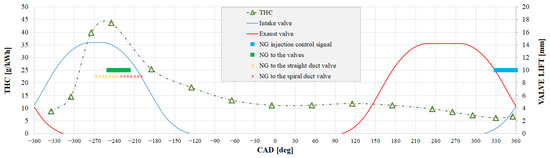
Figure 5.
THC emissions by varying the injection timing compared with the valve lift and injection under optimal conditions.
Fundamentally, the lowest THC values are achieved by injecting gas during full valve overlap. While this may not seem optimal, timing is crucial: considering the time in CAD required for the mixture to reach the intake valves, the mixture enters the cylinder precisely when the two exhaust valves are closed (overlap ended) and the intake valves are at maximum opening.
To determine the optimal injection timing, the angular intervals required for the arrival of the injected NG at the valves were evaluated using the simplified interpretative model, as depicted in Figure 6. Each volume in the diagram is accurately represented to scale, with additional air from the external compressor being imagined behind the gas volume.
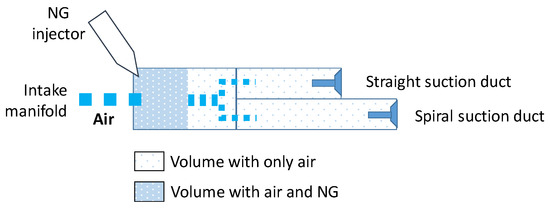
Figure 6.
Scheme of the intake ducts and positioning of gas and air inside them under the best operating conditions (SOI = 330 CAD).
Under optimal conditions, gas injection starts just as the intake valve begins to open during the overlap. The injected gas package is preceded by air accumulated from the moment the intake valve was closed in the previous cycle. With the intake valve closed, there is no mixture flow in the intake duct. As the intake valve opens, the gas begins to flow into the intake manifold, preceded by the air present in the ducts, both straight and swirled. This air, consequently, becomes the first to enter the cylinder and may also be the first to exit through the exhaust because of valve overlap. As depicted in Figure 5, the resulting mixture begins to enter the cylinder at approximately 270 CAD BTDC, precisely when the intake valve is fully open and the exhaust valve is closed.
Moving away from this optimal condition, by advancing the injection timing, for example, to an SOI of 120 CAD, ahead of the gas injected into the duct, there will be less air available compared with the optimal scenario illustrated earlier. In the optimal case, air accumulates from 120 CAD ATDC to 315 CAD BTDC, whereas with an SOI of 120 CAD, air is present only from 120 CAD ATDC to 120 CAD BTDC, thus in a lesser quantity. Consequently, the injected gas package is shifted forward relative to the optimal case, closer to the intake valve when it opens to allow the mixture into the cylinder. This behavior explains the trend in THC in the nearly horizontal section of Figure 5.
Continuing to advance the gas injection, for instance, to 240 CAD ATDC, the gas will be near the intake valve immediately after its closure at 120 CAD ATDC. This represents the worst condition because there is no air ahead of the gas, and at the moment of the next intake valve opening, during the overlap phase, a significant portion of the gas upstream of the intake valves will be quickly diverted to the exhaust. This phenomenon leads to emissions that are even higher than continuous feeding. This result aligns with the fact that because of the short time available and the absence of flow with the intake valves closed, the gas does not mix adequately with the air in the manifold but tends to stagnate under almost static conditions, as assumed in the simplified model. This situation is depicted in Figure 7 and Figure 8.
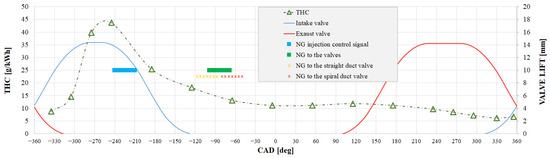
Figure 7.
THC emissions by varying the injection timing compared with the valve lift and injection in the worst conditions.
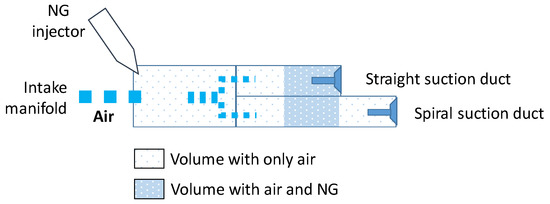
Figure 8.
Scheme of the intake ducts and positioning of gas and air inside them under the worst operating conditions (SOI = 240 CAD).
4.2. Effect of the Boost Pressure on Optimal Conditions
In the previously reported tests, a constant boost pressure of 1.5 bar was maintained for the DF cases. This value optimizes DF combustion without compromising the autoignition conditions of the pilot diesel fuel. Lower values could enhance the combustion of the homogeneous air/NG mixture, at least at the considered load of 8 bar BMEP, but reducing the end-of-compression pressure negatively impacts the autoignition conditions of the diesel fuel. Instead, the increased amount of injected NG requires more air at higher loads, so the lower boost pressure compared with the FD case does not result in excessive reductions in end-of-compression pressure as it does for low and medium loads.
Figure 9 illustrates how increased boost pressure deteriorates the engine’s performance in the DF mode. THC and CO2 emissions were analyzed at varying boost pressures to evaluate the trend in equivalent CO2. This evaluation was conducted for both the brake dynamometer power (gross values) and the corrected power (net values). The difference between these two values becomes more significant with higher boost pressures.
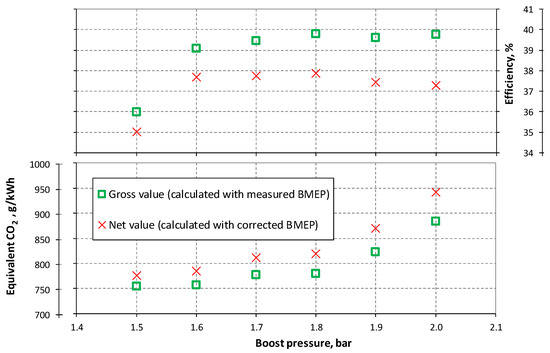
Figure 9.
Efficiency and equivalent CO2 trend as boost pressure varies in DF. Net and gross values.
The tests were conducted with an almost constant fuel flow rate, increasing the boost pressure from 1.5 to 2.0 bar. This approach resulted in BMEP values ranging from 8.3 to 9.5 bar (with BMEPcor in the range of 8.1−8.9 bar). The best results in terms of the lowest equivalent CO2 were obtained at a boost pressure of 1.5 bar, despite the efficiency initially increasing with a higher boost pressure. It can be observed that, under all conditions, as the boost pressure and, consequently, the air index increase (since the tests were conducted at a constant fuel flow rate), the equivalent CO2 also increases. Regarding efficiency, an increase was measured up to a boost pressure of 1.8 bar. Also considering the net efficiency values, which are not influenced by the energy provided by the higher boost, there is an increase up to a boost pressure of approximately 1.8 bar, which then tends to decrease at higher boost values.
The explanation for these trends can be attributed to the increase in THC due to the worsening combustion conditions in the DF mode caused by the leaning of the mixture. The increased dilution of the charge due to excess air not only worsens the propagation conditions of the flame front because of the rarefaction of fuel molecules but also causes a drop in the combustion chamber temperatures. Both factors negatively affect THC formation, increasing emissions.
On the other hand, greater dilution with air at boost pressures higher than 1.5 bar tends to reduce thermal exchanges, improving the engine’s energy balance. Therefore, in the range of boost pressures investigated, favorable conditions for efficiency (lower thermal exchanges) are created, leading to a potential reduction in specific CO2 emissions (compared with the optimal values at 1.5 bar boost), while combustion conditions deteriorate with an increase in the air index, resulting in higher THC emissions. These higher THC emissions are predominant and cause a progressive increase in equivalent CO2 with boost pressure (from about 750 to around 1000 g/kWh).
5. Conclusions
The optimal use of alternative fuels in the maritime sector is of increasing interest. This study focused on a single-cylinder, large-bore research engine fueled in the DF mode with 20% diesel fuel and 80% NG on a mass basis. The boost pressure in the DF mode underwent optimization to facilitate a reduction in THC emissions. The proper timing of NG injection contributed to the reduction in THC emissions to one-third of those observed with continuous fueling. Consequently, there was a substantial decrease in equivalent CO2 emissions of about 20% and an increase in efficiency, approaching levels comparable to those achieved in the conventional FD mode. This achievement was realized by injecting the gas with a timing that ensured that the mixture reached the cylinder with the intake valve open and the exhaust valve closed to prevent losses during valve overlap. The objective was accomplished by considering transit times from the gas injection point in the intake ducts to the mixture entering the cylinder, verified using a simplified model, assuming a not complete mixing of air and NG in the intake ducts. Conversely, improper injection timing could yield even worse outcomes than continuous NG fueling, up to more than 200% of THC emission, if a significant portion of the injected NG enters the cylinder when the exhaust valve is open. In such instances, a substantial amount of gas would be lost to the exhaust, exceeding the losses incurred with continuous fueling, where NG is homogeneously dispersed in the air entering the cylinder. Ultimately, phased injection enables DF operation to achieve marginally higher efficiency levels than those observed in the FD mode (by approximately 5%), with equivalent CO2 emissions similar to or marginally lower than those recorded in the FD mode. This underscores its suitability as a solution for high-efficiency alternative fueling of marine engines, aiming to mitigate particulate matter and sulfur compounds by replacing a significant portion of liquid fuel with NG.
Author Contributions
Conceptualization, L.D.S., L.M., S.I. and V.P.; methodology, L.D.S.; software, L.D.S. and V.P.; validation, L.D.S., L.M. and S.I.; formal analysis, L.D.S.; investigation, L.D.S., L.M., S.I., V.P. and N.A.; resources, S.I. and L.M.; data curation, V.P.; writing—original draft preparation, L.D.S.; writing—review and editing, L.D.S., L.M., S.I. and V.P; visualization, L.D.S. and N.A.; supervision, L.D.S., S.I., and L.M.; project administration, S.I. and L.M.; funding acquisition, S.I. and L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project NAUSICA (PON “R&S 2014-2020”), grant number ARS01_00334, project leader NAVTEC cluster.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to (specify the reason for the restriction).
Acknowledgments
The authors thank Vincenzo Bonanno and Alfredo Mazzei for their technical support during the experimental campaign.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| ATDC | after top dead center |
| BDC | bottom dead center |
| BMEP | brake mean effective pressure |
| BTDC | before top dead center |
| CAD | crank angel degree |
| DF | dual fuel |
| FD | full diesel |
| GHG | greenhouse gas |
| GWP | global warming potential |
| IMEP | indicated mean effective pressure |
| NG | natural gas |
| SOI | start of injection |
| TDC | top dead center |
References
- Rochussen, J.; Jaeger NS, B.; Penner, H.; Khan, A.; Kirchen, P. Development and demonstration of strategies for GHG and methane slip reduction from dual-fuel natural gas coastal vessels. Fuel 2023, 349, 128433. [Google Scholar] [CrossRef]
- Sharafian, A.; Blomerus, P.; Mérida, W. Natural gas as a ship fuel: Assessment of greenhouse gas and air pollutant reduction potential. Energy Policy 2019, 131, 332–346. [Google Scholar] [CrossRef]
- Zhao, R.; Xu, L.; Su, X.; Feng, S.; Li, C.; Tan, Q.; Wang, Z. A Numerical and Experimental Study of Marine Hydrogen-Natural Gas-Diesel Tri-Fuel Engines. Pol. Marit. Res. 2020, 27, 80–90. [Google Scholar] [CrossRef]
- Zhang, Z.; Lv, J.; Li, W.; Long, J.; Wang, S.; Tan, D.; Yin, Z. Performance and emission evaluation of a marine diesel engine fueled with natural gas ignited by biodiesel-diesel blended fuel. Energy 2022, 256, 124662. [Google Scholar] [CrossRef]
- Dierickx, J.; Dejaegere, Q.; Peeters, J.; Sileghem, L.; Verhelst, S. Performance and emissions of a high-speed marine dual-fuel 1 engine operating with methanol-water blends as a fuel. Fuel 2023, 333, 126349. [Google Scholar] [CrossRef]
- Xu, L.; Xu, S.; Bai, X.S.; Repo, J.A.; Hautala, S.; Hyvönen, J. Performance and emission characteristics of an ammonia/diesel dual-fuel marine engine. Renew. Sustain. Energy Rev. 2023, 185, 113631. [Google Scholar] [CrossRef]
- García Valladolid, P.; Tunestål, P.; Monsalve-Serrano, J.; García, A.; Hyvönen, J. Impact of diesel pilot distribution on the ignition process of a dual fuel medium speed marine engine. Energy Convers. Manag. 2017, 149, 192–205. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, H.W.; Huang, Y.P.; Wei, J.H.; Peng, Y.H. Effects of injection timing on combustion and emission performance of dual-fuel diesel engine under low to medium load conditions. Energies 2019, 12, 2349. [Google Scholar] [CrossRef]
- Wang, H.; Gan, H.; Theotokatos, G. Parametric investigation of pre-injection on the combustion, knocking and emissions behaviour of a large marine four-stroke dual-fuel engine. Fuel 2020, 281, 118744. [Google Scholar] [CrossRef]
- Yousefi, A.; Guo, H.; Birouk, M.; Liko, B.; Lafrance, S. Effect of post-injection strategy on greenhouse gas emissions of natural gas/diesel dual-fuel engine at high load conditions. Fuel 2021, 290, 120071. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Zheng, Z.; Yao, M. Numerical investigation on the combustion and emission characteristics of a heavy-duty natural gas-diesel dual-fuel engine. Fuel 2021, 300, 120998. [Google Scholar] [CrossRef]
- Boretti, A. Numerical analysis of high-pressure direct injection dual-fuel diesel-liquefied natural gas (LNG) engines. Processes 2020, 8, 261. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, M.; Wang, T.; Lu, T.; Wang, H.; Feng, Y.; Shi, L. Numerical research of the in-cylinder natural gas stratification in a natural gas-diesel dual-fuel marine engine. Fuel 2023, 337, 126861. [Google Scholar] [CrossRef]
- Gleis, S.; Frankl, S.; Waligorski, D.; Prager, I.M.; Wachtmeister, I.G. Investigation of the High-Pressure-Dual-Fuel (HPDF) combustion process of natural gas on a fully optically accessible research engine. SAE Technical Paper, 19 December 2019. [Google Scholar] [CrossRef]
- Lei, Y.; Wu, Y.; Qiu, T.; Zhou, D.; Lian, X.; Jin, W. Experimental Study of Dual-Fuel Diesel/Natural Gas High-Pressure Injection. ACS Omega 2022, 8, 519–528. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Li, J.; Wang, J.; Wu, C.; Liu, B.; Dong, J.; Liu, T.; Ye, Y.; Wang, H.; Yao, M. Effects of injection strategies on low-speed marine engines using the dual fuel of high-pressure direct-injection natural gas and diesel. Energy Sci. Eng. 2019, 7, 1994–2010. [Google Scholar] [CrossRef]
- Yang, B.; Zeng, K. Effects of natural gas injection timing and split pilot fuel injection strategy on the combustion performance and emissions in a dual-fuel engine fueled with diesel and natural gas. Energy Convers. Manag. 2018, 168, 162–169. [Google Scholar] [CrossRef]
- Ariani, B.; Ariana, I.M.; Fathallah, M.A. Effect of natural gas injection timing on combustion performance & methane slip emission of diesel—NG dual fuel engine: An experimental study. In AIP Conference Proceedings; AIP Publishing: College Park, MD, USA, 2019; Voluime 2187. [Google Scholar] [CrossRef]
- Felayati, F.M.; Semin Cahyono, B.; Bakar, R.A. Investigation of the effect of natural gas injection timing on dual-fuel engine emissions using split injection strategies. Int. Rev. Mech. Eng. 2019, 13, 645–654. [Google Scholar] [CrossRef]
- Kurniawan, M.A.; Yuvenda, D.; Sudarmanta, B. The Effects CNG Injection Timing on Engine Performance and Emissions of A Diesel Dual Fuel Engine. IPTEK J. Technol. Sci. 2019, 30, 64–67. [Google Scholar] [CrossRef]
- You, J.; Liu, Z.; Wang, Z.; Wang, D.; Xu, Y. Impact of natural gas injection strategies on combustion and emissions of a dual fuel natural gas engine ignited with diesel at low loads. Fuel 2020, 260, 116414. [Google Scholar] [CrossRef]
- De Simio, L.; Iannaccone, S.; Pennino, V.; Marchitto, L. Experimental Analysis of a Single-Cylinder Large Bore Engine with External Supercharging in Diesel/CNG Dual-Fuel Mode. SAE Technical Papers, 28 August 2023. [Google Scholar] [CrossRef]
- Gülmez, Y.; Özmen, G. Effects of Exhaust Backpressure Increment on the Performance and Exhaust Emissions of a Single Cylinder Diesel Engine. J. Eta Marit. Sci. 2021, 9, 177–191. [Google Scholar] [CrossRef]
- IPCC. 2021: Climate Change 2021: The Physical Science Basis Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2023; p. 2391. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).