Abstract
In this study, we present the preliminary results of our effort to construct a new high spatial resolution precipitation database (1 km × 1 km) over Greece, on an annual and monthly basis. A variety of spatial parameters (i.e., latitude, longitude, altitude, aspect, distance from water bodies, among others) and ERA5 reanalysis data were used as independent variables in an algorithm combined with the Regression Kriging with a Histogram-Based Gradient-Boosting Regression Tree. The dependent variable in the algorithm was the gauge data covering most of the area studied. Μaps were constructed for the ERA5 reanalysis and the modelled mean precipitation totals on an annual and monthly basis for the 1980–2010 study period. The findings of the analysis show that the applied methodology improves the spatial resolution and distribution of the ERA5 reanalysis precipitation totals over Greece. Furthermore, when comparing the modelled high spatial resolution datasets against ERA5 datasets over the gauge precipitation totals, the model achieved an average R2 improvement of 31.7%, with the largest improvement recorded on an annual basis, while the RMSE decreased by 16.6% on average and more than 40% on an annual basis.
1. Introduction
Precipitation in Greece exhibits very high spatial variability, as documented by many researchers in this field [1,2]. Greece is defined by the Pindos Mountain range, where the bulk of precipitation occurs. The mountain range gives precipitation in Greece a longitudinal shift [3], while the many small islands make precipitation even harder to simulate. The greater Mediterranean area also experiences a lot of extreme precipitation events [4] in the winter and a lot of droughts in the summer [5]. This high inter-seasonal variability also creates additional issues with simulating the precipitation, particularly in the spring and summer months since, precipitation is extremely rare.
Currently, the ERA5 datasets are given at a spatial resolution of 0.25° × 0.25°. This makes the datasets unsuitable to study precipitation in Greece, as precipitation can change a lot within such a large grid cell. In particular, spatial precipitation variabilities regarding small islands cannot be fully interpreted. The aim of this paper is to downscale the ERA5 precipitation totals on an annual and monthly basis, on a 1 km × 1 km spatial resolution, over the Greek area.
2. Materials and Methods
The ERA5 reanalysis data use the same Integrated Forecasting System that was used in the ERA Interim Reanalysis, but correcting the biases that were found. The data are given on a 0.25° × 0.25° grid, and this is the reanalysis input used to downscale the precipitation totals. Towards this goal, the constructed model based on Regression Kriging with a Histogram-Based Gradient-Boosting Regression Tree was fed with geographical parameters derived from a 12 m resolution TanDEM-X Elevation Model, which is a product generated from the TerraSAR-X satellite mission. This raster was upscaled to 1 km × 1 km and then the geographical parameters were calculated for each station. The shapefiles used to calculate the distance from shore and water bodies like lakes and rivers were acquired from the government platform https://geodata.gov.gr/ (accessed on 22 September 2022). The daily precipitation totals, the elevation of the precipitation gauges and their coordinates were provided from the Hellenic National Meteorological Service (HNMS). A total of 103 precipitation gauges were used, covering most of the Greek mainland, as well as the islands. The study period refers to 1980–2010, and this is primarily since the reanalysis datasets were given for this period. For the stations studied, 77.7% of the gauge dataset has more than 50% of the data for the period studied, 67% has more than 70% of the data, while 40.8% has more than 90% of the data.
The constructed regression model used as independent variables the climatic elements from ERA5 reanalysis datasets (air temperature, wind speed, evaporation, surface solar radiation, surface pressure, cloud cover, precipitation); the geographical variables from the gauge position (longitude, latitude, elevation); the geospatial variables (distance from lakes, distance from river, distance from shore, slope) from the high resolution 1 km × 1 km Greek domain; and the North Atlantic Circulation index (NAOI) (Table 1). The independent variables entered in the statistical downscaling model to achieve optimal results for each month are presented in Table 1. These variables were chosen based on statistically significant correlation (p < 0.05) with the precipitation datasets (dependent variable), along with a trial-and-error analysis, during the training stages of the model. The training dataset consisted of the 90% precipitation totals (dependent variable) for each one of the gauges used in the study along with the aforementioned independent variables. The used climate elements from the ERA5 reanalysis datasets concerned the nearest cell to the gauge. The validation of the model was based on a random split of 10% of the gauge precipitations totals.

Table 1.
Table of independent variables used in each month (grey colour).
The statistical downscaling approach used in the study was the Regression Kriging with a Histogram-Based Gradient-Boosting Regression Tree (HBGBRT), which is a spatial interpolation technique, where the residuals from a regression model are spatially interpolated using a Kriging technique. The regression model is usually a linear or multilinear model; however, we used a more complex HBGBRT. Gradient Boosting is an ensemble machine learning technique where a tree model is added to a previous tree model ensemble to correct the prediction errors. An HBGBRT technique essentially means that the model is using a histogram approach to categorise the input data and train the trees on the most optimal set of input variables. This technique was used to accelerate the training process dramatically.
3. Results and Discussion
Table 2 summarises the improvements that were made (R2 and RMSE) in the resulting high-resolution precipitation totals compared with the standalone reanalysis data. It is obvious that the newly generated High-Resolution PREcipitation totals (HRPRE) show massive improvement over the original ERA5 reanalysis datasets. The only exception appears in some spring and summer months, where the model does not improve the original ERA5 reanalysis datasets. This shortcoming in accuracy probably happens because the precipitation is very scarce (even zero) in most of these months. Additionally, the best-performing results concern annual precipitation against monthly precipitation, which is due to the scarcity of precipitation even in January or December in specific areas of Greece.

Table 2.
Statistic metrics, on the one hand, between the generated HRPRE and the gauge precipitation totals and, on the other hand, between ERA5 datasets (nearest to the gauge cell) and the gauge precipitation totals.
In the following Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, the spatial distributions of annual and mean monthly precipitation totals for selected months of the generated HRPRE and ERA5 datasets are presented for the period 1980–2010 over Greece. The generated annual HRPRE and ERA5 datasets correctly simulate (Figure 1), the longitudinal shift that exists in the Greek region because of the Pindus Mountain range. Additionally, the model performs much closer to ERA5; however, the values seem to be smaller. This could be since most of the stations used are at low elevations. Additionally, Crossett et al. [6] also found that the model overestimated the precipitation on an annual basis. However, in the Crete region, where a lot of stations at high elevations are included, the downscaled data show an increase in the mountainous regions.
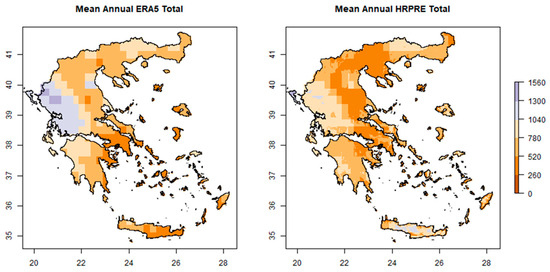
Figure 1.
Mean annual precipitation totals for HRPRE (right graph) and ERA5 (left graph), 1980–2010.
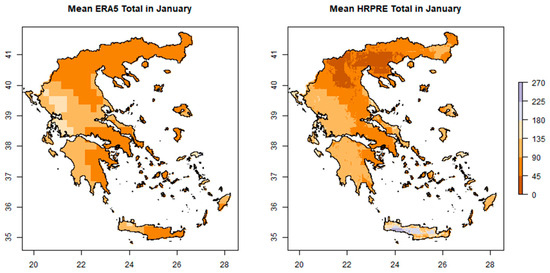
Figure 2.
Mean precipitation totals for HRPRE (right graph) and ERA5 (left graph) in January, 1980–2010.
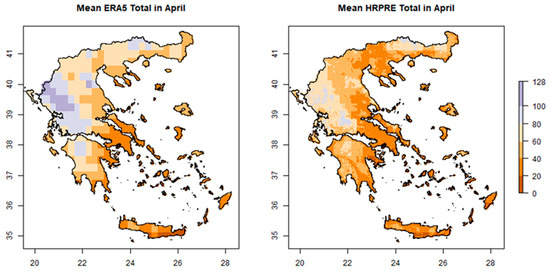
Figure 3.
Mean precipitation totals for HRPRE (right graph) and ERA5 (left graph) in April, 1980–2010.
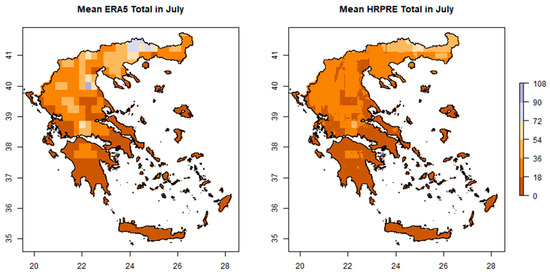
Figure 4.
Mean precipitation totals for HRPRE (right graph) and ERA5 (left graph) in July, 1980–2010.
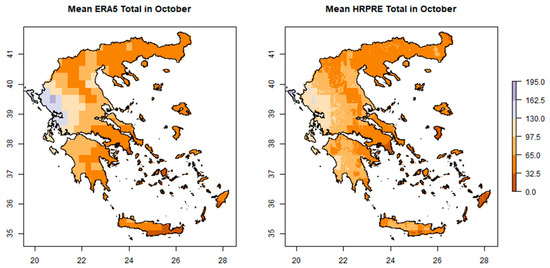
Figure 5.
Mean precipitation totals for HRPRE (right graph) and ERA5 (left graph) in October, 1980–2010.
Summer months are the worst performing; namely, the precipitation in these months usually exists only in the northern parts of the country. Table 1 depicts that fewer independent variables appear to be included in the model with respect to summer months. Furthermore, the inter-seasonal variability is something in which models usually reach their limits in the region, as in some areas very heavy precipitation falls in some winter months and virtually no precipitation falls in summer. This is obvious in Crete, where, during winter, the mountainous regions record some of the highest precipitation in the country against very little precipitation within the summer period. Additionally, in Crete the downscaled data simulate much higher precipitation in the mountainous region and do not simulate the very pronounced longitudinal shift that ERA5 simulates. The shortcoming of the ERA5 in Crete is probably due to its coarser resolution, which does not help in simulating the mountainous regions of the island.
From the results, we can remark that the ERA5 is driving the predictions made by the HRPRE model. However, this is to be expected, as most of the parameters used in the model were derived from the ERA5 dataset. From the metrics used when comparing the HRPRE with the ERA5, we can see that the HRPRE does increase the accuracy of the ERA5, and the maps produced further validate the model, as it does follow the basic patterns that exist in the Greek region. Additionally, it is clear the benefits from the higher resolution as the different geomorphologies are more accurately mapped. In high elevation regions, more stations are needed to increase the accuracy and further test whether the model is correct in reducing some of the precipitation simulated by the ERA5.
4. Conclusions
A high-resolution (1 km × 1 km) precipitation database (HRPRE) over Greece was generated, using Regression Kriging with a Histogram-Based Gradient-Boosting Regression Tree. Towards this, a total of 103 precipitation gauges from the Hellenic National Meteorological Service were used for the period 1980–2010. Climatic elements from ERA5 reanalysis datasets, geographical variables from the gauge positions, geospatial variables from the high resolution 1 km × 1 km Greek domain and the North Atlantic Circulation index were used as independent variables, while the dependent variables were the gauge precipitation totals. The contribution of the ERA5 reanalysis climatic elements in the constructed regression model seems to be the main driver of the spatial precipitation pattern change on both a monthly and annual basis. The results showed large improvement in the statistic metrics (R2 and RMSE) between the generated HRPRE and the ERA5 datasets (nearest to the gauge cell) over the Greek area. Overall, the algorithm tested seems to be a good fit for creating precipitation datasets. Future research will concern extreme precipitation indices focusing on daily precipitation totals.
Author Contributions
Conceptualisation, G.E.N. and Y.K.; methodology, G.E.N.; data analysis and validation, G.E.N.; formal analysis, G.E.N. and Y.K.; investigation, G.E.N.; resources, P.T.N. and G.E.N.; data curation, G.E.N. and Y.K.; writing—original draft preparation, G.E.N.; writing—review and editing, P.T.N.; visualisation, G.E.N.; supervision, P.T.N.; project administration, P.T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The gauge data used in this study were provided by the Hellenic National Meteorological Service, the reanalysis data by the ECMWF, the Digital Elevation Model by the TerraSAR-X satellite mission and the shoreline, lake and river datasets by the https://geodata.gov.gr/platform, accessed on 22 September 2022. The datasets generated during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feidas, H.; Noulopoulou, C.; Makrogiannis, T.; Bora-Senta, E. Trend analysis of precipitation time series in Greece and their relationship with circulation using surface and satellite data: 1955–2001. Theor. Appl. Climatol. 2007, 87, 155–177. [Google Scholar] [CrossRef]
- Nastos, P.T.; Zerefos, C.S. Spatial and temporal variability of consecutive dry and wet days in Greece. Atmos. Res. 2009, 94, 616–628. [Google Scholar] [CrossRef]
- Sindosi, O.A.; Bartzokas, A.; Kotroni, V.; Lagouvardos, K. Influence of orography on precipitation amount and distribution in NW Greece; a case study. Atmos. Res. 2015, 152, 105–122. [Google Scholar] [CrossRef]
- Toreti, A.; Xoplaki, E.; Maraun, D.; Kuglitsch, F.G.; Wanner, H.; Luterbacher, J. Characterisation of extreme winter precipitation in Mediterranean coastal sites and associated anomalous atmospheric circulation patterns. Nat. Hazards Earth Syst. Sci. 2010, 10, 1037–1050. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.; Zhang, T.; Pegion, P. On the increased frequency of Mediterranean drought. J. Clim. 2012, 25, 2146–2161. [Google Scholar] [CrossRef]
- Crossett, C.C.; Betts, A.K.; Dupigny-Giroux, L.A.L.; Bomblies, A. Evaluation of daily precipitation from the ERA5 global reanalysis against GHCN observations in the northeastern United States. Climate 2020, 8, 148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).