Fatigue of Mechanical Structures from Cyclic Wind Actions ^†

Abstract

It is difficult to analyse the action force of the wind in a way that considers the change in the height of its action, the change in direction, or the momentum required for the time of its action. Depending on the design codes of structures and buildings, wind action can be static or dynamic. In this article, we study the dynamic action of the wind on engineering structures (the object of study in this paper is truss structures), analysing in detail the phenomenon of pulsating cyclic loads and the fatigue of the elements of the structures because of its impact. First, we determine the cycle of the wind action, after which we extract its characteristics, such as the average load, the asymmetry of the cycle, the amplitude, and the frequency of the action using the data obtained for the wind from the meteorological services. Then, we evaluate the structure’s life by assessing the damage caused by this loading and cumulative accumulation. Also, in this material, we treat a specific case of a crane structure, where all the characteristics of wind action in the case of cyclic loads have been determined and the construction factor has been extracted as a characteristic that can be used in fast calculation by different engineers.

1. Introduction

Often, in the calculation of engineering structures, the action of the wind load is taken as a static load based on the design procedures [1]. To perform dynamic calculation from the action of the wind, it would be necessary to predict the dynamic cycle of loading, accurately determining all the dynamic parameters of the wind load. Taking them into account will make it possible to obtain the correct loading of each element of the structure and to find the real reason for the destruction of the object excited by the force of the wind, that is, destruction from a loss of solidity or due to rigidity, vibrations, failure or fatigue.

As for the static loads, their determination is relatively easy since their data are obtained through standards [2] for specific areas, different heights of structures, structural factors, etc. Conversely, the dynamic load [3,4] is more difficult to determine since the recognition of the cyclic characteristics of the wind load is more difficult.

In this article, referring to the wind data obtained from the static loads and the factors for calculating the wind speed, we will further analyse the dynamic loads. What is new in this article is the practice of determining the characteristics of the load cycle from the dynamic action of the wind in different structures. The maximum load, minimum load, amplitude load, and the characteristics of the load cycle (load ratio) [5] are quantities that will be determined as normalized and then used for other calculations by different engineers. Also, through the accumulation method of the damage, we will determine the lifespan of a structure from the dynamic action of the wind [6,7].

2. Static Load from Wind Action

As mentioned above, the study of the load from the wind action has its own difficulties since the wind is a quantity that changes not only in the function of the geographical position of the structure but also in function of height. For engineering calculations, it is often recommended that practitioners use the tabular method of assessing the geographical area and height where the structure is as a more appropriate method compared to analytical methods.

Table 1. The factor for average speeds and forces for 3 s in height 10 m [1,3].

Heigh	Factor	Heigh	Factor
10 m	1	110 m	1.285
20 m	1.073	120 m	1.297
30 m	1.119	130 m	1.309
40 m	1.153	140 m	1.319
50 m	1.181	150 m	1.329
60 m	1.204	160 m	1.339
70 m	1.224	170 m	1.348
80 m	1.241	180 m	1.356
90 m	1.257	190 m	1.364
100 m	1.272	200 m	1.372

presents a material according to [1], where the factor for the speed and average force for 3 s at a height of 10 m is given as a function of height.

So, the above data from the standards show the factors we must consider in order to perform the speed or wind force calculation at different heights. As seen above, there is considered to be an average speed or strength of 3 s. Based on the calculations of the machine elements [8,9], the average force is equivalent to a static force, and so the dynamic action of the wind [10,11] is not considered. Let us analyse these data further.

3. Dynamic Load from Wind Action

Starting from the wind speed, measured at the height of 10 m for 10 min, i.e., 600 s, the value meteorological stations give, it is possible to move to the instantaneous wind speed measured at the height of 10 m for 3 s (sometimes given as wind gust).

3.1. Average Wind Speed for 600 Seconds and 3 Seconds

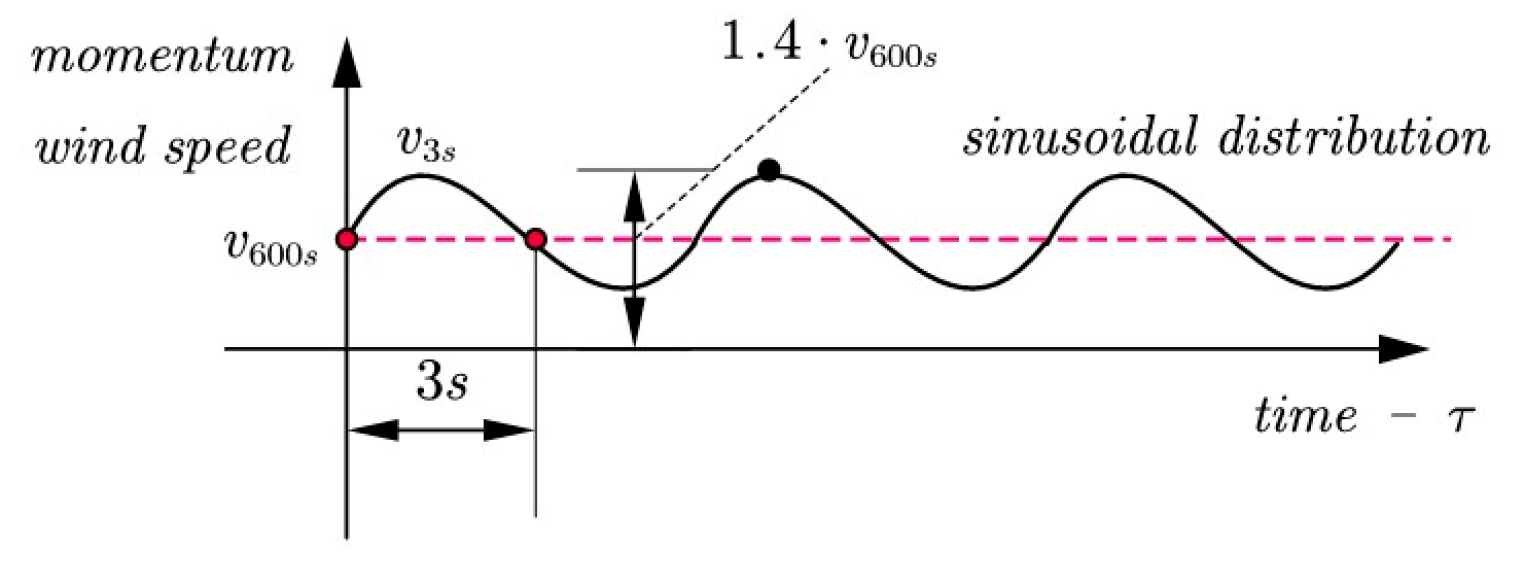
Calculating from the average speed measured by meteorological services for 600 s to the average speed for 3 s or, in special cases, to 1 s, can be performed by multiplying the average speed for 600 s by the coefficient. In this article, we consider sinusoidal distribution, as shown in Figure 1. The coefficient 1.4 for 3 s or, in special cases, 1.51 for 1 s, which we consider in the dynamic calculation, is taken from the ISO standard (en1991.1.4.2005) [1]. It is also worth emphasizing that the sinusoidal distribution shown in Figure 1 is used for the general (almost ideal) case without considering the structure factors, c_s c_d, pressure coefficients for buildings, terrain effects, etc. This distribution is accepted as the theory of fatigue in machine elements [5].

The equation for determining the wind speed per second will be:

$$v\left(t\right)=1.4·v_{600\mathrm{s}}·\sin \omega t,$$

(1)

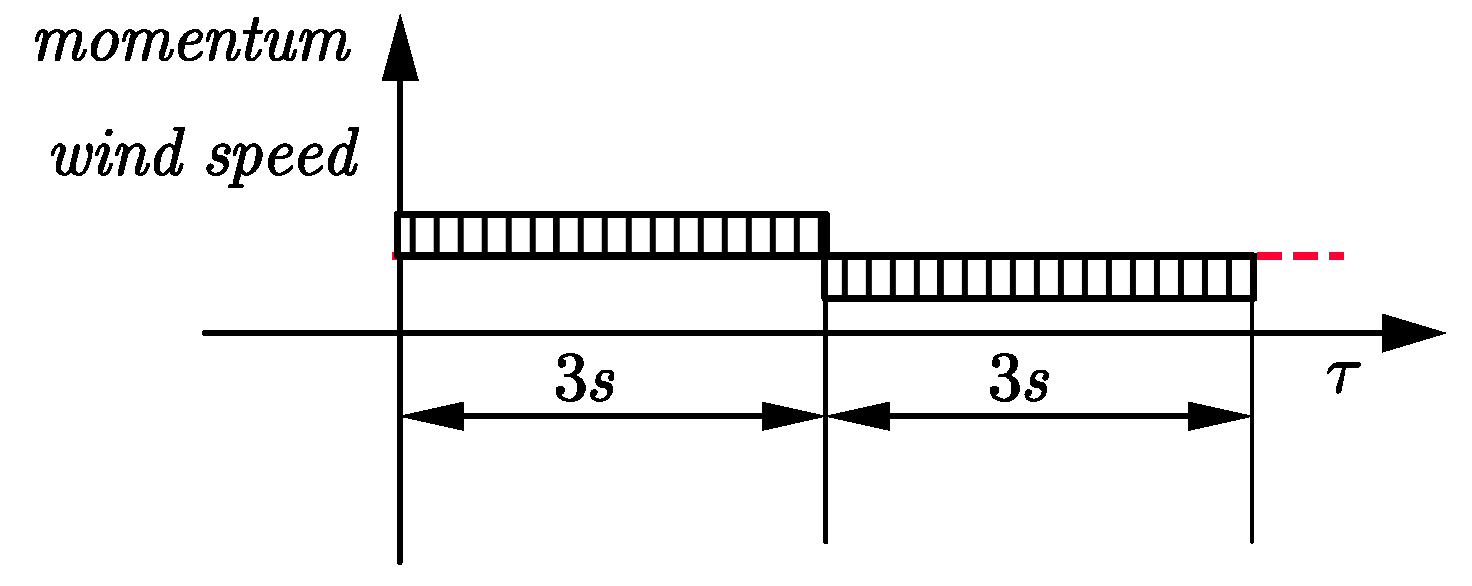
Analysing only for 3 s, we will have the distribution of the speed as shown in Figure 2.

So, for the time 3 s, a part of the wind speed will be above the average value and the other part will be below the average. Based on this approximation, we draw the conclusion that the cycle period of the wind is $T=6$ s.

3.2. Active Forces in Costruction

The same reasoning applies to active force in the construction, which is a dynamic force and causes damage from vibrations and fatigue. Knowing the dynamic force expression, we will write:

$$F\left(t\right)\approx c_{w.eq}·A·\frac{v^2}{1.6}=c_{w.eq}·A·\frac{{\left(1.4·v_{600\mathrm{s}}·\sin \omega t\right)}^2}{1.6}=c_{w.eq}·A·\frac{1.96·{v_{600\mathrm{s}}}^2}{1.6}\left(\frac{1-\cos 2\omega t}{2}\right),$$

(2)

where $c_{w.eq}$ is structure form factor, $A$ is the projected surface in the wind direction.

Average force $F_m$ can be determined from the wind speed $v_{600}$ as above:

$$F_m=c_{w.eq}·A·\frac{{\left(v_{600\mathrm{s}}\right)}^2}{1.6}=c_{w.eq}·A·q_{10m},$$

(3)

Then the maximal dynamic force can be determined as:

$$F_{max}={1.4}^2·F_m=1.96·F_m,$$

(4)

The amplitude force for further calculation, such as fatigue calculation, and the minimal dynamic force can be expressed as:

$$F_a=0.96·F_m,$$

(5)

$$F_{min}=F_m-F_a=0.04·F_m,$$

(6)

Now, we can also calculate the cyclic loading characteristic $\kappa$.

$$\kappa =\frac{F_{min}}{F_{max}}=\frac{0.04·F_m}{1.96·F_m}=0.02\approx 0$$

(7)

We see that this characteristic is almost zero, which means that we are in the case of loading with the pure pulsating cycle of the mechanical structure.

3.3. Swing Period

The period of this speed oscillation was taken to be $T=6 \mathrm{s}$. By analogy with the theory of vibrations, we can find the circular frequency of the excitation force:

$$\omega =\frac{2\pi }{T}=\frac{2\pi }{6 \mathrm{s}}=1.047 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},$$

(8)

and the wind speed will be written in the form:

$$v\left(t\right)=1.4·v_{600\mathrm{s}}·\sin \left(1.047·t\right),$$

(9)

3.4. Active Impulse from the Wind Action

From the pulse and momentum theorem we obtain:

$${\int }_0^{T/2}F·dt=m·v_2-m·v_1,$$

(10)

where $m$ is object mass, and $v_2$ and $v_1$ are the velocity of the mass before and after the action of the wind force. As well as knowing the dynamic force expression from Equation (3), we can derive the active impulse as follows:

$${\int }_0^{T/2}F·dt={\int }_0^{T/2}{c}_{w.eq}·A·\frac{{1.96·v_{600\mathrm{s}}}^2}{1.6}\left(\frac{1-\cos 2\omega t}{2}\right)·dt=c_{w.eq}·A·\frac{{1.96·v_{600\mathrm{s}}}^2}{1.6·2}\left(t-\frac{\sin 2\omega t}{2\omega }\right)\begin{array}{c}\frac{T}{2}\\ 0\end{array},$$

(11)

$${\int }_0^{T/2}F·dt=c_{w.eq}·A·\frac{1.96·{v_{600\mathrm{s}}}^2·T}{6.4}=0.306·c_{w.eq}·A·{v_{600\mathrm{s}}}^2,$$

(12)

An object at rest under the influence of the active force of the wind and a constant resistance force R, such as sliding or rolling friction, will gain speed

$$v_2=\frac{0.306·c_{w.eq}·A·{v_{600\mathrm{s}}}^2·T-\mathrm{R}·\mathrm{T}}{m}$$

(13)

4. Case Study

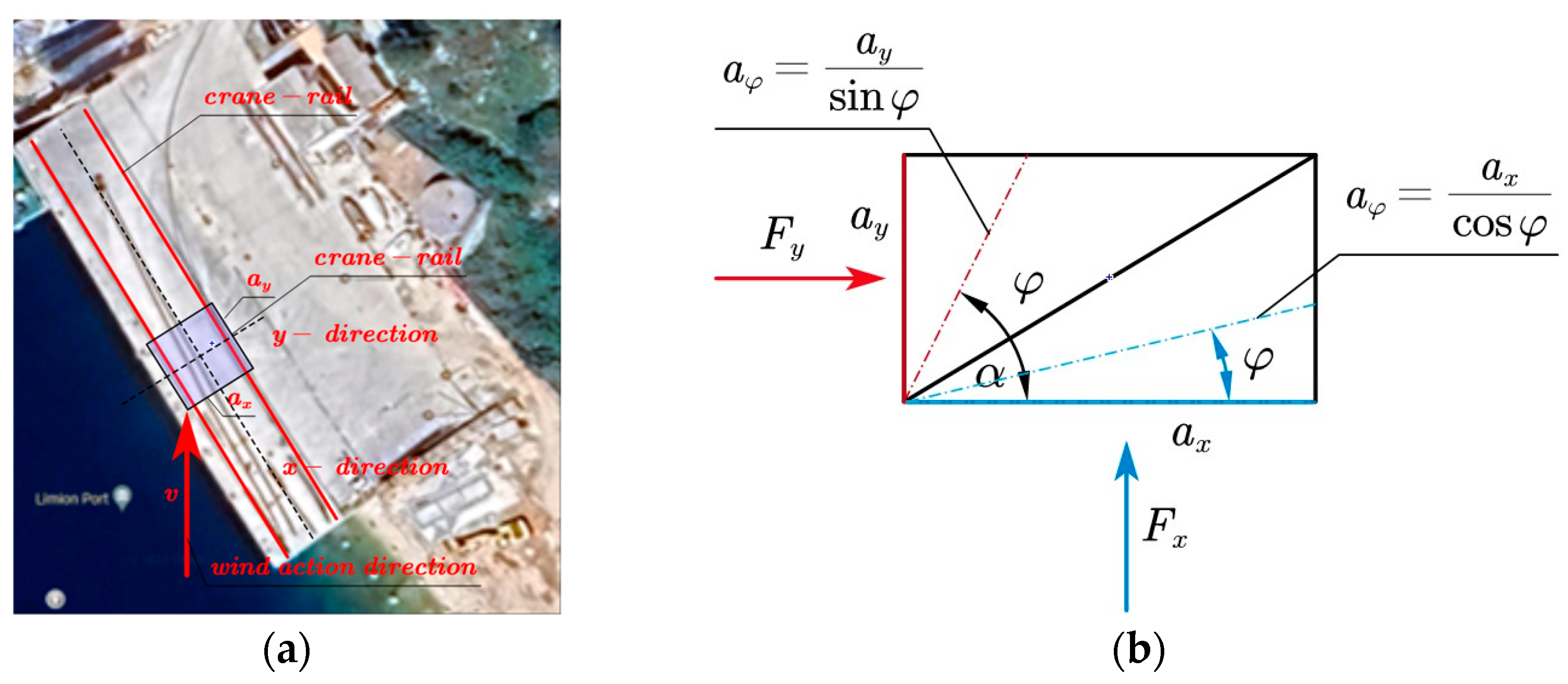
In the following section, we will briefly show a case study for the calculation of the minimum force caused by the wind that can move a port crane. As mentioned at the beginning, the characteristics of the surface of the structure, the mass of the GANZ 50 kN portal crane, as shown in Figure 3, and the equivalent wind coefficient were obtained according to [3] and are shown in

Table 2. Portal Crane GANZ 50 kN [3].

${\mathit{c}}_{\mathit{w}.\mathit{e}\mathit{q}}$	Area [m2]	${\mathit{v}}_{600\mathbf{s}}$ [m/s]	Mass [kg]
2.59	92	110 m	50,000

.

Based on the above dynamic analysis for these characteristics found, it is possible to calculate the minimum wind speed that starts the crane movement after the forces of resistance have been overcome (unwanted case, accident, falling into the sea even though there was a mechanical stop).

$$v_2=\frac{0.306·2.59·92·{8.9}^2·6-3187·6}{50000}=0.976 \mathrm{m}/\mathrm{s},$$

(14)

This speed is the critical wind speed for this crane, which could move if it were not equipped with a braking system (free state). This speed is equivalent to a wind force that will overcome the wind’s rolling resistance.

Change of Wind Diraction Action

The crane has two possibilities of movement: parallel to the rails or in the direction that does not move, which is perpendicular to the rails. So, the direction of the wind plays an important role because we require the component of the wind force in the direction of movement to be greater than the resistance forces of movement (or the equivalent wind speed found above). In the specific case examined, the wind speed was greater before the event, but this was not in the direction of movement. Hence, we needed the angle that the wind speed vector took to make it possible to defeat the rolling forces.

In the case of crane crash analysis, the wind direction changed during the day and at 12:20 it became parallel to the tracks (rails), that is, to the direction of movement (This is a case that happens rarely, but which has a probability of happening). But even if the wind is in a different direction, it produces forces of different sizes. Variation depends on the projected surface and shape coefficients and can also be understood on the basis of the wind speed.

If we design a structure with a rectangular cross-section, that is, with two axes, x and y, then we would derive the coefficients of the structure according to these axes:

$$A_x·c_{w.eq.x}=\frac{F_{e.x}}{\frac{{v_{600\mathrm{s}}}^2}{1.6}},$$

(15)

and,

$$A_y·c_{w.eq.y}=\frac{F_{e.y}}{\frac{{v_{600\mathrm{s}}}^2}{1.6}},$$

(16)

Keeping the real height $H$ constant (unchanged), weobtain two equivalent dimensions for the cross section of the structure according to $x$ and $y$, which are:

$$a_{x}H=A_x·c_{w.eq.x}$$

(17)

and

$$a_{y}H=A_y·c_{w.eq.y}$$

(18)

the force of the wind in any direction can be approximated knowing the only coefficient in the two directions of movement and perpendicular to it. Figure 4 shows the projections of these characteristics from different angles.

From the Figure 4 we have:

$$\tan \alpha =\frac{a_y}{a_x},$$

(19)

For the angel $\phi :\left(0^0-\alpha \right)$ have

$$a_{\phi }=\frac{a_x}{\cos \phi },$$

(20)

For the angel $\phi :\left(\alpha -{90}^0\right)$ have:

$$a_{\phi }=\frac{a_y}{\sin \phi }$$

(21)

Then, the force in any direction of wind action will be easier to calculate

$$F_{e.\phi }=a_{\phi }H\frac{{v_{600\mathrm{s}}}^2}{1.6}$$

(22)

These characteristics for different angles can be used in the calculation of the critical wind speed for our case.

5. Conclusions

In the literature or standards, calculations are only given for static loads from the wind action. In this article, we have tried to approximate the data for the average wind speed (which is equivalent to static load) to dynamic loads, and we can conclude that:

• In dynamic loads, the wind is considered as a pure pulsating load;
• We have a maximum load which is 1.96 times greater than the average load;
• We also have as a minimum load 0.04 for the average load (almost 0);
• Based on the analysis of the active impulse, the minimum speed needed to overcome the resistance forces can be calculated using Equation (14).

In our case of the portal crane GANZ 50 kN, the minimum wind and crane speed are calculated (note that we found out whether the crane is connected or not) when the wind is in the direction of the rails. If the wind were in different directions, we would have to find the wind speed in different directions. To complete this, we would have to use Equations (20)–(22).