Investigation of the Influence of Stratospheric Shear on Baroclinic Instability ^†

Abstract

Baroclinic instability is one of the main mechanisms for the formation of synoptic scale systems. Previous studies examined the exponential growth of small perturbations for a stably stratified troposphere in the case of a constant meridional temperature gradient ignoring the stratosphere (Eady’s model). However, since stratospheric flow also affects to some extent the motions in the troposphere, in this work we investigate the effect of stratospheric wind shear on baroclinic instability using the tools of Generalized Stability Theory (GST). GST is a linear stability theory that addresses both the exponential growth of perturbations that is pertinent in the large time asymptotic limit and the transient growth of perturbations at finite time. The optimal initial perturbations leading to the largest growth over a specified time interval are calculated for three main cases of stratospheric shear: positive, zero and negative shear over the stratosphere. It is found that the inclusion of stratospheric shear in all three cases decreases perturbation growth and influences the scale of the structures that will dominate the flow. For optimizing times of the order of a week, the development of systems with larger spatial scale compared to the prediction of the Eady model is expected, while for optimizing times of the order of a day, smaller scale systems are found to develop.

1. Introduction

Baroclinic instability in the atmosphere is one of the main processes leading to the genesis of synoptic scale systems. It exists due to meridional temperature gradients that support a vertical shear of the mean flow through thermal wind balance. One of the commonly used models for the study of baroclinic instability is Eady’s model [1], which describes the evolution of small perturbations on a constant vertical wind shear in the quasi-geostrophic limit. This model assumes that the perturbations extend only until the tropopause, ignoring the stratospheric layer above along with the stratospheric flow. However, the stratospheric circulation can affect the tropospheric dynamics as illustrated by recent studies showing the downward propagation and tropospheric influence of stratospheric anomalies [2].

Previous studies have examined the effect of stratospheric flow on baroclinic instability using the classical method of modal analysis [3,4], which is based on the identification of eigenmodes of the linear dynamics that are growing exponentially. However, the drawback of this analysis is that it examines the stability of the flow in the infinite time asymptotic limit, where the exponential growth is the most rapid. Such a large time limit might not be relevant for baroclinic instability, as cyclogenesis occurs over finite time periods of the order of days.

In this work, we investigate the influence of the stratospheric flow on baroclinic instability using the tools of Generalized Stability Theory (GST) [5] that addresses perturbation growth over finite time scales regardless of whether this is exponential or algebraic. We study a modified version of Eady’s model that is coupled with a stratospheric stably stratified layer and study the influence of three cases of stratospheric shear (positive, zero and negative) on baroclinic instability and on the finite time development of small perturbations.

2. The Evolution of Small Perturbations in the Quasi-Geostrophic Limit

In this work, we extend the classical Eady model to take into account the stably stratified stratospheric layer and the flow therein. We consider an inviscid, adiabatic and hydrostatically balanced flow on an f-plane in the quasi-geostrophic limit. In this limit, the dynamics reduce to the conservation of potential vorticity:

$$\left(\frac{\partial }{\partial \tilde{t}}+{\tilde{u}}_g\frac{\partial }{\partial \tilde{x}}+{\tilde{v}}_g\frac{\partial }{\partial \tilde{y}}\right)\tilde{q}=0,$$

(1)

where the tildes denote dimensional variables, $\left({\tilde{u}}_g,{\tilde{v}}_g\right)$ is the geostrophic wind and $\tilde{q}$ is the potential vorticity that is given by

$$\tilde{q}={\tilde{\nabla }}^2\tilde{\psi }+f+f^2\frac{\partial }{\partial \tilde{z}}\left(\frac{1}{{\tilde{N}}^2}\frac{\partial \tilde{\psi }}{\partial \tilde{z}}\right),$$

(2)

with ${\tilde{\nabla }}^2$ the horizontal Laplacian, $\tilde{\psi }$ the streamfunction, $f$ the Coriolis parameter at the center of the f-plane and $\tilde{N}\left(\tilde{z}\right)$ the Brunt–Väisälä frequency. A zonal flow $\left({\tilde{u}}_g,{\tilde{v}}_g\right)=\left(\tilde{U}\left(\tilde{z}\right),0\right)$, with streamfunction $\tilde{\Psi }=-\tilde{U}\left(\tilde{z}\right)\tilde{y}$ is an equilibrium of the dynamics. The stability of this flow is addressed by considering the evolution of small perturbations $\tilde{\psi }=\tilde{\Psi }+{\tilde{\psi }}^{\prime }$. Substituting into (1) and linearizing the dynamics, we obtain the following non-dimensional equation for the evolution of perturbations:

$$\left(\frac{\partial }{\partial t}+U\left(z\right)\frac{\partial }{\partial x}\right)\left[{\nabla }^2{\psi }^{\prime }+\frac{\partial }{\partial z}\left(\frac{1}{N^2}\frac{\partial {\psi }^{\prime }}{\partial z}\right)\right]+\frac{d}{dz}\left(\frac{1}{N^2}\frac{dU}{dz}\right)\frac{\partial {\psi }^{\prime }}{\partial x}=0.$$

(3)

The vertical scales have been non-dimensionalized by the height of the troposphere $H$, the horizontal scales by $N_{o}H/f$, where $N_o$ is a typical value of the Brunt–Väisälä frequency in the troposphere, time is non-dimensionalized by the Coriolis parameter $f$ and velocities are non-dimensionalized by $N_{o}H$. The velocity and the temperature perturbations have to be bounded away from the stratosphere, implying that the streamfunction is bounded for $z\to \infty$ and the vertical velocity should be zero at the ground. From the thermodynamic equation, this yields

$${\left(\frac{\partial }{\partial t}\frac{\partial {\psi }^{\prime }}{\partial z}-\frac{\partial {\psi }^{\prime }}{\partial x}\right)}_{z=0}=0.$$

(4)

We consider wave solutions of the form ${\psi }^{\prime }=\widehat{\psi }\left(z,t\right)e^{i\mathit{k}·\mathit{x}},$ where $\mathit{k}=\left(K\cos \theta ,K\sin \theta \right)$ is the wavevector with amplitude $K$ and $\theta$ is the angle between the lines of constant phase of the waves and the meridional direction. The waves satisfy the equation:

$$\frac{\partial \widehat{\psi }}{\partial t}=A\widehat{\psi },$$

(5)

with

$$A=iK\cos \theta {\left(\frac{\partial }{\partial z}\left(\frac{1}{N^2}\frac{\partial }{\partial z}\right)-{{\rm K}}^2\right)}^{-1}\left[\frac{d}{dz}\left(\frac{1}{N^2}\frac{dU}{dz}\right)-U\left(\frac{\partial }{\partial z}\left(\frac{1}{N^2}\frac{\partial }{\partial z}\right)-{{\rm K}}^2\right)\right].$$

(6)

The equation is solved by discretizing the functions in a vertical grid with a small grid size $\delta z$. The streamfunction then becomes a vector $\mathit{\psi }$ along with the other functions and the linear operator incorporating also the boundary conditions becomes a matrix $\mathit{A}$ acting on the vector $\mathit{\psi }$.

We consider four cases of flows. The first is the classical Eady model with $U\left(z\right)=z$, $N\left(z\right)=1$ and with atmospheric motions bounded by the tropopause at $z=1$. In this case, there is the additional boundary condition of zero vertical velocity at the tropopause

$${\left(\frac{\partial }{\partial t}\frac{\partial {\psi }^{\prime }}{\partial z}+\frac{\partial }{\partial x}\frac{\partial {\psi }^{\prime }}{\partial z}-\frac{\partial {\psi }^{\prime }}{\partial x}\right)}_{z=1}=0.$$

(7)

This is the control case, as it ignores the motions in the stratosphere. In the other cases, we consider that the stratosphere is a very stable layer with a static stability $2N_o$. The non-dimensional Brunt–Väisälä frequency transitions smoothly between the two values using the function shown in Figure 1. To investigate the influence of the stratospheric flow, we consider three typical cases. The first is that the tropospheric shear continues unabated into the stratosphere. The second is that there is no stratospheric shear and the third is that the shear is reversed. The mean flow $U$(z) in these three cases is also shown in Figure 1. We therefore calculate the evolution of small perturbations in the three different cases and compare it to the corresponding evolution in the Eady model.

3. The Effect of Stratospheric Shear

We first investigate the modal stability of the flow by calculating the eigenvalues $\lambda$ of the $\mathit{A}$ matrix as a function of wavevector $\mathit{k}$ for each case of the stratospheric flow and compare them to the corresponding eigenvalues in the Eady model. The flow is unstable if the real part of the eigenvalues is positive as the perturbations grow exponentially with growth rate $\sigma =real\left(\lambda \right)$. For long time scales, the perturbations with the largest growth rate are expected to dominate the flow as their amplitude will be much larger compared to all others. For all cases, the maximum growth rate is found for meridionally oriented perturbations ($\theta =0$). 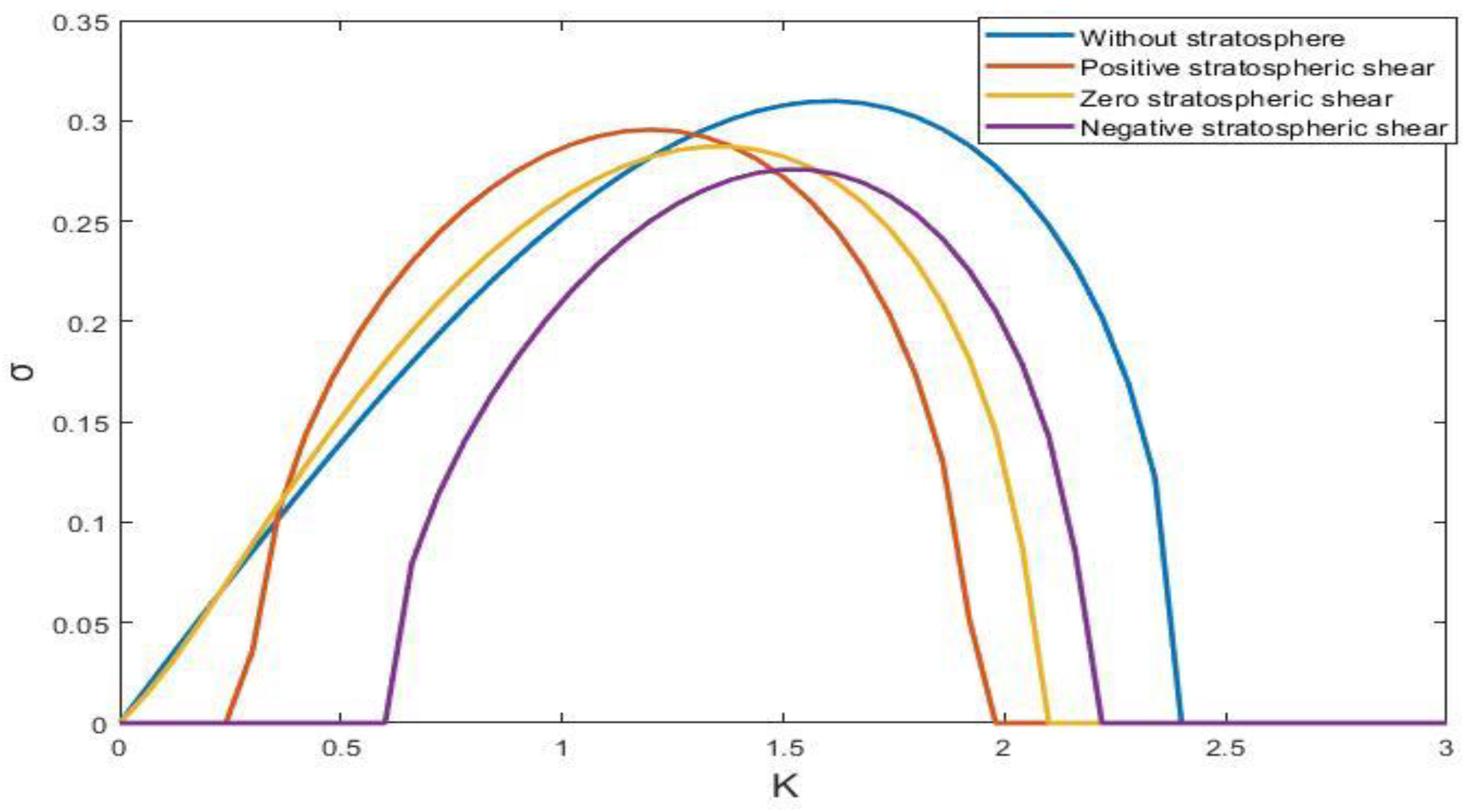This maximum growth rate is shown in Figure 2 as a function of the wavenumber $K$. We observe that in the absence of the stratosphere, perturbations with $K<2.4$, which correspond to perturbations with scales larger than about 2500 km for typical values of the parameters, are unstable. The maximum growth rate in the Eady model is achieved for a perturbation with $K_{max}\approx 1.6$ (horizontal scale of 4000 km) that grows at a rate of ~0.03 day⁻¹. In all cases of stratospheric flows, the growth rate of the most unstable perturbation is smaller than the growth rate in the Eady model, with the largest growth rate achieved in the positive shear and the lowest in the negative shear case. The scale of the maximally growing perturbation decreases as we move from positive to negative shear, but remains in all cases larger than the corresponding scale in the Eady model. It is also worth noting that in the cases of positive and negative shear, there is a low wavenumber cut-off for the instability. That is, the flow is stable to perturbations with very large scales. The range of scales for the unstable perturbations is approximately the same in these two cases and is shifted towards smaller scales for negative stratospheric shear. So, by taking into account the stratospheric flow, we expect perturbations with larger scales growing at a slower rate compared to the Eady model.

As it was noted in the introduction, modal analysis determines the stability of the flow at large times. However, perturbations grow at a finite time scale. To investigate perturbation growth at finite time, we define a positive definite norm for their amplitude, which is their energy density. This is given in terms of the state vector $\mathit{\psi }$ as $E={\mathit{\psi }}^{+}\mathit{M}\mathit{\psi },$ where

$$\mathit{M}=-\frac{1}{4} \left[\frac{\partial }{\partial z}\left(\frac{1}{N^2}\frac{\partial }{\partial z}\right)-K^2\right] \delta z,$$

(8)

is the energy metric. We then seek the initial perturbation that has the largest increase in energy over a specified time interval $T_{opt}$, that is the largest ratio of its energy in the optimal time $E\left(T_{opt}\right)$ over its initial energy $E\left(0\right)$. To calculate this ratio, we assume a coordinate system where $\mathit{w}={\mathit{M}}^{\frac{1}{2}}\mathit{\psi }$, so that the energy is given by the Euclidean norm $E={\mathit{w}}^{+}\mathit{w}$ with + denoting the Hermitian transpose. Then, $\mathit{w}$ evolves according to $\dot{\mathit{w}}=\mathit{D}\mathit{w}$ where $\mathit{D}={\mathit{M}}^{1/2}\mathit{A}{\mathit{M}}^{-1/2}$ and the energy ratio is given by

$$G=\frac{E\left(T_{opt}\right)}{E\left(0\right)}=\frac{{\mathit{w}}^{+}\left(0\right)e^{{\mathit{D}}^{+}{T}_{opt}}{e}^{\mathit{D}{T}_{opt}}\mathit{w}\left(0\right)}{{\mathit{w}}^{+}\left(0\right)\mathit{w}\left(0\right)}.$$

(9)

The optimal growth is then given by the maximum eigenvalue of the matrix $e^{{\mathit{D}}^{+}{T}_{opt}}{e}^{\mathit{D}{T}_{opt}}$.

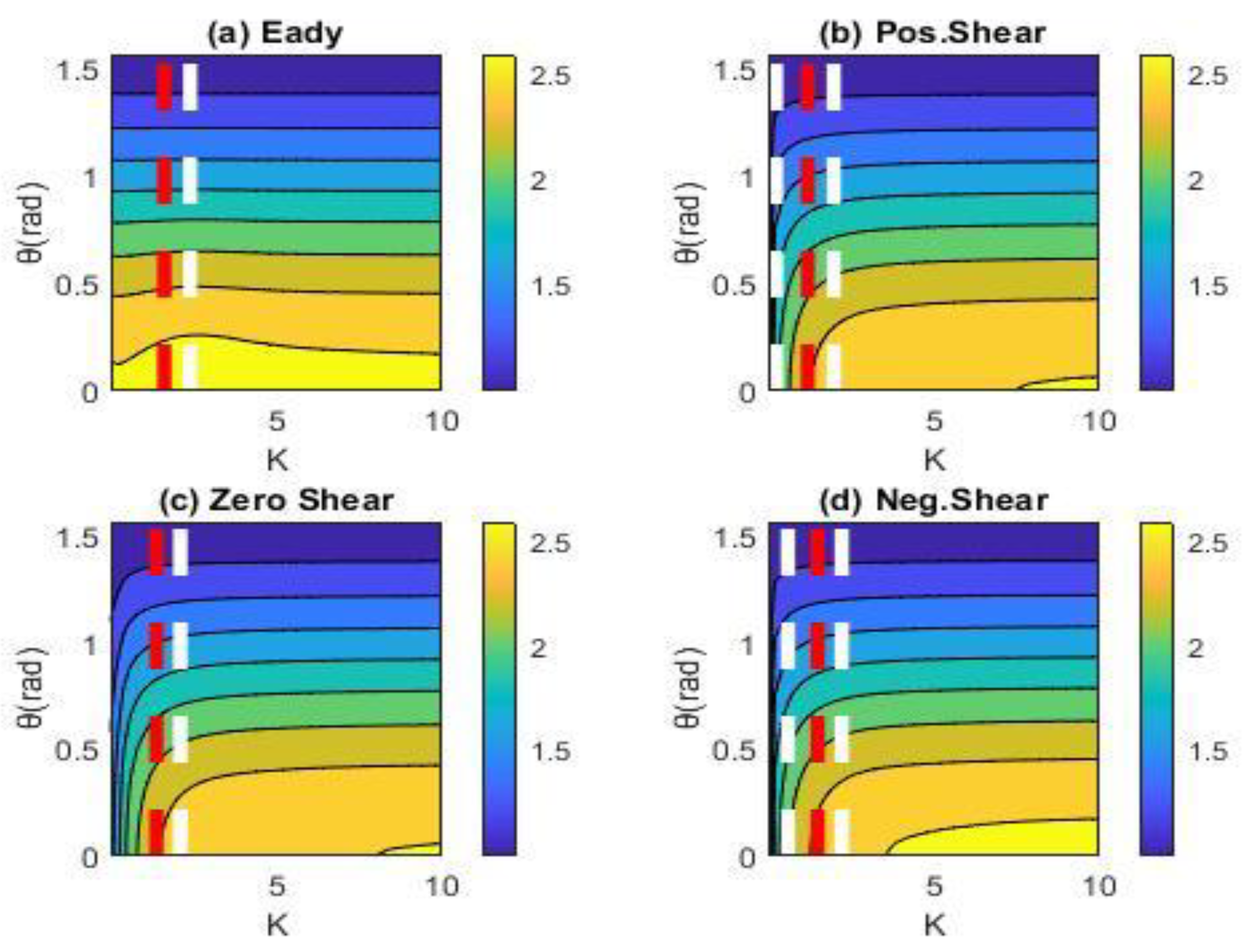
In Figure 3, the optimal energy growth at time $T_{opt}=1$ (corresponding to 1 day) is shown as a function of the wavenumber $K$ and the orientation $\theta$ of the perturbations, for the Eady model and the three different cases of stratospheric flow. The white dotted lines indicate the range of wavenumbers for exponentially growing perturbations and the red dotted line indicates the wavenumber $K_{max}$ with the maximum exponential growth rate. As we can see, $G$ is a monotonically decreasing function of $\theta$ with a maximum at $\theta =0$. For the Eady model, we observe that the optimal growth is almost independent of $K$ regardless of the region of exponential instability. This means that smaller scale perturbations that are modally stable grow within one day at the same rate as the exponentially unstable large-scale perturbations. For all cases of stratospheric flow, we observe approximately the same values of growth as in the Eady model, with smaller scale perturbations ($K>3.5$ corresponding to scales lower than 1800 km) achieving slightly larger values of growth compared to exponentially unstable waves with larger scale.

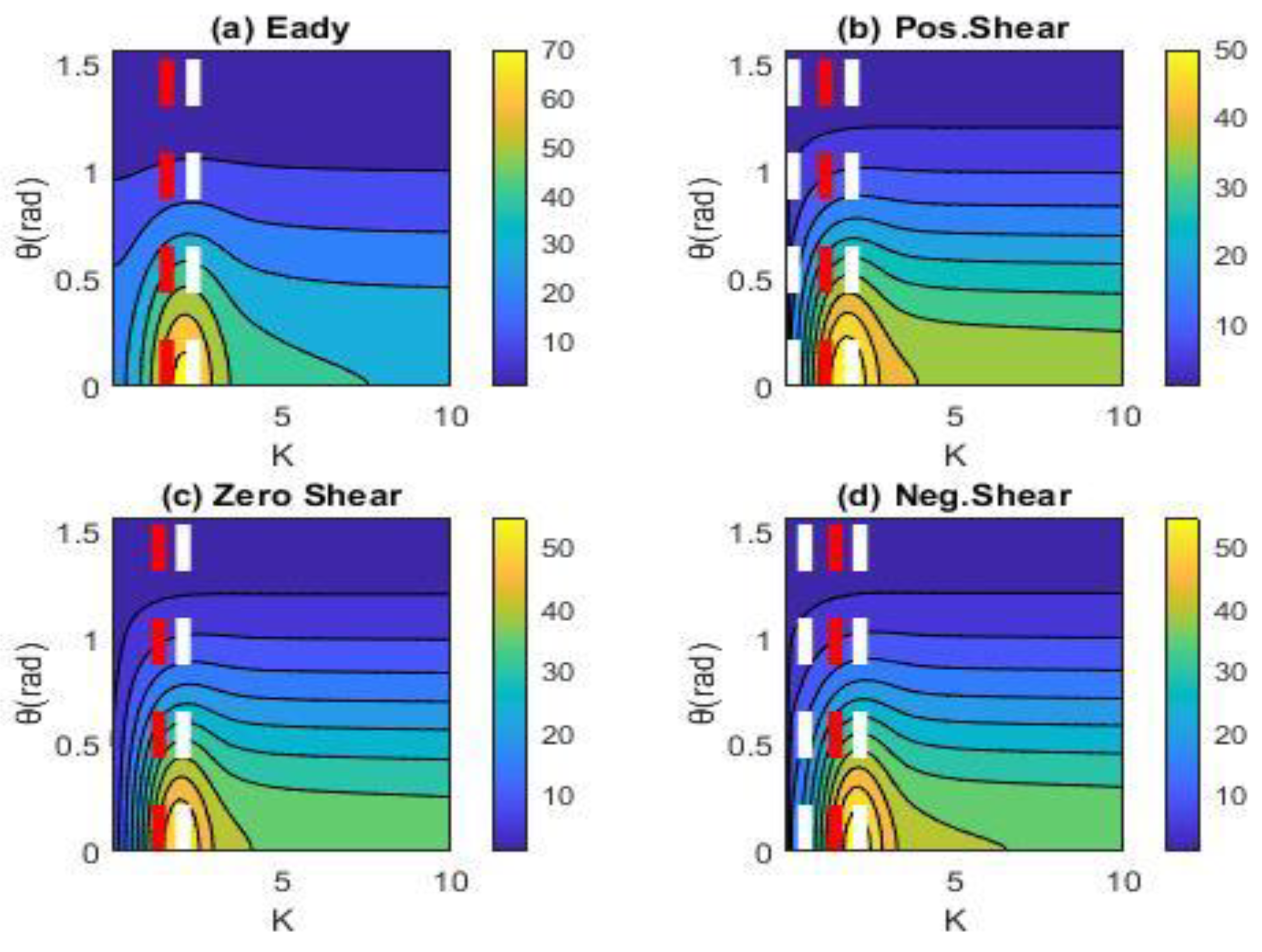
Figure 4 shows the corresponding growth for $T_{opt}=5$ days. We can see that considering the stratospheric flow results in a reduction of optimal growth between 20% and 30%. The maximum energy growth is observed in the case of negative shear in contrast to the exponential growth discussed above. The largest energy growth is observed again for meridionally oriented perturbations with $\theta =0$ and with large scales as now the maximum of $G$ occurs for wavenumbers less than 2. However, these wavenumbers are larger than $K_{max}$. That is, the perturbations growing the most over a time scale of a week have smaller scales compared to the scales predicted by the modal stability analysis. As in the case of exponential growth, the scale corresponding to the maximum value of $G$ is larger in all cases of stratospheric shear compared to the corresponding scale in the Eady model.

4. Conclusions

In this work, the influence of stratospheric shear on baroclinic instability was investigated. The evolution of small perturbations on a zonal shear flow that extends to the stable stratospheric layer was calculated for the quasi-geostrophic dynamics using the tools of Generalized Stability Theory. Three paradigms of flows were considered with positive, zero and negative stratospheric shear and the results were compared to the Eady model in which the stratospheric layer is absent. The perturbation growth for all three cases was found to be lower than the growth in the Eady model. For growth within time periods of the order of a day, small scale systems (with scales lower than 1800 km) are expected to grow more quickly, while for time periods of the order of a week, the systems growing the most have larger horizontal scales of the order of 3000 km. Compared to the Eady model, the scale of the perturbations that are expected to emerge is larger. For larger times for which exponentially growing perturbations are expected to dominate, the same conclusion holds. That is the influence of the stratospheric flow is to weaken perturbation growth and to lengthen the scale of the emerging systems.