Next Article in Journal
Bias Correction of Daily Precipitation on Two Eastern Mediterranean Stations with GAMs
Previous Article in Journal
The Detection of Plastic and Petroleum Hydrocarbon Pollution at Sea with Laser-Induced Fluorescence
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Environmental Sciences Proceedings
Volume 26
Issue 1
10.3390/environsciproc2023026002
environsciproc-logo
Submit to this Journal
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
Please note that, as of 4 December 2024, Environmental Sciences Proceedings has been renamed to Environmental and Earth Sciences Proceedings and is now published here.
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Proceeding Paper

Machine Learning Regression to Predict Pollen Concentrations of Oleaceae and Quercus Taxa in Thessaloniki, Greece †

by
Sofia Papadogiannaki
*,
Serafeim Kontos
,
Daphne Parliari
and
Dimitrios Melas
Laboratory of Atmospheric Physics, School of Physics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
*
Author to whom correspondence should be addressed.
†
Presented at the 16th International Conference on Meteorology, Climatology and Atmospheric Physics—COMECAP 2023, Athens, Greece, 25–29 September 2023.
Environ. Sci. Proc. 2023, 26(1), 2; https://doi.org/10.3390/environsciproc2023026002
Published: 23 August 2023
(This article belongs to the Proceedings of 16th International Conference on Meteorology, Climatology and Atmospheric Physics—COMECAP 2023)
Browse Figures
Versions Notes

Abstract

:
Airborne pollen triggers allergic reactions in up to 40% of the global population. The incidence of pollen allergies is increasing in Thessaloniki, Greece and it is predicted that more than 50% of the European Union’s inhabitants will suffer from allergic rhinitis by 2025. Thus, it is essential to investigate and predict high pollen concentrations to address this growing concern. This study utilized the Gradient Boosting Regression (GBR) technique, a machine learning approach, to estimate pollen concentrations of Oleaceae and Quercus taxa, using daily meteorological and land surface data obtained from the European Center for Medium-Range Weather Forecasts (ECMWF). The method accurately predicted pollen concentrations for both species, with an Index of Agreement (IoA) of 0.86 for Oleaceae and 0.78 for Quercus, despite the limited size of the dataset.

1. Introduction

Pollen, a significant environmental factor, has a considerable impact on human health, triggering various respiratory diseases in urban European cities and affecting up to 40% of the global population [1,2]. Allergy-related respiratory diseases are among the critical public health concerns of the 21st century [3,4]. The European Union has estimated that over half of its population will suffer from allergic rhinitis and/or asthma by 2025, resulting in reduced quality of life, decreased workplace productivity, and increased healthcare costs [5,6,7]. Atmospheric pollen concentration doubles every decade [8,9]; therefore, predicting and monitoring pollen concentrations are of utmost importance.
Machine learning techniques integrate pollen observations, meteorological data, and algorithms to accurately predict daily pollen concentrations. The most commonly applied techniques, including Deep Neural Networks (DNN) [10,11], Random Forests [10,11,12], Light Gradient Boosting Machine (LightGBM) [13], Least Absolute Shrinkage and Selection Operator (LASSO) [10], Artificial Neural Networks (ANN) [13,14,15,16], Extreme Gradient Boosting (XGBoost) [11], a K-mean cluster analysis [15,17], and a Bayesian ridge [11] can estimate phenological metrics and pollen intensity parameters. These techniques have been utilized for predicting pollen concentrations of various species such as Ambrosia [10,11,12,17], Oleaceae [13], Quercus [12], Cupressaceae [12], and Poaceae [12,15,17], and thus constitute valuable tools for allergiological and ecological implementations.
Previous studies on predicting pollen concentrations in Thessaloniki, Greece have been based only on observational data [8,18] and in-field measurements [19,20]. Current research on the prediction of pollen concentrations using machine learning techniques is limited and usually depends on extensive datasets. The primary focus has been on the use of K-means clustering algorithms [17] and data-driven modeling methods such as the multi-layer perceptron, support vector regression, and regression trees [21]. These methods have been applied to develop effective prediction models for mean daily pollen concentrations of highly allergenic taxa, such as Oleaceae. Nonetheless, there is presently no commensurate investigation regarding the application of machine learning techniques to forecast pollen concentrations of Quercus taxa or for constrained datasets.
The objective of this research is to develop a machine learning approach based on Gradient Boosting Regression (GBR) to estimate pollen concentrations for Oleaceae and Quercus taxa. The proposed method leverages daily meteorological and land surface data obtained from the European Center for Medium-Range Weather Forecasts (ECMWF). The training dataset comprises 6 years of daily pollen concentration measurements from 2016 to 2021. The final year of the dataset, 2022, is allocated for conducting an independent testing phase to evaluate the machine learning model’s performance. In addition, the main pollen season for all years is determined.

2. Materials and Methods

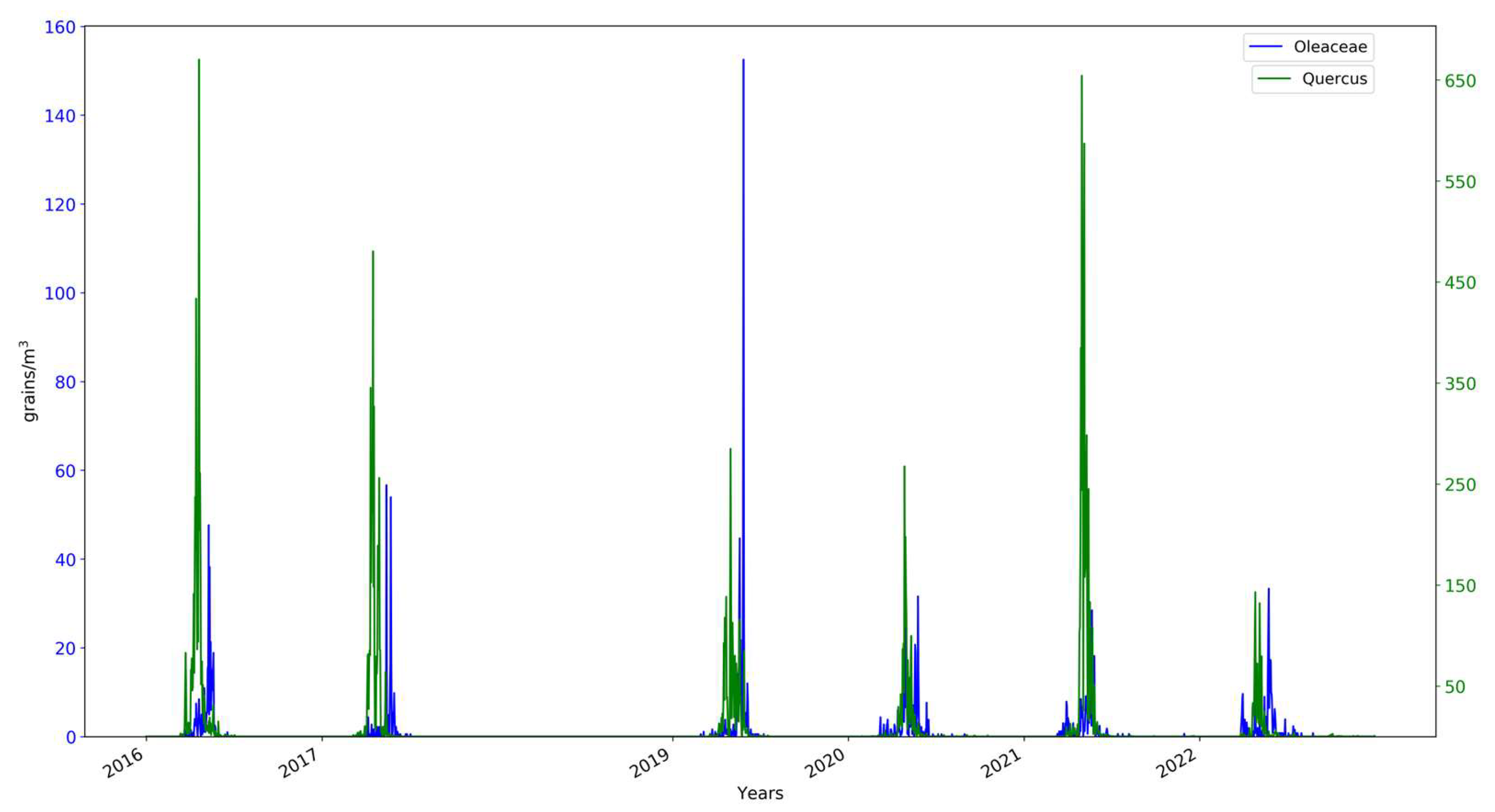
2.1. Pollen Data

Airborne pollen in Thessaloniki was collected using a 7-day recording volumetric spore trap of the Hirst design [22], located at 30 m a.g.l. on the roof of the Department of Biology at Aristotle University of Thessaloniki in the city center (40°37′ N, 22°57′ E) [19,20]. The station has been continuously operating since 1987, following the standard guidelines of the European Aerobiology Society for pollen counting [23]. Measurements are expressed as average daily pollen concentrations (grains/m3). The identification of the main pollen season of Oleaceae and Quercus taxa was executed by utilizing the 95% method [24].

2.2. ECMWF Data

The daily meteorological and land surface contextual data were sourced from the ECMWF reanalysis [25]. A range of 22 predictor variables were utilized based on the methodology of Zewdie et al. [11], including the total water column, cloud cover, surface and mean sea level pressures, vertical and horizontal wind speed, soil temperature at various levels, skin temperature, surface albedo, total column ozone, volumetric soil water, dew point temperature at 2 m, surface and 2 m temperature, precipitation, and high and low vegetation cover.

2.3. GBR and Analysis

Gradient Boosting Regression (GBR) is a widely used machine learning algorithm that is particularly suited for analyzing tabular datasets. This approach is capable of identifying complex, nonlinear relationships between a model’s target and its associated features, and is highly adaptable, able to effectively handle both missing values and outliers [26,27].
The GBR model was developed using pollen and ECMWF data collected from 2016 to 2021 (year 2018 is missing due to a lack of data), with the data from 2022 used for testing the model’s predictive performance. All input parameters were time-lagged up to 30 days back, including the sine of the Julian day, to identify the relationship between pollen abundance and previous days’ atmospheric weather and land surface parameters. The GBR algorithm, with Friedman’s mean squared error criterion as the splitting criterion, was implemented, and normalization was not required. To identify the best combination of hyperparameters, the RandomizedSearchCV function from the scikit-learn library was employed [28]. The function performed 1000 iterations on the training data, exploring various hyperparameter settings. The loss function used was Huber, and the ensemble comprised 300 estimators.

3. Results and Discussion

Figure 1 depicts the time series of pollen concentrations for the Oleaceae and Quercus taxa for the years 2016 to 2022. Notably, the Oleaceae exhibits elevated concentrations in 2019, reaching a peak of 152 grains/m3 on 28 May. In the remaining years, a consistent pattern is observed, where the main pollen season commences in mid- to late March and ends in early July, with concentrations staying below 60 grains/m3. In contrast, the Quercus exhibits higher concentrations, with peak values observed in 2016 (670 grains/m3 on 20 April) and 2021 (654 grains/m3 on 1 May). However, in 2022, the concentrations decrease compared to previous years, not exceeding 150 grains/m3. The pollination period for Quercus exceeds from mid-April to mid-June.
Figure 2 illustrates the time series of observed and predicted daily concentrations for the Oleaceae and Quercus species for 2022. The GBR model demonstrates satisfactory performance in predicting the observed pollen concentrations for both taxa, albeit with a slight underestimation of the peaks. Specifically, during the onset of the main pollen period, the model underestimates the concentrations of Oleaceae, resulting in an overestimation during the occurrence of secondary peaks. Conversely, for the Quercus species, the model initially overestimates the concentrations, followed by an underestimation at the peaks.
The statistical metrics (Appendix A) presented in Table 1 (MB Equation (A1), MAE Equation (A2), NMAE Equation (A3), IoA Equation (A4)) further demonstrate the satisfactory correlation and estimation of daily concentrations using the GBR model. The observed and predicted values exhibit a significant agreement, with an IoA of 0.86 for Oleaceae and 0.78 for Quercus, highlighting the model’s effectiveness in accurately capturing the pollen concentrations for both species.
Table 2 confirms the GBR model’s successful prediction of the peak day and timing of the main pollen season. The actual and predicted peak days for Oleaceae aligned closely, occurring on DOY 145 (25 May) and DOY 146 (26 May), respectively. Similarly, the actual and predicted peak days for the Quercus coincided, observed on DOY 117 (27 April) and DOY 118 (28 April), respectively. Furthermore, there was notable agreement between the predicted and observed start and end dates for both taxa. The GBR model accurately estimated the start and end dates for the Oleaceae as DOY 89 (30 March) and DOY 196 (15 July), respectively, and for the Quercus, as DOY 111 (21 April) and DOY 165 (14 June), respectively. These findings demonstrate the GBR model’s reliable estimation of the main pollen season’s timing, providing valuable insights for allergy management and preventive measures.

4. Conclusions

The present study effectively utilized the Gradient Boosting Regression (GBR) technique to precisely estimate daily pollen concentrations for the Oleaceae and Quercus taxa in Thessaloniki, Greece. The model’s accuracy was confirmed through the agreement between the observed and predicted values, while its capability to forecast the timing of the main pollen season was successfully demonstrated. These findings hold significant implications for the management of allergies and the implementation of preventive measures, addressing the mounting apprehension surrounding pollen allergies in the population.

Author Contributions

Conceptualization, S.P. and D.M.; methodology, S.P.; investigation, S.P.; formal analysis, S.P.; resources, S.P.; writing—original draft preparation, S.P.; writing—review and editing, S.P., S.K., D.P. and D.M.; supervision, D.M.; project administration, D.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The pollen observations of the Department of Biology of the Aristotle University of Thessaloniki are provided from the Municipality of Thessaloniki (MoT) at https://envdimosthes.gr/fisika-aerioallergiogona/, accessed on 15 April 2023.

Acknowledgments

We would like to acknowledge the Department of Environment and Adaptation to Climate Change of the Municipality of Thessaloniki (MoT) for its participation in a Programmatic Agreement with the Department of Ecology of the Department of Biology, AUTH, for the operation of a natural Air Allergen Recording Station in MoT. Daphne Parliari acknowledges the support provided by Greece and the European Union (European Social Fund—ESF) through the Operational Program «Human Resources Development, Education and Lifelong Learning» in the context of the Act “Enhancing Human Resources Re-search Potential by undertaking a Doctoral Research”, Sub-action 2: «IKY Scholarship Programme for PhD candidates in the Greek Universities».

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The statistical metrics, which were utilized to assess the performance of the parameterizations, are defined as follows:
  • Mean Bias (MB):
    MB = ∑ i = 1 N ( P i − O i ) N
  • Mean Absolute Error (MAE):
    MAE = ∑ i = 1 N | P i − O i | N
  • Normalized Mean Absolute Error (NMAE):
    NMAE = ∑ i = 1 N | P i − O i | N O ¯
  • Index of Agreement (IoA):
    IoA = 1 − ∑ i = 1 N ( P i − O i ) 2 ∑ i = 1 N ( P i − O ¯ + | O i − O ¯ | ) 2
    where N is the number of values, Pi is the predicted values, Oi is the observed values, and O ¯   is the observation’s mean. The MB ranges from −∞ to +∞ with an optimal value of 0, while MAE and NMAE range from 0 to +∞ with an optimal value of 0. IoA ranges from 0 to 1, with an optimal value above 0.7 indicating a good performance of the predictions. The optimal value is 1 [29,30].

References

  1. D’Amato, G.; Cecchi, L.; Bonini, S.; Nunes, C.; Annesi-Maesano, I.; Behrendt, H.; Liccardi, G.; Popov, T.; Van Cauwenberge, P. Allergenic pollen and pollen allergy in Europe. Allergy Allerg. Immunother. 2017, 62, 287–306. [Google Scholar] [CrossRef]
  2. Bousquet, J.; Schünemann, H.; Samolinski, B.; Demoly, P.; Baena-Cagnani, C.; Bachert, C.; Bonini, S.; Boulet, L.; Bousquet, P.; Brozek, J.; et al. Allergic Rhinitis and its Impact on Asthma (ARIA): Achievements in 10 years and future needs. J. Allergy Clin. Immunol. 2012, 130, 1049–1062. [Google Scholar] [CrossRef] [PubMed]
  3. Pawankar, R. Allergic diseases and asthma: A global public health concern and a call to action. World Allergy Organ. J. 2014, 7, 1–3. [Google Scholar] [CrossRef] [PubMed]
  4. D’amato, G.; Holgate, S.T.; Pawankar, R.; Ledford, D.K.; Cecchi, L.; Al-Ahmad, M.; Al-Enezi, F.; Al-Muhsen, S.; Ansotegui, I.; Baena-Cagnani, C.E.; et al. Meteorological conditions, climate change, new emerging factors, and asthma and related allergic disorders. A statement of the World Allergy Organization. World Allergy Organ. J. 2015, 8, 25–52. [Google Scholar] [CrossRef]
  5. European Academy of Allergy And Clinical Immunology. Advocacy Manifesto, Tackling the Allergy Crisis in Europe—Concerted Policy Action Needed. Brussels. 2015. Available online: https://www.veroval.info/-/media/diagnostics/files/knowledge/eaaci_advocacy_manifesto.pdf (accessed on 24 April 2023).
  6. Blaiss, M.S. Pediatric allergic rhinitis: Physical and mental complications. Allergy Asthma Proc. 2008, 29, 1–6. [Google Scholar] [CrossRef]
  7. Meltzer, E.O.; Nathan, R.; Derebery, J.; Stang, P.E.; Campbell, U.B.; Yeh, W.-S.; Corrao, M.; Stanford, R. Sleep, quality of life, and productivity impact of nasal symptoms in the United States: Findings from the Burden of Rhinitis in America survey. Allergy Asthma Proc. 2009, 30, 244–254. [Google Scholar] [CrossRef]
  8. Damialis, A.; Halley, J.M.; Gioulekas, D.; Vokou, D. Long-term trends in atmospheric pollen levels in the city of Thessaloniki, Greece. Atmos. Environ. 2007, 41, 7011–7021. [Google Scholar] [CrossRef]
  9. Lake, I.R.; Jones, N.R.; Agnew, M.; Goodess, C.M.; Giorgi, F.; Hamaoui-Laguel, L.; Semenov, M.A.; Solomon, F.; Storkey, J.; Vautard, R.; et al. Climate Change and Future Pollen Allergy in Europe. Environ. Health Perspect. 2017, 125, 385–391. [Google Scholar] [CrossRef]
  10. Liu, X.; Wu, D.; Zewdie, G.K.; Wijerante, L.; Timms, C.I.; Riley, A.; Levetin, E.; Lary, D.J. Using machine learning to estimate atmospheric Ambrosia pollen concentrations in Tulsa, OK. Environ. Health Insights 2017, 11, 1178630217699399. [Google Scholar] [CrossRef]
  11. Zewdie, G.K.; Lary, D.J.; Levetin, E.; Garuma, G.F. Applying Deep Neural Networks and Ensemble Machine Learning Methods to Forecast Airborne Ambrosia Pollen. Int. J. Environ. Res. Public Health 2019, 16, 1992. [Google Scholar] [CrossRef]
  12. Lo, F.; Bitz, C.M.; Hess, J.J. Development of a Random Forest model for forecasting allergenic pollen in North America. Sci. Total. Environ. 2021, 773, 145590. [Google Scholar] [CrossRef] [PubMed]
  13. Cordero, J.M.; Rojo, J.; Gutiérrez-Bustillo, A.M.; Narros, A.; Borge, R. Predicting the Olea pollen concentration with a machine learning algorithm ensemble. Int. J. Biometeorol. 2020, 65, 541–554. [Google Scholar] [CrossRef]
  14. Rodríguez-Rajo, F.; Astray, G.; Ferreiro-Lage, J.; Aira, M.; Jato-Rodriguez, M.; Mejuto, J. Evaluation of atmospheric Poaceae pollen concentration using a neural network applied to a coastal Atlantic climate region. Neural Netw. 2010, 23, 419–425. [Google Scholar] [CrossRef] [PubMed]
  15. Sánchez-Mesa, J.A.; Galan, C.; Martínez-Heras, J.A.; Hervás-Martínez, C. The use of a neural network to forecast daily grass pollen concentration in a Mediterranean region: The southern part of the Iberian Peninsula. Clin. Exp. Allergy 2002, 32, 1606–1612. [Google Scholar] [CrossRef] [PubMed]
  16. Valencia, J.A.; Astray, G.; Fernández-González, M.; Aira, M.J.; Rodríguez-Rajo, F.J. Assessment of neural networks and time series analysis to forecast airborne Parietaria pollen presence in the Atlantic coastal regions. Int. J. Biometeorol. 2019, 63, 735–745. [Google Scholar] [CrossRef]
  17. Makra, L.; Sánta, T.; Matyasovszky, I.; Damialis, A.; Karatzas, K.; Bergmann, K.-C.; Vokou, D. Airborne pollen in three European cities: Detection of atmospheric circulation pathways by applying three-dimensional clustering of backward trajectories. J. Geophys. Res. Atmos. 2010, 115, D24220. [Google Scholar] [CrossRef]
  18. Gioulekas, D.; Papakosta, D.; Damialis, A.; Spieksma, F.; Giouleka, P.; Patakas, D. Allergenic pollen records (15 years) and sensitization in patients with respiratory allergy in Thessaloniki, Greece. Allergy 2004, 59, 174–184. [Google Scholar] [CrossRef]
  19. Damialis, A.; Kaimakamis, E.; Konoglou, M.; Akritidis, I.; Traidl-Hoffmann, C.; Gioulekas, D. Estimating the abundance of airborne pollen and fungal spores at variable elevations using an aircraft: How high can they fly? Sci. Rep. 2017, 7, 44535. [Google Scholar] [CrossRef]
  20. Charalampopoulos, A.; Damialis, A.; Lazarina, M.; Halley, J.M.; Vokou, D. Spatiotemporal assessment of airborne pollen in the urban environment: The pollenscape of Thessaloniki as a case study. Atmos. Environ. 2021, 247, 118185. [Google Scholar] [CrossRef]
  21. Voukantsis, D.; Niska, H.; Karatzas, K.; Riga, M.; Damialis, A.; Vokou, D. Forecasting daily pollen concentrations using data-driven modeling methods in Thessaloniki, Greece. Atmos. Environ. 2010, 44, 5101–5111. [Google Scholar] [CrossRef]
  22. Hirst, J.M. An automatic volumetric spore trap. Ann. Appl. Biol. 1952, 39, 257–265. [Google Scholar] [CrossRef]
  23. Galan, C.; Smith, M.; Thibaudon, M.; Frenguelli, G.; Oteros, J.; Gehrig, R.; Berger, U.E.; Clot, B.; Brandao, R.; EAS QC Working Group. Pollen monitoring: Minimum requirements and reproducibility of analysis. Aerobiologia 2014, 30, 385–395. [Google Scholar] [CrossRef]
  24. Andersen, T.B. A model to predict the beginning of the pollen season. Grana 1991, 30, 269–275. [Google Scholar] [CrossRef]
  25. Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
  26. Hastie, T.; Tibshirani, R.; Friedman, J.; Hastie, T.; Tibshirani, R.; Friedman, J. Boosting and additive trees. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 337–387. [Google Scholar]
  27. Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
  28. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. JMLR 2011, 12, 2825–2830. [Google Scholar]
  29. Emery, C.; Tai, E.; Yarwood, G. Enhanced Meteorological Modeling and Performance Evaluation for Two Texas Ozone Episodes. Final Report Submitted to Texas Natural Resources Conservation Commission, Prepared by ENVIRON 2001; International Corp.: Novato, CA, USA, 2001. [Google Scholar]
  30. Kontos, S.; Papadogiannaki, S.; Parliari, D.; Steiner, A.L.; Melas, D. High resolution modeling of Quercus pollen with an Eulerian modeling system: A case study in Greece. Atmos. Environ. 2021, 268, 118816. [Google Scholar] [CrossRef]
Environsciproc 26 00002 g001
Figure 1. Oleaceae and Quercus daily pollen concentrations (2016–2022) in Thessaloniki, Greece.
Figure 1. Oleaceae and Quercus daily pollen concentrations (2016–2022) in Thessaloniki, Greece.
Environsciproc 26 00002 g001
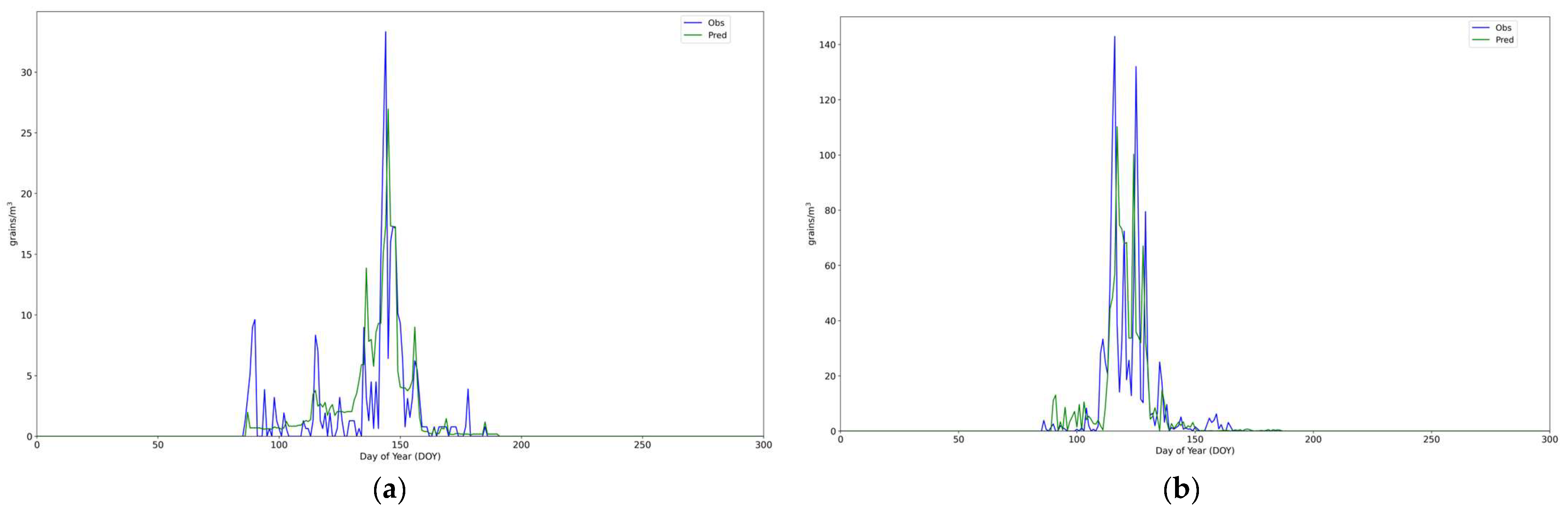
Environsciproc 26 00002 g002
Figure 2. Time series of the observed and predicted (a) Oleaceae and (b) Quercus daily pollen concentrations (2022).
Figure 2. Time series of the observed and predicted (a) Oleaceae and (b) Quercus daily pollen concentrations (2022).
Environsciproc 26 00002 g002
Table 1. Statistical metrics for the evaluation of GBR model.
Table 1. Statistical metrics for the evaluation of GBR model.
ΜΒΜAΕΝΜAΕΙοA
Oleaceae0.282.810.550.86
Quercus−0.3811.020.640.78
Table 2. Actual and Expected Dates of Start, End, and Peak of the Main Pollen Season (2022) in Day of Year (DOY).
Table 2. Actual and Expected Dates of Start, End, and Peak of the Main Pollen Season (2022) in Day of Year (DOY).
Actual DateExpected Date
StartEndPeakStartEndPeak
Oleaceae89 (30 March)196 (15 July)145 (25 May)96 (6 April)185 (4 July)146 (26 May)
Quercus111 (21 April)165 (14 June)117 (27 April)101 (11 April)171 (20 June)118 (28 April)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Papadogiannaki, S.; Kontos, S.; Parliari, D.; Melas, D. Machine Learning Regression to Predict Pollen Concentrations of Oleaceae and Quercus Taxa in Thessaloniki, Greece. Environ. Sci. Proc. 2023, 26, 2. https://doi.org/10.3390/environsciproc2023026002

AMA Style

Papadogiannaki S, Kontos S, Parliari D, Melas D. Machine Learning Regression to Predict Pollen Concentrations of Oleaceae and Quercus Taxa in Thessaloniki, Greece. Environmental Sciences Proceedings. 2023; 26(1):2. https://doi.org/10.3390/environsciproc2023026002

Chicago/Turabian Style

Papadogiannaki, Sofia, Serafeim Kontos, Daphne Parliari, and Dimitrios Melas. 2023. "Machine Learning Regression to Predict Pollen Concentrations of Oleaceae and Quercus Taxa in Thessaloniki, Greece" Environmental Sciences Proceedings 26, no. 1: 2. https://doi.org/10.3390/environsciproc2023026002

APA Style

Papadogiannaki, S., Kontos, S., Parliari, D., & Melas, D. (2023). Machine Learning Regression to Predict Pollen Concentrations of Oleaceae and Quercus Taxa in Thessaloniki, Greece. Environmental Sciences Proceedings, 26(1), 2. https://doi.org/10.3390/environsciproc2023026002

Article Metrics

Back to TopTop