Simulations of Tesla Valve Micromixer for Water Purification with Fe₃O₄ Nanoparticles ^†

Abstract

Heavy metals can contaminate water through both natural processes and anthropogenic activities. Unlike organic contaminants, heavy metals are toxic, not biodegradable, and possess the ability to accumulate in organisms. Effective mixing between contaminated water and nanoparticles is of great importance in various purification applications of microfluidics, especially when heavy metals are involved. In these terms, a series of simulations were performed to succeed in an effective mixing of iron oxide nanoparticles in the duct. The selected geometry for the simulations was the Tesla valve which was used as a micromixer. In the present work, a stream loaded with nanoparticles and a stream with contaminated water are numerically studied for various inlet velocity ratios of the two streams. Better mixing is achieved, compared with relative works, under V_p/V_c = 10, for an inlet rate of the Fe₃O₄ nanoparticles per second equal to 1000.

1. Introduction

The combined properties of heavy metals, i.e., non-biodegradable, unmetabolized, or decomposed, and their ability to accumulate in environmental systems make them extremely dangerous for human health [1]. Moreover, heavy metals are categorized as essential (Zn, Cu, Fe, and Co) and nonessential (Cd, Hg, As, and Cr). This classification is based on their toxicity, for example, even at low concentrations essential heavy metals are harmless, unlike nonessential metals, which are highly toxic [2]. Several studies investigate the synthesis of nanoparticles and adsorption properties of Fe₃O₄ magnetic nanoparticles for the removal of heavy metal ions. Chang and Chen [3] found that the adsorption equilibrium time was 1 min for monodisperse Fe₃O₄ magnetic nanoparticles with a mean diameter size of 13.5 nm. In addition to synthesis of nanoparticles, several parameters affect the adsorption efficiency of heavy metals, such as pH, contact time, temperature, adsorbent dose, and initial ion concentration [2].

Modern water flow simulations explore novel mechanisms occurring at the nanoscale for water purification [4]. The main purpose of this numerical study was to achieve the optimum mixing between streams of nanoparticles and contaminated water, where the heavy metal could be captured by nanoparticles through chemical reactions under various initial conditions [2]. Passive micromixing systems are defined through virtue of their geometry and any natural flow features that arise [5]. Generally, passive micromixers [1] are more reliable in comparison to active micromixers [6], mostly due to a reduction in moving parts. In micromixers, the flow rates and the regime of the fluids are significantly low and laminar, respectively. The mixing of the fluids is mainly dependent on diffusion with a very low mixing efficiency [7].

Many variations of Tesla’s geometries which were used either as valves [8,9] or as micromixers [10] have been investigated during the last years. The main factors affecting the mixing efficiency are the Reynolds number (Re) and geometric parameters [11]. In previous studies, the Reynolds number varied from 0.05 to 100 [10,11], while the mixing efficiency reached up to 96.47% for Re = 52.5 and eight Tesla units [12]. The geometric parameters of existing micromixers show a high variety of lengths and contact angles (θ°). It should be noted that Tesla valves can be used as forward or inverse flow micromixers.

In the present study, a Tesla valve was used as a passive micromixer where a heavy-metal-contaminated water stream and a freshwater stream loaded with nanoparticles are inserted in a microfluidic duct with variable inlet velocity ratios. The novelty of this work is that discrete methods are used in order to simulate the nanoparticle trajectories inside the single Tesla’s valve geometry. Numerical simulations were performed for the study of the effect of inflow on the particle distribution in the duct. The methodology for water flow and particle motion simulation is described in Section 2. The results of the mixing performance are discussed in Section 3 and Section 4, respectively. Finally, the most important conclusions are summarized in Section 5.

2. Materials and Methods

The slow water flow in the micromixer duct is expected to be laminar and steady state. The inlet of the micromixer is a squared cross section with height and width of W = H = 10⁻⁴ m. The angle θ = 30◦ and the length ratio of L₁/L₂ = 2 were selected from an existing Tesla structure [12]. The two water streams enter the micromixer from different inlets (with the same dimensions), are mixed, and then leave the domain from the common outlet as is shown in Figure 1. Additionally, the physical and mechanical properties of Fe₃O₄ have an impact on interactions and thus they were numerically embedded in the simulations. The values of these properties found from the literature correspond to a density equal to 5180 kg/m³ [13], Poisson’s ratio equal to 0.31, and Young’s modulus 200 × 10⁹ Pa [14].

The incompressible Navier–Stokes equations are solved in the Eulerian frame, for the pressure p and velocity u, together with a model for the discrete motion of particles in a Lagrangian frame. Due to microfluidic duct size, nanoscale effects such as wall interference on fluid properties and transport properties [15] are suppressed. Governing equations of the fluid phase are given by [1]:

$$\nabla ·u=0$$

(1)

$$\frac{\partial u}{\partial t}+u·\nabla u=-\nabla p+v{\nabla }^{2}u$$

(2)

where t is time and v the kinematic viscosity of the water. The motion equations of each single particle in the discrete frame are based on the Newton law and may read as follows:

$$m_i\frac{\partial u_i}{\partial t}=F_{nc,i}+F_{tc,i}+F_{drag,i}+F_{grav,i}$$

(3)

$$I_i\frac{\partial {\omega }_i}{\partial t}={{\rm M}}_{drag,i}+{{\rm M}}_{con,i}$$

(4)

where the index i stands for the ith-particle and diameters d_i, u_i, and ω_i are its transversal and rotational velocities, respectively, and m_i is its mass. The mass moment of inertia matrix is I_i and the terms ∂u_i/∂t and ∂ω_i/∂t correspond to the linear and angular accelerations, respectively. F_nc,i and F_tc,i are the normal and tangential contact forces, respectively. F_drag,i stands for the hydrodynamic drag force, and F_grav,i is the total force due to buoyancy. M_drag,i and M_con,i are the drag and contact moments, respectively.

The Reynolds number (Re) is defined as:

$$Re=\frac{\rho VD}{\mu }=\frac{VD}{v}$$

(5)

where ρ = 10³ kg/ m³ is the density of the fluid, μ is the fluid dynamic viscosity coefficient, while ν = 10⁻⁶ m²/s is the kinematic viscosity of the fluid. D is a characteristic linear dimension that is equal to the hydraulic diameter (D_h); for a square inlet duct D_h = W = H = 10⁻⁴ m. Finally, V is the maximum velocity that is developed inside the duct. Re was found to be 0.63 and 0.1 for the V_p/V_c = 10 and V_p/V_c = 1, respectively, in the present work.

Mixing efficiency (n) of the Tesla micromixer is defined as [16]:

$$n=1-\sqrt{\frac{{\sigma }_C^2}{{\sigma }_{max}^2}}=1-\frac{\sqrt{\frac{1}{N-1}{{\displaystyle \sum }}_{i=1}^N{\left(C_i-\overline{C}\right)}^2}}{\overline{C}\left(1-\overline{C}\right)}$$

(6)

where σ and σ_max are the standard deviation and the maximum deviation, respectively. N is the number of sampling points and N − 1 is given by applying Bessel’s correction. C_i is the point concentration and $\overline{C}$ is the mean concentration from sampling points.

The OpenFoam platform is used for the calculation of the flow field and the uncoupled equations of particle motion [17,18]. The simulation process reads as follows: initially, the fluid flow is found using the incompressible Navier–Stokes equations and the pressure correction method. Upon finding the flow field, pressure and velocity, the motion of particles is evaluated by the Lagrangian method. The equations are evolved in time by Euler’s time marching method. An unstructured computational grid composed of 62,899 (tetrahedra) cells is used here as shown in Figure 2, which is adequate for the low Reynolds number of the flow. Details of the numerical models, force, and moment terms used on equations may be found in [19,20].

3. Results

A series of simulations were performed with different velocity ratios of the contaminated water (V_c) and the nanoparticle solution (V_p) streams for optimum mixing. Simulation parameters as well as the boundary conditions are presented in

Table 1. Simulation parameters.

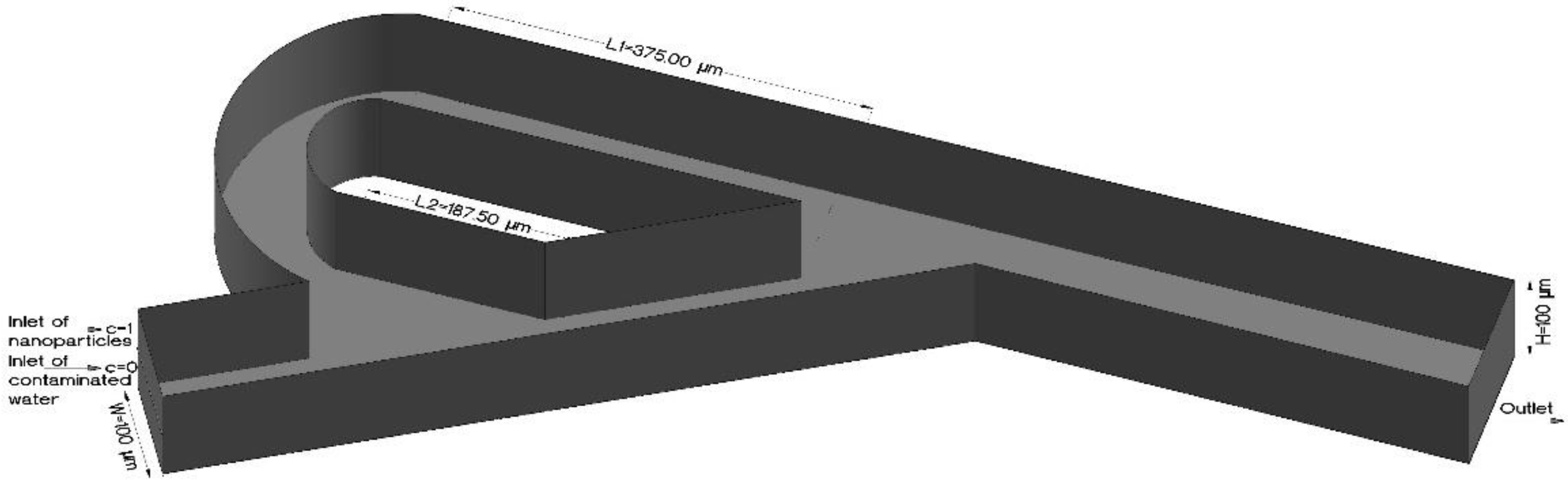
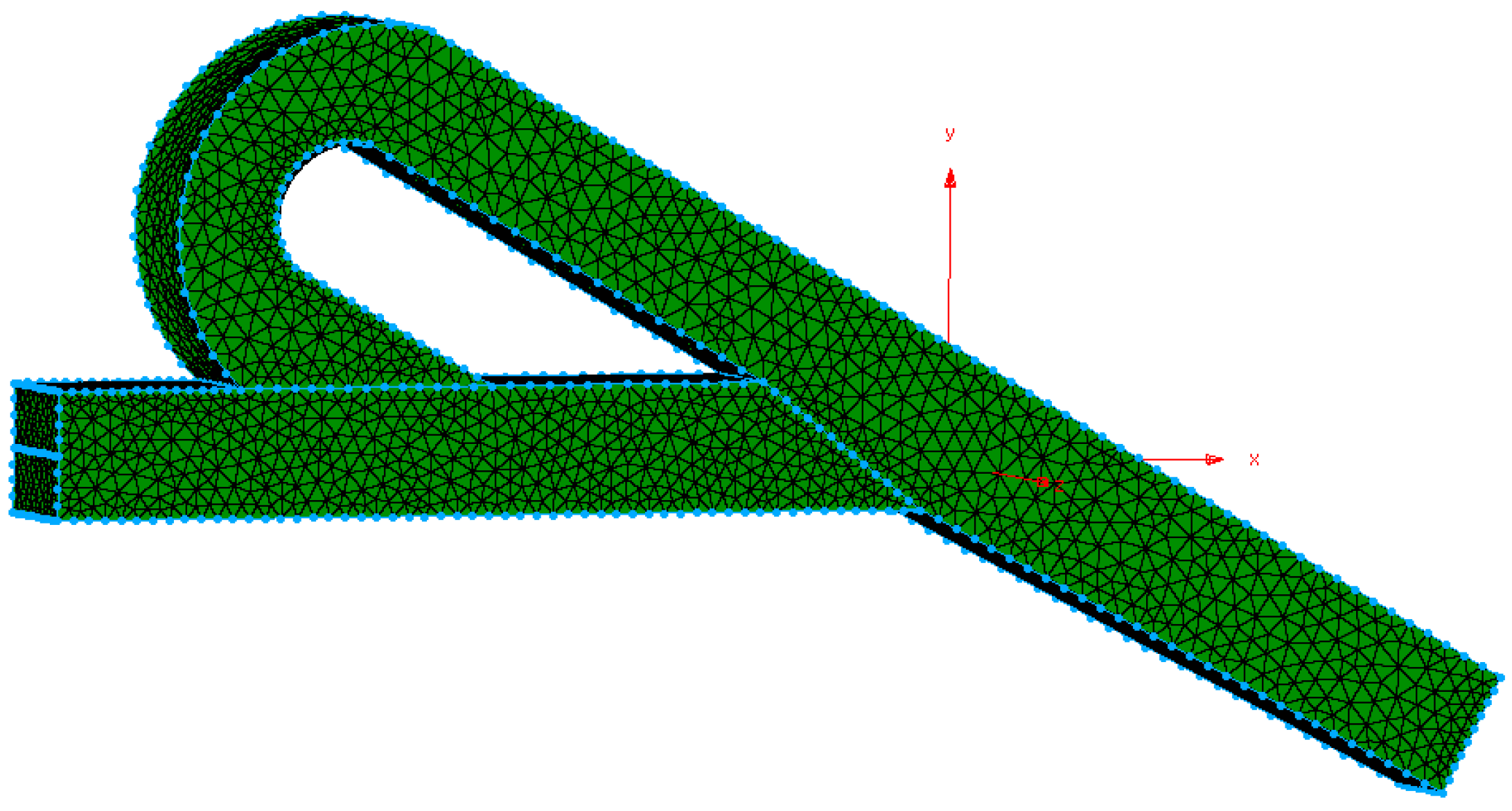
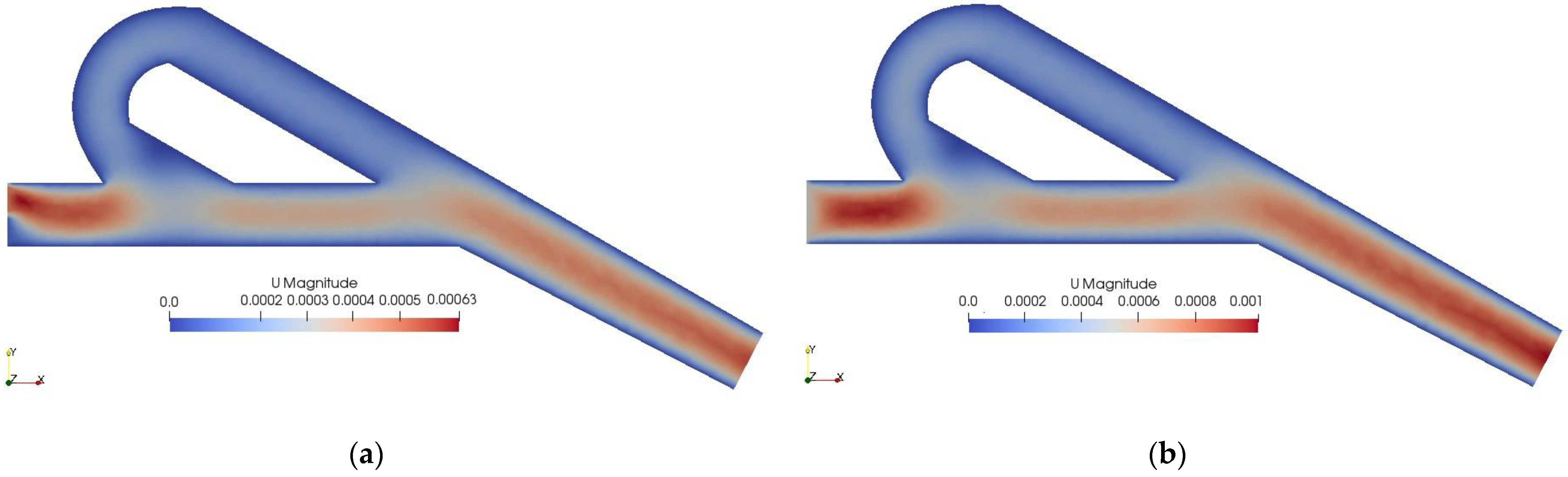
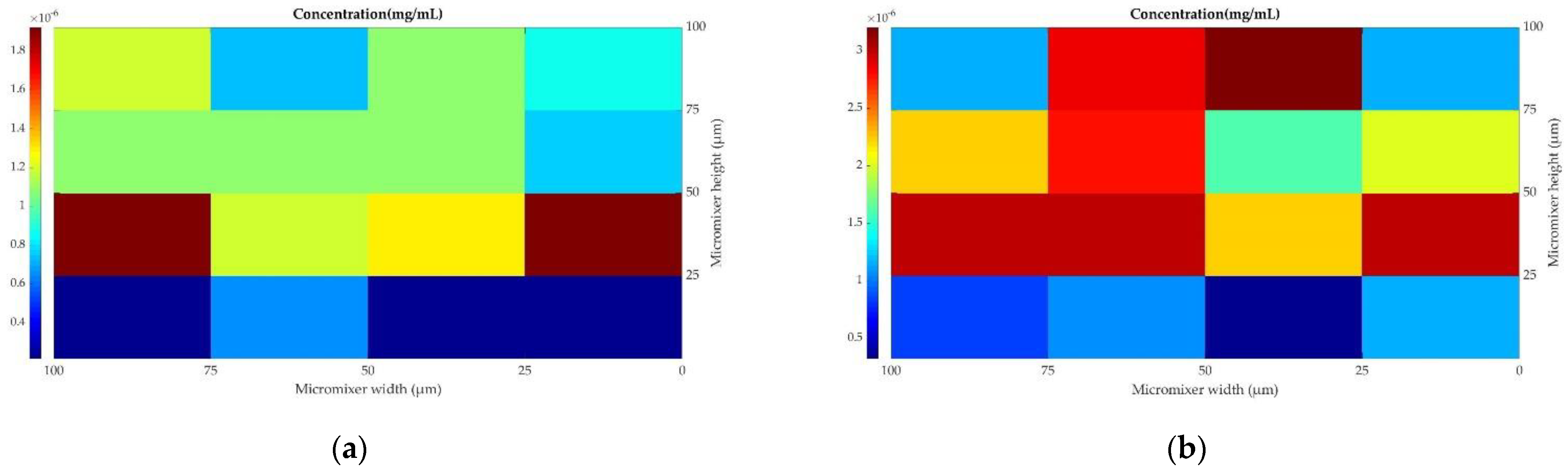
Inlet, outlet dimensions of geometry	Height (H) = Width (W) = 1 × 10−4 m
Diameter of nanoparticles	13.5 nm
Nanoparticles per second	500 and 1000
Boundary conditions	Velocity (U) (m/s)	Pressure (p) (pa)
Contaminated water–heavy metals (Vc)	0.0005, 0.00005	zero gradient
Nanoparticles (Vp)	0.0005	zero gradient
Outlet	zero gradient	0
Walls	0	zero gradient

. Initially, the examination of the inlet velocity ratio occurs as shown in Figure 3a,b, which represents the velocity field inside the micromixer for the V_p/V_c = 10 and V_p/V_c = 1, respectively. It is clear that for the higher velocity ratio the velocity field is decreased inside the duct.

The first outcomes (before mathematical analysis) of the investigation for optimum mixing under various inlet velocities ratios of the micromixer are presented in Figure 4a,b. The rate of nanoparticles remains constant for the entire simulation. In Figure 4a,b, we provide 500 Fe₃O₄ nanoparticles per second at the upper half inlet of the micromixer. Under V_p/V_c = 10 (4a), a satisfying distribution is observed at the begging of the micromixer. In addition, the upper part (loop) of the micromixer is full of Fe₃O₄ nanoparticles. Near the common outlet, a very satisfying mixing is observed for all inlet rates of nanoparticles. It should be noticed that in the present simulations only one Tesla valve is used compared with previous works. However, under V_p/V_c = 1 (4b), no mixing is observed inside the whole length of the micromixer. Hence, there is no need for further investigation of the case study V_p/V_c = 1.

Nanoparticle concentrations were calculated for N samples near the exit of the duct. The quantification of the results show that mixing efficiency increased with the increase in the inlet rate of Fe₃O₄ nanoparticles. When the rate was equal to 500 Fe₃O₄ nanoparticles per second, the mixing efficiency was 46.5%, while for 1000 Fe₃O₄ nanoparticles per second, the mixing efficiency was 52.8%.

The distribution of nanoparticles is visualized in Figure 5 through a cross section of the micromixer near the exit. An inlet rate equal to 500/s nanoparticles was determined in all regions of the micromixer (Figure 5a). The majority of nanoparticles are localized in the middle layers of the micromixer. At the bottom of the micromixer, the concentration is minimized. Additionally, for rates equal to 1000/s, the nanoparticles also exist in all regions and seem to be more distributed across the micromixer (Figure 5b). Moreover, it is encouraging that for both inlet ratio cases, the second layer (from bottom) has a high concentration. This may be a counterbalance for the first layer where the concentration is at a minimum.

4. Discussion

To summarize the existing results, mixing is not achieved for all the cases with V_p/V_c = 1 under all the selected rates of Fe₃O₄ nanoparticles. As the V_p/V_c increases, the nanoparticles are spread to almost the full height of the micromixer as shown in Figure 3a. The results of the estimation of the mixing index in Equation (6) show that for an inlet rate equal to 500 Fe₃O₄ nanoparticles per second, the mixing efficiency was 46.5%, while for 1000 Fe₃O₄ nanoparticles per second, the mixing efficiency was 52.8%. Hence, mixing efficiency seems to have a correlation with the inlet rates of Fe₃O₄ nanoparticles. Additionally, the inlet velocity ratio seems to be crucial for the mixing efficiency of micromixers, since for the simplest geometries [19] with or [1] without an external magnetic field, the factor V_p/V_c dominates over other factors such as radius ratio and frequency of the magnetic field.

Moreover, comparing with previous works where a Tesla valve was used as a micromixer, our results seem encouraging. Weng found 26.10% [12] for a single Tesla micromixer which is half of the present work. It should be noted that the present geometry is based on Weng. Additionally, our mixing efficiency for 1000 Fe₃O₄ nanoparticles per second (52.8%) is comparable with Weng (51.93%) after the second Tesla valve. Hence, the selected initial conditions in the present work result in successful mixing with fewer Tesla units. Additionally, for an inverse type micromixer, Wang found mixing efficiency equal to 45.7% [10] with the first Tesla unit.

5. Conclusions

In the present work, Tesla’s valve geometry was used as a micromixer. In order to succeed in creating a uniform distribution of Fe₃O₄ nanoparticles inside the micromixer, various inlet velocity ratios were investigated, while forward flow was selected. The results from simulations show that as the velocity is equal to V_p/V_c = 10, the nanoparticles are spread uniformly across the length of the micromixer and occupy a large percent of the height of the micromixer near the common exit. The lower boundary of the velocity ratio is found where an effective mix is achieved. Hence, the next concern is to determine the upper boundary of the velocity ratio. Above the upper boundary, the velocity ratio will not intensively affect the mixing efficiency. The initial rates of nanoparticles seem to have a secondary role to mixing efficiency. Moreover, further investigation of mixing performance is needed either for reverse flow or adding Tesla’s valves in a series according to the bibliography. In addition, an external magnetic field for further investigation of micromixing enhancement will be embedded to expand this simplified model.