Abstract
Countermeasures against local scour at bridge piers and abutments can be grouped into two categories: (1) flow-altering and (2) bed-armouring countermeasures. In this work, long-term laboratory-scale experiments of clear-water scour at bridge piers with different configurations were performed in order to investigate the effects of an unprotected cylindrical pier, of a cylindrical pier with a classic collar countermeasure and of a cylindrical pier with a modified collar countermeasure. Tests were performed in a flume with movable sediment bed, and the scoured bathymetries at the equilibrium stage were acquired and used in numerical simulations of small-scale hydrodynamics at the piers. The modified collar countermeasure resulted in a significant reduction of the scour hole dimensions.
1. State of the Art
The erosion at bridge piers and/or abutments can be attributed to the combination of different phenomena: (1) general erosion, (2) contraction scour and (3) local scour. General erosion depends on the evolution of the river reach, whereas contraction scour is due to the interaction between the bridge structure and the river, causing local flow acceleration, which triggers bed erosion. Occurrence of these two phenomena is not compulsory. On the contrary, local scour, generated by the turbulent interaction between the flow and submerged bridge elements, is always present. In the past, several countermeasures against local scour at piers have been proposed. These can be grouped into two main categories [1,2]: (1) flow-altering countermeasures, aimed at contrasting the downflow at the upstream face of the pier and mitigating the erosion processes of the ensuing horseshoe vortex; and (2) bed-armouring countermeasures, which provide a physical barrier to contrast local scour [1,2]. The second group includes solutions like the riprap of natural rocks [3,4,5], the installation of man-made elements or the combination of both (e.g., bed sill) [2,6,7]. The pier collar is a popular countermeasure. It can be considered both as a flow-altering countermeasure if placed above the riverbed, acting as an obstacle to the downward flux upstream of the pier, and as a bed-armouring countermeasure, if it is placed flush with the bed or buried [8,9,10]. In the literature, several collar shapes have been proposed, e.g., winged collar and conical collar [11], as well as hooked collar and double hooked collar [12], obtaining in all cases a reduction of the maximum scour depth between 42% and 50% with respect to the plain pier.
Here, a bordered collar is investigated as a countermeasure to contrast the pier local scouring. Long-term laboratory tests under clear-water conditions were carried out in a tilting flume with an erodible bed. The experiments were stopped once that the quasi-equilibrium phase had been reached. A reference test was performed with an unprotected cylindrical pier (test T0), later adding to the same pier both a standard collar (test T1) and a collar with an upper border (test T2).
Numerical simulations were then performed, investigating the small-scale flow field around the pier for the different configurations under both flat-bed and equilibrium scoured conditions, corresponding to the initial and final stages of the scour process, respectively. Similar numerical experiments have already been performed in literature [13,14,15,16,17]. Our simulations allowed for exploring the flow alteration brought about by the different collar configurations with respect to the unprotected case. Three-dimensional (3D) Reynolds-Averaged Navier-Stokes (RANS) simulations were performed. Although RANS simulations cannot describe the unsteady nature of vortex shedding, they still reveal the mean steady characters of the flow field around the pier and the protection structures, allowing for the identification of the main hydrodynamic differences between the different tested configurations.
2. Laboratory Tests
Laboratory tests were carried out at the Laboratorio “Grandi Modelli Idraulici” of the Dipartimento di Ingegneria Civile, Università della Calabria (Italy). A 9.6 m long rectangular tilting flume with width B = 0.485 m was employed, equipped with a 1.5 m long and 0.20 m deep recess box, placed 6 m downstream of the inlet section. Steady, uniform flow conditions were set up in the test region. The flume inlet is equipped with a honeycomb flow straightener, whereas a tailgate regulates the water level at the outlet.
2.1. Test Conditions
The maximum equilibrium scour depth was obtained under clear-water conditions, i.e., for a flow intensity U/Uc < 1, where U is the mean velocity within the flume and Uc is the critical velocity for the inception of sediment motion, here estimated through Neill’s equation [18]. The bed sediment grading was uniform, with median diameter d50 = 1.53 mm and geometric standard deviation of the grain size distribution σg = (d84/d16)0.5 < 1.5, thus avoiding bed armouring. The depth of the approaching flow was set to h = 0.13 m, as measured by a ± 0.1 mm accurate point gauge placed upstream of the recess box.
2.2. Test Setup and Procedure
Three cylindrical pier models with diameter b = 0.04 m were used: the unprotected pier model was used for reference test T0; the pier model with a classic 3b-wide and b/10-thick collar placed flush with the unscoured sand bed was employed for test T1; the pier model with the same collar and a b/10-wide and b/10-thick upper border, its top surface being at the undisturbed bed level, served for test T2. The collar width was chosen according to the limit dimension for practical applications [19].
As reported in Ferraro et al. [20], the experimental tests satisfy all the conditions on non-dimensional parameters present in literature, determining that only local scour occurs at the pier model and that equilibrium scour conditions have been reached [1,21,22,23,24]. The list of the non-dimensional parameters characterising the laboratory experiments is given in Table 1, in which the Reynolds number of the pier is defined as Rep = U b/ν, ν being the water kinematic viscosity.

Table 1.
Non-dimensional parameters characterising the laboratory experiments of clear-water scour at the pier models.
Prior to each test, the pier model was attached to the bottom of the recess box at the centre of the test section. The recess box was then filled in with compacted and levelled sand. The flume was slowly filled with water to protect the bed from initial uncontrolled scouring, up to the achievement of the experimental design conditions. Maximum scour depth around the pier during the tests was measured through a ± 0.1 mm accurate point gauge installed on a movable carriage. The tests were stopped according to the Coleman criterion [25]: namely, the maximum scour depth observed within the last 24 h of experimentation had to be smaller than 5% of the smallest value between the pier diameter and the flow depth. Once that this quasi-equilibrium scour depth had been achieved, the discharge was slowly reduced to zero, and the residual water volume flushed out through sinks placed along the flume bottom. Landslip phenomena were not observed in the scour hole.
2.3. Scoured Bathymetry Survey
A 3D survey of the emptied scoured flume in the pier area was made through the photogrammetry technique. A Nikon D3000 camera (Nikon, Tokyo, Japan) with a Nikon R AF-S DX Zoom-Nikkor 18-55 mm lens was used to take a large number of pictures (about 80 for each test) from different positions, catching also markers placed into the flume. The shots were imported into the Agisoft PhotoScan software (Agisoft LLC, St. Petersburg, Russia), creating in the end a high-density 3D point cloud. The position of markers, which allowed for referencing the photogrammetry points, was identified using a Terrestrial Laser Scanner (TLS, Leica ScanStation P20, Heerbrugg, Switzerland). Finally, the 3D scoured bathymetry was processed through a Matlab code determining the dimensions of the scour hole, the deposit mound and the scoured volume. The surveyed 3D scoured bed surfaces were furthermore used in the numerical modelling.
3. Numerical Simulations
Five numerical simulations were performed, reproducing the equilibrium scour conditions of laboratory experiments T0, T1 and T2, as well as the flat-bed initial conditions of both tests T0 and T1, with the collar top face flush with the bed in the latter case, and of test T2, in which the sediments on the plate of the bordered collar were transported downstream in the first instants of the laboratory experiment.
The results of the numerical model are here shown in non-dimensional form for the purpose of generalisation. The magnitude of the local mean velocity u and the turbulence dissipation rate ϵ are displayed and made non-dimensional as follows:
where = 0.024 m/s is the undisturbed shear velocity, being determined from a preliminary flat-bed simulation of the flume without the pier.
Numerical Model
Three-dimensional simulations were performed with the Siemens Simcenter STAR-CCM+ v2019.1 (Siemens Digital Industries Software, Munich, Germany) computational fluid dynamics package [26]. The model solves the RANS equations through a projection method, based on the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm. Integration is performed through a finite-volume second-order upwind scheme. Eddy viscosity is parameterised through the realisable k-ϵ turbulence model [27]. For proper modelling of stagnation upstream of the pier leading to the downflow, the Volume-of-Fluid (VoF) method was employed to determine the position of the free surface, placing a gaseous incompressible phase of air above the water liquid phase. The liquid phase was identified for the purpose of displaying the results by the mesh elements with a water volume fraction ≥ 0.5.
The numerical domain reproduces the recess-box portion of the experimental flume, with the surveyed bottom surfaces and the pier models. The domain was extended in the upstream direction by 0.6 m with respect to the limit of the recess box to ensure the achievement of a correct velocity distribution upstream of the pier. The domain stretches vertically to a distance of 2 h from the reference initial bed elevation, so that a suitable volume is given to air, avoiding the development of excess fictitious currents. The numerical mesh is made of cubic elements trimmed at the boundaries. The base resolution is 5 mm, being refined down to 1.25 mm in the proximity of the pier. The geometric details of the mesh refinement are given in Ferraro et al. [20].
Simulations start with the interface between the water and air phases being placed at a distance h from the reference bed elevation and a static pressure distribution throughout the domain. The water volume is initially set in motion at constant velocity U = Q/A = 0.37 m/s, with A = B h being the undisturbed wetted area, while air is set still. Numerical runs were performed with time-invariant boundary conditions, iterating until the achievement of steady flow. For liquid flow, a constant normal inflowing velocity U was set at the upstream water boundary, while a static pressure distribution was set at the downstream water boundary, both extending up to h. A static pressure distribution was set at the upstream and downstream air boundaries above h, in addition to the top of the numerical domain. A rough no-slip wall condition, i.e., with explicit modification for wall roughness in the wall law [26], was set to the bottom, employing a ks = d50 =1.53 mm roughness height. Smooth no-slip wall conditions, i.e., without modifications to the wall law for roughness [26], were set instead to the sidewall and pier boundaries, given the negligible roughness of the plastic material they are made of.
4. Results and Discussion
4.1. Results of the Laboratory Tests
The evolution of the scour depth for test T0 (unprotected pier) follows a logarithmic trend [28,29,30], whereas in tests T1 and T2 (collar-protected piers) scour evolves through different stages, as reported in some works [31,32,33,34].
Figure 1 shows the evolution in time of the maximum scour depth Δys (made non-dimensional with respect to the pier diameter b) in the laboratory tests. In the experiments with collar-protected piers (tests T1 and T2), in addition to the reduction of the maximum equilibrium scour depth Δyse, a delay in the scour development is observed.
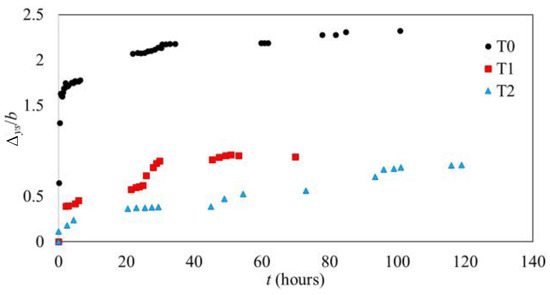
Figure 1.
Temporal evolution of the non-dimensional maximum scour depth.
In fact, in tests with collars, an S-shaped evolution of Δys is observed until the upstream side of the collar is uncovered, a typical log-like scour depth evolution occurring afterwards. While in test T0 the position of maximum scour is located upstream of the pier throughout the scouring process, in tests T1 and T2, it starts at the collar side and later migrates upstream.
For the laboratory tests, Table 2 shows the maximum equilibrium scour depth Δyse, the equilibrium scoured volume vse and the countermeasure efficiencies for tests T1 and T2 in terms of both Δyse and vse, respectively, which are computed as follows:
where Δyse,u and Δyse,p are the maximum equilibrium scour depths observed for the unprotected (test T0) and collar-protected (tests T1 and T2) pier model experiments, respectively, vse,u and vse,p being the related equilibrium scour volumes.

Table 2.
Maximum equilibrium scour depths, equilibrium scoured volumes and collar countermeasure efficiencies in the laboratory tests.
The standard collar mitigates the maximum scour depth by 59.63% with respect to the unprotected pier, whereas the upper border promotes a reduction of 63.51%. The additional scour reduction of test T2 is mirrored in the 60.00% decrease of the scoured volume, which is 16.20% more than the correspondent efficiency obtained for the standard collar.
4.2. Numerical Simulations
The flow field in the proximity of the bed around the pier determines the scour mechanism, thus shaping the scour hole dimensions. The hydrodynamics in the pier region are strongly shaped by the pier and collar geometry, which impacts on the entity of the downward flow upstream of the pier and, in turn, impacts the magnitude of the horseshoe vortex and of bed shear stress [35]. In Figure 2, the contour maps of the non-dimensional velocity magnitude u+ along the flume longitudinal centreline in the pier area are shown under both initial and equilibrium scour stages for the different pier configurations.
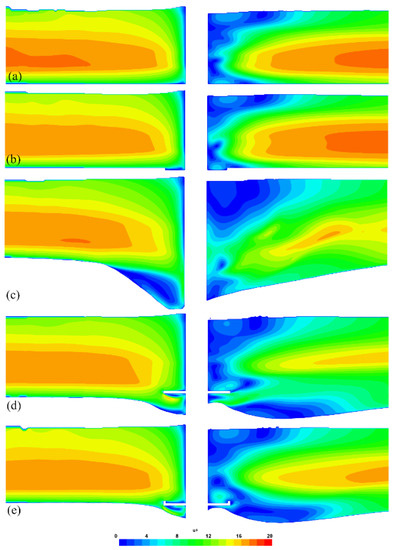
Figure 2.
Non-dimensional velocity magnitude u+ along the longitudinal centreline in the pier area for simulations of the initial conditions of tests T0 and T1 (a) and of test T2 (b) and of the final equilibrium scour conditions of tests T0 (c), T1 (d) and T2 (e).
No significant differences were observed among the simulations of the initial stages of tests T0 and T1 (Figure 2a) and of test T2 (Figure 2b), apart from the confinement of flow recirculation upstream of the pier and of flow acceleration occurring downstream of it within the upper border of the collar in the latter case. As regards the simulations of the equilibrium scour configurations, the mean velocity strongly reduces within the scour hole in the unprotected pier case (Figure 2c), owing to stable vortical structures that are recognisable both upstream and downstream of the pier [15,36]. In the classic (Figure 2d) and bordered (Figure 2e) collar configurations, the mean flow fields are very similar above the countermeasure, yet differences occur below it. Specifically, the standard collar (Figure 2d) halts the downflow upstream of the pier from proceeding below it, triggering the formation of two counter-rotating vortices underneath, a counter-clockwise one near the collar and a clockwise one near the bed. The bordered collar (Figure 2e) still blocks the upstream downflow, and, thanks to the border, confines the horseshoe vortex. Here, however, a single counter-clockwise recirculation forms below the collar upstream of the pier.
The turbulence dissipation rate ϵ is linked to the velocity gradient and, in turn, to the shear stress and to the shear velocity. Therefore, large values of ϵ are obtained where large values of shear velocity are present [37]. For flow around a pier, according to the Richardson–Kolmogorov principle of turbulence cascade, the largest eddies arise from the fluid–structure interaction of the mean flow, but then they are subject to inertial instabilities and break down into smaller vortices.
Assuming that sediment resuspension is due to the energy of the smallest eddies, whose size is of the order of the grain size of bed sediments [38], then the ϵ field can be seen as a proxy for the erosive attitude of the flow.
In Figure 3, the non-dimensional ϵ+ field along the flume longitudinal centreline in the pier area is shown for all the performed numerical simulations. Simulations of the initial conditions of tests T0 and T1 (Figure 3a) and of test T2 (Figure 3b) display very similar ϵ+ fields. An extended region of high ϵ+ is located for both simulations downstream of the pier, where the horseshoe vortex breaks up. A cluster with high ϵ+ values is also present at the upstream toe of the pier in both cases, revealing the erosive potential of the downflow upstream of the pier. Lower values of ϵ+ are legitimately obtained in the near-bed area for the simulations of quasi-equilibrium scour conditions (Figure 3c–e), proving the ceased scouring action. The classic collar (Figure 3d) deflects the high-ϵ+ region where the horseshoe vortex breaks up downstream of itself, detaching it from the bed downstream of the collar, thus reducing downstream scour. The largest values of ϵ+ among all simulations were reproduced in this case, occurring below the collar upstream of the pier. Intense sediment saltation was observed in laboratory test T1 in that same location, confirming the link between ϵ and bed erosion. As a matter of fact, lower values of ϵ+ were simulated in the same region for the bordered-collar configuration (Figure 3e), with lower sediment saltation and local scour having been observed in laboratory test T2 compared to T1. Above the collar, the upper border locks the whole downstream high ϵ+ area far from the bed, also increasing the efficiency of such a countermeasure with respect to the scour downstream of the pier.
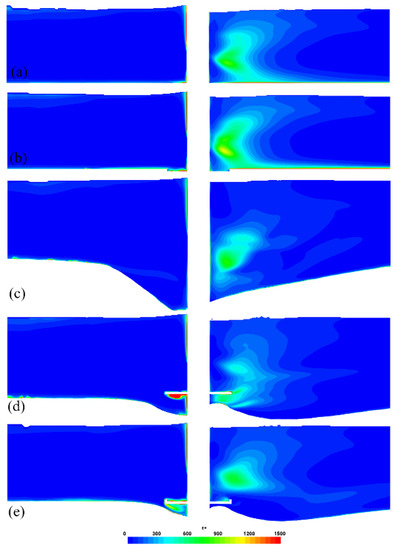
Figure 3.
Non-dimensional turbulence dissipation rate ϵ+ along the longitudinal centreline in the pier area for simulations of the initial conditions of tests T0 and T1 (a) and of test T2 (b) and of the final equilibrium scour conditions of tests T0 (c), T1 (d) and T2 (e).
5. Conclusions
The experimental campaign displayed the increasing efficiency of a classic collar and of a new-collar shape with an upper border as countermeasures against local scour at bridge piers. The bordered collar showed a reduction of maximum scour depth compared to the unprotected pier of 63.51%, outdoing by 3.88% the standard collar countermeasure.
In terms of scoured volume, the bordered collar allowed for a 60.00% reduction, outclassing the standard collar by 16.20%. The numerical simulations of the laboratory tests helped to understand the variations in the flow fields for the different pier model configurations, which explain the dissimilar scouring observed among the laboratory tests. Both collars block the upstream downflow, confining the horseshoe vortex, yet the bordered collar better keeps high turbulence dissipation far from the near-bed region, thus explaining the smaller scour observed with respect to the classic collar countermeasure.
Author Contributions
D.F. designed and ran the experiments and wrote the paper. A.F. prepared and ran the numerical simulations and reviewed the paper. R.G. supervised the entire study and reviewed the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data in this study can be obtained from the following link: https://drive.google.com/drive/folders/1In5NZt299AMSvym7LpAjFREMw-MOjkug?usp=sharing (accessed on 10 October 2022).
Acknowledgments
We thank Maria Chiara Corrado, who took part in the experimental activity as part of her M.Sc. thesis. We are grateful to the technicians of the Laboratorio “Grandi Modelli Idraulici” at Università della Calabria for their help in the experimental activity.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tafarojnoruz, A.; Gaudio, R.; Dey, S. Flow-altering countermeasures against scour at bridge piers: A review. J. Hydraul. Res. 2010, 48, 441–452. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Calomino, F. Evaluation of flow-altering countermeasures against bridge pier scour. J. Hydraul. Eng. 2012, 138, 297–305. [Google Scholar] [CrossRef]
- Froehlich, D.C. Protecting bridge piers with loose rock riprap. J. Appl. Water Eng. Res. 2013, 1, 39–57. [Google Scholar] [CrossRef]
- Lauchlan, C.S.; Melville, B.W. Riprap protection at bridge piers. J. Hydraulic Eng. 2001, 127, 412–418. [Google Scholar] [CrossRef]
- Mashahir, M.B.; Zarrati, A.R.; Mokallaf, E. Application of riprap and collar to prevent scouring around rectangular bridge piers. J. Hydraul. Eng. 2010, 136, 183–187. [Google Scholar] [CrossRef]
- Hamidifar, H.; Omid, M.H.; Nasrabadi, M. Reduction of scour using a combination of riprap and bed sill. Proc. Inst. Civ. Eng.-Water Manag. 2018, 171, 264–270. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Chamani, M.R.; Shafaie, A.; Latifi, M. Scour countermeasures for cylindrical piers using riprap and combination of collar and riprap. Int. J. Sediment Res. 2010, 25, 313–322. [Google Scholar] [CrossRef]
- Richardson, J.; Richardson, E. Discussion of ‘Local Scour at Bridge Abutments’ by BW Melville (April, 1992, Vol. 118, No. 4). J. Hydraulic Eng. 1993, 119, 1069–1071. [Google Scholar] [CrossRef]
- Wang, S.; Wei, K.; Shen, Z.; Xiang, Q. Experimental investigation of local scour protection for cylindrical bridge piers using anti-scour collars. Water 2019, 11, 1515. [Google Scholar] [CrossRef]
- Alabi, P.D. Time Development of Local Scour at a Bridge Pier Fitted with a Collar. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2006. [Google Scholar]
- Bestawy, A.; Eltahawy, T.; Alsaluli, A.; Almaliki, A.; Alqurashi, M. Reduction of local scour around a bridge pier by using different shapes of pier slots and collars. Water Supply 2020, 20, 1006–1015. [Google Scholar] [CrossRef]
- Chen, S.C.; Tfwala, S.; Wu, T.Y.; Chan, H.C.; Chou, H.T. A hooked-collar for bridge piers protection: Flow fields and scour. Water 2018, 10, 1251. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Characteristics of horseshoe vortex in developing scour holes at piers. J. Hydraul. Eng. 2007, 133, 399–413. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G.; Ettema, R. Detached eddy simulation investigation of turbulence at a circular pier with scour hole. J. Hydraul. Eng. 2009, 135, 888–901. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredsøe, J. Numerical investigation of flow and scour around a vertical circular cylinder. Phil. Trans. R. Soc. A 2015, 373, 20140104. [Google Scholar] [CrossRef]
- Neill, C. Mean-velocity criterion for scour of coarse uniform bed-material. In Proceedings of the International Association of Hydraulic Research 12th Congress, Fort Collins, CO, USA, 11–14 September 1967. [Google Scholar]
- Zarrati, A.; Nazariha, M.; Mashahir, M. Reduction of local scour in the vicinity of bridge pier groups using collars and riprap. J. Hydraul. Eng. 2006, 132, 154–162. [Google Scholar] [CrossRef]
- Ferraro, D.; Fenocchi, A.; Gaudio, R. Hydrodynamics of a bordered collar as a countermeasure against pier scouring. Proc. R. Soc. A 2020, 476, 20200393. [Google Scholar] [CrossRef]
- Chiew, Y.M.; Melville, B.W. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Ettema, R. Scour at Bridge Piers; Technical Report no. 216; University of Auckland: Auckland, New Zealand, 1980. [Google Scholar]
- Jiménez, J. Computing turbulent channels at experimental Reynolds numbers. In Proceedings of the 15th Australasian Fluid Mechanics Conference the University of Sydney, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Ferraro, D.; Servidio, S.; Gaudio, R. Velocity scales in steady-nonuniform turbulent flows with low relative submergence. Environ. Fluid Mech. 2019, 19, 1025–1041. [Google Scholar] [CrossRef]
- Coleman, S.E. Clearwater local scour at complex piers. J. Hydraul. Eng. 2005, 131, 330–334. [Google Scholar] [CrossRef]
- Siemens. Simcenter STAR-CCM+ v2019.1; Siemens: Melville, NY, USA, 2019. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-epsilon eddy viscosity model for high Reynolds number turbulent flows: Model development and validation. Comput. Fluids 1994, 24, 227–238. [Google Scholar] [CrossRef]
- Ballio, F.; Orsi, E. Time evolution of scour around bridge abutments. Water Eng. Res. 2001, 2, 243–259. [Google Scholar]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Chang, W.Y.; Lai, J.S.; Yen, C.L. Evolution of scour depth at circular bridge piers. J. Hydraul. Eng. 2004, 130, 905–913. [Google Scholar] [CrossRef]
- Ferraro, D.; Tafarojnoruz, A.; Gaudio, R.; Cardoso, A.H. Effects of pile cap thickness on the maximum scour depth at a complex pier. J. Hydraul. Eng. 2013, 139, 482–491. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Baratian-Ghorghi, Z.; Beheshti, A. Experimental investigation of clearwater local scour of compound piers. J. Hydraul. Eng. 2010, 136, 343–351. [Google Scholar] [CrossRef]
- Moreno, M.; Maia, R.; Couto, L.; Cardoso, A. Evaluation of local scour depth around complex bridge piers. Proc. River Flow 2012, 2, 935–942. [Google Scholar]
- Ramos, P.X.; Bento, A.M.; Maia, R.; Pêgo, J.P. Characterization of the scour cavity evolution around a complex bridge pier. J. Appl. Water Eng. Res. 2016, 4, 128–137. [Google Scholar] [CrossRef]
- Salaheldin, T.M.; Imran, J.; Chaudhry, M.H. Numerical modeling of three-dimensional flow field around circular piers. J. Hydraul. Eng. 2004, 130, 91–100. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Aslani-Kordkandi, A. Flow field around side-by-side piers with and without a scour hole. Eur. J. Mech.-B/Fluids 2012, 36, 152–166. [Google Scholar] [CrossRef]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Gioia, G.; Chakraborty, P. Turbulent friction in rough pipes and the energy spectrum of the phenomenological theory. Phys. Rev. Lett. 2006, 96, 044502. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).