Experimental Comparison between Hydrokinetic Turbines: Darrieus vs. Gorlov ^†

Abstract

In this research, the influence of blade geometry on the power stage characterization of cross-flow hydrokinetic turbines and vertical axis under conditions of low current velocity (<1 m/s) has been studied. To carry out the characterization of the power stage, two turbines have been used. The first has three straight blades and corresponds to a SC-Darrieus-type rotor, while the second has three corresponding helical blades with a Gorlov-type rotor. The experimental study has been performed by using a hydrodynamic tunnel and a high precision torque meter with an electric brake, which allows one to obtain the necessary mechanical parameters (torque, rotation speed) for the characterization of the power stage. Analyzing the data obtained from the results of the experimental study, it is determined that, for the same water speed, the Gorlov rotor obtains greater mechanical power than the Darrieus type. In all cases, power coefficient values greater than 1 have been obtained, thus verifying the influence of the blocking phenomenon on the performance of the turbines when they are in confined flow conditions. In turn, the TSR values obtained indicate that these turbines will work mainly by lift since they are higher than unity.

1. Introduction

Hydrokinetic turbines are devices that transform the kinetic energy of sea currents, rivers or canals into mechanical energy, to then obtain electrical energy through the use of a generator coupled to it [1]. These turbines are especially attractive since their design allows a reducing of the harmful impacts caused by traditional turbines on the environment, it not being necessary to build large elements such as dams or reservoirs since they take advantage of the natural course of the current [2].

The amount of energy that a turbine can extract from a fluid flow can be described mathematically:

$$P=\frac{1}{2} \rho A C_p v_{}^3,$$

(1)

where P is power, $\rho$ is the density of the fluid and $v$ its velocity.

The Power Coefficient (C_p) is the ratio between the available energy and the energy that is finally generated:

$$C_p=\frac{P_e}{P_k},$$

(2)

where P_e is the power generated and P_k is the available power.

To define the operating characteristics of a turbine, it is necessary to obtain the evolution of C_p with respect to the relative speed at the tip of the turbine blade determined by TSR. The term Tip Speed Ratio (TSR) is defined as the ratio between the tangential velocity of the blade at a given time instant and the current velocity at the tip of the blade. Equation (3) shows the mathematical expression to obtain it:

$$TSR=\left(\frac{\omega R}{v}\right),$$

(3)

where TSR is the Tip Speed Ratio, ω is the rotational speed in rad/s, R is the turbine radius (m) and v is the current velocity at the blade tip (m/s).

Hydrokinetic turbines can be classified according to the orientation of the axis of rotation with respect to the direction of water flow (Figure 1), differentiating between the horizontal axis and cross-flow turbines [3]. Axial flow or horizontal axis turbines are those in which the axis of rotation is parallel to the direction of the water. These systems are developed based on the knowledge of horizontal axis wind turbines, adapting their design to the characteristics of water. In this regard, it should be noted that density is one of the most important factors, since it is approximately 800 times greater than that of air [4]. One of the major problems with this type of turbine is their arrangement in the water, since the electric generator is generally totally submerged, making it necessary to use watertight chambers to avoid contact with the water (Figure 2).

Cross-flow turbines have been developed to overcome the problems of axial flow turbines in water. These turbines have the axis of rotation perpendicular to the direction of the water and operate independently of the direction of the fluid, which makes them particularly attractive since water currents, especially in marine environments, change direction frequently [5]. Although they have a lower efficiency than horizontal axis turbines, the possibility of being able to arrange them in a matrix form, thus increasing the effective cross-sectional area of the stream, allows power generation from low velocities (<1 m/s) [6]. The Darrieus, Gorlov or Savonius-type turbines stand out in this typology.

Savonius turbines (Figure 3) have a simple design in which their blades are formed by two hollow half-cylinders displaced to simulate an S. Their operating system is based on aerodynamic drag force, where the concave areas capture the fluid, making the rotor rotate in the direction of least resistance. They offer low efficiencies but ensure operation even at low current velocities [7].

Darrieus turbines base their operation on the lift force where the rotational movement is produced by the difference in pressure between the blades, achieving high efficiencies. In fact, the velocity in the blade is higher than that of the fluid. There are unique designs and configurations for this type of rotor. An example is the H-Darrieus turbine, which consists of vertical blades attached to the shaft by means of horizontal supports. The main disadvantage of this configuration is the need to implement an additional starting system, as they have problems in starting rotation at low current speeds. The SC-Darrieus rotors are a variant of the previous ones. This system is composed of two discs located at the top and bottom of the device that serve as support for the blades that are arranged vertically. The advantage over the H-Darrieus type turbine is that the introduction of the discs allows the turbine to withstand centrifugal forces acting on the blades, and reduces its rotational speed variations [9,10,11].

Gorlov turbines (Figure 4) have a similar geometry to the SC-Darrieus, but in this case the blades are helical, which is an advantage over straight blades as it improves the self-starting problem of Darrieus turbines. Thus, the helical shape allows a part of the blade to have an optimal angle of attack during the rotational movement [12]. In order to improve parameters such as performance, self-start or tip speed, hybrid systems (Figure 5) combining Darrieus and Savonius rotors are being investigated. As mentioned above, Savonius rotors have high self-starting capability but low efficiencies while Darrieus turbines have high efficiencies but self-starting problems. Their combination makes them devices with high efficiency and high starting torque.

The objective of the present investigation is the comparative study of the power stage of two vertical axis hydrokinetic turbines of Darrieus and Gorlov type under low current velocity conditions. For this purpose, experimental tests will be carried out in the hydrodynamic tunnel of the Hydraulic Engineering Area of the University of Oviedo.

2. Materials and Methods

The following materials were used for the tests, as detailed below:

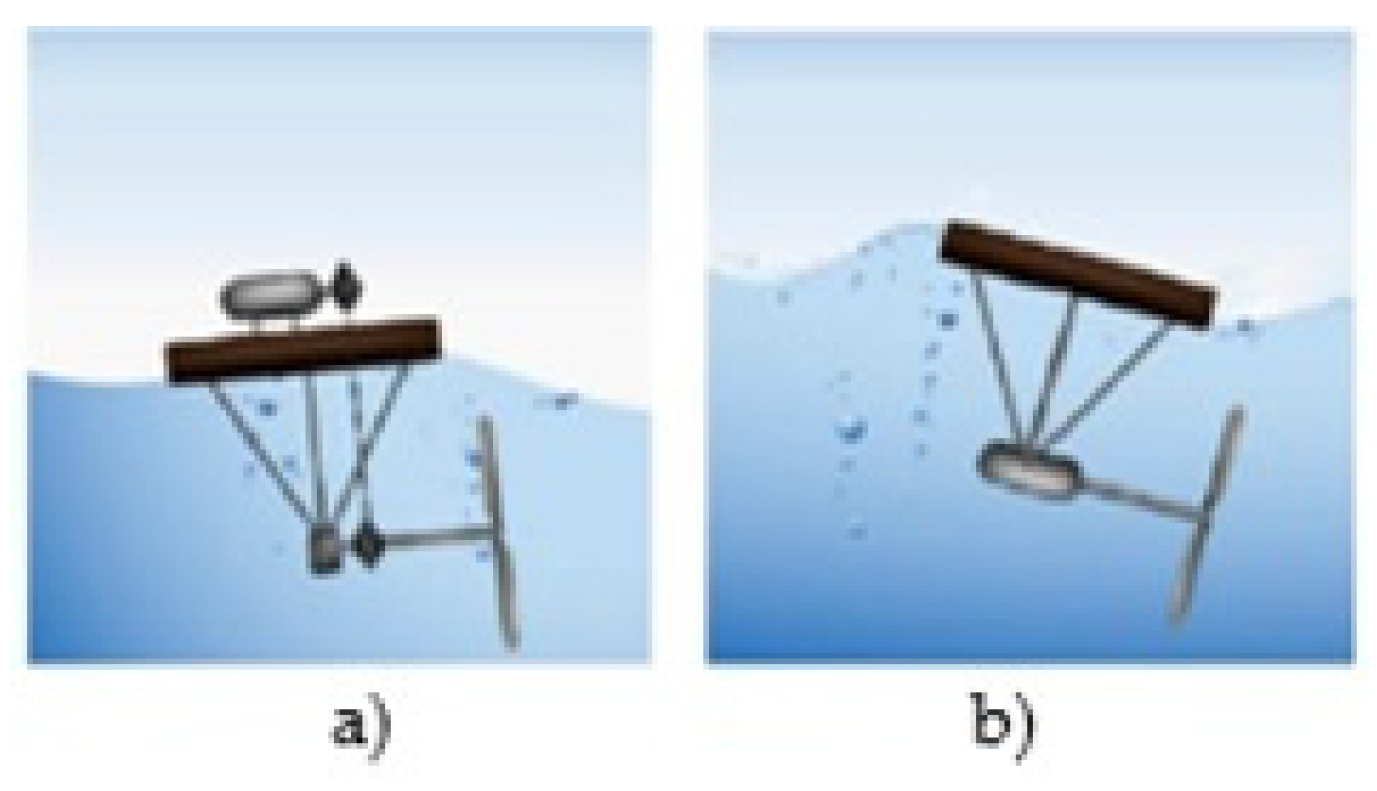
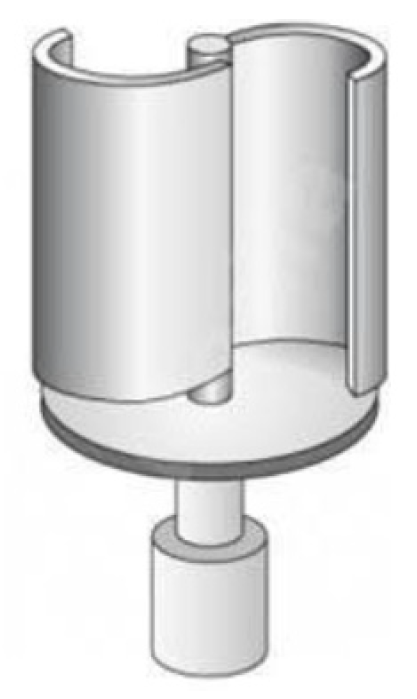
• Hydrokinetic turbines.
• Hydrodynamic tunnel.
• Data acquisition system.

2.1. Hydrokinetic Turbines

Two cross-flow, vertical axis turbines with different blade types will be used for testing in the hydrodynamic tunnel. Both rotors have been designed and printed using 3D technology based on nylon filament (PA) in University of Oviedo laboratories. The first turbine (Figure 6a) is a Darrieus Squirrel Cage (SC-Darrieus)-type rotor composed of three straight blades of standard NACA0015 profile, which are spaced 120 degrees apart and whose dimensions are specified in the

Table 1. Turbine dimensions.

	SC-Darrieus	Gorlov
Height (m)	0.15	0.15
Diameter (m)	0.175	0.175
Chord (m)	0.05	0.05

. The turbine also has a system of wedges and threads for coupling the rotor to the 10 mm diameter metal shaft, which facilitates interchangeability between different types of turbines. The other turbine to be used for testing will be a Gorlov-type helical turbine with three NACA0015 type blades spaced 120° apart and a 45° angle of rotation (Figure 6b) whose measurements are also specified in Table 1.

2.2. Hydrodynamic Tunnel

The experimental tests were carried out in a hydrodynamic water tunnel (HWT) (Figure 7) made up of tanks (reassuring and recirculation), hydraulic pumps, adjustable frequency drive (AFD), glass channel (0.5 m height, 0.3 m width and 1.5 length) and a monitoring-control system.

2.3. Data Acquisition System

The data acquisition system consists of the following elements:

• Torque measuring equipment.
• Electric brake.
• Data acquisition software.

For the characterization of the rotor power stage, a high precision torque meter (MAGTROL TSR 103) (Figure 8) with a nominal torque of 0.5 Nm and a maximum torque of 1 Nm was used and the following data were obtained: Rotation angle (°), Torque (Nm), Rotation speed (rpm), Mechanical power (W), Time (s). These data were collected thanks to the “TORQUE Tool” V10 software, which allows immediate visualization and storage of the results. A DC electric brake (MAGTROL HB140M, Magtrol SA, Rossens-Switzerland) controlled by a current source was placed on the torque meter to apply a resistive torque to the rotor in order to characterize its power stage. The electrical source varied the current flowing through the brake, which caused the resistive torque to vary as well, thus making it possible to obtain the mechanical power for each braking torque.

Data collection and recording were performed using the software provided by the manufacturer of the torque measurement equipment (TORQUE TOOL V10). This software allows one to store data of rotation angle (°), mechanical torque (Nm), rotation speed (rpm) and test time (s). In addition, it allows one to represent in real time the different parameters so that the behavior of the rotor or the appearance of errors in the measurements can be seen.

2.4. Methodology

In order to obtain the necessary data for the characterization of the turbine power stage by means of mechanical parameters, the following experimental procedure has been used:

• The turbine to be characterized was placed inside the methacrylate box (Figure 9). The rotor was positioned at the correct elevation and coupled to the torque meter through the rotation axis.
• Once the whole assembly was placed inside the hydraulic channel, the water circulation was started so that the turbine began to rotate. At that moment, the first measurement called “no-load” was performed, where the voltage of the electric brake is 0 V, so no braking torque is applied to the turbine. Under these conditions, the mechanical power is zero but the rotational speed is maximum.
• Subsequently, by means of the current source, the electrical intensity of the brake was increased in 1 V intervals during 35 s. For each of the measurements, a value of mechanical torque and rotational speed was obtained. The characterization of the power stage continued until the turbine stopped rotating.

To characterize the power stage of each turbine, three different tests were performed using three different water current speeds. The minimum speed (0.60 m/s) corresponds to the current speed at which the turbine starts to rotate (cut-in speed), while the maximum speed (0.65 m/s) corresponds to the maximum speed that can be simulated inside the hydrodynamic tunnel. It should be noted that an additional test has been performed with an intermediate speed (0.63 m/s) in order to obtain the complete characterization of the turbine. With the data obtained during the tests, the Power vs Speed and TSR vs. C_p graphs were obtained to determine the best turbine design through the characterization of its power stage.

3. Results

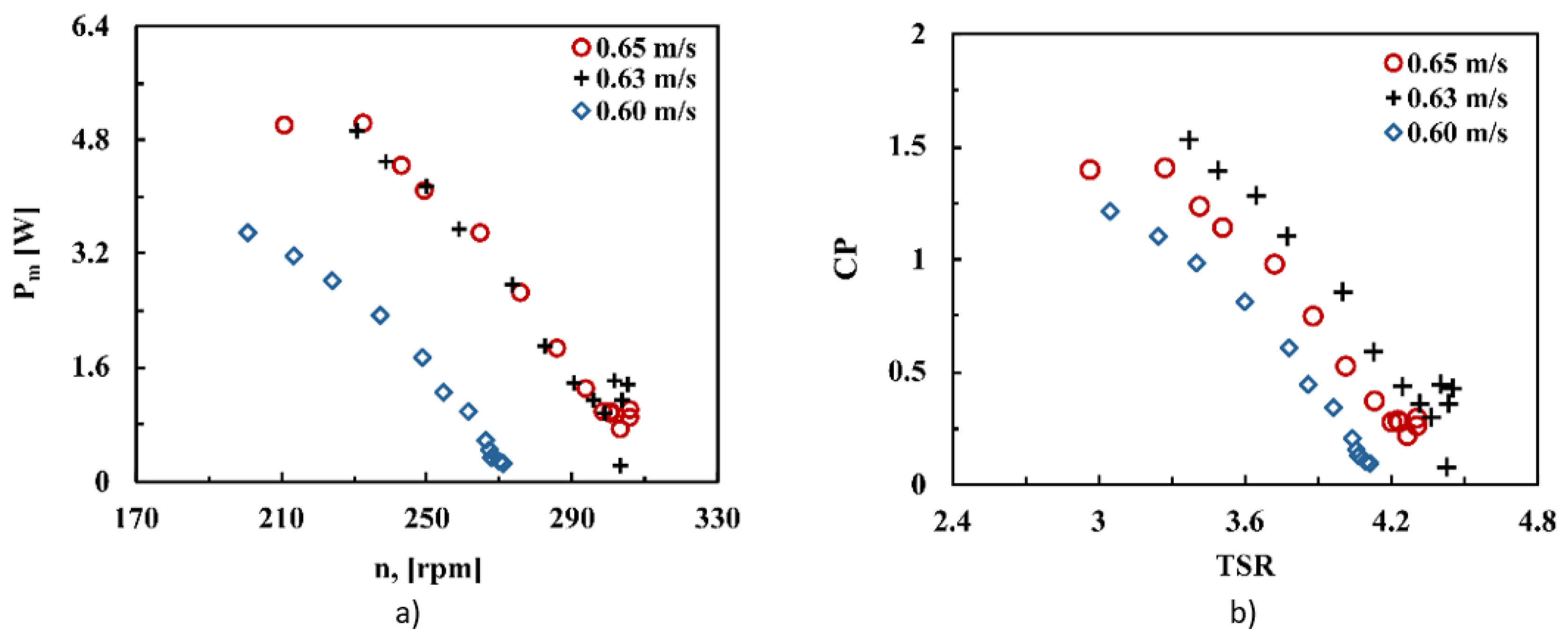
3.1. Darrieus Type Rotor Characterization

First, the characterization of the Darrieus turbine power stage was performed, obtaining the values of mechanical power (P_m) and rotational speed (n) shown in Figure 10a. As can be seen, as the current speed increased, the mechanical power of the rotor also increased, although the difference between the maximum and intermediate speeds was negligible (≈5 W). By applying the dimensionless TSR and C_p coefficients, a first approximation of the Darrieus-type rotor performance was obtained (Figure 10b).

It is observed how for the three water current velocities the Darrieus rotor managed to reach maximum C_p values between 1.2 and 1.5 for TSR of 3 and 3.4, respectively. It should be noted that all the obtained results presented high TSR values, which could indicate a good performance of the airfoil to lift (TSR > 1).

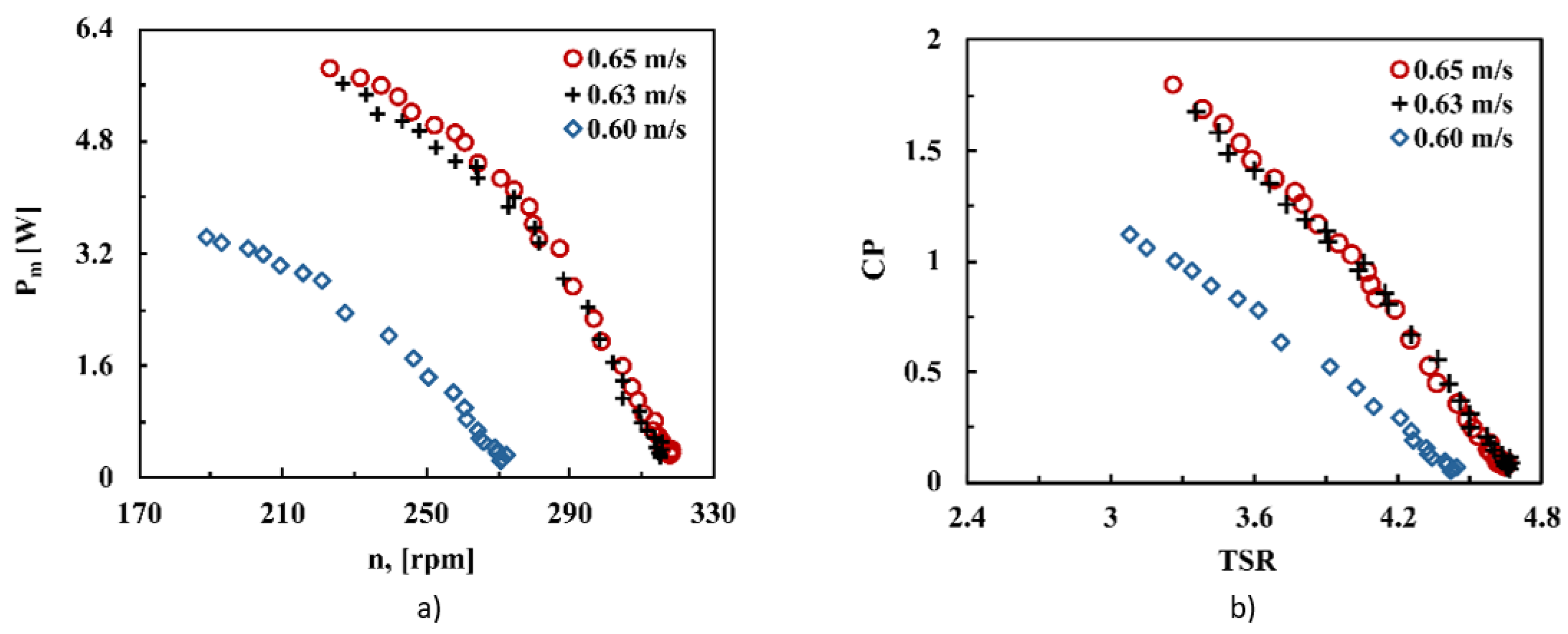
3.2. Gorlov Type Rotor Characterization

Secondly, the results obtained from the characterization of the Gorlov-type rotor under the same hydrodynamic conditions as the Darrieus rotor are shown (Figure 11a). In this case, the rotational speeds of the turbine were very similar to those of the Darrieus rotor as they reached 250–350 rpm. However, for the higher speeds tested, the Gorlov turbine managed to obtain higher mechanical power (P ≈ 5.8 W). While that power difference is very small, it should be noted that they worked with very small designs and under very low current velocities (<1 m/s). Similarly, the dimensionless parameters TSR and C_p have been obtained for the Gorlov-type rotor (Figure 11b). In this case, there has been an increase in the maximum values of TSR and C_p compared to those obtained with the Darrieus-type rotor. More specifically, for the maximum speed, a maximum value of C_p = 1.8 has been reached for a TSR ≈ 3.3.

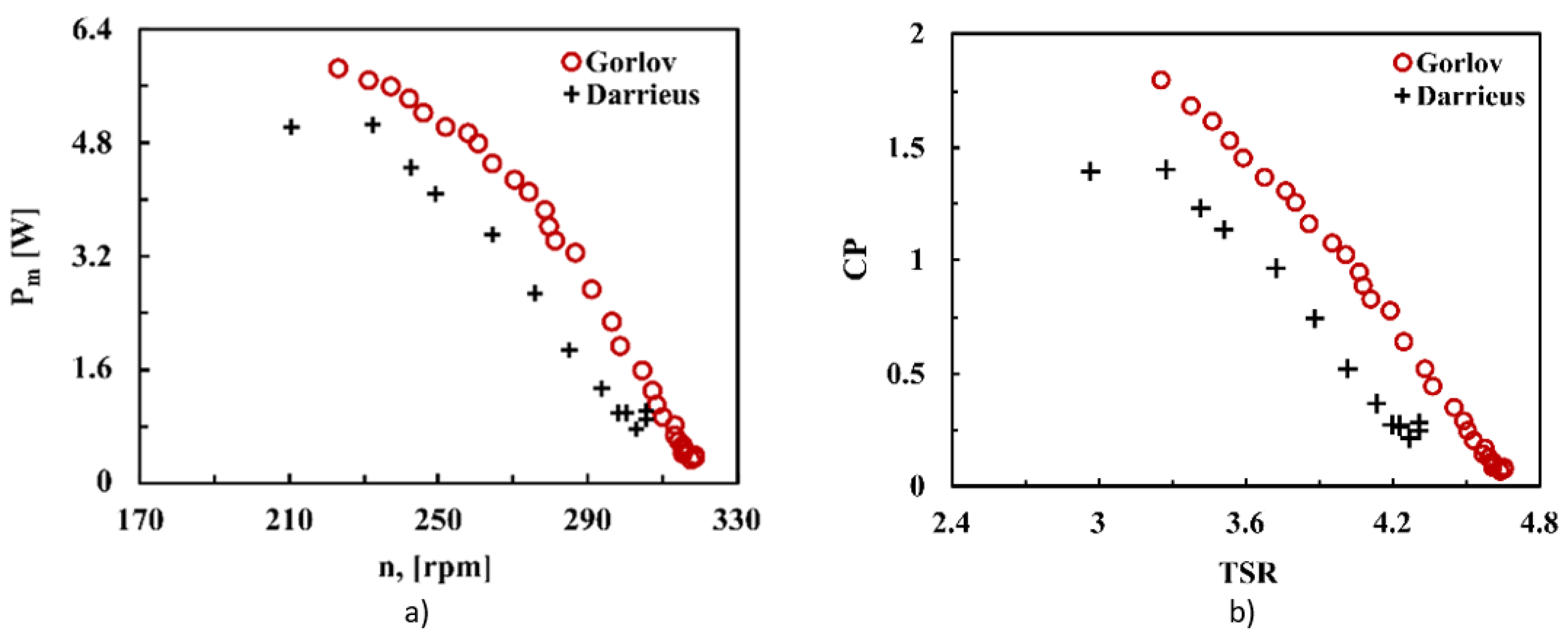
3.3. Rotor Comparison

Finally, a comparison between both turbine designs has been performed to contrast their behavior during the power phase and determine which of the two designs performs better. Figure 12a shows the mechanical power results obtained for the maximum water flow velocity for both designs. It is clearly observed how, for the same water speed, the Gorlov rotor was able to obtain a higher mechanical power than the Darrieus type. Moreover, in both designs, the maximum measured power was reached at a very similar rotational speed. For the same speed, a comparative graph is shown between both designs, but representing the dimensionless parameters TSR vs. C_p (Figure 12b).

4. Conclusions

This paper analyzes the influence of blade geometry on the characterization of vertical axis turbines at low current speeds (<1 m/s) in the power stage of a turbine. For this purpose, a Darrieus turbine and a Gorlov turbine of identical dimensions are analyzed at identical velocities and flow conditions.

Analyzing the data obtained from the results of the experimental study, it can be seen that the Gorlov rotor obtains a maximum C_p value much higher than that of the Darrieus turbine and, in addition, it achieves it for a TSR value also higher than that of the Darrieus turbine. It is determined that, for the same water speed, the Gorlov rotor obtains greater mechanical power than the Darrieus rotor.

It should be noted that power coefficient values greater than 1 have been obtained in all cases, which verifies the influence of the blockage phenomenon on the performance of the turbines when they are in confined flow conditions. In turn, the TSR values obtained indicate that these turbines will work mainly by lift as they are higher than unity.