1. Introduction
The diffusion of contaminants in Urban Drainage Networks (UDNs) is a relevant topic that has attracted the attention of many researchers and water utilities, especially in recent years. The presence of industrial and commercial activities continuously exposes UDNs to many polluting sources. The study of the diffusion of contaminants in UDNs is typically based on hydraulic modelling, considering the flow rates, decay times and concentrations of contaminants as key factors [
1,
2,
3,
4,
5,
6]. These methodologies, although effective, presume a detailed knowledge of the systems (both topological and hydraulic) and high computational costs. Therefore, they may not be easily applicable to large and complex networks.
In recent years, with the aim of evaluating how the diffusion of pollutants is influenced by the geometry of systems and to what extent, the topological component of UDNs has been increasingly considered in such studies. In this sense, the Complex Network Theory (CNT) intervenes with specific metrics, based on the network topology, that are effective in both detecting the process of spreading contaminants in the network and in ensuring lower computational efforts for such analyses [
7,
8,
9,
10].
At the same time, the topology of urban systems also lies at the basis of strategies/algorithms of backtracking. These algorithms solve problems recursively, trying to build a solution incrementally, one piece at a time, by removing those solutions that fail to satisfy the constraints of the problem at any point. This approach has already been used in the past to assess the presence and diffusion of contaminants in water distribution networks (WDNs) [
11,
12,
13,
14].
Starting from the network’s topology, this work proposes the application of an innovative methodology, based on the CNT tools and on a backtracking algorithm, to analyse and model the diffusion of pollutants along the UDN. The goals are to highlight the role of the topology in the diffusion of pollutants and to simplify the computational effort compared with other methodologies without the need to perform hydraulic and quality simulations. The presented strategy allows the calculation of a topological metric, called contamination index
IC, that informs about the effect that a contaminant spill originated in given nodes would have on the whole system. In this way, it is possible to establish the extent of contaminated areas. In the proposed innovative approach, information related to the flow rates along the various pipes is surrogated with information obtained from the Horton’s hierarchy [
15] of the system.
The analysis is performed on a schematic literature network. The results indicate the performance of the metric in evaluating the spread of pollutants in UDNs without the use of hydraulic and quality simulations, which require a large effort for large, complex networks.
2. Methodology
The typical analyses to study the contaminant spread in UDNs are based on systems of mass balance and momentum equations within pipes and nodes. In contrast, the strategy presented here is based only on the UDN topology. It refers to CNT concepts and to a backtracking algorithm to simulate the diffusion of contaminants.
It is assumed that the distribution of contaminants in the network is similar to a process of diffusion, whereby the contaminant placed in the network propagates in the direction of the flow, and the concentration decays along the pipes depending on the type of contaminant, the length of the pipes, as well as the hydrodynamic conditions. Moreover, each contaminated node spreads the contaminant to the pipes downstream.
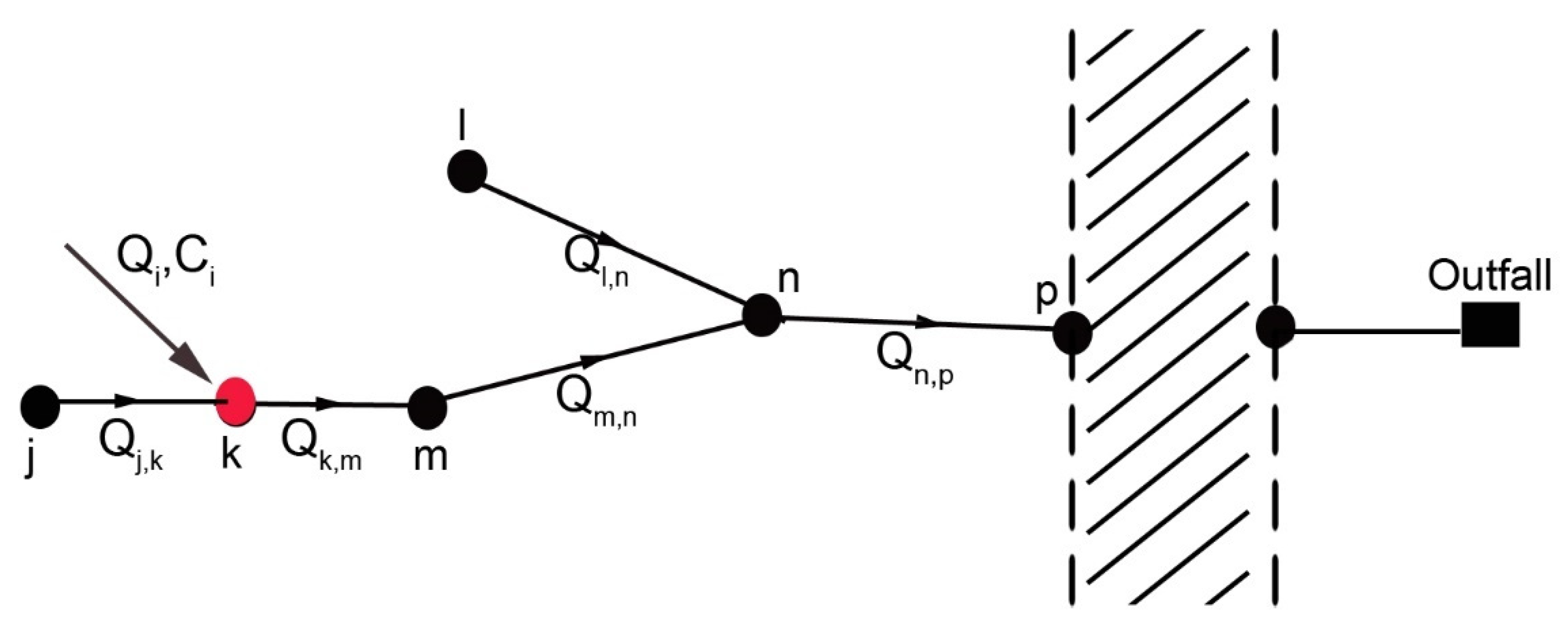
As shown in
Figure 1, UDNs are direct graphs where the set of links
L represents the sewer pipes and the set of nodes
N represents manholes. The links are directed according to the flow direction, i.e., diffusion from a node
k towards a generic node
m is possible only if there is a link
l directed from
k to
m. Once contaminated, the target node
m is modelled as a new source and the spreading process carries on towards the farthest nodes.
The proposed methodology foresees initiating the analysis directly from the source nodes and, following the direction of the network, monitoring the contaminant. For the pipes upstream of the source node, or in any case located in network areas not connected to it, the contaminant value is zero. For the pipes downstream of the contaminated node, the strategy proposes different formulations to evaluate the contaminant value according to the characteristics of the scheme.
The Horton’s hierarchy of the system is herein used as topological information instead of the flow rate along the sewer pipe. This choice has both the advantage of being able to guarantee a purely topological analysis, without the necessity of hydraulic simulations, and to obtain information on the diffusion process at an early stage in the study of the system.
Supposing the injection of the contaminant into node
k (
Figure 1), pipes that precede it have no traces of contaminant; therefore
.
The pipe where the contaminant is injected (pipe
k-m) has an amount of contaminant defined by the formula:
where
Ci is the concentration of the contaminant at node
k;
Qi is the flow rate introduced with the contaminant, set equal to the lowest Horton order,
Qi =
Hi = 1; and
Hd is the Horton’s order of the pipes downstream of the source node. In this specific case, there is only one pipe downstream of the contamination (pipe
k-m).
To determine the quantity of contaminant for pipe
m-n due to the introduction of the contaminant into node
k, it is important to keep in mind that node
m has only one inlet pipe, i.e., there are no confluences that dilute the contaminant arriving in the node, nor there are inputs that increase the amount of contaminant. In this case, the quantity of the contaminant is defined by the formulation:
where
and
Hu are the concentration of the contaminant and the Horton’s order along the pipe upstream of pipe
m-n (pipe
k-m) and
is the Horton’s order of the pipes following
k-m (pipe
m-n in this specific case).
Pipe
l-n is not affected by the introduction of the contaminant, but intervenes in the dilution of the contaminant in node
n. Therefore, to determine the quantity of contaminant in pipe
n-p, it is necessary to calculate a weighted average of the concentration along the pipes entering node
n. In particular, if only one of the pipes entering node
n is contaminated, the flow of other pipes has only a diluting effect, i.e., it dilutes the concentration; otherwise, it increases the amount of the contaminant. Generally, the quantity of the contaminant is defined by the formula:
where
and
Hu are the concentrations of the contaminant and the Horton’s order along the pipes entering in pipe
n,
p (pipe
m-n) and
is the Horton’s order of the pipes leaving
m-n (pipe
n-p in this specific case).
In this way, the strategy calculates the amount of contaminant in each pipe with respect to the injection into each node of the network, considering the dilution due to the connection among the pipes.
The concentration of contaminant that spreads in the system according to the direction of the flow is also subject to an exponential decay, which varies according to the considered substance and determines the reduction in the concentration with time. Following the topological approach, it is possible to assume that the decay is a function of the length of the path crossed to reach the outfall. Hence, the concentration decay along the pipes is also replaced by the geometric characteristics of the system, in particular the length.
Then, for each node
s, a contamination index
IC is calculated, indicative of the amount of contaminant detected at the outfall, evaluated as:
where
is the contamination of the generic pipe
l belonging to a specific path due to a spill in the source node
s,
Ll is the length of the generic pipe
l belonging to the path and the term
f is a scale factor used to align the term
Ll to
. The term
considers the dilution in the path due to convergences. It is important to note that, having considered the Horton hierarchy instead of the flow rates, the dilutions take place only at the confluences that provide an increase in the Horton order. The term
, instead, simulates the decay of the contaminant along the pipes.
High values of IC indicate high values of the contaminant detected at the outfall for the specific source node.
3. Case Study
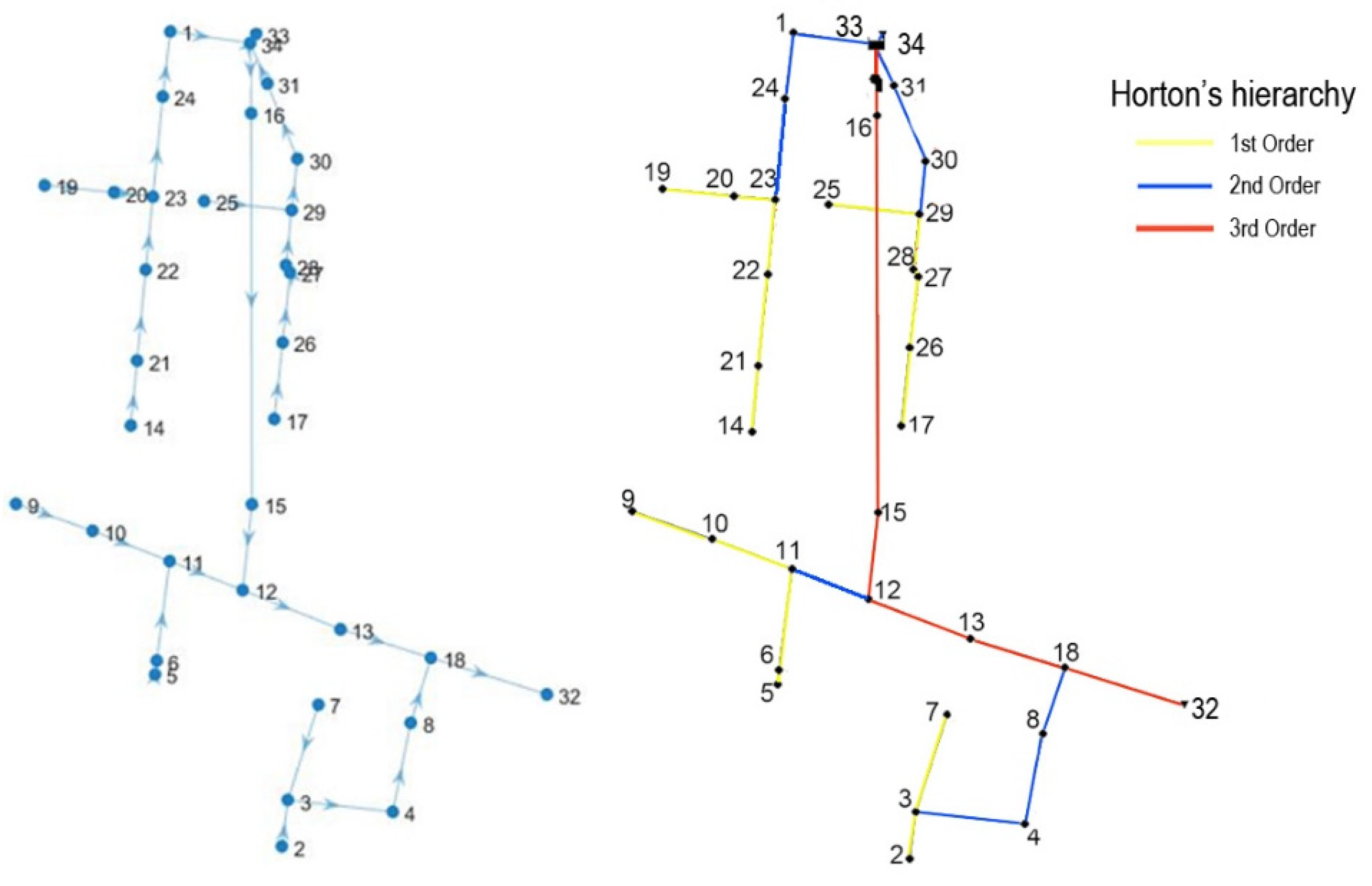
The proposed strategy was applied to SWMM example 3. The aim was to detect useful information regarding the contaminant spreading based on the network topology without accounting for the hydraulic simulations.
SWMM example 3 is a simple urban drainage network composed of 32 nodes, 32 pipes, 1 outfall (node 32), 1 storage (node 34) and 1 pump. Its layout, with direction and Horton’s hierarchy, is reported in
Figure 2.
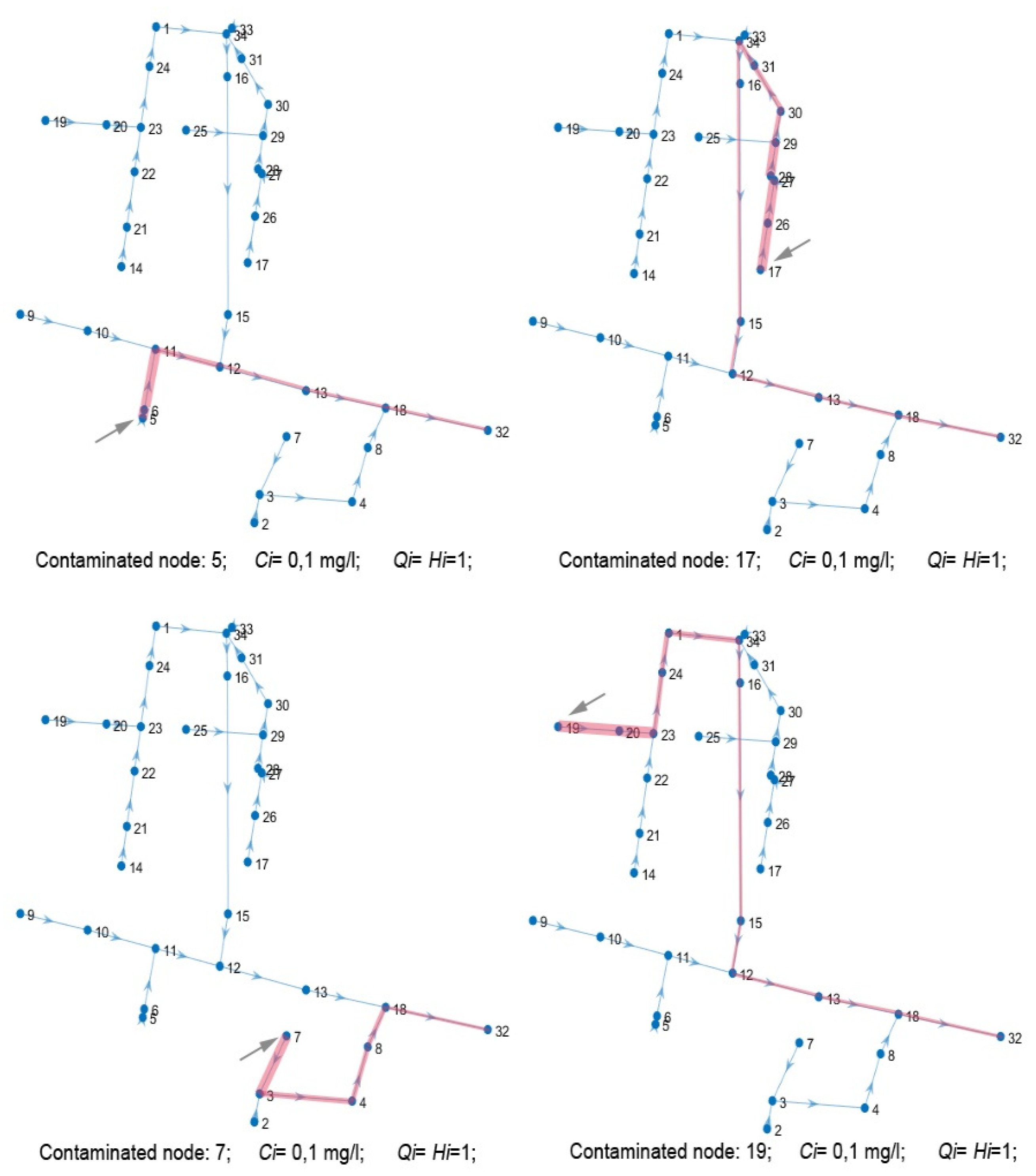
Knowing the Horton’s hierarchy of the system, the strategy allows the propagation of contaminants in the pipes to be identified. As an example, the injection into four nodes of the network (5, 17, 7 and 19) is considered (
Figure 3). The contaminant concentration value is set to 0. g/L and the corresponding flow rate is set to be equal to the lowest Horton order, i.e.,
Ci =
Hi = 1. It is evident that the pipes with the highest concentration of contaminant are those located immediately downstream of the pollutant spill and that the concentration decreases moving towards the outfall.
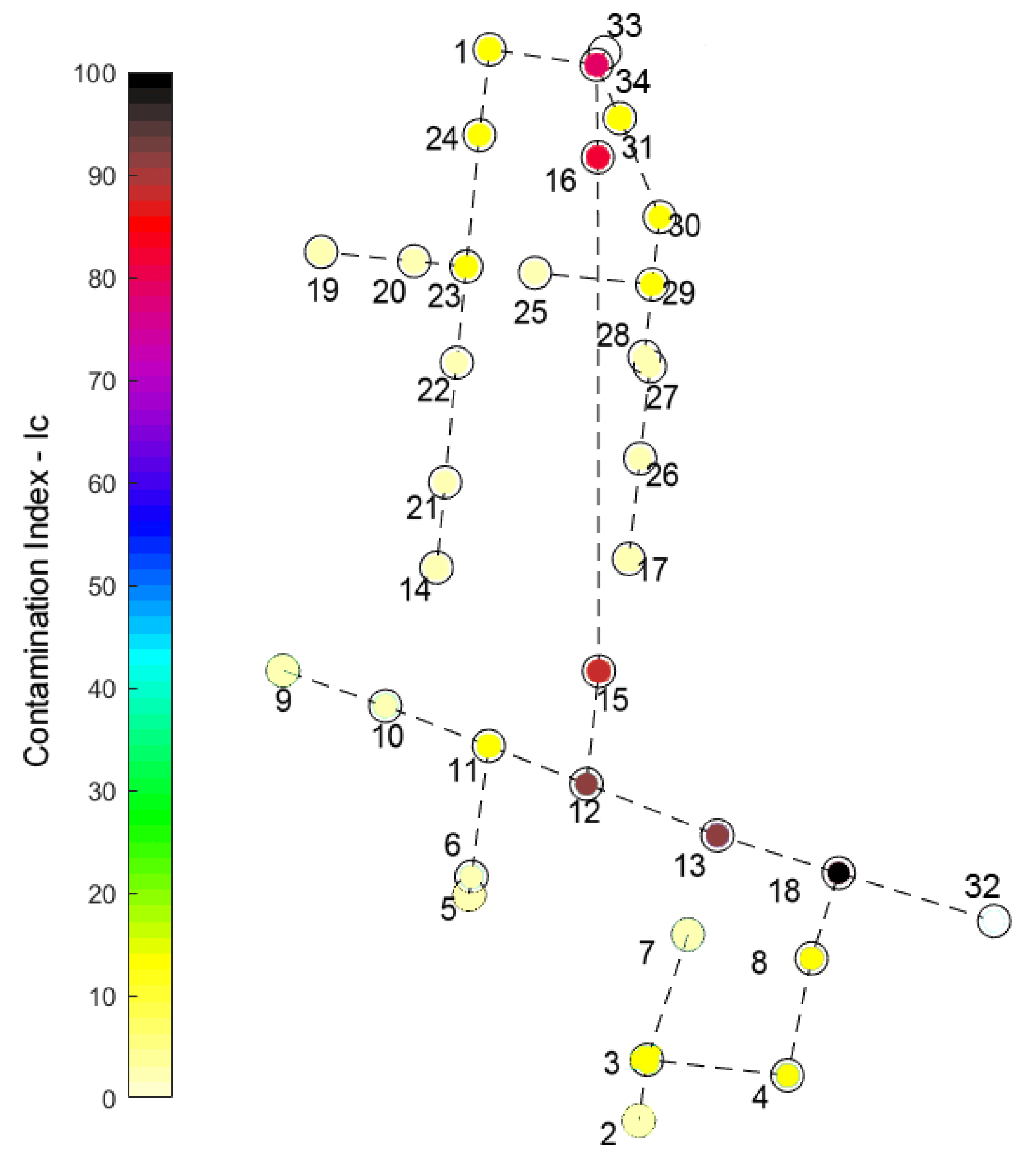
When considering the same injection of 0.1 mg/L in each node of the network, assuming one contaminated node at a time, the strategy identifies the contamination process for all pipes of the network and, based on the quantity of contaminant
, calculates the contamination index
IC for all nodes.
Figure 4 reports the contamination index
IC for all nodes of the network.
The results show that the contamination index IC assumes maximum values for the nodes close to the outfall and decreasing values moving away from it and moving more and more upstream. Nodes with a high value of IC (from red to black) represent the points in which any contaminant input is easily detected at the outfall, while nodes with a very low IC (light yellow) represent the points in which any contaminant input is difficult to detect at the outfall, precisely because of the dilution and decay phenomena that occur along the path.
The results are coherent with the physics of the phenomenon, which could be easily predicted in the considered simple example scheme. Of course, the strategy is especially useful in the study of large, complex networks that are not easy to operate.
4. Conclusions
In recent years, the use of appropriate tools to analyse UDNs has become more important for the need to monitor the system and to control the spread of substances, such as contaminants and pathogenic agents. Many strategies have been proposed based on hydraulic modelling, and monitoring systems have been designed using optimization algorithms. These methodologies, although effective, presume detailed knowledge of the systems (both topological and hydraulic) and high computational costs. The idea of resorting to strategies based on the CNT and backtracking algorithms for UDN analysis is related to the need to solve different critical tasks, such as the individuation of illicit intrusion and the control of the presence of target substances for either environmental or epidemiological purposes.
This work proposes a new index, called the node contamination index IC, to evaluate the effect that contaminant spill in each node will have on the entire system. The strategy uses a network model that is based only on the network topology and does not implement hydraulic analysis. These conditions ensure that the strategy entails a low computational burden and is easily implemented, even for complex networks of large cities, where data are usually not completely available. In fact, the advantage of this strategy is to provide a realistic preliminary/qualitative analysis regardless of the system’s operation in complex networks whose hydraulic behaviour is often uncertain or difficult to model.
Future work will focus on testing this strategy on a real complex scheme and comparing it with other methodologies based on the hydraulic and quality simulations of the system.