Abstract
Water distribution networks suffer from high levels of water losses due to leaks and breaks, mainly due to high operating pressure. One of the most well-known methods to reduce water losses is pressure management. However, when the operating pressure in a water distribution network reduces, the time the water stays within the network (called water age) increases. Increased water age means deteriorated water quality. In this paper, water pressure in relation to water age is addressed in a water distribution network in Greece. Using simulation and optimization tools, the optimum solution is found to reduce water age and operating pressure at the same time. In addition, District Metered Areas are formed and water age is optimized.
1. Introduction
The ultimate aim of a water distribution network (WDN) is to supply the consumers with safe water of good quality at their taps, at an acceptable pressure level. However, to achieve this aim is a challenging task, as WDNs are complex systems. WDNs suffer from high levels of water losses due to leaks or breaks. One of the main reasons for this high level of losses is high operating pressure. Especially when the water utility does not apply any Non-Revenue Water (NRW) management strategy, operating pressure is high. A minimum level of pressure is necessary for the WDN to operate and for water to be supplied in all consumers’ taps. However, due to topological characteristics (e.g., altitude variations within the cities), water operators maintain a high operating pressure to satisfy water demand. One of the most known measures to reduce physical (real) losses in a WDN is pressure management [1]. It is proven that reduced pressure has a positive impact on the WDN’s economic life, as water losses due to leaks and breaks are less and the equipment (pipes etc.) are burdened less due to pressure variations within 24 h [2]. When water losses are reduced, the water entering the network is also reduced, resulting in the sustainable use of water resources. A WDN is better managed and inspected when it is divided in district metered areas (DMAs). Various studies have shown that water volume entering the WDN may be reduced by as much as 30–40% [2,3,4,5]. DMAs are smaller areas within the WDN which are usually hydraulically isolated, meaning that there is one inlet point and one outlet point. Normally, when DMAs are formed, pressure management takes place in WDNs, installing a pressure reduction valve (PRV) at the inlet point, to control pressure. DMA formation is a challenging task taking into consideration various factors [6,7].
When pressure is reduced within a WDN, water age values increase. Water age is the retention time of water within the WDN. The average water age in a network has been measured at 1.3 days, while the maximum is 3.0 days, according to the results of a survey involving over 800 water supply networks in the USA [3,8]. Increased water age values are connected to water quality problems such as formation of disinfection-by-products, nitrification, microbial re-growth, pathogens intrusion, increased temperature, sediment deposition, etc. [8,9]. Studies mention that recently installed pipes along with effective pressure control may also drive water to be stagnant in rural areas during the night, as well as in industrial areas when the water demand is minimized during low production periods [2]. Water age is considered as a water quality indicator in WDNs. Water quality deterioration is caused due to reactions taking place between the pipes’ walls and water and due to several other reactions taking place in water. Pipes’ material, water flow, and the materials deposited such as sand, ferrum, etc. are factors affecting water quality deterioration. Water age values get higher when DMAs are formed because more pipes lead to dead ends. Water age cannot be measured, but it can be estimated using hydraulic mathematical models. There are not maximum or minimum values for water age, as every WDN is unique, having its own characteristics. In general, water age values should be low.
Hydraulic simulation models estimate the average water age, assuming that water age at the joints is the average water age at the pipes. Based on the water demand, the average water age is estimated. Water age depends on: (a) water demand, as increased water demand means lower water age as water flow is increased; (b) the distance from the water reservoirs, as increased distance means that the water travels for a long time and residual chlorine is reduced, resulting in increased microbial growth risk; (c) the WDN design (radial or looped); and (d) the oversizing of the pipes in order to meet the future water demand. Therefore, it is crucial to find the optimum point between water age and water pressure.
2. Materials and Methods
To find the optimum water age and pressure in a WDN, several tools are used, starting from a hydraulic simulation software to develop the hydraulic model of the WDN and to estimate the age of the water in each node/pipe. In this specific study, the EPANET 2.0 solver was used. Then, the combination of Matlab and EPANET software packages is used for optimization purposes. Eliades et al. [10] reported that combining Matlab and EPANET software packages unfolds numerous possibilities and takes the study of WDNs to another level of complexity, providing fast and well-aimed solutions to optimization problems. In this study, the following software tools are used: (a) EPANET, to control and inspect the case study network’s hydraulic model; and (b) Matlab, to develop the optimization algorithm and its optimization toolbox/toolkit [3]. In this study, the EPANET-Matlab-Toolkit based on Epanet 2.1 is used [10]. Using these tools, several solutions derived resulting in the optimal segmentation of the case study WDN by closing isolation valves in water pipes. Genetic algorithms (GAs) are used to solve both constrained and unconstrained optimization problems, based on the natural selection principle, the process that drives biological evolution [5,11]. The use of GA in optimization processes requires the formation of an objective function which describes the optimal solution of the problem.
Several heuristic methods and artificial intelligence-based algorithms have been used to optimize the operation of WDNs. GAs have been used for the optimization of cost, reliability, and water quality [12] and for leakage optimization [13]. Other algorithms based on artificial intelligence have been used to model and optimize WDNs’ operation [14,15,16]. Literature review revealed that many optimization techniques (Genetic Algorithms; Hybrid Algorithms; Geometric Partitioning; Gaussian Mixture Models; etc.) have been developed to assist in pressure management through the optimal formation of DMAs and the minimization of the number of PRVs and isolation valves used [2,3,4,5]. However, the combination of water pressure and water age is a subject not thoroughly studied. Lately, there are some studies examining pressure regulation and water age [2] and the optimization of DMA formation taking into consideration water age along with pressure, diving the WDN into smaller areas using advance modeling techniques [4,5].
3. The Case Study
The case study is the WDN of Eani, a municipal district of Kozani municipality, in Greece. Kozani municipality has a population of 71,388 people (2011 census) and Eani district’s population is 3429 people. The district covers an area of 152.9 Km2 and its altitude ranges from 432 m to 547 m. The municipal water utility (DEYAK) supplies with water the municipal district. The WDN consists of 329 pipes of total length 28,846 m, made from PVC. The pipes’ diameters range from 63 mm to 225 mm. The people are supplied with water through 809 water meters. The total water supply entering the network was 571,939 m3 in 2014, coming from springs and boreholes (Figure 1).
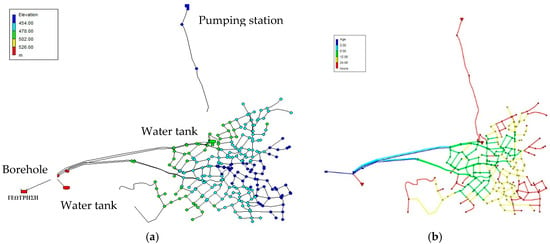
Figure 1.
(a) Eani water supply and distribution network; (b) water age in water distribution network (WDN).
The billed authorized consumption in 2014 was 104,486 m3 and the Non-Revenue Water (NRW) accounted for was 467,453 m3 (81.7% of the water volume entering the network), of which 85,791 m3 were apparent losses and 370,223 m3 were real losses. The remaining 11,439 m3 were unbilled authorized consumption due to several uses, such as schools, public gardens watering, etc. It is obvious that water losses account for a big volume of water in this municipal district. The reasons are mainly that the water utility does not implement any NRW reduction measures, such as pressure management, active leakage control, etc. Operating pressure is high as there are significant altitude variations in the district.
3.1. Water Age and Water Pressure
The first step of the methodology followed in this study is the hydraulic simulation of the WDN using mathematical models. The software tool used in this study is Epanet 2.0. The WDN’s model has been developed taking into consideration all the data for the tanks, the pipes, and all the equipment, together with topological data. Water demand and water losses data are also incorporated in the model. Water demand patterns (residential and commercial) were considered over a 24-h (daily) period using a hydraulic time step of 1 h. Hydraulic and water age analyses were both performed for seven consecutive days of the network’s operation (simulated week). The developed model has been verified and calibrated with real data. Water pressure and water age values are shown in Figure 2 and Figure 3. Average water pressure values range from 73.7 to 119 psi. Water age increases and gets its maximum value of 22.46 h after about 153 h of simulation.
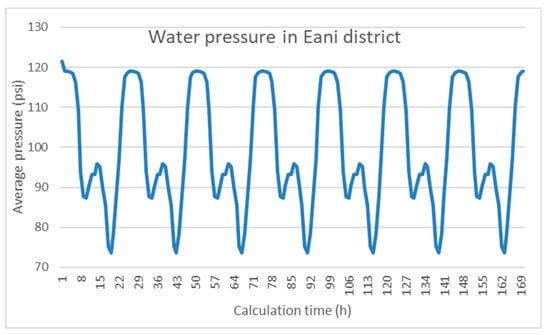
Figure 2.
Average water pressure (psi) per hour for Eani WDN.
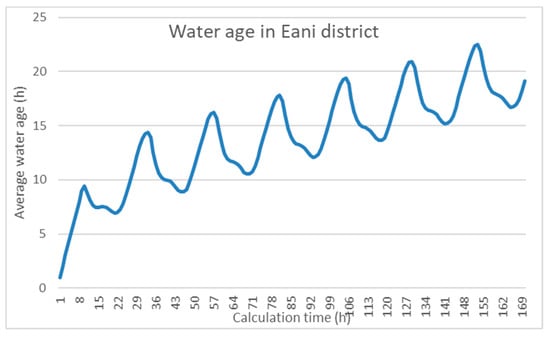
Figure 3.
Average water age (h) per hour for Eani WDN.
The next step is to optimize the water age. Matlab was used together with Epanet 2.0. The optimization was focused on the reduction of the retention time of water (water age) inside the WDN. The objective function is:
where i is the network’s joint, t is the time step for the water quality analysis (h), Age is the water age (h), and n is the maximum number of joints in the network. The constraint is that the pressure at every joint should exceed 29 psi (200 KPa), according to the national legislation:
Pmin ≥ 29 psi
The optimization aim is to minimize the objective function z (Equation (1)) during a simulation period of continuous network operation (one week). The first step of the optimization process setup is to develop an algorithm that links EPANET and Matlab software tools, collects all the data needed, and performs calculations. The algorithm should be able to simulate the hydraulic operation of the network and collect the values of nodal water demands and pressures. Considering the specific boundary constraint of a minimum nodal pressure at 29 psi (200 KPa) (imposed by the national legislation), the algorithm computes Equation (1). It is important to note that the tool only works if the user defines the number of closed pipes (the number of pipes directly relevant to the position and number of isolation valves). The results from the first 24 h (t = 0 to t = 24) were excluded, as this is the time the system needs to arrive to a balance. Thus, the remaining time (6 days or 25 ≤ t ≤ 168 h) was the actual time frame for the model. Based on the objective function (Equation (1)) and the constraint (Equation (2)), the network’s model is tested for various scenarios formed and studied regarding water age reduction. The scenarios involved combinations of isolation valves that need to be closed in pipes in the WDN. The scenarios included the installation of isolation valves in groups of 4 to 18 isolation valves in pipes, at a step of two pipes at a time.
From the analysis of the scenarios, the best combination of the closed pipes is found to determine the lowest water age. Basic presupposition was the pressure not to drop below the threshold of 29 psi (200 KPa), according to the guidelines provided by the water utilities and the legislation. Based on this, the scenarios with 16 and 18 pipes with closed valves are excluded from the analysis, as the pressure was below the minimum threshold.
3.2. DMA Formation and Water Age
Based on the water pipes’ scenarios described above, the WDN is divided into DMAs. Four DMAs are formed using the hydraulic simulation software (Figure 4). The following scenarios are then examined: (a) base scenario where there are no DMAs and no PRVs; (b) scenario 1 where the WDN is divided in four DMAs but operates without pressure reduction valves; and scenario 2 where the WDN is divided in DMAs and pressure reduction valves are installed at the inlet points of each DMA. Thus, at first, the network operates without any DMAs being formed and no PRVs installed. Then, a minimum level of pressure management is performed by forming DMAs without any PRVs being installed too. The ultimate level of pressure management takes place when PRVs are installed in an optimal way, based also on the actual field restrictions. In every scenario, the water age and the water pressure are being calculated. The use of PRVs reduces operating pressure in all DMAs but water age is increased or remains the same. To check the scenarios described, the same objective function (Equation (1)) and constraint (Equation (2)) are used.
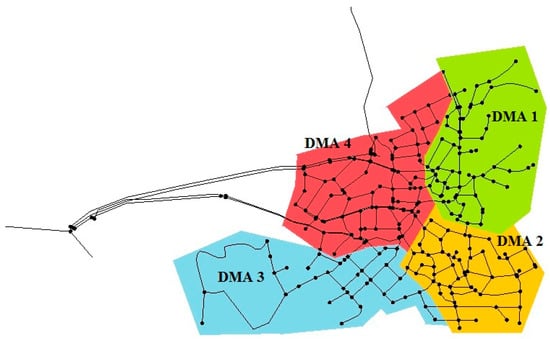
Figure 4.
Four DMAs formed in the WDN of Eani.
4. Results and Discussion
4.1. Water Age and Water Pressure
From the analysis above, the critical pipe with the highest water age is determined. In addition, the critical joint having the lowest pressure value is determined. The critical pipe, the average and maximum water age, and the critical joint and the minimum and average pressure values are presented in Table 1. The results show that the pipe with ID 69 is the critical pipe for three out of the six scenarios studied with an average water age 42.056 h. For the other scenarios, the pipe with ID number 255 is the critical pipe with an average water age of 50.242 when four pipes are closed; pipe ID 203 is critical with an average water age of 35.040 h when 12 pipes are closed; and pipe with ID 289 is critical with an average water age of 47.357 h when 14 pipes are closed. In all cases, joint ID 59 is the critical one with an average pressure ranging from 8.132 to 8.270 psi and a minimum pressure ranging from 4.64 to 4.93 psi.

Table 1.
Number of pipes closed, critical pipe, max and average water age; and critical joint, min and average pressure.
Average (nodal) water age in the WDN has been estimated in all scenarios and at the initial conditions. Water age value without any intervention is estimated to 13.59 h (Figure 5). Average water age ranges from 13.18 (scenario 3) to 14.12 h (scenario 5). Average water age has high values in scenarios 2 and 5 (Figure 5). The results show that the number of closed pipes does not directly affect water age inside the network, which is also found in other studies [3]. Average water pressure has been estimated for all scenarios and the initial conditions. Average pressure values range from 97.5 (scenario 3) to 99.1 psi (initial conditions without interventions) (Figure 5). The lowest water pressure values are met in scenarios 3 and 4. From the results, scenario 3 shows the lowest water age value (13.18 h) and the lowest water pressure value (97.5 psi) (Figure 5). In scenario 3, eight pipes are closed (with ID 216,171,165,155,106,332,319,287), and the critical pipe is the one with ID69.
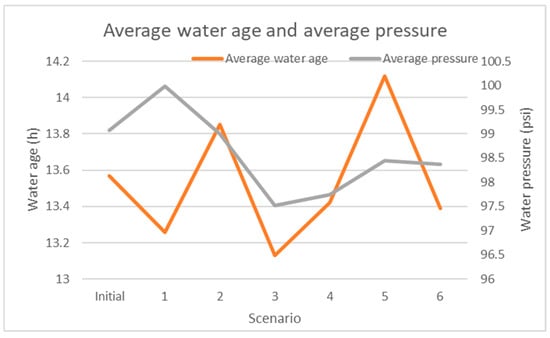
Figure 5.
Average water age and pressure for various scenarios.
4.2. DMAs and Water Age
The results for the three scenarios show that, as pressure management is implemented, water pressure is reduced, while water age is increased. When PRVs are installed in DMAs (scenario 3), average water pressure reduces radically (Figure 6). Based on the results, the scenario with closed pipes (base scenario) provides the best solution for water age, while the scenario with DMAs and PRVs (scenario 2) provides the best solution for water pressure. Water age gets its lower value (13.7 h) when the pipes are closed (base scenario) and water pressure gets its lower value (75.2 psi) when DMAs are formed and PRVs are used (scenario 2).
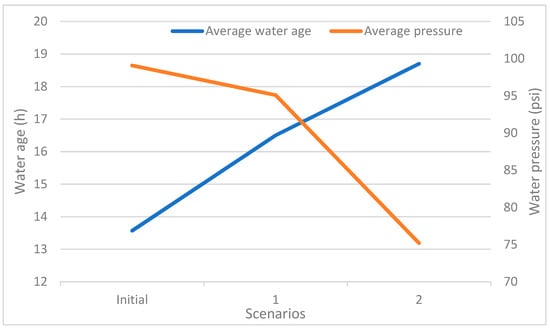
Figure 6.
Average water age and pressure for the initial state, and the DMA formation with PRVs or without PRVs.
The study of Chatzivasili et al. [4] combined the optimization (minimization) of water age and the product of pressure x demand at nodes at the same time. A two-phase hybrid approach based on mixture models has been used in the study. The network was divided using the Geometric Partitioning method and then the SMM-EM algorithm was implemented [4]. The results showed that the pressure x demand product is reduced by 43.69% and average water age was reduced by 7.3%, compared to the initial state of the network. Additional benefits of this hybrid methodology are that seven pipes are closed (compared to 8 with GAs), fewer PRVs are installed, and less computational time is needed for the model to “run”.
5. Conclusions
In this paper, water age and water pressure are studied in the WDN of Eani. GAs are used through EPANET and the Matlab software tool to provide the optimal water age–water pressure relation, when isolation valves are used to close certain water pipes within the network. Six scenarios are studied to determine the optimal number of closed pipes, meaning that, during this scenario, the water age takes its lowest value while water pressure remains low as well. As each network has its own characteristics, the optimum solutions differ from one WDN to the other. The methodology (use of GAs through EPANET and Matlab) can be used universally. During this study, DMAs are formed in the WDN and the scenarios of installing PRVs or not are also investigated. The results showed that the use of PRVs reduces water pressure but increases water age. Thus, when forming DMAs, optimization processes should be used in order to install PRVs and optimize both water age and water pressure. Therefore, the criterion of water age should be included as one of the criteria for the DMA formation in WDNs. The use of residual chlorine can also be used as an additional criterion in the optimization process. As water quality is extremely important for the consumers’ health, water age and residual chlorine should not be underestimated in the design stage or when NRW reduction strategies are studied.
Author Contributions
All authors have read and agreed to the published version of the manuscript. Conceptualization, V.K.; methodology, V.K., M.P., and N.K.; formal analysis, N.K., M.P., and S.T.; writing—original draft preparation, S.T.; writing—review and editing, S.T. and V.K.; supervision, V.K.
Funding
The research is elaborated within the framework of the invitation “Granting of scholarship for Post-Doctoral Research” of the University of Thessaly, which is being implemented by the University of Thessaly and was funded by the Stavros Niarchos Foundation.
Acknowledgments
The research is elaborated within the framework of the invitation “Granting of scholarship for Post-Doctoral Research” of the University of Thessaly, which is being implemented by the University of Thessaly and was funded by the Stavros Niarchos Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kanakoudis, V.; Muhammetoglu, H. Urban Water Pipe Networks Management Towards Non-Revenue Water Reduction: Two Case Studies from Greece and Turkey. CLEAN-Soil Air Water 2013, 42, 880–892. [Google Scholar] [CrossRef]
- Patelis, M.; Kanakoudis, V.; Kravvari, A. Pressure Regulation vs. Water Aging in Water Distribution Networks. Water 2020, 12, 1323. [Google Scholar] [CrossRef]
- Chondronasios, A.; Gonelas, K.; Kanakoudis, V.; Patelis, M.; Korkana, P. Optimizing DMAs’ formation in a water pipe network: The water aging and the operating pressure factors. J. Hydroinformatics 2017, 19, 890–899. [Google Scholar] [CrossRef]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V. Optimizing the Formation of DMAs in a Water Distribution Network through Advanced Modelling. Water 2019, 11, 278. [Google Scholar] [CrossRef]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V.; Patelis, M. Optimizing the Formation of DMAs in a Water Distribution Network Applying Geometric Partitioning (GP) and Gaussian Mixture Models (GMMs). Proceedings 2018, 2, 601. [Google Scholar] [CrossRef]
- Savic, D.; Ferrari, G. Design and Performance of District Metering Areas in Water Distribution Systems. Procedia Eng. 2014, 89, 1136–1143. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Non-revenue water reduction through pressure management in Kozani’s water distribution network: From theory to practice. Desalin. Water Treat. 2015, 57, 11436–11446. [Google Scholar] [CrossRef]
- AWWA; AWWARF. Water Industry Database: Utility Profiles; American Water Works Association: Denver, CO, USA; American Water Works Association Research Foundation: Denver, CO, USA, 1992. [Google Scholar]
- Shamsaei, H.; Jaafar, O.; Basri, N.E.A. Effects Residence Time to Water Quality in Large Water Distribution Systems. Engineering 2013, 5, 449–457. [Google Scholar] [CrossRef]
- Eliades, D.G.; Kyriakou, M.; Polycarpou, M. Sensor Placement in Water Distribution Systems Using the S-PLACE Toolkit. Procedia Eng. 2014, 70, 602–611. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.; Savic, D. Evolutionary multi-objective optimization of the design and operation of water distribution network: Total cost vs. reliability vs. water quality. J. Hydroinformatics 2006, 8, 165–179. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G. Multiobjective Optimization of Pipe Replacements and Control Valve Installations for Leakage Attenuation in Water Distribution Networks. J. Water Resour. Plan. Manag. 2015, 141, 04014059. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Kumar, A.R.S.; Sudheer, K.P.; Jain, S.K.; Agarwal, P.K. Rainfall-runoff modelling using artificial neural networks: Comparison of network types. Hydrol. Process. 2005, 19, 1277–1291. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal Layout of Early Warning Detection Stations for Water Distribution Systems Security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).