Enhancement of Socioeconomic Criteria for the Assessment of the Vulnerability to Flood Events with the Use of Multicriteria Analysis †
Abstract
1. Introduction
2. Materials and Methods
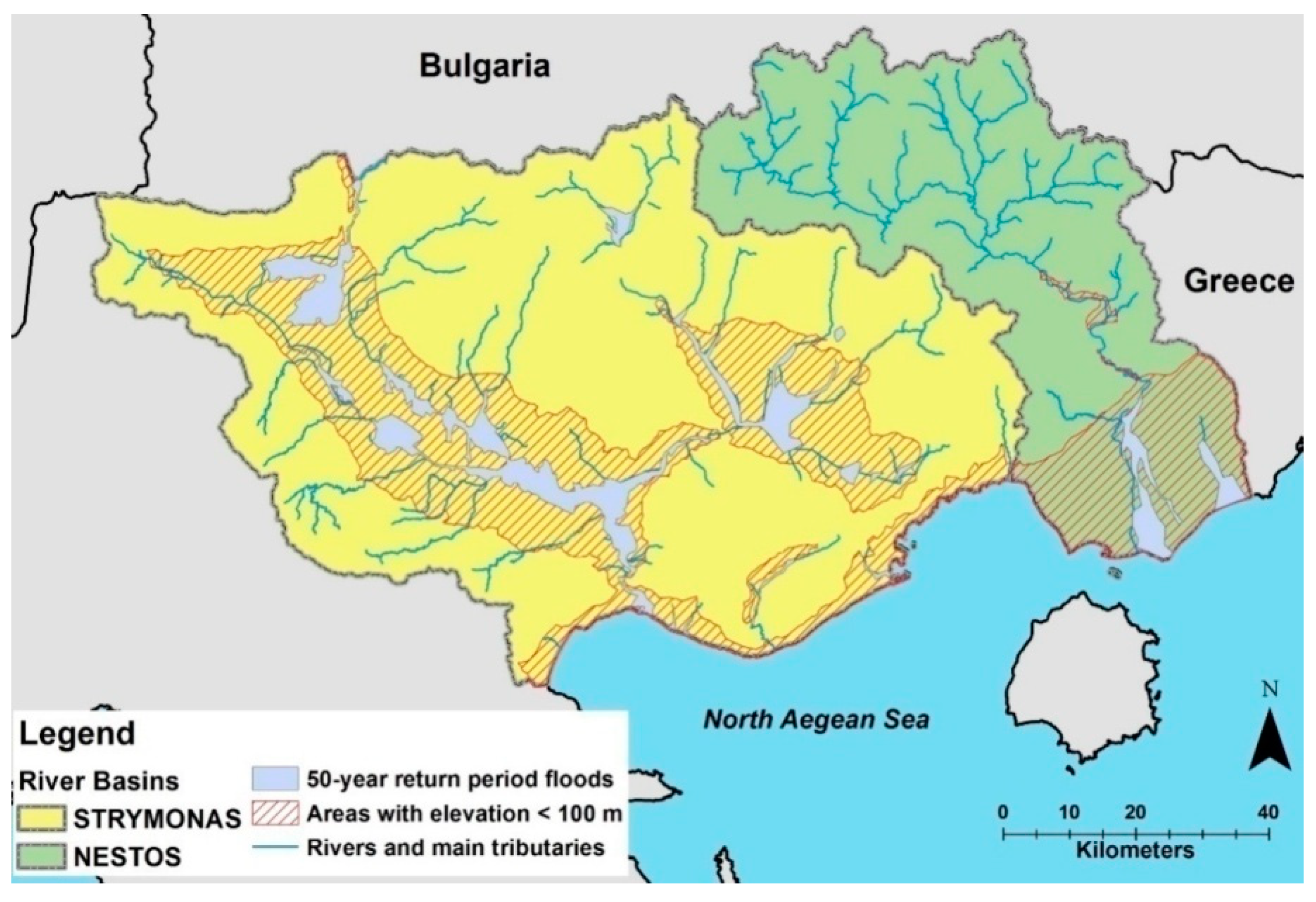
2.1. Case Study Areas
2.2. TOPSIS Method Based on a Fuzzy Pattern Recognition
2.3. Proxy Variables and Input Data
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tsakiris, G. Flood risk assessment: Concepts, modelling, applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1361–1369. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Tateishi, R. Urban Flood Vulnerability and Risk Mapping Using Integrated Multi-Parametric AHP and GIS: Methodological Overview and Case Study Assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Rani, N.N.V.S.; Satyanarayana, A.N.V.; Bhaskaran, P.K. Coastal vulnerability assessment studies over India: A review. Nat. Hazards 2015, 77, 405–428. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2001: Impacts, Adaptation Vulnerability, Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; McCarthy, J.J., Canziani, O.F., Leary, N.A., Dokken, D.J., White, K.S., Eds.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Jun, K.-S.; Chung, E.-S.; Kim, Y.-G.; Kim, Y. A fuzzy multi-criteria approach to flood risk vulnerability in South Korea by considering climate change impacts. Expert Syst. Appl. 2013, 40, 1003–1013. [Google Scholar] [CrossRef]
- Ramieri, E.; Hartley, A.; Barbanti, A.; Santos, F.; Gomes, A.; Hildén, M.; Laihonen, P.; Marinova, N.; Santini, M. Methods for Assessing Coastal Vulnerability to Climate Change, ETC CCA Technical Paper 1/2011; European Environment Agency: Copenhagen, Denmark, 2011; pp. 1–93.
- Chung, E.-S.; Lee, K.S. Identification of Spatial Ranking of Hydrological Vulnerability Using Multi-Criteria Decision Making Techniques: Case Study of Korea. Water Resour. Manag. 2009, 23, 2395–2416. [Google Scholar] [CrossRef]
- Skoulikaris, C.; Zafirakou, A. River Basin Management Plans as a tool for sustainable transboundary river basins’ management. Environ. Sci. Pollut. Res. 2019, 26, 14835–14848. [Google Scholar] [CrossRef] [PubMed]
- Special Secretariat for Water. In Flood Risk Management Plan of Thrace Water District (GR12); Ministry of Environment and Energy: Athens, Greece, 2018.
- Special Secretariat for Water. In Flood Risk Management Plan of Eastern Macedonia Water District (GR11); Ministry of Environment and Energy: Athens, Greece, 2018.
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making; Springer Science and Business Media LLC: Berlin, Germany, 1981; Volume 186, pp. 128–140. [Google Scholar]
- Spiliotis, M.; Iglesias, A.; Garrote, L. A multicriteria fuzzy pattern recognition approach for assessing the vulnerability to drought: Mediterranean region. Evol. Syst. 2020, 1–14, in press. [Google Scholar] [CrossRef]
- Balioti, V.; Tzimopoulos, C.; Evangelides, C. Multi-Criteria Decision Making Using TOPSIS Method Under Fuzzy Environment. Application in Spillway Selection. Proceedings 2018, 2, 637. [Google Scholar]
- Huicheng, Z.; Guoli, W.; Qing, Y. A multi-objective fuzzy pattern recognition model for assessing groundwater vulnerability based on the DRASTIC system. Hydrol. Sci. J. 1999, 44, 611–618. [Google Scholar] [CrossRef]
- Shouyu, C.; Guangtao, F. A DRASTIC-based fuzzy pattern recognition methodology for groundwater vulnerability evaluation. Hydrol. Sci. J. 2003, 48, 211–220. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. Cost–volume–profit analysis under uncertainty: A model with fuzzy estimators based on confidence intervals. Int. J. Prod. Res. 2009, 47, 5977–5999. [Google Scholar] [CrossRef][Green Version]
- Weis, S.W.M.; Agostini, V.N.; Roth, L.M.; Gilmer, B.; Schill, S.R.; Knowles, J.E.; Blyther, R. Assessing vulnerability: An integrated approach for mapping adaptive capacity, sensitivity, and exposure. Clim. Chang. 2016, 136, 615–629. [Google Scholar] [CrossRef]
- Chakraborty, A.; Joshi, P.K. Mapping disaster vulnerability in India using analytical hierarchy process. Geomat. Nat. Hazards Risk 2014, 7, 1–19. [Google Scholar] [CrossRef]
- Chung, E.-S.; Abdulai, P.J.; Park, H.; Kim, Y.; Ahn, S.R.; Kim, S. Multi-Criteria Assessment of Spatial Robust Water Resource Vulnerability Using the TOPSIS Method Coupled with Objective and Subjective Weights in the Han River Basin. Sustainability 2016, 9, 29. [Google Scholar] [CrossRef]
- Panagiotou, L.; Spiliotis, M.; Latinopoulos, D.; Kagalou, I. Evaluation of management options for implementing water framework directive: Application of fuzzy TOPSIS method. In Proceedings of the 14th Conference of Hellenic Hydrotechnical Association (H.H.A.), Volos, Greece, 16–17 May 2019; pp. 209–218. [Google Scholar]
- Ye, J. Expected value method for intuitionistic trapezoidal fuzzy multicriteria decision-making problems. Expert Syst. Appl. 2011, 38, 11730–11734. [Google Scholar] [CrossRef]
| River | Extend (km2) | Mean Elevation (m) | River Length (km) | Annual Precipitation (mm) | Annual Discharge (×106m3) |
|---|---|---|---|---|---|
| Nestos | 2834 | 606 | 130 | 678 | 687 |
| Strymonas | 7282 | 430 | 110 | 675 | 1514 |
| Vulnerability Components | Weights [5] | Criterion | Criterion Description | Individual Weights [5] | Source of Data |
|---|---|---|---|---|---|
| Sensitivity | 0.37 | C1 | Areas with elevation < 100m | 0.31 | GTOPO30 Digital elevation Model & GIS Analysis |
| C2 | Settlements located in areas with elevation < 100 m | 0.23 | National statistics & GIS Analysis | ||
| C3 | Flooded areas for T = 50 years | 0.19 | National Flood Risk Plans | ||
| C4 | Population density (persons/km2) | 0.16 | National statistics & GIS Analysis | ||
| C5 | Total population | 0.11 | National statistics | ||
| C6 | Regional average slope (°) | 0.10 | GIS Analysis | ||
| C7 | Percentage of road area (%) | 0.10 | Egnatia Street Observatory | ||
| Adaptive capacity | 0.30 | C8 | Financial independence (%) | 0.10 | National statistics |
| C9 | Number of civil servants per population (persons/103 people) | 0.11 | National statistics | ||
| C10 | Number of civil servants related to water | 0.16 | National statistics | ||
| Exposure | 0.33 | ||||
| C11 | Surface runoff (mm/day) | National Flood Risk Plans |
| Criteria | Area 1 | Area 2 | Area 3 | Area 4 |
|---|---|---|---|---|
| (+) sensitivity×0.37 | 0.092 | 0.066 | 0.240 | 0.217 |
| (−) adaptive capacity×0.30 | 0.159 | 0.006 | 0.157 | 0.060 |
| (+) exposure×0.33 | 0.245 | 0.030 | 0.330 | 0.000 |
| Scores | Area 1 | Area 2 | Area 3 | Area 4 |
|---|---|---|---|---|
| 0.332 | 0.427 | 0.204 | 0.369 | |
| 0.297 | 0.303 | 0.432 | 0.324 | |
| (+) membership degree (ideal solution) (μi+) | 0.445 | 0.335 | 0.818 | 0.435 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skoulikaris, C.; Papadopoulos, C.; Spiliotis, M.; Maris, F. Enhancement of Socioeconomic Criteria for the Assessment of the Vulnerability to Flood Events with the Use of Multicriteria Analysis. Environ. Sci. Proc. 2020, 2, 52. https://doi.org/10.3390/environsciproc2020002052
Skoulikaris C, Papadopoulos C, Spiliotis M, Maris F. Enhancement of Socioeconomic Criteria for the Assessment of the Vulnerability to Flood Events with the Use of Multicriteria Analysis. Environmental Sciences Proceedings. 2020; 2(1):52. https://doi.org/10.3390/environsciproc2020002052
Chicago/Turabian StyleSkoulikaris, Charalampos, Christopher Papadopoulos, Mike Spiliotis, and Fotis Maris. 2020. "Enhancement of Socioeconomic Criteria for the Assessment of the Vulnerability to Flood Events with the Use of Multicriteria Analysis" Environmental Sciences Proceedings 2, no. 1: 52. https://doi.org/10.3390/environsciproc2020002052
APA StyleSkoulikaris, C., Papadopoulos, C., Spiliotis, M., & Maris, F. (2020). Enhancement of Socioeconomic Criteria for the Assessment of the Vulnerability to Flood Events with the Use of Multicriteria Analysis. Environmental Sciences Proceedings, 2(1), 52. https://doi.org/10.3390/environsciproc2020002052








