Exploring the Potential of Mathematical Self-Purification Models Used for Evaluating Water Quality in Rivers
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Process
2.2. Protocol and Focus Questions
2.3. Systematic Search According to PRISMA
3. Results and Discussion
3.1. Research Question 1: What Are the Most Used Mathematical Models to Evaluate River Self-Purification, and What Are Their Theoretical Foundations?
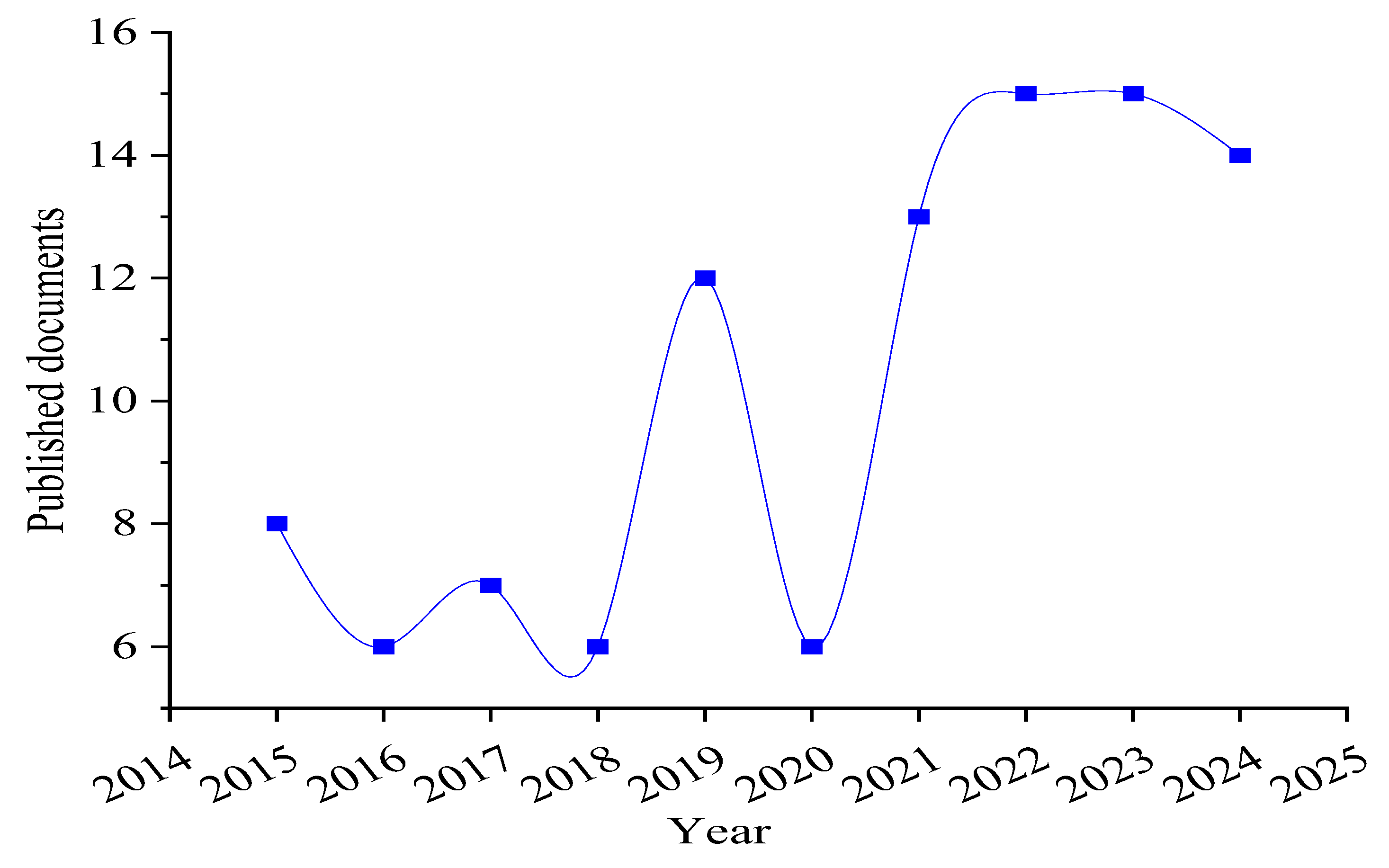
3.1.1. Temporal Trends in the Publication of Studies on Self-Purification Models Used to Assess Water Quality in Rivers
3.1.2. Geographic Distribution of Studies on River Self-Purification Models
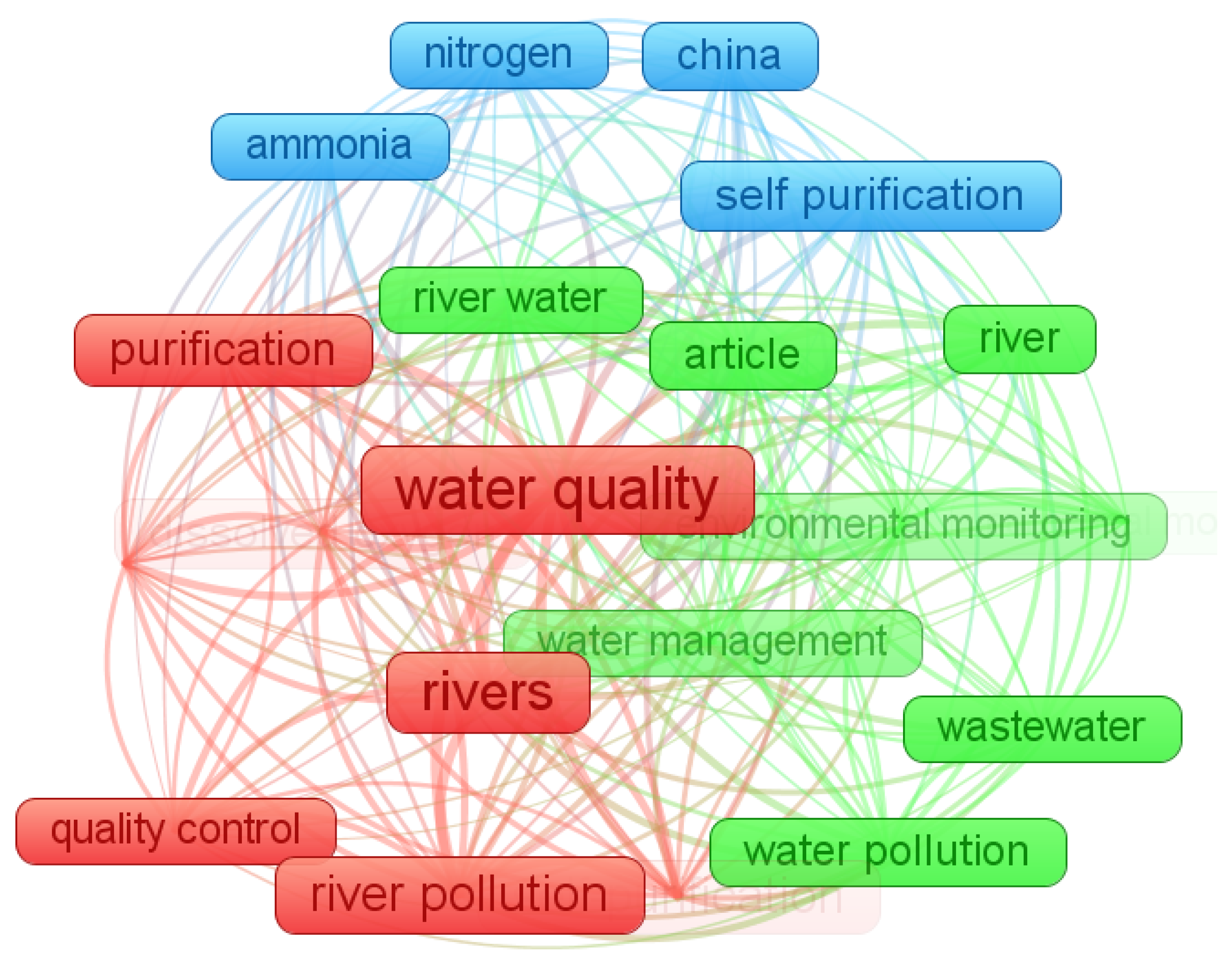
3.1.3. Analysis of Keyword Trends in Research on River Self-Purification Models
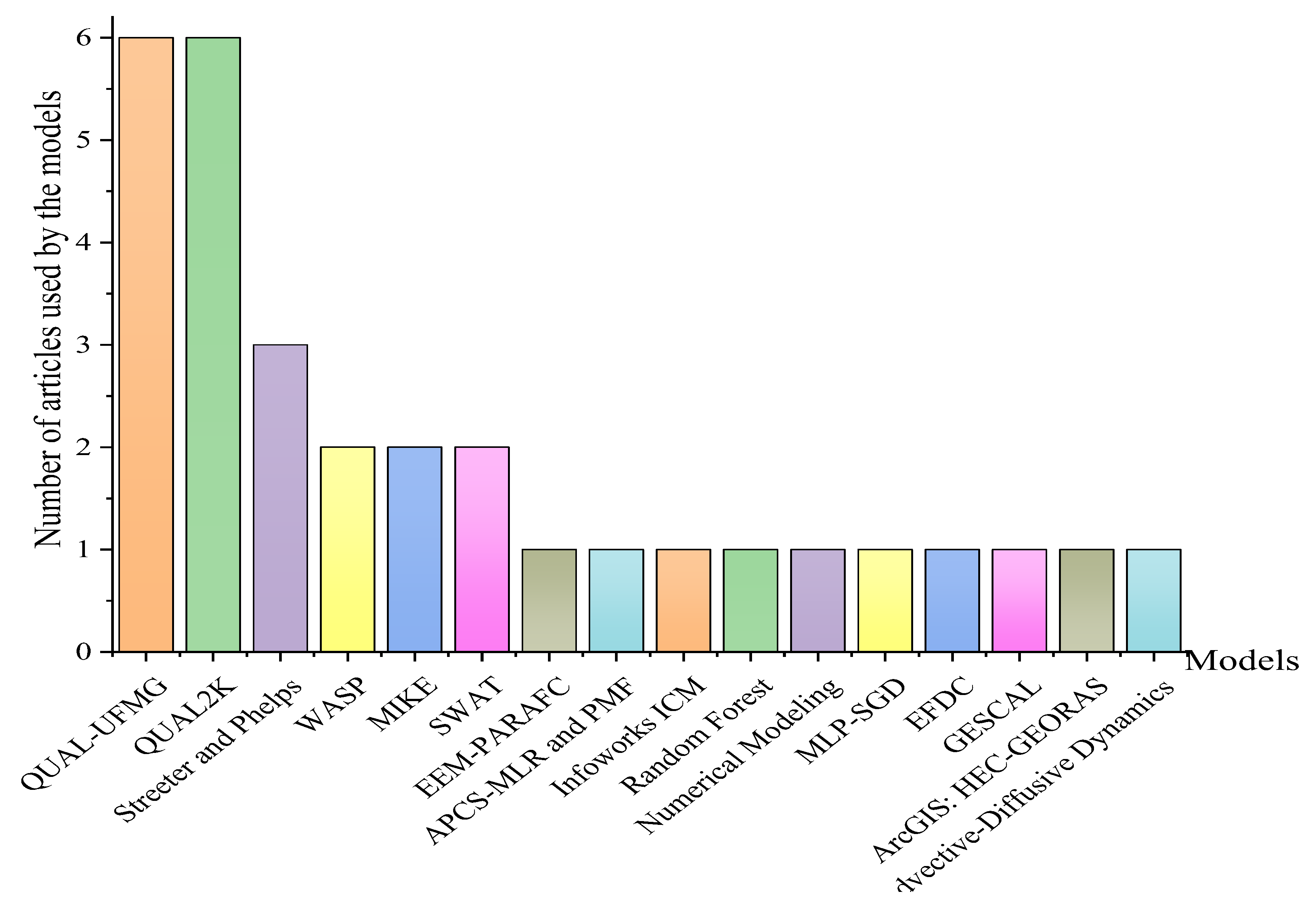
3.1.4. Most Commonly Used Mathematical Models for Evaluating Self-Purification in Rivers: Frequencies, Characteristics and Limitations
| Authors | Model | N° Articles | Theoretical Foundation | Application | Limitations |
|---|---|---|---|---|---|
| [28,62,63,71,72,73] | QUAL-UFMG | 6 | It is an adaptation of the QUAL2E model from USEPA developed by the Federal University of Minas Gerais (Portuguese: Universidade Federal de Minas Gerais, UFMG) in Brazil. The calculation is done by processing coupled differential equations in Microsoft Excel. It uses the equations from the QUAL family with the corresponding adaptations. Main parameters
| Given that the model is developed in Brazil, its application mainly focuses on tropical zones (similar to the design conditions) and in studies that require simple tools of easy access based on Excel to evaluate the impact of discharges. | It is limited to zones of tropical conditions. It has less effective precision for other climate zones [71]. According to the work of Da Luz et al. [63], for the DO calibration a good data fit was shown, but this was not the case for BOD5. This adjustment was presented due to the fact that real conditions in which effluents are discharged are unknown. The discharge of pollutant loads in a water body has to be analyzed with much caution because misinterpreted data and incorrect results compromise predominant applications [63]. |
| [18,65,74,75,76,77] | QUAL2K | 6 | The QUAL2K model is an evolution of the QUAL2E model, designed to improve water quality simulations through the inclusion of variables such as algae growth, denitrification, and an adjustment in the calculation of dissolved oxygen. Main parameters
| The application of this model is used in simulations of dissolved oxygen and biochemical oxygen demand. | If the model uses variables such as nitrogen or phosphorous, it can extend to problems with these pollutants. Also, it presents significant challenges due to the quantity of detailed data that is required, which is why the information is often very limited [18]. Many times the behavior of variables in the section studied may tend to underestimate in this case the concentration of DO [18] The adjustment to the QUAL2K model may be significantly lower [77]. |
| [64,65,78] | Streeter-Phelps | 3 | The Streeter-Phelps model is the main historical basis model from which many other models for the evaluation of water quality in rivers and other water bodies are derived through the explication of the interaction between BOD and DO. It is specially designed in response to wastewater discharges. Main parameters
| It is a model used for water quality simulation in rivers. It is a classic approach that does not include advanced technological tools. The model allows the identification of natural recovery zones and critical pollution points, considering the organic matter decomposition rate, and the process of reoxygenation. | The authors mention that for this model homogeneous, stationary, and constant flux conditions have to be assumed [64,65,78] According to the work of Díaz et al. [64], the precision of the model is lowered by the presence of diffuse sources of pollution, and in cases of high hydrodynamic complexity. According to the work of Pazmiño-Rodríguez et al. [65], neither multiple pollutants nor seasonal variability are considered. |
| [58,66] | WASP | 2 | The WASP model is a tool developed in 1980 by USEPA. It is designed to simulate various parameters and their interaction for the evaluation of water quality in such a way that the effect of pollutant loads over water bodies can be predicted. It basically uses a set of differential equations to describe transport, dispersion, and reaction of pollutants. Main parameters
| The model is used to simulate water quality under different pollution scenarios, allowing the analysis of impacts of either anthropogenic or natural pollutant loads. Speaking of environmental management, the model helps to design optimal strategies for control measures of pollutant sources such as optimal systems and for future decisions based on the information provided on water quality. | According to the work of Żelazny et al. [60], there are limitations for precise representation of extreme events, such as runoff caused by extreme rainfall. According to the work of Ma et al. [67], there is a precision dependency on input data, and on the simplification of assumptions in the behavior of the interception system. |
| [69,79] | MIKE | 2 | The MIKE model was developed in 1972 by the Danish Hydraulic Institute. It is a deterministic model that allows the simulation of fluxes in a non-permanent state within river systems, adapting both to simple and complex configurations. This model can be used to evaluate the impact of discharges on water quality in rivers, besides working as a hydraulic model for the analysis of floods. It integrates specialized modules, among which those of rainfall-runoff, advection-dispersion, and hydrodynamics are included. Main parameters Physicochemical
| It is an advanced model that allows hydrodynamic and water quality simulation in water bodies, evaluating diverse pollutant dispersion scenarios, such as the optimal location of pumping stations. The model analyzes self-purification processes, identifies critical pollution zones, and allows the design of environmental management strategies for improving water quality. | According to the work of S. Han et al. [79], the precision of the model depends on the quantity of input data. Also, the accuracy of the predictions may be affected by the complexity of the fluvial system that may require simplifications. According to the work of H. Wang et al. [69], the model is limited by the accuracy and availability of input data. The unidimensionality of the MIKE 11 model may not fully capture the complexity of fluvial systems with significant tridimensional variations. |
3.2. Research Question 2: What Are the Most Relevant Variables Used in Self-Purification Models, and How Do They Influence the Prediction of Water Quality?
3.3. Research Question 3: What Are the Strengths and Weaknesses of the Self-Purification Models in Polluted Rivers?
3.4. Final Considerations Between Models
3.5. Recent Developments and Prospects for Self-Purification Models
Recent Advances and Perspectives for Self-Purification Models
3.6. Applicability of the Findings Identified in the Review
3.7. Strengths, Limitations, and Knowledge Gaps
3.7.1. Fundamental Limitations: The Trade-Off Between Complexity and Utility
3.7.2. Uncertainty Analysis, Sensitivity, and Hybrid Models in Water Quality Prediction
3.7.3. Practical Implications and Recommendations for Water Management
3.8. Comparative Analysis and Methodological Limitations of the Compared Models
3.9. Future Direction of Next-Generation Research and Modeling
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, J.; Yang, T.; Wang, Y.; Jiang, H.; He, C. Effects of ecological restoration on water quality and benthic macroinvertebrates in rural rivers of cold regions: A case study of the Huaide River, Northeast China. Ecol. Indic. 2022, 142, 109169. [Google Scholar] [CrossRef]
- González, L.; Zhiña, D.X.; Avilés, A.; Astudillo, A.; Peralta, X.; Verdugo, T. Exploring habitat quality dynamics in an equatorial Andean basin under scenarios of land use change. Earth 2025, 6, 10. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Cui, G.; Cao, Y. Water quality attribution and simulation of non-point source pollution load flux in the Hulan River basin. Sci. Rep. 2020, 10, 3012. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Shen, Y.; Huang, Y.; Hu, N. A comparative study of aeration, biostimulation and bioaugmentation in contaminated urban river purification. Environ. Technol. Innov. 2018, 11, 276–285. [Google Scholar] [CrossRef]
- Cui, Y.; Zhou, Y.; Jin, J.; Zhang, L.; Wu, C.; Ning, S. Coordinated development evaluation and diagnosis of regional water resources-social economy-ecological environment system based on mechanical model and risk matrix. J. Hydrol. 2024, 633, 131013. [Google Scholar] [CrossRef]
- Kantamaneni, K.; Whitton, J.; Panneer, S.; Ahmad, I.; Gautam, A.; Sen, D. An assessment of bio-physical and social drivers of river vulnerability and risks. Earth 2025, 6, 77. [Google Scholar] [CrossRef]
- Das, A. Water pollution and water quality assessment and application of criterion impact loss (CILOS), geographical information system (GIS), artificial neural network (ANN) and decision-learning technique in river water quality management: An experiment on the Mahanadi catchment, Odisha, India. Desalination Water Treat. 2025, 321, 100969. [Google Scholar] [CrossRef]
- Deng, S.; Li, C.; Jiang, X.; Zhao, T.; Huang, H. Research on surface water quality assessment and its driving factors: A case study in taizhou city, China. Water 2022, 15, 26. [Google Scholar] [CrossRef]
- Roldán-Arias, A.; García-Ávila, F.; Pesántez-Quintuña, K.; Cabello-Torres, R.; Valdiviezo-Gonzales, L. Spatiotemporal dynamics of a peri-urban stream water quality and its relationship with land use. Case Stud. Chem. Environ. Eng 2023, 8, 100420. [Google Scholar] [CrossRef]
- Hounkpe, J.; Bossa, Y.A.; Badou, F.D.; Nouasse, F.; Sinasson, K.G.S.; Yangouliba, I.; Bio Salifou, A.L.D.; Kodjogbe, I.; Yira, Y.; Hounkpatin, O.; et al. Local Perspectives on the Role of Dams in Altering River Ecosystem Services in West Africa. Earth 2025, 6, 93. [Google Scholar] [CrossRef]
- Zuo, D.; Bi, Y.; Song, Y.; Xu, Z.; Wang, G.; Ma, G.; Abbaspour, K.C.; Yang, H. The response of non-point source pollution to land use change and risk assessment based on model simulation and grey water footprint theory in an agricultural river basin of Yangtze River, China. Ecol. Indic. 2023, 154, 110581. [Google Scholar] [CrossRef]
- Islam, M.A.S.; Hossain, M.E.; Majed, N. Assessment of physicochemical properties and comparative pollution status of the Dhaleshwari river in Bangladesh. Earth 2021, 2, 696–714. [Google Scholar] [CrossRef]
- Long, B.T. Inverse algorithm for Streeter–Phelps equation in water pollution control problem. Math. Comput. Simul. 2020, 171, 119–126. [Google Scholar] [CrossRef]
- Medupe, M.; Letshwenyo, M.W. Investigation of self-purification and water quality index during dry and rainy seasons in the Khurumela Stream (Botswana). J. Ecohydraulics 2024, 10, 1–18. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Fakhreddine, S.; Rateb, A.; De Graaf, I.; Famiglietti, J.; Gleeson, T.; Grafton, R.Q.; Jobbagy, E.; Kebede, S.; Kolusu, S.R.; et al. Global water resources and the role of groundwater in a resilient water future. Nat. Rev. Earth Environ. 2023, 4, 87–101. [Google Scholar] [CrossRef]
- Popa, V.-I.; Rusu, E.; Chirosca, A.-M.; Arseni, M. Danube River: Hydrological features and risk assessment with a focus on navigation and monitoring frameworks. Earth 2025, 6, 70. [Google Scholar] [CrossRef]
- Capodaglio, A.; Callegari, A. Can Payment for Ecosystem Services Schemes Be an Alternative Solution to Achieve Sustainable Environmental Development? A Critical Comparison of Implementation between Europe and China. Resources 2018, 7, 40. [Google Scholar] [CrossRef]
- Zurita, A.; Aguayo, M.; Arriagada, P.; Figueroa, R.; Díaz, M.E.; Stehr, A. Modeling Biological Oxygen Demand Load Capacity in a Data-Scarce Basin with Important Anthropogenic Interventions. Water 2021, 13, 2379. [Google Scholar] [CrossRef]
- Mummidivarapu, S.K.; Rehana, S.; Rao, Y.S. Mapping and assessment of river water quality under varying hydro-climatic and pollution scenarios by integrating QUAL2K, GEFC, and GIS. Environ. Res. 2023, 239, 117250. [Google Scholar] [CrossRef]
- Saravia-Maldonado, S.A.; Fernández-Pozo, L.F.; Ramírez-Rosario, B.; Rodríguez-González, M.Á. Analysis of Deforestation and Water Quality in the Talgua River Watershed (Honduras): Ecosystem Approach Based on the DPSIR Model. Sustainability 2024, 16, 5034. [Google Scholar] [CrossRef]
- Cacal, J.C.; Mehboob, M.S.; Bañares, E.N. Integrating Water Evaluation and Planning modeling into Integrated Water Resource Management: Assessing climate change impacts on future surface water supply in the Irawan Watershed of Puerto Princesa, Philippines. Earth 2024, 5, 905–927. [Google Scholar] [CrossRef]
- United Nations. The United Nations World Water Development Report 2023: Partnerships and Cooperation for Water; UNESCO: Paris, France, 2023. [Google Scholar]
- Darji, J.; Lodha, P.; Tyagi, S. Assimilative capacity and water quality modeling of rivers: A review. J. Water Supply Res. Technol. —AQUA 2022, 71, 1127–1147. [Google Scholar] [CrossRef]
- UN-Water 2021. UN-Water. Integrated Monitoring of Initiative SDG 6. 2021. Available online: https://www.unwater.org/our-work/integrated-monitoring-initiative-sdg-6 (accessed on 2 May 2020).
- World Health Organization. World Health Day 2022. 2022. Available online: https://www.who.int/campaigns/world-health-day/2022 (accessed on 14 May 2020).
- Perujo, N.; Neuert, L.; Fink, P.; Weitere, M. Saturation of intracellular phosphorus uptake and prevalence of extracellular phosphorus entrapment in fluvial biofilms after long-term P pulses: Implications for river self-purification. Sci. Total Environ. 2024, 952, 175976. [Google Scholar] [CrossRef] [PubMed]
- Mureithi, P.W.; Aine, A.; Basooma, R.; Namumbya, J.; Nansumbi, F.; Yegon, M.J.; Meimberg, H.; Graf, W. Advancements in macroinvertebrate-based river bioassessment research in the Afrotropical region: Review and steps towards a regional framework. Environ. Monit. Assess. 2025, 197, 935. [Google Scholar] [CrossRef] [PubMed]
- Zubaidah, T.; Karnaningroem, N.; Slamet, A. The self-purification ability in the rivers of Banjarmasin, Indonesia. Inżynieria Ekol. 2019, 20, 177–182. [Google Scholar] [CrossRef]
- Pani, D.F.; Reis, J.A.T.D.; Rodrigues, M.B.; Mendonça, A.S.F.; Marques, S.M.; Da Silva, F.D.G.B. Prospects for reducing the contribution of organic load in a water basin with significant urban occupation. Eng. Sanit. E Ambient. 2024, 29, e20230079. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, Y.; Liu, T. Purification-analysis of urban rivers by combining graphene photocatalysis with sewage treatment improvement based on the MIKE11 model. Environ. Technol. 2020, 43, 585–594. [Google Scholar] [CrossRef]
- Macêdo, B.d.S.; Lima, L.; Fonseca, D.L.; Boratto, T.H.A.; Saporetti, C.M.; Fetoshi, O.; Hajrizi, E.; Bytyçi, P.; Aires, U.R.V.; Yonaba, R.; et al. Evolutionary-assisted data-driven approach for dissolved oxygen modeling: A case study in Kosovo. Earth 2025, 6, 81. [Google Scholar] [CrossRef]
- Higashino, M.; Stefan, H.G. Oxygen uptake prediction in rivers and streams: A stochastic approach. J. Environ. Manag. 2017, 203 Pt 1, 200–207. [Google Scholar] [CrossRef]
- Qiu, L.; Li, J.; Yu, P.; Ma, H.; Li, D.; Wang, A. Study on seasonal floating treatment wetland combination water purification based on numerical simulation. J. Water Process Eng. 2023, 56, 104305. [Google Scholar] [CrossRef]
- Zheng, Y.; He, J.; Zhang, W.; Lv, A. Assessing Water Security and Coupling Coordination in the Lancang–Mekong River Basin for Sustainable Development. Sustainability 2023, 15, 16880. [Google Scholar] [CrossRef]
- Rifai, R.M.; Lahardo, D.R.; Fahmi, A.F.R.; Siswahyudi, D. Investigating the Availability of Domestic Wastewater Pollution Load Capacity in Brantas River, Malang. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2023; Volume 445, p. 01019. [Google Scholar] [CrossRef]
- Lee, J.-W.; Lee, S.-W.; Lee, H.; Park, S.-R. Impact of environmental factors of stream ecosystems on aquatic invertebrate communities. Sustainability 2025, 17, 1252. [Google Scholar] [CrossRef]
- Bouriqi, A.; Ouazzani, N.; Deliege, J.-F. Modeling the impact of urban and industrial pollution on the quality of surface water in intermittent rivers in a semi-arid Mediterranean climate. Hydrology 2024, 11, 150. [Google Scholar] [CrossRef]
- Xiao, C.; Chai, Z.; Chen, D.; Luo, Z.; Li, Y.; Ou, Q.; Zhang, Y. Research on the influence of river morphological changes on water self-purification capacity: A case study of the Shiwuli River in chaohu basin. Water 2025, 17, 1694. [Google Scholar] [CrossRef]
- Hu, C.; Liu, Z.; Xiong, K.; Lyu, X.; Li, Y.; Zhang, R. Characteristics of and Influencing Factors of Hydrochemistry and Carbon/Nitrogen Variation in the Huangzhouhe River Basin, a World Natural Heritage Site. Int. J. Environ. Res. Public Health 2021, 18, 13169. [Google Scholar] [CrossRef]
- Ghafoor, J.; Forio, M.A.E.; Goethals, P.L.M. Spatially explicit river basin models for cost-benefit analyses to optimize land use. Sustainability 2022, 14, 8953. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, L.; Xu, B.; Li, J.; Feng, P. Analysis of the Water Temperature and Quality Characteristics of the Daheiting Reservoir Based on Coupled Hydrology–Hydrodynamic–Water Quality Simulations. Phys. Chem. Earth Parts A/B/C 2024, 135, 103632. [Google Scholar] [CrossRef]
- Cumpston, M.S.; McKenzie, J.E.; Thomas, J.; Brennan, S.E. The use of ‘PICO for synthesis’ and methods for synthesis without meta-analysis: Protocol for a survey of current practice in systematic reviews of health interventions [version 2; peer review: 2 approved]. F1000Research 2021, 9, 678. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. Declaración PRISMA 2020: Una guía actualizada para la publicación de revisiones sistemáticas. Rev. Española De Cardiol. 2021, 74, 790–799. [Google Scholar] [CrossRef]
- Khan, K.; Cavanillas, A.B.; Zamora, J. Revisiones sistemáticas en cinco pasos: I. Cómo formular una pregunta para la que se pueda obtener una respuesta válida. Medicina de Familia. SEMERGEN 2022, 48, 356–361. [Google Scholar] [CrossRef]
- Eriksen, M.B.; Frandsen, T.F. The impact of patient, intervention, comparison, outcome (PICO) as a search strategy tool on literature search quality: A systematic review. J. Med. Libr. Assoc. JMLA 2018, 106, 420. [Google Scholar] [CrossRef]
- Linares-Espinós, E.; Hernández, V.; Domínguez-Escrig, J.; Fernández-Pello, S.; Hevia, V.; Mayor, J.; Padilla-Fernández, B.; Ribal, M. Metodología de una revisión sistemática. Actas Urológicas Españolas 2018, 42, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Hossain, T.; Tushar, M.A.N.; Murshed, S.; Basak, U.; Islam, M.A. Landslide studies in the context of disaster management in Bangladesh—A systematic literature review. Earth 2024, 5, 784–811. [Google Scholar] [CrossRef]
- Ojo, S.; Asamoah, S.; Albrecht, E.; Ibrahim, B. Integrating sustainable development and disaster mitigation into climate policies to support water security in Africa. Earth 2025, 6, 57. [Google Scholar] [CrossRef]
- García-Ávila, F.; García-Pizarro, E.; Malla-Aguilar, G.; Sánchez-Cabrera, C.; Cadme-Galabay, M.; Valdiviezo-Gonzales, L.; Cabello-Torres, R. Influence of nutrients on aquatic vegetation and trophic status of lakes: Analysis of eutrophication and mitigation. Results Eng. 2025, 27, 106381. [Google Scholar] [CrossRef]
- García-Ávila, F.; Cabello-Torres, R.; Iglesias-Abad, S.; García-Mera, G.; García-Uzca, C.; Valdiviezo-Gonzales, L.; Donoso-Moscoso, S. Cleaner production and drinking water: Perspectives from a scientometric and systematic analysis for a sustainable performance. S. Afr. J. Chem. Eng. 2023, 45, 136–148. [Google Scholar] [CrossRef]
- Fu, B.; Liu, Y.; Meadows, M.E. Ecological restoration for sustainable development in China. Natl. Sci. Rev. 2023, 10, nwad033. [Google Scholar] [CrossRef]
- Hordones, R.H.; Boëchat, I.G.; Cunha, D.G.F.; Brauns, M.; Gücker, B. Toward effective river restoration in Brazil: A systematic review of current practices, regional disparities, and success metrics. Restor. Ecol. 2025, 33, e70041. [Google Scholar] [CrossRef]
- Mohamad Noor, S.S.; Saad, N.A. A review on QUAL2K water quality model: Comparative analysis with other models, recent advances and future directions. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2024; Volume 599, p. 02008. [Google Scholar] [CrossRef]
- Fitriana, F.; Yudianto, D.; Seo, Y.C. Comparative analysis of water quality models for the Cibarani Irrigation Channel using WASP and QUAL2Kw. Sustinere J. Environ. Sustain. 2025, 9, 162–172. [Google Scholar] [CrossRef]
- Slaughter, A.R.; Mantel, S.K. Water quality modelling of an impacted semi-arid catchment using flow data from the WEAP model. Proc. Int. Assoc. Hydrol. Sci. 2018, 377, 25–33. [Google Scholar] [CrossRef]
- Ouermi, K.S.; Paturel, J.-E.; Adounpke, J.; Lawin, A.E.; Goula, B.T.A.; Amoussou, E. Comparison of hydrological models for use in climate change studies: A test on 241 catchments in West and Central Africa. Comptes Rendus Geosci. 2019, 351, 477–486. [Google Scholar] [CrossRef]
- Hadgu, L.T.; Nyadawa, M.O.; Mwangi, J.K.; Kibetu, P.M.; Mehari, B.B. Application of water quality model QUAL2K to model the dispersion of pollutants in river ndarugu, Kenya. Comput. Water Energy Environ. Eng. 2014, 03, 162–169. [Google Scholar] [CrossRef]
- Mustafa, A.O.; Sulaiman, S.H.; Shahooth, S. Application of QUAL2K for Water Quality Modeling and Management in the lower reach of the Diyala river. Iraqi J. Civ. Eng. 2017, 11, 66–80. [Google Scholar] [CrossRef]
- Raeisi, N.; Moradi, S.; Scholz, M. Surface water resources assessment and planning with the QUAL2KW model: A case study of the Maroon and Jarahi basin (Iran). Water 2022, 14, 705. [Google Scholar] [CrossRef]
- Mengistu, A.G.; van Rensburg, L.D.; Woyessa, Y.E. Techniques for calibration and validation of SWAT model in data scarce arid and semi-arid catchments in South Africa. J. Hydrol. Reg. Stud. 2019, 25, 100621. [Google Scholar] [CrossRef]
- Burigato Costa, C.M.d.; da Silva Marques, L.; Almeida, A.K.; Leite, I.R.; de Almeida, I.K. Applicability of water quality models around the world-a review. Environ. Sci. Pollut. Res. Int. 2019, 26, 36141–36162. [Google Scholar] [CrossRef]
- Teodoro, A.; Ide, C.N.; Ribeiro, M.L.; Broch, S.A.O.; Da Silva, J.B. Implementação do conceito Capacidade de Diluiçãode Efluentes no modelo de qualidade da água QUAL-UFMG: Estudo de caso no Rio Taquarizinho (MS). Eng. Sanit. E Ambient. 2013, 18, 275–288. [Google Scholar] [CrossRef]
- Da Luz, E.; Tomazoni, J.C.; Pokrywiechi, T.S. Monitoramento Da Qualidade Da Água E Avaliação Da Capacidade De Autodepuração Do Rio Ligeiro No Município E Pato Branco—PR. Geociências 2019, 38, 755–768. [Google Scholar] [CrossRef]
- Díaz, J.J.F.; Salgado, D.N.; Pérez, S.J.M. Tasas de desoxigenación y reaireación para el río Sinú. Ing. Y Desarro. 2017, 35, 8–17. [Google Scholar]
- Pazmiño-Rodríguez, J.C.; Zambrano-Ganchozo, G.L.; Coello-Burgos, H.A. Modelización de la calidad del agua del estero aguas Claras, cantón Quevedo, Ecuador. Dyna 2018, 85, 204–214. [Google Scholar] [CrossRef]
- Żelazny, M.; Bryła, M.; Ozga-Zielinski, B.; Walczykiewicz, T. Applicability of the WASP Model in an Assessment of the Impact of Anthropogenic Pollution on Water Quality—Dunajec River Case Study. Sustainability 2023, 15, 2444. [Google Scholar] [CrossRef]
- Ma, C.; Huang, Y.; Kao, C. Development of Optimal Management Strategies for the Interception System Using River Water Quality Modeling. MATEC Web Conf. 2018, 175, 03024. [Google Scholar] [CrossRef]
- Han, Z.; Xiao, M.; Yue, F.; Yi, Y.; Mostofa, K. Seasonal Variations of Dissolved Organic Matter by Fluorescent Analysis in a Typical River Catchment in Northern China. Water 2021, 13, 494. [Google Scholar] [CrossRef]
- Wang, H.; Xu, W.; Liu, P.; Zhu, J. Coastal water environment regulation and simulation based on tidal power control. MATEC Web Conf. 2018, 246, 02027. [Google Scholar] [CrossRef]
- Tenreiro, T.R.; García-Vila, M.; Gómez, J.A.; Jimenez-Berni, J.A.; Fereres, E. Water modelling approaches and opportunities to simulate spatial water variations at crop field level. Agric. Water Manag. 2020, 240, 106254. [Google Scholar] [CrossRef]
- Da Silva, S.R.; Da Silva, M.A.B.; Junior De Lima, E.E.S. Analysis and modeling of water quality as a contribution to the preliminary framework proposal for the Una River (Pernambuco/Brazil). Ambiente E Agua—Interdiscip. J. Appl. Sci. 2018, 13, 1. [Google Scholar] [CrossRef]
- Guimarães, T.M.H.; Salla, M.R.; Pereira, C.E.; Justo, B.B.; Riquieri, J.C. Interferência Do Uso E Ocupação Do Solo Na Qualidade Da Água Em Bacia Hidrográfica Com Disponibilidade Hídrica Crítica. Geociências 2019, 38, 229–240. [Google Scholar] [CrossRef]
- Calmon, A.; Souza, J.; Reis, J.; Mendonça, A. Uso combinado de curvas de permanência de qualidade e modelagem da autodepuração como ferramenta para suporte ao processo de enquadramento de cursos d-água superficiais. RBRH 2016, 21, 118–133. [Google Scholar] [CrossRef]
- Gutiérrez, J.V.R. Determinación de las tasas de oxidación, nitrificación y sedimentación en el proceso de autopurificación de un río de montaña. Rev. Chil. Ing. 2016, 24, 314–326. [Google Scholar] [CrossRef]
- Jaramillo, M.F.; Cardona-Zea, D.A.; Galvis, A. Reutilización de las aguas residuales municipales como estrategia de prevención y control de la contaminación hídrica. Caso de estudio: Cuencas de los ríos Bolo y Frayle (Colombia). Ing. Y Compet. 2020, 22. [Google Scholar] [CrossRef]
- Rivera-Gutiérrez, J.V. Evaluación de la cinética de oxidación y remoción de materia orgánica en la autopurificación de un río de montaña. Dyna 2015, 82, 183–193. [Google Scholar]
- Asadisharif, E.; Namin, J.I.; Taheriyoun, M. Biomonitoring, simulation, and evaluation of anthropogenic pollution in Disam River, Iran: Use of macroinvertebrate-based biotic indices and Qual2kw model. Biologia 2023, 79, 775–789. [Google Scholar] [CrossRef]
- De Menezes, J.P.C.; Bittencourt, R.P.; De Sá Farias, M.; Bello, I.P.; De Oliveira, L.F.C.; Fia, R. Deoxygenation rate, reaeration and potential for self-purification of a small tropical urban stream. Rev. Ambiente Água 2015, 10, 748–757. [Google Scholar] [CrossRef][Green Version]
- Han, S.; Yu, X.; Zhang, W.; Sang, G.; Liu, Y.; Xu, S. Rationality Research on Pumping Station Location Based on MIKE Model: A Case Study of the Wanfu River Re-Navigation Project. Water 2023, 15, 4207. [Google Scholar] [CrossRef]
- Zhalmagambetova, U.; Assanov, D.; Neftissov, A.; Biloshchytskyi, A.; Radelyuk, I. Implications of water quality index and multivariate statistics for improved environmental regulation in the Irtysh River Basin (Kazakhstan). Water 2024, 16, 2203. [Google Scholar] [CrossRef]
- Mamani Larico, A.J.; Zúñiga Medina, S.A. Application of WASP model for assessment of water quality for eutrophication control for a reservoir in the Peruvian Andes. Lakes Reserv. 2019, 24, 37–47. [Google Scholar] [CrossRef]
- López, I.D.; Figueroa, A.; Corrales, J.C. Un mapeo sistemático sobre predicción de calidad del agua mediante técnicas de inteligencia computacional. Rev. Ing. Univ. Medellín 2016, 15, 35–52. [Google Scholar] [CrossRef]
- Arifin, A.; Mohamed, R.M.S.R.; Al-Gheethi, A.; Kassim, A.H.M.; Yaakob, M.A. Assessment of household greywater discharge from village houses using Streeter–Phelps model in stream. Desalination Water Treat. 2020, 179, 8–18. [Google Scholar] [CrossRef]
- Tian, L.; Gu, S.; Wu, H.; Meng, Q.; Shao, S. Smoothed particle hydrodynamics for modeling nutrient transport in shallow lakes. Results Eng. 2025, 28, 106944. [Google Scholar] [CrossRef]
- Yavuz, V.S. Impact of temperature and flow rate on oxygen dynamics and water quality in major Turkish rivers. Sci. Rep. 2025, 15, 22830. [Google Scholar] [CrossRef]
- Sridharan, V.K.; Quinn, N.W.T.; Kumar, S.; McCutcheon, S.C.; Ahmadisharaf, E.; Fang, X.; Zhang, H.X.; Parker, A. Selecting reliable models for total maximum daily load development: Holistic protocol. J. Hydrol. Eng. 2021, 26, 04021031. [Google Scholar] [CrossRef]
- Ejigu, M.T. Overview of water quality modeling. Cogent Eng. 2021, 8, 1891711. [Google Scholar] [CrossRef]
- Fernandez, N.; Camacho, L.A. Water quality modeling in headwater catchments: Comprehensive data assessment, model development and simulation of scenarios. Water 2023, 15, 868. [Google Scholar] [CrossRef]
- Slaughter, A.R.; Hughes, D.A.; Retief, D.C.H.; Mantel, S.K. A management-oriented water quality model for data scarce catchments. Environ. Model. Softw. Environ. Data News 2017, 97, 93–111. [Google Scholar] [CrossRef]
- Salila, E.; Sharma, M.P.; Singh, R. Climate change impacts on water quality of water bodies-A review. Int. J. Environ. Clim. Change 2020, 10, 26–37. [Google Scholar] [CrossRef]
- Dorado-Guerra, D.Y.; Paredes-Arquiola, J.; Pérez-Martín, M.Á.; Corzo-Pérez, G.; Ríos-Rojas, L. Effect of climate change on the water quality of Mediterranean rivers and alternatives to improve its status. J. Environ. Manag. 2023, 348, 119069. [Google Scholar] [CrossRef]
- Hosseini, N.; Johnston, J.; Lindenschmidt, K.-E. Impacts of climate change on the water quality of a regulated Prairie River. Water 2017, 9, 199. [Google Scholar] [CrossRef]
- Mendivil-García, K.; Amabilis-Sosa, L.E.; Salinas-Juárez, M.G.; Pat-Espadas, A.; Rodríguez-Mata, A.E.; Figueroa-Pérez, M.G.; Roé-Sosa, A. Climate change impact assessment on a tropical river resilience using the Streeter-Phelps dissolved oxygen model. Front. Environ. Sci. 2022, 10, 903046. [Google Scholar] [CrossRef]
- Nwerem, J.O.; Ekere, N.R.; Ibeto, C.N.; Ejikeme, E.M.; Ihedioha, J.N.; Abugu, H.O. Impact of industrial effluent on the self-purification characteristics and oxygen sag level of Ajali River, South east Nigeria. PLoS Water 2025, 4, e0000320. [Google Scholar] [CrossRef]
- Huang, J.; Yin, H.; Chapra, S.; Zhou, Q. Modelling dissolved oxygen depression in an urban river in China. Water 2017, 9, 520. [Google Scholar] [CrossRef]
- Fan, C.; Wang, W.-S.; Liu, K.F.-R.; Yang, T.-M. Sensitivity analysis and water quality modeling of a tidal river using a modified Streeter–Phelps equation with HEC-RAS-calculated hydraulic characteristics. Environ. Model. Assess. 2012, 17, 639–651. [Google Scholar] [CrossRef]
- Quiñones Huatangari, L.; Milla Pino, M.E.; Gamarra Torres, O.A.; Salas López, R.; Bazán Correa, J.F. Empleo del Modelo Streeter-Phelps para estimar el oxígeno disuelto del Río Utcubamba. Ecuadorian Sci. J. 2020, 4, 12–16. [Google Scholar] [CrossRef]
- Yuan, L.; Sinshaw, T.; Forshay, K.J. Review of watershed-scale water quality and Nonpoint Source Pollution models. Geosciences 2020, 10, 25. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Kang, G.; Chu, C.; Qiu, Y.; Xu, Z.; Wang, Y. Comparison of SWAT and GWLF model simulation performance in humid south and semi-arid north of China. Water 2017, 9, 567. [Google Scholar] [CrossRef]
- Das, S.K.; Ahsan, A.; Khan, M.H.R.B.; Yilmaz, A.G.; Ahmed, S.; Imteaz, M.; Tariq, M.A.U.R.; Shafiquzzaman, M.; Ng, A.W.M.; Al-Ansari, N. Calibration, validation and uncertainty analysis of a SWAT water quality model. Appl. Water Sci. 2024, 14, 86. [Google Scholar] [CrossRef]
- Darji, J.; Lodha, P. QUAL2Kw—A water quality modeling tool for rivers and streams: A review. Int. J. Sci. Technol. 2025, 16, 1–17. [Google Scholar] [CrossRef]
- Asresu, A.T.; Furlan, E.; Horneman, F.; Zennaro, F.; Nguyen, N.D.; Torresan, S.; Critto, A.; Marcomini, A. A systematic review of climate change impacts on water quality in transitional environments from a multi-hazard perspective. Estuar. Coast. Shelf Sci. 2025, 317, 109194. [Google Scholar] [CrossRef]
- Terry, J.; Lindenschmidt, K.-E. Modelling climate change and water quality in the Canadian Prairies using loosely coupled WASP and CE-QUAL-W2. Water 2023, 15, 3192. [Google Scholar] [CrossRef]
- Gil-García, L.; Montilla-López, N.M.; Gutiérrez-Martín, C.; Sánchez-Daniel, Á.; Saiz-Santiago, P.; Polanco-Martínez, J.M.; Pindado, J.; Pérez-Blanco, C.D. Actionable human–water system modelling under uncertainty. Hydrol. Earth Syst. Sci. 2024, 28, 4501–4520. [Google Scholar] [CrossRef]
- Hellweger, F.L. 100 years since Streeter and Phelps: It is time to update the biology in our water quality models. Environ. Sci. Technol. 2015, 49, 6372–6373. [Google Scholar] [CrossRef]
- Brum, M.; Fan, F.M.; Salla, M.R.; von Sperling, M. Analysis of a probabilistic approach for modelling and assessment of the water quality of rivers. J. Hydroinformatics 2022, 24, 783–797. [Google Scholar] [CrossRef]
- Gomides, C.E.; de Matos, M.P.; Fia, R.; Fonseca, A.R. Deterministic and probabilistic modeling of microbiological quality using the QUAL-UFMG: A water resource management tool applied on the slope waters of the Grande River, Brazil. Water Sci. Technol. A J. Int. Assoc. Water Pollut. Res. 2023, 87, 2020–2042. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Zhu, X.; Xi, W.; Pan, H.; Yao, H.; Du, Y. Purification capacity of natural biofilms and their physiochemical and biological properties: A case study in the Jishan River, a heavily polluted river. Water Sci. Technol. Water Supply 2023, 23, 1611–1625. [Google Scholar] [CrossRef]
- Cheng, S.; Meng, F.; Wang, Y.; Zhang, J.; Zhang, L. The potential linkage between sediment oxygen demand and microbes and its contribution to the dissolved oxygen depletion in the Gan River. Front. Microbiol. 2024, 15, 1413447. [Google Scholar] [CrossRef]
- Huang, J.; Borchardt, D.; Rode, M. How do inorganic nitrogen processing pathways change quantitatively at daily, seasonal, and multiannual scales in a large agricultural stream? Hydrol. Earth Syst. Sci. 2022, 26, 5817–5833. [Google Scholar] [CrossRef]
- Sarkar, A.; Pandey, P. River water quality modelling using artificial neural network technique. Aquat. Procedia 2015, 4, 1070–1077. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A review of the artificial neural network models for water quality prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Isık, H.; Akkan, T. Water quality assessment with artificial neural network models: Performance comparison between SMN, MLP and PS-ANN methodologies. Arab. J. Sci. Eng. 2025, 50, 369–387. [Google Scholar] [CrossRef]
- Lindenschmidt, K.-E.; Carr, M.; Lindenschmidt, K.-E.; Carr, M. Geospatial Modeling of River Systems. Water 2018, 10, 282. [Google Scholar] [CrossRef]
- Wang, K.; Liu, L.; Ben, X.; Jin, D.; Zhu, Y.; Wang, F. Hybrid deep learning based prediction for water quality of plain watershed. Environ. Res. 2024, 262 Pt 2, 119911. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, Y.; Wei, Q.; Yin, H. A hybrid deep learning approach to improve real-time effluent quality prediction in Wastewater treatment plant. Water Res. 2024, 250, 121092. [Google Scholar] [CrossRef]
- Santos Santos, T.F.; Camacho, L.A. An integrated water quality model to support multiscale decisions in a highly altered catchment. Water 2022, 14, 374. [Google Scholar] [CrossRef]
- Herzog, S.P.; Ward, A.S.; Wondzell, S.M. Multiscale feature-feature interactions control patterns of hyporheic Exchange in a simulated headwater mountain stream. Water Resour. Res. 2019, 55, 10976–10992. [Google Scholar] [CrossRef]
- Mimouni, E.-A.; Ridal, J.J.; Skufca, J.D.; Twiss, M.R. A multiscale approach to water quality variables in a river ecosystem. Ecosphere 2020, 11, e03014. [Google Scholar] [CrossRef]
- Beck, M.W.; de Valpine, P.; Murphy, R.; Wren, I.; Chelsky, A.; Foley, M.; Senn, D.B. Multi-scale trend analysis of water quality using error propagation of generalized additive models. Sci. Total Environ. 2022, 802, 149927. [Google Scholar] [CrossRef] [PubMed]
- Pratiwi, D.; Sumiarsa, D.; Oktavia, D.; Sunardi, S. Water quality influences self-purification in the Cihawuk and Majalaya segments upstream of the Citarum River, West Java, Indonesia. Water 2023, 15, 2998. [Google Scholar] [CrossRef]
- Nascimento, J.R.; dos Santos, J.F.; Pinha, G.D.; de Barros Cabral, J.; Simões, N.R. Influence of aquatic biodiversity on the self-purification of tropical rivers. Ecol. Eng. 2025, 212, 107540. [Google Scholar] [CrossRef]
- Varadharajan, C.; Appling, A.P.; Arora, B.; Christianson, D.S.; Hendrix, V.C.; Kumar, V.; Lima, A.R.; Müller, J.; Oliver, S.; Ombadi, M.; et al. Can machine learning accelerate process understanding and decision-relevant predictions of river water quality? Hydrol. Process. 2022, 36, e14565. [Google Scholar] [CrossRef]
- Buonocore, C.; Gomiz Pascual, J.J.; Pérez Cayeiro, M.L.; Mañanes Salinas, R.; Bruno Mejías, M. Modelling the impacts of climate and land use changes on water quality in the Guadiana basin and the adjacent coastal area. Sci. Total Environ. 2021, 776, 146034. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, P.; Han, Y.; Chang, X.; Dai, S. Quantitative analysis of self-purification capacity of non-point source pollutants in watersheds based on SWAT model. Ecol. Indic. 2022, 143, 109425. [Google Scholar] [CrossRef]
- Chatrabhuj Meshram, K.; Mishra, U.; Omar, P.J. Integration of remote sensing data and GIS technologies in river management system. Discov. Geosci. 2024, 2, 67. [Google Scholar] [CrossRef]
- Mustamin, M.R.; Maricar, F.; Lopa, R.T.; Karamma, R. Integration of UH SUH, HEC-RAS, and GIS in flood mitigation with flood forecasting and early warning system for Gilireng watershed, Indonesia. Earth 2024, 5, 274–293. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016, 52, 3599–3622. [Google Scholar] [CrossRef]
- Babamiri, O.; Vanaei, A.; Guo, X.; Wu, P.; Richter, A.; Ng, K.T.W. Numerical Simulation of Water Quality and Self-Purification in a Mountainous River Using QUAL2KW. J. Environ. Inform. 2021, 37, 26–35. [Google Scholar] [CrossRef]
- Salla, M.R.; Fernandes, L.E.; Pereira, C.E.; Silva, H.C.D.; Lima, G.D. Importance of calibration for mathematical modeling of self-purification of lotic environments. Acta Limnol. Bras. 2016, 28, e27. [Google Scholar] [CrossRef]
- Manfreda, S.; Miglino, D.; Saddi, K.C.; Jomaa, S.; Eltner, A.; Perks, M.; Rode, M. Advancing river monitoring using image-based techniques: Challenges and opportunities. Hydrol. Sci. J. 2024, 69, 657–677. [Google Scholar] [CrossRef]
- Jackson-Blake, L.A.; Sample, J.E.; Wade, A.J.; Helliwell, R.C.; Skeffington, R.A. Are our dynamic water quality models too complex? A comparison of a new parsimonious phosphorus model, SimplyP, and INCA-P: OVER-COMPLEXITY IN WATER QUALITY MODELS. Water Resour. Res. 2017, 53, 5382–5399. [Google Scholar] [CrossRef]
- Ishikawa, M.; Gonzalez, W.; Golyjeswski, O.; Sales, G.; Rigotti, J.A.; Bleninger, T.; Mannich, M.; Lorke, A. Effects of dimensionality on the performance of hydrodynamic models for stratified lakes and reservoirs. Geosci. Model Dev. 2022, 15, 2197–2220. [Google Scholar] [CrossRef]
- Man, X.; Lei, C.; Carey, C.C.; Little, J.C. Relative performance of 1-D versus 3-D hydrodynamic, water-quality models for predicting water temperature and oxygen in a shallow, eutrophic, managed reservoir. Water 2021, 13, 88. [Google Scholar] [CrossRef]
- Abdi, B.; Bozorg-Haddad, O.; Chu, X. Uncertainty analysis of model inputs in riverine water temperature simulations. Sci. Rep. 2021, 11, 19908. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Fu, W. Utilizing the Sobol’ sensitivity analysis method to address the multi-objective operation model of reservoirs. Water 2023, 15, 3795. [Google Scholar] [CrossRef]
- Del Castillo, A.F.; Garibay, M.V.; Díaz-Vázquez, D.; Yebra-Montes, C.; Brown, L.E.; Johnson, A.; Garcia-Gonzalez, A.; Gradilla-Hernández, M.S. Improving river water quality prediction with hybrid machine learning and temporal analysis. Ecol. Inform. 2024, 82, 102655. [Google Scholar] [CrossRef]
- Obin, N.; Tao, H.; Ge, F.; Liu, X. Research on water quality simulation and water environmental capacity in Lushui River based on WASP model. Water 2021, 13, 2819. [Google Scholar] [CrossRef]
- Rozemeijer, J.; Jordan, P.; Hooijboer, A.; Kronvang, B.; Glendell, M.; Hensley, R.; Rinke, K.; Stutter, M.; Bieroza, M.; Turner, R.; et al. Best practice in high-frequency water quality monitoring for improved management and assessment; a novel decision workflow. Environ. Monit. Assess. 2025, 197, 353. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A review of the application of machine learning in water quality evaluation. Eco-Environ. Health 2022, 1, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Nugraha, W.D.; Sarminingsih, A.; Alfisya, B. The study of self purification capacity based on biological oxygen demand (BOD) and dissolved oxygen (DO) parameters. IOP Conf. Ser. Earth Environ. Sci. 2020, 448, 012105. [Google Scholar] [CrossRef]
- Bui, H.; Ha, N.H.; Nguyen, T.N.D.; Nguyen, A.T.; Pham, T.T.H.; Kandasamy, J.; Nguyen, T.V. Integration of SWAT and QUAL2K for water quality modeling in a data scarce basin of Cau River basin in Vietnam. Ecohidrología E Hidrobiol. 2019, 19, 210–223. [Google Scholar] [CrossRef]
- Nguyen TTy Willems, P. The Influence of Model Structure Uncertainty on Water Quality Assessment. Gestión De Recur. Hídricos 2016, 30, 1567–1584. [Google Scholar] [CrossRef]
- Milišić, H.; Hadžić, E.; Šuvalija, S. Modeling of Water Self-purification in Rivers. In Advanced Technologies, Systems, and Applications VII; Springer: Berlin/Heidelberg, Germany, 2022; pp. 197–228. [Google Scholar] [CrossRef]
- Almeida, M.; Coelho, P.; Almeida, M.; Coelho, P. Evaluating the performance of CE-QUAL-W2 version 4.5 sediment diagenesis model. Geosci. Model Dev. 2022, 18, 6135–6165. [Google Scholar] [CrossRef]
- Kim, S.; Park, Y. An improved model for water quality management accounting for the spatiotemporal benthic flux rate. Water 2023, 15, 2219. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, T. Recalibration of a three-dimensional water quality model with a newly developed autocalibration toolkit (EFDC-ACT v1.0.0): How much improvement will be achieved with a wider hydrological variability? Geosci. Model Dev. 2023, 16, 4315–4329. [Google Scholar] [CrossRef]
- Novita, E.; Setyono, P.; Setiyo Rini, T.; Andriyani, I.; Andiananta Pradana, H.; Verynikaningrum, V. Water quality assessment in the Bedadung River using self-purification optimisation and water quality allocation in Indonesia. J. Water Land Dev. 2024, 71–78. [Google Scholar] [CrossRef]
- Masi, M.; Masseroni, D.; Castelli, F. Coupled hydrologic, hydraulic, and surface water quality models for pollution management in urban–rural areas. J. Hydrol. 2025, 657, 133172. [Google Scholar] [CrossRef]
- Fenocchi, A.; Pella, N.; Copetti, D.; Buzzi, F.; Magni, D.; Salmaso, N.; Dresti, C. Use of process-based coupled ecological-hydrodynamic models to support lake water ecosystem service protection planning at the regional scale. J. Contam. Hydrol. 2025, 268, 104469. [Google Scholar] [CrossRef] [PubMed]
- Nong, X.; He, Y.; Chen, L.; Wei, J. Machine learning-based evolution of water quality prediction model: An integrated robust framework for comparative application on periodic return and jitter data. Environ. Pollut. 2025, 369, 125834. [Google Scholar] [CrossRef] [PubMed]
- Anand, V.; Oinam, B.; Wieprecht, S. Machine learning approach for water quality predictions based on multispectral satellite imageries. Ecol. Inform. 2024, 84, 102868. [Google Scholar] [CrossRef]
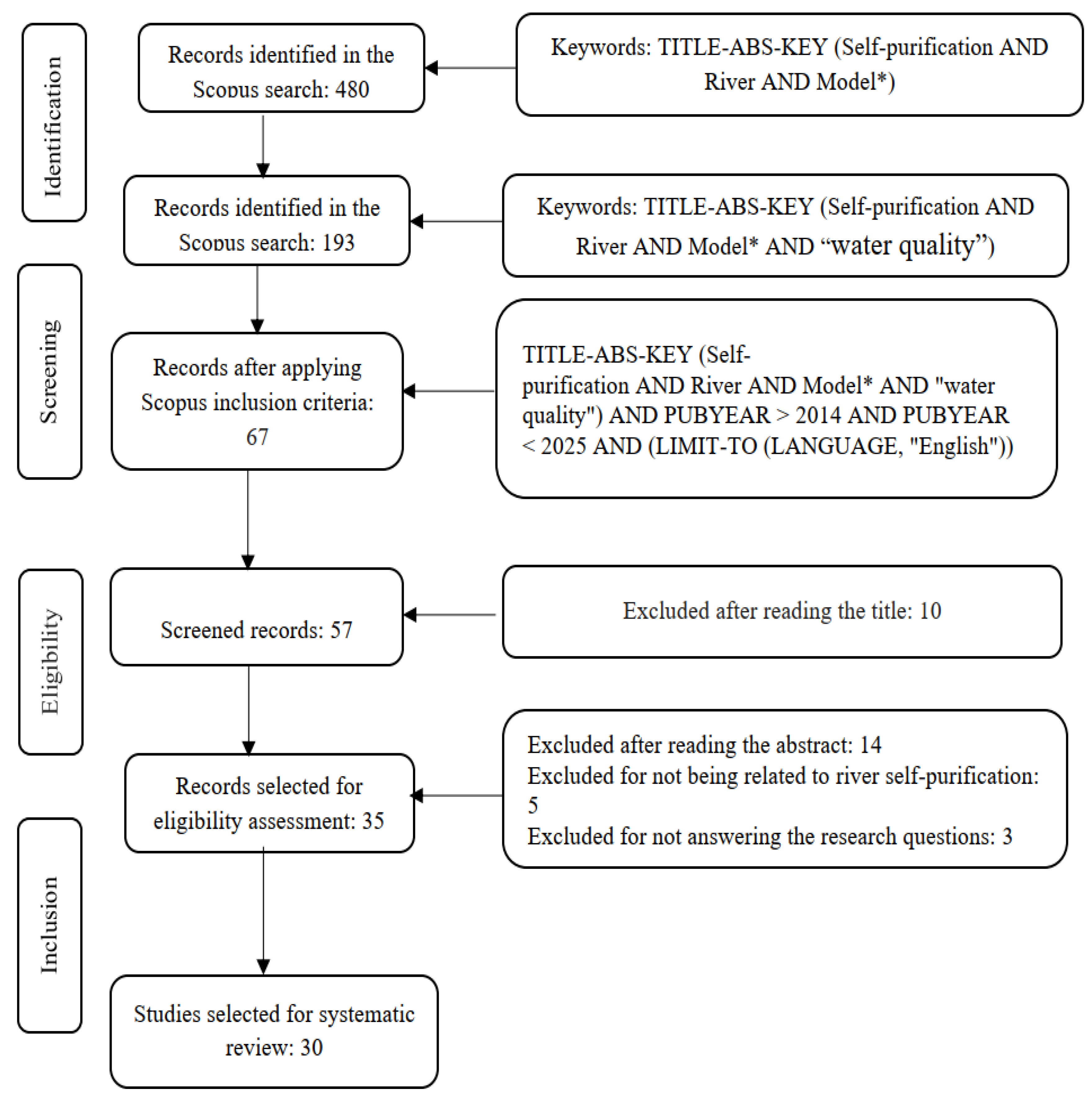

| Population/Problem | Pollution of rivers that affect water quality |
| Intervention | Application of models to analyze the self-purification of rivers |
| Comparison | Analysis of different river self-purification models |
| Outcomes | Determination of the most effective self-purification models, and their applicability in the restoration of water quality in rivers |
| Model | Variables | Category | Evaluation Method | Calibration | Model Robustness | Reference |
|---|---|---|---|---|---|---|
| QUAL-UFMG | BOD5, DO, Total nitrogen and its fractions, Total phosphorous and its fractions, Thermotolerant coliforms | Biochemistry, Physical chemistry, Chemistry, Microbiology | Coupled differential equations from the QUAL equations family, Microsoft Excel spreadsheet simulation. | The associated coefficients to the DO and BOD5 variables, as well as the organic matter decomposition coefficient are manually calibrated in this model. The calibration method consists of varying the coefficients until obtaining the minimum sum of squares through a process that integrates a database of observed and modeled data, making the determination of the coefficient more precise. Coefficient values described in the literature are equally considered as in Pani et al. [28] or in Da Luz et al. [63]. | High, as long as it is applied in tropical zones and according to the calculation of the coefficients for their appropriate calibration. | [28,63,71,73] |
| QUAL2K | pH, Temperature, Sedimentable solids, BOD5, DO, Electrical conductivity, Nitrogen (organic, ammoniacal, nitric), Phosphorous (organic, inorganic) | Physics, Biochemistry, Physical chemistry, Chemistry | Mass balance using differential equations; specific parameter analysis. | For this model, calibration is performed on the constants associated with the main variables (DO, BOD) as well as those associated with chemical and physical variables. The calibration methodology is described as a Montecarlo simulation using the GLUE method based on databases of the considered variables. Calibrations from literature are also taken into account, like Gutiérrez [73] | High, although it depends on the modeling processes and the calibration performed. | [18,65,74,76,77] |
| Streeter-Phelps | DO, BOD5 | Physical chemistry, Biochemistry | Simulates the dynamics of DO and BOD based on natural self-purification processes, including degradation and reoxygenation. | The deoxygenation (k1) and reoxygenation (k2) constants are used. These are obtained from equation calculations proposed by different authors. In De Menezes et al. [78] the equations proposed by von Sperling are used, in Pazmiño-Rodríguez et al. [65] the equations from Owen and Gibbs are used, and in Díaz et al. [64] a statistical approach is taken. | Average since it does not integrate other variables for modeling. | [64,65,78] |
| WASP | DO, BOD5, Nitrogen, Phosphorous, Suspended solids, Pathogens | Physical chemistry, Chemistry, Physics, Microbiology | The dynamic analysis allows the modeling of multiple pollutants and their interactions in water bodies. | In this model, a series of coefficients are considered according to the variables used. It is a more complex model, so only the coefficients for physical variables were calculated, while for the other variables, data were considered from the existing literature. | Average | [67,68] |
| MIKE | Velocity, Flow rate, Water level, Water quality, Sediment transport BOD5, DO, NO3-N, NH4-N, Heavy metals, Coliform bacteria | Physics, Biochemistry, Physical chemistry, Chemistry, Microbiology | 1D, 2D, and 3D detailed simulations based on advanced numerical methods. | More general coefficients are considered for each variable, they can be summarized in the diffuse convection coefficient and the matter attenuation coefficient. These are usually extracted from existing literature. For hydraulic variables, the most relevant coefficient is the Manning coefficient. | High, due to the integration of multiple modules that allow a more complete modeling. | [69,79] |
| Model | Advantages | Disadvantages |
|---|---|---|
| QUAL -UFMG | Model mostly used in Brazil for its adaptation to tropical conditions [71]. | Limited for tropical conditions, so its accuracy will be less effective in other climates [71]. |
| DO and BOD5 parameters have the greatest presence in most of the literature and studies reviewed. These 2 parameters are considered key evaluation parameters [28,62,63,71,72,73] | According to the work of Da Luz et al. [63], for the DO calibration a good data fit was shown, but this was not the case for BOD5. This adjustment was presented due to the fact that real conditions in which effluents are discharged are unknown. | |
| The QUAL-UFMG excel platform provided by this model is an easy-to-use and highly productive tool for modeling water quality. It is a bidimensional model [28,53,54,62,63,64]. | The discharge of pollutant loads in a water body has to be analyzed with much caution because misinterpreted data and incorrect results compromise predominant applications [63]. | |
| The model reproduces physical, chemical, and biological processes, considering point and diffuse inputs of pollutant loads, as well as point extractions, both consumptive and non-consumptive [62,72]. | ||
| QUAL2K | The QUAL2K model complies with the study of the behavior of water quality of surface sources. Its simulation determines the behavior of the pollutant quality in a certain time for a specific section [18,65,74,75,76,77] | If the model uses variables such as nitrogen or phosphorous, it can extend to problems with these pollutants. Also, it presents significant challenges due to the quantity of detailed data that is required, which is why the information is often very limited [18]. |
| QUAL2K can estimate and simulate an unknown location of the pollution source, it provides a dynamic and accurate estimation of the following factors: TEM, EC, pH, DO, and BOD5 [76]. | Many times the behavior of variables in the section studied may tend to underestimate in this case the concentration of DO [18]. | |
| The QUAL2K model is based on differential equations for unidimensional systems, and a stationary flux. It is an efficient method to simulate water quality and hydrologic conditions in rivers, as well as in systems with diffuse pollutant loads [77]. | The adjustment to the QUAL2K model may be significantly lower [77]. | |
| This model can solve the Streeter–Phelps equation. It makes an analytic expansion for the DO and BOD5 relation. The QUAL2K model is a good approximation for estimating the BOD5 load capacity [18]. | ||
| Streeter-Phelps | It facilitates the development of other advanced numerical models like QUAL-I, II, E, and QUAL-2K. This model describes how oxygen demand decreases in a river over distance due to BOD5 degradation [78]. | It tends to overestimate the DO concentration and the efficiency of atmospheric reaeration in certain sections [65]. |
| The Streeter-Phelps classic model is a reference point in sanitary and environmental engineering, being the precursor of water quality models [64]. | The mass balance of the model is only performed at a specific point, unlike more advanced models that do it throughout the entire section [65]. | |
| It is a simple and useful model to evaluate water quality in rivers, even with limited data. It achieves a good fit in dissolved oxygen simulations with a high coefficient of determination and Nash-Sutcliffe index [65]. | It may present an error in the prediction of DO of up to 40% in some cases [65]. | |
| WASP | The WASP model can also be used for operational purposes. With advective and dispersive transport between discrete physical compartments it can be applied in 1D, 2D, or 3D for any type of water [18]. | This model does not determine the extent of the intermediate zone, because the short section of the river covered by the selected model is selected as an analysis example [18]. |
| The WASP model can handle multiple types of pollutants in one single run. It has two kinetic models: advanced toxic transformation and advanced eutrophication [18]. | The WASP model does not have adequate treatment facilities [18]. | |
| Using the model, it is possible to determine the hazards that can be generated by the facilities already present in the watersheds [18]. | ||
| MIKE | This model is responsible for analyzing complex problems with a certain precision [79]. | The specialization level has to be high for its configuration and operation, limiting the use of modeling [69]. |
| Using the water quality module, the MIKE software allows the user to create different templates of pollutant composition, which helps to achieve greater modeling accuracy [79]. | It is limited by license costs and software access, restricting its use [69]. | |
| It is widely used for hydrodynamic analysis, water quality modeling, pollutant migration, and quality improvement [79]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Avila, F.; Sinche-Morales, A.; Sagal-Bustamante, F.; Criollo-Illescas, F.; Valdiviezo-Gonzales, L. Exploring the Potential of Mathematical Self-Purification Models Used for Evaluating Water Quality in Rivers. Earth 2025, 6, 131. https://doi.org/10.3390/earth6040131
García-Avila F, Sinche-Morales A, Sagal-Bustamante F, Criollo-Illescas F, Valdiviezo-Gonzales L. Exploring the Potential of Mathematical Self-Purification Models Used for Evaluating Water Quality in Rivers. Earth. 2025; 6(4):131. https://doi.org/10.3390/earth6040131
Chicago/Turabian StyleGarcía-Avila, Fernando, Andrés Sinche-Morales, Fátima Sagal-Bustamante, Freddy Criollo-Illescas, and Lorgio Valdiviezo-Gonzales. 2025. "Exploring the Potential of Mathematical Self-Purification Models Used for Evaluating Water Quality in Rivers" Earth 6, no. 4: 131. https://doi.org/10.3390/earth6040131
APA StyleGarcía-Avila, F., Sinche-Morales, A., Sagal-Bustamante, F., Criollo-Illescas, F., & Valdiviezo-Gonzales, L. (2025). Exploring the Potential of Mathematical Self-Purification Models Used for Evaluating Water Quality in Rivers. Earth, 6(4), 131. https://doi.org/10.3390/earth6040131






