Abstract
Quantifying land–atmosphere transport remains crucial for advancing climate prediction and weather forecasting efforts. To improve turbulent flux estimation, the anisotropy of turbulence is taken into consideration. The parameters and , which quantify anisotropy degrees across motion scales, form trajectories in the barycentric map. Using the Hilbert–Huang transform, the scale-dependent properties of anisotropy in observational data from multiple sites are investigated. Analysis reveals consistent patterns in the average trajectories across stratification conditions: as scale increases, increases from 0.4 to 0.9, while initially climbs from 0.5 to 0.7 before declining to 0. Meanwhile, individual case trajectories sometimes deviate from this pattern, indicating contamination by non-turbulent motions that typically cause turbulent flux overestimation. Crucially, identifying the scale at which deviations occur allows effective separation of atmospheric turbulence from non-turbulent motions, which enables the reconstruction of turbulence data. Results demonstrate that corrected fluxes reduce overestimation inherent in traditional eddy covariance systems by approximately 30%, with enhancements for CO2 and air pollutants reaching 45–83%. Furthermore, the correlation between anisotropy and stratification suggests potential for refining similarity theories into a broader scope, such as carbon cycle assessment and pollution control. Therefore, anisotropy shows promise in quantifying the land–atmosphere transport.
1. Introduction
The dominant form of land–atmosphere transport is the turbulent flux, which is the primary mechanism for the exchange of energy, heat, greenhouse gases and air pollutants [1,2,3,4,5]. The eddy covariance (EC) system is recognized as the most universal method [6,7,8] to quantify the turbulent flux as the covariance of vertical wind and a second quantity of interest. However, turbulent transport quantification faces significant challenges under non-ideal conditions, in which the heterogeneity of the land surface (e.g., roughness, height, and humidity [9,10,11,12]) and the non-stationary nature of atmospheric conditions [13,14,15,16,17] usually affect the identification and analysis of atmospheric turbulence, causing deviations in the estimation of turbulent fluxes from traditional theories [18].
Extensive studies have confirmed that non-turbulent motions occur across stable and unstable conditions [19,20,21], significantly impacting turbulent transport quantification. While both turbulent and non-turbulent motions are crucial for land–atmosphere transport [15,22,23,24], a key challenge arises: large-scale motions (including coherent turbulence structures) may be redundantly incorporated into turbulence parameterizations within different simulation models focusing on varied scales [25,26,27]. Thus, systematic identification and removal of non-turbulent motions are essential for accurate turbulent transport quantification. Efforts like the cospectral gap [28] and spectral plateau [29] stem from spectral analysis, marking boundaries between turbulent and non-turbulent motions. Advanced techniques such as the Hilbert–Huang Transform [30,31,32] (HHT) and multiresolution decomposition [33,34,35] enhance spectral analysis effectiveness. Methods beyond spectra also exist, like anisotropy analysis for turbulence time scales [36], Eulerian autocorrelation function diagnostics [37], Mexhat-wavelet techniques [38], and amplitude probability distribution algorithms [39]. Nevertheless, significant challenges persist. Non-turbulent (or submesoscale) motions exhibit complex, superimposed, and interactive forms [15,40,41], resisting precise mathematical definition; existing methods often focus mainly on statistical characteristics/effects. Many techniques are also stratification-specific, limiting practical application. Furthermore, accurate material flux estimation (including carbon dioxide and air pollutants such as PM2.5) remains underexplored due to complex transport mechanisms [11,42,43] and demanding observational requirements [44,45,46].
Emerging approaches leveraging novel parameters show promise in addressing these limitations. Examples include aerosol composition-visibility correlations for pollutant density [45,47,48] and fractal dimensions characterizing turbulent flow properties [49,50], highlighting the value of moving beyond traditional spectral analysis by incorporating parameters capturing turbulence’s multiscale nature for robust flux estimation. Herein, anisotropy, a key turbulence characteristic derived from the Reynolds stress tensor and quantified on a 2D barycentric map (BAM) [51], offers significant potential. It influences near-surface similarity theories for atmospheric turbulence properties [52,53]. There is a wealth of studies demonstrating the validity of anisotropy. The anisotropy of flow over two-dimensional rigid dunes proves to deviate from the traditional isotropic hypothesis and demonstrates that anisotropy can reliably represent turbulent properties in numerical models [54]. The return-to-isotropy phenomenon, in which the turbulence kinetic energy (TKE) tends to be equally redistributed at small scales, is also detected and analyzed [55]. The applicability of isotropy is evaluated through simulations of fluidized gas-particle suspensions [56] and the internal gravity wave detection in a stable boundary layer [57]. Introducing anisotropy into scaling relations of atmospheric turbulence is also justified for its potential in generalizing MOST in non-ideal conditions, which is supported by evidence from comprehensive analyses from the aspect of normalized standard deviations [58] and the flux–profile relationships [59]. While anisotropy’s role in scaling is established, few studies focus on the intrinsic connection between anisotropy, fundamental turbulence, and atmospheric boundary-layer (ABL) characteristics. The application for identifying non-turbulent motions and improving flux quantification is limited to single-point observations and lacks further exploration. Thus, examining the scale-dependent properties of anisotropy across diverse conditions holds great promise for revealing new turbulence characteristics, effectively distinguishing non-turbulent motions, and ultimately enhancing turbulent flux quantification.
This study investigates how the application of anisotropy can enhance the land–atmosphere transport estimation through the analysis of dynamic and thermodynamic properties of atmospheric turbulence. The investigation involves exploration of scale-dependent anisotropy properties using observational data from three stations representing diverse underlying surfaces, and the evaluation of the effectiveness of anisotropy incorporation across different stratification conditions. Section 2 introduces the observational sites and data, together with the data processing approaches. Section 3 describes the methods for investigating the scale-dependent properties of atmospheric turbulence. Section 4 applies anisotropy to provide criteria for distinguishing non-turbulent motions and correcting turbulent fluxes. Section 5 summarizes the methods, conclusions, and discussions of the study, exploring the application prospects of anisotropy.
2. Data
2.1. Observational Site
To investigate the effectiveness of anisotropy in reflecting characteristics of atmospheric turbulence, the data are selected from multiple observational sites across different underlying surfaces and in different seasons.
The 255 m meteorological tower in Tianjin () is located in the PBL Meteorological Observation Station, Tianjin Meteorological Administration, which is representative of the typical urban landscape with profound anthropogenic influences. Turbulent data are acquired from sonic anemometers (CSAT-3, Campbell Scientific, Inc., Logan, UT, USA) from the meteorological tower at 80 m orienting towards East, which can provide the three-dimensional wind speed and the sonic temperature data. Fast-response observations of gases are conducted with the Open Path CO2/H2O Analyzer (LI-7500, LI-COR, Inc., Lincoln, NE, USA) installed at 80 m, providing density time series of CO2 and water vapor. The sampling frequencies of the instruments above are all 10 Hz. There are also observations of mean wind speed (Cup and vane anemometer, Changchun Meteorological Instrument Ltd., Changchun, China) and mean temperature and humidity (HMP45C, Campbell Scientific, Inc., Logan, UT, USA) at a total of 15 levels. The gradient data are calculated as the averaged finite difference in the mean variables from 5 levels, from 40 m to 120 m. The observational data were collected from 1 July to 31 August 2017. There is more information about the Tianjin Station [60,61].
The Naiman station is located in Horqin Sandy Land () in the Naiman County of Inner Mongolia. The underlying surface is nearly flat and homogeneous, consisting mainly of sandy land with low and open shrubs, which is typical of a semiarid continental monsoon climate, and there are few anthropogenic activities. The sonic anemometers and Open Path CO2/H2O Analyzer are the same as Tianjin Station at 8 m, orienting towards the west, with the same sampling frequencies of 10 Hz. The mean wind speed (010C, MetOne Instruments Inc., Grants Pass, OR, USA), air temperature, and humidity (HMP45C, Campbell Scientific, Inc., Logan, UT, USA) are observed at four levels from 2 to 20 m. The gradient data are obtained from the finite difference between the two levels of 4 m and 16 m. The observational data were collected from 1 July to 31 July 2022. More information concerning the Naiman station can be found in references [62,63].
The Dezhou station is located at the Pingyuan County Meteorological Bureau () in Shandong Province. The underlying surface is typical flat farmland in the North China Plain. The station is equipped with a set of instruments at a height of 2.8 m, including a three-dimensional sonic anemometer (IRGASON, Campbell Scientific, Inc., Logan, UT, USA) orienting towards North, and a continuous particle measuring instrument, E-sampler (Met One, Inc., Grants Pass, OR, USA). The sampling frequency of wind speed is 10 Hz, and that of PM2.5 density is 1 Hz. The gradient data is acquired from a near-surface observation of a GPS low-altitude electronic sonde (XHD-403, Institute of Atmospheric Physics of the Chinese Academy of Sciences). The sonde collects data every 10 m, and the averaged finite difference within 100 m from the land surface is calculated as the gradient of each meteorological parameter. Observations are repeated every 3 h from 27 December 2018 to 24 January 2019, and the data are interpolated to match the sampling frequency of other instruments. There is a comprehensive introduction on the Dezhou station and the methodology of the measurement of PM2.5 density [45].
The comparison among the three observational stations is given in Table 1, and their locations are shown in Figure 1.

Table 1.
Comparison of the conditions around different observational stations.
Figure 1.
The location of 3 observational stations from Google Earth.
2.2. Data Processing
The raw turbulence observational data were pre-processed using the EddyPro software (ver. Advanced 7.0.9, LI-COR Biosciences, Inc., Lincoln, NE, USA), including error flags, despiking [10], double coordinate rotation [64], and linear detrending. The turbulent fluxes are also corrected to eliminate the influence of tilt, time lag, and WPL terms within the software and the following reconstructions. The averaging time span for Naiman and Dezhou is 30 min following the standardized calculation of EddyPro. To address non-stationarity arising from complex conditions at the Tianjin station, the averaging time span is set to 1 hr. This extended duration better captures large-scale turbulence components, notably coherent structures, while enabling comparative analysis of varying averaging spans across heights and observational sites to strengthen result robustness. The calculations in the following sections use the same time spans.
From the observational data, several important scales and parameters can be defined: The Obukhov Length is
where is the von Kármán constant, is the numerical value of gravitational acceleration, and is the average potential temperature. is called the friction velocity, which is a characteristic scale of the turbulent wind stress generated by surface friction. The definition of sensible heat flux , momentum flux , latent heat flux , and turbulent flux of specific materials are defined as follows:
where and are the air density and specific heat capacity at constant pressure; is the latent heat, is the concentration of water vapor, and is the density of a certain kind of material. To ensure data quality for anisotropy evaluation, the data where the angle between the wind direction and the sensing probe axis exceeded ±120° were excluded. This threshold minimizes errors associated with flow distortion and acoustic shadowing inherent to sonic anemometry at extreme angles. The other criteria in the standard EC system, such as the mean wind speed range and the friction velocity , are NOT applied to ensure the inclusion of properties that could be reflected by anisotropy.
3. Methods
3.1. Hilbert–Huang Transform (HHT)
The HHT effectively analyzes nonlinear and non-stationary atmospheric turbulence by adaptively decomposing signals while isolating non-ideal components as residuals [30,65]. Through Empirical Mode Decomposition (EMD), the original signal separates into components spanning distinct frequency ranges, enabling scale-specific characterization. Low-index IMFs (small ) capture high-frequency, small-scale motions, whereas high-index IMFs (large ) represent low-frequency, large-scale phenomena. The residual , being monotonic or having at most one extremum, embodies the non-oscillatory trend. The multivariate EMD extension further processes combined signals (e.g., wind components u, v, w) through redefined local mean calculations [66,67]. Applying the Hilbert transform to each IMF generates an analytical signal with instantaneous amplitude and frequency. Further analysis integrates the joint probability density function to define the arbitrary-order Hilbert marginal spectrum in amplitude-frequency space. The second-order spectrum corresponds to energy density at frequency , sharing the physical significance of the Fourier transform spectrum.
The fundamental steps of the HHT, including the EMD process and the calculation of Hilbert spectra, are detailed in Appendix A.
3.2. Anisotropy and Turbulent Motion
The Reynolds stress tensor characterizes the stress distribution caused by turbulent fluctuations in the fluid flow and is defined as
where are the wind speeds in the directions of prevailing wind, cross wind, and vertical wind. The non-dimensional anisotropy tensor is defined as the normalized subtracting the isotropic components, which holds the definition as
where is the Kronecker delta, and the index appearing twice in a single term follows the Einstein summation notation. From the three eigenvalues of the normalized anisotropy tensor, , , and , and the different states can be depicted graphically through the Barycentric Anisotropy Map (BAM) with respect to the parameters and [51], which is considered in this study from a linearized point of view:
where , , are the weights determined by the Reynolds stress, and , , are the three vertices of a unit equilateral triangle, which corresponds to the different limiting states of turbulence anisotropy.
Figure 2 shows the distribution of the anisotropy of the observational data from three different stations. It reveals that the data from different stations collectively reflect a broad range of atmospheric turbulence conditions. For the data from Tianjin, the complex terrain, weather, and anthropogenic conditions cause the anisotropy to be widely distributed in the BAM, revealing both idealized and extreme cases. Furthermore, multiple strongly unstable conditions are observed, in which the turbulence is fully developed and reaches the isotropic limit. For the latter two stations, the turbulence is less disturbed as a result of the high homogeneity and minimal change in characteristics of the underlying surface, and the anisotropy concentrates around specific areas in the BAM. Specifically, in Dezhou, there are more stable cases, the horizontal motions are driven by the dominant wind, with vertical motions constrained by the near-surface inversion layer. Therefore, the turbulence is highly anisotropic, as reflected by the scatters at the bottom of BAM in Figure 2c,f. It can be observed that has positive correlations with the absolute value of the stability parameter . There is also a strong positive correlation between and , especially in Figure 2d, but there are also cases where the correlation becomes weaker or even slightly opposite.
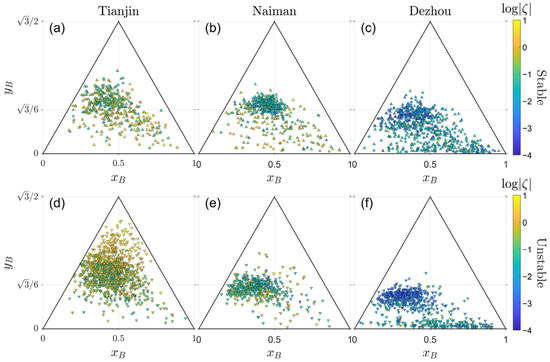
Figure 2.
The barycentric map of the observational data, with three columns representing different stations. The first row (a–c) represents stable conditions, and the second row (d–f) represents unstable conditions. The color of the points reflects the logarithm of stability parameter with base 10.
Incorporating the multivariate EMD process in Section 3.1, the anisotropy of each IMF can also be analyzed to reveal a comprehensive view of different scales. The analysis at different scales can be applied in two ways:
- (1)
- By calculating the anisotropy of each IMF. Note the kth IMF of the wind speed component as
The non-dimensional anisotropy tensor of the kth IMF can be defined by
The eigenvalues and parameters and of the kth IMF are calculated accordingly, yielding the trajectory.
- (2)
- By superimposing the IMFs of the signal from high frequencies to low frequencies (namely from small to large scale), the superimposed signal from 1st to kth IMF is given by
The anisotropy tensor, eigenvalues, and the parameters and are calculated the same way as the 1st way, and are denoted as the superimposed trajectory. The residuals are not considered as they correspond with motions around Hz, which typically fall beyond the energy-containing eddies of atmospheric turbulence.
To separate and retrieve the turbulence signal from the data series, the upper limit scale of turbulence can be evaluated by an anisotropy analysis in the frequency domain [39]. Technically, atmospheric turbulence and non-turbulent motions typically differ in scale and can be distinguished using several criteria [20,39]. Non-turbulent motions generally exhibit a lower frequency of motion. In such cases, a boundary frequency, , can be proposed to mark the transition between turbulent transport and other forms of transport. In this study, the boundary frequency is determined using the properties of anisotropy, given that all turbulent transport is closely related to the dynamics of atmospheric turbulence. The time series can then be expressed as
where contains the signal with frequencies higher than , and contains the signal with frequencies lower than . Note the number of IMF with a frequency closest to as . These two kinds of signals can be calculated as
In this way, the turbulence data is reconstructed as , and all the turbulent fluxes calculated by Equations (2)–(5) should be replaced with the reconstructed turbulent variables to eliminate other forms of transport.
4. Results
4.1. Scale-Dependent Properties of Anisotropy
Figure 3 illustrates the changes in anisotropy properties with the scale of motions through the parameters and calculated from different IMFs across the averaging time span (introduced in Section 2.2), and data from all three observational stations are used for the general analysis. Each trajectory in Figure 3a,c,e,g corresponds to the average changing pattern of anisotropy with frequency in a specific range of stratification conditions. The trajectories in Figure 3a,e represent the trajectory calculated from the shift in single IMFs, while the ones in Figure 3c,g represent the superimposed IMFs. As shown in Figure 3a,e, under different stratification conditions, the trajectory follows a regular pattern:
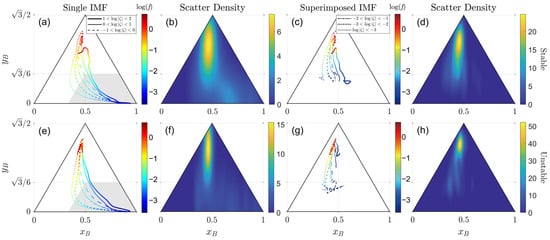
Figure 3.
Scale-dependent anisotropy trajectories (single IMFs: (a,b,e,f); superimposed IMFs: (c,d,g,h)) and parameter density distributions in the BAM under stable (a–d) and unstable (e–h) conditions. Trajectory color indicates motion scale (logarithm of frequency with base 10); line type indicates stability parameter () range. The line types for (a,c,e,g) are consistent.
- (1)
- From small scale to large scale, the initially remains constant around 0.4 to 0.5. When the average frequency of motions decreases below , the starts to increase rapidly, reaching up to 0.8 to 0.9.
- (2)
- From small scale to large scale, the initially increases slightly from 0.6 to 0.7 before the average frequency decreases to , and for larger scales (lower frequencies), continues to decrease until it approaches 0.
- (3)
- With the increase in the absolute values of stability parameters, the bending of the trajectory is weakened. The location where the bending occurs is roughly limited in the trapezoidal gray area in Figure 3a,e, which holds the boundary at , , , and .
These findings align with the results of previous studies [55,68], confirming that the atmospheric turbulence approaches isotropy at small scales, and the anisotropy primarily originates from larger-scale motions. The comparable anisotropy patterns in Figure 3a,e implicates minimal variations between unstable and stable stratification conditions [55]. The fluctuation of near the small-scale ends exist for most trajectories, which can be attributed to the loss of accuracy of high-frequency observations and the decomposition of signals. However, in extremely stable conditions, the end of the trajectory appears away from the isotropic limit, implying that in stable boundary layers, the development of turbulence becomes non-Kolmogorov where local isotropy is not achieved [69,70]. It can be observed from the differentiated lines within the same panels that for different ranges of the absolute value of the stability parameter the difference in the bending of trajectory is revealed, which originates from different physical processes. In near-neutral cases marked by dotted lines, the vertical forcing is limited, and the motions of middle scales () transition to the axisymmetric two-component state near the left-bottom vertex of BAM, before bending to the one-component limit (right-bottom vertex) with the dominant parameter following the dominant wind speed. On the contrary, under extreme conditions (), turbulence dynamics become vertically dominated in two opposing regimes, both resulting in the weakened bending in the middle of the trajectory. For strongly unstable cases, the enhanced vertical forcing and efficient vertical mixing lead to the balanced distribution of the Reynolds stress tensor. In this situation, both the TKE and the covariances of wind speed are similar, with less dominant or minor values favoring the two-component state (in the direction of bending). For strongly stable cases, the turbulence generation is mechanically weakened for a considerable time, resulting in both minimal horizontal and vertical winds with frequent turbulent intermittency. In this situation, the distribution of the Reynolds stress tensor is also balanced, making the two-component state also no longer favored. The above discussion can be corroborated from the overall density distribution shown in Figure 3b,f. There are high-density areas in the upper-middle of the BAM, indicating the high importance of the parameter. However, considering the anisotropy properties at larger scales, the parameter may also be significant. Between the frequency range and , the change in is faster than that in , suggesting its potential relevance.
Figure 3c,d,g,h depict the changes in the superimposed anisotropy properties, which are similar to Figure 3a,b; however, each point on the trajectories corresponds to the superimposition of IMFs, starting from the smallest scale. The main physical difference between trajectory and the superimposed trajectory is that the former decomposes and reveals the anisotropy properties of the motion within specific scales, while the latter visualizes the anisotropy as an aggregation of a certain scale together with all the smaller scales. As shown in Figure 3c,g, in most cases, the changing patterns of the trajectory of parameters and from superimposed IMFs reveal similar information to that from a single IMF. However, the differentiation in the converging points allows for more conclusions to be drawn. The superimposition of IMFs results in the trajectory reaching the center of the BAM, rather than the bottom, which indicates a transition from isotropic to a balanced state the three limiting states contribute equally. However, the convergence points for the large-scale end of the superimposed trajectory are highly dependent on the stratification condition. In stable conditions, the final of the trajectories are close, while the shows an increasing trend with the increase of , making the cluster of trajectories resemble branches away from the small-scale isotropic end and towards the 1-component limit [57,70]. In contrast, both the final and increase together with , indicating that the more unstable the stratification is, the turbulence becomes closer to isotropic. These properties shape the overall density distribution, as Figure 3d,h. The change in anisotropy in the superimposed trajectory is more influenced by the parameter for small-scale motions, which explains the prominence of in previous studies [58,59]. However, it can be judged by all the results in Figure 3 that also plays an important role, especially for larger scales.
The analysis above focuses on the differentiation of anisotropy at large-scale ends. Conversely, from the perspective of the scales from large to small, a return-to-isotropy pattern can also be observed, which is consistent with previous scale-dependent analysis in the BAM [71]. There are also studies concerning both the phenomenon of isotropic turn with the relaxed development of turbulence [72,73,74], and the isotropic transition of the multi-scale turbulence data samples [55,68]. The results in this study reveal a similar transition to isotropic from different anisotropic states of various stratification conditions, providing a novel view that enables the decomposition and reconstruction of turbulence data. Practically, the scale-dependent anisotropy is relevant when examining the properties of motions at a specific scale. Section 3.1 has demonstrated that a high index of IMFs and the residual of EMD correspond to large-scale motions within the observational data, where non-turbulent motions often arise. From the above analysis, the properties of these motions are more accurately reflected through the parameter and dominate the point distribution in BAM. Therefore, analyzing the large-scale ends of trajectories can provide heuristic insights into identifying non-turbulent motions within the observational data.
4.2. Distinguishing Non-Turbulent Motions
Section 4.1 has demonstrated that the anisotropy of atmospheric turbulence is scale-dependent, exhibiting a regular pattern in the trajectory with the shift in IMFs in the BAM. The trapezoidal area introduced in the last section warrants focus due to its -dominant and monotonous characteristics. However, in individual cases, this pattern happens to be violated at IMFs of larger scales, as reflected by outliers from the mean trajectory in the trapezoidal area. In previous studies, the violation of statistical characteristics of atmospheric turbulence tends to be taken as the criterion of the existence of non-turbulent motions, such as the spectral gap [20,75] and the transport properties [39]. To distinguish non-turbulent motions from observed signals, an integrated criterion can be proposed. Note that the trajectory in the trapezoidal area is monotonic for all the conditions (as the left-top boundary marks the bending place of the trajectory), the criterion can be summarized by identifying the violation of the regular pattern through the following steps:
- (1)
- Collect the points violating the monotonicity of within the trapezoidal area.
- (2)
- Collect the points violating the monotonicity of within the trapezoidal area.
- (3)
- Determine whether the collected points are statistical outliers: if they are, the points are kept for the next step; otherwise, they are discarded.
- (4)
- Locate the index of IMFs for these outliers and the average frequencies.
The statistical outliers are defined as values that exceed three times the standard deviation from the local median within a sliding window of 5 points. If more than one point meets the criterion, the one with the highest frequency is considered the boundary between turbulent and non-turbulent motions. If no points satisfy the criterion, the boundary frequency is set to the IMF of the largest scale, and the residual of EMD is considered as the non-turbulent motion. The identification of statistical outliers is determined through established statistical principles such as the three-sigma rule, which aims at avoiding misinterpreting data fluctuations and enhancing the reliability of the algorithm. However, the distribution of anisotropy is not necessarily Gaussian, which requires multiple tests on this criterion. The results have proven that the anisotropy-based algorithm effectively distinguishes the existence of non-turbulent motions from the anomaly of trajectory under different conditions, and Figure 4 presents two typical cases of stable and unstable stratifications and visualizes the outliers as the boundaries between turbulent and non-turbulent motions. As seen in Figure 4a, the trajectory may appear to bend in individual cases, but generally aligns with the overall pattern observed in Figure 3a. However, certain points deviate from this pattern, mostly in the form of the violation of the monotonicity of the trajectory, which indicates the presence of non-turbulent motions. The right column in Figure 4 displays the time series of the two cases shown in Figure 4a. It can be seen from the time series that the original observational signal is strongly non-stationary, with both meanderings in direction and mutations in amplitude, which complies well with the definitions in the form of non-turbulent motions [15,41]. After the reconstruction through anisotropy properties, the turbulence signal is successfully separated with steadier amplitudes and smaller scales.
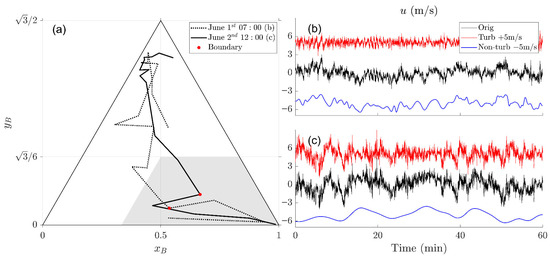
Figure 4.
The trajectory in 2 individual cases from Tianjin station (a) and the comparison of time series of turbulent and non-turbulent motions (b,c). The dotted line and (b) for the case of stable stratification, the solid line and (c) for unstable case. The gray patch visualizes the searching area, and the red points in (a) locate the boundary of turbulent and non-turbulent motion.
In stable conditions reflected in Figure 4b, the non-stationary component in the original signal, together with the local motions that affect the amplitude, can be mostly attributed to the non-turbulent motion. Moreover, in stable conditions, the complexity of non-turbulent motion is higher and the average scale is smaller, as seen from the comparison between Figure 4b,c. This is primarily due to static and steady meteorological conditions limiting motions in the stable boundary layer and often inducing intermittency in turbulence. In unstable conditions, however, the scale of both turbulence and non-turbulent motion is larger, and they happen to interact and are thus difficult to distinguish. From Figure 5c, it can be observed that non-turbulent motion is identified as the large-scale component of the original signal, conforming to the typical definitions. Meanwhile, the coherent structure, a large-scale form of atmospheric turbulence (see the ramp-like structure in the time series from 0 to 15 min [21], is not misidentified and is effectively preserved. This demonstrates the good performance of anisotropy in distinguishing non-turbulent motions without compromising the original turbulent structure in observational data. As the residual of EMD is automatically identified as non-turbulent motions in the algorithm, the application for small-size data samples (~10 min) and for intensely convective/non-stationary boundary layers should be evaluated twice to ensure the large-scale structures of atmospheric turbulence are not mistakenly filtered.
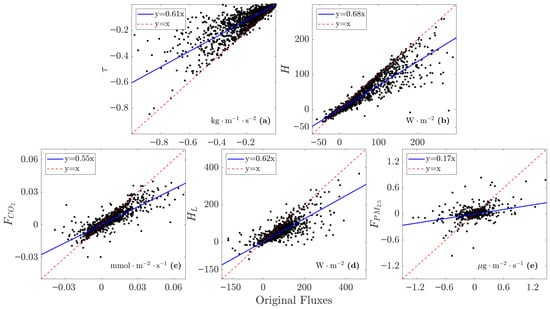
Figure 5.
The comparison between reconstructed fluxes and the original fluxes: (a) for momentum, (b) for sensible heat, (c) for CO2, (d) for latent heat, and (e) for PM2.5. The black dots are the data points, the blue lines mark the linear fit of the comparison relationship, and the red dashed lines denote the 1:1 reference line.
Once the non-turbulent motions are identified, the turbulent time series can be reconstructed following the instructions in Section 3.2. Figure 5 presents a comparison of turbulent fluxes, which reveals that the absolute value of the reconstructed fluxes tends to be smaller than the original fluxes (calculated using the standardized EC system), with the turbulent momentum flux overestimated by an average of 39%, sensible heat flux by 32%, latent heat flux by 38%, CO2 flux by 45%, and the PM2.5 flux by 83%. This result suggests that non-turbulent motions, which hold larger scales and evident non-stationary characteristics, typically lead to a significant overestimation of turbulent fluxes [39,76]. In the meantime, there are minor instances where the reconstructed flux is higher than the original flux, indicating underestimation and corresponding to counter-gradient transport [13,14]. The results reveal that non-turbulent motions typically generate large-scale transport aligned with turbulent flux directions. The corrections of turbulent flux demonstrate broader applicability for momentum and sensible heat fluxes, as these incorporate measurements from all three stations. The misjudgment of material fluxes can be attributed to non-stationarity from the sources and sinks, and for PM2.5, the predominant stable boundary layer (and possibly, the different season of winter) within the observational span of Dezhou station also makes a great difference. Similarly to prior studies, misjudgment of greenhouse gas and pollutant transport is more profound in stable conditions, where the calm and steady synoptic conditions limit the development of turbulence and result in turbulence intermittency [20,75]. Although some of the values above are based on specific conditions, the flux corrections can be representative in an arbitrary region based on historical data under characteristic synoptic conditions, and are transferable to future observations. For example, for summer and flat underlying surfaces, sufficient mixing favors the isotropy turbulence, with smaller bending for trajectory and fewer misjudgments of turbulent fluxes. Correspondingly, in other seasons (and complex surfaces), the turbulent fluxes tend to need larger corrections as the locality and anisotropy of turbulence (and thereby the influence of non-turbulent motions) become higher. The analysis above reveals that the anisotropy-based turbulence reconstruction provides substantial reference for critical applications like carbon cycle assessment and pollution control, where traditional methods falter.
Once non-turbulent motions are eliminated, the spectra change accordingly, with the energy of larger scales of motion decreasing, as shown in Figure 6. Following the procedures of HHT, the 2nd order of Hilbert marginal spectra is shown to reveal the scale-dependent energy distribution. The horizontal axes in the spectra are standardized into 40 bins. In higher frequency ranges, where there is no non-turbulent motion, the points of the original and reconstructed spectra overlap, resembling hexagrams. In lower frequency ranges, however, the spectra deviate. The location of this deviation marks the boundary frequency between turbulent and non-turbulent motions and is marked in the spectra as dashed lines. Comparing the 1st and 2nd columns of Figure 6, it can be judged that non-turbulent motions tend to occur around , corresponding to a time scale of s. For unstable stratification conditions, most boundary frequencies take place at frequencies lower than in most cases, while for stable conditions, tends to be slightly higher than . The boundary frequency also proves to be dependent on the stability parameter , as shown by the interesting dispersion of the dashed lines in Figure 6a–j. In unstable conditions, the lines are spread wider with a regular pattern of sequence, except for PM2.5, where many lines overlap. In stable conditions, the lines are closer to each other, and the overlapping phenomenon is more evident. This serves as evidence that for different stratification conditions, the non-turbulent motions might have various forms, different scales, and potential interaction with turbulence. However, based on the scale-dependent anisotropy properties, the existence of non-turbulent motions can be effectively identified and eliminated. Therefore, the anisotropy-based turbulence reconstruction provides a robust correction framework for land–atmosphere transport.
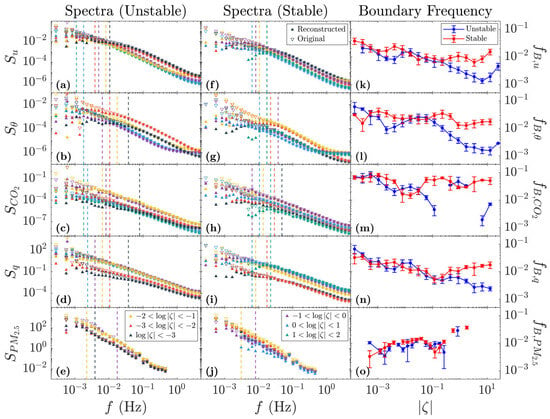
Figure 6.
Hilbert marginal spectra of original (hollow points) and reconstructed (solid points) data under unstable (a–e) and stable (f–j) conditions, colored by stability parameter (ζ). Panels (k–o) show the relationship between boundary frequency () and with error bars visualizing the standard deviation. The term “log” denotes a logarithm with base 10.
The 3rd column in Figure 6 works in concert with the dashed lines in the left two columns and provides a more detailed illustration of the relationship between and . With the increase in the absolute values of , the boundary frequency usually decreases. For unstable stratifications with strong surface heating or convective instability, atmospheric turbulence intensifies and exhibits an increased characteristic scale, and the observations capture a broader spectrum of motion scales, extending from fine turbulent eddies to larger organized structures. The effects of non-turbulent motions tend to interact and blur with the coherent structures of turbulence, with overlapped spectra, favoring a larger size of data samples. On the contrary, in stable stratifications, the turbulence itself is limited in strength and scale by the static and steady meteorological conditions, and its deviation from the non-turbulent motions only depends on the maximum scale of turbulence, making the decreasing trend of less significant. This behavior makes it easier to distinguish non-turbulent motions in the stable boundary layer, whose other characteristics, such as the spectral gap [20,75], are also more evident. For both scenarios, the non-turbulent motions lack involvement in the Kolmogorov energy cascade, and most of them can be resolved by large-scale models, which should not be recalculated via parameterization schemes and can be effectively eliminated from the turbulent reconstruction based on the anisotropy of atmospheric turbulence.
4.3. Similarity Relationships and Anisotropy
Compared with the direct calculation and correction of turbulent fluxes in the EC system, in which intensive computations are involved, introducing anisotropy into similarity relationships may hold significant promise for the estimation of land–atmosphere transport across multiple datasets under a substantially reduced cost. Previous studies have sufficiently analyzed the effectiveness of anisotropy in generalizing MOST in both normalized standard deviations and the flux-gradient profiles [58,59], and the analyses above suggest that both and are promising for advancing the performance of MOST in the prediction of atmospheric turbulence properties in different stratification conditions. To further investigate the joint influence of the two anisotropy parameters, Figure 7 compares the similarity relationships and the anisotropy parameters using turbulence data reconstructed in Section 4.2, where and are the normalized standard deviations of wind speed and potential temperature. The results conform well to the M-O similarity theory (the relationships of and are similar to and are therefore omitted), even though the data were not strictly selected for near-ideal conditions. Figure 7a–d indicates that as the stability parameter changes from small to large absolute values, the average varies from small to large values. However, for points that deviate significantly from the empirical curves, exhibits larger values. This phenomenon demonstrates that the anisotropy parameter is closely related to the dynamic properties of atmospheric turbulence, providing a physical basis for incorporating into similarity relationships. Similarly, Figure 7e–h shows increasing trends of with increasing absolute values of , and the outliers from the scaling curves correspond with particularly low . The correlation relationships of , and align well with the results in Figure 3.
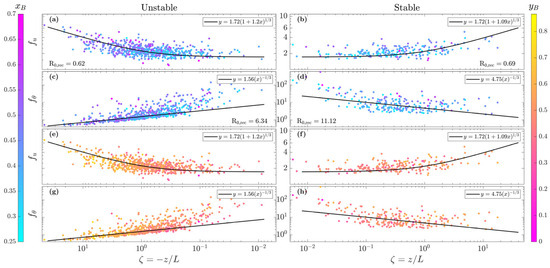
Figure 7.
The comparison between the similarity relationships and the dispersion of anisotropy parameters for the reconstructed turbulence data. The solid lines give the empirical scaling curves, and the color of the points in (a–d) marks the value of , and the color of the points in (e–h) marks the value of .
Figure 7’s heuristic approach effectively addresses limitations in traditional MOST under non-ideal conditions. By deliberately incorporating anisotropy parameters ( and )—both critically linked to turbulent flux characteristics—the modified similarity relationships demonstrate superior performance, even when tested against observational data selected solely by wind direction without excluding non-ideal conditions. This robust validation confirms that anisotropy integration simultaneously enhances similarity relationship precision and expands its applicability across diverse atmospheric regimes. Similar analysis can also be applied to the normalized standard deviations and flux–profile relationships concerning CO2, water vapor, and PM2.5, which holds promise for enhancing predictive accuracy for critical sustainability applications, including weather/climate prediction, greenhouse effect quantification, and urban pollution mitigation. Therefore, the advances above based on anisotropy enable reconstruction of pure turbulence data and significantly improve turbulent flux estimates, providing essential theoretical foundations for optimizing parameterization schemes of land–atmosphere transport.
5. Conclusions
In this study, anisotropy derived from the Reynolds stress tensor is quantified using two parameters, and , based on turbulence data acquired from multiple observational stations with different underlying surfaces and stratification conditions. The properties of anisotropy are investigated across different scales using HHT, and the scale-dependent properties are summarized.
From small to large-scale turbulent motions, exhibits an overall increasing trend from 0.4 to 0.9, while initially increases to 0.7 before decreasing to 0. This regular pattern forms the circuitous curve of the trajectory in the BAM for both unstable and stable stratification conditions. However, in individual cases, the trajectory sometimes deviates from the average pattern. Using a comprehensive algorithm, these outliers can be identified and serve as the boundary between turbulent and non-turbulent motions, occurring at a time scale of approximately seconds. Once non-turbulent motions are identified, the turbulence data can be reconstructed, with the spectra at large scales being weaker than the original data. Moreover, the turbulent fluxes calculated from the reconstructed data are typically lower than those from the standardized EC system. The overestimation of turbulent momentum, sensible heat, and latent heat fluxes can vary around 30%, and even higher for CO2 and PM2.5, with occasional instances of flux underestimation. The application of flux correction highlights the potential of anisotropy in refining similarity theory, which is intrinsically linked to turbulent transport. It is demonstrated that and vary consistently with the stability parameter, making them suitable for incorporation into similarity relationships. Introducing anisotropy into the similarity theory outperforms direct correction of turbulent flux in both computational efficiency and reliability. These findings demonstrate that the modified similarity relationships not only improve predictions of turbulent transport characteristics but also extend their applicability across a wider range of atmospheric conditions, showing enhanced utilities for both fundamental turbulence research and practical applications.
In conclusion, the stable statistical pattern in the properties of anisotropy serves as a new indicator of the scale-dependent characteristics of atmospheric turbulence and is effective in the accurate estimation of land–atmosphere transport. On the one hand, it provides a systematic scheme for reconstructing pure-turbulent motions, allowing for more precise estimation of turbulent transport. On the other hand, the use of anisotropy in similarity relationships enables a broader application of atmospheric turbulence properties. Consequently, anisotropy-based turbulence reconstruction offers an operationally robust approach for refining land–atmosphere transport quantification and warrants further investigations, which may involve the evaluation of anisotropy’s effectiveness across spatially distributed datasets beyond single-point observations, and the transformation of these findings into parameterization schemes through atmospheric turbulence simulations. Such advancements would benefit diverse domains, including climate projection, greenhouse gas monitoring, and pollution management.
Author Contributions
Conceptualization: Z.L. and H.Z.; formal analysis: Z.L.; resources: H.Z.; data curation: H.Z. and X.C.; writing—original draft preparation: Z.L.; writing—review and editing: H.Z., X.C. and Y.S.; funding acquisition: H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2023YFC3706300), the Science and Technology Plan Project of Beijing (Z241100009124014), and the National Natural Science Foundation of China (42175092, 42475184, 42305071).
Data Availability Statement
The data are available at Zhang, Hongsheng; Liu, Zihan (2025). Identification of non-turbulent motions for enhanced estimation of turbulent transport using the anisotropy of atmospheric Turbulence [Dataset]. Dryad. https://doi.org/10.5061/dryad.c866t1gh6.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABL | Atmospheric Boundary-Layer |
| HHT | Hilbert–Huang Transform |
| EMD | Empirical Mode Decomposition |
| TKE | Turbulence Kinetic Energy |
| MOST | Monin–Obukhov Similarity Theory |
| BAM | Barycentric Map |
Appendix A
The fundamental steps of the Hilbert–Huang Transform (HHT) are as follows:
- (1)
- Conducting EMD on multiple variables:
EMD is an adaptive method to decompose nonlinear/nonstationary signals into Intrinsic Mode Functions (IMFs, ) through an iterative “sifting” process. The key steps are as follows:
- A.
- Local Extrema Detection: identify all local maxima and minima in the signal.
- B.
- Envelope Construction: the upper envelope is defined as the cubic spline interpolation of local maxima, and the lower envelope as the interpolation of local minima (Figure A1, black solid lines in IMF8 panel).
- C.
- Local Mean Calculation: compute the running mean of upper/lower envelopes (Figure A1, dashed line in IMF8 panel).
- D.
- Sifting Iteration: subtract the local mean from the signal, and repeat Steps A–C on the residual until two criteria are met:
- (a)
- The number of extrema and zero-crossings differ by ≤1 (avoiding over-decomposition).
- (b)
- The mean of upper/lower envelopes approaches zero (ensuring symmetry).
When criteria (a)–(b) are satisfied, the residual is designated as an IMF, . The remaining signal (original minus IMF) undergoes further sifting to extract subsequent IMFs, and the final residual, , represents the signal’s secular trend, which is non-oscillatory and decoupled from IMFs. The EMD process for a real signal can be written as
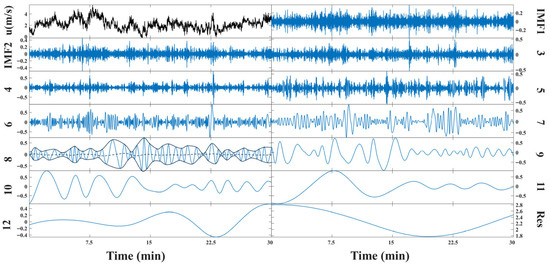
Figure A1.
The comparison of original signal of u-wind and the IMFs generated by EMD. The envelopes of the signal are visualized through the black solid lines in the panel of IMF 8, and their running mean value is marked by the dashed line.
- (2)
- Performing the Hilbert transform on each IMF:
The definition of the Hilbert transform is
where is the transformed signal of the kth IMF, and the original signal can be generalized into analytical signal :
where is the instantaneous amplitude, is the instantaneous phase, and the instantaneous frequency can be defined as . One can also calculate the average frequency, , within every analytical signal.
- (3)
- Calculating the Hilbert marginal spectrum:
Within the data sample of size , the frequency–time distribution of the amplitude, , is defined as the Hilbert spectrum, and the joint probability density functions (JPDF), , can also be calculated. The arbitrary-order Hilbert marginal spectrum can be defined in an amplitude–frequency space by a marginal integration of the JPDF:
where the and are instantaneous frequency and instantaneous amplitude at time , respectively. Specifically, the 2nd order Hilbert marginal spectrum is essentially the energy density at frequency , which shares the same physical significance as the Fourier transform:
References
- Caughey, S.J.; Wyngaard, J.C.; Kaimal, J.C. Turbulence in the Evolving Stable Boundary Layer. J. Atmos. Sci. 1979, 36, 1041–1052. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; Volume 13. [Google Scholar]
- Garratt, J.R. Review: The atmospheric boundary layer. Earth-Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Robinson, S.K. Coherent Motions in the Turbulent Boundary Layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Marusic, I.; McKeon, B.J.; Monkewitz, P.A.; Nagib, H.M.; Smits, A.J.; Sreenivasan, K.R. Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 2010, 22, 065103. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Hincks, B.B.; Meyers, T.P. Measuring Biosphere-Atmosphere Exchanges of Biologically Related Gases with Micrometeorological Methods. Ecology 1988, 69, 1331–1340. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Burba, G. Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates; LI-COR Biosciences: Lincoln, NE, USA, 2013. [Google Scholar]
- Moore, C.J. Frequency response corrections for eddy correlation systems. Bound.-Layer Meteorol. 1986, 37, 17–35. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality Control and Flux Sampling Problems for Tower and Aircraft Data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Aubinet, M. Eddy covariance CO2 flux measurements in nocturnal conditions: An analysis of the problem. Ecol. Appl. 2008, 18, 1368–1378. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Anderson, W.; Katul, G.G.; Mahrt, L. The Persistent Challenge of Surface Heterogeneity in Boundary-Layer Meteorology: A Review. Bound. Layer Meteorol. 2020, 177, 227–245. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. A Solution for Flux Contamination by Mesoscale Motions With Very Weak Turbulence. Bound. Layer Meteorol. 2006, 118, 431–447. [Google Scholar] [CrossRef]
- Mahrt, L. The influence of nonstationarity on the turbulent flux–gradient relationship for stable stratification. Bound. Layer Meteorol. 2007, 125, 245–264. [Google Scholar] [CrossRef]
- Mahrt, L. Stably Stratified Atmospheric Boundary Layers. Annu. Rev. Fluid Mech. 2014, 46, 23–45. [Google Scholar] [CrossRef]
- Mahrt, L. Microfronts in the nocturnal boundary layer. Q. J. R. Meteorol. Soc. 2019, 145, 546–562. [Google Scholar] [CrossRef]
- Pfister, L.; Lapo, K.; Mahrt, L.; Thomas, C.K. Thermal Submeso Motions in the Nocturnal Stable Boundary Layer. Part 2: Generating Mechanisms and Implications. Bound. Layer Meteorol. 2021, 180, 203–224. [Google Scholar] [CrossRef]
- Mahrt, L.; Bou-Zeid, E. Non-stationary Boundary Layers. Bound. Layer Meteorol. 2020, 177, 189–204. [Google Scholar] [CrossRef]
- Lan, C.; Wang, B.; Zheng, D.; Wang, Y.; Zhang, Z.; Fang, R. Decreased dissimilarity of turbulent transport attributed to large eddies. Q. J. R. Meteorol. Soc. 2022, 148, 1262–1279. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.; Wei, W.; Wu, B.; Cai, X.; Song, Y. Effects of turbulence structure and urbanization on the heavy haze pollution process. Atmos. Chem. Phys. 2019, 19, 1041–1057. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Cai, X.; Song, Y.; Zhang, X. Characteristics of Turbulence Intermittency, Fine Structure, and Flux Correction in the Taklimakan Desert. J. Atmos. Sci. 2024, 81, 459–475. [Google Scholar] [CrossRef]
- Mahrt, L. Computing turbulent fluxes near the surface: Needed improvements. Agric. For. Meteorol. 2010, 150, 501–509. [Google Scholar] [CrossRef]
- Serafin, S.; Adler, B.; Cuxart, J.; De Wekker, S.F.J.; Gohm, A.; Grisogono, B.; Kalthoff, N.; Kirshbaum, D.J.; Rotach, M.W.; Schmidli, J.; et al. Exchange Processes in the Atmospheric Boundary Layer Over Mountainous Terrain. Atmosphere 2018, 9, 102. [Google Scholar] [CrossRef]
- Sun, J.; Nappo, C.J.; Mahrt, L.; Belušić, D.; Grisogono, B.; Stauffer, D.R.; Pulido, M.; Staquet, C.; Jiang, Q.; Pouquet, A.; et al. Review of wave-turbulence interactions in the stable atmospheric boundary layer. Rev. Geophys. 2015, 53, 956–993. [Google Scholar] [CrossRef]
- Siebesma, A.P.; Soares, P.M.M.; Teixeira, J. A Combined Eddy-Diffusivity Mass-Flux Approach for the Convective Boundary Layer. J. Atmos. Sci. 2007, 64, 1230–1248. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, Q.; Li, D.; Zhong, Q. Contributions of very large-scale motions to turbulence statistics in open channel flows. J. Fluid Mech. 2020, 892, A3. [Google Scholar] [CrossRef]
- Fan, J.; Hao, J.; Wen, C.-Y. Role of very large-scale motions in shock wave/turbulent boundary layer interactions. Phys. Fluids 2024, 36. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. The Cospectral Gap and Turbulent Flux Calculations. J. Atmos. Ocean. Technol. 2003, 20, 660–672. [Google Scholar] [CrossRef]
- Muschinski, A.; Frehlich, R.G.; Balsley, B.B. Small-scale and large-scale intermittency in the nocturnal boundary layer and the residual layer. J. Fluid Mech. 2004, 515, 319–351. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Huang, Y.X.; Schmitt, F.G.; Hermand, J.P.; Gagne, Y.; Lu, Z.M.; Liu, Y.L. Arbitrary-order Hilbert spectral analysis for time series possessing scaling statistics: Comparison study with detrended fluctuation analysis and wavelet leaders. Phys. Rev. E 2011, 84, 016208. [Google Scholar] [CrossRef]
- Wei, W.; Schmitt, F.G.; Huang, Y.X.; Zhang, H.S. The Analyses of Turbulence Characteristics in the Atmospheric Surface Layer Using Arbitrary-Order Hilbert Spectra. Bound. Layer Meteorol. 2016, 159, 391–406. [Google Scholar] [CrossRef]
- Howell, J.F.; Mahrt, L. Multiresolution Flux Decomposition. Bound. Layer Meteorol. 1997, 83, 117–137. [Google Scholar] [CrossRef]
- Mahrt, L. Characteristics of Submeso Winds in the Stable Boundary Layer. Bound. Layer Meteorol. 2009, 130, 1–14. [Google Scholar] [CrossRef]
- Nilsson, E.O.; Sahlée, E.; Rutgersson, A. Turbulent momentum flux characterization using extended multiresolution analysis. Q. J. R. Meteorol. Soc. 2014, 140, 1715–1728. [Google Scholar] [CrossRef]
- Falocchi, M.; Giovannini, L.; de Franceschi, M.; Zardi, D. A method to determine the characteristic time-scales of quasi-isotropic surface-layer turbulence over complex terrain: A case-study in the Adige Valley (Italian Alps). Q. J. R. Meteorol. Soc. 2019, 145, 495–512. [Google Scholar] [CrossRef]
- Urbancic, G.H.; Suomi, I.; Vihma, T. A general theory for the characterization of submeso-scale motions and turbulence in the atmospheric surface layer. Q. J. R. Meteorol. Soc. 2021, 147, 660–678. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Y.; Tang, J.; Zhu, P.; Gao, Z.; Yang, Y. Quantitative Evaluation of Wavelet Analysis Method for Turbulent Flux Calculation of Non-Stationary Series. Geophys. Res. Lett. 2023, 50, e2022GL101591. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H.; Wei, W.; Cai, X.; Song, Y.; Zhang, X. Non-turbulent motion identified from properties of transport and its influence on the calculation of turbulent flux. Q. J. R. Meteorol. Soc. 2024, 150, 2223–2241. [Google Scholar] [CrossRef]
- Deb Burman, P.K.; Prabha, T.V.; Morrison, R.; Karipot, A. A Case Study of Turbulence in the Nocturnal Boundary Layer During the Indian Summer Monsoon. Bound. Layer Meteorol. 2018, 169, 115–138. [Google Scholar] [CrossRef]
- Cava, D.; Mortarini, L.; Anfossi, D.; Giostra, U. Interaction of Submeso Motions in the Antarctic Stable Boundary Layer. Bound. Layer Meteorol. 2019, 171, 151–173. [Google Scholar] [CrossRef]
- Moncrieff, J.B.; Malhi, Y.; Leuning, R. The propagation of errors in long-term measurements of land-atmosphere fluxes of carbon and water. Glob. Change Biol. 1996, 2, 231–240. [Google Scholar] [CrossRef]
- Finnigan, J. The storage term in eddy flux calculations. Agric. For. Meteorol. 2006, 136, 108–113. [Google Scholar] [CrossRef]
- Honkanen, M.; Tuovinen, J.P.; Laurila, T.; Mäkelä, T.; Hatakka, J.; Kielosto, S.; Laakso, L. Measuring turbulent CO2 fluxes with a closed-path gas analyzer in a marine environment. Atmos. Meas. Tech. 2018, 11, 5335–5350. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.; Wei, W.; Cai, X.; Song, Y. Determining the fluctuation of PM2.5 mass concentration and its applicability to Monin–Obukhov similarity. Sci. Total Environ. 2020, 710, 136398. [Google Scholar] [CrossRef]
- Rinne, J.; Ammann, C.; Pattey, E.; Paw U, K.T.; Desjardins, R.L. Alternative Turbulent Trace Gas Flux Measurement Methods; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1505–1530. [Google Scholar]
- Qu, W.J.; Wang, J.; Zhang, X.Y.; Wang, D.; Sheng, L.F. Influence of relative humidity on aerosol composition: Impacts on light extinction and visibility impairment at two sites in coastal area of China. Atmos. Res. 2015, 153, 500–511. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.; Zhang, X.; Li, Q.; Cai, X.; Song, Y.; Kang, L.; Zhu, T. Temporal and spatial characteristics of turbulent transfer and diffusion coefficient of PM2.5. Sci. Total Environ. 2021, 782, 146804. [Google Scholar] [CrossRef] [PubMed]
- Carbone, F.; Alberti, T.; Faranda, D.; Telloni, D.; Consolini, G.; Sorriso-Valvo, L. Local dimensionality and inverse persistence analysis of atmospheric turbulence in the stable boundary layer. Phys. Rev. E 2022, 106, 064211. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, H.; Fu, Z.; Cai, X.; Song, Y. Analysis of Fractal Properties of Atmospheric Turbulence and the Practical Applications. Fractal Fract. 2024, 8, 483. [Google Scholar] [CrossRef]
- Banerjee, S.; Krahl, R.; Durst, F.; Zenger, C. Presentation of anisotropy properties of turbulence, invariants versus eigenvalue approaches. J. Turbul. 2007, 8, N32. [Google Scholar] [CrossRef]
- Stiperski, I.; Calaf, M. Dependence of near-surface similarity scaling on the anisotropy of atmospheric turbulence. Q. J. R. Meteorol. Soc. 2018, 144, 641–657. [Google Scholar] [CrossRef]
- Stiperski, I.; Calaf, M.; Rotach, M.W. Scaling, Anisotropy, and Complexity in Near-Surface Atmospheric Turbulence. J. Geophys. Res. Atmos. 2019, 124, 1428–1448. [Google Scholar] [CrossRef]
- Dey, S.; Paul, P.; Ali, S.Z.; Padhi, E. Reynolds stress anisotropy in flow over two-dimensional rigid dunes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20200638. [Google Scholar] [CrossRef]
- Stiperski, I.; Katul, G.G.; Calaf, M. Universal Return to Isotropy of Inhomogeneous Atmospheric Boundary Layer Turbulence. Phys. Rev. Lett. 2021, 126, 194501. [Google Scholar] [CrossRef]
- Dabbagh, F.; Schneiderbauer, S. Anisotropy characterization of turbulent fluidization. Phys. Rev. Fluids 2022, 7, 094301. [Google Scholar] [CrossRef]
- Gucci, F.; Giovannini, L.; Stiperski, I.; Zardi, D.; Vercauteren, N. Sources of anisotropy in the Reynolds stress tensor in the stable boundary layer. Q. J. R. Meteorol. Soc. 2023, 149, 277–299. [Google Scholar] [CrossRef]
- Stiperski, I.; Calaf, M. Generalizing Monin-Obukhov Similarity Theory (1954) for Complex Atmospheric Turbulence. Phys. Rev. Lett. 2023, 130, 124001. [Google Scholar] [CrossRef]
- Mosso, S.; Calaf, M.; Stiperski, I. Flux-gradient relations and their dependence on turbulence anisotropy. Q. J. R. Meteorol. Soc. 2024, 150, 3346–3367. [Google Scholar] [CrossRef]
- Ye, X.; Wu, B.; Zhang, H. The turbulent structure and transport in fog layers observed over the Tianjin area. Atmos. Res. 2015, 153, 217–234. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, H.; Wu, B.; Huang, Y.; Cai, X.; Song, Y.; Li, J. Intermittent turbulence contributes to vertical dispersion of PM2.5 in the North China Plain: Cases from Tianjin. Atmos. Chem. Phys. 2018, 18, 12953–12967. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H. Size distribution of dust aerosols observed over the Horqin Sandy Land in Inner Mongolia, China. Aeolian Res. 2015, 17, 231–239. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, H.; Ren, Y.; Li, Q.; Cai, X.; Song, Y.; Kang, L. Study on the characteristics of the pressure fluctuations and their contribution to turbulence kinetic energy. Atmos. Res. 2021, 258, 105634. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic Anemometer Tilt Correction Algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P.; Lilly, J.M. Bivariate Empirical Mode Decomposition. IEEE Signal Process. Lett. 2007, 14, 936–939. [Google Scholar] [CrossRef]
- Klipp, C. Near-Surface Turbulent Temperature Variances and Anisotropy at Multiple Scales of Motion; SPIE: Bellingham, WA, USA, 2012; Volume 8380. [Google Scholar]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. The Critical Richardson Number and Limits of Applicability of Local Similarity Theory in the Stable Boundary Layer. Bound. Layer Meteorol. 2013, 147, 51–82. [Google Scholar] [CrossRef]
- Vercauteren, N.; Boyko, V.; Faranda, D.; Stiperski, I. Scale interactions and anisotropy in stable boundary layers. Q. J. R. Meteorol. Soc. 2019, 145, 1799–1813. [Google Scholar] [CrossRef]
- Klipp, C. Near-Surface Anisotropic Turbulence; SPIE: Bellingham, WA, USA, 2010; Volume 7685. [Google Scholar]
- Sarkar, S.; Speziale, C.G. A simple nonlinear model for the return to isotropy in turbulence. Phys. Fluids A Fluid Dyn. 1990, 2, 84–93. [Google Scholar] [CrossRef]
- Choi, K.-S.; Lumley, J.L. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 2001, 436, 59–84. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ren, Y.; Zhang, H.; Zhang, L.; Liang, J. Quantitative description and characteristics of submeso motion and turbulence intermittency. Q. J. R. Meteorol. Soc. 2023, 149, 1726–1744. [Google Scholar] [CrossRef]
- Mazzola, M.; Viola, A.P.; Choi, T.; Tampieri, F. Characterization of Turbulence in the Neutral and Stable Surface Layer at Jang Bogo Station, Antarctica. Atmosphere 2021, 12, 1095. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).