Abstract
Landslides are among the most hazardous natural phenomena affecting Greater Abidjan, causing significant economic and social damage. Strategic planning supported by geographic information systems (GIS) can help mitigate potential losses and enhance disaster resilience. This study evaluates landslide susceptibility using logistic regression and frequency ratio models. The analysis is based on a dataset comprising 54 mapped landslide scarps collected from June 2015 to July 2023, along with 16 thematic predictor variables, including altitude, slope, aspect, profile curvature, plan curvature, drainage area, distance to the drainage network, normalized difference vegetation index (NDVI), and an urban-related layer. A high-resolution (5-m) digital elevation model (DEM), derived from multiple data sources, supports the spatial analysis. The landslide inventory was randomly divided into two subsets: 80% for model calibration and 20% for validation. After optimization and statistical testing, the selected thematic layers were integrated to produce a susceptibility map. The results indicate that 6.3% (0.7 km2) of the study area is classified as very highly susceptible. The proportion of the sample (61.2%) in this class had a frequency ratio estimated to be 20.2. Among the predictive indicators, altitude, slope, SE, S, NW, and NDVI were found to have a positive impact on landslide occurrence. Model performance was assessed using the area under the receiver operating characteristic curve (AUC), demonstrating strong predictive capability. These findings can support informed land-use planning and risk reduction strategies in urban areas. Furthermore, the prediction model should be communicated to and understood by local authorities to facilitate disaster management. The cost function was adopted as a novel approach to delineate hazardous zones. Considering the landslide inventory period, the increasing hazard due to climate change, and the intensification of human activities, a reasoned choice of sample size was made. This informed decision enabled the production of an updated prediction map. Optimal thresholds were then derived to classify areas into high- and low-susceptibility categories. The prediction map will be useful to planners in helping them make decisions and implement protective measures.
1. Introduction
Landslides (LS), defined as the downward movement of rock, debris, or soil along a slope [1], represent a significant geohazard in many parts of the world, causing thousands of fatalities annually [2]. This threat is particularly severe in tropical urban areas, where rapidly expanding populations and unplanned development increase exposure to LS events. The high frequency of LS in these regions is driven by a combination of demographic pressure, land-use changes, and climate change [3]. As urban expansion pushes settlements onto steep and unstable hillslopes, the vulnerability of local populations to LS hazards intensifies [3]. Consequently, the reduction and prevention of LS-related damage have become major research areas in natural disaster risk management [4]. In light of the severe impacts of these mass movements, assessing LS susceptibility is crucial for mitigating damage and loss of life. The development of LS susceptibility maps enables the identification of areas with elevated landslide risk, thereby supporting effective planning and early warning strategies [5].
Over the past decade, various models have been applied in LS susceptibility assessment [6]. These approaches are generally classified into qualitative and quantitative categories. Qualitative methods rely heavily on expert judgment and are often considered subjective and context-dependent [7]. In contrast, quantitative approaches are data-driven and provide a more objective means of assessing LS susceptibility [8]. Quantitative techniques primarily include deterministic models, specific machine learning algorithms, and conventional statistical methods. Deterministic models, which are grounded in the physical laws governing LS processes, are theoretically robust. However, their application to regional-scale LS susceptibility mapping is limited due to the complexity of input parameters and the high computational demands involved.
With the rapid development of artificial intelligence (AI), machine learning (ML) algorithms, particularly ensemble learning methods, have gained prominence in modeling complex nonlinear relationships. In the context of LS prediction assessment, ensemble techniques such as bagging, boosting, and stacking have produced promising results [9]. For instance, Zhang et al. [4] applied the bagging method in combination with decision tree (DT), logistic model tree (LMT), and reduced error pruning tree (REPT) algorithms to develop three hybrid models: Bag-DT, Bag-LMT, and Bag-REPT. In Chenggu County, China, the Bag-REPT model achieved the highest prediction accuracy (92.5%) among the three. Similarly, Zhang et al. [10] conducted LS susceptibility mapping in Fengjie County, China, using two ensemble methods: random forest (RF) and extreme gradient boosting (XGBoost). The models achieved area under the curve (AUC) values of 0.866 (RF) and 0.864 (XGBoost), respectively, highlighting their strong predictive performance. In another study conducted in Turkey, Sahin [11] compared the predictive capabilities of four ensemble models-gradient boosting machine (GBM), categorical boosting (CatBoost), XGBoost, and light gradient boosting machine (LightGBM). Among them, CatBoost demonstrated the highest predictive accuracy, with an AUC of 0.8975.
Although machine learning (ML) techniques often yield better predictive performance, traditional mathematical statistical methods still offer distinct advantages in specific contexts. These methods are generally grouped into two main categories: (1) bivariate statistical approaches and (2) multivariate statistical approaches. Bivariate approaches include the frequency ratio (FR) [12,13], weight of evidence (WoE) [13], statistical index (SI) [14], index of entropy (IoE) [15], certainty factors (CF) [13,16], Dempster–Shafer models (DSM) [12], Bayesian probability model (BPM) [12], and evidential belief function (EBF) [13,17]. Among multivariate approaches, support vector machine (SVMs), artificial neural networks (ANNs), and logistic regression models have been used for LS susceptibility mapping. The logistic regression (LR) method [18,19] has been extensively applied in LS susceptibility assessment due to its simplicity and interpretability.
Ivory Coast, located in West Africa, has experienced significant LS events, primarily due to intense rainfall during the rainy season [20]. These geohazard events pose serious threats to life, livelihoods, and infrastructure, especially in coastal urban areas such as Greater Abidjan, situated in the southern part of the country. In this study, the municipality of Attecoube, located centrally within Greater Abidjan, was selected as a representative LS-prone area of interest. This urban area typifies all LS-prone zones in Greater Abidjan. For instance, between 2005 and 2007, heavy rainfall triggered LSs that resulted in ten fatalities and the destruction of buildings [21]. Similarly, during 2014–2015, LSs caused sixteen fatalities and damaged numerous buildings [22]. Most recently, on 11 June 2023, five people were killed by LSs in the Mossikro and Boribana districts [23].
Despite the frequent LS occurrence, this area is subject to anthropogenic disturbances (clearing of hillslopes, construction of buildings at the top of hillslopes, etc.). These human activities may contribute to the destabilization of hillslopes. Several studies have focused on assessing LS susceptibility [21]. However, those studies are limited because they are based solely on the spatial overlay of topographical data without integrating field observations or they lack validation by field data. Therefore, the resulting maps are overly abstract and do not provide comprehensive LS susceptibility analysis. Moreover, they rely heavily on geomorphological expertise. To address these gaps, we propose an ensemble approach combining logistic regression (LR) and frequency ratio (FR) models to evaluate LS susceptibility in this urban area. The assessment of LS susceptibility is based on the integration of factors that influence the occurrence of LSs. Using these models and applying the LS prediction model in practice results in economic consequences due to the classification of land according to its susceptibility. For example, a unit of land (in this case, a pixel) classified as stable can be used without restriction, which increases its economic value. In contrast, an unstable unit of land is subject to restrictions on use and, therefore, sees its market value reduced. The inclusion of a cost function in a logistic regression model significantly affects the accuracy of LS susceptibility mapping, particularly in urban contexts where the consequences of classification errors can be severe.
The main objective of this paper is to identify LS-susceptible areas by selecting the most appropriate logistic regression model and evaluating its effectiveness in minimizing costs through testing the sensitivity of the threshold to variations in the cost ratio. This study aims to provide valuable support to administrators and policymakers for the planning and implementation of infrastructure projects, such as building and road construction.
2. Study Area
The study area was located in the central part of Greater Abidjan (Figure 1A) at latitude 5°20′01″ N and longitude 4°02′16″ W. Attecoube (Figure 1B) extends over ~70 km2, of which the Banco forest covers 40 km2 on its northern side, the Lake Ebrie occupies 5 km2 in the southern part, and the remaining 25 km2 are inhabited by approximately 260,911 residents [24]. Divided into two distinct halves by the lake, the area is characterized by altitudes ranging from ~0 m.a.s.l in the flat plain around the lake and valleys to ~65 m.a.s.l on the northern strips of the dissected low plateau.
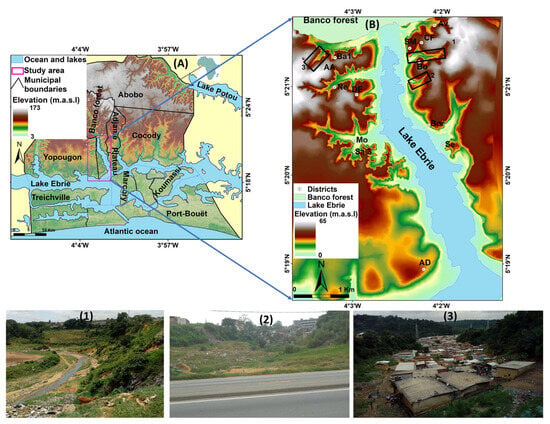
Figure 1.
Location map of the study area in central Abidjan, on a background digital elevation model (DEM). (A) The pink rectangle indicates the position of Attecoube within the city. (B) Location of districts and main valleys investigated in the study area. Av, Agban-village. CF, Cite Fairmont. SM, Sanctuaire Marial. Bo, Bobito. Bor, Boribana. Se, Sebroko. Ba1, Banco1. AA, Agban-Attié. Ne, Nematoulaye. DE, Djene-Ecare. Mo, Mossikro. Sa 3, Sante 3. AD, Abobo-Doume. The numbers 1, 2, and 3 in Figure 1B represent main valley respectively pictures 1, 2 & 3.
In the eastern half, the relief is characterized by two main, steep-sided, W-flowing, U-shaped valleys that deeply incise the low plateau, exhibiting geomorphological evidence of active slope processes. These valleys’ transverse sections are asymmetric, with steeper N-facing slopes. Especially in the north, where the plateau reaches its highest altitudes, the part of the study area west of the lake is also characterized by deeply incised ravines and valleys, albeit with a more dendritic pattern (Figure 1, pictures 1–3). Although this makes the sector less suitable for urban development than Abobo-Doume to the south, urban sprawl has completely invaded it, with poorly built houses and precarious dwellings set in every imaginable location.
Geologically, Attecoube lies within the coastal sedimentary basin of Abidjan, which is filled with Mesozoic deposits overlain by Mio-Pliocene sediments of the Continental Terminal. At Attecoube, these ~100–200 m thick deposits mainly consist of, from top to bottom, clayey sands, fine to middle sands, and coarse sands resting on a granitic basement [25]. No data exist about possible spatial variations in facies (in particular grain size) of the shallow clayey sands, which are thus commonly considered uniform throughout the study area, except for their thickness varying from 10 to 25 m [26].
The determination of soil types and characteristics is key to slope stability analysis [27]. Based on the harmonized soil map of the Soil Atlas of Africa, which uses the World Reference Base for Soil Resources [28,29], the dominant soil types in Attecoube are arenosols. They developed on sands with a variable content in clay (10–45%), themselves derived from the weathering of the basement and deposited in a marine environment. The arenosols are categorized as moderately well-drained soils with sand to clay texture due to the presence of clay in the lower horizon, which reduces the absorption capacity of the soils under saturated conditions.
Hydrologically, the main U-shaped valleys are occupied by perennial streams that flow directly into Lake Ebrie, whereas their tributaries exhibit ephemeral flow. Attecoube has a humid tropical climate with two humid seasons (the main one from May to July, and a minor one from October to November) and two dry seasons (August to September and December to March) and is classified as Aw (tropical savannah climate) in the Köppen–Geiger classification [30,31]. The rainfall seasons are largely controlled by the movement of the tropical rain belt associated with the Intertropical Convergence Zone (ITCZ), which oscillates between the northern and southern tropics throughout the year. Monthly rainfall data for the study area are available only for the 1981–2012 period. Moreover, average values cannot represent their high interannual variability. The most humid months are May and June, each with an average rainfall of more than 350 mm, during which the LS hazard is high (Figure 2). Temperatures generally range between 25 °C and 29 °C.
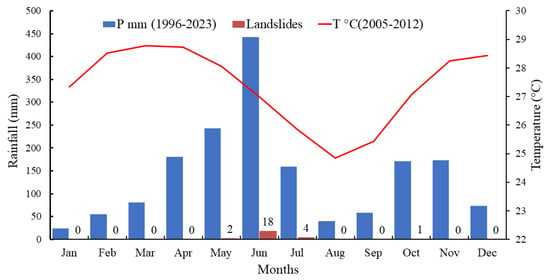
Figure 2.
Monthly averages of rainfall (P) and temperature (T°) in the Abidjan region over the period 1996–2023. The red line displays average monthly temperatures over the period 2005–2012. The red bar graph represents the number of LSs occurring and identified during the period 1996–2023.
In recent years, Attecoube has experienced a rapid change in land cover. Population growth has increased the demographic pressure, resulting in uncontrolled and wild construction, first at the foot of slopes and then on the slopes themselves. The current demographic growth is a result of the birth rate, estimated at 8%, and the proximity of cities, notably Yopougon, Adjamé, and Plateau, where attractive economic activities are taking place.
3. Materials and Methods
3.1. Landslide Inventory and Dataset Preparation
Before carrying out the LS susceptibility modeling, acquiring information about LS data in the study area is vital. For our surveyed area, no reports of LS were found. Three steps were considered to address this problem of LS inventory. Firstly, we examined several archives: scientific articles, newspapers, and website information. Unfortunately, these archival sources explored appeared to be of very limited use, delivering frequently incomplete basic information about LSs. For example, the terminology used to describe types of LS is unclear, randomly confusing LS and debris or soil fall. Moreover, the number of LS occurrences during a particularly rainy day is not provided. The lack of clear temporal information and vagueness in the location of LSs were noted.
In response to these data scarcities, we undertook intensive fieldwork during multiple rainy seasons between 2015 and 2023 to develop a comprehensive and reliable landslide inventory. Consequently, LSs were mapped using a Garmin eTrex-10 GPS (KS, USA) receiver, which provided planimetric accuracy within a few meters. Furthermore, all identified mass movements were systematically described and classified according to the updated Varnes’ classification [32]. Moreover, morphometric attributes including scarp height, length, and width were measured whenever LSs were physically accessible. The LSs were further categorized as shallow or deep-seated based on the 2 m depth threshold proposed by [33].
To finalize the LS inventory, we employed a combined human–computer visual interpretation approach to identify and delineate observed LSs. This process was supported by the analysis of multiple data sources (Table 1). Specifically, we used Pleiades satellite imagery acquired on 29 April 2015; a 2016 orthophoto covering the eastern portion of the study area; post-2015 Google Earth images to detect more recent LS events; and high-resolution imagery from SAS Planet 2023. These data enabled us to accurately delineate landslides as polygons within the ArcGIS 10.3.1 environment [34] (Figure 3).

Table 1.
Information used. BNETD: Bureau National d’Etudes Technique et de Développement (or National Office of Technical Studies and Development); CCT: Centre de Cartographie et de Télédétection (Centre for Cartography and Remote Sensing); ONPC: Office National de la Protection Civile (or National Agency for Civil Protection); N.A.: not applicable.
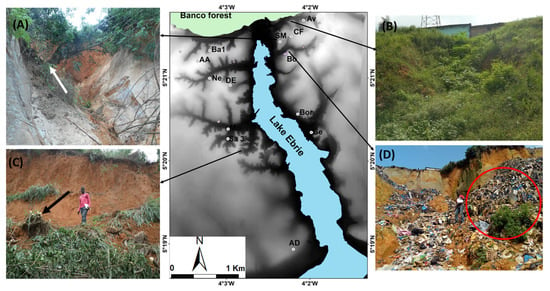
Figure 3.
Examples of mass movements identified in the digital elevation model (DEM). (A) Recent rotational slide in altered material (regolith) surveyed in the study area. The photo was taken in August 2017 (−4.036°, 5.356°). The white arrow shows the tilted tree. (B) The planar slide is covered by grasses. The photo was taken in August 2017 (−4.036°, 5.361°). (C) Shallow planar slide occurred in clayed sandy material. The photo was taken in June 2015 (−4.045°, 5.337°). The black arrow indicates an uprooted tree that has been cut by inhabitants. (D) Deep-seated planar slide. The photo was taken in August 2019 (−4.037°, 5.355°). The red circle indicates waste discharged in this LS.
In total, 67 LSs were recorded, most of which were small in size. The inventory comprised 54 planar slides and 13 rotational slides. A large majority (55) of these landslides were classified as deep-seated, while 5 were shallow, and the depth of 7 could not be determined. These landslides are predominantly located in the western part of Lake Ebrie, where the higher density is linked to the presence of steep-sided valleys.
The surface area of the smallest LS was 24 m2, while the largest reached 2100 m2, with an average of 301 m2. Altogether, the 67 landslides covered 0.0193 km2 (~2 ha), representing approximately 0.30% of the total study area.
Most of the LSs in the study area appeared to exhibit a climatic triggering pattern. The dates of occurrence, gathered through archival sources and field investigations, were correlated with daily rainfall data collected over the past 42 years (1981–2023) from SODEXAM (Société d’Exploitation et de Développement Aéroportuaire, Aéronautique et de la Météorologie, Ivory Coast), located 44 km from the site (Table 2). This external dataset was used due to the lack of local rainfall records.

Table 2.
LS occurrence dates associated with cumulative rainfall from 1996 to 2023.
Table 2 provides records for 25 landslides with precisely known dates between 1996 and 2023. Based on these data, two types of rainfall regimes were identified [35]: (i) high-intensity rainfall episodes (0–182.09 mm within the 3 days preceding the event), and (ii) moderately intense rainfall episodes (25.3–435.1 mm over the 15 days before those 3 days).
A comprehensive and reliable landslide inventory is critical for susceptibility modeling. According to [36], landslide susceptibility assessment is a complex and multivariate challenge, often involving considerable uncertainty in estimating the probability of occurrence. One major difficulty lies in the spatial variability of different types of mass movements, which are typically driven by distinct threshold conditions of contributing factors. When all types of movements are treated as a single input, weak correlations can arise between landslide distribution and causative factors [36].
To overcome this, it has been suggested [37] that the type of mass movement should be defined before the modeling stage. In this study, we focused solely on the 54 planar slides for the susceptibility analysis.
Another essential step in landslide modeling involves identifying representative samples of the failure zones. Various approaches exist for sampling, including using the full extent of the landslide, the source zone (scarps), or the centroid of either. In this study, only the scarps were selected for analysis. This decision was based on the fact that deposition zones are often altered by human activity, which complicates the accurate delineation. While using centroids can reduce spatial autocorrelation [38], it may also introduce model uncertainty [39]. Furthermore, a single value of a landslide-predisposing factor may not fully capture the complex mechanisms responsible for slope failure.
The scarp polygons of the 54 planar slides were converted into raster format at a spatial resolution of 5 m. From this, 443 pixels were identified and assigned a value of “1”, representing positive instances. For negative instances, pixels from non-landslide areas were randomly selected and assigned a value of “0”. A 1:5 ratio between LS and non-LS pixels was applied, resulting in a dataset of 2658 samples.
This dataset was randomly divided into calibration and validation subsets, using an 80:20 ratio. Although there are no fixed rules for determining this division, the 80% calibration and 20% validation split is commonly used [40] to balance the amount of data used for model training and performance testing.
3.2. Landslide Conditioning Factors
Estimating the probability of landslide (LS) occurrence requires the careful selection of relevant environmental factors. However, there are currently no universally accepted guidelines for identifying these influencing parameters. In this study, factor selection was guided by three main criteria: data availability, the typology of landslides observed, and findings from previous research [41]. Based on these considerations, nine primary factors were selected as input variables: altitude, slope, aspect, profile curvature, plan curvature, flow accumulation, distance to drainage networks, the normalized difference vegetation index (NDVI), and an urban-related layer (Table 3).

Table 3.
Database of explanatory variables for the current study.
To derive topographic attributes, a high-resolution digital elevation model (DEM) with a spatial resolution of 5 × 5 m was created using the Spatial Analyst toolbox in ArcGIS. This DEM was constructed from contour lines (2 m interval, 1.5 m planimetric accuracy), produced through photogrammetric processing of aerial photographs at a scale of 1:14,500 (Table 1). These primary datasets were enhanced with 766 ground control points and break lines. A triangulated irregular network (TIN) interpolation method, implemented in ArcGIS, was used to generate the DEM. The resulting DEM had a vertical root mean square error (RMSE) of 0.75 m, which provided sufficient detail for geomorphological analysis.
Several morphometric variables, derived from this DEM, benefit from the fine spatial resolution, allowing improved representation of local terrain characteristics [42]. The final dataset consisted of 16 explanatory variables: eight continuous and eight categorical variables derived from aspect reclassification. These variables formed the basis for assessing LS susceptibility in the study area.
Altitude (A) (Figure 4a): The altitude factor is a variable frequently used in studies of LS susceptibility and is quite often recognized as a significant predisposing factor. In the study area, the altitude range is very small (0–65 m), and we cannot expect any orographic effect on the amount of rain that would link the latter to altitude. Furthermore, altitude is frequently a derived predisposition factor linked to a primary factor such as lithology or slope. This low-relief area is characterized by sandy-clayed formation—on the scale for which information is available—uniform throughout the area. We paid close attention to the possible relationship between slope and altitude, two factors included in the list of potential predisposing factors.
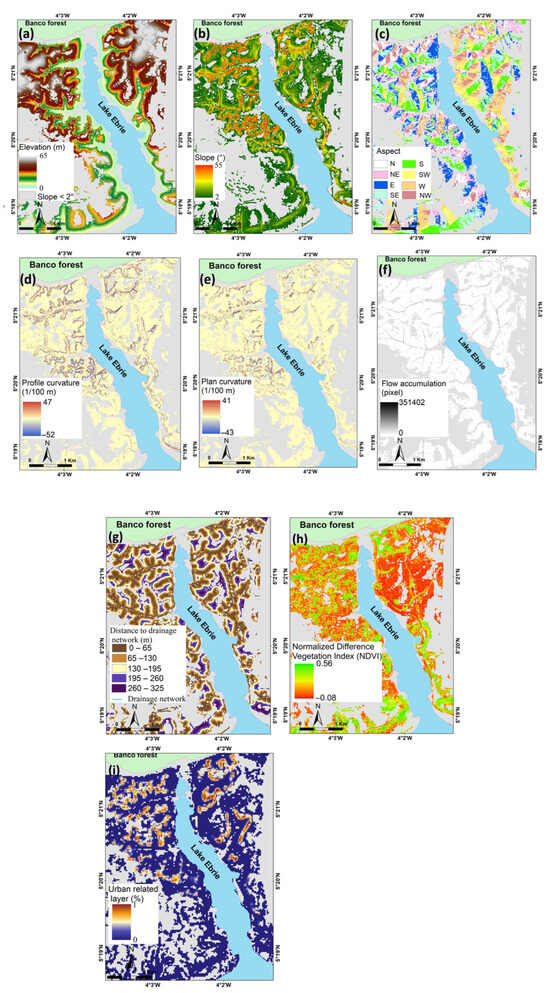
Figure 4.
Thematic maps of LS controlling factors. (a) Elevation; (b) slope; (c) aspect; (d) profile curvature; (e) plan curvature; (f) flow accumulation (g) distance to drainage network; (h) Normalized difference vegetation index (NDVI); (i) URL (artificial loading of upper hillslopes). The grey background represents slope values below 2° and is a non-susceptible area.
Slope (S) (Figure 4b): The slope factor is an essential variable in slope stability analysis. Physically, it is directly linked to the seepage process, shear stress, and gravitational effect, which directly affect LS stability [43]. The slope map in this study area was produced by the DEM and ranged from 2° to 45°.
Aspect (As) (Figure 4c): The aspect is considered to be a significant predisposing factor in LS susceptibility assessment [44,45]. It is decisive in specific climatic characteristics, such as the predominant direction of precipitation and the amount of solar radiation [46]. This factor was derived from DEM and divided into eight directions: north (N), northeast (NE), east (E), southeast (SE), south (S), southwest (SW), west (W), and northwest (NW).
Plan curvature (Cpa) (Figure 4d): The Plan curvature was used to describe the contour curvature of the slope surface. This factor controls the convergence/divergence of surface runoff and is derived from DEM produced, ranging from −43.67 to 41.48.
Profile curvature (Cpo) (Figure 4e): The profile curvature indicates the rate of slope change in the direction of the maximum slope. It corresponds to the curvature of the topographic surface along the line of greatest slope. This parameter controls the acceleration/deceleration of surface water flows and erosion/accumulation processes; it was extracted from DEM and ranged from −52.28 to 47.12.
Flow accumulation (Fa) (Figure 4f): The area drained by the pixel controls the degree of water saturation of the slopes and, hence, their stability. The relationship between flow accumulation, runoff concentration, flow rate, and LS occurrence has frequently been highlighted [47]. The greater the surface area drained upstream of a scarp, the greater the quantity of water that infiltrates the soil at the head of LS, bringing the slopes made of loose materials even closer to their failure threshold. This factor was extracted from DEM and ranged from 0 to 351,402 (pixels).
Distance to drainage network (Ddr) (Figure 4g): The cutting and erosion of the river-to-bank slope is considered the critical factor of LS stability. This factor’s influence is probably related primarily to the fact that the top of the water table is closer to the surface of the ground near valley bottoms and perhaps also to changes in the terrain caused by more effective gully erosion in this same topographical position. The distance ranged from 0 to 300 m from the buffer of the drainage work.
Normalized difference vegetation index (NDVI) (Figure 4h): The nature and density of ground vegetation cover can affect the resistance of slopes to LS, mainly through the strong control it exerts over the balance between infiltration and surface runoff during rainfall and through the effect of interception of drops and evapotranspiration on soil water content. This factor was derived from an overlay of bands 4 (PIR) and 3 (R) of the Pleiades multispectral image from 29 April 2015, using the “Image Analysis” window in ArcMap, and ranged from −0.23 to 0.62.
Urban-related layer (URL) (Figure 4i): This factor represents the artificial loading of upper hillslopes. “Construction” is considered to be human actions that can, to some extent, cause LS incidence. This parameter provides information about the percentage of built-up area on the tops of hillslopes. Using a topographic contour map and Pleiades image, constructions were digitized within a 100 m buffer from the edges of the interfluve plateau, considering a slope angle of 15°, and then converted to raster format in ArcMap. The values ranged from 0 to 1.
Before extracting the thematic layers, we delineated the area covered by our LS susceptibility modeling. We know that the identified LSs were exclusively distributed on the steep slopes separating the lowlands connected to Lake Ebrie from the residual plateau areas in the interfluves. Intensive fieldwork allowed us to confirm that interfluves and subhorizontal lowlands will never constitute LS starting zones. For this reason, to quantify the hazard inherent in the slopes alone more realistically, we reduced the area for which the modeling was carried out to only those surfaces with slopes greater than 2°.
3.3. Multicollinearity Analysis
Effective selection of LS-favoring variables is essential to produce reliable results when using the logistic regression (LR) model. A high correlation between independent variables can test the models produced in terms of performance and generalizability. Two stages were adopted for the optimal selection of variables.
The first phase consisted of estimating the Pearson coefficient (r). This assesses the linear relationship between continuous independent variables [48]. A variable with an r value of 0.7 or more indicates a strong linear correlation and should be excluded from predictive modeling. This coefficient was calculated using the following expression:
where are the values taken by the independent variables. and represent their respective means.
The second stage involved estimating 2 statistical indicators, such as the variance inflation factor (VIF) and the tolerance (TOL), in order to detect and reject strongly related variables. These were calculated as follows:
where is the coefficient of determination of a regression of j explanatory variables on the prediction variables. The exclusion or not of a variable from the model is based on the critical values of these 2 indicators. The elimination of a variable occurred when TOL < 0.1 and VIF > 10 occurred simultaneously [49].
The calculations were performed using the pixels of the calibration sets of scarps, corresponding to the pixels of the 8 explanatory variables.
3.4. Preliminary Assessment of the Individual Explanatory Power of Predictor Variables
Here, the frequency ratio (FR) was used as a complementary approach to assess the spatial correlation between the distribution of LS and potential LS-favoring variables [50], which helped to explain the role of the variables in contributing to LS occurrence. FR values were computed by dividing the LS frequency for a given predictor factor class by the frequency of LS incidence for the whole. If FR is more significant than 1, this indicates that the relationship between LS events and the influencing factors is stronger. This index is calculated as follows:
FR: Frequency ratio
Npix (LSi): Number of LS pixels into class (i) of the factor
Npix (Ci): Number of pixels belonging to class (i) over the whole study area
: Total number of LS pixels in the study area
: Total number of pixels in the study area
3.5. Logistic Regression Model
Logistic regression (LR) is a generalized linear model that predicts the probability of spatial occurrence based on a binary response (0 or 1) [51]. LR consists of finding the best fit of the model, establishing the relationship between LS (from an inventory and represented by a binary variable—LS presence: 1; absence: 0) and the independent variables. The basic equation for predicting future occurrence is as follows:
where represents the probability of LS occurrence and takes values between 0 and 1, is the intercept of the model, represents the jth of n predictive variables, and is the coefficient of respective variable that is needed to build the model. All calculations were performed in the RStudio environment (version 1.4.1717).
All coefficients obtained allowed predicted probabilities to be estimated, and these were classified into one of the response levels (i.e., 1 or 0) based on probability, with a cut-off value of 0.5. Then, cells with a probability above this cut-off value were classified as LS cells while those with lower probabilities were classified as non-LS cells.
During this process, we carried out backward elimination, which consisted of introducing all the explanatory variables into the model at the start and progressively eliminating them, depending on whether or not they were statistically significant. Then, we looked for models that minimized the loss of information by comparing their Akaike information criterion values [52]. Models with a low AIC value were considered to be robust. It should not be forgotten that AIC is a measure of the quality of a statistical model. It is calculated using the following expression:
where L is the maximized likelihood, and k is the number of LS-favoring variables in the model. AIC represents a compromise between bias (which decreases with the number of independent variables) and parsimony (the need to describe the data with as few variables as possible). Based on the AIC quality criterion, we simplified the model(s) produced. Assume a model M with the following parameters: spatial resolution of 5-m, X corresponding to scarps (E), the sampling ratio 1:5, where n is the number of explanatory input variables. This model is written as follows: 5X€ (1:5)|n.
AIC = −2 × log (L) + 2 × k
3.6. Model Performance
After building the LS susceptibility models (LSMs), it was essential to evaluate their performance. According to [53], LS susceptibility models that have not been validated hold no scientific value. For this reason, we used different accuracy metrics to evaluate the performance of the models obtained. In this study, overall accuracy (OA), RMSE, and area under the receiver operating characteristic curve (AUC-ROC) metrics were used to validate the results of the models. Regarding AUC-ROC, this metric represents a measure of the model’s predictive power. Thus, an AUC value close to 1 indicates that the model has high predictive power. An AUC value of 1 would indicate perfect discrimination of the danger zones. On the other hand, an AUC value slightly above 0.5 indicates a poorly predictive model, while an AUC of 0.5 means that the model’s performance is equal to that of a random prediction. Except for RMSE, the performance evaluation metrics were computed using the components of the confusion matrix. In Equation (6), TP (true positive) and TN (true negative) express the number of pixels correctly classified as LS and non-LS, respectively; FP (false positive) and FN (false negative) denote the number of pixels misclassified as LS and non-LS, respectively [54].
where n is the number of calibration or validation data sets, XP corresponds to the probabilities predicted by the models (LS pixels), and XO represents the events (LS pixels) or non-events (non-LS pixels).
3.7. Cost Functions and Risk Classes
3.7.1. Cost Curve
In a binary classification problem, the input vectors (variables) are X = {x1, …, xm} with xi ∈ Rd, and the landslide classes are Y = {y1, …, ym} with yi ∈ {0, 1}. Here, xi is the i-th value of the variable described by dimension d, yi = 1 represents the class of events, and yi = 0 represents the class of non-events. In this scenario, each event/non-event pixel i is associated with a specific cost Ci. For example, for correctly classified pixels, i.e., true negatives and true positives, the associated costs are CTN and CTP, respectively. Furthermore, the costs associated with model-induced misclassification of pixels are the cost of false negatives (CFN) and the cost of false positives (CFP), respectively. [54]. In general, the costs associated with CTN and CTP equal zero. Therefore, for the classifier hi (x) (here, the decision threshold), the total expected cost based on this cost matrix is given by the following expression:
where yi ∈ {0, 1} is the observed category and hi ∈ {0, 1} is the predicted category for observation i, with n being the number of observations. represents the logistic regression model (5X (=E) (1:5)|n) obtained in Section 3.5.
The (arbitrary) sample ratio of 1:5 shows a disproportion between event and non-event pixels. This significant imbalance logically calls for the application of rare event modeling. However, our sample was sufficient to train a standard logistic regression. To better reflect reality, we reconsidered the sampling ratio. Our sample spanned several years (up to 10 years), during which the inventory could not be constructed systematically. Nevertheless, the prediction map derived from this inventory is likely to remain valid for several decades (up to 50 years), during which LS hazard is expected to increase due to climate change [55] and the impact of human activities on hillslopes [3,9]. Consequently, the number of events is likely to be significantly higher than what we initially observed. Our dataset indicates that one pixel out of 1000 experienced a LS, which is a very low rate. Considering the extended time span covered by the susceptibility map, along with climate change and anthropogenic alterations, we anticipate a higher frequency of LSs in this urban area. We can reasonably assume that the future number of events will be twenty times greater than our current observation, that is, 20 out of 1000 pixels, or 2%, equating to a 1:50 ratio between LS and non-LS pixels. This defines the new model, expressed as follows: (5X (=E) (1:50)|n).
3.7.2. Data Description
Estimating the costs associated with model misclassification (CFN and CFP) ideally requires detailed socio-economic data. However, due to the unavailability of such information, we empirically assessed these costs based on specific considerations that would give a realistic character to the data sets envisaged. To this end, we defined a false positive to false negative (FN/FP) cost ratio. The cost associated with false positives (CFP) is interpreted as an additional investment in prevention measures, which we estimate to be around 10% of the total investment, particularly since some buildings are located in areas of potential instability. Given the sparsity of the study area, false positives were assigned a weight of 1. In contrast, the occurrence of a LS can expose certain elements to high socio-economic losses and, potentially, human fatalities. Therefore, the cost of false negatives was estimated at 150% of the investment, relative to CFP. Based on a projected LS frequency increase by a factor of 20 (see Section 3.7.1), we assigned a weight of 300 (20 × 15) to FN and 1 to FP, to examine the sensitivity of the threshold to variations in the cost ratio. Additional scenarios were tested using alternative cost ratios of 250 (12.5 × 20) and 350 (17.5 × 20).
4. Results
4.1. Multicollinearity Analysis
The selection of LS conditioning variables is essential for developing reliable models that can accurately distinguish between areas susceptible to mass movement and stable zones. In this study, variable selection was performed using Pearson correlation, the variance inflation factor (VIF), and tolerance (TOL). The results of the correlation matrix are presented in Table 4. As shown in this table, none of the LS-conditioning variable pairs exceed the critical correlation threshold of 0.7. This indicates the absence of multicollinearity among predictor variables, confirming their suitability for LS hazard assessment.

Table 4.
Pearson correlation between pairs of predictor variables.
The next step in the variable selection phase was to analyze the VIF and TOL statistical indicators. A VIF > 10 and TOL < 0.1 indicate significant multicollinearity between these factors [56]. The results (Table 5) showed that variables such as profile curvature (1.48), plan curvature (1.44), altitude (1.29), and urban-related layer (1.23) had the highest VIF values, indicating low tolerance values. These results satisfied the critical thresholds, i.e., VIF > 10 and TOL < 0.1, which means that there was no multicollinearity between these eight LS-favoring variables. Therefore, these factors were used as input factors of LS susceptibility mapping for model calibration.

Table 5.
Multicollinearity analysis of the evaluation factors.
4.2. Relationship Between Explanatory Variables Using FR
The frequency ratio (FR) establishes the correlation between LS and the factors that cause failures. If a class has an FR value > 1, then this class has a high correlation with LS events; in contrast, if a class has an FR value < 1, then this class has a low correlation with LS events [57]. The FR values for each class of the 16 factors that cause mass movements are shown in Table 6. In the table, altitude values between 20 and 50 m have FR values > 1, indicating the high probability of LS occurring in these classes of variables. In the case of the slope variable, the higher its value, the greater the probability of LS. For the classes 5–15° (1.03), 15–30° (2.65), 30–45° (4.94), and >45°, the FR values are greater than 1, showing the association between these classes of independent variables and the dependent variable (LS). Regarding the drainage network variable, the 0–75 m and 75–150 m classes have high FR > 1 values. However, no LSs were observed as the distance from the network increased (classes 150–225 m and 225–300 m). In the case of the urban-related layer, classes 0–0.22 and 0.22–0.44 have FR > 1 values, indicating the high susceptibility to mass movement in these classes. It can be seen from this table that NDVI values between 0.11 and 0.62 have FR values > 1, indicating the association between areas (wooded or grassy) and the occurrence of failures. The FR values for the flow accumulation class (0–57,274 pixels) are greater than 1. As can be seen from this table, aspect classes such as north (1.29), south (1.27), and northwest (3.56) have FR > 1 values. This shows the strong correlation between these variable classes and LS. However, the remainder of the aspect classes have a FR value < 1. The FR values for the plan curvature classes −43.67–−2.93 (5.65) and 2.93–41.48 (7.27) are greater than 1, indicating a high probability of mass movement. However, the class −2.93–2.41 has a FR (0.77) value < 1, indicating a low probability of LS. In the case of curvature in profile, the classes −52.28–−3.16 (6.08) and 3.07–47.12 (3.10) have FR values greater than 1.

Table 6.
Spatial relationship between each prediction variable and LS. Legend: Npci = number of pixels belonging to class (i) over the whole study area; NpLS = number of pixels of LS in class (i) of the variable; Ppci = percentage of pixels belonging to class (i) over the whole study area; PpLSci = percentage of pixels of LS in class (ci); Fri = frequency ratio.
4.3. LS Occurrence Model
The LS occurrence model was built after carrying out an exploratory analysis of all LS-favoring variables. The final model was built using the backward elimination approach. In this process, three LS susceptibility models (M1 = 5E1:5|16, M2 = 5E1:5|11 and M3 = 5E1:5|10) were produced (Table 7). Based on the AIC criterion, models M2 and M3 fit the sampled variables well. These two models have similar AICs, and this does not facilitate the choice of the best model. Adopting the principle of parsimony, we selected M3 (5E1:5|10), because of the reduced number of independent variables (10) and its AIC quality (Table 7). For the prediction of susceptibility to mass movements, variables such as altitude, aspect (NW, SE, S, and SW), urban-related layer, flow accumulation, NDVI, profile curvature, and slope were included in the model, because of their statistical significance (significance level α = 5%). Table 8 presents the coefficients for these predictor variables.

Table 7.
Models and their respective AICs.

Table 8.
Estimated variable coefficients, odds ratios, coefficient confidence (95%), and p-value for the final LR model M3.
4.4. Performance Assessment
In this study, different metrics, including overall accuracy (OA), RMSE, and area under the receiver operating characteristic (ROC) curve (AUC), were used to evaluate the performance of the LR model (Table 9). These metrics were applied for both calibration and validation stages. Based on the calibration datasets, the model 5E1:5|10 presented OA equal to 87.5%, while a value of 89.5% was obtained for validation datasets. One of the commonly used metrics to measure the accuracy of models is RMSE [58]. This is used to measure the prediction error of the model; the closer it is to 0, the better the performance of the model [58]. Thus, the RMSE was 0.291 for the calibration datasets and 0.267 for the validation datasets. In this study, we also used the AUC metric to evaluate the models’ performance in terms of calibration and validation datasets. As can be seen, Figure 5 shows the ROC curves and AUC values of the model 5E1:5|10. Examining this figure, it can be seen that the model had an AUC value (0.915) using calibration datasets, while this value was 0.938 for validation datasets. It may be noted that the AUC value obtained with the testing datasets was greater than the AUC value acquired with the training datasets.

Table 9.
Performance of the LR (5E1:5|10) models in the calibration and validation stages.
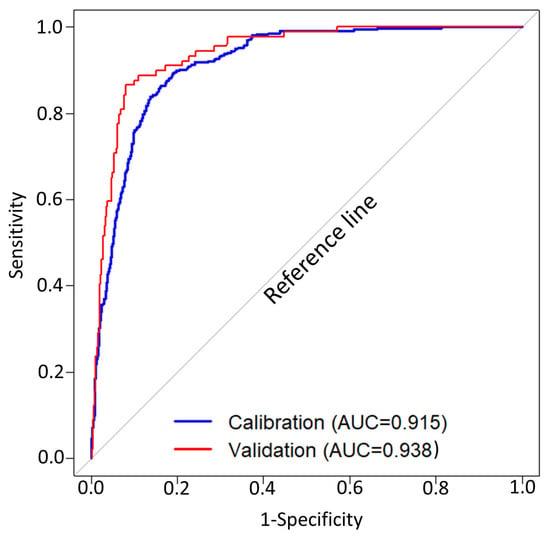
Figure 5.
ROC curves and AUC values of the model (5E1:5|10).
4.5. Landslide Susceptibility Map (LSM)
LR was used to build the model 5E1:5|10 to find the optimal regression coefficients (Table 8). These were used to generate probabilities of LS occurrence based on a scale of 0 to 1. These estimated probabilities associated with LS were classified into five levels of susceptibility according to the natural breaks–Jenks approach: very low (0–0.06), low (0.06–0.2), moderate (0.2–0.4), high (0.4–0.7), and very high (0.7–1). Visual inspection of the susceptibility maps after classification revealed the distribution of the LS susceptibility level (very high) throughout the entire study area (Figure 6). To better analyze the classification of the LS susceptibility maps, two indicators were used in this case: the proportion of area and LS pixels.
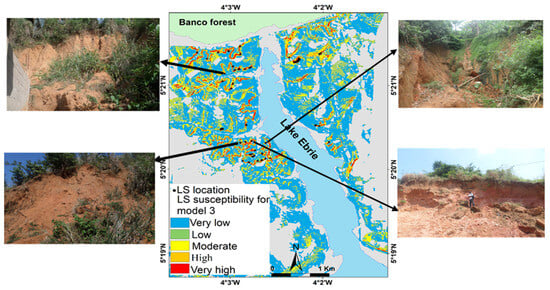
Figure 6.
LS susceptibility map using model 3, showcasing several identified LSs.
In model 5E1:5|10 (Table 10), the susceptibility classes (very low and low) covered more than half (86.7% or 9.5 km2) of the study area (slope > 2°), with a proportion of LS equal to 15.6% and an estimated frequency ratio of 0.6. The model’s susceptibility levels (high and very high) covered only 6.3% (0.7 km2) of the built-up area, with values of 61.2% and 20.2% attributed to the LS proportion and FR, respectively.

Table 10.
Classification statistics for LS susceptibility based on the model (5E1:5|10).
4.6. ROC and Cost Curves
In the LS risk management context, the definition of a decision threshold associated with the ROC curves enables the determination of whether a given area (pixel) is hazardous or not, leading to the consideration of preventive measures. In this study, the threshold value was determined using the model (5E1:50|10) and data derived from empirical costs. Considering the cost ratio (300/1), Figure 7 shows an estimated global optimum threshold of 0.04, and the total cost associated with this value equaled 75,000 (an arbitrary value). for the additional scenarios, the results revealed a negligible threshold value similar to the first. This shows the low sensitivity of the threshold to changes in cost ratios.
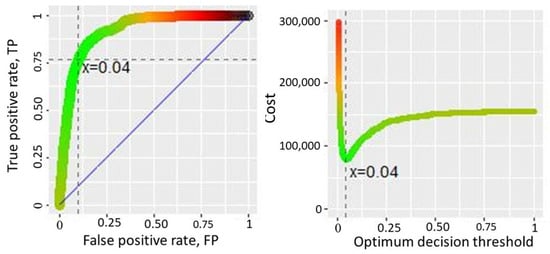
Figure 7.
ROC curve and cost function showing optimal threshold for the scenario (FN/FP). This scenario indicates an optimal threshold equal to 0.04. The cyan dotted line on the cost function curves indicates where the optimal point is for plotting costs. For the ROC curve, the intersection shows the location of the FP rate and the TP rate corresponding to the optimal threshold value. The color of the curve indicates the cost associated with this point: greener means that the cost is lower, while blacker means the opposite.
The ROC curves constructed from the different threshold values show the rate of true positives identified as a function of the false positives misclassified. The area under these curves, estimated at 0.92, shows the performance of our model (AUC > 0.90, excellent).
The optimal thresholds, as shown on the ROC curves, were used to evaluate statistical indicators (Table 11) and obtain an overall view of cost minimization. Taking into account the optimum threshold (X = 0.04), we note that the dangerous (or unstable) areas are concentrated in the upper part of the hillslopes, and a large part of the study area is classified as stable and available for construction (Figure 8). Although a clear difference was not observed, these susceptibility maps associated with costs constitute decision-making tools for local authorities responsible for land use and urban space planning. This could be improved by taking accurate socio-economic data into account.

Table 11.
Evaluation of statistics using optimal threshold values for cost ratio (300/1).
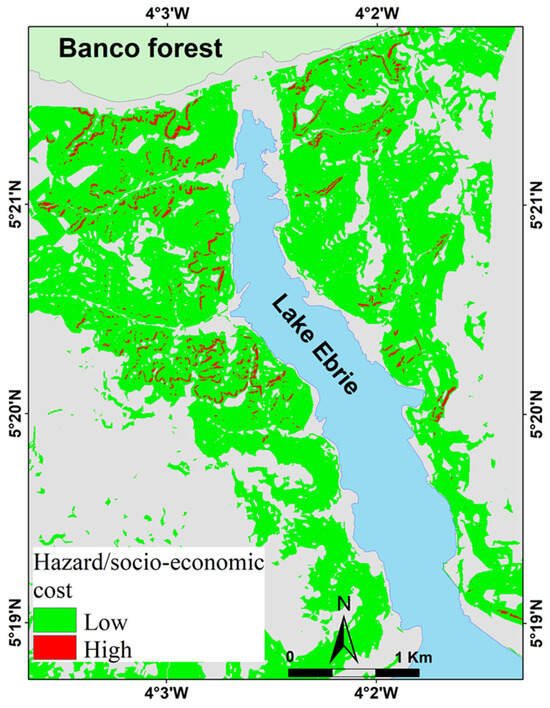
Figure 8.
Susceptibility patterns classified into stable/unstable zones using optimal threshold value for the scenario (FN/FP).
5. Discussion
5.1. Determination of Unsafe Slopes Using the Model and the Influence of Individual Variables
The study area, located in the central part of Greater Abidjan, is frequently subject to LSs. This study aims to fill the knowledge gap about LSs and to produce a LS susceptibility map for the study area. Some research has been conducted in this urbanized area [22] focused on the impacts of meteorological conditions on slope classification. Marcel et al. [23] have assessed the socio-economic impacts of LS occurrence. However, they did not assess the LS-driving variables or LS susceptibility.
Field observations and the interpretation of satellite images revealed that many natural and human-made factors contribute to triggering these mass movements. In the study area, LS are mainly affected by morphological factors, precipitation, geological formations, and changes in land use. To determine the relationship between LS occurrence and the driving variables, the FR approach was produced using weights for each class of conditioning factors (Table 6). Table 6 represents the relationship between LS events and the classes of each conditioning factor. In the case of the relationship between LS occurrence and altitude, the failure mainly occurred at altitude between 30 and 40 m. For areas with a slope angle > 45°, the area’s susceptibility to the LS occurrence is higher. Regarding distance to drainage, susceptibility to LS increases with class 75–150 m. The ratio for the urban driving variable is higher for the 0.22–0.44% class. NDVI is one of the conditioning factors that directly impact the presence of LS.
For this driving variable, the highest FR ratio (2.35) was obtained for forested slopes, which amplified the LS occurrence. For flow accumulation, the increase in LS occurrence was obtained for class 0–57,274 (pixels). The impact of each aspect was assessed as contributing to the occurrence of LS. The ratio was highest (3.56) for the NW class. A high value of the FR ratio for the slope curvature class is characteristic of concave slopes, indicating a high probability of landslides.
The multivariate statistical analysis (MSA) was performed using LR, and the relationship between the LS incidence and LS driving factors was assessed. The LS favouring factors are obtained and listed in Table 8. As shown in this table, driving variables (altitude, slope, southeast, south, northwest, and NDVI) positively influenced LS occurrence in this urban area. Among these six significant driving factors, NDVI was the main conditioning factor. This predictive variable had a high magnitude positive coefficient (), revealing vegetated areas where slopes are likely to be stable. Some studies have pointed out that the presence of vegetated surfaces may be more effective in reducing susceptibility [59]. Similarly, other work [60] highlighted that vegetated areas are commonly related to increased slope stability. However, we note the inverse relationship between NDVI and LS occurrence in the study area. The density of LS occurrence increases and decreases with increasing NDVI values. Surfaces with NDVI values of 0.24–0.38 are most susceptible to LS incidence. The presence of plants (Rottboellia Cochinchinensis and Panicum Maximum) and urban crops such as maize, cassava, potato, and peanut along the hillslopes does not offer protection against LS, because these plants have shallow roots. Recent studies [61] in Lin’an, a city in Zhejiang Province, China, have revealed that shrub forests with shallow root systems (0 to 30 cm) favor the occurrence of LS. On the other hand, low NDVI values are primarily concentrated in valleys and interfluves where human activities are prevalent. These areas are relatively flat and are not conducive to the formation of LSs.
In this study, the results showed that the most susceptible class of the aspect factor was the northwest (), followed by the south () and southeast () classes. This may be due to the prevailing wind direction coming from the south and southeast (Greater Abidjan). These hillslopes, exposed to the wind during the rainy season, receive rainfall that infiltrates the clayed sand units. This water infiltration reduces the shear strength of this formation and triggers a LS. Regarding the slope, our results revealed that slope angle plays a role in the occurrence of LSs in the study area. The frequency distribution of LSs shows that slopes above 5° are potentially subject to landsliding. This is consistent with results found in other tropical regions [62]. However, our results do not align with those of [63]. Those authors reported that, at a constant altitude, the probability of LS occurrence increased, then decreased with the increasing slope, reaching its maximum between 28° and 50°. These findings were confirmed by the work of [64], who indicated that the probability of LS increased with the slope, but decreased with slopes greater than 70°. We note that the altitude variable has a minor influence on the occurrence of LS in this urbanized area, as its odds ratio () is close to unity. The interelationship between LSs and altitude is more pronouced at elevations ranging from 20 m.a.s.l to 40 m.a.s.l. The weak association of LSs with altitude has been investigated in previous studies. For example, Van Den Eeckhaut et al. [65] used a “rare event logistic regression” model to assess LS susceptibility prediction in W Belgium (altitude ranging from 10 m.a.s.l to 150 m.a.s.l) and stressed that terrain height had a relatively minor influence, with an odds value estimated at ().
Although altitude has little impact on the initiation of LSs, hillslopes concentrate anthropogenic activities such as clearing of slopes, construction of informal settlements at the tops of slopes, and inadequate solid waste management, which can lead to an increase in LSs in areas with gentle slopes [66]. In this highly urbanized context, we introduced an anthropogenic variable (URL) that describes artificial loading (informal settlements) of upper hillslopes to assess its real contribution to LS occurrence. Incorporated into the dataset to assess the prediction map, the model revealed that this variable had no significant influence (= 0.23) on LS development. Several reasons may explain this situation. Firstly, this variable reflected the low levels of construction at the immediate edges of the hillslopes, especially since distributed loads created by buildings with diffuse local stress presented a weak intensity of surcharge. Secondly, the size of the map unit (25 m2) may not be appropriate to cover a sufficient portion of the buildings. Therefore, increasing the pixel size will be necessary in future research. Notwithstanding its lesser contribution, this variable remains important when modeling LSs in a continuously changing urban context. On the other hand, in addition to this, it would be desirable to include other anthropogenic variables such as huge amounts of waste, pedestrian paths, and makeshift pipes, to improve understanding of their influence on LS incidence. Given the spatial dynamics, it will be important to update our construction dataset (polygons) by considering recent satellite images of urban sprawl.
Based on the coefficients derived from the LR, the LS probability map was generated from the (5E1:5|10) model. This LS probability map shows that the probability of failure is high along hillslopes with steep slopes and altitudes. The obtained LS probability map was categorized into five susceptibility levels, using the Jenks Breaks method. This classification approach was used because it minimizes intra-class variance and maximizes inter-class variance. Finally, the LS susceptibility map for Attecoube, using only the main escarpments, included values as follows: very low (0–0.06), low (0.06–0.2), medium (0.2–0.4), high (0.4–0.7), and very high (0.7–1); map is shown in Figure 6. Based on the LS susceptibility map acquired, most areas (around Lake Ebrie, interfluves, and valley bottoms) are located in very low and low susceptibility zones, covering more than 86.7% or 9.5 km2, with a proportion of LS equal to 15.6% and an estimated frequency ratio (FR) of 0.6. The high and very high susceptibility zones cover only 6.3% (0.7 km2) of the urban area, with values of 61.2% and 20.2% attributed to the proportion of LS and the FR, respectively. These zones are distributed over almost the entire study area and are located along the slopes. The (5E1:5|10) model obtained during this research was evaluated using the area under the curve (AUC-ROC). The performance and predictive capacity of the model were determined by considering different configurations of calibration and validation samples. The AUC-ROC values obtained were described as excellent (AUC-ROC > 0.9). This result suggests that the model produced in this study demonstrates a high level of accuracy in predicting the spatial probability of LS in Attecoube. Having been used in several publications, logistic regression has produced promising AUC-ROC results ranging from 0.79 to 0.93 [67].
The results of this study can help urban planners and decision-makers reduce the areas where LSs are likely to occur. The prediction model used in this study has proven to be very useful for effective land management.
5.2. ROC and Cost Curves
The adoption of the prediction model enabled the assessment of the minimum costs for the study area, based on various cost ratios. Figure 7 shows a negligible optimum threshold value, which was used to estimate these two costs. Integrating a cost function into a logistic regression model (5E1:50|10) enables the determination of optimum thresholds, which are useful for discriminating between areas susceptible to mass movement and stable zones (Figure 7). The threshold (X = 0.04) shows a low frequency of pixels exposed (unsafe/unstable) to mass movements in the study area. However, a significant fraction of pixels were classified as safe or stable. This was due to the sufficient quantity of non-events derived from the sampling ratio (1:50), which was introduced to calibrate the susceptibility model.
The increase in stable zones (FN) coupled with the reduction in unstable zones (FP) constitutes a significant housing problem in the study area (Table 11). Unstable areas, characterized by high economic costs, are concentrated on the upper parts of the hillslopes. To a certain extent, these areas, which are considered dangerous, are unsuitable or even unfit for construction. The current planning regulations adopted by the Attecoube municipal authorities (and, indeed, the Ivorian government) are very close to this situation. In this context, residents reported the destruction of several buildings at the top of the hillslopes during our fieldwork. This was linked to the recurrent occurrence of mass movements with their attendant loss of life and injuries. Stable zones with low economic costs occupy a significant proportion of the study area (talwegs, slopes, and hilltops). Analysis of the costs associated with misclassification reveals that the probability of committing a type II error (false negative rate) is almost three times higher than that of committing a type I error (false positive rate). Given the evolution of the hillslopes in this urban area, except for the gentle slopes (talwegs, tops of slopes, around the bay lagoon), the other slopes can be assumed to be hazardous. It is, therefore, essential to recommend preventive measures to stabilize hillslopes, especially as human activities and the effects of climate change have adverse consequences on the balance of slopes in urban areas.
This study assessed the costs associated with classification errors based on empirical data (extracted from LS datasets). Using real socio-economic conditions, which control the cost of elements exposed to LS risk, would be interesting. This approach would enable the susceptibility model to effectively determine the real costs associated with type I and type II misclassifications. These costs could also be allocated based on the decision-maker’s approach to the hazard, which reflects society’s perception of the risk. For example, suppose a given company is prepared to tolerate a high level of risk. In that case, decision-makers will depreciate the cost of false negatives, reducing the cost ratio (FN/FP). On the other hand, if the company tolerates a low level of risk, decision-makers will have to increase the cost of false negatives. In the first case (low cost ratio), a cost-sensitive criterion would favor a model that classifies a small part of the zone as unstable and of course, the opposite would apply in the second case.
6. Conclusions
Accurate LS prediction maps are essential tools for urban planners and decision-makers to reduce the risk of human casualties and infrastructure damage. In this study, we applied logistic regression (LR) and frequency ratio (FR) models to assess LS susceptibility maps for the municipality of Attecoube, situated in the central part of Greater Abidjan. The dataset used consisted of 54 scarps from planar slides and 16 LS-conditioning variables. Among these, altitude, slope, southeast, south, northwest orientations, and NDVI were identified as significant positive contributors to LS occurrence. The most at-risk areas are located in hilly zones where clayed sands are saturated and anthropogenic activities are concentrated. The LR-based model (5E1:5|10) classified the study area into five susceptibility categories: very low, low, moderate, high, and very high. High and very high susceptibility zones together covered approximately 0.7 km2, accounting for 6.3% of the total study area (12.4 km2). Model validation using the ROC curve yielded a prediction rate of 0.938, indicating strong predictive performance and reliability for application in LS hazard forecasting within Attecoube. To further support risk planning, we recommend that local authorities integrate susceptibility maps with detailed escarpment information (E). The integration of a cost function into a logistic regression model made it possible to test the sensitivity of thresholds to variations in the cost ratios of FN and FP, using a reasoned sample size (1:50). The optimal thresholds obtained were similar and negligible in their differences, allowing clear distinction between zones of low and high susceptibility. Overall, the resulting maps constitute practical tools for guiding protection strategies and land-use planning within the municipality.
Author Contributions
Conceptualization and writing—original draft, F.L.G., A.D. and S.S.; methodology, F.L.G., H.B.K., A.H.-F. and J.B.; investigation, F.L.G.; formal analysis, F.L.G. and A.D.; supervision, S.S. and A.D.; review, F.L.G., A.D. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors declare no external funding.
Data Availability Statement
The used data in the present manuscript are confidential.
Acknowledgments
The authors thank the Office National de la Protection Civile (ONPC, or National Agency for Civil Protection) and the municipality of Attecoube for providing reports on past landslides. Also, they gratefully acknowledge the support of BNETD (Bureau National d’Etudes Technique et de Développement) and CCT (Centre de Cartographie et de Télédetection, or Cartography and Remote Sensing Centre) for the topographical data provided.
Conflicts of Interest
The authors declare no potential conflicts of interest.
References
- Cruden, D.M. A simple definition of a landslide. Bull. Int. Assoc. Eng. Geol. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Petley, D.N. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Ozturk, U.; Bozzolan, E.; Holcombe, E.A.; Shukla, R.; Pianosi, F.; Wagener, T. How climate change and unplanned urban sprawl bring more landslides. Nature 2022, 608, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.Y.; Quevedo, R.P.; Wang, H.Y.; Fu, Q.; Luo, D.; Wang, T.; de Oliveira, G.G.; Guasselli, L.A.; Renno, C.D. Improved tree-based machine learning algorithms combining with bagging strategy for landslide susceptibility modeling. Arab. J. Geosci. 2022, 15, 183. [Google Scholar] [CrossRef]
- Ye, P.; Yu, B.; Chen, W.; Liu, K.; Ye, L. Rainfall-induced landslide susceptibility mapping using machine learning algorithms and comparison of their performance in hilly area of Fujian Province. China Nat. Hazards 2022, 113, 965–995. [Google Scholar] [CrossRef]
- Orhan, O.; Bilgilioglu, S.S.; Kaya, Z.; Ozcan, A.K.; Bilgilioglu, H. Assessing and mapping landslide susceptibility using different machine learning methods. Geocarto Int. 2022, 37, 2795–2820. [Google Scholar] [CrossRef]
- Yan, F.; Zhang, Q.; Ye, S.; Ren, S. A novel hybrid approach for landslide susceptibility mapping integrating analytical hierarchy process and normalized frequency ratio methods with the cloud model. Geomorphology 2019, 327, 170–187. [Google Scholar] [CrossRef]
- Wang, X.; Ma, X.; Guo, D.; Yuan, G.; Huang, Z. Construction and Optimization of Landslide Susceptibility Assessment Model Based on Machine Learning. Appl. Sci. 2024, 14, 6040. [Google Scholar] [CrossRef]
- Li, Y.; Duan, W. Decoding vegetation’s role in landslide susceptibility mapping: An integrated review of techniques and future directions. Biogeotechnics 2023, 2, 100056. [Google Scholar] [CrossRef]
- Zhang, W.G.; He, Y.W.; Wang, L.Q.; Liu, S.L.; Meng, X.Y. Landslide susceptibility mapping using random forest and extreme gradient boosting: A case study of Fengjie, Chongqing. Geol. J. 2023, 58, 2372–2387. [Google Scholar] [CrossRef]
- Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2022, 37, 2441–2465. [Google Scholar] [CrossRef]
- Achu, A.L.; Aju, C.D.; Reghunath, R. Spatial modelling of shallow landslide susceptibility:A study from the Southern Western Ghats region of Kerala, India. Ann. GIS 2020, 26, 113–131. [Google Scholar] [CrossRef]
- Chen, W.; Sun, Z.; Han, J. Landslide susceptibility modeling using integrated ensemble weights of evidence with logistic regression and random forest models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (Wi) and adaptive neuro-fuzzy inference system (ANFIS) model at Alborz Mountains (Iran). Environ. Earth Sci. 2016, 75, 553. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Ding, D.; Wu, Y.; Wu, T.; Gong, C. Landslide susceptibility assessment in Tongguan District Anhui China using information value and certainty factor models. Sci. Rep. 2025, 15, 12275. [Google Scholar] [CrossRef]
- Cui, K.; Lu, D.; Li, W. Comparison of landslide susceptibility mapping based on statistical index, certainty factors, weights of evidence and evidential belief function models. Geocarto Int. 2017, 32, 935–955. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Traore, H.K.; De Angeli, S.; Lebaut, S.; Drogue, G.; Konan Kouadio, E. A spatio-temporal analysis of the risks of flooding and landslides in Greater Abidjan, Ivory Coast, by applying a multi-risk framework. In Proceedings of the EGU General Assembly, Vienna, Austria, 14–19 April 2024. [Google Scholar]
- Hauhouot, C. Analyse du risque pluvial dans les quartiers précaires d’Abidjan. Etude de cas à Attécoubé. Géo-Eco-Trop 2008, 10, 75–82. [Google Scholar]
- Marcel, B.K.; Athanase, A.A.; Joël, K.K.; Della André, A. Accidents related to the 2014 rains and their socio-economic consequences in the city of Abidjan: The case of the municipalities of Abobo and Attécoubé (Côte d’Ivoire). J. Geosci. Environ. Prot. 2021, 9, 195–208. [Google Scholar] [CrossRef]
- Fraternité Matin. Les pluies font six morts à Abidjan. Fratern. Matin 2023, 17536, 9. [Google Scholar]
- Recensement Général de la Population et de L’habitat; Agence Nationale de la Statistique: Abidjan, Côte d’Ivoire, 2014.
- N’dri, B.E.; Niamke, K.H.; Bakayoko, S.; Soro, G.; Niangoran, K.C.; N’go, Y.A. Dynamique de l’occupation des sols de la commune urbaine d’Attécoubé (Côte D’Ivoire). LARHYSS J. 2016, 26, 129–147. [Google Scholar]
- Kouassi, A.; Kouassi, F.; Mangoua, J.; Savane, I. Modèle conceptuel de l’aquifère du Continental Terminal d’Abidjan. IAHS Publ. 2014, 363, 256–262. [Google Scholar]
- Sidle, R.C.; Ochiai, H. Landslides: Processes, Prediction and Land Use; Water Resources Monograph; American Geophysical Union: Washington, DC, USA, 2006. [Google Scholar]
- Dewitte, O.; Jones, A.; Spaargaren, O.; Breuning-Madsen, H.; Brossard, M.; Dampha, A.; Deckers, J.; Gallali, T.; Hallett, S.; Jones, R.; et al. Harmonisation of the soil map of Africa at the continental scale. Geoderma 2013, 211–212, 138–153. [Google Scholar] [CrossRef]
- Jones, A.; Breuning-Madsen, H.; Brossard, M.; Dampha, A.; Deckers, J.; Dewitte, O.; Gallali, T.; Hallett, S.; Jones, R.; Kilasara, M.; et al. Soil Atlas of Africa; European Commission Publications Office of the European Union: Gasperich, Luxembourg, 2013; p. 176. [Google Scholar]
- Kouakou, K.E.; Moussa, H.; Kouassi, A.M.; Goula, B.T.A.; Savane, I. Redefinition of homogeneous climatic zones in Côte d’Ivoire in a context of climate change. Int. J. Sci. Eng. Res. 2017, 8, 453–462. [Google Scholar]
- Peel, M.; Finlayson, B.; McMahon, T. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types: An update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth-Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop: Release 10.1; Environmental Systems Research Institute: Redlands, CA, USA, 2015. [Google Scholar]
- Chleborad, A.F.; Baum, R.L.; Godt, J.W. Rainfall Thresholds for Forecasting Landslides in the Seattle, Washington, Area-Exceedance and Probability; U.S. Geological Survey Open-File Report 2006–1064; U.S. Geological Survey: Reston, VA, USA, 2006; 31p. [Google Scholar]
- Zêzere, J.L. Landslide susceptibility assessment considering landslide typology. A case study in the area north of Lisbon (Portugal). Nat. Hazards Earth Syst. Sci. 2002, 2, 73–82. [Google Scholar] [CrossRef]
- Irigaray, C.; Chac’on, J.; Fern’andez, T. Methodology for the analysis of landslide determinant factors by means of a GIS: Application to the Colmenar area (Malaga, Spain). In Landslides, Proceedings of the Eighth International Conference and Field Trip on Landslides, Granada, Spain, 27–28 September 1996; Balkema: Rotterdam, The Netherlands, 1996; pp. 163–172. [Google Scholar]
- Kubwimana, D.; Ait Brahim, L.; Nkurunziza, P.; Dille, A.; Depicker, A.; Nahimana, L.; Abdelouafi, A.; Dewitte, O. Characteristics and Distribution of Landslides in the Populated Hillslopes of Bujumbura, Burundi. Geosciences 2021, 11, 259. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; McDonald, E.V.; Vitek, J.D. A comparison of logistic regression-based models of susceptibility to landslides in western Colorado, USA. Landslides 2014, 11, 247–262. [Google Scholar] [CrossRef]
- Kainthura, P.; Sharma, N. Hybrid machine learning approach for landslide prediction. Uttarakhand India Sci. Rep. 2022, 12, 20–101. [Google Scholar]
- Achour, Y.; Pourghasemi, R.H. How do machine learning techniques help in increasing the accuracy of landslide susceptibility maps? Geosci. Front. 2019, 11, 871–883. [Google Scholar] [CrossRef]
- Cavazzi, S.; Corstanje, R.; Mayr, T.; Hannam, J.; Fealy, R. Are fine resolution digital elevation models always the best choice in digital soil mapping? Geoderma 2013, 195–196, 111–121. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region. Saudi Arab. Geosci Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Saha, A.K.; Gupta, R.P.; Sarkar, I.; Arora, M.K.; Csaplovics, E. An approach for GIS-based statistical landslide susceptibility zonation- with a case study in the Himalayas. Landslides 2005, 2, 61–69. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Gokceoglu, C. Use of fuzzy relations to produce landslide susceptibility map of a landslide prone area (West Black Sea Region, Turkey). Eng. Geol. 2004, 75, 229–250. [Google Scholar] [CrossRef]
- Mohammad, A. The Effect of Slope Aspect on Soil and Vegetation Characteristics in Southern West Bank. Bethlehem Univ. J. 2008, 27, 9–25. [Google Scholar]
- Glade, T. Landslide occurrence as a response to land use change: A review of evidence from New Zealand. Catena 2003, 51, 297–314. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Amir Naghibi, S.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 2, 49–69. [Google Scholar] [CrossRef]
- Nanda, A.M.; Lone, F.A.; Ahmed, P. Prediction of rainfall-induced landslide using machine learning models along highway Bandipora to Gurez road, India. Nat. Hazards 2024, 120, 6169–6197. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2000; p. 375. [Google Scholar]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Usta, Z.; Akıncı, H.; Akin, T.A. Comparison of tree-based ensemble learning algorithms for landslide susceptibility mapping in Murgul (Artvin), Turkey. Earth Sci. Inform. 2024, 17, 1459–1481. [Google Scholar] [CrossRef]
- Günnemann, N.; Pfeffer, J. Cost matters: A new example-dependent cost-sensitive logistic regression model. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Cham, Switzerland, 2017; pp. 210–222. [Google Scholar]
- Alcântara, E.; Baião, C.F.; Guimarães, Y.C.; Marengo, A.J.; Mantovani, J.R. Climate change-induced shifts in landslide susceptibility in São Sebastião (southeastern Brazil). Nat. Hazards Res. 2024, 5, 321–334. [Google Scholar] [CrossRef]
- Pham, B.T.; Phong, T.V.; Nguyen-Thoi, T.; Trinh, P.T.; Prakash, I. GIS-based ensemble soft computing models for landslide susceptibility mapping. Adv. Space Res. 2020, 66, 1303–1320. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, D.; Wen, H.; Zhang, H.; Zhang, F. Comparison of Random Forest Model and Frequency Ratio Model for Landslide Susceptibility Mapping (LSM) in Yunyang County (Chongqing, China). Int. J. Environ. Res. Public Health 2020, 17, 4206. [Google Scholar] [CrossRef]
- Trinh, T.; Luu, B.T.; Le, T.T.H.; Nguyen, D.H.; Tran, T.V.; Nguyen, T.H.V.; Nguyen, K.Q.; Nguyen, L.T. A comparative analysis of weight-based machine learning methods for landslide susceptibility mapping in Ha Giang area. Big Earth Data 2023, 7, 1005–1034. [Google Scholar] [CrossRef]
- Quevedo, R.P.; Velastegui-Montoya, A.; Montalvan-Burbano, N.; Morante-Carballo, F.; Korup, O.; Renno, C.D. Land use and land cover as a conditioning factor in landslide susceptibility: A literature review. Landslides 2023, 20, 967–982. [Google Scholar] [CrossRef]
- Cohen, D.; Schwarz, M. Tree-root control of shallow landslides. Earth Surf. Dyn. 2017, 5, 451–477. [Google Scholar] [CrossRef]
- Chen, C.; Shen, Z.; Weng, Y.; You, S.; Lin, J.; Li, S.; Wang, K. Modeling Landslide Susceptibility in Forest-Covered Areas in Lin’an, China, Using Logistical Regression, a Decision Tree, and Random Forests. Remote Sens. 2023, 15, 4378. [Google Scholar] [CrossRef]
- Jacobs, L.; Dewitte, O.; Poesen, J.; Maes, J.; Mertens, K.; Sekajugo, J.; Kervyn, M. Landslide characteristics and spatial distribution in the Rwenzori Mountains, Uganda. J. Afr. Earth Sci. 2016, 134, 917–930. [Google Scholar] [CrossRef]
- Liu, Q.; Norbu, N. Modeling of landslides susceptibility prediction using deep belief networks with optimized learning rate control. Geocarto Int. 2024, 39, 2322060. [Google Scholar] [CrossRef]
- Ali, N.; Chen, J.; Fu, X.; Ali, R.; Hussain, M.A.; Daud, H.; Hussain, J.; Altalbe, A. Integrating Machine Learning Ensembles for Landslide Susceptibility Mapping in Northern Pakistan. Remote Sens. 2024, 6, 988. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Vanwalleghem, T.; Poesen, J.; Govers, G.; Verstraeten, G.; Vandekerckhove, L. Prediction of landslide susceptibility using rare events logistic regression: A case-study in the Flemish Ardennes (Belgium). Geomorphology 2006, 76, 392–410. [Google Scholar] [CrossRef]
- MacAfee, E.; Lohr, A.J.; Jong, E. Leveraging local knowledge for landslide disaster risk reduction in an urban informal settlement in Manado, Indonesia. Int. J. Disaster Risk Reduct. 2024, 111, 104710. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Landslide susceptibility mapping using a modified decision tree classifier in the Xanthi Perfection, Greece. Landslides 2016, 13, 305–320. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).