Interpretation of a Machine Learning Model for Short-Term High Streamflow Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
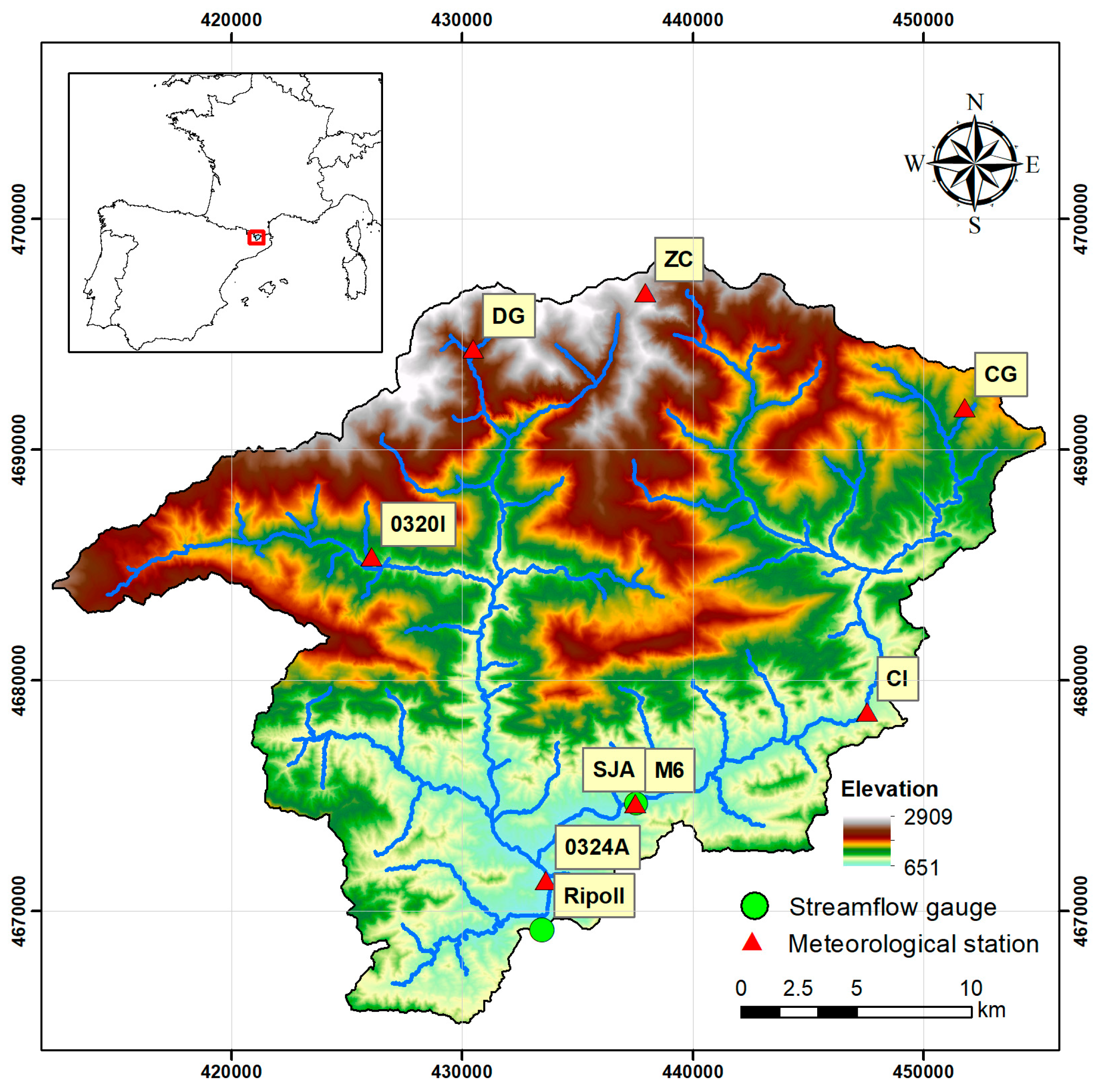
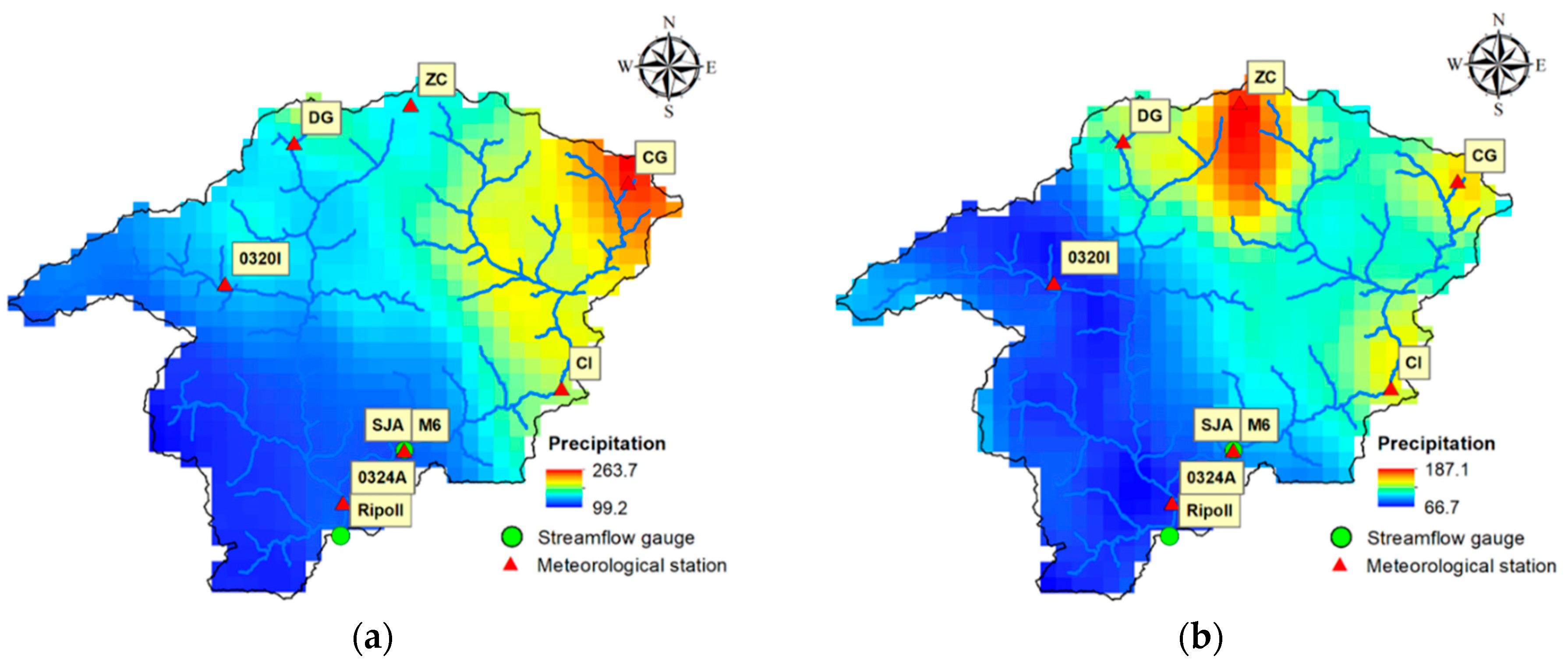
2.2. Data and Study Area
2.3. The ML Predictive Model Based on Random Forest
2.4. Feature Selection
2.5. Hyperparameter Tuning
3. Model Interpretation Methods
3.1. Mean Decrease Impurity
3.2. Mean Decrease Accuracy
- The error of the OOB values for a tree is computed based on the mean squared error (MSE).
- The feature is permuted in the same group of OOB values, and the MSE is calculated.
- The difference between the MSE of the permuted and original set of OOB values is summed and divided by the number of trees (3) [30,62]:where and correspond to the MSE of the OOB values with feature permuted and not permuted, respectively. is the number of trees. The higher , the higher the importance of feature . Both MDA and MDI are computed using ranger package.
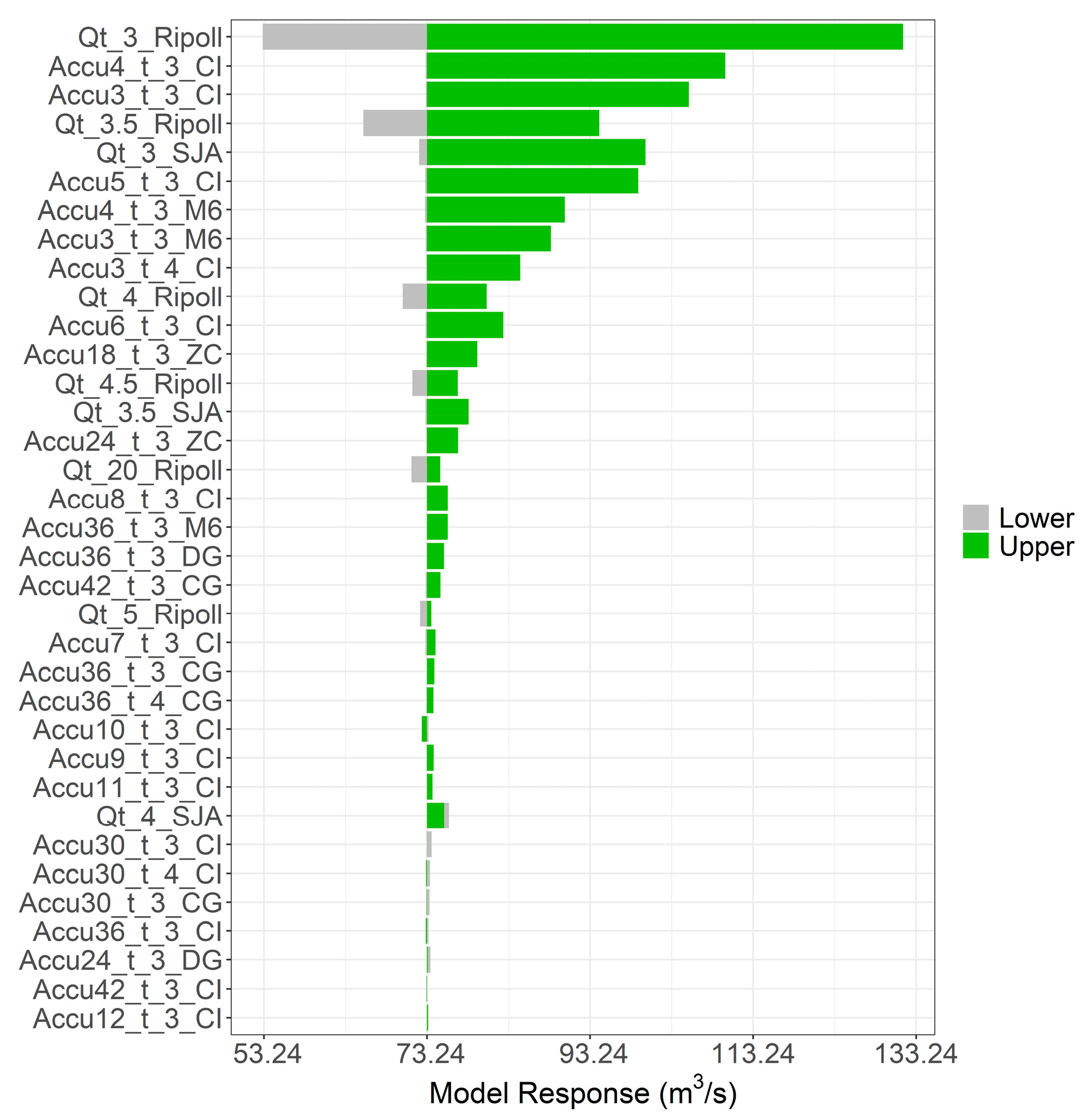
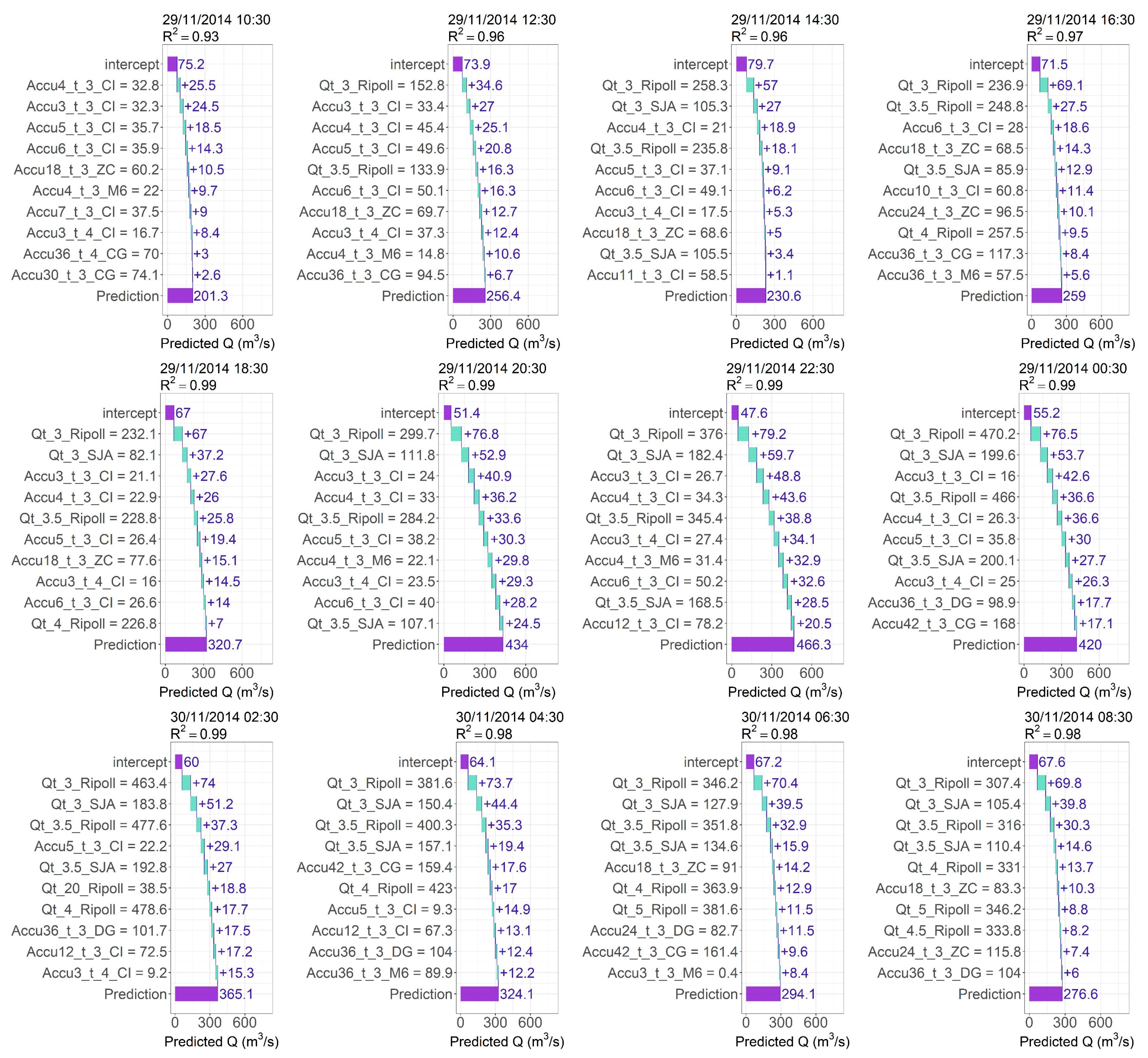
3.3. Tornado Diagrams
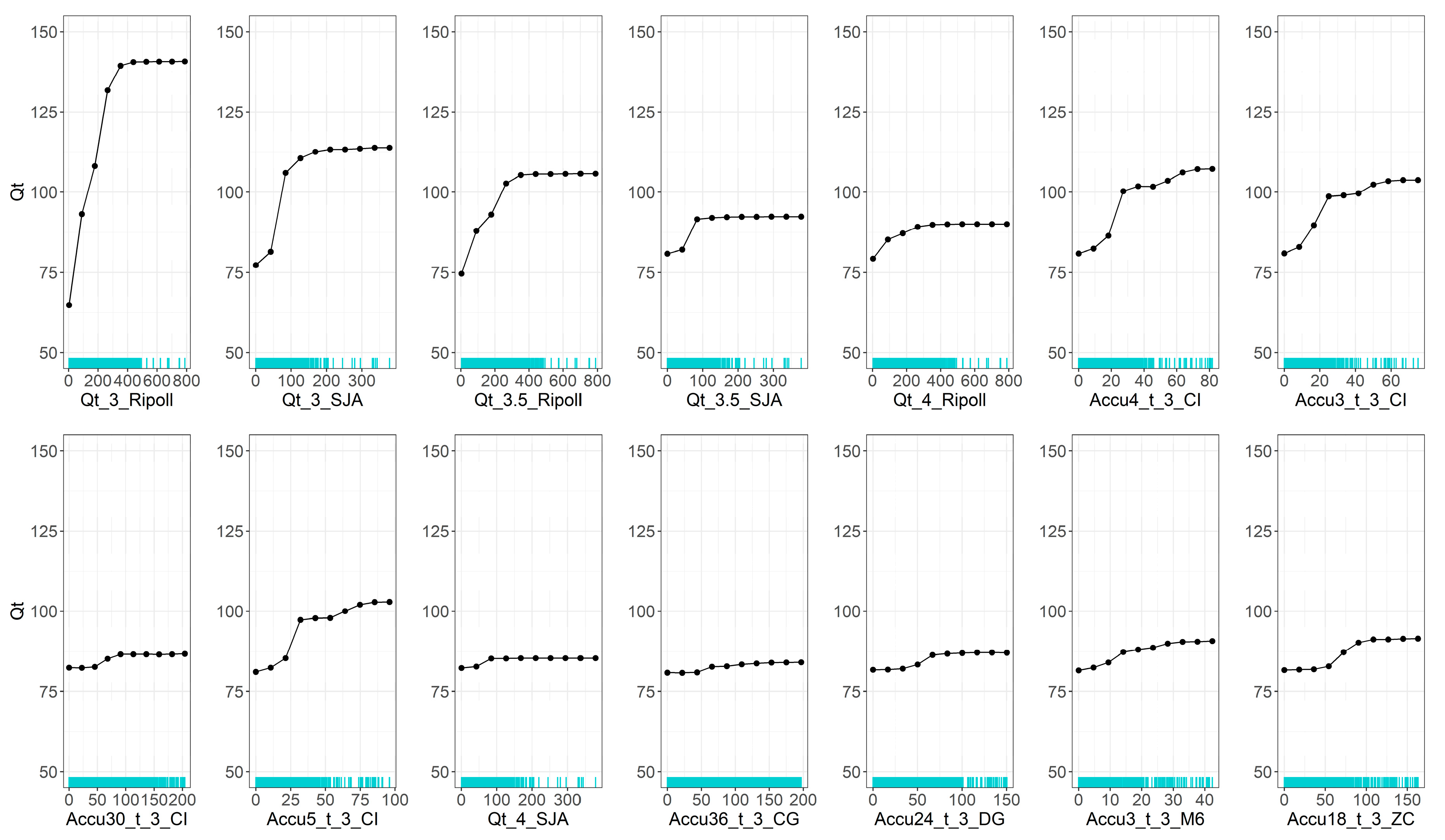
3.4. Partial Dependence Plots
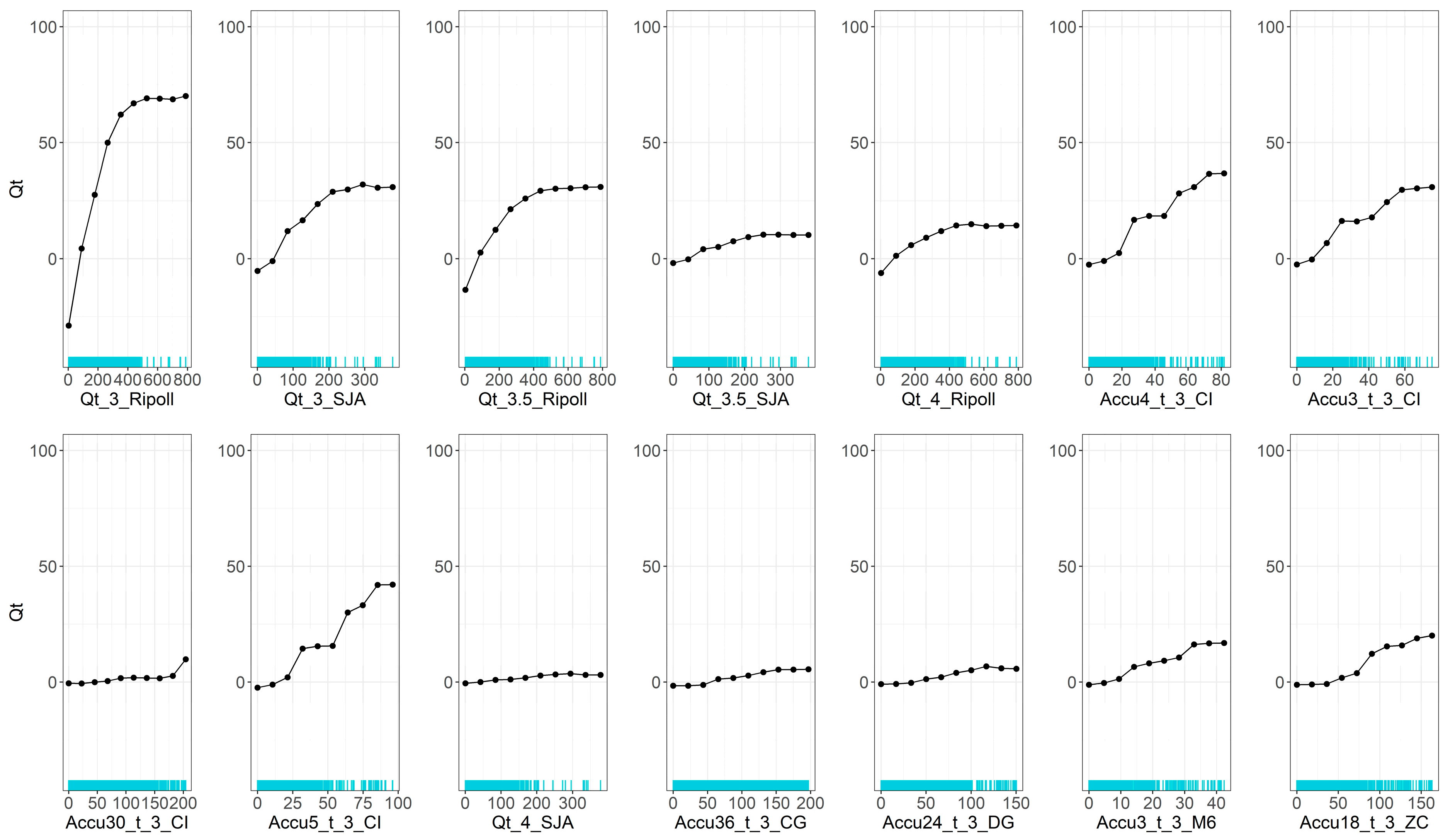
3.5. Accumulated Local Effect
3.6. Local Interpretable Model-Agnostic Explanations
3.7. Shapley Values
3.8. Shapley Additive Explanations (SHAP)
4. Results and Discussion
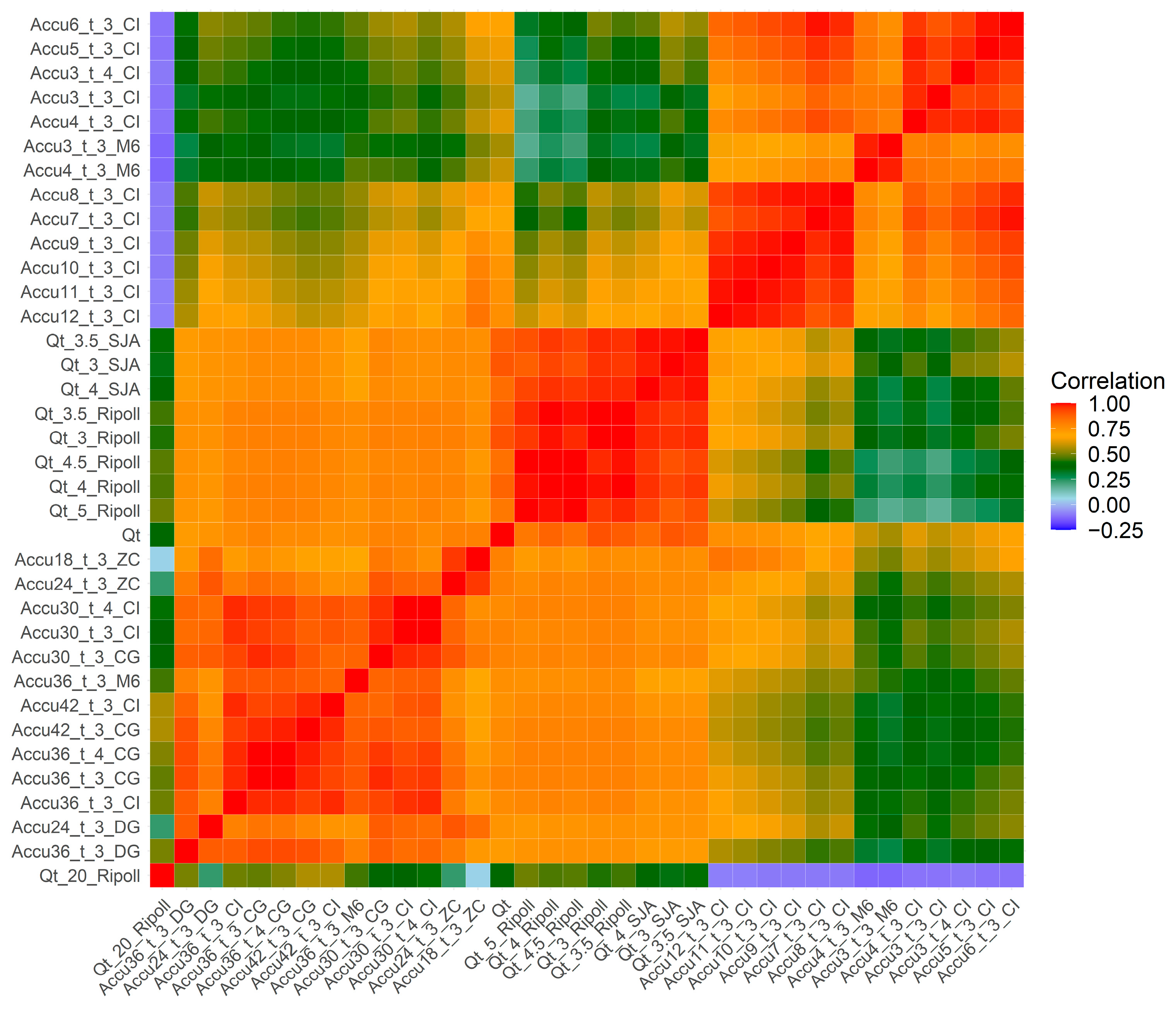
4.1. General Feature Importance Analysis
4.2. Partial Dependence Analysis
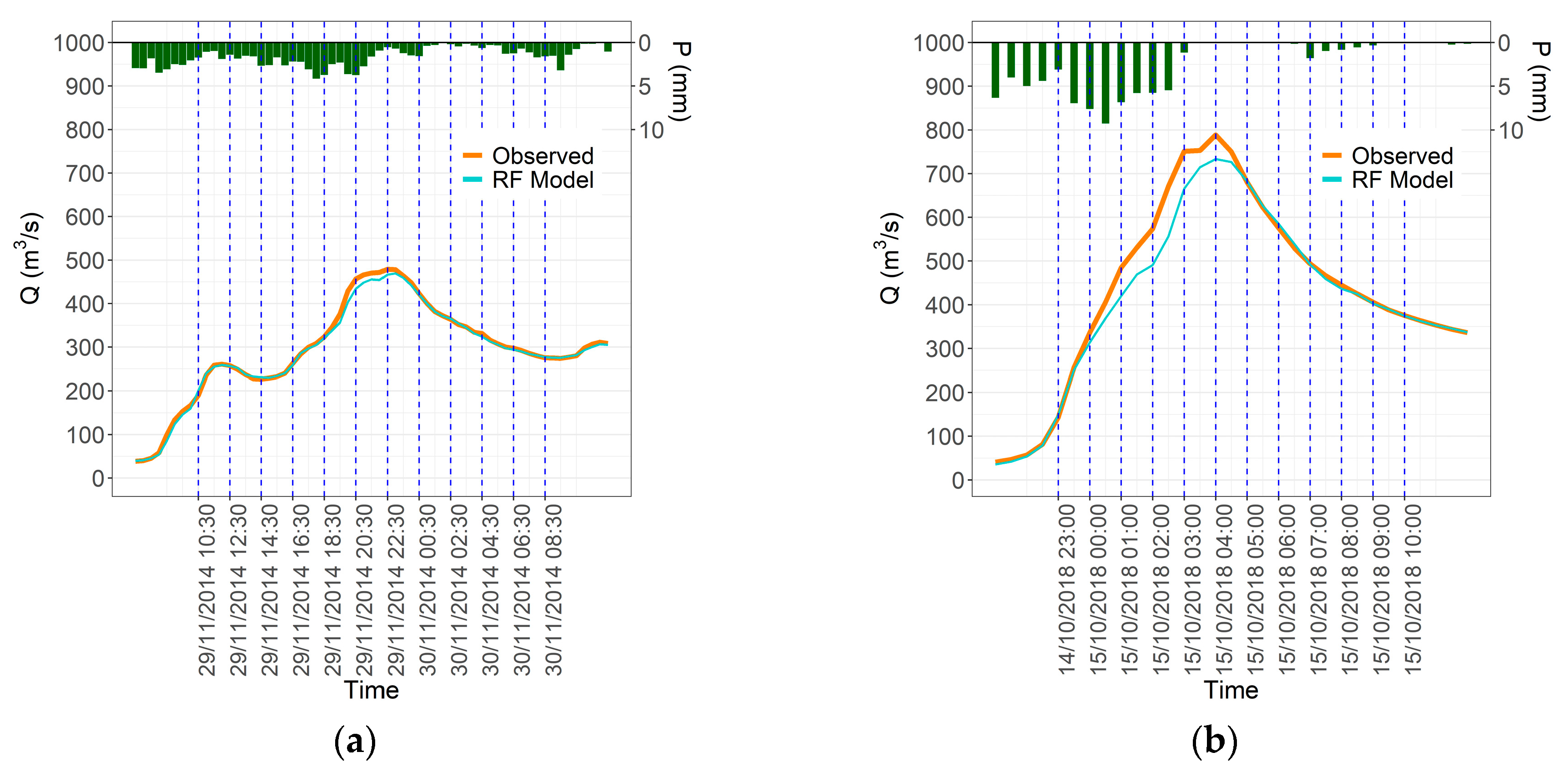
4.3. Local Analysis
4.4. Comparative Analysis and Overall Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Inputs | Output | |
|---|---|---|
| {3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 18, 24, 30, 36, 42, 48}; k ∈ {3, 4, 5} | ||
| Qt_h; h ∈ {3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5, 7, 7.5, 8, 8.5, 9, 9.5, 10, 10.5, 11, 11.5, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36} | ||
| Value | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 |
|---|---|---|---|---|---|
| Minimum Observed (m3/s) | 5.94 | 9.78 | 9.89 | 10.91 | 3.21 |
| Maximum observed (m3/s) | 380.85 | 196.12 | 271.02 | 788.51 | 788.51 |
| Mean (m3/s) | 59.97 | 46.82 | 54.11 | 109.22 | 129.91 |
| Standard deviation (m3/s) | 70.45 | 40.84 | 47.60 | 132.43 | 139.81 |
| Set of LIME Parameters | Selected Combination |
|---|---|
| {10, 1} |
References
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Frame, J.M.; Kratzert, F.; Gupta, H.V.; Ullrich, P.; Nearing, G.S. On Strictly Enforced Mass Conservation Constraints for Modelling the Rainfall-Runoff Process. Hydrol. Process 2023, 37, e14847. [Google Scholar] [CrossRef]
- Yifru, B.A.; Lim, K.J.; Lee, S. Enhancing Streamflow Prediction Physically Consistently Using Process-Based Modeling and Domain Knowledge: A Review. Sustainability 2024, 16, 1376. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- López-Chacón, S.R.; Salazar, F.; Bladé, E. Combining Synthetic and Observed Data to Enhance Machine Learning Model Performance for Streamflow Prediction. Water 2023, 15, 2020. [Google Scholar] [CrossRef]
- Konapala, G.; Kao, S.C.; Painter, S.L.; Lu, D. Machine Learning Assisted Hybrid Models Can Improve Streamflow Simulation in Diverse Catchments across the Conterminous US. Environ. Res. Lett. 2020, 15, 104022. [Google Scholar] [CrossRef]
- Roy, A.; Kasiviswanathan, K.S.; Patidar, S.; Adeloye, A.J.; Soundharajan, B.S.; Ojha, C.S.P. A Novel Physics-Aware Machine Learning-Based Dynamic Error Correction Model for Improving Streamflow Forecast Accuracy. Water Resour. Res. 2023, 59, e2022WR033318. [Google Scholar] [CrossRef]
- Goulet, J.-A. Probabilistic Machine Learning for Civil Engineers; The MIT Press: Cambridge, MA, USA, 2020; ISBN 9780262538701. [Google Scholar]
- Nwanganga, F.; Chapple, M. Practical Machine Learning in R; John Wiley & Sons: New York, NY, USA, 2020; ISBN 9781119591542. [Google Scholar]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A Hybrid Deep Learning Algorithm and Its Application to Streamflow Prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Sellars, S.L. “Grand Challenges” in Big Data and the Earth Sciences. Bull. Am. Meteorol. Soc. 2018, 99, ES95–ES98. [Google Scholar] [CrossRef]
- Mushtaq, H.; Akhtar, T.; Hashmi, M.Z.U.R.; Masood, A.; Saeed, F. Hydrologic Interpretation of Machine Learning Models for 10-Daily Streamflow Simulation in Climate Sensitive Upper Indus Catchments. Theor. Appl. Climatol. 2024, 155, 5525–5542. [Google Scholar] [CrossRef]
- Guthery, F.S.; Bingham, R.L. A Primer on Interpreting Regression Models. J. Wildl. Manag. 2007, 71, 684–692. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Tiefenbacher, J.P. Using Optimized Deep Learning to Predict Daily Streamflow: A Comparison to Common Machine Learning Algorithms. Water Resour. Manag. 2022, 36, 699–716. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.C.; Molnar, C. Beyond Prediction: Methods for Interpreting Complex Models of Soil Variation. Geoderma 2022, 422, 115953. [Google Scholar] [CrossRef]
- Pham, L.T.; Luo, L.; Finley, A. Evaluation of Random Forests for Short-Term Daily Streamflow Forecasting in Rainfall- And Snowmelt-Driven Watersheds. Hydrol. Earth Syst. Sci. 2021, 25, 2997–3015. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine Learning Methods for Empirical Streamflow Simulation: A Comparison of Model Accuracy, Interpretability, and Uncertainty in Seasonal Watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Liu, J.; Ren, K.; Ming, T.; Qu, J.; Guo, W.; Li, H. Investigating the Effects of Local Weather, Streamflow Lag, and Global Climate Information on 1-Month-Ahead Streamflow Forecasting by Using XGBoost and SHAP: Two Case Studies Involving the Contiguous USA. Acta Geophys. 2023, 71, 905–925. [Google Scholar] [CrossRef]
- Sushanth, K.; Mishra, A.; Mukhopadhyay, P.; Singh, R. Real-Time Streamflow Forecasting in a Reservoir-Regulated River Basin Using Explainable Machine Learning and Conceptual Reservoir Module. Sci. Total Environ. 2023, 861, 160680. [Google Scholar] [CrossRef]
- Vilaseca, F.; Castro, A.; Chreties, C.; Gorgoglione, A. Assessing Influential Rainfall–Runoff Variables to Simulate Daily Streamflow Using Random Forest. Hydrol. Sci. J. 2023, 68, 1738–1753. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, X. A New Interpretable Streamflow Prediction Approach Based on SWAT-BiLSTM and SHAP. Environ. Sci. Pollut. Res. 2024, 31, 23896–23908. [Google Scholar] [CrossRef]
- Abbasi, M.; Farokhnia, A.; Bahreinimotlagh, M.; Roozbahani, R. A Hybrid of Random Forest and Deep Auto-Encoder with Support Vector Regression Methods for Accuracy Improvement and Uncertainty Reduction of Long-Term Streamflow Prediction. J. Hydrol. 2021, 597, 125717. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, X.; Li, B.; He, X.; Zhang, Y.; Fu, Y. Improving Short-Term Streamflow Forecasting by Flow Mode Clustering. Stoch. Environ. Res. Risk Assess. 2023, 37, 1799–1819. [Google Scholar] [CrossRef]
- Núñez, J.; Cortés, C.B.; Yáñez, M.A. Explainable Artificial Intelligence in Hydrology: Interpreting Black-Box Snowmelt-Driven Streamflow Predictions in an Arid Andean Basin of North-Central Chile. Water 2023, 15, 3369. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Interpretable Machine Learning for Assessing the Cumulative Damage of a Reinforced Concrete Frame Induced by Seismic Sequences. Sustainability 2023, 15, 2768. [Google Scholar] [CrossRef]
- Latif, I.; Banerjee, A.; Surana, M. Explainable Machine Learning Aided Optimization of Masonry Infilled Reinforced Concrete Frames. Structures 2022, 44, 1751–1766. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.T.; Oñate, E.; Suárez, B. Interpretation of Dam Deformation and Leakage with Boosted Regression Trees. Eng. Struct. 2016, 119, 230–251. [Google Scholar] [CrossRef]
- Ishwaran, H. The Effect of Splitting on Random Forests. Mach. Learn. 2015, 99, 75–118. [Google Scholar] [CrossRef] [PubMed]
- Janitza, S.; Tutz, G.; Boulesteix, A.L. Random Forest for Ordinal Responses: Prediction and Variable Selection. Comput. Stat. Data Anal. 2016, 96, 57–73. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Eschenbach, T.G. Spiderplots versus Tornado Diagrams for Sensitivity Analysis. Interfaces 1992, 22, 40–46. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Apley, D.W.; Zhu, J. Visualizing the Effects of Predictor Variables in Black Box Supervised Learning Models. J. R. Statist. Soc. B 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?” Explaining the Predictions of Any Classifier. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Giandotti, M. Previsione Delle Piene e Delle Magre Dei Corsi d’acqua. Ist. Poligr. Dello Stato 1934, 8, 107–117. [Google Scholar]
- Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Temps de Concentration: Un Paradoxe Dans l’hydrologie Moderne. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef]
- Llasat, M.C.; Llasat-Botija, M.; Rodriguez, A.; Lindbergh, S. Flash Floods in Catalonia: A Recurrent Situation. Adv. Geosci. 2010, 26, 105–111. [Google Scholar] [CrossRef]
- Gallart, F.; Delgado, J.; Beatson, S.J.V.; Posner, H.; Llorens, P.; Marcé, R. Analysing the Effect of Global Change on the Historical Trends of Water Resources in the Headwaters of the Llobregat and Ter River Basins (Catalonia, Spain). Phys. Chem. Earth 2011, 36, 655–661. [Google Scholar] [CrossRef]
- Lana, X.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Serra, C.; Martínez, M.D.; Kirchner, R. Rainfall Regime Trends at Annual and Monthly Scales in Catalonia (NE Spain) and Indications of CO2 Emissions Effects. Theor. Appl. Climatol. 2021, 146, 981–996. [Google Scholar] [CrossRef]
- ICGC Elevation Model 15 × 15. Available online: http://www.icc.cat/vissir3/ (accessed on 2 November 2023).
- INUNCAT. Plan Especial de Emergencias Para Inundaciones; INUNCAT: Barcelona, Spain, 2017. [Google Scholar]
- Lana, X.; Burgueño, A.; Martínez, M.D.; Serra, C. Statistical Distributions and Sampling Strategies for the Analysis of Extreme Dry Spells in Catalonia (NE Spain). J. Hydrol. 2006, 324, 94–114. [Google Scholar] [CrossRef]
- López-Chacón, S.R.; Salazar, F.; Bladé, E. Hybrid Physically Based and Machine Learning Model to Enhance High Streamflow Prediction. Hydrol. Sci. J. 2024, 70, 311–333. [Google Scholar] [CrossRef]
- Reed, S.; Schaake, J.; Zhang, Z. A Distributed Hydrologic Model and Threshold Frequency-Based Method for Flash Flood Forecasting at Ungauged Locations. J. Hydrol. 2007, 337, 402–420. [Google Scholar] [CrossRef]
- Toth, E. Estimation of Flood Warning Runoff Thresholds in Ungauged Basins with Asymmetric Error Functions. Hydrol. Earth Syst. Sci. 2016, 20, 2383–2394. [Google Scholar] [CrossRef]
- Harman, C.; Stewardson, M.; DeRose, R. Variability and Uncertainty in Reach Bankfull Hydraulic Geometry. J. Hydrol. 2008, 351, 13–25. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Khan, Z.; Gul, N.; Faiz, N.; Gul, A.; Adler, W.; Lausen, B. Optimal Trees Selection for Classification via Out-of-Bag Assessment and Sub-Bagging. IEEE Access 2021, 9, 28591–28607. [Google Scholar] [CrossRef]
- Islam, K.I.; Elias, E.; Carroll, K.C.; Brown, C. Exploring Random Forest Machine Learning and Remote Sensing Data for Streamflow Prediction: An Alternative Approach to a Process-Based Hydrologic Modeling in a Snowmelt-Driven Watershed. Remote Sens. 2023, 15, 3999. [Google Scholar] [CrossRef]
- Lantz, B. Machine Learning with R; Packt Publishing: Birmingham, UK, 2013; ISBN 9781782162148. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and Tuning Strategies for Random Forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Scornet, E. Tuning Parameters in Random Forests. ESAIM Proc. Surv. 2017, 60, 144–162. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.-L. To Tune or Not to Tune the Number of Trees in Random Forest. J. Mach. Learn. Res. 2018, 18, 1–18. [Google Scholar]
- Contreras, P.; Orellana-Alvear, J.; Muñoz, P.; Bendix, J.; Célleri, R. Influence of Random Forest Hyperparameterization on Short-Term Runoff Forecasting in an Andean Mountain Catchment. Atmosphere 2021, 12, 238. [Google Scholar] [CrossRef]
- Han, S.; Kim, H. Optimal Feature Set Size in Random Forest Regression. Appl. Sci. 2021, 11, 3428. [Google Scholar] [CrossRef]
- Van Rijn, J.N.; Hutter, F. Hyperparameter Importance across Datasets. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery, London, UK, 19–23 August 2018; pp. 2367–2376. [Google Scholar]
- Jibril, M.; Bello, A.; I Aminu, I.; Ibrahim, A.S.; Bashir, A.; Malami, S.I.; Habibu, M.A.; Magaji, M.M. An Overview of Streamflow Prediction Using Random Forest Algorithm. GSC Adv. Res. Rev. 2022, 13, 50–57. [Google Scholar] [CrossRef]
- Cerqueira, V.; Torgo, L.; Mozetič, I. Evaluating Time Series Forecasting Models: An Empirical Study on Performance Estimation Methods. Mach. Learn. 2020, 109, 1997–2028. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Package RandomForest—Breiman and Culter’s Random Forest for Classification and Regression. 2022. Version 4.7-1.1. Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 9 December 2022).
- Benard, C.; Da Veiga, S.; Scornet, E. Mean Decrease Accuracy for Random Forests: Inconsistency, and a Practical Solution via the Sobol-MDA. Biometrika 2022, 109, 881–900. [Google Scholar] [CrossRef]
- Anderson, R.N.; Xie, B.; Wu, L.; Kressner, A.A.; Frantz, J.H.; Ockree, M.A.; Brown, K.G. Petroleum Analytics Learning Machine to Forecast Production in the Wet Gas Marcellus Shale. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference 2016, Unconventional Resources Technology Conference (URTEC), San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Carnell, R. Package “tornado” Plots for Model Sensitivity and Variable Importance. 2024. Version 0.1.3. Available online: http://cran.r-project.org/web/packages/tornado/tornado.pdf (accessed on 14 February 2025).
- Molnar, C. Interpretable Machine Learning A Guide for Making Black Box Models Explainable; Lean Publishing: Victoria, BC, Canada, 2019. [Google Scholar]
- Casalicchio, G. Package “iml” Interpretable Machine Learning. 2024. Version 0.11.3. Available online: https://cran.r-project.org/web/packages/iml/iml.pdf (accessed on 6 June 2024).
- Zhang, Y.; Song, K.; Sun, Y.; Tan, S.; Udell, M. “Why Should You Trust My Explanation?” Understanding Uncertainty in LIME Explanations. arXiv 2019, arXiv:1904.12991. [Google Scholar]
- Garreau, D.; von Luxburg, U. Looking Deeper into Tabular LIME. arXiv 2020, arXiv:2008.11092. [Google Scholar]
- Hvitfeldt, E.; Pedersen, T.L.; Benesty, M. Package “lime” Local Interpretable Model-Agnostic Explanations. CRAN Repos. 2022. Version 0.5.3. Available online: https://cran.r-project.org/web/packages/lime/lime.pdf (accessed on 14 November 2024).
- Shapley, L.S. A Value for N-Person Games, Contributions to the Theory of Games; Princeton University Press: Princeton, NJ, USA, 1953; Volume II. [Google Scholar]
- Štrumbelj, E.; Kononenko, I. An Efficient Explanation of Individual Classifications Using Game Theory. J. Mach. Learn. Res. 2010, 11, 1–18. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Alabi, R.O.; Elmusrati, M.; Leivo, I.; Almangush, A.; Mäkitie, A.A. Machine Learning Explainability in Nasopharyngeal Cancer Survival Using LIME and SHAP. Sci. Rep. 2023, 13, 8984. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Kalin, L.; Isik, S.; Schoonover, J.E.; Lockaby, B.G. Predicting Water Quality in Unmonitored Watersheds Using Artificial Neural Networks. J. Environ. Qual. 2010, 39, 1429–1440. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance Evaluation of Hydrological Models: Statistical Significance for Reducing Subjectivity in Goodness-of-Fit Assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Nicodemus, K.K.; Malley, J.D. Predictor Correlation Impacts Machine Learning Algorithms: Implications for Genomic Studies. Bioinformatics 2009, 25, 1884–1890. [Google Scholar] [CrossRef] [PubMed]
- Nicodemus, K.K.; Malley, J.D.; Strobl, C.; Ziegler, A. The Behaviour of Random Forest Permutation-Based Variable Importance Measures under Predictor Correlation. BMC Bioinform. 2010, 11, 110. [Google Scholar] [CrossRef] [PubMed]
- Van Zyl, C.; Ye, X.; Naidoo, R. Harnessing EXplainable Artificial Intelligence for Feature Selection in Time Series Energy Forecasting: A Comparative Analysis of Grad-CAM and SHAP. Appl. Energy 2024, 353, 122079. [Google Scholar] [CrossRef]
- Palar, P.S.; Zuhal, L.R.; Shimoyama, K. Enhancing the Explainability of Regression-Based Polynomial Chaos Expansion by Shapley Additive Explanations. Reliab. Eng. Syst. Saf. 2023, 232, 109045. [Google Scholar] [CrossRef]
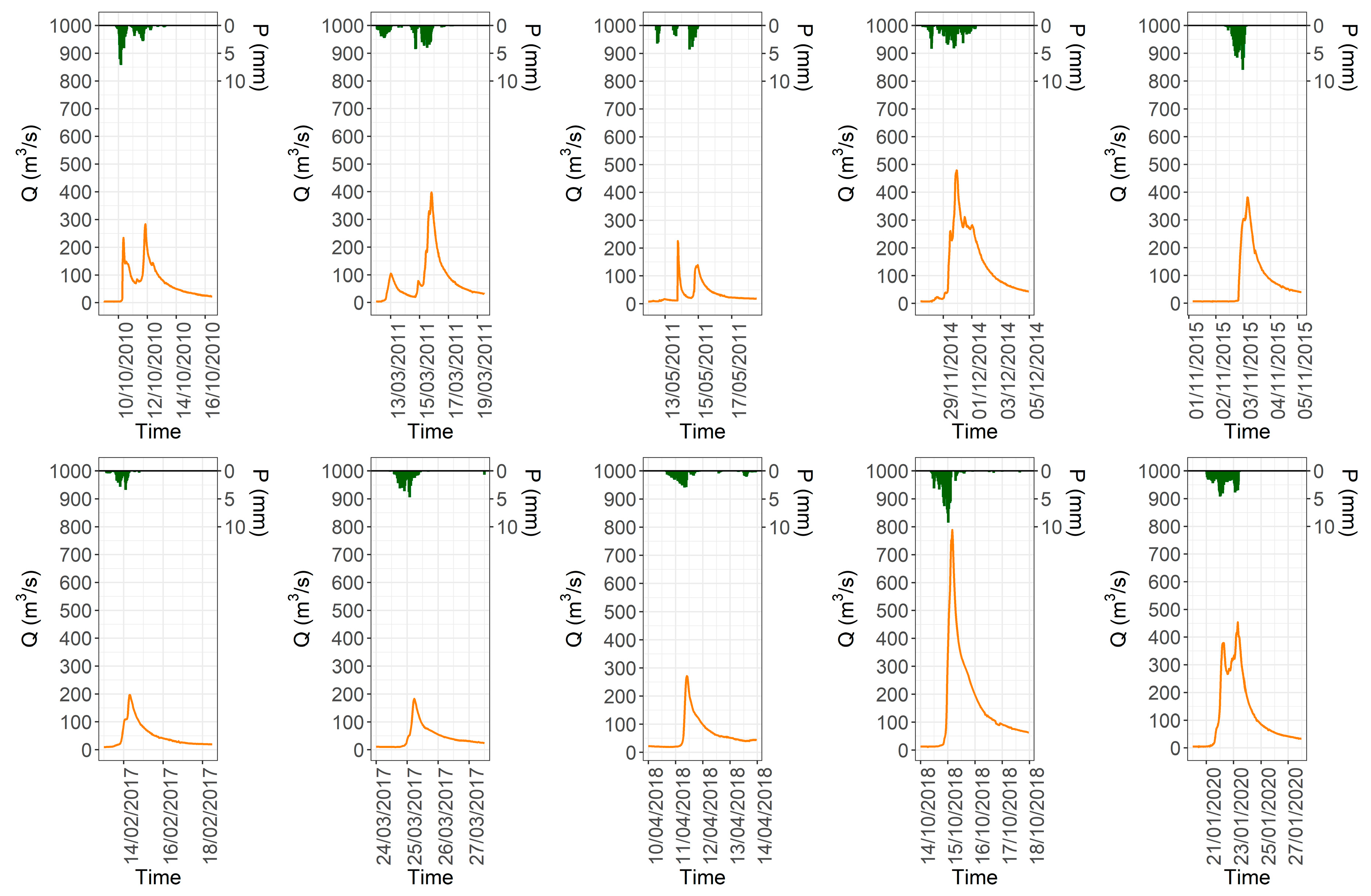
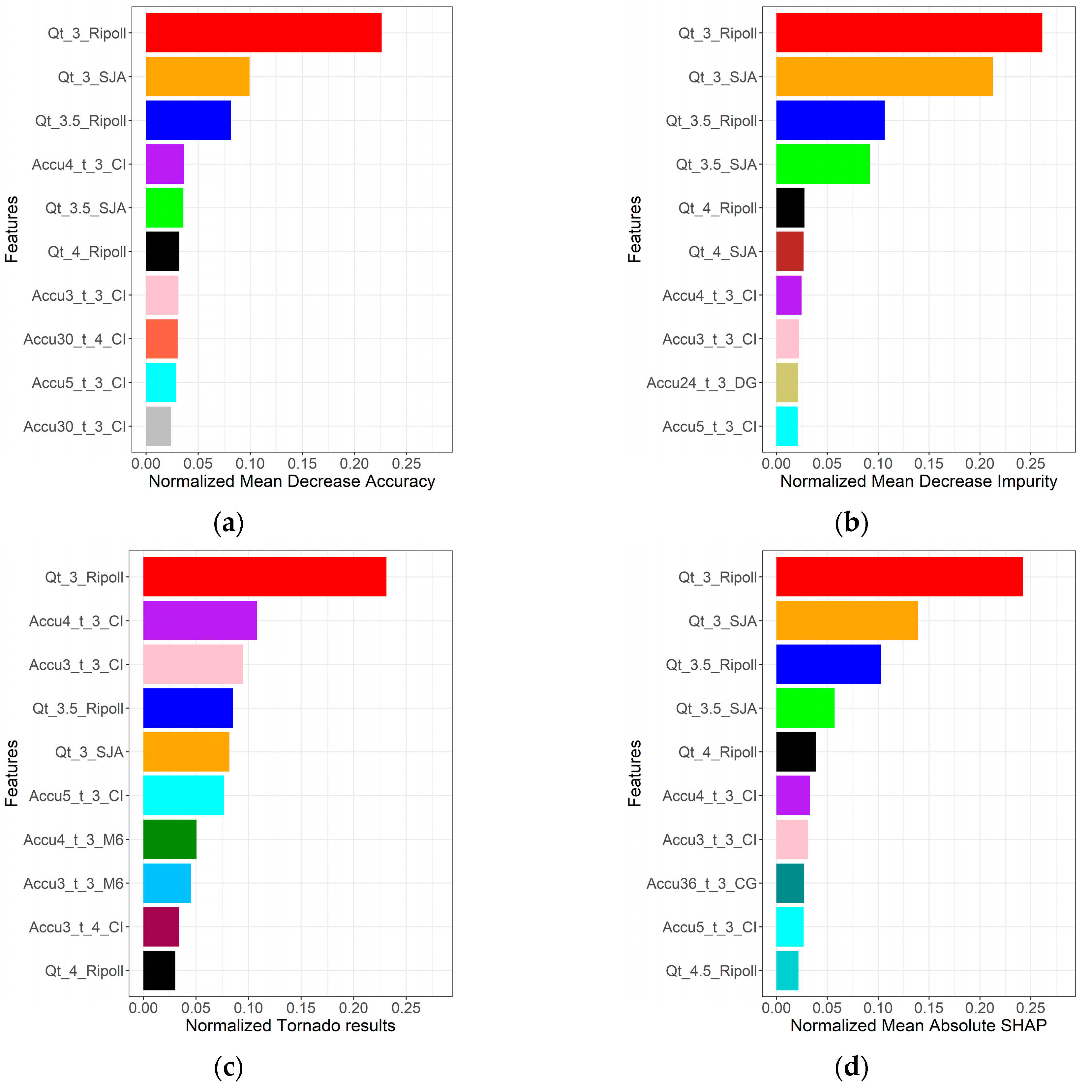
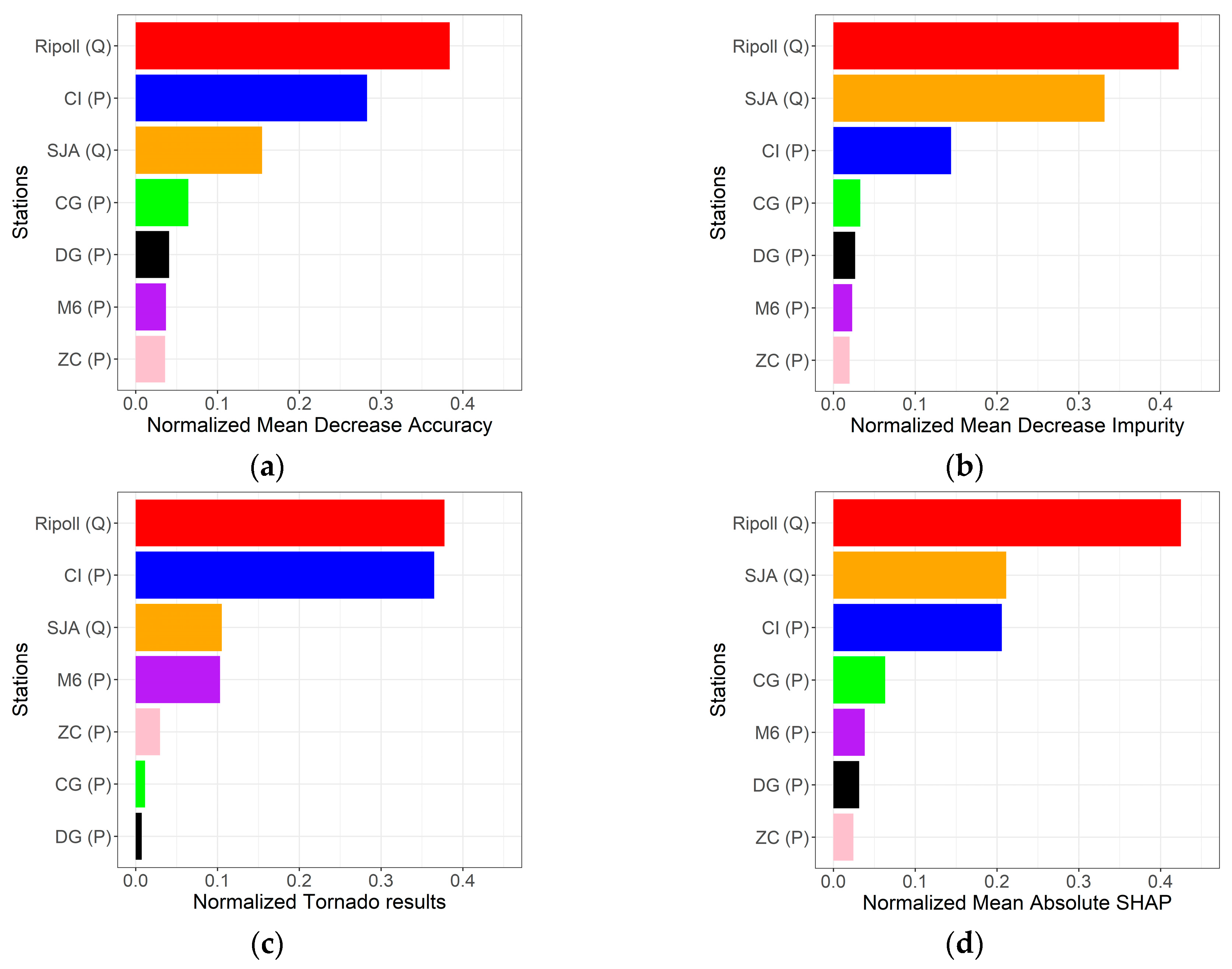
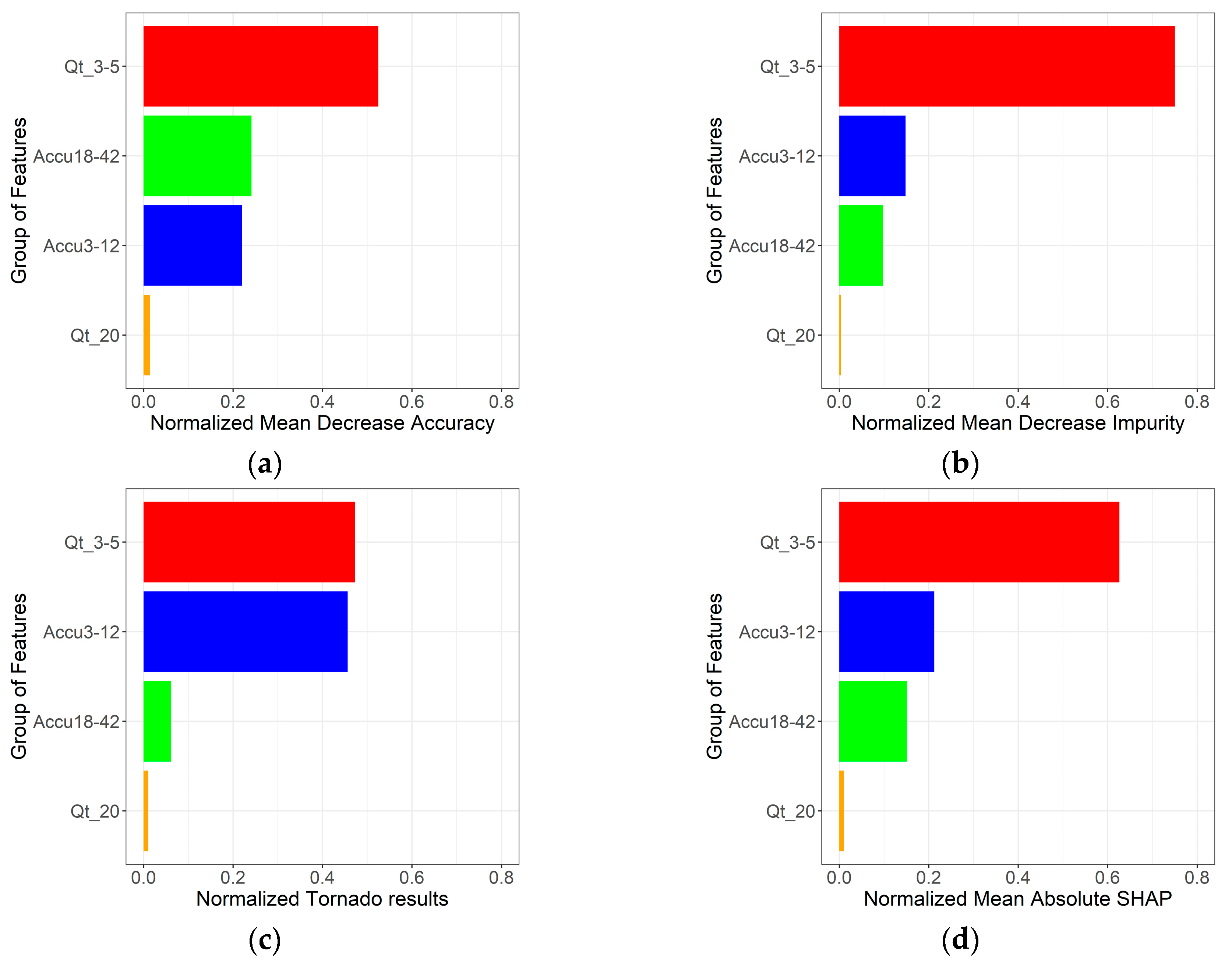

| Station | Inputs | Output |
|---|---|---|
| Ripoll | ||
| SJA | ||
| CI | ||
| CG | ||
| DG | ||
| M6 | ||
| ZC |
| Set of Hyperparameters | Selected Combination |
|---|---|
| Error Metric | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Average |
|---|---|---|---|---|---|---|
| RMSE (m3/s) | 21.06 | 10.29 | 17.85 | 61.42 | 50.66 | 32.26 |
| PBIAS (%) | 11.41 | 5.06 | 0.47 | −14.52 | −6.91 | −0.90 |
| NSE | 0.91 | 0.94 | 0.86 | 0.78 | 0.87 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Chacón, S.R.; Salazar, F.; Bladé, E. Interpretation of a Machine Learning Model for Short-Term High Streamflow Prediction. Earth 2025, 6, 64. https://doi.org/10.3390/earth6030064
López-Chacón SR, Salazar F, Bladé E. Interpretation of a Machine Learning Model for Short-Term High Streamflow Prediction. Earth. 2025; 6(3):64. https://doi.org/10.3390/earth6030064
Chicago/Turabian StyleLópez-Chacón, Sergio Ricardo, Fernando Salazar, and Ernest Bladé. 2025. "Interpretation of a Machine Learning Model for Short-Term High Streamflow Prediction" Earth 6, no. 3: 64. https://doi.org/10.3390/earth6030064
APA StyleLópez-Chacón, S. R., Salazar, F., & Bladé, E. (2025). Interpretation of a Machine Learning Model for Short-Term High Streamflow Prediction. Earth, 6(3), 64. https://doi.org/10.3390/earth6030064







