Allometric Models to Estimate the Merchantable Wood Volume and Biomass of the Most Abundant Miombo Species in the Miombo Woodlands in Mozambique
Abstract
1. Introduction
2. Materials and Methods
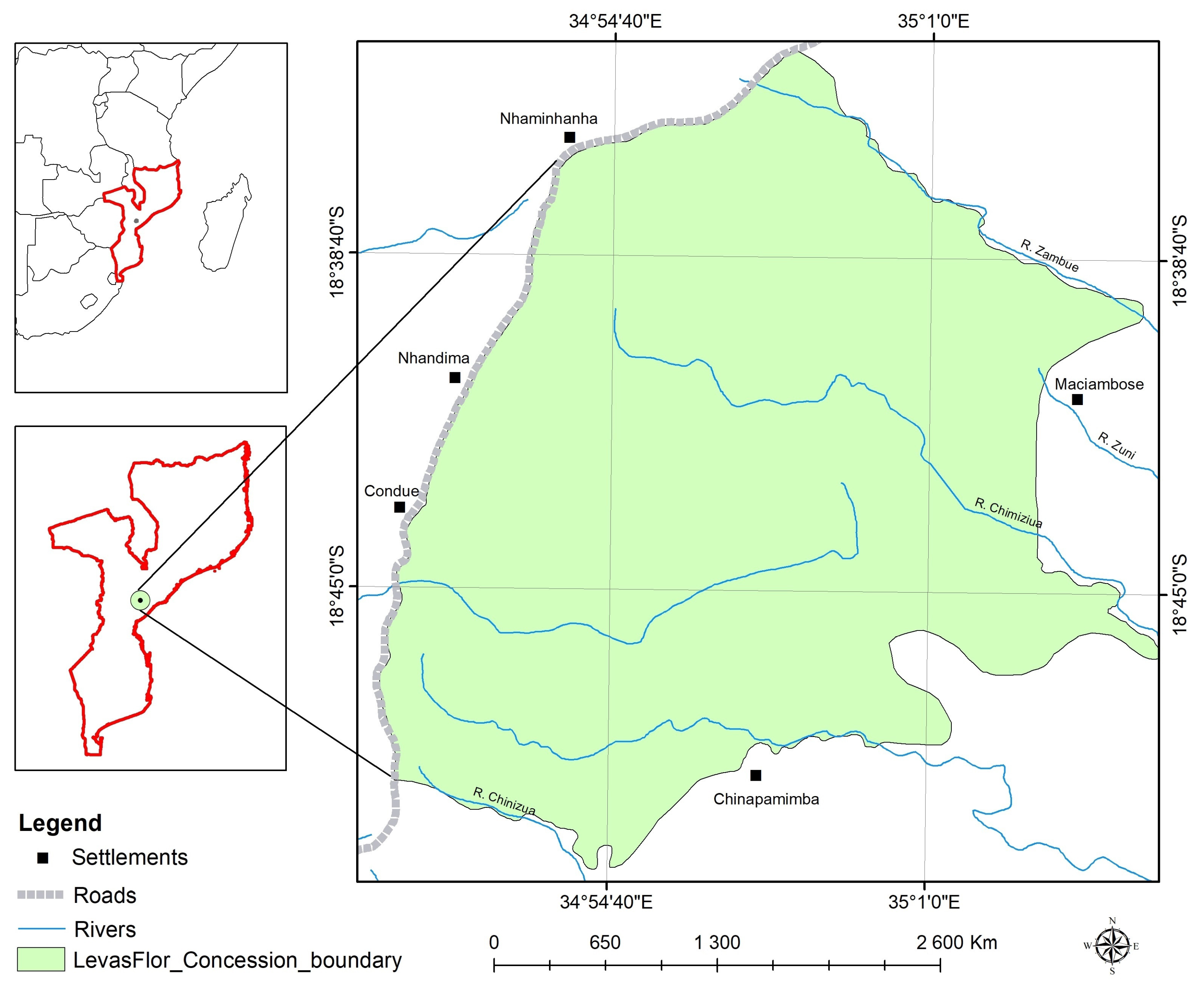
2.1. Study Area
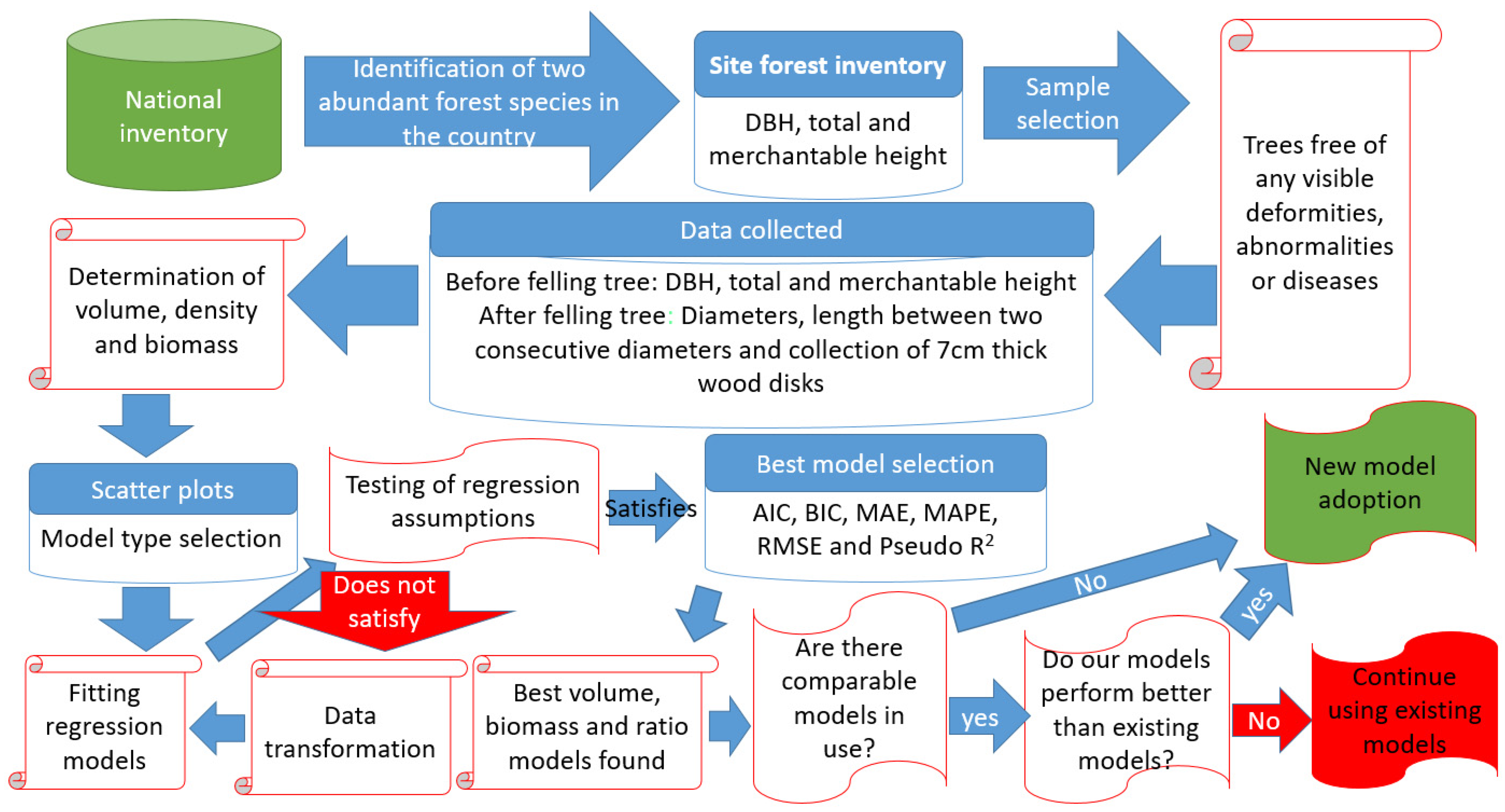
2.2. Data Collection
2.3. Determination of Volumes, Ratios, and Biomass
- Vm = total volume of the section (under bark and heartwood) (m3);
- Ab = cross-sectional area at the bottom of the section (m2);
- Au = cross-sectional area at the top of the section (m2);
- L = length of the section (m).
2.4. Selection of Candidate Models
2.5. Model Evaluation and Validation
2.6. Comparison with Existing Allometric Equations
3. Results
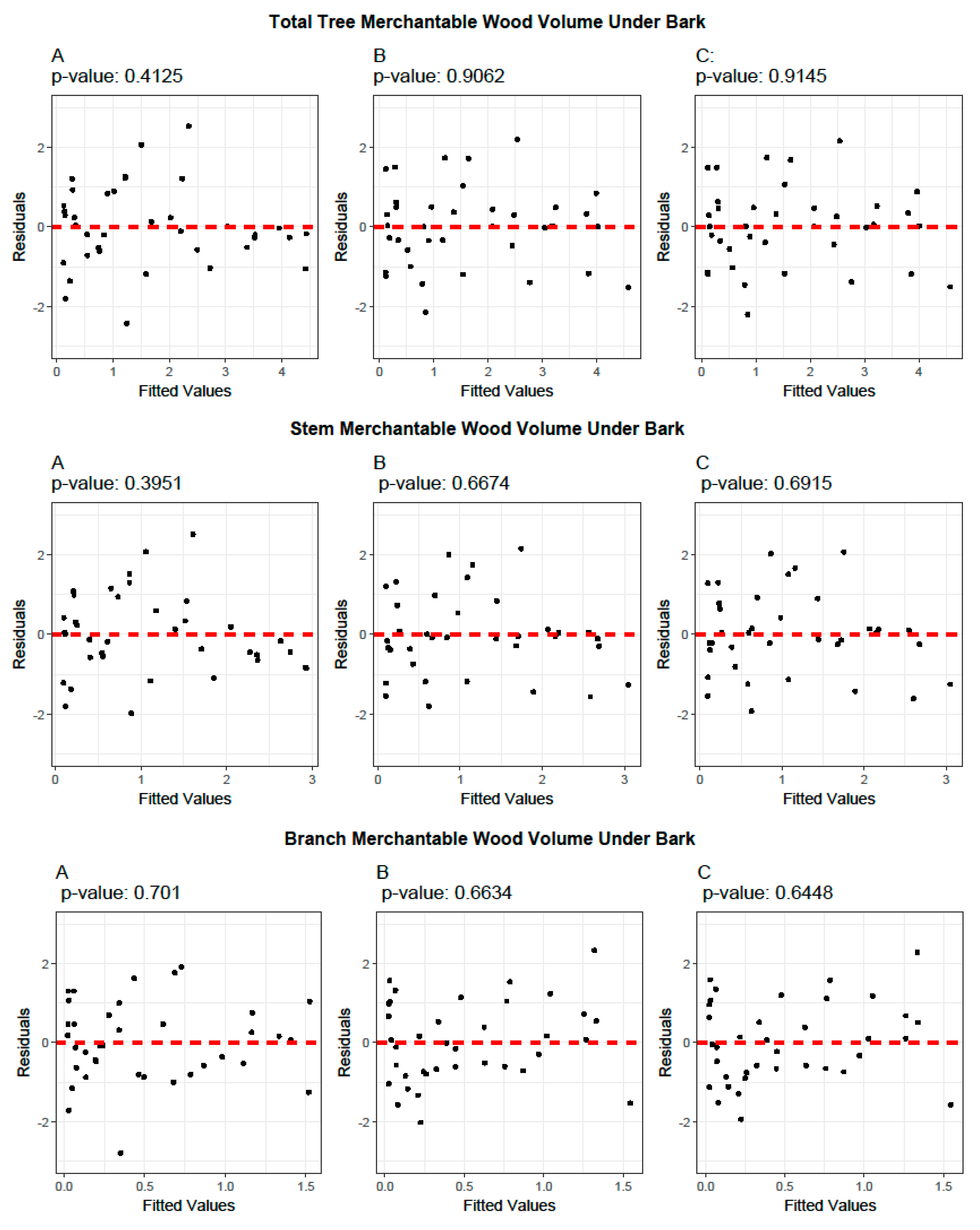
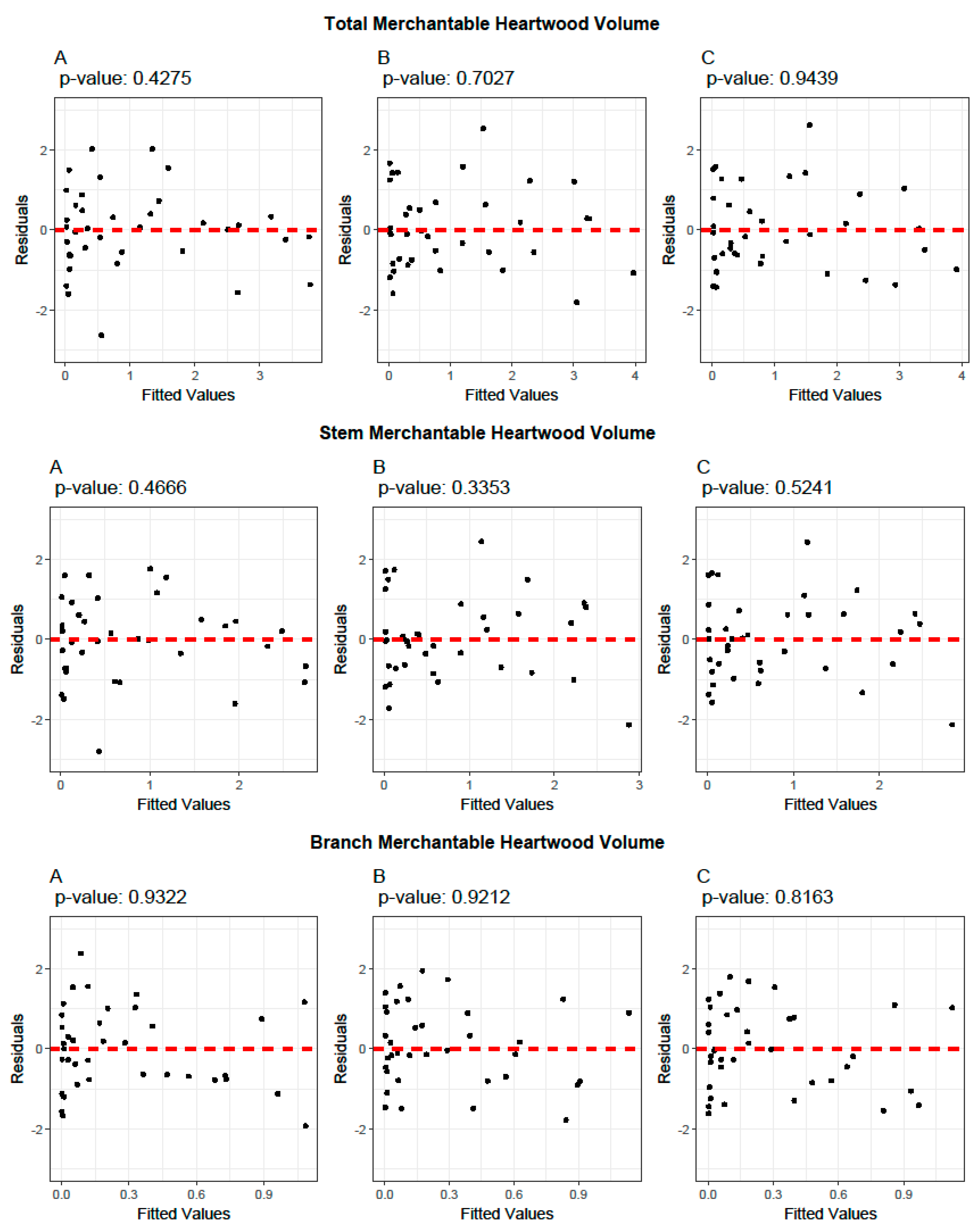
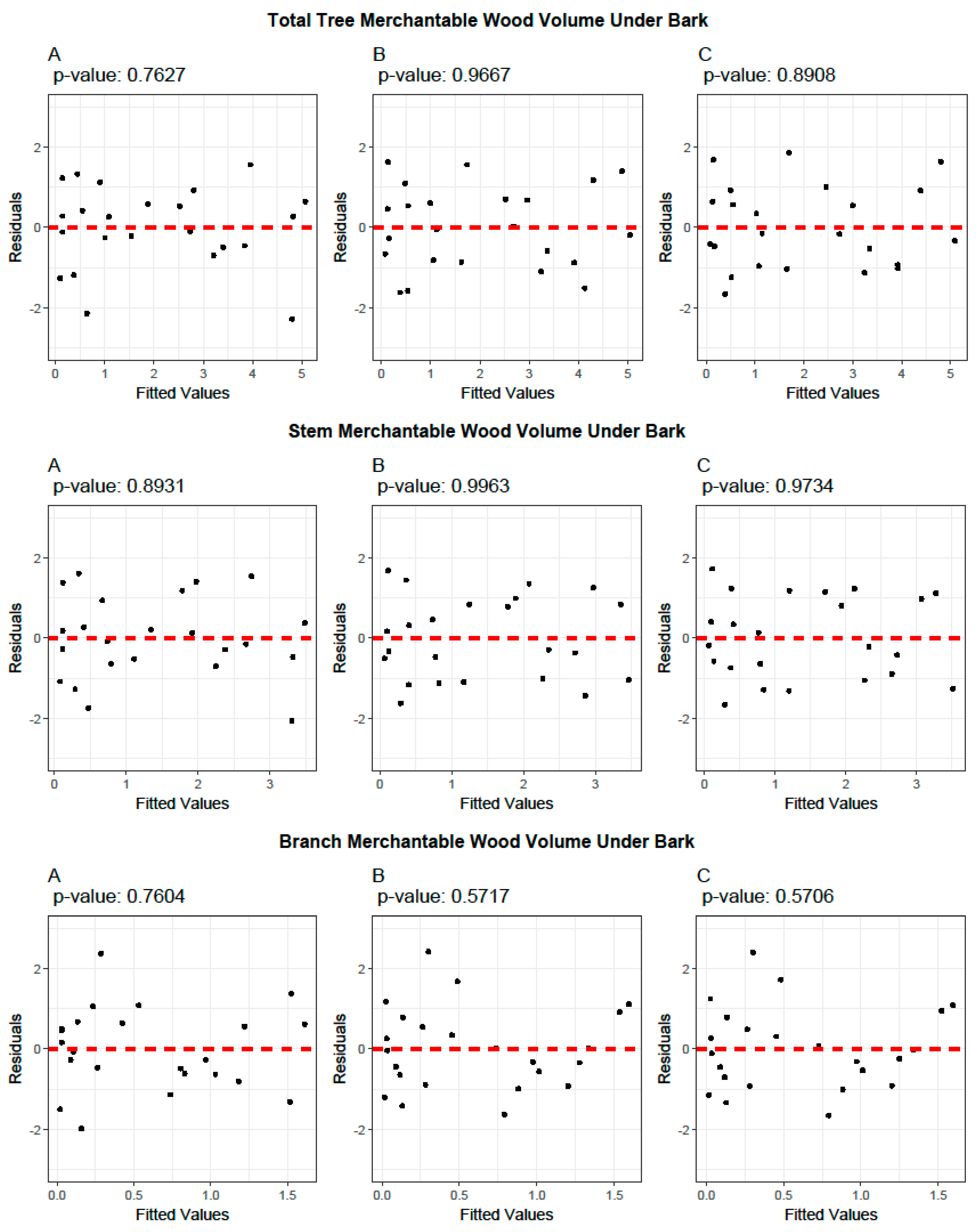
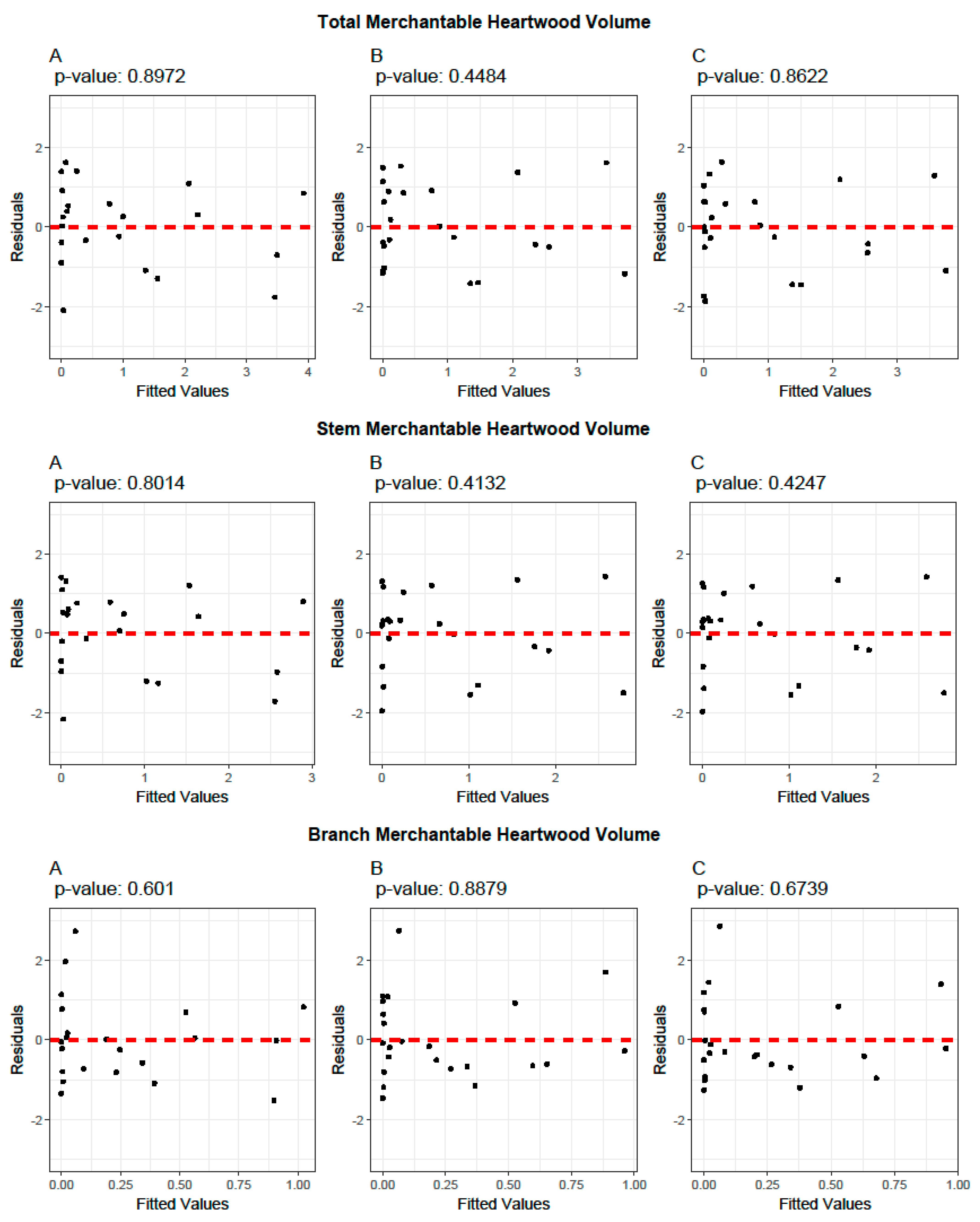
3.1. Allometric Equations for Volume Estimation
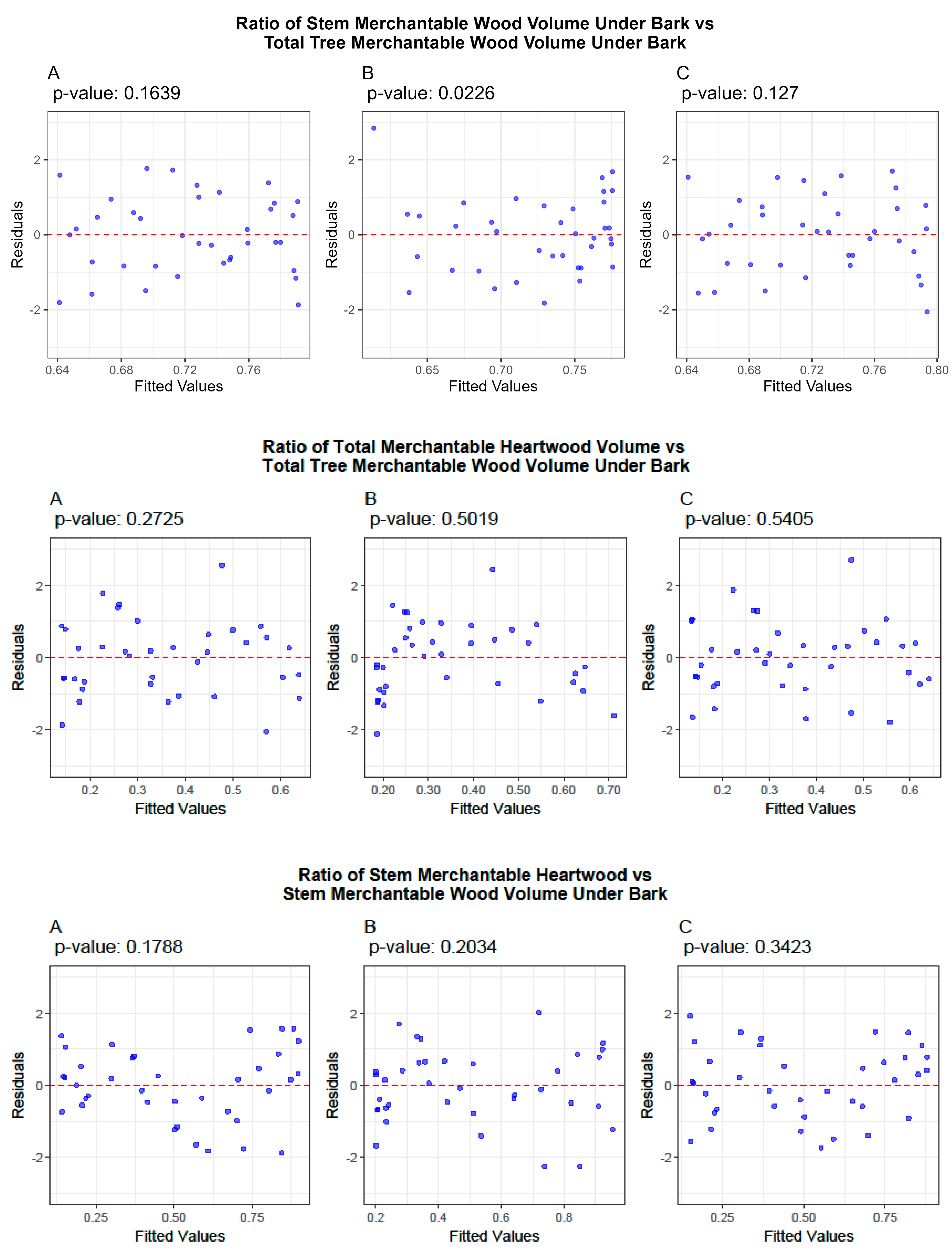
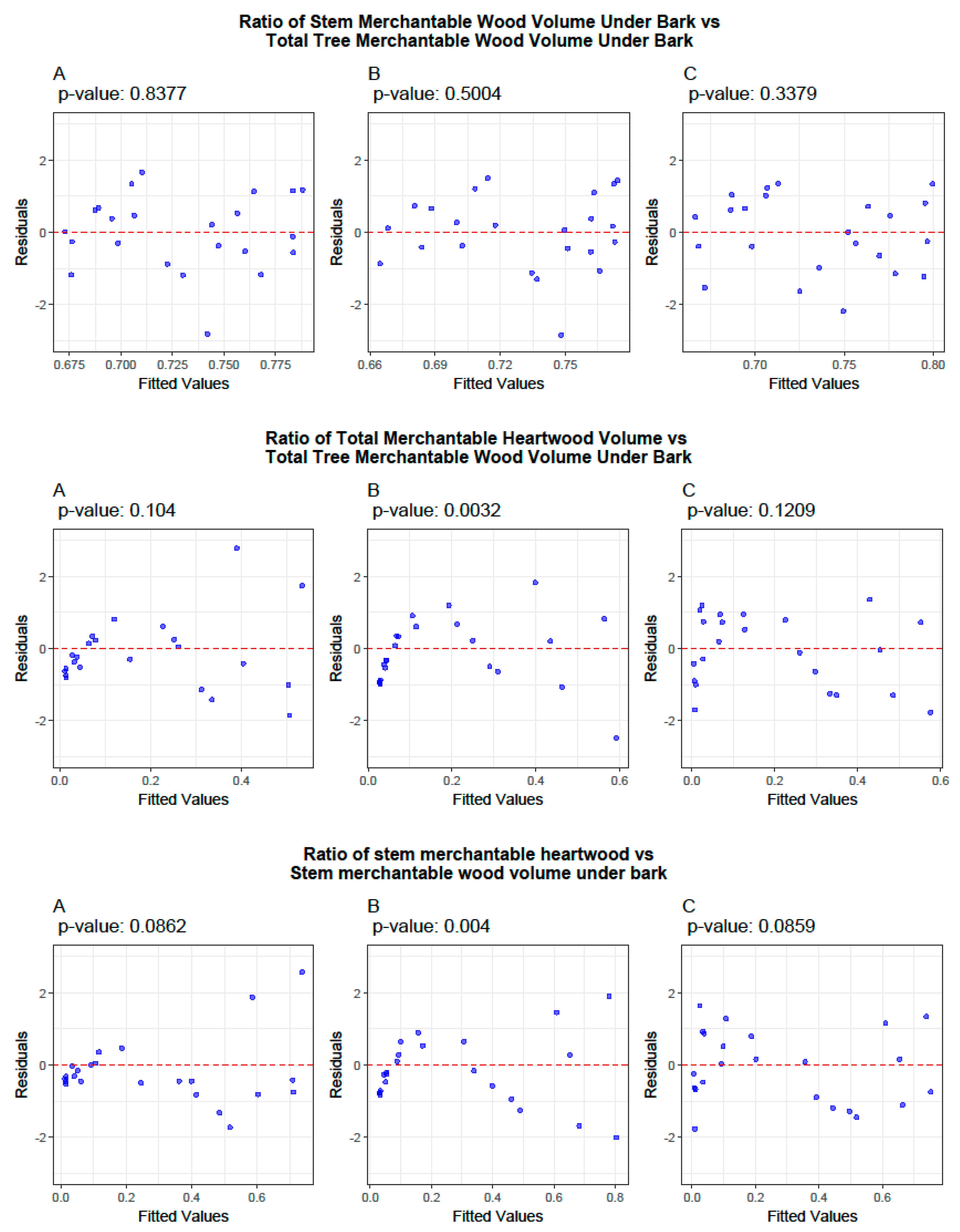
3.2. Ratio Models
3.3. Biomass Equations
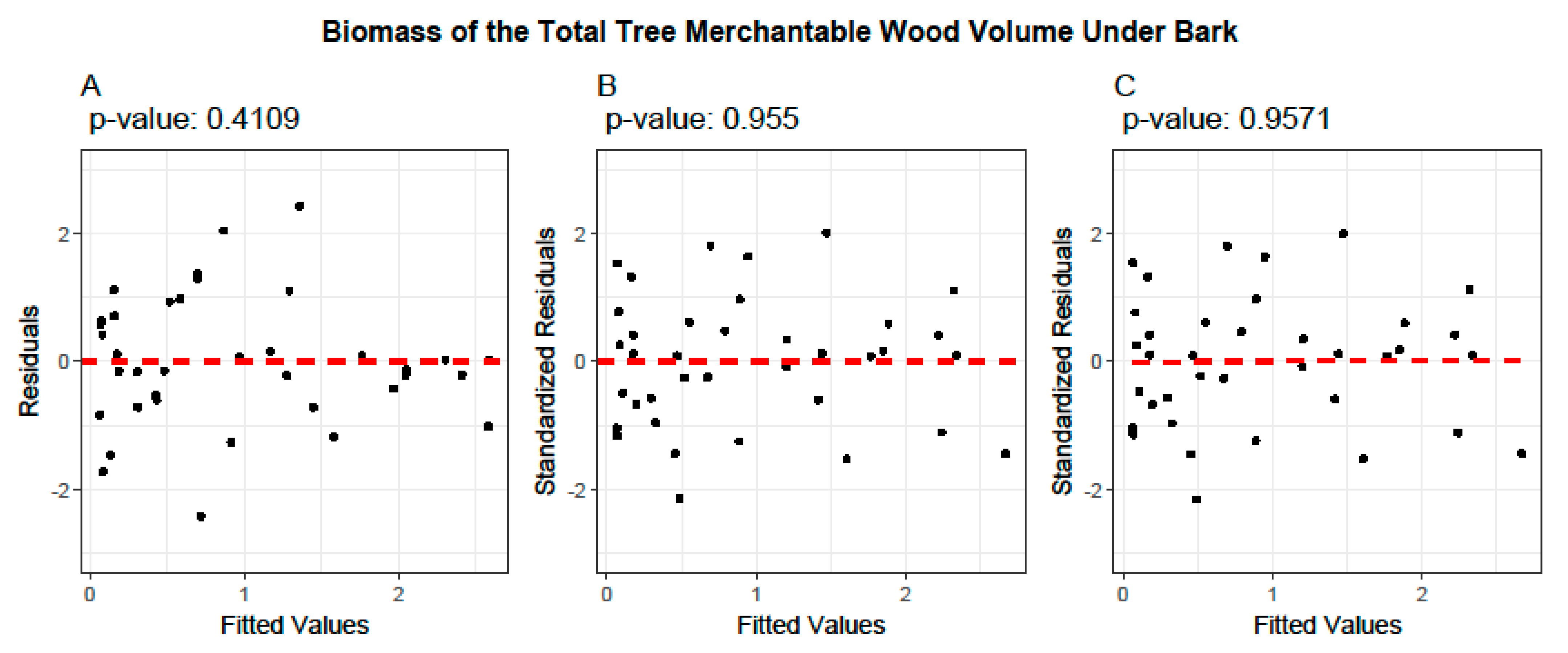
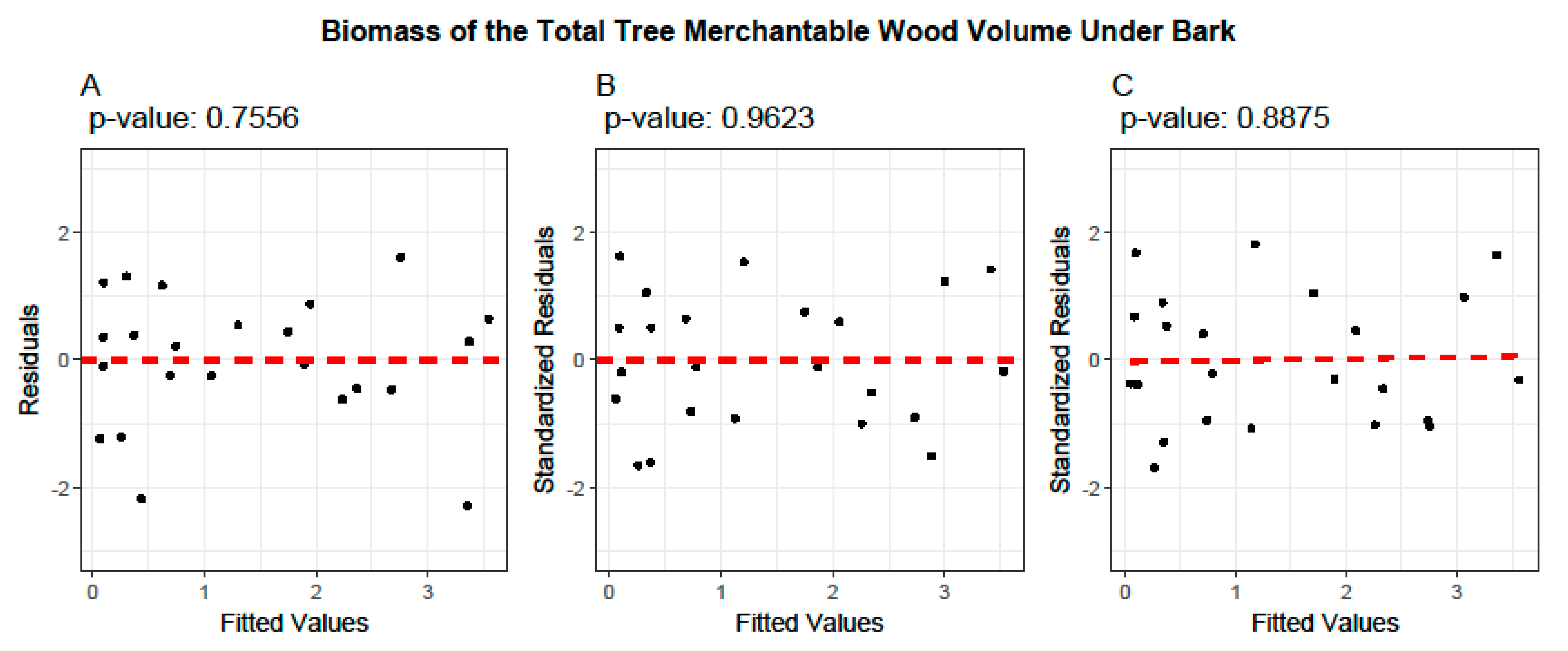
3.4. Cross-Validation of Volume and Ratio Biomass Equations
3.5. Evaluation of the Predictive Performance of Developed and Existing Allometric Equations
4. Discussion
- Wood volume equations
- Heartwood volume equations
- Ratio models
- Practical use of volume and ratio models
- Biomass models
- Model Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Campbell, B.M.; Angelsen, A.; Cunningham, A.; Katerere, Y.; Sitoe, A.; Wunder, S. Miombo Woodlands—Opportunities and Barriers to Sustainable Forest Management; Campbell, B., Ed.; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2007. [Google Scholar]
- Dziba, L.; Ramoelo, A.; Ryan, C.; Harrison, S.; Pritchard, R.; Tripathi, H.; Sitas, N.; Selomane, O.; Engelbrecht, F.; Pereira, L.; et al. Scenarios for Just and Sustainable Futures in the Miombo Woodlands. In Miombo Woodlands in a Changing Environment: Securing the Resilience and Sustainability of People and Woodlands; Ribeiro, N., Katerere, Y., Chirwa, P.W., Grundy, I.M., Eds.; Springer Nature: Cham, Switzerland, 2020; pp. 191–234. [Google Scholar]
- Chiteculo, V.; Surovy, P. Dynamic Patterns of Trees Species in Miombo Forest and Management Perspectives for Sustainable Production—Case Study in Huambo Province, Angola. Forests 2018, 9, 321. [Google Scholar] [CrossRef]
- Gumbo, D.J.; Dumas-Johansen, M.; Muir, G.; Boerstler, F.; Xia, Z. Sustainable Management of Miombo Woodlands. Food Security, Nutrition, and Wood Energy; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2018; ISBN 9789251304235. [Google Scholar]
- Magalhães, T. Inventário Florestal Nacional; Ministério da Terra, Ambiente e Desenvolvimento Rural: Maputo, Mozambique, 2018. [Google Scholar]
- MITADER. Desflorestamento em Moçambique (2003–2016); Direção Nacional de Florestas: Maputo, Mozambique, 2018. [Google Scholar]
- Aquino, A.; Lim, C.; Kaechele, K.; Taquidir, M. Mozambique Country Forestry Note; World Bank: Washington, DC, USA, 2018; pp. 1–33. [Google Scholar] [CrossRef]
- Magalhães, T.M. What is left in miombo woodlands? Rarity and commonness of woody species, commercial timber species, and lawful harvestable diameter classes. Heliyon 2025, 11, e41821. [Google Scholar] [CrossRef] [PubMed]
- Bila, N.F.; Trianoski, R.; Iwakiri, S.; Bila, N.F.; Manhiça, A.A.; Rocha, M.P.D. Bonding Quality of Two Lesser-Used Wood Species Brachystegia spiciformis and Julbernardia globiflora from Mozambique. Maderas. Cienc. y Tecnol. 2021, 23, 1–12. [Google Scholar] [CrossRef]
- DINAF. Relatorio Anual 2023; Brazilian Development Bank: Rio de Janeiro, Brazil, 2023. [Google Scholar]
- Bila, N.F.; Trianoski, R.; Da Rocha, M.P.; Da Silva, J.R.M.; Iwakiri, S.; Egas, A.F.; Mussana, A.F. Machining Operations on Messassa Wood. Wood Res. J. 2020, 11, 12–19. [Google Scholar] [CrossRef]
- De Lima, R.B.; Rutishauser, E.; Da Silva, J.A.A.; Guedes, M.C.; Herault, B.; De Oliveira, C.P.; Da Silva Aparício, P.; Sotta, E.D.; Da Silva, D.A.S.; Ferreira, R.L.C. Accurate Estimation of Commercial Volume in Tropical Forests. For. Sci. 2020, 67, 14–21. [Google Scholar] [CrossRef]
- Kachamba, D.J.; Eid, T. Total tree, merchantable stem and branch volume models for miombo woodlands of Malawi Total tree, merchantable stem and branch volume models for miombo. South. For. 2016, 78, 41–51. [Google Scholar] [CrossRef]
- Romero, F.M.B.; Jacovine, L.A.G.; Ribeiro, S.C.; Torres, C.M.M.E.; da Silva, L.F.; Gaspar, R.d.O.; da Rocha, S.J.S.S.; Staudhammer, C.L.; Fearnside, P.M. Allometric equations for volume, biomass, and carbon in commercial stems harvested in a managed forest in the southwestern amazon: A case study. Forests 2020, 11, 874. [Google Scholar] [CrossRef]
- Miranda, D.L.C.; Loch, V.M.; Silva, F.; dos Santos Lisboa, G.; de Goes Canalez, G.; Condé, T.M.; Castelo, P.A.R. Porcentagem de cerne, alburno e casca de cinco espécies madeireiras da Amazônia. Nativa 2017, 5, 619–627. [Google Scholar] [CrossRef]
- Bor, N.C.; Muchiri, M.N.; Kigomo, J.N.; Hyvönen, P.; Muga, M.; Nduati, P.N.; Haakana, H.; Owuor, N.O. Compartmentalized Allometric Equation for Estimating Volume and Biomass of Eucalyptus in Agroforestry Systems in Kenya. East African J. For. Agrofor. 2021. Special Issue 1–9. Available online: https://www.kefri.org/assets/publications/articles/Compartmentalized%20Allometric%20Equation%20for%20estimating%20volume%20and%20biomass%20of%20eucalyptus%20in%20agroforestry%20systems%20in%20Kenya.pdf (accessed on 31 March 2025).
- Ver Planck, N.R.; MacFarlane, D.W. Modelling vertical allocation of tree stem and branch volume for hardwoods. Forestry 2014, 87, 459–469. [Google Scholar] [CrossRef]
- Steel, E.A. Carbon Storage and Climate Change Mitigation Potential of Harvested Wood Products; The Food and Agriculture Organization of the United Nations (FAO): Roma, Italy, 2021. [Google Scholar]
- Johnston, C.M.T.; Radeloff, V.C. Global mitigation potential of carbon stored in harvested wood products. Proc. Natl. Acad. Sci. USA 2019, 116, 14526–14531. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Y.; Song, T.; Xu, J. Harvested wood products as a carbon sink in China, 1900–2016. Int. J. Environ. Res. Public Health 2019, 16, 445. [Google Scholar] [CrossRef] [PubMed]
- Jasinevičius, G.; Lindner, M.; Pingoud, K.; Tykkylainen, M. Review of models for carbon accounting in harvested wood products. Int. Wood Prod. J. 2015, 6, 198–212. [Google Scholar] [CrossRef]
- Tadese, S.; Soromessa, T.; Aneseyee, A.B.; Gebeyehu, G.; Noszczyk, T.; Kindu, M. Carbon Storage Dynamics and its Economic Values in Tropical Moist Afromontane Forests, South-West. Res. Sq. 2023, 1–41. [Google Scholar]
- Parobek, J.; Paluš, H.; Moravčík, M.; Kovalčík, M.; Dzian, M.; Murgaš, V.; Šimo-Svrček, S. Changes in carbon balance of harvested wood products resulting from different wood utilization scenarios. Forests 2019, 10, 590. [Google Scholar] [CrossRef]
- Tupenaite, L.; Kanapeckiene, L.; Naimaviciene, J.; Kaklauskas, A.; Gecys, T. Timber Construction as a Solution to Climate Change: A Systematic Literature Review. Buildings 2023, 13, 976. [Google Scholar] [CrossRef]
- Guedes, B.S.; Sitoe, A.A.; Olsson, B.A. Allometric models for managing lowland miombo woodlands of the Beira corridor in Mozambique. Glob. Ecol. Conserv. 2018, 13, e00374. [Google Scholar] [CrossRef]
- Mugasha, W.A.; Mwakalukwa, E.E.; Luoga, E.; Malimbwi, R.E.; Zahabu, E.; Silayo, D.S.; Sola, G.; Crete, P.; Henry, M.; Kashindye, A. Allometric Models for Estimating Tree Volume and Aboveground Biomass in Lowland Forests of Tanzania. Int. J. For. Res. 2016, 2016, 8076271. [Google Scholar] [CrossRef]
- Mate, R.; Johansson, T.; Sitoe, A. Biomass equations for tropical forest tree species in mozambique. Forests 2014, 5, 535–556. [Google Scholar] [CrossRef]
- Mauya, E.W.; Mugasha, W.A.; Zahabu, E.; Bollandsås, O.M.; Tron, E. Models for estimation of tree volume in the miombo woodlands of Tanzania. South. For. 2014, 76, 209–219. [Google Scholar] [CrossRef]
- Falcão, M.P. Plano de Maneio Revisto 2017–2022 Levasflor; Administração Nacional das Áreas de Conservação: Maputo, Mozambique, 2017.
- Ministério da Administração Estatal. Perfil do Distrito do Nhamatanda Prov Í Ncia de Sofala Edi ç ão 2005; Ministério da Administração Estatal: Maputo, Mozambique, 2005.
- Ulak, S.; Ghimire, K.; Gautam, R.; Bhandari, S.K.; Poudel, K.P.; Timilsina, Y.P.; Pradhan, D.; Subedi, T. Predicting the upper stem diameters and volume of a tropical dominant tree species. J. For. Res. 2022, 33, 1725–1737. [Google Scholar] [CrossRef]
- Koirala, A.; Montes, C.R.; Bullock, B.P.; Wagle, B.H. Developing taper equations for planted teak (Tectona grandis L.f.) trees of central lowland Nepal. Trees For. People 2021, 5, 100103. [Google Scholar] [CrossRef]
- Subedi, T.; Bhandari, S.K.; Pandey, N.; Timilsina, Y.P.; Mahatara, D. Form factor and volume equations for individual trees of Shorea robusta in Western low land of Nepal. Austrian J. For. Sci. 2021, 138, 143–166. [Google Scholar]
- Kozak, A. Methods for Ensuring Additivity of Biomass Components by Regression Analysis. For. Chron. 1970, 46, 402–405. [Google Scholar] [CrossRef]
- van Laar, A.; Akça, A. Forest Mensuration—Managing Forest Ecosystems; von Gadow, K., Pukkala, T., Tomé, M., Eds.; Springer: Dordrecht, The Netherlands, 2007; Volume 13, ISBN 9781402059902. [Google Scholar]
- Kershaw, J.J.A.; Ucey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; John Wiley & Sons: West Sussex, UK, 2017; ISBN 9781118902035. [Google Scholar]
- ISO 13061-2:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 2: Determination of Density for Physical and Mechanical Tests. International Organization for Standardization: Geneva, Switzerland, 2014.
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volume and Biomass Allometric Equations: From Field Measurement to Prediction; Food and Agricultural Organization of the United Nations: Rome, Italy; Centre de Coopération Internationale en Recherche Agronomique pour le Développement: Montpellier, France, 2012.
- Dutcă, I.; McRoberts, R.E.; Næsset, E.; Blujdea, V.N.B. Accommodating heteroscedasticity in allometric biomass models. For. Ecol. Manag. 2021, 505, 119865. [Google Scholar] [CrossRef]
- Mascaro, J.; Litton, C.M.; Hughes, R.F.; Uowolo, A.; Schnitzer, S.A. Minimizing Bias in Biomass Allometry: Model Selection and Log-Transformation of Data. Biotropica 2011, 43, 649–653. [Google Scholar] [CrossRef]
- Li, W.; Cook, D.; Tanaka, E.; VanderPlas, S. A Plot is Worth a Thousand Tests: Assessing Residual Diagnostics with the Lineup Protocol. J. Comput. Graph. Stat. 2024, 33, 1497–1511. [Google Scholar] [CrossRef]
- Halunga, A.G.; Orme, C.D.; Yamagata, T. A heteroskedasticity robust Breusch–Pagan test for Contemporaneous correlation in dynamic panel data models. J. Econom. 2017, 198, 209–230. [Google Scholar] [CrossRef]
- Waldman, D.M. A note on algebraic equivalence of White’s test and a variation of the Godfrey/Breusch-Pagan test for heteroscedasticity. Econ. Lett. 1983, 13, 197–200. [Google Scholar] [CrossRef]
- Bruce, P.; Bruce, A. Practical Statistics for Data Scientists 50 Essential Concepts; Shannon, C., Ed.; O’Reilly Media: Sebastopol, CA, USA, 2017; ISBN 978-4-87311-828-4. [Google Scholar]
- Menin, B. Objective Model Selection in Physics: Exploring the Finite Information Quantity Approach. J. Appl. Math. Phys. 2024, 12, 1848–1889. [Google Scholar] [CrossRef]
- Pham, H. A new criterion for model selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef]
- Höge, M.; Wöhling, T.; Nowak, W. A Primer for Model Selection: The Decisive Role of Model Complexity. Water Resour. Res. 2018, 54, 1688–1715. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?-Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Hyndman, R.J. Another Look at Forecast Accuracy Metrics for Intermittent Demand. Foresight Int. J. Appl. Forecast. 2006, 4, 43–46. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Magalhães, T.M.; Mate, R.S. Least squares-based biomass conversion and expansion factors best estimate biomass than ratio-based ones: Statistical evidences based on tropical timber species. MethodsX 2018, 5, 30–38. [Google Scholar] [CrossRef]
- Spiess, A.-N.; Neumeyer, N. An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol 2010, 10, 6. [Google Scholar] [CrossRef]
- Magalhães, T.M.; Cossa, V.N.; Guedes, B.S.; Fanheiro, A.S.M. Species-specific biomass allometric models and expansion factors for indigenous and planted forests of the Mozambique highlands. J. For. Res. 2021, 32, 1047–1065. [Google Scholar] [CrossRef]
- Asigbaase, M.; Dawoe, E.; Abugre, S.; Kyereh, B.; Ayine Nsor, C. Allometric relationships between stem diameter, height and crown area of associated trees of cocoa agroforests of Ghana. Sci. Rep. 2023, 13, 14897. [Google Scholar] [CrossRef]
- Wirabuana, P.Y.A.P.; Setiahadi, R.; Sadono, R.; Lukito, M.; Martono, D.S.; Matatula, J. Allometric equations for estimating biomass of community forest tree species in Madiun, Indonesia. Biodiversitas 2020, 21, 4291–4300. [Google Scholar] [CrossRef]
- Yates, L.A.; Aandahl, Z.; Richards, S.A.; Brook, B.W. Cross validation for model selection: A review with examples from ecology. Ecol. Monogr. 2023, 93, e1533. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Goussanou, C.A.; Guendehou, S.; Assogbadjo, A.E.; Kaire, M.; Sinsin, B.; Cuni-Sanchez, A. Specific and generic stem biomass and volume models of tree species in a West African tropical semi-deciduous forest. Silva Fenn. 2016, 50, 1474. [Google Scholar] [CrossRef]
- Mwaluseke, M.L.; Mwakalukwa, E.E.; Maliondo, S.M.S. Volume and aboveground biomass models for a dry evergreen montane forest in Tanzania. Asian J. For. 2023, 7, 45–53. [Google Scholar] [CrossRef]
- Mate, R.; Johansson, T.; Sitoe, A. Stem Volume Equations for Valuable Timber Species in Mozambique. J. Sustain. For. 2015, 34, 787–806. [Google Scholar] [CrossRef]
- Fernández-Sólis, D.; Berrocal, A.; Moya, R. Heartwood formation and prediction of heartwood parameters in Tectona grandis L.f. trees growing in forest plantations in Costa Rica. Bois Forets des Trop. 2018, 335, 25–37. [Google Scholar] [CrossRef]
- Yang, B.; Jia, H.; Zhao, Z.; Pang, S.; Cai, D. Horizontal and vertical distributions of heartwood for teak plantation. Forests 2020, 11, 225. [Google Scholar] [CrossRef]
- Ekoungoulou, R.; Nzala, D.; Liu, X.; Niu, S. Tree Biomass Estimation in Central African Forests Using Allometric Models. Open J. Ecol. 2018, 8, 209–237. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Banin, L.; Phillips, O.L.; Baker, T.R.; Lewis, S.L.; Quesada, C.A.; Affum-Baffoe, K.; Arets, E.J.M.M.; Berry, N.J.; Bird, M.; et al. Height-diameter allometry of tropical forest trees. Biogeosciences 2011, 8, 1081–1106. [Google Scholar] [CrossRef]
- Fortier, J.; Truax, B.; Gagnon, D.; Lambert, F. Allometric equations for estimating compartment biomass and stem volume in mature hybrid poplars: General or site-specific? Forests 2017, 8, 309. [Google Scholar] [CrossRef]
- Halle, F.; Oldeman, R.A.A.; Tomlinson, P.B. Tropical Trees and Forests: An Architectural Analysis; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1978; ISBN 2013206534. [Google Scholar]
- Pulido-Rodríguez, E.; López-Camacho, R.; Tórres, J.; Velasco, E.; Salgado-Negret, B. Traits and trade-offs of wood anatomy between trunks and branches in tropical dry forest species. Trees-Struct. Funct. 2020, 34, 497–505. [Google Scholar] [CrossRef]
- Cushman, K.C.; Machado, J.L. Plasticity in branching and crown architecture helps explain how tree diversity increases tropical forest production. New Phytol. 2020, 228, 1163–1165. [Google Scholar] [CrossRef] [PubMed]
- Boczniewicz, D.; Mason, E.G.; Morgenroth, J.A. Developing fully compatible taper and volume equations for all stem components of Eucalyptus globoidea Blakely trees in New Zealand. N. Z. J. For. Sci. 2022, 52, 6. [Google Scholar] [CrossRef]
- Arisandi, R.; Marsoem, S.N.; Sutapa, J.P.G.; Lukmandaru, G. A Review of the Factors Influencing Variations in the Heartwood Proportion for Solid Wood. South-East Eur. For. 2023, 14, 245–253. [Google Scholar] [CrossRef]
- Igartúa, D.; Moreno, K.; Monteoliva, S. Acacia melanoxylon in Argentina: Heartwood content and its relationship with site, growth and age of the trees. For. Syst. 2017, 26, 9. [Google Scholar] [CrossRef]
- Kokutse, A.D.; Baillères, H.; Stokes, A.; Kokou, K. Proportion and quality of heartwood in Togolese teak (Tectona grandis L.f.). For. Ecol. Manag. 2004, 189, 37–48. [Google Scholar] [CrossRef]
- Ramanan, S.S.; Kunhamu, T.K.; Anoop, E.V.; George, A.K. Does stand thinning influence wood physical properties? An investigation in a tropical hardwood, Acacia mangium Willd. J. Trop. Agric. 2018, 56, 137–144. [Google Scholar]
- Pérez Cordero, L.D.; Kanninen, M. Heartwood, sapwood and bark content, and wood dry density of young and mature teak (Tectona grandis) trees grown in Costa Rica. Silva Fenn. 2003, 37, 45–54. [Google Scholar] [CrossRef]
- Tewari, V.P.; Mariswamy, K.M. Heartwood, sapwood and bark content of teak trees grown in Karnataka, India. J. For. Res. 2013, 24, 721–725. [Google Scholar] [CrossRef]
- Tewari, V.P.; Singh, B. Total and merchantable wood volume equations for Eucalyptus hybrid trees in Gujarat State, India. Arid L. Res. Manag. 2006, 20, 147–159. [Google Scholar] [CrossRef]
- Teshome, T. Compatible volume-taper equations for predicting merchantable volume to variable merchantable limits for Cupressus lusitanica, Ethiopia. SINET Ethiop. J. Sci. 2005, 28, 15–22. [Google Scholar] [CrossRef]
- Ali, A.; Wang, L.Q. Big-sized trees and forest functioning: Current knowledge and future perspectives. Ecol. Indic. 2021, 127, 107760. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Laurance, W.F. The ecology, distribution, conservation and management of large old trees. Biol. Rev. 2017, 92, 1434–1458. [Google Scholar] [CrossRef]
- Sitoe, A.; Chidumayo, E.; Alberto, M. Timber and wood products. In The Dry Forests and Woodlands of Africa: Managing for Products and Services; Chidumayo, E.N., Gumbo, D.J., Eds.; Center for International Forestry Research: London, UK; Washington, DC, USA, 2010; pp. 131–153. ISBN 9781136531385. [Google Scholar]
- Syampungani, S.; Chirwa, P.W.; Geldenhuys, C.J.; Handavu, F.; Chishaleshale, M.; Rija, A.A.; Mbanze, A.A.; Ribeiro, N.S. Managing Miombo: Ecological and Silvicultural Options for Sustainable Socio-Economic Benefits. In Miombo Woodlands in a Changing Environment: Securing the Resilience and Sustainability of People and Woodlands; Ribeiro, N.S., Katerere, Y., Chirwa, P.W., Grundy, I.M., Eds.; Springer Nature: Cham, Switzerland, 2020; pp. 101–131. [Google Scholar]
- Kapinga, K.; Syampungani, S.; Kasubika, R.; Yambayamba, A.M.; Shamaoma, H. Species-specific allometric models for estimation of the above-ground carbon stock in miombo woodlands of Copperbelt Province of Zambia. For. Ecol. Manag. 2018, 417, 184–196. [Google Scholar] [CrossRef]
- Romero, F.M.B.; de Nazaré Oliveira Novais, T.; Jacovine, L.A.G.; Bezerra, E.B.; de Castro Lopes, R.B.; de Holanda, J.S.; Reyna, E.F.; Fearnside, P.M. Wood Basic Density in Large Trees: Impacts on Biomass Estimates in the Southwestern Brazilian Amazon. Forests 2024, 15, 734. [Google Scholar] [CrossRef]
- Mwakalukwa, E.E.; Meilby, H.; Treue, T. Volume and Aboveground Biomass Models for Dry Miombo Woodland in Tanzania. Int. J. For. Res. 2014, 2014, 31256. [Google Scholar] [CrossRef]
- Teshome, M.; Torres, C.M.M.E.; Sileshi, G.W.; de Mattos, P.P.; Braz, E.M.; Temesgen, H.; da Rocha, S.J.S.S.; Alebachew, M. Mixed-Species Allometric Equations to Quantify Stem Volume and Tree Biomass in Dry Afromontane Forest of Ethiopia. Open J. For. 2022, 12, 263–296. [Google Scholar] [CrossRef]
- Daba, D.E.; Soromessa, T. Allometric equations for aboveground biomass estimation of Diospyros abyssinica (Hiern) F. White tree species. Ecosyst. Health Sustain. 2019, 5, 86–97. [Google Scholar] [CrossRef]
- Grundy, I.M. Wood biomass estimation in dry miombo woodland in Zimbabwe. For. Ecol. Manag. 1995, 72, 109–117. [Google Scholar] [CrossRef]
- Lisboa, S.N.; Macôo, S.; Sitoe, A. Allometric equations and height-diameter models for estimating above-and below-ground biomass of Colophospermum mopane J. Léonard. in Mozambique. Nature 2025, 15, 3464. [Google Scholar] [CrossRef]
| Brachystegia spiciformis | Julbernardia globiflora | |||||
|---|---|---|---|---|---|---|
| DBH (cm) | Hc (m) | Ht (m) | DBH (cm) | Hc (m) | Ht (m) | |
| Min | 17.1 | 4.46 | 12.5 | 14.5 | 4.46 | 12.03 |
| Max | 80.7 | 18.7 | 25.4 | 61.2 | 13.9 | 22.17 |
| Mean | 47.04 | 10.26 | 19.92 | 38.93 | 9.17 | 18.28 |
| SD | 20.62 | 3.92 | 3.42 | 15.71 | 3.17 | 2.77 |
| CV | 43.84 | 38.22 | 17.18 | 40.34 | 34.55 | 15.15 |
| SE | 3.39 | 0.65 | 0.56 | 3.28 | 0.66 | 0.58 |
| Category | Wood Component | Tree Part | Analyzed Volume and Biomass Categories |
|---|---|---|---|
| Total wood | Heartwood plus sapwood | Stem plus branches | Total tree merchantable wood volume under bark (stem merchantable wood volume under bark plus branch merchantable wood volume under bark) (stem or branches from 15cm diameter over bark) |
| Total tree merchantable biomass under bark (biomass of stem merchantable wood volume under bark plus biomass of branches merchantable wood volume under bark) (stem or branches from 15 cm diameter over bark) | |||
| Components | Heartwood and sapwood | Merchantable stem | Stem merchantable wood volume under bark (stem from 15 cm diameter over bark) |
| Merchantable branches | Branches merchantable wood volume under bark (branches from 15 cm top diameter over bark) | ||
| Heartwood | Stem plus branches | Total merchantable heartwood volume (stem merchantable heartwood plus branch merchantable heartwood) | |
| Merchantable stem | Stem merchantable heartwood (stems from 15 cm diameter over bark) | ||
| Merchantable branches | Branches merchantable heartwood (branches from 15 cm diameter over bark) |
| Model | Power Models | Model | Ratio Models |
|---|---|---|---|
| 1 | ε | 4 | ε |
| 2 | × ε | 5 | ε |
| 3 | ε | 6 | ε |
| ID | Models | AIC | BIC | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|---|
| Total tree merchantable wood volume under bark | ||||||
| 1 | Y = 1.67 × 10−4 × DBH2.319 | −33.017 | −21.741 | 0.200 | 0.128 | 10.631 |
| 2 | Y = 2.59 × 10−5 × (DBH2 × Ht)1.008 | −57.394 | −46.117 | 0.192 | 0.115 | 7.411 |
| 3 | Y = 2.42 × 10−5 × DBHb2.002 × Ht1.047 | −49.439 | −31.719 | 0.194 | 0.116 | 7.365 |
| Stem merchantable wood volume under bark | ||||||
| 1 | Y = 2.03 × 10−4 × DBH2.181 | −51.701 | −40.425 | 0.155 | 0.109 | 11.680 |
| 2 | Y = 3.32 × 10−5 × (DBH2 × Ht)0.953 | −72.116 | −60.840 | 0.142 | 0.083 | 8.111 |
| 3 | Y = 2.75 × 10−5 × DBH1.873 × Ht1.058 | −64.373 | −46.653 | 0.143 | 0.084 | 8.077 |
| Branch merchantable wood volume under bark | ||||||
| 1 | Y = 1.17 × 10−5 × DBH2.682 | −123.212 | −111.935 | 0.078 | 0.051 | 12.187 |
| 2 | Y = 1.58 × 10−6 × (DBH2 × Ht)1.150 | −145.192 | −133.915 | 0.091 | 0.048 | 8.832 |
| 3 | Y = 1.78 × 10−6 × DBH2.327 × Ht5.130 | −137.316 | −119.596 | 0.089 | 0.047 | 8.895 |
| Total merchantable heartwood volume | ||||||
| 1 | Y = 7.99 × 10−7 × DBH3.500 | −98.802 | −87.525 | 0.135 | 0.075 | 11.649 |
| 2 | Y = 4.36 × 10−8 × (DBH2 × Ht)1.528 | −117.166 | −105.890 | 0.118 | 0.070 | 9.408 |
| 3 | Y = 1.13 × 10−7 × DBH3.198 × Ht1.035 | −115.792 | −98.071 | 0.101 | 0.061 | 9.080 |
| Stem merchantable heartwood | ||||||
| 1 | Y = 9.39 × 10−7 × DBH3.391 | −112.714 | −101.438 | 0.113 | 0.068 | 12.657 |
| 2 | Y = 5.78 × 10−8 × (DBH2 × Ht)1.478 | −130.199 | −118.923 | 0.114 | 0.063 | 9.380 |
| 3 | Y = 1.29 × 10−7 × DBH3.081 × Ht1.053 | −126.200 | −108.480 | 0.103 | 0.057 | 9.529 |
| Branch merchantable heartwood | ||||||
| 1 | Y = 2.83 × 10−8 × DBH43.977 | −184.658 | −173.382 | 0.082 | 0.045 | 18.862 |
| 2 | Y = 1.12 × 10−9 × (DBH2 × Ht)1.729 | −191.102 | −179.826 | 0.067 | 0.038 | 16.989 |
| 3 | Y = 3.65 × 10−9 × DBH3.649 × Ht1.099 | −185.938 | −168.218 | 0.069 | 0.040 | 16.820 |
| ID | Models | AIC | BIC | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|---|
| Total tree merchantable wood volume under bark | ||||||
| 1 | Y = 6.53 × 10−5 × DBH2.737 | −2.588 | 5.360 | 0.342 | 0.204 | 13.502 |
| 2 | Y = 6.98 × 10−6 × (DBH2 × Ht)1.196 | −16.500 | −8.552 | 0.230 | 0.160 | 10.474 |
| 3 | Y = 3.55 × 10−6 × DBH2.286 × Ht1.559 | −9.560 | 2.931 | 0.219 | 0.156 | 10.135 |
| Stem merchantable wood volume under bark | ||||||
| 1 | Y = 7.05 × 10−5 × DBH2.627 | −10.365 | −2.417 | 0.277 | 0.169 | 15.070 |
| 2 | Y = 8.34 × 10−6 × (DBH2 × Ht)1.1470 | −20.879 | −12.931 | 0.204 | 0.153 | 12.802 |
| 3 | Y = 3.02 × 10−6 × DBH2.134 × Ht1.694 | −14.382 | −1.892 | 0.191 | 0.145 | 12.193 |
| Branch merchantable wood volume under bark | ||||||
| 1 | Y = 5.41 × 10−6 × DBH3.064 | −50.336 | −42.387 | 0.129 | 0.089 | 18.202 |
| 2 | Y = 4.72 × 10−7 × (DBH2 × Ht)1.333 | −56.293 | −48.344 | 0.112 | 0.075 | 15.003 |
| 3 | Y = 3.73 × 10−7 × DBH2.624 × Ht1.464 | −48.346 | −35.855 | 0.112 | 0.075 | 14.908 |
| Total merchantable heartwood volume | ||||||
| 1 | Y = 1.86 × 10−11 × DBH6.337 | −89.882 | −81.934 | 0.391 | 0.198 | 19.621 |
| 2 | Y = 1.28 × 10−13 × (DBH2 × Ht)2.748 | −120.782 | −112.834 | 0.350 | 0.173 | 11.342 |
| 3 | Y = 2.67 × 10−13 × DBH5.639 × Ht2.325 | −116.228 | −103.737 | 0.343 | 0.176 | 11.359 |
| Stem merchantable heartwood | ||||||
| 1 | Y = 1.88 × 10−11 × DBH6.261 | −100.158 | −92.210 | 0.284 | 0.149 | 21.231 |
| 2 | Y = 1.29 × 10−13 × (DBH2 × Ht)2.722 | −126.579 | −118.630 | 0.263 | 0.131 | 12.303 |
| 3 | Y = 1.38 × 10−13 × DBH5.457 × Ht2.682 | −118.595 | −106.105 | 0.263 | 0.131 | 12.354 |
| Branch merchantable heartwood | ||||||
| 1 | Y = 1.88 × 10−12 × DBH6.568 | −147.223 | −139.275 | 0.116 | 0.051 | 20.823 |
| 2 | Y = 1.09 × 10−14 × (DBH2 × Ht)2.847 | −153.325 | −145.376 | 0.099 | 0.047 | 17.715 |
| 3 | Y = 5.17 × 10−14 × DBH5.950 × Ht1.999 | −146.343 | −133.853 | 0.098 | 0.048 | 17.835 |
| ID | Model | AIC | BIC | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|---|
| Ratio of stem merchantable wood volume under bark vs. total tree merchantable wood volume under bark | ||||||
| 4 | Y = 1.533 − 0.012 × DBH | −187.216 | −182.383 | 0.018 | 0.015 | 2.128 |
| 5 | Y = 1.261 − 4.9 × 10−6 × (DBH2 × Ht) | −183.582 | −178.749 | 0.019 | 0.015 | 2.129 |
| 6 | Y = 1.656 − 0.011 × DBH − 0.009 × Ht | −184.099 | −174.433 | 0.018 | 0.014 | 2.029 |
| Ratio of total merchantable heartwood volume vs. total tree merchantable wood volume under bark | ||||||
| 4 | Y = −2.452 + 0.037 × DBH | −120.798 | −115.965 | 0.045 | 0.036 | 13.392 |
| 5 | Y = −1.543 + 1.52 × 10−5 (DBH2Ht) | −99.164 | −94.331 | 0.058 | 0.048 | 19.468 |
| 6 | Y = −2.834 + 0.034 × DBH + 0.027 × Ht | −117.079 | −107.413 | 0.043 | 0.034 | 12.733 |
| Ratio of stem merchantable heartwood vs. stem merchantable wood volume under bark | ||||||
| 4 | Y = −2.893 + 0.063 × DBH | −84.558 | −79.726 | 0.073 | 0.059 | 14.469 |
| 5 | Y = −1.498 + 2.82 × 10−5 × (DBH2Ht) | −93.142 | −88.309 | 0.066 | 0.053 | 15.298 |
| 6 | Y = −2.679 + 0.058 × DBH − 0.003 × Ht | −88.089 | −78.424 | 0.072 | 0.060 | 14.290 |
| ID | AIC | BIC | RMSE | MAE | MAPE (%) | |
|---|---|---|---|---|---|---|
| Ratio of stem merchantable wood volume under bark to total tree merchantable wood volume under bark | ||||||
| 4 | Y = 1.497 − 0.013 × DBH | −74.966 | −71.560 | 0.042 | 0.034 | 4.708 |
| 5 | Y = 1.250 − 7.14 × 10−6 × (DBH2 × Ht) | −72.716 | −69.310 | 0.044 | 0.035 | 4.857 |
| 6 | Y = 1.146 − 0.016 × DBH + 0.005 × Ht | −74.667 | −67.854 | 0.043 | 0.034 | 4.825 |
| Ratio of total merchantable heartwood volume to total tree merchantable wood volume under bark | ||||||
| 4 | Y = −5.892 + 0.098 × DBH | −97.364 | −93.957 | 0.048 | 0.030 | 43.407 |
| 5 | Y = −3.728 + 5.18 × 10−5 (DBH2Ht) | −82.850 | −79.444 | 0.058 | 0.040 | 104.198 |
| 6 | Y = −8.505 + 0.094 × DBH + 0.145 × Ht | −106.714 | −99.901 | 0.056 | 0.034 | 21.837 |
| Ratio of stem merchantable heartwood to stem merchantable wood volume under bark | ||||||
| 4 | Y = −6.061 + 0.166 × DBH | −71.651 | −68.244 | 0.071 | 0.046 | 39.758 |
| 5 | Y = −3.564 + 6.40 × 10−5 × (DBH2Ht) | −69.126 | −65.720 | 0.073 | 0.054 | 92.633 |
| 6 | Y = −8.566 + 0.110 × DBH − 0.140 × Ht | −93.239 | −86.426 | 0.076 | 0.049 | 20.017 |
| ID | Models | AIC | BIC | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|---|
| Total tree merchantable biomass of the total merchantable wood under bark | ||||||
| 1 | Y = 8.83 × 10−5 × DBH2.343 | −74.835 | −63.558 | 0.111 | 0.071 | 10.657 |
| 2 | Y = 1.35 × 10−5 × (DBH2 × Ht)1.017 | −98.324 | −87.048 | 0.112 | 0.069 | 7.682 |
| 3 | Y = 1.33 × 10−5 × DBH2.030 × Ht1.028 | −90.328 | −72.608 | 0.112 | 0.069 | 7.670 |
| ID | Models | AIC | BIC | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|---|
| Total tree merchantable biomass of the total merchantable wood under bark | ||||||
| 1 | Y = 4.10 × 10−5 × DBH2.763 | −20.095 | −12.147 | 0.237 | 0.138 | 13.250 |
| 2 | Y = 4.29 × 10−6 × (DBH2 × Ht)1.207 | −34.244 | −26.295 | 0.237 | 0.110 | 10.298 |
| 3 | Y = 2.26 × 10−6 × DBH2.314 × Ht1.551 | −27.216 | −14.726 | 0.151 | 0.108 | 9.995 |
| Species | Parameter | TWuB | SWuB | BWuB | THwV | SHwV | BHwV |
|---|---|---|---|---|---|---|---|
| B. spiciformis | MAPE (%) | 7.80 | 8.55 | 9.31 | 9.88 | 9.96 | 18.03 |
| J. globiflora | MAPE (%) | 11.66 | 13.96 | 16.33 | 13.09 | 14.15 | 19.84 |
| Species | Parameter | Ratio SWUB vs. TWUB | Ratio THWV vs. TWUB | Ratio SMHW vs. SWUB |
|---|---|---|---|---|
| B. spiciformis | MAPE (%) | 2.23 | 14.12 | 16.05 |
| J. globiflora | MAPE (%) | 4.93 | 25.84 | 23.01 |
| Species | Parameter | Biomass |
|---|---|---|
| B. spiciformis | MAPE (%) | 8.03 |
| J. globiflora | MAPE (%) | 11.66 |
| References | Models | MAPE (%) | |||
|---|---|---|---|---|---|
| TWuB | SWuB | BWuB | THwV | ||
| Present study | B. spiciformis (data set used) | 7 | 8 | 9 | 9 |
| Present study | J. globiflora | 81 | 155 | 108 | 159 |
| [58] | Holoptelea grandis | 46 | - | - | - |
| [58] | Cynometra megalophylla | 29 | - | - | - |
| [59] | Mixed species | 86 | - | - | - |
| [26] | Mixed species | 82 | 53 | 205 | - |
| [60] | Pterocarpus angolensis | - | 217 | - | - |
| [60] | Afzelia quanzensis | - | 76 | - | - |
| [13] | Mixed species | - | 64 | 98 | - |
| [28] | Mixed species | - | - | 334 | - |
| [61] | Tectona grandis | - | - | - | 61 |
| [62] | Tectona grandis | - | - | - | 100 |
| References | Models | MAPE (%) |
|---|---|---|
| Biomass | ||
| Present study | B. spiciformis (data set used) | 8 |
| Present study | J. globiflora | 166 |
| [53] | B. spiciformis | 25 |
| [27] | Pterocarpus angolensis | 29 |
| [27] | Afzelia quanzensis | 128 |
| Mixed species | 89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manjate, A.; Goodman, R.; Zahabu, E.; Ilstedt, U.; Egas, A. Allometric Models to Estimate the Merchantable Wood Volume and Biomass of the Most Abundant Miombo Species in the Miombo Woodlands in Mozambique. Earth 2025, 6, 52. https://doi.org/10.3390/earth6020052
Manjate A, Goodman R, Zahabu E, Ilstedt U, Egas A. Allometric Models to Estimate the Merchantable Wood Volume and Biomass of the Most Abundant Miombo Species in the Miombo Woodlands in Mozambique. Earth. 2025; 6(2):52. https://doi.org/10.3390/earth6020052
Chicago/Turabian StyleManjate, Americo, Rosa Goodman, Eliakimu Zahabu, Ultrik Ilstedt, and Andrade Egas. 2025. "Allometric Models to Estimate the Merchantable Wood Volume and Biomass of the Most Abundant Miombo Species in the Miombo Woodlands in Mozambique" Earth 6, no. 2: 52. https://doi.org/10.3390/earth6020052
APA StyleManjate, A., Goodman, R., Zahabu, E., Ilstedt, U., & Egas, A. (2025). Allometric Models to Estimate the Merchantable Wood Volume and Biomass of the Most Abundant Miombo Species in the Miombo Woodlands in Mozambique. Earth, 6(2), 52. https://doi.org/10.3390/earth6020052






