Inferential Approach for Evaluating the Association Between Land Cover and Soil Carbon in Northern Ontario
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Collection and Processing of Soil Samples
2.3. Statistical Analysis
2.3.1. Kruskal–Wallis Test
2.3.2. Generalized Estimating Equations
3. Results
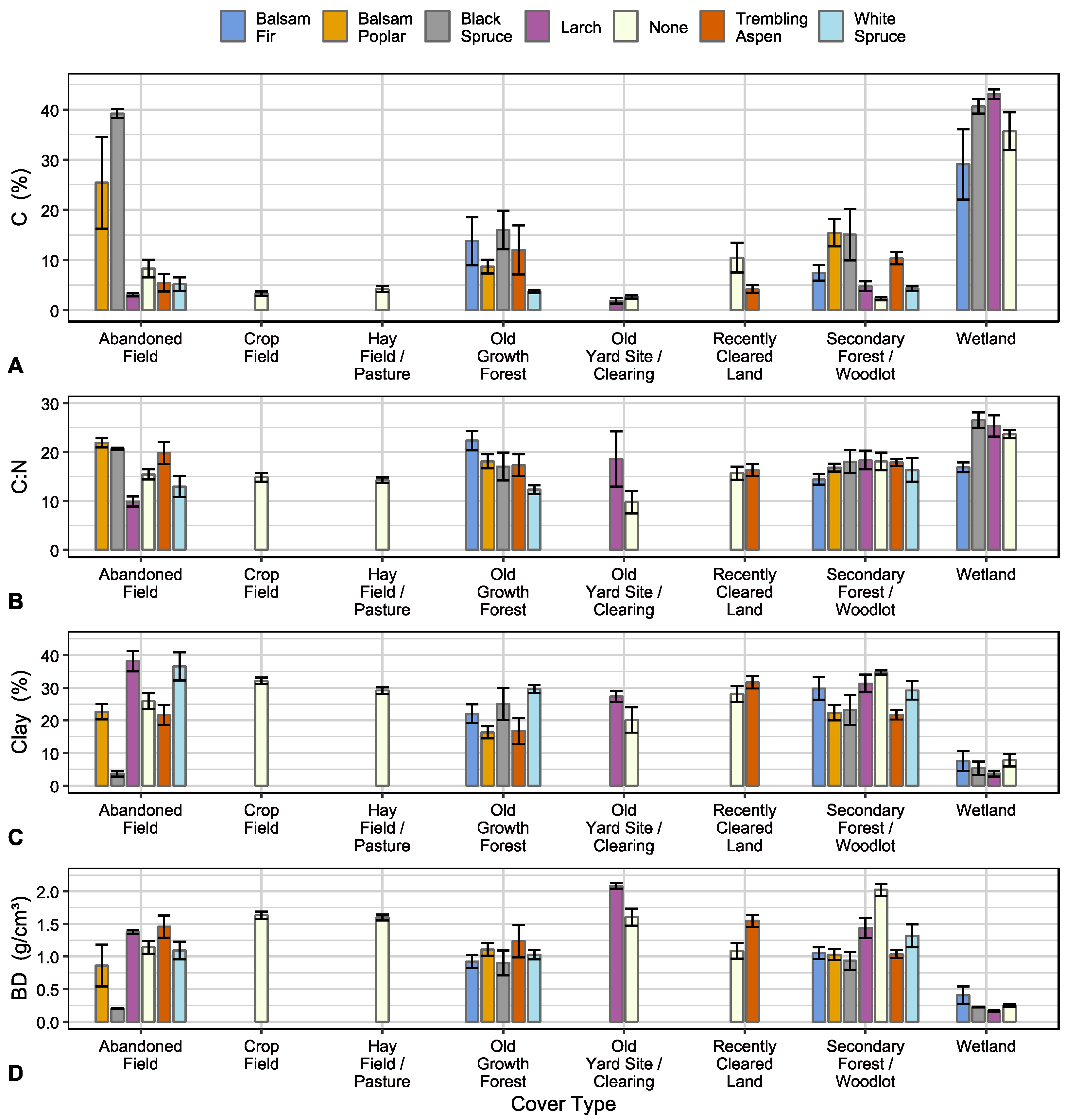
3.1. Bar Plots
3.2. Kruskal–Wallis Testing
3.3. Generalized Estimating Equations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Soil Property | Summary | Depth Layer | |||||
|---|---|---|---|---|---|---|---|
| 0–5 cm | 5–15 cm | 15–30 cm | 30–45 cm | 90–105 cm | |||
| C | (%) | Number of Samples (n) | 263 | 431 | 106 | 115 | 29 |
| Mean | 10.3 | 9.9 | 6.5 | 4.7 | 4.2 | ||
| Standard Deviation | 9.9 | 12.9 | 11.0 | 9.0 | 0.8 | ||
| Maximum | 47.5 | 91.7 | 47.8 | 48.6 | 5.6 | ||
| Minimum | 1.6 | 0.6 | 0.6 | 0.4 | 1.9 | ||
| C:N | Number of Samples (n) | 263 | 431 | 106 | 112 | 29 | |
| Mean | 15.7 | 16.2 | 13.1 | 25.1 | 170.2 | ||
| Standard Deviation | 7.1 | 6.4 | 18.2 | 18.2 | 91.6 | ||
| Maximum | 75.3 | 43.6 | 170.5 | 121.3 | 430.7 | ||
| Minimum | 3.4 | 2.1 | 1.9 | 6.1 | 32.6 | ||
| Clay | (%) | Number of Samples (n) | 229 | 424 | 99 | 106 | 23 |
| Mean | 30.3 | 25.9 | 44.9 | 41.3 | 46.1 | ||
| Standard Deviation | 11.7 | 12.9 | 15.8 | 13.6 | 17.8 | ||
| Maximum | 54.6 | 68.6 | 78.6 | 68.1 | 70.2 | ||
| Minimum | 6.6 | 1.0 | 11.4 | 2.0 | 7.6 | ||
| BD | (g/cm3) | Number of Samples (n) | 431 | 431 | |||
| Mean | 1.03 | 1.21 | |||||
| Standard Deviation | 0.55 | 0.56 | |||||
| Maximum | 2.44 | 2.55 | |||||
| Minimum | 0.10 | 0.13 | |||||
References
- Minasny, B.; Berglund, Ö.; Connolly, J.; Hedley, C.; de Vries, F.; Gimona, A.; Kempen, B.; Kidd, D.; Lilja, H.; Malone, B.; et al. Digital Mapping of Peatlands—A Critical Review. Earth-Sci. Rev. 2019, 196, 102870. [Google Scholar] [CrossRef]
- Beguin, J.; Fuglstad, G.A.; Mansuy, N.; Paré, D. Predicting Soil Properties in the Canadian Boreal Forest with Limited Data: Comparison of Spatial and Non-Spatial Statistical Approaches. Geoderma 2017, 306, 195–205. [Google Scholar] [CrossRef]
- Lempriere, T.C.; Kurz, W.A.; Hogg, E.H.; Schmoll, C.; Rampley, G.J.; Yemshanov, D. Canadian Boreal Forests and Climate Change Mitigation. Environ. Rev. 2013, 21, 293–321. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52, ISBN 0016-7061. [Google Scholar] [CrossRef]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The Use of Remote Sensing in Soil and Terrain Mapping—A Review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Mansuy, N.; Thiffault, E.; Paré, D.; Bernier, P.; Guindon, L.; Villemaire, P.; Poirier, V.; Beaudoin, A. Digital Mapping of Soil Properties in Canadian Managed Forests at 250m of Resolution Using the K-Nearest Neighbor Method. Geoderma 2014, 235–236, 59–73. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An Overview and Comparison of Machine-Learning Techniques for Classification Purposes in Digital Soil Mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Laganière, J.; Paré, D.; Bergeron, Y.; Chen, H.Y.H.; Brassard, B.W.; Cavard, X. Stability of Soil Carbon Stocks Varies with Forest Composition in the Canadian Boreal Biome. Ecosystems 2013, 16, 852–865. [Google Scholar] [CrossRef]
- Vesterdal, L.; Clarke, N.; Sigurdsson, B.D.; Gundersen, P. Do Tree Species Influence Soil Carbon Stocks in Temperate and Boreal Forests? For. Ecol. Manag. 2013, 309, 4–18. [Google Scholar] [CrossRef]
- Suratno, A.; Seielstad, C.; Queen, L. Tree Species Identification in Mixed Coniferous Forest Using Airborne Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2009, 64, 683–693. [Google Scholar] [CrossRef]
- Simfukwe, P.; Hill, P.W.; Emmett, B.A.; Jones, D.L. Soil Classification Provides a Poor Indicator of Carbon Turnover Rates in Soil. Soil Biol. Biochem. 2011, 43, 1688–1696. [Google Scholar] [CrossRef]
- Fang, H.; Ji, B.; Deng, X.; Ying, J.; Zhou, G.; Shi, Y.; Xu, L.; Tao, J.; Zhou, Y.; Li, C.; et al. Effects of Topographic Factors and Aboveground Vegetation Carbon Stocks on Soil Organic Carbon in Moso Bamboo Forests. Plant Soil 2018, 433, 363–376. [Google Scholar] [CrossRef]
- Han, X.; Tsunekawa, A.; Tsubo, M.; Li, S. Effects of Land-Cover Type and Topography on Soil Organic Carbon Storage on Northern Loess Plateau, China. Acta Agric. Scand. Sect. B Soil Plant Sci. 2010, 60, 326–334. [Google Scholar] [CrossRef]
- Li, M.; Del Giorgio, P.A.; Parkes, A.H.; Prairie, Y.T. The Relative Influence of Topography and Land Cover on Inorganic and Organic Carbon Exports from Catchments in Southern Quebec, Canada. J. Geophys. Res. Biogeosci. 2015, 120, 2562–2578. [Google Scholar] [CrossRef]
- Kothawala, D.N.; Ji, X.; Laudon, H.; Ågren, A.M.; Futter, M.N.; Köhler, S.J.; Tranvik, L.J. The Relative Influence of Land Cover, Hydrology, and in-Stream Processing on the Composition of Dissolved Organic Matter in Boreal Streams. J. Geophys. Res. Biogeosci. 2015, 120, 1491–1505. [Google Scholar] [CrossRef]
- Lantz, B. The Impact of Sample Non-Normality on ANOVA and Alternative Methods. Br. J. Math. Stat. Psychol. 2013, 66, 224–244. [Google Scholar] [CrossRef] [PubMed]
- Driscoll, W.C. Robustness of the ANOVA and Tukey-Kramer Statistical Tests. Comput. Ind. Eng. 1996, 31, 265–268. [Google Scholar] [CrossRef]
- Bargagliotti, A.E.; Greenwell, R.N. Combinatorics and Statistical Issues Related to the Kruskal-Wallis Statistic. Commun. Stat. Simul. Comput. 2015, 44, 533–550. [Google Scholar] [CrossRef]
- Vargha, A.; Delaney, H.D. The Kruskal-Wallis Test and Stochastic Homogeneity. J. Educ. Behav. Stat. 1998, 23, 170–192. [Google Scholar] [CrossRef]
- Lung-Yut-Fong, A.; Lévy-Leduc, C.; Cappé, O. Robust Retrospective Multiple Change-Point Estimation for Multivariate Data. In Proceedings of the 2011 IEEE Statistical Signal Processing Workshop (SSP), Nice, France, 28–30 June 2011; pp. 405–408. [Google Scholar]
- An, Y.; Zhang, L.; Wang, Q.; Han, Y. Soil Quality Assessment of Different Land Use Types Based on TOPSIS Method in Hilly Sandy Area of Loess Plateau, Northern China. Int. J. Environ. Res. Public Health 2022, 19, 17059. [Google Scholar] [CrossRef]
- Jung, K.M. Local Influence in Generalized Estimating Equations. Scand. J. Stat. 2008, 35, 286–294. [Google Scholar] [CrossRef]
- Dahmen, G.; Ziegler, A. Generalized Estimating Equations in Controlled Clinical Trials: Hypotheses Testing. Biom. J. 2004, 46, 214–232. [Google Scholar] [CrossRef]
- Salazar, A.; Ojeda, B.; Dueñas, M.; Fernández, F.; Failde, I. Simple Generalized Estimating Equations (GEEs) and Weighted Generalized Estimating Equations (WGEEs) in Longitudinal Studies with Dropouts: Guidelines and Implementation in R. Stat. Med. 2016, 35, 3424–3448. [Google Scholar] [CrossRef]
- Zeger, S.L.; Liang, K.-Y.; Albert, P.S. Models for Longitudinal Data : A Generalized Estimating Equation Approach. Biometrics 1988, 44, 1049–1060. [Google Scholar] [CrossRef]
- Kroetsch, D.J.; Geng, X.; Chang, S.X.; Saurette, D.D. Organic Soils of Canada: Part 1. Wetland Organic Soils. Can. J. Soil Sci. 2011, 91, 807–822. [Google Scholar] [CrossRef]
- Fradette, O.; Marty, C.; Faubert, P.; Dessureault, P.L.; Paré, M.; Bouchard, S.; Villeneuve, C. Additional Carbon Sequestration Potential of Abandoned Agricultural Land Afforestation in the Boreal Zone: A Modelling Approach. For. Ecol. Manag. 2021, 499, 119565. [Google Scholar] [CrossRef]
- Pittman, R.; Hu, B. Constructing Rasterized Covariates from LiDAR Point Cloud Data via Structured Query Language. Proceedings 2024, 110, 1. [Google Scholar] [CrossRef]
- Environment Canada Canadian Climate Normals 1981–2010 Station Data: Mattice TCPL Ontario. Available online: https://climate.weather.gc.ca/climate_normals/results_e.html?searchType=stnProx&txtRadius=100&selCity=&selPark=&optProxType=custom&txtCentralLatDeg=49&txtCentralLatMin=30&txtCentralLatSec=00&txtCentralLongDeg=84&txtCentralLongMin=00&txtCentralLongSec=00&t (accessed on 27 June 2023).
- Environment Canada Canadian Climate Normals 1981–2010 Station Data: Cochrane Ontario. Available online: https://climate.weather.gc.ca/climate_normals/results_e.html?searchType=stnProv&lstProvince=ON&txtCentralLatMin=0&txtCentralLatSec=0&txtCentralLongMin=0&txtCentralLongSec=0&stnID=4142&dispBack=0 (accessed on 27 June 2023).
- Pittman, R.; Hu, B. Soil Sampling Protocol for York University Field Campaigns; Department of Earth and Space Science and Engineering, York University: Toronto, ON, Canada, 2024. [Google Scholar]
- Dexter, A.R. Soil Physical Quality: Part I. Theory, Effects of Soil Texture, Density, and Organic Matter, and Effects on Root Growth. Geoderma 2004, 120, 201–214. [Google Scholar] [CrossRef]
- Marín-Sanleandro, P.; Gómez-García, A.M.; Blanco-Bernardeau, A.; Gil-Vázquez, J.M.; Alías-Linares, M.A. Influence of the Type and Use of Soil on the Distribution of Organic Carbon and Other Soil Properties in a Sustainable and Resilient Agropolitan System. Forests 2023, 14, 1085. [Google Scholar] [CrossRef]
- Petaja, G.; Bārdule, A.; Zalmanis, J.; Lazdiņa, D.; Daugaviete, M.; Skranda, I.; Zvaigzne, Z.A.; Purviņa, D. Changes in Organic Carbon Stock in Soil and Whole Tree Biomass in Afforested Areas in Latvia. Plants 2023, 12, 2264. [Google Scholar] [CrossRef]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- De Neve, J.; Thas, O. A Regression Framework for Rank Tests Based on the Probabilistic Index Model. J. Am. Stat. Assoc. 2015, 110, 1276–1283. [Google Scholar] [CrossRef]
- Johnson, R.W. Alternate Forms of the One-Way ANOVA F and Kruskal–Wallis Test Statistics. J. Stat. Data Sci. Educ. 2022, 30, 82–85. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Avery, L.; Del Bel, R.; Espin-Garcia, O.; Pittman, T.; Wang, Y.; Weiss, J.; Xu, W. ReportRmd: Tidy Presentation of Clinical Reporting; University Health Network: Toronto, ON, Canada, 2023. [Google Scholar]
- Norouzian, R.; Plonsky, L. Eta- and Partial Eta-Squared in L2 Research: A Cautionary Review and Guide to More Appropriate Usage. Second. Lang. Res. 2018, 34, 257–271. [Google Scholar] [CrossRef]
- Hojat, M.; Xu, G. A Visitor’s Guide to Effect Sizes—Statistical Significance versus Practical (Clinical) Importance of Research Findings. Adv. Health Sci. Educ. 2004, 9, 241–249. [Google Scholar] [CrossRef]
- Ferguson, C.J. Is Psychological Research Really as Good as Medical Research? Effect Size Comparisons Between Psychology and Medicine. Rev. Gen. Psychol. 2009, 13, 130–136. [Google Scholar] [CrossRef]
- Shieh, G. Sample Size Calculations for Precise Interval Estimation of the Eta-Squared Effect Size. J. Exp. Educ. 2015, 83, 203–217. [Google Scholar] [CrossRef]
- McShane, B.B.; Böckenholt, U. Supplemental Material for Planning Sample Sizes When Effect Sizes Are Uncertain: The Power-Calibrated Effect Size Approach. Psychol. Methods 2016, 21, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Eta-Squared and Partial Eta-Squared in Fixed Factor ANOVA Designs. Educ. Psychol. Meas. 1973, 33, 107–112. [Google Scholar] [CrossRef]
- Richardson, J.T.E. Eta Squared and Partial Eta Squared as Measures of Effect Size in Educational Research. Educ. Res. Rev. 2011, 6, 135–147. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioural Sciences, 2nd ed.; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Zeger, L.; Liang, S. Longitudinal Data Analysis for Discrete and Continuous Outcomes. Biometrics 1986, 42, 121–130. [Google Scholar] [CrossRef]
- Muggeo, V.M.R.; Ferrara, G. Fitting Generalized Linear Models with Unspecified Link Function: A P-Spline Approach. Comput. Stat. Data Anal. 2008, 52, 2529–2537. [Google Scholar] [CrossRef]
- Li, B. On the Consistency of Generalized Estimating Equations. Lect. Notes-Monogr. Ser. 1997, 32, 115–136. [Google Scholar] [CrossRef]
- Yan, J.; Fine, J. Estimating Equations for Association Structures. Stat. Med. 2004, 23, 859–874. [Google Scholar] [CrossRef]
- Fan, C.; Zhang, D. Wald-Type Rank Tests: A GEE Approach. Computational Stat. Data Anal. 2014, 74, 1–16. [Google Scholar] [CrossRef]
- Goeman, J.J.; Solari, A. Comparing Three Groups. Am. Stat. 2022, 76, 168–176. [Google Scholar] [CrossRef]
- Wu, X.; Wu, K.; Zhao, H.; Hao, S.; Zhou, Z. Impact of Land Cover Changes on Soil Type Mapping in Plain Areas: Evidence from Tongzhou District of Beijing, China. Land 2023, 12, 1696. [Google Scholar] [CrossRef]
- Halekoh, U.; Højsgaard, S.; Yan, J. The R Package Geepack for Generalized Estimating Equations. J. Stat. Softw. 2006, 15, 1–11. [Google Scholar] [CrossRef]
- Smith, R.J.; Jovan, S.; Gray, A.N.; McCune, B. Sensitivity of Carbon Stores in Boreal Forest Moss Mats—Effects of Vegetation, Topography and Climate. Plant Soil 2017, 421, 31–42. [Google Scholar] [CrossRef]
- Ste-Marie, C.; Paré, D.; Gagnon, D. The Contrasting Effects of Aspen and Jack Pine on Soil Nutritional Properties Depend on Parent Material. Ecosystems 2007, 10, 1299–1310. [Google Scholar] [CrossRef]
- Paloniemi, J. FRI Field Guide; Forest Resources Inventory; Ontario Ministry of Natural Resources and Forestry: Peterborough, ON, Canada, 2018.
- Gunsolley, J.C.; Getchell, C.; Chinchilli, V.M. Small Sample Characteristics of Generalized Estimating Equations. Commun. Stat. Simul. Comput. 1995, 24, 869–878. [Google Scholar] [CrossRef]
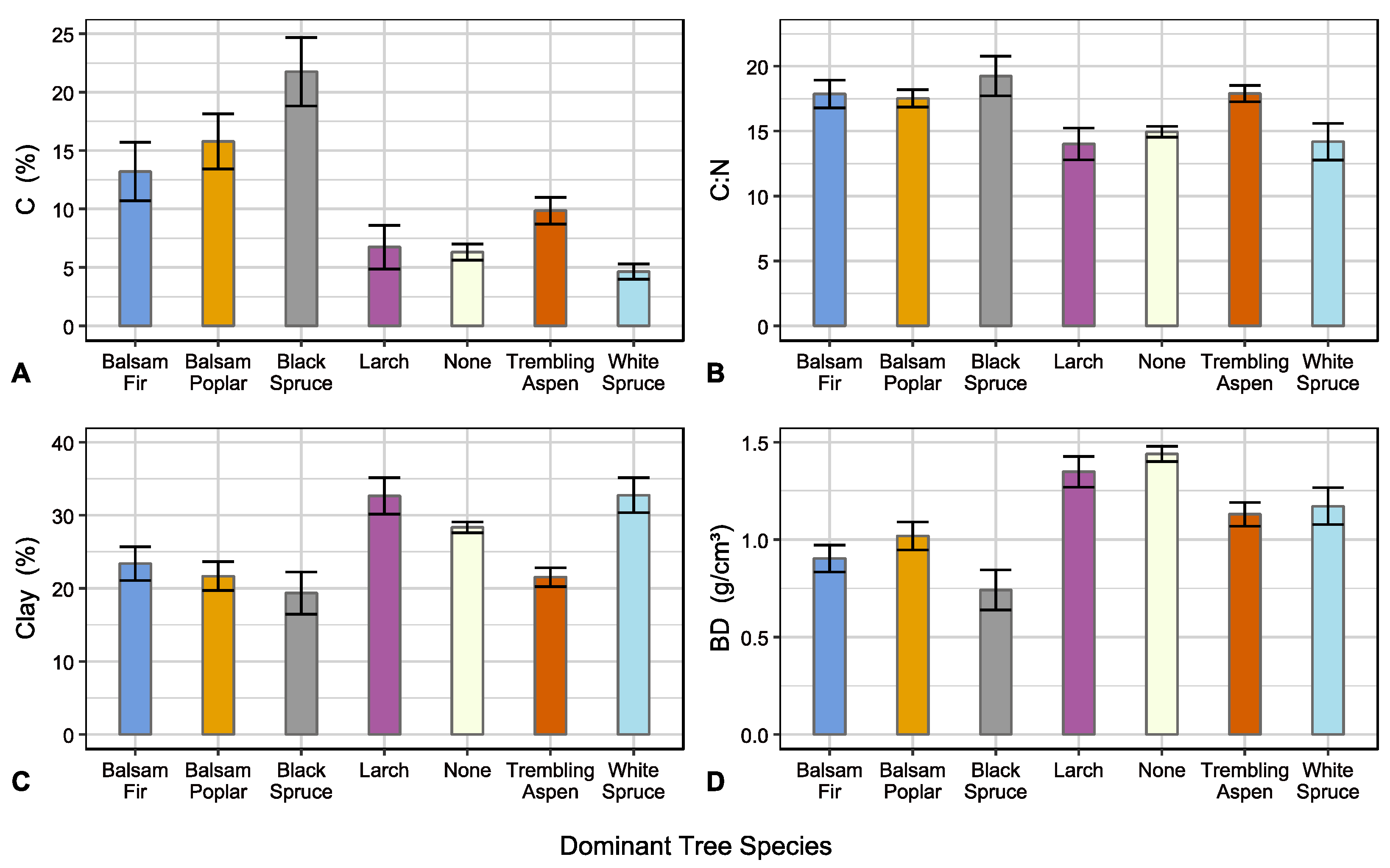
| Soil Property | Full Sample | Balsam Fir | Balsam Poplar | Black Spruce | Larch | None | Trembling Aspen | White Spruce | Unnested | Nested | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (n = 431) | (n = 39) | (n = 54) | (n = 36) | (n = 36) | (n = 180) | (n = 63) | (n = 23) | Effect Size | p-Value | p-Value | ||
| C | (%) | 4.3 | 5.8 | 7.9 | 23.4 | 3.2 | 3.0 | 7.1 | 4.2 | 0.15 | <0.001 *** | 0.88 |
| C:N | 16.0 | 17.7 | 17.8 | 20.5 | 13.3 | 15.1 | 17.7 | 13.1 | 0.07 | <0.001 *** | 0.88 | |
| Clay | (%) | 27.0 | 25.1 | 20.0 | 14.0 | 29.0 | 29.0 | 21.0 | 32.6 | 0.11 | <0.001 *** | 0.90 |
| BD | (g/cm3) | 1.31 | 1.01 | 1.15 | 0.33 | 1.37 | 1.50 | 1.06 | 1.22 | 0.18 | <0.001 *** | 0.74 |
| Soil Property | Full Sample | Abandoned Field | Crop Field | Hay Field/ Pasture | Old Growth Forest | Old Yard Site/ Clearing | Recently Cleared Land | Secondary Forest/ Woodlot | Wetland | Unnested | Nested | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (n = 431) | (n = 74) | (n = 42) | (n = 75) | (n = 48) | (n = 9) | (n = 24) | (n = 138) | (n = 21) | Effect Size | p-Value | p-Value | ||
| C | (%) | 4.3 | 4.6 | 2.6 | 2.8 | 5.2 | 2.4 | 3.9 | 6.2 | 40.6 | 0.28 | <0.001 *** | 0.93 |
| C:N | 16.0 | 15.3 | 15.7 | 13.8 | 17.5 | 11.4 | 16.1 | 16.6 | 23.6 | 0.11 | <0.001 *** | 0.80 | |
| Clay | (%) | 27.0 | 28.0 | 32.0 | 29.0 | 22.5 | 24.0 | 28.0 | 25.0 | 4.0 | 0.18 | <0.001 *** | 0.75 |
| BD | (g/cm3) | 1.31 | 1.32 | 1.71 | 1.59 | 1.08 | 1.91 | 1.34 | 1.11 | 0.22 | 0.33 | <0.001 *** | 0.92 |
| Comparison | Estimate | Confidence Bound Lower 95% | Confidence Bound Upper 95% | Standard Error | p-Value |
|---|---|---|---|---|---|
| (%) | (%) | (%) | |||
| Balsam Fir—None | 8.70 | −3.81 | 21.20 | 4.34 | 0.370 |
| Balsam Poplar—None | 8.42 | −0.66 | 17.50 | 3.15 | 0.088 |
| Black Spruce—None | 15.63 | 2.00 | 29.26 | 4.73 | 0.014 * |
| Larch—None | 0.95 | −9.03 | 10.93 | 3.46 | 1.000 |
| Trembling Aspen—None | 3.06 | −1.79 | 7.91 | 1.68 | 0.492 |
| White Spruce—None | −1.07 | −5.70 | 3.56 | 1.61 | 0.993 |
| Balsam Poplar—Balsam Fir | −0.27 | −15.15 | 14.61 | 5.17 | 1.000 |
| Black Spruce—Balsam Fir | 6.93 | −11.09 | 24.95 | 6.25 | 0.912 |
| Larch—Balsam Fir | −7.75 | −23.19 | 7.70 | 5.36 | 0.744 |
| Trembling Aspen—Balsam Fir | −5.64 | −18.38 | 7.11 | 4.42 | 0.841 |
| White Spruce—Balsam Fir | −9.77 | −22.43 | 2.90 | 4.40 | 0.248 |
| Black Spruce—Balsam Poplar | 7.20 | −8.63 | 23.04 | 5.50 | 0.822 |
| Larch—Balsam Poplar | −7.48 | −20.31 | 5.35 | 4.45 | 0.589 |
| Trembling Aspen—Balsam Poplar | −5.36 | −14.77 | 4.04 | 3.27 | 0.614 |
| White Spruce—Balsam Poplar | −9.49 | −18.79 | −0.20 | 3.23 | 0.042 * |
| Larch—Black Spruce | −14.68 | −31.05 | 1.69 | 5.68 | 0.111 |
| Trembling Aspen—Black Spruce | −12.57 | −26.42 | 1.29 | 4.81 | 0.102 |
| White Spruce—Black Spruce | −16.70 | −30.47 | −2.92 | 4.78 | 0.007 ** |
| Trembling Aspen—Larch | 2.11 | −8.17 | 12.39 | 3.57 | 0.996 |
| White Spruce—Larch | −2.02 | −12.20 | 8.16 | 3.53 | 0.997 |
| White Spruce—Trembling Aspen | −4.13 | −9.37 | 1.11 | 1.82 | 0.225 |
| Comparison | Estimate | Confidence Bound Lower 95% | Confidence Bound Upper 95% | Standard Error | p-Value |
|---|---|---|---|---|---|
| (%) | (%) | (%) | |||
| Abandoned Field—Old Growth Forest | −4.54 | −16.64 | 7.57 | 4.17 | 0.940 |
| Crop Field—Old Growth Forest | −10.33 | −20.53 | −0.12 | 3.51 | 0.045 * |
| Hay Field/Pasture—Old Growth Forest | −9.21 | −19.53 | 1.12 | 3.55 | 0.116 |
| Old Yard Site/Clearing—Old Growth Forest | −11.40 | −21.57 | −1.24 | 3.50 | 0.017 * |
| Recently Cleared Land—Old Growth Forest | −3.19 | −19.64 | 13.26 | 5.66 | 0.999 |
| Secondary Forest/Woodlot—Old Growth Forest | −3.15 | −14.02 | 7.72 | 3.74 | 0.985 |
| Wetland—Old Growth Forest | 22.94 | 10.49 | 35.39 | 4.28 | <0.001 *** |
| Crop Field—Abandoned Field | −5.79 | −12.46 | 0.88 | 2.29 | 0.138 |
| Hay Field/Pasture—Abandoned Field | −4.67 | −11.52 | 2.18 | 2.36 | 0.412 |
| Old Yard Site/Clearing—Abandoned Field | −6.87 | −13.48 | −0.26 | 2.28 | 0.036 * |
| Recently Cleared Land—Abandoned Field | 1.35 | −13.18 | 15.87 | 5.00 | 1.000 |
| Secondary Forest/Woodlot—Abandoned Field | 1.38 | −6.27 | 9.03 | 2.63 | 0.999 |
| Wetland—Abandoned Field | 27.48 | 17.72 | 37.23 | 3.36 | <0.001 *** |
| Hay Field/Pasture—Crop Field | 1.12 | −0.99 | 3.23 | 0.73 | 0.719 |
| Old Yard Site/Clearing—Crop Field | −1.08 | −2.19 | 0.04 | 0.38 | 0.065 |
| Recently Cleared Land—Crop Field | 7.14 | −5.84 | 20.12 | 4.47 | 0.682 |
| Secondary Forest/Woodlot—Crop Field | 7.17 | 3.17 | 11.18 | 1.38 | <0.001 *** |
| Wetland—Crop Field | 33.27 | 26.00 | 40.53 | 2.50 | <0.001 *** |
| Old Yard Site/Clearing—Hay Field/Pasture | −2.20 | −4.12 | −0.28 | 0.66 | 0.014 * |
| Recently Cleared Land—Hay Field/Pasture | 6.02 | −7.05 | 19.09 | 4.50 | 0.841 |
| Secondary Forest/Woodlot—Hay Field/Pasture | 6.05 | 1.75 | 10.36 | 1.48 | 0.001 ** |
| Wetland—Hay Field/Pasture | 32.15 | 24.72 | 39.58 | 2.56 | <0.001 *** |
| Recently Cleared Land—Old Yard Site/Clearing | 8.22 | −4.73 | 21.17 | 4.46 | 0.507 |
| Secondary Forest/Woodlot—Old Yard Site/Clearing | 8.25 | 4.34 | 12.16 | 1.35 | <0.001 *** |
| Wetland—Old Yard Site/Clearing | 34.34 | 27.13 | 41.55 | 2.48 | <0.001 *** |
| Secondary Forest/Woodlot—Recently Cleared Land | 0.04 | −13.47 | 13.55 | 4.65 | 1.000 |
| Wetland—Recently Cleared Land | 26.13 | 11.32 | 40.93 | 5.09 | <0.001 *** |
| Wetland—Secondary Forest/Woodlot | 26.09 | 17.92 | 34.27 | 2.81 | <0.001 *** |
| Univariable | Multivariable | ||||
|---|---|---|---|---|---|
| Predictor | Number of Samples | Estimate and 95% CI | p-Value | Estimate and 95% CI | p-Value |
| (n) | (%) | (%) | |||
| Clay | 424 | −0.67 (−0.74, −0.60) | <0.001 *** | −0.48 (−0.59, −0.37) | <0.001 *** |
| Land Cover Type | 431 | <0.001 *** | <0.001 *** | ||
| 42 | Reference | Reference | ||
| 74 | 5.46 (1.28, 9.64) | 0.01 * | 2.35 (−1.02, 5.72) | 0.17 |
| 75 | 0.88 (−3.28, 5.05) | 0.68 | −0.59 (−2.71, 1.53) | 0.58 |
| 48 | 9.57 (5.00, 14.14) | <0.001 *** | 1.85 (−4.11, 7.81) | 0.54 |
| 9 | −0.94 (−8.88, 7.01) | 0.82 | −5.79 (−8.74, −2.85) | <0.001 *** |
| 24 | 6.39 (0.85, 11.92) | 0.02 * | 4.74 (−2.77, 12.25) | 0.22 |
| 138 | 7.70 (3.88, 11.51) | <0.001 *** | 2.68 (−1.40, 6.76) | 0.2 |
| 21 | 32.98 (27.20, 38.76) | <0.001 *** | 18.00 (11.43, 24.56) | <0.001 *** |
| Dominant Tree Species | 431 | <0.001 *** | 0.16 | ||
| 180 | Reference | Reference | ||
| 39 | 6.91 (2.76, 11.06) | 0.001 ** | 1.17 (−5.08, 7.43) | 0.71 |
| 54 | 9.49 (5.84, 13.14) | <0.001 *** | 2.96 (−3.11, 9.04) | 0.34 |
| 36 | 15.45 (11.15, 19.74) | <0.001 *** | 7.42 (0.86, 13.99) | 0.03 * |
| 36 | 0.44 (−3.85, 4.73) | 0.84 | 0.71 (−3.12, 4.55) | 0.71 |
| 63 | 3.55 (0.11, 7.00) | 0.04 * | −1.31 (−5.56, 2.95) | 0.55 |
| 23 | −1.63 (−6.84, 3.57) | 0.54 | −0.76 (−4.85, 3.33) | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pittman, R.; Hu, B.; Pittman, T.; Webster, K.L.; Shang, J.; Nelson, S.A. Inferential Approach for Evaluating the Association Between Land Cover and Soil Carbon in Northern Ontario. Earth 2025, 6, 1. https://doi.org/10.3390/earth6010001
Pittman R, Hu B, Pittman T, Webster KL, Shang J, Nelson SA. Inferential Approach for Evaluating the Association Between Land Cover and Soil Carbon in Northern Ontario. Earth. 2025; 6(1):1. https://doi.org/10.3390/earth6010001
Chicago/Turabian StylePittman, Rory, Baoxin Hu, Tyler Pittman, Kara L. Webster, Jiali Shang, and Stephanie A. Nelson. 2025. "Inferential Approach for Evaluating the Association Between Land Cover and Soil Carbon in Northern Ontario" Earth 6, no. 1: 1. https://doi.org/10.3390/earth6010001
APA StylePittman, R., Hu, B., Pittman, T., Webster, K. L., Shang, J., & Nelson, S. A. (2025). Inferential Approach for Evaluating the Association Between Land Cover and Soil Carbon in Northern Ontario. Earth, 6(1), 1. https://doi.org/10.3390/earth6010001






