Quantum Tensor DBMS and Quantum Gantt Charts: Towards Exponentially Faster Earth Data Engineering
Abstract
1. Introduction
2. Quantum Computing: Preliminaries
|
2.1. Mathematical Model

| Symbol | Definition |
|---|---|
| Complex conjugate of : , | |
| Norm of vector v: , | |
| Conjugate transpose of column vector v: | |
| ⊗ | Kronecker product: |
| n-fold repeated Kronecker product: | |
| Matrix multiplication: | |
| ket: , , | |
| same as | |
| bra: , e.g., | |
| braket: | |
| H | Hadamard operator: |
| T | T-gate or -gate (8, not 4): |
| Oracle e that acts only on the first qubits; acts on the last qubits | |
| Notes | Note that , , , |
| Frequently used notations from Quantum Array (Tensor) Data Model, Section 4.1: | |
| N | the number of array (tensor) dimensions |
| NA | a missing cell value; other popular names: null,NoData,n/a,NaN, etc. |
| a hyperslab, an N-d subarray of A, Equation (5) | |
| ⋈ | array (tensor) join, Section 4.7 |
| a 1d array with d elements, where and | |
| Quantum memory I/O (, and read/write from/to both QRAM and RAQM), Section 4.4: | |
| a quantum pointer , where j is the cell index that occupies qubits | |
| (read operation), where is the value of the jth memory cell | |
| quantum memory write operation | |
| read-and-append, read memory cells addressed by the first qubits () of | |
| and entangle them with as well, Equation (24) | |
| Notations used for complexity (asymptotic) analysis: | |
| type of array (tensor) cells, Equations (3) and (4) | |
| the number of bits or qubits for type | |
| the size of array (tensor) A, Section 4.1.1 | |
| the number of qubits for keeping cell indexes in a quantum pointer, Section 4.4 | |
| the number of qubits to keep the whole array (tensor) A in a quantum register | |
| £ | runtime asymptotic cost; note that symbols T and are already reserved |
| O | big O, defined in [131] |
| the asymptotic cost of function or oracle e on qubits; note that the notation | |
| accounts for multiple operands and ancillary qubits for e | |
2.2. Quantum Memory
2.3. Visualization in Quantum Computing
- Vector notation represents a state of single qubit quite well: . However, as the number of qubits for visualization grows, the size of the resulting matrix grows exponentially and the vector notation becomes bulky and impractical:
- Dirac notation was developed, in particular, to address the aforementioned limitation of the vector notation. It is typical to write a superposition as a sum. However, it becomes hard to track the progression of the applied transformations. For example, which parts of the sum generated the subsequent parts in Equation (2) which has only three summands and one transformation. The growth of the transformation chain and the number of summands hinder the comprehension of the situation.
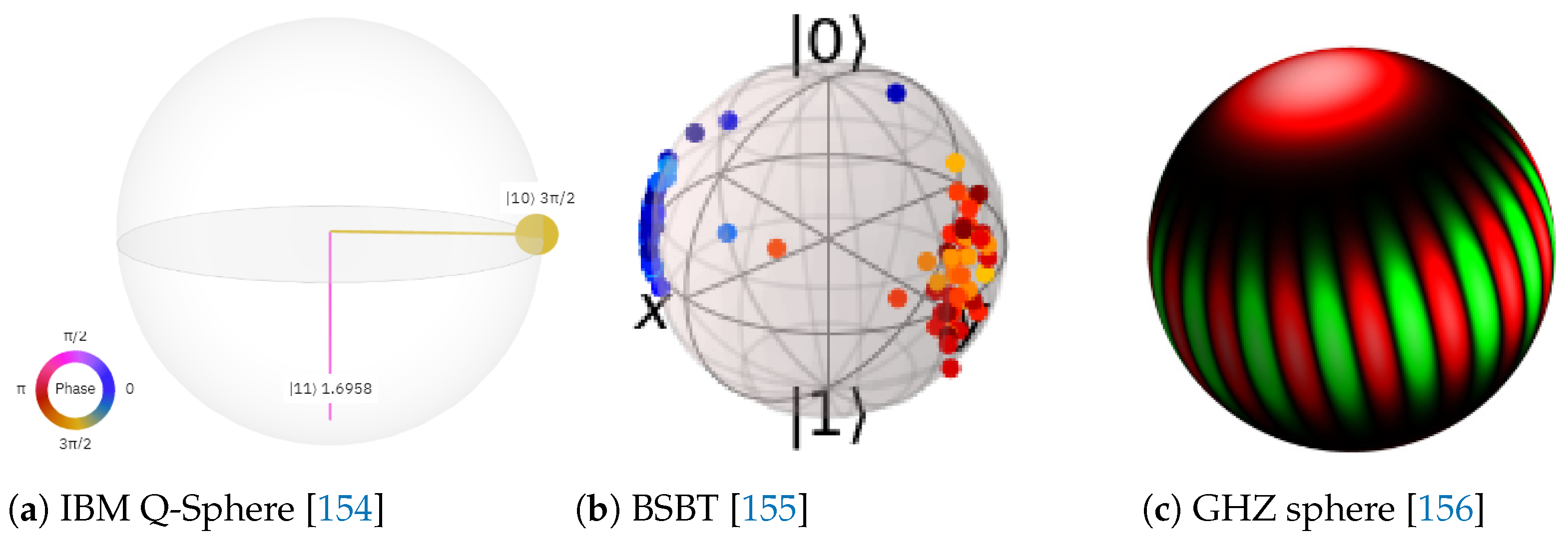
- Bloch sphere displays the state of only a single qubit, Figure 1.
- Majumdar-Ghosh model qubism representation [159] focuses on the same family of states as the previous approach, but utilizes 2-d grids for visualization.
- Quantum circuit diagram is a fundamental way to graphically illustrate a quantum program using a set of connected operators, Figure 3. Many exciting and powerful quantum circuit visualizers exist, for example, IBM Qiskit [160] and Quirk [161]. However, circuits display the sequence of operations, not the data flow, e.g., values of quantum registers and their source-target relationships.
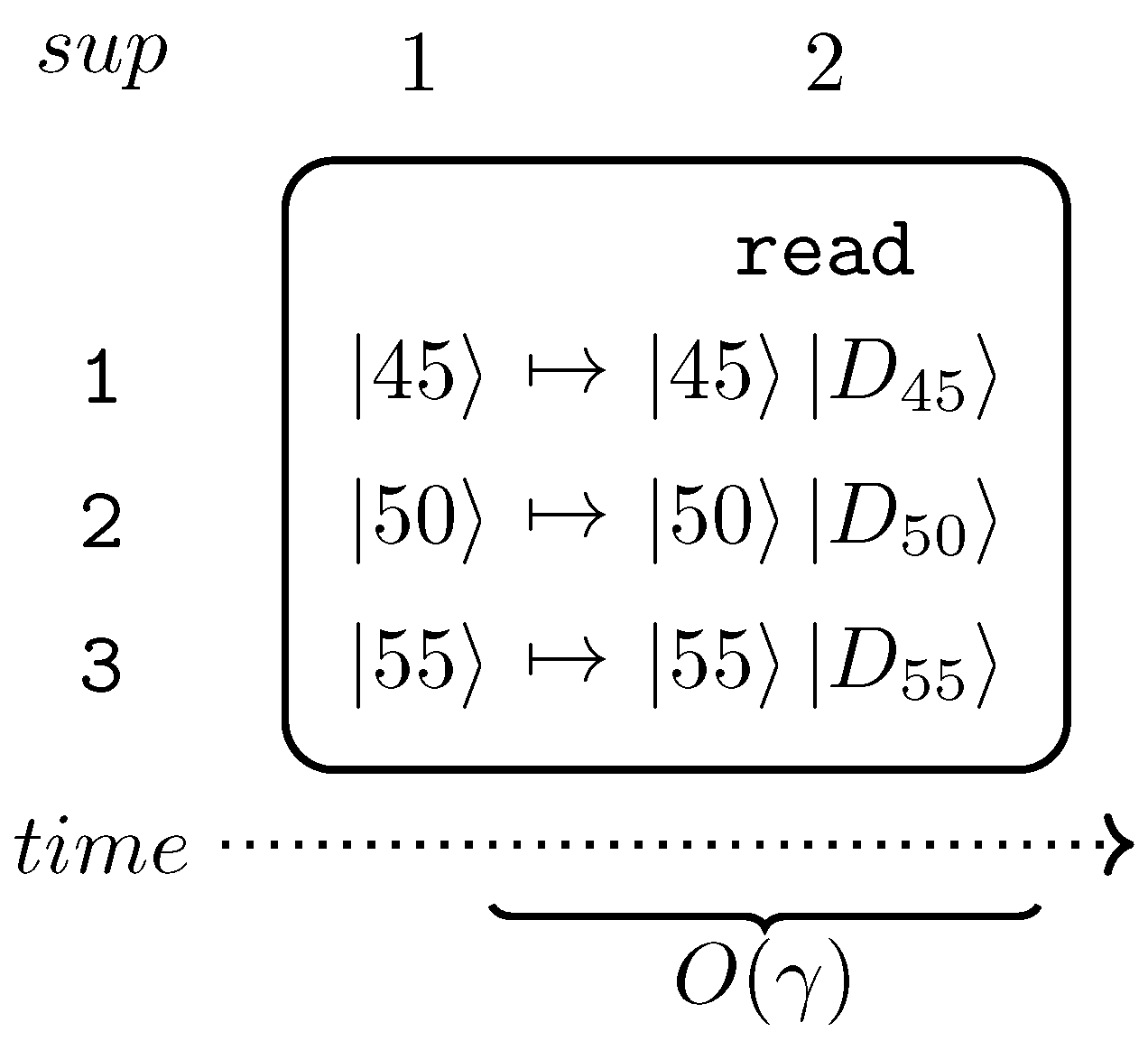
3. Quantum Gantt Chart (QGantt)
 due to aesthetic reasons. However, it is possible to render QGantt charts in an ASCII art or HTML versions, which are very flexible, similar to the way quantum circuits are presented in popular frameworks [160,161]. An example of an ASCII art version of a QGantt chart is in Section 5.4. Graphs are also good for displaying QGantt charts for practical reasons: diverse software can be used to manipulate graphs interactively. We will present increasingly complex QGantt charts during the progression of this article. For now, consider the following examples. We show that QGantt charts can naturally complement existing visualization techniques, including algebraic expressions with vector or Dirac notation, spherical representations, as well as quantum circuits. QGantt charts can also be used autonomously without additional visualization techniques, because QGantt charts are self-contained. In some cases, for example for operations with quantum memory or other data-centric algorithms, a QGantt chart can be the first visualization tool to try.
due to aesthetic reasons. However, it is possible to render QGantt charts in an ASCII art or HTML versions, which are very flexible, similar to the way quantum circuits are presented in popular frameworks [160,161]. An example of an ASCII art version of a QGantt chart is in Section 5.4. Graphs are also good for displaying QGantt charts for practical reasons: diverse software can be used to manipulate graphs interactively. We will present increasingly complex QGantt charts during the progression of this article. For now, consider the following examples. We show that QGantt charts can naturally complement existing visualization techniques, including algebraic expressions with vector or Dirac notation, spherical representations, as well as quantum circuits. QGantt charts can also be used autonomously without additional visualization techniques, because QGantt charts are self-contained. In some cases, for example for operations with quantum memory or other data-centric algorithms, a QGantt chart can be the first visualization tool to try.3.1. QGantt: Reading Data from Quantum Memory
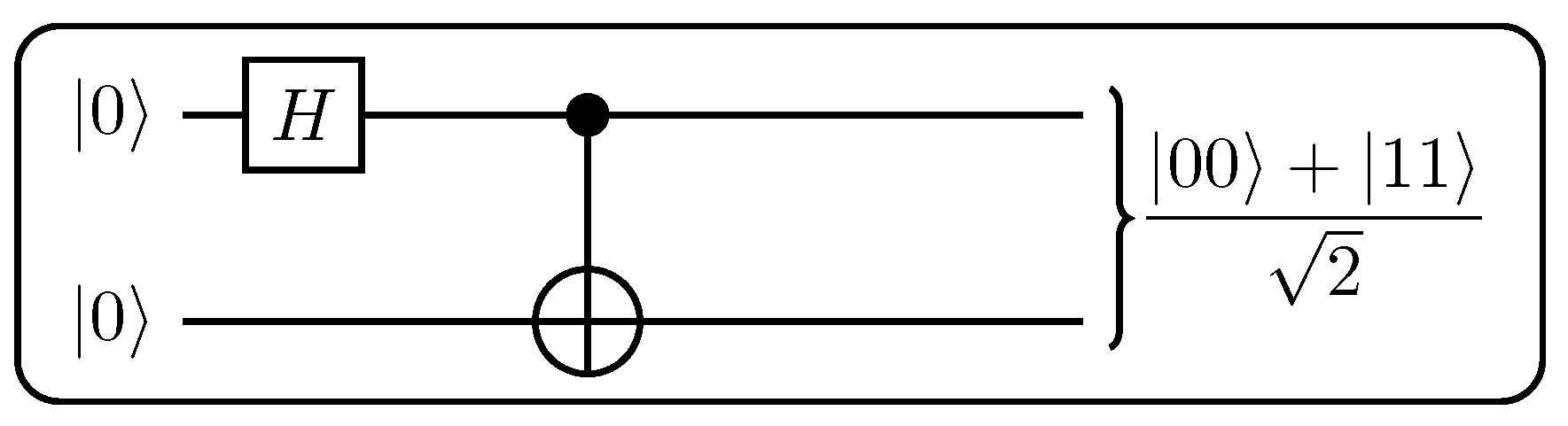
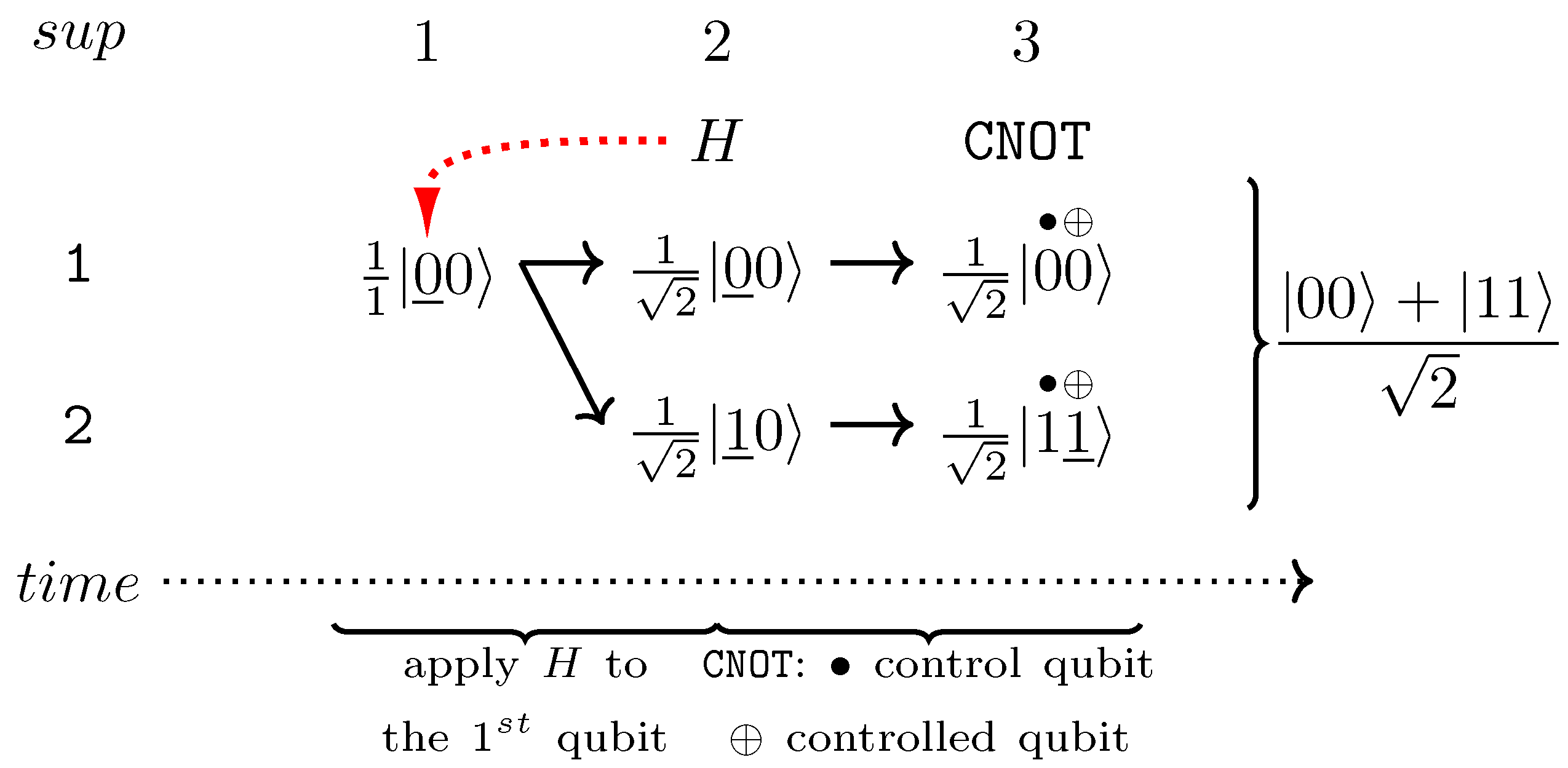
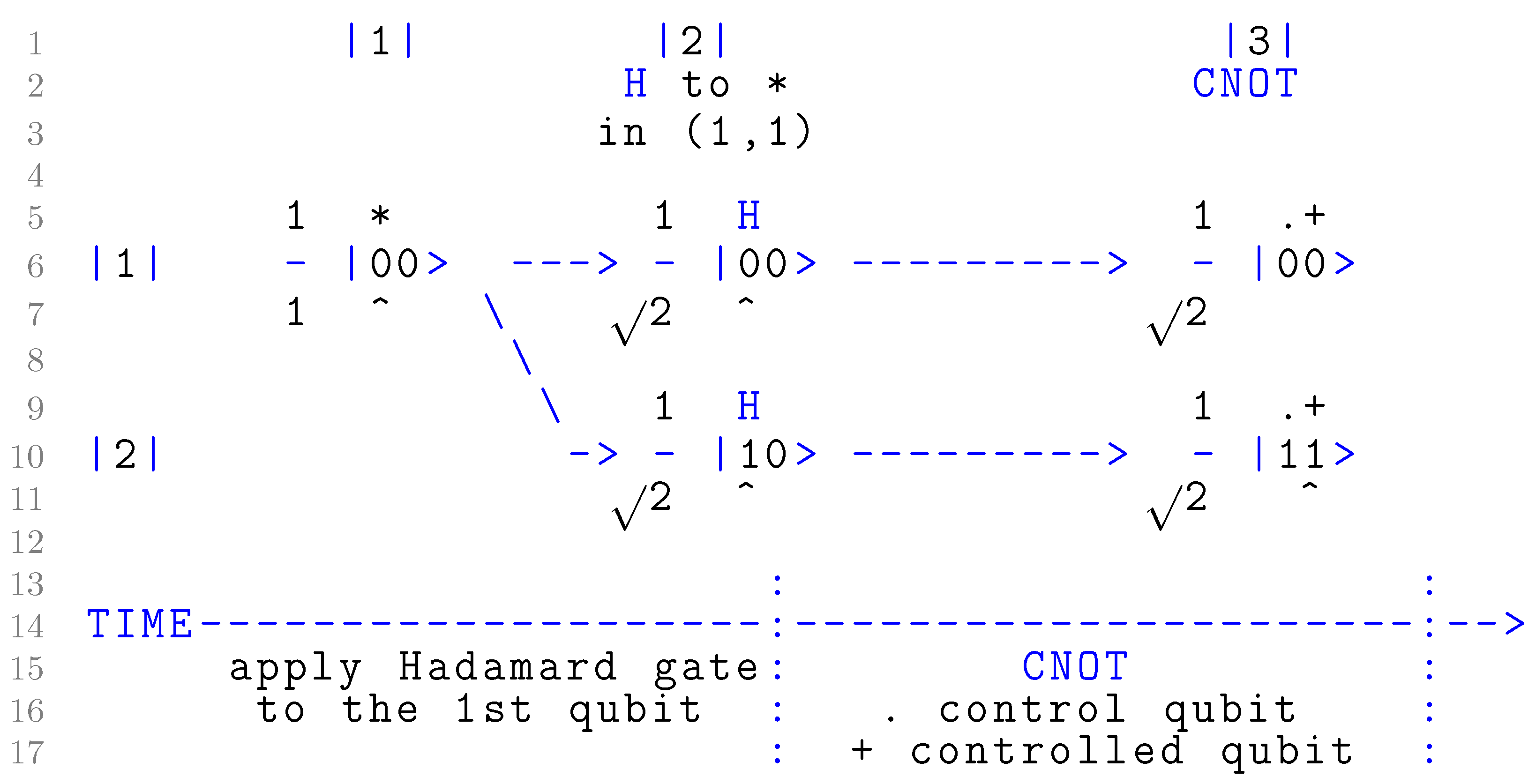
3.2. QGantt: Creating Bell State
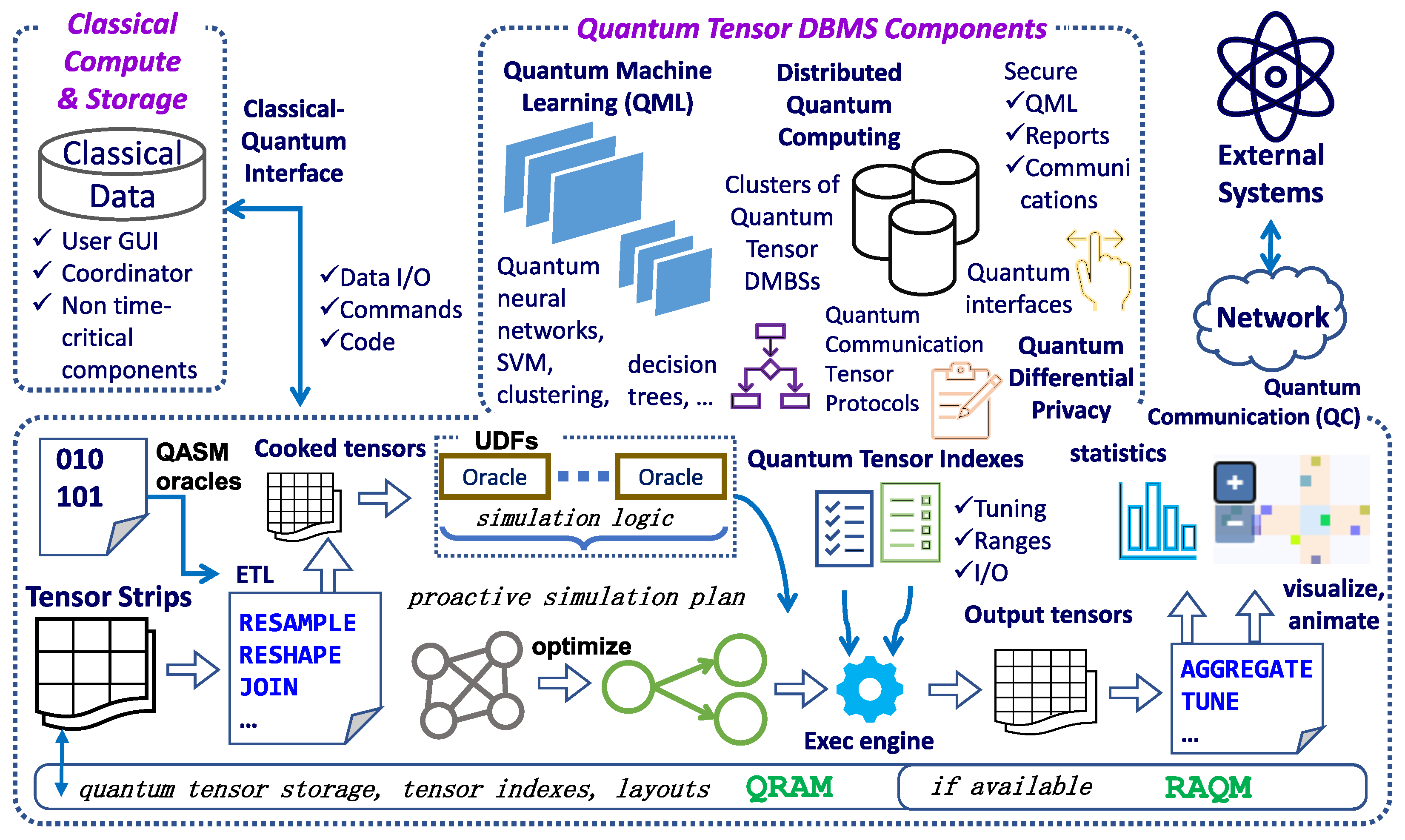
4. Quantum Array (Tensor) DBMS Techniques
4.1. Quantum Array (Tensor) Data Model
4.1.1. Logical Array (Tensor)
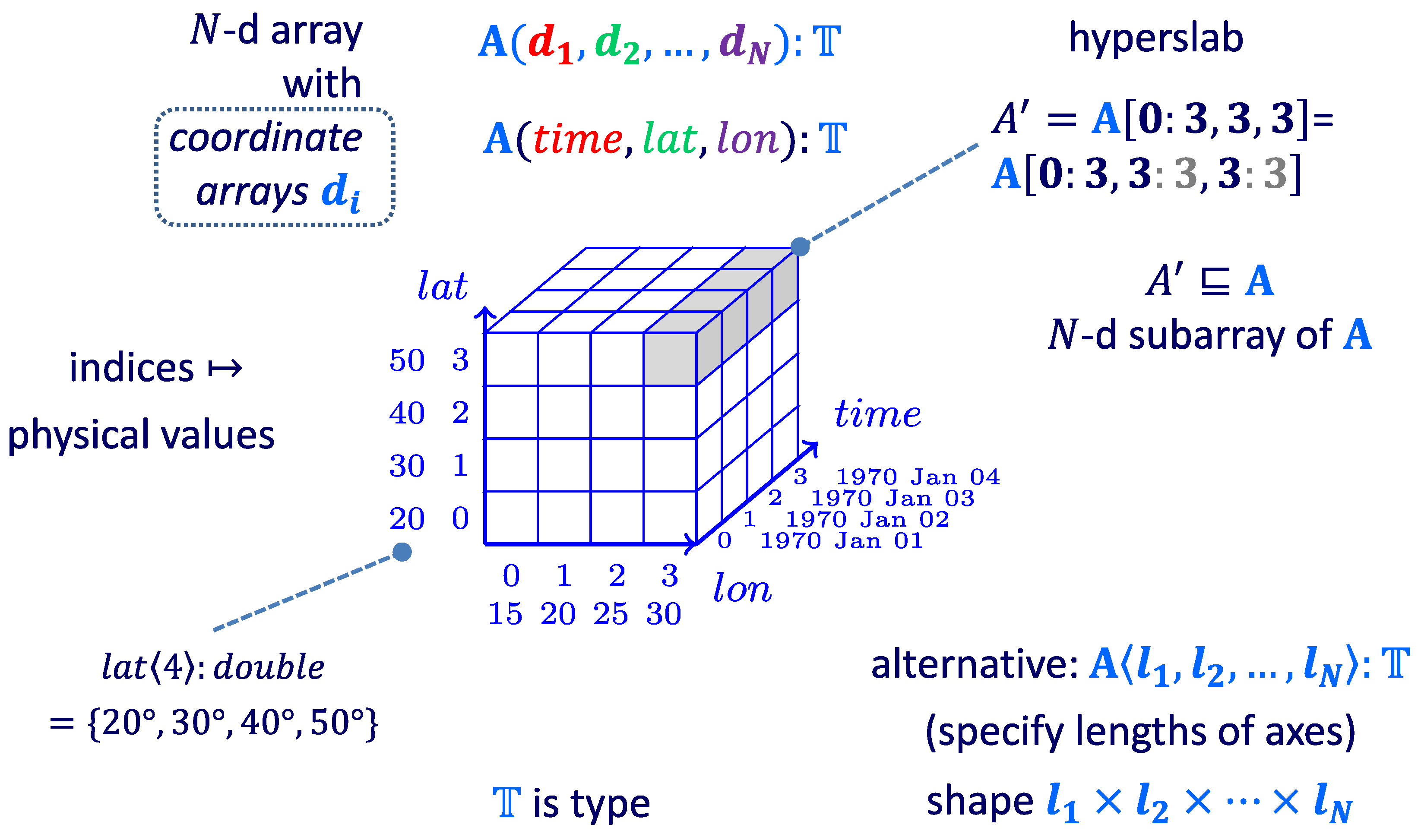
4.1.2. Quantum Model Aspects
 .
.4.2. Array (Tensor)
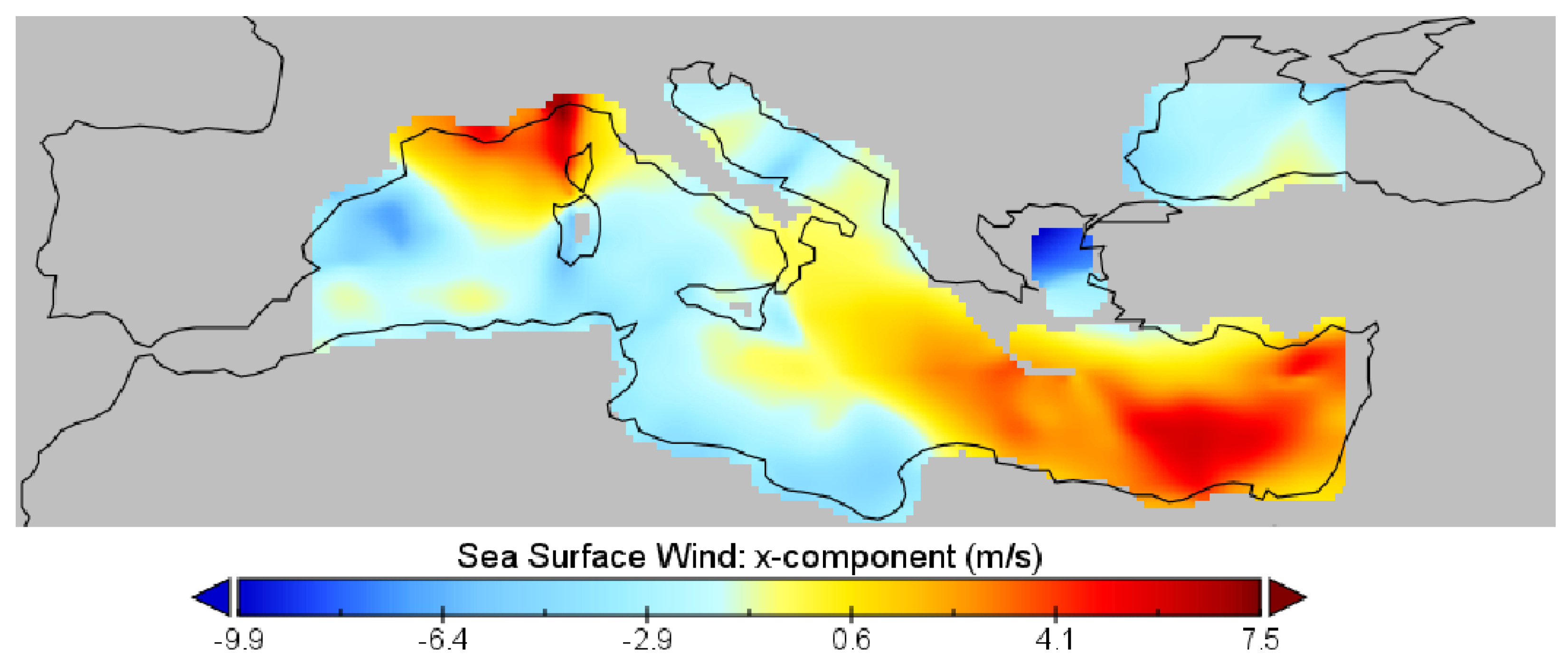
4.3. Illustrative Datasets

4.4. Quantum Memory Operations
4.4.1. NA in Tensor Cell Values
4.4.2. NA in Address Indexes
4.5. Quantum Sparse Arrays (Tensors)
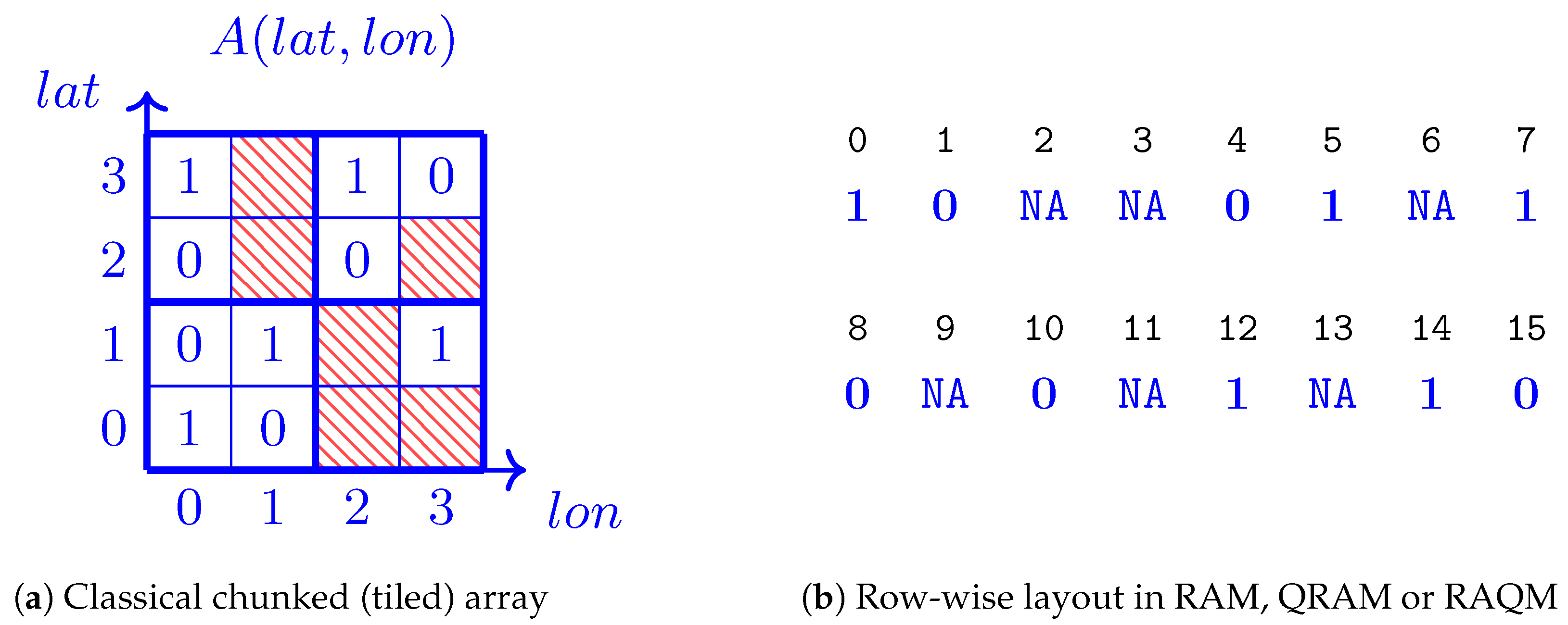
 Quantum Look at Challenge 1. A Quantum Array (Tensor) DBMS Data Model is a radical departure from a classical array data model which splits a large Nd array into multiple chunks or tiles to create a more manageable dataset. Quantum Array (Tensor) DBMSs can now operate on quantum strips, or simply strips, Section 4.5.1 and Section 4.5.2. We introduce a new term, quantum strips, to clearly distinguish quantum array (tensor) formats (layouts) from chunks, tiles, and other classical entities.
Quantum Look at Challenge 1. A Quantum Array (Tensor) DBMS Data Model is a radical departure from a classical array data model which splits a large Nd array into multiple chunks or tiles to create a more manageable dataset. Quantum Array (Tensor) DBMSs can now operate on quantum strips, or simply strips, Section 4.5.1 and Section 4.5.2. We introduce a new term, quantum strips, to clearly distinguish quantum array (tensor) formats (layouts) from chunks, tiles, and other classical entities.4.5.1. Wide Quantum Strips
- read A in for or in compared to for the classical case: an exponential speedup
- read arrays of significantly different sizes with almost the same performance: may not be too different from given the appropriate hidden constants
- atomically read any list of indexes in a single go by providing a superposition of QRAM indexes for
- atomically write/update any list of values indexed by a superposition which can contain non-continuous index values
4.5.2. Narrow Quantum Strips
4.5.3. Quantum Strip Layouts
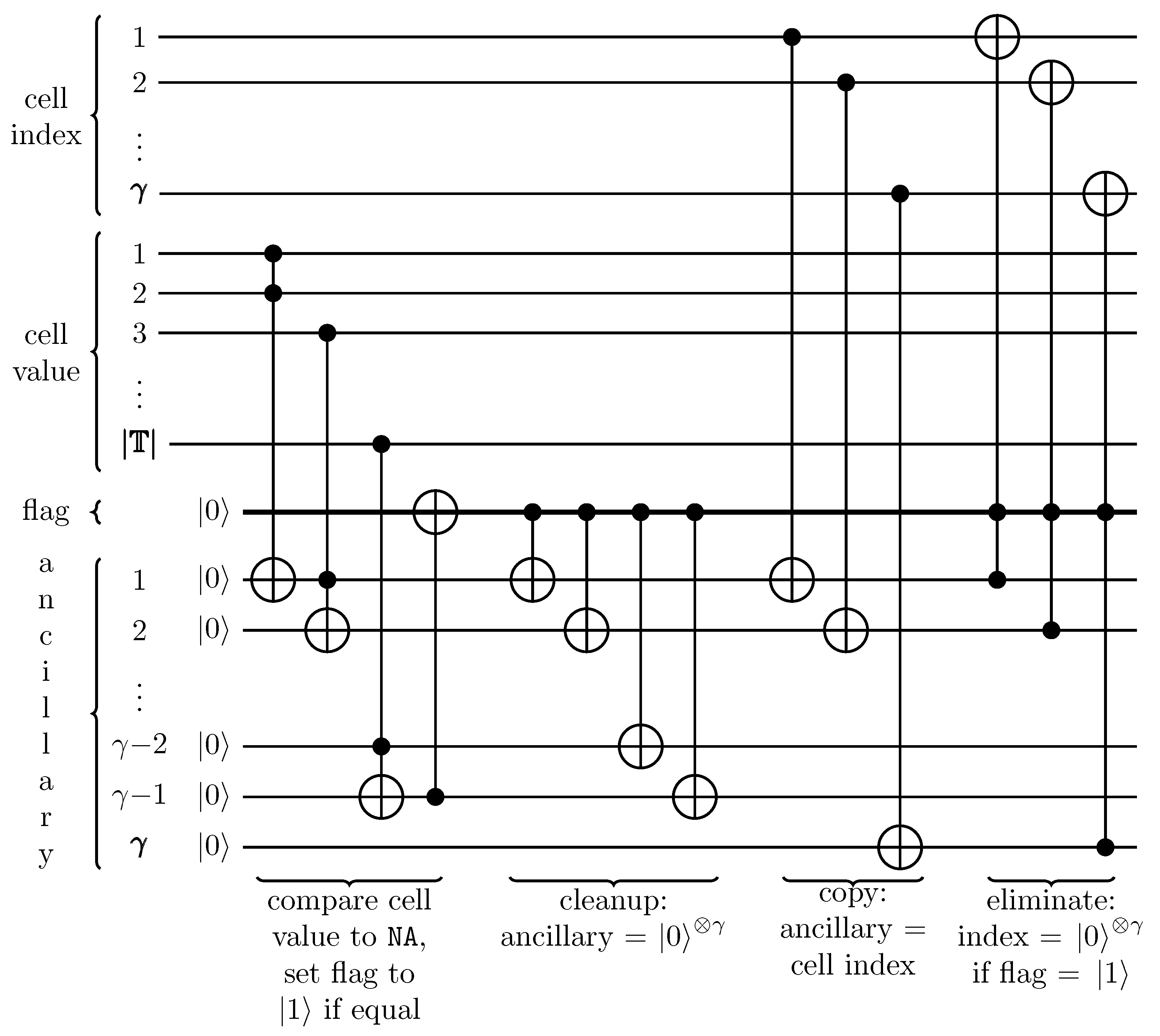
4.5.4. NA Elimination Technique (Deleting Terms from Quantum Superposition)
- removes only 1 term at a time, but we need to remove all terms with NA and we do not know the quantity of such NA terms
- assumes that all terms are present in the superposition (for qubits there should be terms in the input superposition): in a quantum strip we may not have all terms after a sequence of operations or just because its length is less than and is generally unknown
- assumes that the terms have the same amplitudes ( for and ) which may not hold and is hard to guarantee in practice due to the aforementioned reasons
- needs to perform floating point operations which are hard to implement without bias; nearly complete deletion means that the certainty of the operation is less than 100% and, therefore, subsequent algorithms still need to account for the deleted value as if it was not deleted; in our case, algorithms must still do additional checks to avoid NA even after deleting them: this renders such a deletion operation pointless
4.6. Quantum Array (Tensor) Hyperslabbing
 Let us complement the model in Section 4.1.2 with quantum hyperslabbing using classical indexes (QHCI):
Let us complement the model in Section 4.1.2 with quantum hyperslabbing using classical indexes (QHCI):
 Let us further complement the model in Section 4.1.2 with Quantum Hyperslabbing using Quantum Indexes (QHQI):
Let us further complement the model in Section 4.1.2 with Quantum Hyperslabbing using Quantum Indexes (QHQI):

4.7. Quantum Array (Tensor) Joins
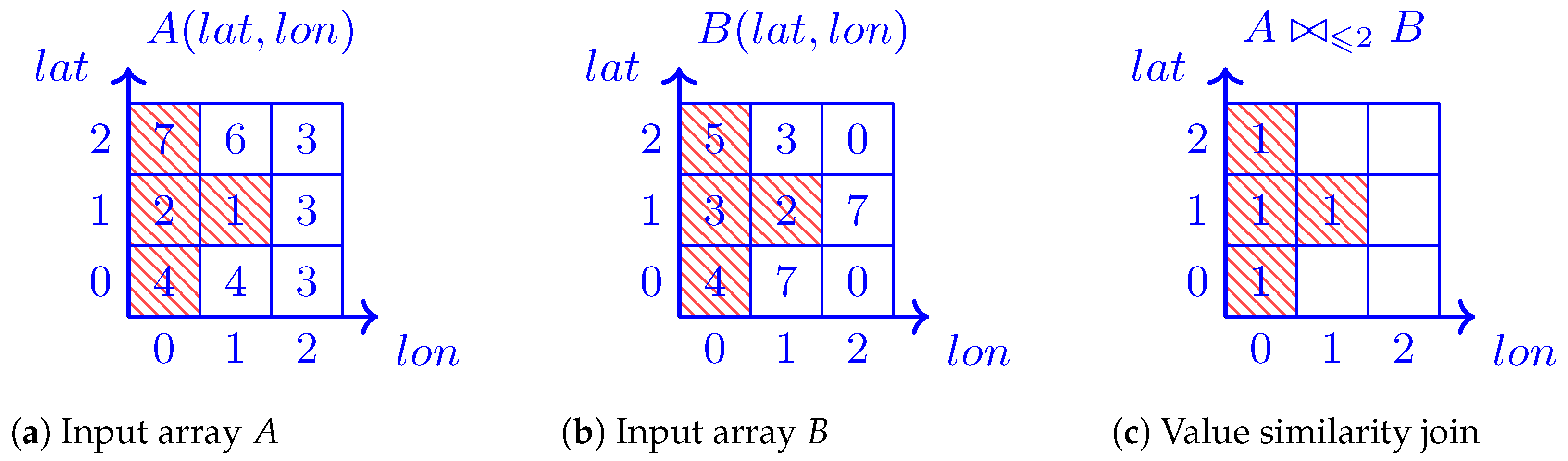

4.8. Quantum Array Algebra
4.9. Quantum Array (Tensor) Indexes
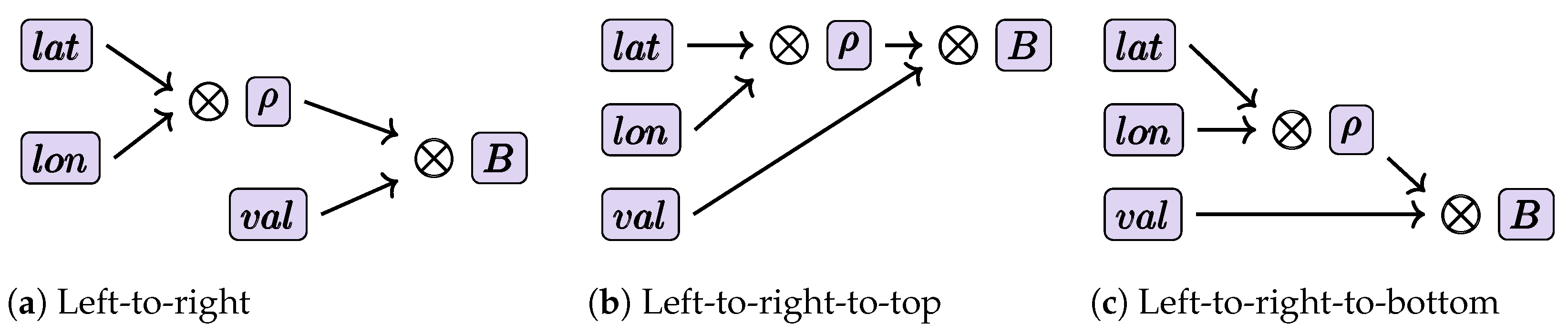
5. Quantum Network Diagrams (QND)
5.1. Quantum Network Diagrams: A Bird’s-Eye View
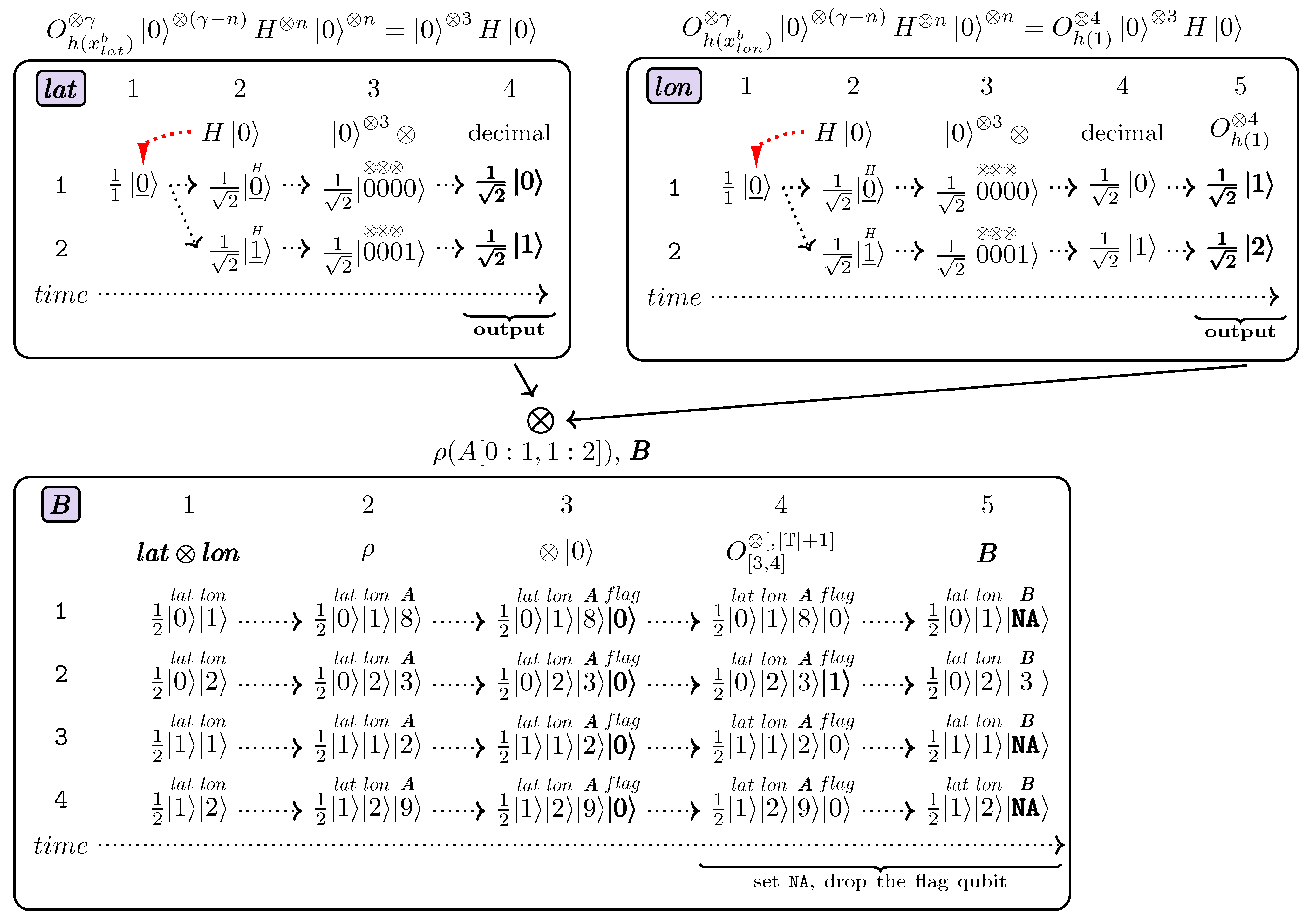
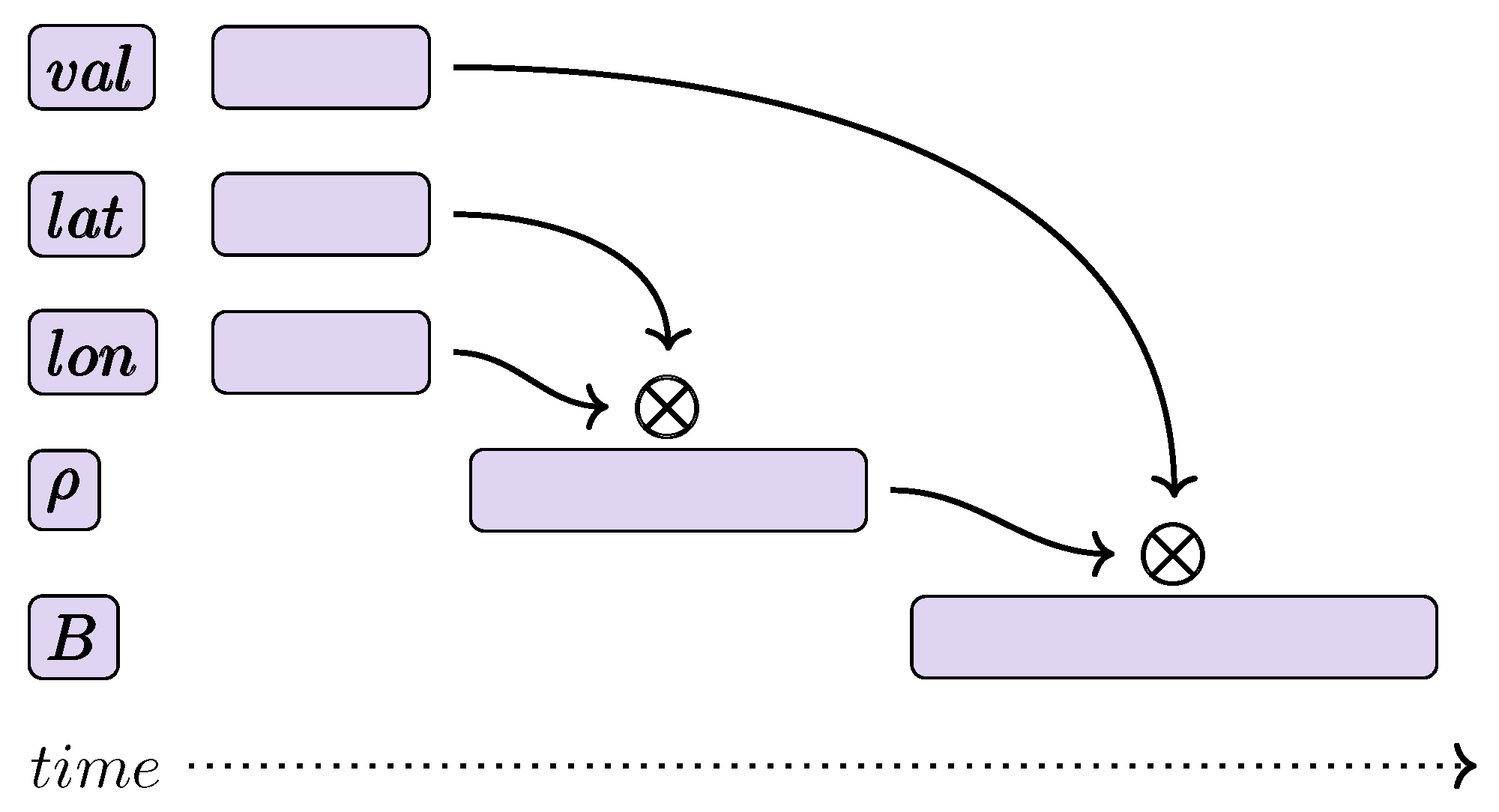
- Each QGantt chart in a Quantum Network Diagram is surrounded with a rectangle to clearly distinguish and visually separate its contents from other QGantt charts that belong to the same Quantum Network Diagram.
- In Quantum Network Diagrams, each QGantt chart has its name (can also be called tag or label) located in the top left corner of each QGantt chart. In Figure 18, QGantt chart names are in bold italic font, placed inside a filled rectangle to better emphasize the names visually, for example,
- QGantt charts can have annotating formulas associated with a whole chart to explain what a QGantt chart aims to produce as its output. A chart annotating formula describes its QGantt chart as a whole in addition to short formulas that can mark superpositions inside a QGantt chart. In Figure 18, such chart annotating formulas are located above QGantt charts and resemble figure captions.
- Symbol ⊗ appears above annotating formulas for QGantt charts which take superpositions as inputs. In Figure 18, the symbol ⊗ appears at the very top of
and
, because the chronological order of QGantt charts (the order in which their output superpositions must be generated) coincides with their vertical order, from top to bottom. Of course, the symbol ⊗ can appear at any other side of a QGantt chart if the charts are laid out in a different way. We laid out ⊗ above the annotating formula for
to indicate that the the output superpositions of
and
are used in the operation. Similarly, ⊗ appears exactly above in
, not or B, to show that the tensor product of outputs of
and
forms —the output of the first stage of the algorithm, Section 4.9.
- Finally, arrows output connect QGantt charts in a DAG (Directed Acyclic Graph). Typically, the last column of a QGantt chart is its output superposition. We additionally mark each such column in
,
,
, and
by a curly brace at the bottom of the last column (superposition) with caption “output”. Each arrow that connects QGantt charts starts near this curly brace or its caption. The arrows point to the symbol ⊗ indicating that the superpositions at the beginning of the arrows participate in the tensor product operation. For example, the superposition № 1 in
represents the tensor products of
and
outputs, so the column № 1 is marked as . Similarly, the first column (superposition) of
equals to , which is the tensor product of outputs of
and
.
 that completes the illustration of the execution of the algorithm from Figure 18 by providing step-by-step actions that lead to getting the dimension- and value-based query result B.
that completes the illustration of the execution of the algorithm from Figure 18 by providing step-by-step actions that lead to getting the dimension- and value-based query result B.5.2. Efficiently Answering Dimension- and Value-Based Queries Step-by-Step
 and
and  respectively, in accordance with the algorithm in Section 4.6. As the hyperslabbing algorithm has been already discussed in Section 4.6, we omit the desciption of
respectively, in accordance with the algorithm in Section 4.6. As the hyperslabbing algorithm has been already discussed in Section 4.6, we omit the desciption of  and
and  which is similar to Figure 12. Therefore, the reader can refer to the description of Figure 12 to understand
which is similar to Figure 12. Therefore, the reader can refer to the description of Figure 12 to understand  and
and  .
.
 is that it does not require an addition oracle as its output index range starts from 0, representing a special case.
is that it does not require an addition oracle as its output index range starts from 0, representing a special case. and
and  come to the QGantt chart named
come to the QGantt chart named 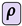 which illustrates reading the hyperslab of A, namely , from QRAM. For more clarity, we show a wide quantum strip for instead of its narrow version. Recall that it is straightforward to switch between wide and narrow strip layouts. The QGantt chart
which illustrates reading the hyperslab of A, namely , from QRAM. For more clarity, we show a wide quantum strip for instead of its narrow version. Recall that it is straightforward to switch between wide and narrow strip layouts. The QGantt chart 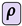 completes the execution of the dimension-based portion of the query.
completes the execution of the dimension-based portion of the query.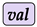 performs this step in accordance with Equations (31) and (39). Recall that the idea is to perform an exhaustive, direct 1:1 equality test of each value in the hyperslab with each value within the queried range . This is the worst case for classical computing, but it can be executed in asymptotically constant time on a quantum machine.
performs this step in accordance with Equations (31) and (39). Recall that the idea is to perform an exhaustive, direct 1:1 equality test of each value in the hyperslab with each value within the queried range . This is the worst case for classical computing, but it can be executed in asymptotically constant time on a quantum machine.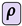 with each value of superposition № 5 of
with each value of superposition № 5 of 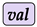 . To accomplish this, we form superposition № 1 called in
. To accomplish this, we form superposition № 1 called in  based on the outputs of
based on the outputs of 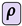 and
and 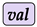 . For the sake of clarity, each value in each term of superposition № 1 in
. For the sake of clarity, each value in each term of superposition № 1 in  is marked by the symbols , , A, and which indicate that the marked values represent and indexes, the cell values of the hyperslab , and the generated values by
is marked by the symbols , , A, and which indicate that the marked values represent and indexes, the cell values of the hyperslab , and the generated values by 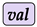 within the submitted cell value range respectively. has 4 values while the range has 2 values. We compare each value of with each value in the range , so we get 8 terms in superposition , column № 1 of
within the submitted cell value range respectively. has 4 values while the range has 2 values. We compare each value of with each value in the range , so we get 8 terms in superposition , column № 1 of  .
. displays the superposition after appending the flag qubit. Initially it is set to . The flag qubit is marked by the word flag and appears in bold in column № 2 to show that this qubit is new compared to the previous superposition in column № 1, QGantt chart
displays the superposition after appending the flag qubit. Initially it is set to . The flag qubit is marked by the word flag and appears in bold in column № 2 to show that this qubit is new compared to the previous superposition in column № 1, QGantt chart  .
. displays the resulting superposition after applying the equality test oracle. The oracle acts on the values marked by A and , saving the equality test result to the flag qubit; in total on qubits, excluding possible ancillary qubits. It turns out, that now only term has the flag qubit equal to . The flag qubit in term is bold and underlined to visually indicate that it is different compared to its previous state in term . Flag qubits in other terms remain equal to and, thus, appear in usual font style in column № 3.
displays the resulting superposition after applying the equality test oracle. The oracle acts on the values marked by A and , saving the equality test result to the flag qubit; in total on qubits, excluding possible ancillary qubits. It turns out, that now only term has the flag qubit equal to . The flag qubit in term is bold and underlined to visually indicate that it is different compared to its previous state in term . Flag qubits in other terms remain equal to and, thus, appear in usual font style in column № 3. contains terms whose cell indexes and values are set to if the qubit flag equals , Figure 18. All terms where the flag qubit is will collapse to . If we drop the ancillary qubits and the flag qubit, we will obtain and as the result. Again, with the respective hardware support, we could just write the superposition in column № 4 to QRAM, omitting term .
contains terms whose cell indexes and values are set to if the qubit flag equals , Figure 18. All terms where the flag qubit is will collapse to . If we drop the ancillary qubits and the flag qubit, we will obtain and as the result. Again, with the respective hardware support, we could just write the superposition in column № 4 to QRAM, omitting term .- Append a flag qubit that indicates whether cell values contain NA. Continuing our example, we will have 2 terms: and . We can reuse the flag from the previous step. In addition, we can integrate this algorithm with the main indexing approach, thus skipping some steps, e.g., Step № 3, by setting to cell indexes instead of .
- Convert the array (tensor) from a 0-based to a 1-based indexed array (tensor): increment the index the corresponds to the last dimension (the most frequently varying) in terms where flag equals . We get and .
- Using the ideas illustrated in Figure 10, set cell indexes to where flag equals : and .
- Reserve in QRAM the number of cells equal to starting at and initialize them to : we know the shape of , because we can compute it using the dimension-based part of the query. We also need an additional dummy cell at the very beginning of the reserved QRAM space to write the cell whose value is equal to . The index of such a cell is or in the case of an N-dimensional array (tensor). Write the superposition to QRAM starting at .
- Read cells from QRAM starting at , thus, omitting the dummy cell. In our example, we obtain exactly the same result as provided in Equation (33). Note that the array (tensor) at this stage, after reading from QRAM, will already be a 0-based indexed array (tensor).

 and
and 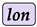 in Figure 20 are the same as in Figure 18. Column № 1 and column № 2 of
in Figure 20 are the same as in Figure 18. Column № 1 and column № 2 of  in Figure 20 are also equal to column № 1 and column № 2 of
in Figure 20 are also equal to column № 1 and column № 2 of  in Figure 18.
in Figure 18. in Figure 20 displays the superposition after appending the flag qubit, which is initially . Column № 4 is the result of applying the test-in-range oracle, Equation (30). For our example, . We found that only satisfies both the dimension- and value-based parts of the query. If we set NA to cell values where the flag qubit is and drop the flag qubit, we will obtain the query result B, Equation (33).
in Figure 20 displays the superposition after appending the flag qubit, which is initially . Column № 4 is the result of applying the test-in-range oracle, Equation (30). For our example, . We found that only satisfies both the dimension- and value-based parts of the query. If we set NA to cell values where the flag qubit is and drop the flag qubit, we will obtain the query result B, Equation (33).5.3. QGantt Charts and Quantum Network Diagrams: Effect and Value
- Research. QGantt charts and Quantum Network Diagrams (QND) excel at visual clarity and structure when graphically presenting, step-by-step, new quantum algorithms utilizing publication-quality vector graphics. Consider Quantum Network Diagrams in Figure 18 and Figure 20 and other QGantt charts introduced in this article.
- Development. IDEs (Integrated Development Environments) as well as quantum computing frameworks can provide step-by-step visualization of program execution or enable debugging with the help of QGantt charts and/or Quantum Network Diagrams which can be displayed in ASCII art, Section 5.4, or rendered using high-quality formula engines comparable to
, for example, in ASCII Math [176,177,178].
- Education. Drawing QGantt charts and Quantum Network Diagrams on paper, tablet, or whiteboard by hand is easy, as the ideas underlying the spatial organization of the entities are intuitive and clear. In addition, the static step-by-step nature of QGantt charts and Quantum Network Diagrams can assist teachers in presenting quantum algorithms and concepts. Furthermore, QGantt charts and Quantum Network Diagrams can support self-study for anyone interested in quantum computing.
5.4. Alternative Ways to Display Quantum Network Diagrams and QGantt Charts
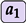 ,
, 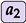 , …,
, …,  provide their inputs to QGantt chart
provide their inputs to QGantt chart  . Therefore, QGantt chart
. Therefore, QGantt chart  depends on the outputs of all QGantt charts
depends on the outputs of all QGantt charts 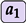 ,
, 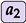 , …,
, …,  . In the time-aware top-to-bottom layout, QGantt chart
. In the time-aware top-to-bottom layout, QGantt chart  appears below all QGantt charts
appears below all QGantt charts 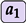 ,
, 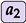 , …,
, …,  .
.
 symbols found in Figure 5 are replaced with textual symbols that can be found on any PC keyboard, except the square root which is a Unicode character. We can enhance the QGantt chart in Figure 23 even more by using Unicode characters for symbols • and ⊕ as well as diverse arrows [179]. However, Figure 23 looks understandable even without additional Unicode symbols. We slightly enhanced the ASCII art in Figure 23 by treating H,TIME,CNOT,-,|,>,->,:,\ as keywords and coloring them blue.
symbols found in Figure 5 are replaced with textual symbols that can be found on any PC keyboard, except the square root which is a Unicode character. We can enhance the QGantt chart in Figure 23 even more by using Unicode characters for symbols • and ⊕ as well as diverse arrows [179]. However, Figure 23 looks understandable even without additional Unicode symbols. We slightly enhanced the ASCII art in Figure 23 by treating H,TIME,CNOT,-,|,>,->,:,\ as keywords and coloring them blue.6. Discussion
| |
|
6.1. Challenges and Opportunities
6.1.1. Quantum Array (Tensor) DBMSs and Simulation Data
6.1.2. Utilizing Other Types of Quantum Memory
6.1.3. Quantum Array Layouts
6.1.4. Quantum-Classical Interface
6.1.5. Query Parsing
6.1.6. New Cost Models and Benchmarks
6.1.7. Hardware-Software Co-Design
6.2. Improving QGantt Charts and Quantum Network Diagrams
 shows the time 15 min past noon. This mnemonics can indicate that the amplitude value is . Another way is to render the amplitudes as icons, e.g., WiFi or similar:
shows the time 15 min past noon. This mnemonics can indicate that the amplitude value is . Another way is to render the amplitudes as icons, e.g., WiFi or similar:  . In this case, the amplitude values become somewhat proportional to the signal strength.
. In this case, the amplitude values become somewhat proportional to the signal strength.6.3. A Roadmap for a Future Quantum Array (Tensor) DBMS
7. Concluding Remarks
Funding
Data Availability Statement
Conflicts of Interest
References
- Donoho, D. 50 years of data science. J. Comput. Graph. Stat. 2017, 26, 745–766. [Google Scholar]
- Chai, C.P. The importance of data cleaning: Three visualization examples. Chance 2020, 33, 4–9. [Google Scholar]
- ECMWF. 2022. Available online: https://www.ecmwf.int/en/computing/our-facilities/data-handling-system (accessed on 22 August 2024).
- Sentinel Data Access Annual Report. 2021. Available online: https://sentinels.copernicus.eu/web/sentinel/-/copernicus-sentinel-data-access-annual-report-2021 (accessed on 22 August 2024).
- Nativi, S.; Caron, J.; Domenico, B.; Bigagli, L. Unidata’s Common Data Model mapping to the ISO 19123 Data Model. Earth Sci. Inform. 2008, 1, 59–78. [Google Scholar]
- Balaji, V.; Adcroft, A.; Liang, Z. Gridspec: A standard for the description of grids used in Earth System models. arXiv 2019, arXiv:1911.08638. [Google Scholar]
- Rusu, F. Multidimensional array data management. Found. Trends® Databases 2023, 12, 69–220. [Google Scholar]
- Rodriges Zalipynis, R.A. Array DBMS: Past, Present, and (Near) Future. Proc. VLDB Endow. 2021, 14, 3186–3189. [Google Scholar]
- Baumann, P.; Misev, D.; Merticariu, V.; Huu, B.P. Array databases: Concepts, standards, implementations. J. Big Data 2021, 8, 1–61. [Google Scholar]
- Kingsmore, S.F.; Smith, L.D.; Kunard, C.M.; Bainbridge, M.; Batalov, S.; Benson, W.; Blincow, E.; Caylor, S.; Chambers, C.; Del Angel, G.; et al. A genome sequencing system for universal newborn screening, diagnosis, and precision medicine for severe genetic diseases. Am. J. Hum. Genet. 2022, 109, 1605–1619. [Google Scholar]
- Askenazi, M.; Ben Hamidane, H.; Graumann, J. The arc of Mass Spectrometry Exchange Formats is long, but it bends toward HDF5. Mass Spectrom. Rev. 2017, 36, 668–673. [Google Scholar]
- Rodriges Zalipynis, R.A. BitFun: Fast Answers to Queries with Tunable Functions in Geospatial Array DBMS. Proc. VLDB Endow. 2020, 13, 2909–2912. [Google Scholar]
- Horlova, O.; Kaitoua, A.; Ceri, S. Array-based Data Management for Genomics. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 109–120. [Google Scholar]
- Masseroli, M.; Canakoglu, A.; Pinoli, P.; Kaitoua, A.; Gulino, A.; Horlova, O.; Nanni, L.; Bernasconi, A.; Perna, S.; Stamoulakatou, E.; et al. Processing of big heterogeneous genomic datasets for tertiary analysis of Next Generation Sequencing data. Bioinformatics 2019, 35, 729–736. [Google Scholar]
- Rodriges Zalipynis, R.A. Generic Distributed In Situ Aggregation for Earth Remote Sensing Imagery. In Proceedings of the International Conference on Analysis of Images, Social Networks and Texts, Moscow, Russia, 5–7 July 2018; LNCS. Springer: Cham, Switzerland, 2018; Volume 11179, pp. 331–342. [Google Scholar]
- Xing, H.; Agrawal, G. COMPASS: Compact array storage with value index. In Proceedings of the 30th International Conference on Scientific and Statistical Database Management, Bozen-Bolzano, Italy, 9–11 July 2018; pp. 1–12. [Google Scholar]
- Rodriges Zalipynis, R.A. ChronosDB: Distributed, File Based, Geospatial Array DBMS. Proc. VLDB Endow. 2018, 11, 1247–1261. [Google Scholar]
- Deaton, A.M.; Parker, M.M.; Ward, L.D.; Flynn-Carroll, A.O.; BonDurant, L.; Hinkle, G.; Akbari, P.; Lotta, L.A. Gene-level analysis of rare variants in 379,066 whole exome sequences identifies an association of GIGYF1 loss of function with type 2 diabetes. Sci. Rep. 2021, 11, 21565. [Google Scholar]
- Ward, L.D.; Tu, H.C.; Quenneville, C.B.; Tsour, S.; Flynn-Carroll, A.O.; Parker, M.M.; Deaton, A.M.; Haslett, P.A.; Lotta, L.A.; Verweij, N.; et al. GWAS of serum ALT and AST reveals an association of SLC30A10 Thr95Ile with hypermanganesemia symptoms. Nat. Commun. 2021, 12, 4571. [Google Scholar]
- Aleksandrov, M.; Zlatanova, S.; Heslop, D.J. Voxelisation algorithms and data structures: A review. Sensors 2021, 21, 8241. [Google Scholar] [CrossRef]
- Kim, M.; Lee, H.; Chung, Y.D. Multi-Dimensional Data Compression and Query Processing in Array Databases. IEEE Access 2022, 10, 111528–111544. [Google Scholar]
- Mehta, P.; Dorkenwald, S.; Zhao, D.; Kaftan, T.; Cheung, A.; Balazinska, M.; Rokem, A.; Connolly, A.; Vanderplas, J.; AlSayyad, Y. Comparative evaluation of big-data systems on scientific image analytics workloads. Proc. VLDB Endow. 2017, 10, 1226–1237. [Google Scholar]
- Cudre-Mauroux, P.; Kimura, H.; Lim, K.T.; Rogers, J.; Madden, S.; Stonebraker, M.; Zdonik, S.B.; Brown, P.G. SS-DB: A Standard Science DBMS Benchmark. In Proceedings of the XLDB, 2010. Available online: https://people.csail.mit.edu/jennie/_content/research/ssdb_benchmark.pdf (accessed on 22 August 2024).
- Soroush, E.; Balazinska, M.; Wang, D. ArrayStore: A storage manager for complex parallel array processing. In Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data, Athens, Greece, 12–16 June 2011; pp. 253–264. [Google Scholar]
- Kim, B.; Koo, K.; Enkhbat, U.; Kim, S.; Kim, J.; Moon, B. M2Bench: A Database Benchmark for Multi-Model Analytic Workloads. Proc. VLDB Endow. 2022, 16, 747–759. [Google Scholar]
- Choi, D.; Yoon, H.; Chung, Y.D. ReSKY: Efficient Subarray Skyline Computation in Array Databases. Distrib. Parallel Databases 2022, 40, 261–298. [Google Scholar]
- Choi, D.; Yoon, H.; Chung, Y.D. Subarray skyline query processing in array databases. In Proceedings of the 33rd International Conference on Scientific and Statistical Database Management, Tampa, FL, USA, 6–7 July 2021; pp. 37–48. [Google Scholar]
- Villarroya, S.; Baumann, P. On the Integration of Machine Learning and Array Databases. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 1786–1789. [Google Scholar]
- Rodriges Zalipynis, R.A. Towards Machine Learning in Distributed Array DBMS: Networking Considerations. In Proceedings of the Machine Learning for Networking: Third International Conference, MLN 2020, Paris, France, 24–26 November 2020; LNCS. Springer: Cham, Switzerland, 2021; Volume 12629, pp. 284–304. [Google Scholar]
- Ordonez, C.; Zhang, Y.; Johnsson, S.L. Scalable machine learning computing a data summarization matrix with a parallel array DBMS. Distrib. Parallel Databases 2019, 37, 329–350. [Google Scholar]
- Villarroya, S.; Baumann, P. A survey on machine learning in array databases. Appl. Intell. 2023, 53, 9799–9822. [Google Scholar]
- Alam, M.M.; Torgo, L.; Bifet, A. A survey on spatio-temporal data analytics systems. ACM Comput. Surv. 2022, 54, 1–38. [Google Scholar]
- Xu, C.; Du, X.; Fan, X.; Giuliani, G.; Hu, Z.; Wang, W.; Liu, J.; Wang, T.; Yan, Z.; Zhu, J.; et al. Cloud-based storage and computing for remote sensing big data: A technical review. Int. J. Digit. Earth 2022, 15, 1417–1445. [Google Scholar]
- Lewis, A.; Oliver, S.; Lymburner, L.; Evans, B.; Wyborn, L.; Mueller, N.; Raevksi, G.; Hooke, J.; Woodcock, R.; Sixsmith, J.; et al. The Australian Geoscience Data Cube—Foundations and lessons learned. Remote Sens. Environ. 2017, 202, 276–292. [Google Scholar]
- Baumann, P.; Misev, D.; Merticariu, V.; Huu, B.P.; Bell, B. DataCubes: A technology survey. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 430–433. [Google Scholar]
- Baumann, P. Towards a Model-Driven Datacube Analytics Language. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021; pp. 3740–3746. [Google Scholar]
- Mahecha, M.D.; Gans, F.; Brandt, G.; Christiansen, R.; Cornell, S.E.; Fomferra, N.; Kraemer, G.; Peters, J.; Bodesheim, P.; Camps-Valls, G.; et al. Earth system data cubes unravel global multivariate dynamics. Earth Syst. Dyn. 2020, 11, 201–234. [Google Scholar]
- Baumann, P.; Misev, D. ORBiDANSe: Orbital Big Datacube Analytics Service. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-13002. [Google Scholar]
- Rivera, G.; Porras, R.; Florencia, R.; Sánchez-Solís, J.P. LiDAR applications in precision agriculture for cultivating crops: A review of recent advances. Comput. Electron. Agric. 2023, 207, 107737. [Google Scholar]
- Su, J.; Zhu, X.; Li, S.; Chen, W.H. AI meets UAVs: A survey on AI empowered UAV perception systems for precision agriculture. Neurocomputing 2023, 518, 242–270. [Google Scholar]
- Pande, C.B.; Moharir, K.N. Application of hyperspectral remote sensing role in precision farming and sustainable agriculture under climate change: A review. In Climate Change Impacts on Natural Resources, Ecosystems and Agricultural Systems; Springer: Berlin/Heidelberg, Germany, 2023; pp. 503–520. [Google Scholar]
- Luo, Y.; Huang, H.; Roques, A. Early monitoring of forest wood-boring pests with remote sensing. Annu. Rev. Entomol. 2023, 68, 277–298. [Google Scholar]
- Massey, R.; Berner, L.T.; Foster, A.C.; Goetz, S.J.; Vepakomma, U. Remote Sensing Tools for Monitoring Forests and Tracking Their Dynamics. In Boreal Forests in the Face of Climate Change: Sustainable Management; Springer: Berlin/Heidelberg, Germany, 2023; pp. 637–655. [Google Scholar]
- Yu, D.; Fang, C. Urban Remote Sensing with Spatial Big Data: A Review and Renewed Perspective of Urban Studies in Recent Decades. Remote Sens. 2023, 15, 1307. [Google Scholar] [CrossRef]
- Li, F.; Yigitcanlar, T.; Nepal, M.; Nguyen, K.; Dur, F. Machine Learning and Remote Sensing Integration for Leveraging Urban Sustainability: A Review and Framework. Sustain. Cities Soc. 2023, 96, 104653. [Google Scholar]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Overview of the Application of Remote Sensing in Effective Monitoring of Water Quality Parameters. Remote Sens. 2023, 15, 1938. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, J.; Liu, M.; Yin, Z.; Liu, X.; Yin, L.; Zheng, W. Remote sensing and geostatistics in urban water-resource monitoring: A review. Mar. Freshw. Res. 2023, 74, 747–765. [Google Scholar]
- Kurniawan, R.; Alamsyah, A.R.B.; Fudholi, A.; Purwanto, A.; Sumargo, B.; Gio, P.U.; Wongsonadi, S.K.; Susanto, A.E.H. Impacts of industrial production and air quality by remote sensing on nitrogen dioxide concentration and related effects: An econometric approach. Environ. Pollut. 2023, 334, 122212. [Google Scholar]
- Abu El-Magd, S.; Soliman, G.; Morsy, M.; Kharbish, S. Environmental hazard assessment and monitoring for air pollution using machine learning and remote sensing. Int. J. Environ. Sci. Technol. 2023, 20, 6103–6116. [Google Scholar]
- Sudmanns, M.; Augustin, H.; Killough, B.; Giuliani, G.; Tiede, D.; Leith, A.; Yuan, F.; Lewis, A. Think global, cube local: An Earth Observation Data Cube’s contribution to the Digital Earth vision. Big Earth Data 2023, 7, 831–859. [Google Scholar]
- Mahmood, R.; Zhang, L.; Li, G. Assessing effectiveness of nature-based solution with big earth data: 60 years mangrove plantation program in Bangladesh coast. Ecol. Process. 2023, 12, 11. [Google Scholar]
- Wang, S.; Wang, J.; Zhan, Q.; Zhang, L.; Yao, X.; Li, G. A unified representation method for interdisciplinary spatial earth data. Big Earth Data 2023, 7, 126–145. [Google Scholar]
- Rodriges Zalipynis, R.A.; Pozdeev, E.; Bryukhov, A. Array DBMS and Satellite Imagery: Towards Big Raster Data in the Cloud. In Proceedings of the International Conference on Analysis of Images, Social Networks and Texts, Moscow, Russia, 27–29 July 2017; LNCS. Volume 10716, pp. 267–279. [Google Scholar]
- Ladra, S.; Paramá, J.R.; Silva-Coira, F. Scalable and queryable compressed storage structure for raster data. Inf. Syst. 2017, 72, 179–204. [Google Scholar]
- Leclercq, É.; Gillet, A.; Grison, T.; Savonnet, M. Polystore and Tensor Data Model for Logical Data Independence and Impedance Mismatch in Big Data Analytics. In LNCS; Springer: Berlin/Heidelberg, Germany, 2019; pp. 51–90. [Google Scholar]
- Papadopoulos, S.; Datta, K.; Madden, S.; Mattson, T. The TileDB Array Data Storage Manager. Proc. VLDB Endow. 2016, 10, 349–360. [Google Scholar]
- Rodriges Zalipynis, R.A. ChronosDB in Action: Manage, Process, and Visualize Big Geospatial Arrays in the Cloud. In Proceedings of the 2019 International Conference on Management of Data, Amsterdam, The Netherlands, 30 June–5 July 2019; pp. 1985–1988. [Google Scholar]
- Zhao, W.; Rusu, F.; Dong, B.; Wu, K.; Nugent, P. Incremental view maintenance over array data. In Proceedings of the 2017 ACM International Conference on Management of Data, Chicago, IL, USA, 14–19 May 2017; pp. 139–154. [Google Scholar]
- Zhao, W.; Rusu, F.; Dong, B.; Wu, K. Similarity join over array data. In Proceedings of the 2016 International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 2007–2022. [Google Scholar]
- Zhao, W.; Rusu, F.; Dong, B.; Wu, K.; Ho, A.Y.; Nugent, P. Distributed caching for processing raw arrays. In Proceedings of the 30th International Conference on Scientific and Statistical Database Management, Bozen-Bolzano, Italy, 9–11 July 2018. [Google Scholar]
- Rodriges Zalipynis, R.A. FastMosaic in Action: A New Mosaic Operator for Array DBMSs. Proc. VLDB Endow. 2023, 16, 3938–3941. [Google Scholar]
- Kilsedar, C.E.; Brovelli, M.A. Multidimensional visualization and processing of big open urban geospatial data on the web. ISPRS Int. J.-Geo-Inf. 2020, 9, 434. [Google Scholar]
- Rodriges Zalipynis, R.A.; Terlych, N. WebArrayDB: A Geospatial Array DBMS in Your Web Browser. Proc. VLDB Endow. 2022, 15, 3622–3625. [Google Scholar]
- Battle, L.; Chang, R.; Stonebraker, M. Dynamic prefetching of data tiles for interactive visualization. In Proceedings of the 2016 International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 1363–1375. [Google Scholar]
- Rodriges Zalipynis, R.A. SimDB in Action: Road Trafic Simulations Completely Inside Array DBMS. Proc. VLDB Endow. 2022, 15, 3742–3745. [Google Scholar]
- Rodriges Zalipynis, R.A. Convergence of Array DBMS and Cellular Automata: A Road Traffic Simulation Case. In Proceedings of the 2021 International Conference on Management of Data, Xi’an, China, 20–25 June 2021; pp. 2399–2403. [Google Scholar]
- Cudre-Mauroux, P.; Kimura, H.; Lim, K.T.; Rogers, J.; Simakov, R.; Soroush, E.; Velikhov, P.; Wang, D.L.; Balazinska, M.; Becla, J.; et al. A demonstration of SciDB: A science-oriented DBMS. Proc. VLDB Endow. 2009, 2, 1534–1537. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar]
- Zhao, Q.; Yu, L.; Li, X.; Peng, D.; Zhang, Y.; Gong, P. Progress and trends in the application of Google Earth and Google Earth Engine. Remote Sens. 2021, 13, 3778. [Google Scholar] [CrossRef]
- Wang, Y.; Nandi, A.; Agrawal, G. SAGA: Array Storage as a DB with Support for Structural Aggregations. In Proceedings of the 26th International Conference on Scientific and Statistical Database Management, Aalborg, Denmark, 30 June–2 July 2014. [Google Scholar]
- Baumann, P.; Mazzetti, P.; Ungar, J.; Barbera, R.; Barboni, D.; Beccati, A.; Bigagli, L.; Boldrini, E.; Bruno, R.; Calanducci, A.; et al. Big data analytics for Earth sciences: The EarthServer approach. Int. J. Digit. Earth 2016, 9, 3–29. [Google Scholar]
- GeoTrellis. 2024. Available online: https://geotrellis.io/ (accessed on 22 August 2024).
- Dask. 2024. Available online: https://dask.org/ (accessed on 22 August 2024).
- Microsoft Planetary Computer. 2024. Available online: https://planetarycomputer.microsoft.com/ (accessed on 22 August 2024).
- Earth Engine|Google Cloud. 2024. Available online: https://cloud.google.com/earth-engine (accessed on 22 August 2024).
- Rodriges Zalipynis, R.A. Evaluating Array DBMS Compression Techniques for Big Environmental Datasets. In Proceedings of the 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 18–21 September 2019; Volume 2, pp. 859–863. [Google Scholar]
- Mainzer, J.; Fortner, N.; Heber, G.; Pourmal, E.; Koziol, Q.; Byna, S.; Paterno, M. Sparse Data Management in HDF5. In Proceedings of the 2019 IEEE/ACM 1st Annual Workshop on Large-Scale Experiment-in-the-Loop Computing (XLOOP), Denver, CO, USA, 18 November 2019; pp. 20–25. [Google Scholar]
- Cheng, Y.; Zhao, W.; Rusu, F. Bi-Level Online Aggregation on Raw Data. In Proceedings of the 29th International Conference on Scientific and Statistical Database Management, Chicago, IL, USA, 27–29 June 2017. [Google Scholar]
- Blanas, S.; Wu, K.; Byna, S.; Dong, B.; Shoshani, A. Parallel data analysis directly on scientific file formats. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2014. [Google Scholar]
- Su, Y.; Agrawal, G. Supporting user-defined subsetting and aggregation over parallel NetCDF datasets. In Proceedings of the 2012 12th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing CCGrid, Ottawa, ON, Canada, 13–16 May 2012; pp. 212–219. [Google Scholar]
- Rodriges Zalipynis, R.A. Distributed In Situ Processing of Big Raster Data in the Cloud. In Proceedings of the Perspectives of System Informatics, Moscow, Russia, 27–29 June 2017; LNCS. Springer: Cham, Switzerland, 2018; Volume 10742, pp. 337–351. [Google Scholar]
- Xing, H.; Agrawal, G. Accelerating array joining with integrated value-index. In Proceedings of the 31st International Conference on Scientific and Statistical Database Management, Vienna, Austria, 7–9 July 2020; pp. 145–156. [Google Scholar]
- Choi, D.; Park, C.S.; Chung, Y.D. Progressive top-k subarray query processing in array databases. Proc. VLDB Endow. 2019, 12, 989–1001. [Google Scholar]
- Azure Quantum Homepage. 2024. Available online: https://quantum.microsoft.com/ (accessed on 22 August 2024).
- Cloud Quantum Computing Service—Amazon Braket—AWS. 2024. Available online: https://aws.amazon.com/braket (accessed on 22 August 2024).
- IBM Quantum Computing. 2024. Available online: https://www.ibm.com/quantum (accessed on 22 August 2024).
- Google Quantum AI. 2024. Available online: https://quantumai.google/ (accessed on 22 August 2024).
- Qubit Scorecard. 2024. Available online: https://www.qusecure.com/qubit-scorecard/ (accessed on 22 August 2024).
- Fujitsu Quantum. 2024. Available online: https://www.fujitsu.com/global/about/research/technology/quantum/ (accessed on 22 August 2024).
- Atom Computing. 2024. Available online: https://atom-computing.com/ (accessed on 22 August 2024).
- D-Wave Systems. 2024. Available online: https://www.dwavesys.com/ (accessed on 22 August 2024).
- D-Wave. D-Wave Announces Availability of 1200+ Qubit Advantage2™ Prototype. 2024. Available online: https://www.dwavesys.com/company/newsroom/press-release/d-wave-announces-availability-of-1-200-qubit-advantage2-prototype/ (accessed on 22 August 2024).
- IBM 100,000 Qubit Supercomputer. 2023. Available online: www.ibm.com/quantum/blog/100k-qubit-supercomputer (accessed on 22 August 2024).
- Feynman, R.P. Simulating Physics with Computers. Int. J. Theor. Phys. 1982, 21, 133–153. [Google Scholar]
- Benioff, P. Quantum mechanical Hamiltonian models of Turing machines. J. Stat. Phys. 1982, 29, 515–546. [Google Scholar]
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Chen, J.; Stoudenmire, E.; White, S.R. Quantum Fourier Transform Has Small Entanglement. PRX Quantum 2023, 4, 040318. [Google Scholar]
- Camps, D.; Van Beeumen, R.; Yang, C. Quantum Fourier transform revisited. Numer. Linear Algebra Appl. 2021, 28, e2331. [Google Scholar]
- Acampora, G.; Chiatto, A.; Vitiello, A. Genetic algorithms as classical optimizer for the Quantum Approximate Optimization Algorithm. Appl. Soft Comput. 2023, 142, 110296. [Google Scholar]
- Drias, H.; Drias, Y.; Houacine, N.A.; Bendimerad, L.S.; Zouache, D.; Khennak, I. Quantum OPTICS and deep self-learning on swarm intelligence algorithms for Covid-19 emergency transportation. Soft Comput. 2023, 27, 13181–13200. [Google Scholar]
- Mukhamedov, F.; Souissi, A.; Hamdi, T.; Andolsi, A. Open quantum random walks and quantum Markov Chains on trees II: The recurrence. Quantum Inf. Process. 2023, 22, 232. [Google Scholar]
- Ardelean, S.M.; Udrescu, M. Graph coloring using the reduced quantum genetic algorithm. PeerJ Comput. Sci. 2022, 8, e836. [Google Scholar]
- Gupta, R.; Saxena, D.; Gupta, I.; Makkar, A.; Singh, A.K. Quantum machine learning driven malicious user prediction for cloud network communications. IEEE Netw. Lett. 2022, 4, 174–178. [Google Scholar]
- Melnikov, A.; Kordzanganeh, M.; Alodjants, A.; Lee, R.K. Quantum machine learning: From physics to software engineering. Adv. Phys. X 2023, 8, 2165452. [Google Scholar]
- Biasse, J.F.; Bonnetain, X.; Kirshanova, E.; Schrottenloher, A.; Song, F. Quantum algorithms for attacking hardness assumptions in classical and post-quantum cryptography. IET Inf. Secur. 2023, 17, 171–209. [Google Scholar]
- Herman, D.; Googin, C.; Liu, X.; Sun, Y.; Galda, A.; Safro, I.; Pistoia, M.; Alexeev, Y. Quantum computing for finance. Nat. Rev. Phys. 2023, 5, 450–465. [Google Scholar]
- Cordier, B.A.; Sawaya, N.P.; Guerreschi, G.G.; McWeeney, S.K. Biology and medicine in the landscape of quantum advantages. J. R. Soc. Interface 2022, 19, 20220541. [Google Scholar]
- Huang, D.; Wang, M.; Wang, J.; Yan, J. A survey of quantum computing hybrid applications with brain-computer interface. Cogn. Robot. 2022, 2, 64–176. [Google Scholar]
- Ullah, M.H.; Eskandarpour, R.; Zheng, H.; Khodaei, A. Quantum computing for smart grid applications. IET Gener. Transm. Distrib. 2022, 16, 4239–4257. [Google Scholar]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum principal component analysis. Nat. Phys. 2014, 10, 631–633. [Google Scholar]
- Fritsch, K.; Scherzinger, S. Solving Hard Variants of Database Schema Matching on Quantum Computers. Proc. VLDB Endow. 2023, 16, 3990–3993. [Google Scholar]
- Groppe, S.; Groppe, J.; Çalıkyılmaz, U.; Winker, T.; Gruenwal, L. Quantum data management and quantum machine learning for data management: State-of-the-art and open challenges. In Proceedings of the International Conference on Intelligent Systems and Machine Learning, Guangzhou, China, 5–7 August 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 252–261. [Google Scholar]
- Figgatt, C.; Maslov, D.; Landsman, K.A.; Linke, N.M.; Debnath, S.; Monroe, C. Complete 3-qubit Grover search on a programmable quantum computer. Nat. Commun. 2017, 8, 1918. [Google Scholar]
- Zajac, M.; Störl, U. Towards quantum-based Search for industrial Data-driven Services. In Proceedings of the 2022 IEEE International Conference on Quantum Software (QSW), Barcelona, Spain, 10–16 July 2022; pp. 38–40. [Google Scholar]
- Trummer, I.; Koch, C. Multiple Query Optimization on the D-Wave 2X Adiabatic Quantum Computer. arXiv 2015, arXiv:1510.06437. [Google Scholar]
- Schönberger, M. Applicability of quantum computing on database query optimization. In Proceedings of the 2022 International Conference on Management of Data, Philadelphia, PA, USA, 12–17 June 2022; pp. 2512–2514. [Google Scholar]
- Fankhauser, T.; Solèr, M.E.; Füchslin, R.M.; Stockinger, K. Multiple Query Optimization using a Gate-Based Quantum Computer. IEEE Access 2023, 11, 114043. [Google Scholar]
- Çalikyilmaz, U.; Groppe, S.; Groppe, J.; Winker, T.; Prestel, S.; Shagieva, F.; Arya, D.; Preis, F.; Gruenwald, L. Opportunities for quantum acceleration of databases: Optimization of queries and transaction schedules. Proc. VLDB Endow. 2023, 16, 2344–2353. [Google Scholar]
- Albert Einstein Quote. 2024. Available online: https://www.azquotes.com/quote/905255 (accessed on 22 August 2024).
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar]
- Aaronson, S.; Gottesman, D. Improved simulation of stabilizer circuits. Phys. Rev. A 2004, 70, 052328. [Google Scholar]
- Kitaev, A.Y.; Shen, A.; Vyalyi, M.N. Classical and Quantum Computation; Number 47; American Mathematical Soc.: Washington, DC, USA, 2002. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar]
- IonQ Glossary. 2024. Available online: https://ionq.com/resources/glossary (accessed on 22 August 2024).
- IonQ|Trapped Ion Quantum Computing. 2024. Available online: https://ionq.com/ (accessed on 22 August 2024).
- QuEra. 2024. Available online: https://www.quera.com/ (accessed on 22 August 2024).
- Rigetti Computing. 2024. Available online: https://www.rigetti.com/ (accessed on 22 August 2024).
- Oxford Quantum Circuits. 2024. Available online: https://oxfordquantumcircuits.com/ (accessed on 22 August 2024).
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; OUP Oxford: Oxford, UK, 2006. [Google Scholar]
- Kaiser, S.C.; Granade, C. Learn Quantum Computing with Python and Q#: A Hands-on Approach; Simon and Schuster: New York, NY, USA, 2021. [Google Scholar]
- Vos, J. Quantum Computing in Action; Simon and Schuster: New York, NY, USA, 2022. [Google Scholar]
- Silva, V. Practical Quantum Computing for Developers: Programming Quantum Rigs in the Cloud Using Python, Quantum Assembly Language and IBM QExperience; Apress: New York, NY, USA, 2018. [Google Scholar]
- Combarro, E.F.; Gonzalez-Castillo, S.; Di Meglio, A. A Practical Guide to Quantum Machine Learning and Quantum Optimization: Hands-on Approach to Modern Quantum Algorithms; Packt: Birmingham, UK, 2023. [Google Scholar]
- Q# Programming Language. 2024. Available online: https://github.com/microsoft/qsharp-language (accessed on 22 August 2024).
- OpenQASM. 2024. Available online: https://openqasm.com/ (accessed on 22 August 2024).
- Quantum Computing API for Java. 2024. Available online: https://github.com/redfx-quantum/strange (accessed on 22 August 2024).
- QuTiP—Quantum Toolbox in Python. 2024. Available online: https://qutip.org/ (accessed on 22 August 2024).
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum random access memory. Phys. Rev. Lett. 2008, 100, 160501. [Google Scholar]
- Zidan, M.; Abdel-Aty, A.H.; Khalil, A.; Abdel-Aty, M.; Eleuch, H. A novel efficient quantum random access memory. IEEE Access 2021, 9, 151775–151780. [Google Scholar]
- Park, D.K.; Petruccione, F.; Rhee, J.K.K. Circuit-based quantum random access memory for classical data. Sci. Rep. 2019, 9, 3949. [Google Scholar]
- Phalak, K.; Chatterjee, A.; Ghosh, S. Quantum random access memory for dummies. Sensors 2023, 23, 7462. [Google Scholar] [CrossRef]
- Liu, C.; Wang, M.; Stein, S.A.; Ding, Y.; Li, A. Quantum Memory: A Missing Piece in Quantum Computing Units. arXiv 2023, arXiv:2309.14432. [Google Scholar]
- Jaques, S.; Rattew, A.G. QRAM: A survey and critique. arXiv 2023, arXiv:2305.10310. [Google Scholar]
- Xu, S.; Hann, C.T.; Foxman, B.; Girvin, S.M.; Ding, Y. Systems architecture for quantum random access memory. In Proceedings of the 56th Annual IEEE/ACM International Symposium on Microarchitecture, Toronto, ON, Canada, 28 October–1 November 2023; pp. 526–538. [Google Scholar]
- Hoefler, T.; Häner, T.; Troyer, M. Disentangling hype from practicality: On realistically achieving quantum advantage. Commun. ACM 2023, 66, 82–87. [Google Scholar]
- Customer Success Stories D-Wave. 2024. Available online: https://www.dwavesys.com/learn/customer-success-stories/ (accessed on 22 August 2024).
- Wang, C.; Li, X.; Xu, H.; Li, Z.; Wang, J.; Yang, Z.; Mi, Z.; Liang, X.; Su, T.; Yang, C.; et al. Towards practical quantum computers: Transmon qubit with a lifetime approaching 0.5 milliseconds. npj Quantum Inf. 2022, 8, 3. [Google Scholar]
- Pal, S.; Bhattacharya, M.; Lee, S.S.; Chakraborty, C. Quantum computing in the next-generation computational biology landscape: From protein folding to molecular dynamics. Mol. Biotechnol. 2024, 66, 163–178. [Google Scholar]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar]
- Kazmina, A.S.; Zalivako, I.V.; Borisenko, A.S.; Nemkov, N.A.; Nikolaeva, A.S.; Simakov, I.A.; Kuznetsova, A.V.; Egorova, E.Y.; Galstyan, K.P.; Semenin, N.V.; et al. Demonstration of a parity-time-symmetry-breaking phase transition using superconducting and trapped-ion qutrits. Phys. Rev. A 2024, 109, 032619. [Google Scholar]
- IBM Quantum Composer. 2024. Available online: https://quantum.ibm.com/composer/files/new (accessed on 22 August 2024).
- Barthe, A.; Grossi, M.; Tura, J.; Dunjko, V. Bloch Sphere Binary Trees: A method for the visualization of sets of multi-qubit systems pure states. arXiv 2023, arXiv:2302.02957. [Google Scholar]
- Koczor, B.; Zeier, R.; Glaser, S.J. Fast computation of spherical phase-space functions of quantum many-body states. Phys. Rev. A 2020, 102, 062421. [Google Scholar]
- IBM Quantum Computer with over 1000 Qubits. 2023. Available online: https://www.nature.com/articles/d41586-023-03854-1 (accessed on 22 August 2024).
- IBM Q-Sphere. 2024. Available online: https://quantum-computing.ibm.com/composer/docs/iqx/visualizations#q-sphere-view (accessed on 22 August 2024).
- Migdał, P. Symmetries and self-similarity of many-body wavefunctions. arXiv 2014, arXiv:1412.6796. [Google Scholar]
- IBM Qiskit Circuit Visualization. 2024. Available online: https://docs.quantum.ibm.com/build/circuit-visualization (accessed on 22 August 2024).
- Quirk. 2024. Available online: https://algassert.com/quirk (accessed on 22 August 2024).
- Chang, C.; Moon, B.; Acharya, A.; Shock, C.; Sussman, A.; Saltz, J. Titan: A high-performance remote-sensing database. In Proceedings of the 13th International Conference on Data Engineering, Birmingham, UK, 7–11 April 1997; pp. 375–384. [Google Scholar]
- DeWitt, D.J.; Kabra, N.; Luo, J.; Patel, J.M.; Yu, J.B. Client-Server Paradise. In Proceedings of the VLDB, Santiago de Chile, Chile, 12–15 September 1994; pp. 558–569. [Google Scholar]
- van Ballegooij, A. RAM: A Multidimensional Array DBMS. In Proceedings of the EDBT, Heraklion, Greece, 14–18 March 2004; Volume 3268, pp. 154–165. [Google Scholar]
- Libkin, L.; Machlin, R.; Wong, L. A query language for multidimensional arrays: Design, implementation, and optimization techniques. In Proceedings of the ACM SIGMOD Record, Montreal, QC, Cananda, 4–6 June 1996; Volume 25, pp. 228–239. [Google Scholar]
- Oseledets, I. Tensor-train decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Apache Arrow: A Cross-Language Development Platform for In-Memory Analytics. 2024. Available online: https://arrow.apache.org/ (accessed on 22 August 2024).
- Yuan, G.; Chen, Y.; Lu, J.; Wu, S.; Ye, Z.; Qian, L.; Chen, G. Quantum Computing for Databases: Overview and Challenges. arXiv 2024, arXiv:2405.12511. [Google Scholar]
- Liu, Y.; Long, G.L. Deleting a marked item from an unsorted database with a single query. arXiv 2007, arXiv:0710.3301. [Google Scholar]
- Brassard, G.; Hoyer, P.; Mosca, M.; Tapp, A. Quantum amplitude amplification and estimation. Contemp. Math. 2002, 305, 53–74. [Google Scholar]
- Li, H.S.; Fan, P.; Xia, H.; Peng, H.; Long, G.L. Efficient quantum arithmetic operation circuits for quantum image processing. Sci. China Phys. Mech. Astron. 2020, 63, 1–13. [Google Scholar]
- Cuccaro, S.A.; Draper, T.G.; Kutin, S.A.; Moulton, D.P. A new quantum ripple-carry addition circuit. arXiv 2004, arXiv:0410184. [Google Scholar]
- Zhang, Y. Four arithmetic operations on the quantum computer. J. Phys. Conf. Ser. Iop Publ. 2020, 1575, 012037. [Google Scholar]
- Chou, J.; Wu, K.; Prabhat. FastQuery: A general indexing and querying system for scientific data. In Proceedings of the International Conference on Scientific and Statistical Database Management, Portland, OR, USA, 20–22 July 2011; pp. 573–574. [Google Scholar]
- ASCII Math. 2024. Available online: https://asciimath.org/ (accessed on 22 August 2024).
- CortexJS. 2024. Available online: https://cortexjs.io/mathlive/guides/static (accessed on 22 August 2024).
- MathJax. 2024. Available online: https://www.mathjax.org/ (accessed on 22 August 2024).
- Unicode Arrows. 2024. Available online: https://unicode.org/charts/nameslist/n_2190.html (accessed on 22 August 2024).
- Niels Bohr Quote. 2024. Available online: https://www.azquotes.com/quote/30759?ref=quantum-mechanics (accessed on 22 August 2024).
- Richard Feynman Quotes. 2024. Available online: https://en.wikiquote.org/wiki/Talk:Richard_Feynman (accessed on 22 August 2024).
- Preskill, J. Quantum computing 40 years later. In Feynman Lectures on Computation; CRC Press: Boca Raton, FL, USA, 2023; pp. 193–244. [Google Scholar]
- Céleri, L.C.; Huerga, D.; Albarrán-Arriagada, F.; Solano, E.; de Andoin, M.G.; Sanz, M. Digital-analog quantum simulation of fermionic models. Phys. Rev. Appl. 2023, 19, 064086. [Google Scholar]
- Bringewatt, J.; Davoudi, Z. Parallelization techniques for quantum simulation of fermionic systems. Quantum 2023, 7, 975. [Google Scholar]
- Haah, J.; Fidkowski, L.; Hastings, M.B. Nontrivial quantum cellular automata in higher dimensions. Commun. Math. Phys. 2023, 398, 469–540. [Google Scholar]
- Gillman, E.; Carollo, F.; Lesanovsky, I. Using (1 + 1) Dquantum cellular automata for exploring collective effects in large-scale quantum neural networks. Phys. Rev. E 2023, 107, L022102. [Google Scholar]
- Kent, B.; Racz, S.; Shashi, S. Scrambling in quantum cellular automata. Phys. Rev. B 2023, 107, 144306. [Google Scholar]
- Seyedi, S.; Pourghebleh, B. A new design for 4-bit RCA using quantum cellular automata technology. Opt. Quantum Electron. 2023, 55, 11. [Google Scholar]
- Mohamed, N.A.E.S.; El-Sayed, H.; Youssif, A. Mixed Multi-Chaos Quantum Image Encryption Scheme Based on Quantum Cellular Automata (QCA). Fractal Fract. 2023, 7, 734. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, F.; Fang, L.; Zheng, X.; Qiao, X.; Li, Z.; Meng, Q. Modelling of wildland-urban interface fire spread with the heterogeneous cellular automata model. Environ. Model. Softw. 2021, 135, 104895. [Google Scholar]
- Phalak, K.; Li, J.; Ghosh, S. Approximate quantum random access memory architectures. arXiv 2022, arXiv:2210.14804. [Google Scholar]
- de Paula Neto, F.M.; da Silva, A.J.; de Oliveira, W.R.; Ludermir, T.B. Quantum probabilistic associative memory architecture. Neurocomputing 2019, 351, 101–110. [Google Scholar]
- Sousa, R.S.; dos Santos, P.G.; Veras, T.M.; de Oliveira, W.R.; da Silva, A.J. Parametric probabilistic quantum memory. Neurocomputing 2020, 416, 360–369. [Google Scholar]
- Ezhov, A.; Nifanova, A.; Ventura, D. Quantum associative memory with distributed queries. Inf. Sci. 2000, 128, 271–293. [Google Scholar]
- Ventura, D.; Martinez, T. Quantum associative memory. Inf. Sci. 2000, 124, 273–296. [Google Scholar]
- Ventura, D.; Martinez, T. Quantum associative memory with exponential capacity. In Proceedings of the 1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98CH36227), Anchorage, AK, USA, 4–9 May 1998; Volume 1, pp. 509–513. [Google Scholar]
- Reilly, D. Challenges in scaling-up the control interface of a quantum computer. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 31–37. [Google Scholar]
- De Vos, A. Reversible Computing: Fundamentals, Quantum Computing, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Niemann, P.; de Almeida, A.A.; Dueck, G.; Drechsler, R. Template-based mapping of reversible circuits to IBM quantum computers. Microprocess. Microsyst. 2022, 90, 104487. [Google Scholar]
- Fösel, T.; Niu, M.Y.; Marquardt, F.; Li, L. Quantum circuit optimization with deep reinforcement learning. arXiv 2021, arXiv:2103.07585. [Google Scholar]
- Bae, J.H.; Alsing, P.M.; Ahn, D.; Miller, W.A. Quantum circuit optimization using quantum Karnaugh map. Sci. Rep. 2020, 10, 15651. [Google Scholar]
- Nam, Y.; Ross, N.J.; Su, Y.; Childs, A.M.; Maslov, D. Automated optimization of large quantum circuits with continuous parameters. npj Quantum Inf. 2018, 4, 23. [Google Scholar]
- Stonebraker, M.; Frew, J.; Gardels, K.; Meredith, J. The Sequoia 2000 storage benchmark. SIGMOD Rec. 1993, 22, 2–11. [Google Scholar]
- Patel, J.; Yu, J.; Kabra, N.; Tufte, K.; Nag, B.; Burger, J.; Hall, N.; Ramasamy, K.; Lueder, R.; Ellmann, C.; et al. Building a scalable geo-spatial DBMS: Technology, implementation, and evaluation. In Proceedings of the 1997 ACM SIGMOD International Conference on Management of Data, Tucson, AR, USA, 13–15 May 1997; Volume 26, pp. 336–347. [Google Scholar]
- Merticariu, G.; Misev, D.; Baumann, P. Towards a general array database benchmark: Measuring storage access. In Big Data Benchmarking; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 40–67. [Google Scholar]
- Sajid, M.J.; Khan, S.A.R.; Yu, Z. Implications of Industry 5.0 on Environmental Sustainability; IGI Global: Hershey, PA, USA, 2022. [Google Scholar]
- Graph Formats. 2024. Available online: https://gephi.org/users/supported-graph-formats/ (accessed on 22 August 2024).
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153. [Google Scholar]
- Daley, A.J.; Bloch, I.; Kokail, C.; Flannigan, S.; Pearson, N.; Troyer, M.; Zoller, P. Practical quantum advantage in quantum simulation. Nature 2022, 607, 667–676. [Google Scholar]
- Buluta, I.; Nori, F. Quantum simulators. Science 2009, 326, 108–111. [Google Scholar]
- Sheng, Y.B.; Zhou, L. Distributed secure quantum machine learning. Sci. Bull. 2017, 62, 1025–1029. [Google Scholar]
- Peral-García, D.; Cruz-Benito, J.; García-Peñalvo, F.J. Systematic literature review: Quantum machine learning and its applications. Comput. Sci. Rev. 2024, 51, 100619. [Google Scholar]
- Tychola, K.A.; Kalampokas, T.; Papakostas, G.A. Quantum machine learning—An overview. Electronics 2023, 12, 2379. [Google Scholar] [CrossRef]
- Senokosov, A.; Sedykh, A.; Sagingalieva, A.; Kyriacou, B.; Melnikov, A. Quantum machine learning for image classification. Mach. Learn. Sci. Technol. 2024, 5, 015040. [Google Scholar]
- Zeguendry, A.; Jarir, Z.; Quafafou, M. Quantum machine learning: A review and case studies. Entropy 2023, 25, 287. [Google Scholar] [CrossRef]
- Caleffi, M.; Amoretti, M.; Ferrari, D.; Illiano, J.; Manzalini, A.; Cacciapuoti, A.S. Distributed quantum computing: A survey. Comput. Netw. 2024, 2024, 110672. [Google Scholar]
- Häner, T.; Steiger, D.S.; Hoefler, T.; Troyer, M. Distributed quantum computing with QMPI. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MI, USA, 14–19 November 2021; pp. 1–13. [Google Scholar]
- Zhao, Y.; Zhong, H.; Zhang, X.; Zhang, C.; Pan, M. Bridging Quantum Computing and Differential Privacy: A Survey on Quantum Computing Privacy. arXiv 2024, arXiv:2403.09173. [Google Scholar]
- Hirche, C.; Rouzé, C.; França, D.S. Quantum differential privacy: An information theory perspective. IEEE Trans. Inf. Theory 2023, 69, 5771–5787. [Google Scholar]
- Pan, D.; Lin, Z.; Wu, J.; Zhang, H.; Sun, Z.; Ruan, D.; Yin, L.; Long, G.L. Experimental free-space quantum secure direct communication and its security analysis. Photonics Res. 2020, 8, 1522–1531. [Google Scholar]
- Luo, W.; Cao, L.; Shi, Y.; Wan, L.; Zhang, H.; Li, S.; Chen, G.; Li, Y.; Li, S.; Wang, Y.; et al. Recent progress in quantum photonic chips for quantum communication and internet. Light. Sci. Appl. 2023, 12, 175. [Google Scholar]
- Hasan, S.R.; Chowdhury, M.Z.; Saiam, M.; Jang, Y.M. Quantum communication systems: Vision, protocols, applications, and challenges. IEEE Access 2023, 11, 15855–15877. [Google Scholar]
- WMTS. 2024. Available online: https://www.opengeospatial.org/standards/wmts (accessed on 22 August 2024).
- Dong, B.; Wu, K.; Byna, S.; Liu, J.; Zhao, W.; Rusu, F. ArrayUDF: User-Defined Scientific Data Analysis on Arrays. In Proceedings of the 26th International Symposium on High-Performance Parallel and Distributed Computing, Washington, DC, USA, 26–30 June 2017. [Google Scholar]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 2019, 15, 1273–1278. [Google Scholar]
- Oh, S.; Choi, J.; Kim, J. A tutorial on quantum convolutional neural networks (QCNN). In Proceedings of the 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 21–23 October 2020; pp. 236–239. [Google Scholar]
- Wei, S.; Chen, Y.; Zhou, Z.; Long, G. A quantum convolutional neural network on NISQ devices. AAPPS Bull. 2022, 32, 1–11. [Google Scholar]
- Hur, T.; Kim, L.; Park, D.K. Quantum convolutional neural network for classical data classification. Quantum Mach. Intell. 2022, 4, 3. [Google Scholar]
 [12].
[12].
 [12].
[12].
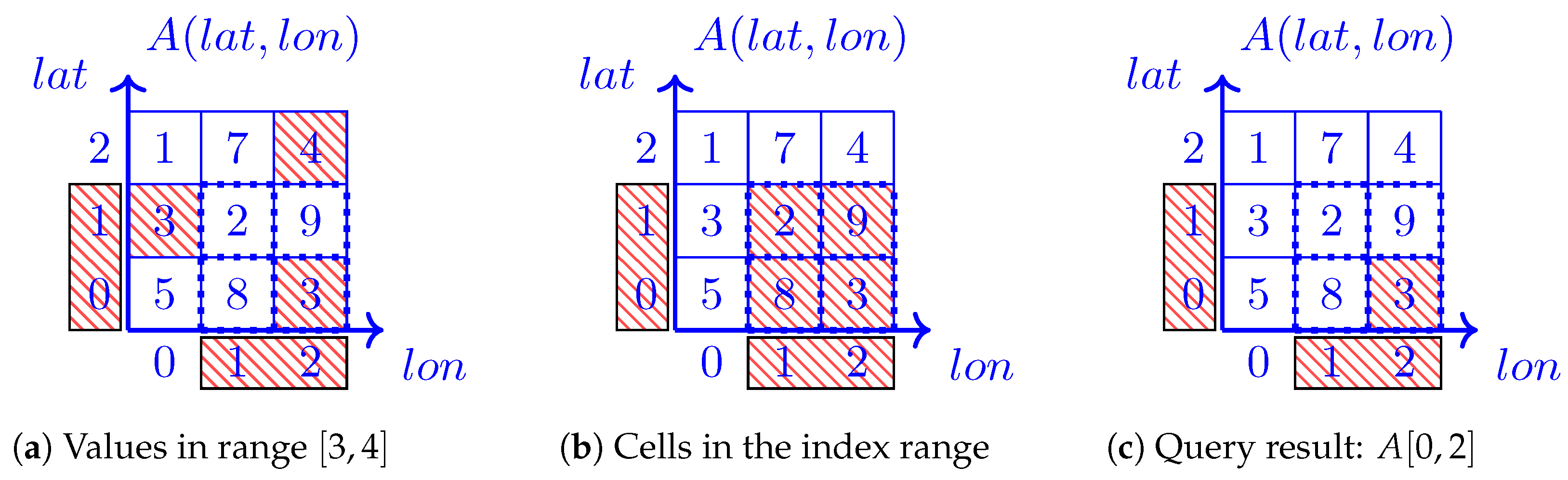
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriges Zalipynis, R.A. Quantum Tensor DBMS and Quantum Gantt Charts: Towards Exponentially Faster Earth Data Engineering. Earth 2024, 5, 491-547. https://doi.org/10.3390/earth5030027
Rodriges Zalipynis RA. Quantum Tensor DBMS and Quantum Gantt Charts: Towards Exponentially Faster Earth Data Engineering. Earth. 2024; 5(3):491-547. https://doi.org/10.3390/earth5030027
Chicago/Turabian StyleRodriges Zalipynis, Ramon Antonio. 2024. "Quantum Tensor DBMS and Quantum Gantt Charts: Towards Exponentially Faster Earth Data Engineering" Earth 5, no. 3: 491-547. https://doi.org/10.3390/earth5030027
APA StyleRodriges Zalipynis, R. A. (2024). Quantum Tensor DBMS and Quantum Gantt Charts: Towards Exponentially Faster Earth Data Engineering. Earth, 5(3), 491-547. https://doi.org/10.3390/earth5030027