Estimating the Statistical Significance of Cross–Correlations between Hydroclimatic Processes in the Presence of Long–Range Dependence

Abstract

Hydroclimatic processes such as precipitation, temperature, wind speed and dew point are usually considered to be independent of each other. In this study, the cross–correlations between key hydrological-cycle processes are examined, initially by conducting statistical tests, then adding the impact of long-range dependence, which is shown to govern all these processes. Subsequently, an innovative stochastic test that can validate the significance of the cross–correlation among these processes is introduced based on Monte-Carlo simulations. The test works as follows: observations obtained from numerous global-scale timeseries were used for application to, and a comparison of, the traditional methods of validation of statistical significance, such as the t-test, after filtering the data based on length and quality, and then by estimating the cross–correlations on an annual-scale. The proposed method has two main benefits: it negates the need of the pre-whitening data series which could disrupt the stochastic properties of hydroclimatic processes, and indicates tighter limits for upper and lower boundaries of statistical significance when analyzing cross–correlations of processes that exhibit long-range dependence, compared to classical statistical tests. The results of this analysis highlight the need to acquire cross–correlations between processes, which may be significant in the case of long-range dependence behavior.

1. Introduction

In recent times, there is an ever-growing need to study processes surrounding our world that are related to the availability of water resources. Many of these resources depend highly on various hydroclimatic conditions and processes that may be cross–correlated (such as temperature and dew point or precipitation and wind speed) [1,2]. Several studies have focused on the relationships between these variables and attempt to simulate them under variate conditions [3,4]. Furthermore, these processes are dominated by high variability at a vast range of scales [5]. Thus, it becomes important to examine possible correlations among hydrological processes such as precipitation, temperature, wind speed and dew point, and the simplest way to evaluate them is to employ the Pearson linear cross–correlation coefficient.

However, hydroclimatic processes may not be independent of each other. In addition, they are shown to exhibit long-range dependence [6,7], which is indicated by fluctuations on a long-term time scale, enhanced patterns and high unpredictability. This justifies the observed variability of these processes, and thus, the uncertainty in estimations, while questioning the use of classical statistical tests that assume independency and serially independent values [8,9].

In this study, the impact of the length of a data series on cross–correlation distributions is first examined using the synthetic series of Gaussian variables, which are then compared to the series with long-term persistence, resembling the variability of the recorded timeseries related to these processes. The reason for this is a need to study the cross–correlations of independently generated numbers to better understand and compare how possibly dependent processes such as hydroclimatic ones perform when under the same statistical analysis. Next, an innovative statistical test is constructed using a stochastic approach, which can determine the upper and lower bounds of statistical significance for cross–correlations of series that exhibit long-range dependence. A key benefit of the proposed method is it allows for generating cross–correlations from inputted timeseries directly, along with an estimate of their statistical significance, without the need of pre-whitening the data series—a process which could disrupt the stochastic properties of hydroclimatic processes.

For illustration, the cross–correlations among key hydrological-cycle processes from numerous global-scale observations are estimated. In turn, an exploratory data analysis including all the examined processes is performed to detect any patterns in their cross–correlations. Finally, using the proposed stochastic test, it is possible to determine which of the calculated cross–correlations can be assumed to be statistically significant.

2. Materials and Methods

We start with an investigation conducted by generating 10,000 series of standardized Gaussian random values (i.e., with a zero mean and a standard deviation of unity), each with a length of 20 values. Then, the zero-lag cross–correlation between each pair of these series is calculated. While the expected value must be zero, since these variables are uncorrelated (and independent), the estimates of cross–correlation values are found to follow a bell-curve distribution [10]. Furthermore, if the number of series is increased to 100,000, this bell-curved distribution becomes even more evident.

However, upon increasing the data length of every series up to 100, for example, more estimated cross–correlation coefficients are close to zero, resulting in a narrower distribution, thus, lowering the variability of the estimation, as seen in Figure 1 (see also results in [11]).

There have been many studies in the literature showing that most hydroclimatic processes are characterized by the so-called Hurst phenomenon, otherwise known as scaling, long-range dependence (LRD) or long-term persistence [6,12]. In this work, we focus on the effect of LRD on cross–correlations between hydroclimatic processes, quantified through the Hurst parameter. In simple terms, this parameter indicates the behavior of a process over a long-time scale. As the Hurst parameter increases and approaches its maximum value of 1, a timeseries of a long-range dependent process exhibits enhanced patterns as well as change, which leads to high uncertainty and unpredictability at large scales. Although these processes may deviate from Gaussianity (even at the annual scale), here, we show results based on the hypothesis that this deviation is small or negligible. By performing a Monte-Carlo analysis and by applying the symmetric moving average (SMA) generation algorithm [13], 1000 timeseries with 20 years of length are generated, and their cross–correlations are estimated for various Hurst parameters (specifically, ranging from 0.5 to 0.95 with a 0.05 step), similarly to the methodology described in [14]. To calculate the Hurst parameters of the timeseries given, there are multiple methods that can be assessed. In this study, the preferred analysis is the classic rescaled-range analysis introduced in [12,15], but there are multiple others that can be selected, such as wavelets [16], or by choosing a maximum likelihood estimator, as described in [17].

A common practice advocated in the literature is to pre-whiten them first before estimating their cross–correlations (e.g., [18]). This process entails a transformation of the two variables using a filter, with the reasoning that it disentangles any autocorrelation between the two variables, while retaining any linear relationships between them. Then, for two mutually independent series, the empirical cross–correlation coefficient follows approximately N(0, 1/sqrt(n)), if at least one of the series is a white-noise process [19]. However, the pre-whitening procedure distorts several stochastic properties and there is no apparent reason to apply it. In our case, the SMA algorithm has been used to generate series in such a way that no pre-whitening is required, and thus, avoiding any added artifacts into the simulation. Thus, to determine the empirical distribution of cross–correlation, an alternative method can be proposed.

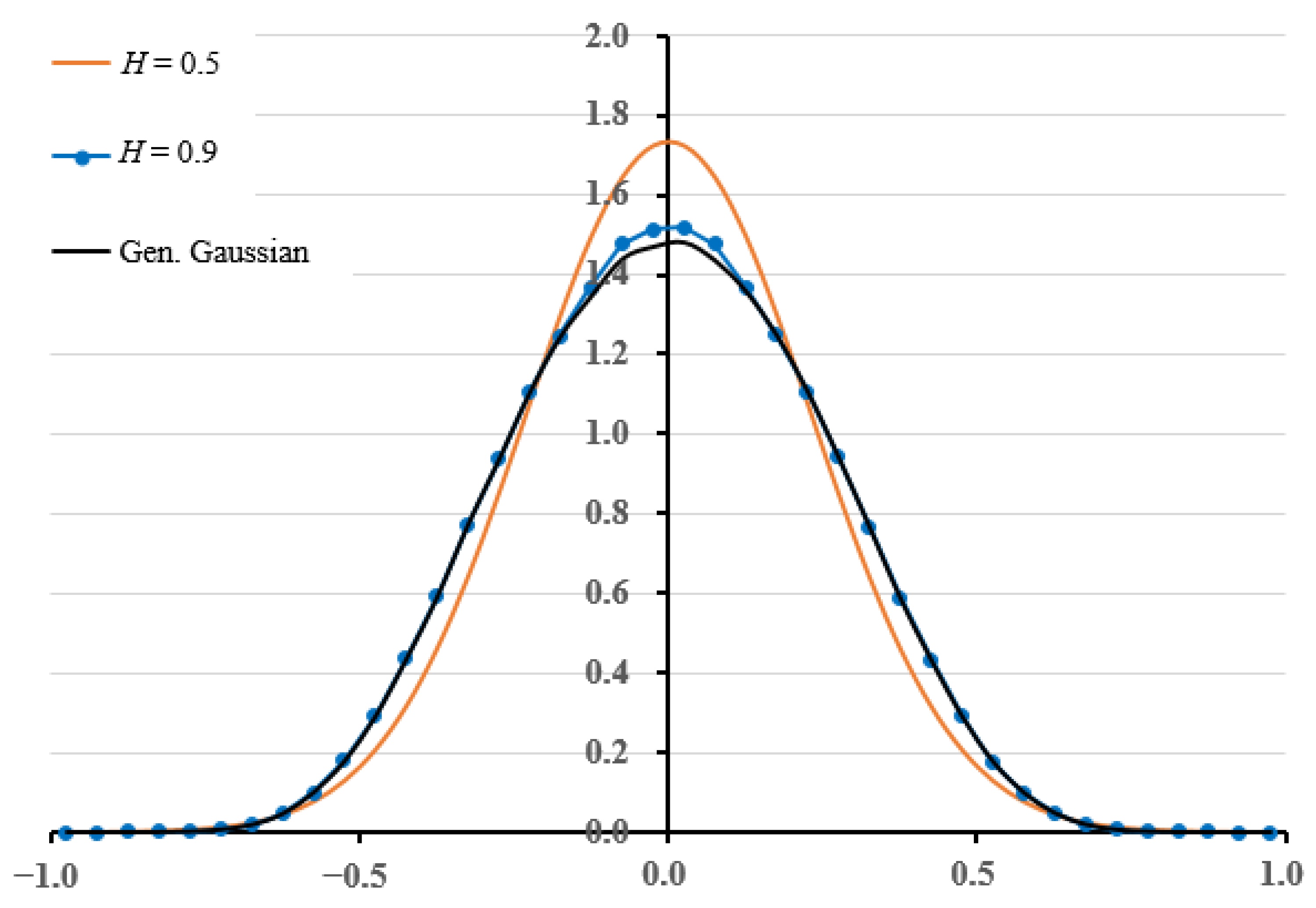
The distribution of the estimator of the cross–correlation between the uncorrelated series is Gaussian, and may be approximately Gaussian when the Hurst parameter is close to 0.5 (i.e., white-noise). Therefore, we can determine the probability that a high cross–correlation value is estimated between uncorrelated samples. Specifically, for series exhibiting LRD (i.e., H > 0.5), the resulting distribution of the estimator of the cross–correlation coefficient is shown to highly deviate from Gaussianity, and becomes flatter than the Gaussian bell, corresponding to a higher kurtosis. Thus, in Figure 2, a comparison is made between the empirical distributions of the cross–correlations estimated from an ensemble of 100,000 normally distributed variables with H = 0.5, and the one estimated from 5,000,000 timeseries with H = 0.9, with each distribution having the same length of 60 years.

Among several candidates, the generalized Gaussian distribution is selected to fit the cross–correlation estimations (Figure 2), which is a parametric family with the following probability density function [20]:

$$f_X\left(x\right)=\frac{\beta }{2\alpha \mathsf{\Gamma }\left(\frac{1}{\beta }\right)}{e}^{-{\left(\frac{\left|x-\mu \right|}{\alpha }\right)}^{\beta }},$$

(1)

where μ denotes location, α denotes scale, Γ denotes the gamma function, and β is a shape parameter. When β = 2, this distribution corresponds to the normal one.

A limitation of the selected distribution for the estimator of the linear cross–correlation is that it cannot accurately represent heavy power-law tails. A more advanced methodology for the estimation of the cross–correlation is described in [21], where an estimator is introduced based on the scale domain rather than the lag domain through the correlation function (as adopted in the current analysis), or the frequency domain through the power-spectrum (see discussion and comparisons in [22]). Nevertheless, it is considered important to perform this analysis using the classical (and most widely applied in the literature) estimator of the linear Pearson cross–correlation to highlight and assess its increased variability in the presence of the long-range dependence behavior.

Besides the Hurst parameter (H), the length (n) of the series is expected to also have a great impact on the cross–correlation estimations. In order to determine the influence of both parameters (i.e., H and n) on the statistical significance of the cross–correlation estimations, multiple synthetic series of normally distributed processes are generated using the SMA algorithm, and by varying both n and H. Specifically, in this test, the series lengths range from 10 to 100 (with a step of 10), and the Hurst parameter ranges from 0.5 to 0.95 (with a 0.05 step). For each combination, 5,000,000 synthetic timeseries are generated, the cross–correlation between them is calculated, and the resulting distributions are compared (for illustration, see Figure 3) to the distribution of cross–correlation estimations generated from a white-noise process (i.e., H = 0.5) with the same length.

From this comparison, the influence of the Hurst parameter on the distributions becomes even more apparent. Initially, a small Hurst parameter (indicating a weak LRD) corresponds to a cross–correlation distribution that is nearly Gaussian, while as the Hurst parameter increases, the distribution of the cross–correlation estimations becomes flatter (i.e., the kurtosis is increased).

Based on the above analysis, it is possible to determine the upper and lower bounds of the statistical significance for any estimated cross–correlation coefficient, using a method similar to the t-test [23], but by also taking into account the LRD. This behavior can be introduced in a statistical significance test through the generalized Gaussian distribution. Specifically, the estimated cross–correlation coefficient between two processes exhibiting long-range dependence is assumed (null hypothesis, H_o)/not assumed (alternative hypothesis, H₁) statistically significant, based on whether it is estimated within/outside of the confidence limits of the generalized Gaussian distribution.

For the determination of the confidence limits, an expression is constructed among the linear cross–correlation coefficient’s quantile c, the length n of the sample, and the Hurst parameter H of the process (see Figure 4 and Figure 5), i.e.,

c(H,q) = a(H,q) n^b(H,q)

a = p₁H² + p₂H + p₃

(2)

b = p₁H² + p₂H + p₃

where H is the Hurst parameter, q is the level of confidence, n is the length of the sample and p₁, p₂, p₃ are coefficients that can be selected from

Table 1. Model parameters a, b, p₁, p₂, p₃ for various confidence limits and Hurst values.

Confidence Interval	70%		80%		95%		99%
H	a	b	a	b	a	b	a	b
0.50	1.281	−0.548	1.526	−0.539	1.829	−0.523	2.276	−0.471
0.55	1.281	−0.547	1.521	−0.537	1.823	−0.522	2.270	−0.469
0.60	1.264	−0.539	1.503	−0.530	1.803	−0.514	2.229	−0.461
0.65	1.244	−0.528	1.479	−0.518	1.770	−0.502	2.184	−0.449
0.70	1.223	−0.512	1.443	−0.501	1.720	−0.484	2.105	−0.429
0.75	1.172	−0.485	1.385	−0.475	1.646	−0.458	1.983	−0.400
0.80	1.116	−0.453	1.317	−0.443	1.551	−0.424	1.847	−0.364
0.85	1.031	−0.410	1.212	−0.399	1.427	−0.380	1.687	−0.321
0.90	1.007	−0.380	1.173	−0.367	1.356	−0.344	1.549	−0.278
0.95	0.933	−0.333	1.080	−0.319	1.244	−0.296	1.404	−0.230
Model Parameters
p1	−1.660	1.119	−2.101	1.148	−2.825	1.204	−4.009	1.273
p2	1.601	−1.138	2.023	−1.169	2.746	−1.234	3.785	−1.301
p3	0.901	−0.259	1.045	−0.242	1.169	−0.208	1.399	−0.139

. It is noted that R² > 0.99 in all expressions. An important remark is that the above expressions correspond to Hurst values between 0.5 and 0.9, while values outside these limits could lead to erroneous extrapolations.

After a thorough analysis of the performance of normal random values and defining the stochastic test, real world timeseries of hydroclimatic processes can be studied. From a global-scale database of the National Oceanic and Atmospheric Association containing more than 15,000 land-based stations [24], the timeseries of temperature, wind speed and dew point are extracted from approximately 7500 stations that are still operational up to 2018 (i.e., access year). Most of these timeseries have a three-hour resolution, whereas some stations in recent years have included 30 min resolution observations. To select high-quality stations, only the ones with twenty or more years of data are included in the analysis. Subsequently, all the extracted timeseries are transformed to the annual resolution, while a year that contains less than 300 days of values is considered null. This choice is made to allow a more realistic comparison and reduce any uncertainty caused by large gaps in some data timeseries [5]. Finally, the zero-lag cross–correlations are estimated for stations containing all three annual timeseries (i.e., temperature, wind speed and dew point). After all filters are applied, the final number of analyzed stations is 2090. Of these 2090 stations, 1479 contain thirty or more years of data, which is ideal for longer-term data analysis. That being said, the coverage of these older stations is mainly limited to Europe and North America, leaving out many newer-built stations in regions such as Africa, Australia and the Southern Pacific Ocean. Therefore, we proceed with the original 2090, as they are more widely spread out throughout the globe. Furthermore, specifically for wind speed, the input stations return both speed and direction. The direction of wind speed was omitted from our analysis to maintain simplicity. To estimate cross–correlations between precipitation and the abovementioned processes, we employ the NOAA’s database containing approximately 100,000 operational land-based stations with daily precipitation measurements [24]. From the latter, we utilize 66,000 daily stations that have more than 20 years of data and aggregate them to an annual resolution timeseries, applying the same quality control as previously described. However, the precipitation timeseries are generally recorded at stations other than the ones at the previous application. Therefore, for the estimation of cross–correlations, we identify pairs of stations in proximity by implementing the following algorithm. A precipitation station and a station measuring temperature, wind speed and dew point are assumed to be within the same region when they are both located within a maximum distance of 0.5 geographical degrees, and the relative elevation difference between them is as small as possible. These two criteria are incorporated as percentages of the maximum possible values, and then combined to be used as an index. Naturally, the lowest possible score of this index indicates the optimum station pairs. For 1032 out of the 2090 stations measuring temperature, wind speed and dew point, there is a corresponding precipitation measurement station at the same location. For the remaining 1058, the above-mentioned algorithm identifies the corresponding precipitation measurement station. For a visualization of the typical distances and elevation differences for these measurement station pairs, see Figure 6.

For the cross–correlations between precipitation and temperature, each process has a different H parameter, and thus, it is necessary to adapt the stochastic test for variables with different H parameters. Using the same model, the simulated series with lengths of 100,000 are generated by selecting the H parameters as 0.6 for precipitation and 0.8 for temperature. The confidence limits of these simulations for different lengths are compared with the ones obtained for the series with equal H parameters, 0.6 and 0.8, respectively (see results in Figure 7). Finally,

Table 2. Model parameters a and b for calculating cross–correlations between precipitation and temperature, for various confidence intervals, assuming H = 0.6 for precipitation and H = 0.8 for temperature.

Confidence Interval	70%		80%		95%		99%
	a	b	a	b	a	b	a	b
Precipitation-Temperature	0.5797	−0.4995	0.899	−0.4919	1.56	−0.4671	1.902	−0.4374

contains the a and b parameters corresponding to Equation (2), as calculated from the analysis, for various confidence intervals.

3. Applications

3.1. Applications to Global-Scale Temperature, Wind Speed and Dew Point

For most of the locations, a strong (i.e., above 0.7) positive cross–correlation is found between the annual mean temperature and dew point (e.g., see a sample of twenty stations located around Norway in

Table 3. A list of stations selected for an example of cross–correlations between hydroclimatic processes and their locations.

Station	Latitude	Longitude	Approximate Location
1	77.00°	15.50°	Svalbard
2	78.25°	15.47°	Adventfjorden, Svalbard
3	69.68°	18.92°	Tromsø, Norway
4	70.25°	19.50°	Karlsøy Municipality, Norway
5	69.02°	23.07°	Kautokeino, Norway
6	69.98°	23.37°	Alta, Norway
7	70.07°	24.98°	Lakselv, Norway
8	71.02°	25.98°	Valan, Norway
9	71.03°	27.83°	Gamvik Municipality, Norway
10	71.10°	28.22°	Gamvik Municipality, Norway
11	70.87°	29.03°	Berlevåg, Norway
12	70.07°	29.85°	Vadsø Municipality, Norway
13	65.20°	11.00°	Sklinna, Norway
14	67.52°	12.10°	Røst, Norway
15	65.47°	12.22°	Toft, Norway
16	66.77°	12.48°	Myken, Norway
17	65.97°	12.47°	Alstahaug Municipality, Norway
18	66.37°	12.62°	Lurøy Municipality, Norway
19	65.78°	13.22°	Kjærstad, Norway
20	66.37°	14.30°	Rana Municipality, Norway

and Figure 8). However, there are exceptions around the globe, with zero or even negative cross–correlations; studying these on a case-by-case basis may yield important results. For example, a previous analysis of similar variables in Australia yielded strong positive correlations between air dry-bulb temperature and global solar irradiation, while at the same time, there was a strong negative correlation between temperature and hourly variations of relative humidity [1]. In regard to the available length of timeseries and any gaps in the data, there seems to be no connection between length and the resulting cross–correlation, provided there are at least twenty years of data with no gaps. A sanity check of stations that did not pass the originally set data filters yields cross–correlation results similar to those of the normal random values described earlier, which likely means that they were correctly not included in the analysis.

Moreover, comparisons between other processes in this study are more inconsistent on a global-scale, and fluctuate between medium (i.e., less than 0.6) positive and negative correlation coefficient values. Additionally, it is noted that both high and low cross–correlation coefficient values seem to form spatial clusters (Figure 9, Figure 10, Figure 11 and Figure 12), which can be further investigated in future studies based on spatial-stochastic analysis [25]. When the humidity in a location remains constant, then the dew point should also be constant, despite changes in temperature [6,26]. This is considered to be the main cause for the zero or negative values of the cross–correlation coefficient clusters between temperature and dew point. Specifically, a high positive cross–correlation value between temperature and dew point is more likely to occur in locations close to the seafront, where the humidity is expected to vary more. Conversely, in arid areas, or in the center of large continents where the absolute humidity varies less, the correlation is often closer to zero.

3.2. Application to Global-Scale Precipitation

The results show that the global cross–correlations are highly inconsistent, with averages close to zero for cross–correlations between precipitation, temperature and wind speed, and approximately 0.2 between precipitation and dew point. Significant strong positive or negative correlations have been found in various locations, and they also appear to form clusters, but no prevailing global pattern is observed. Figure 12 shows an example of a global map of cross–correlations between precipitation and temperature, based on the location of the station measuring temperature. Nevertheless, in the following section, we proceed to estimate the statistical significance of the calculated cross–correlations using the proposed test.

3.3. Application of the Statistical Tests

After analyzing the timeseries of the hydrological-cycle processes and calculating their cross–correlations, it is possible to determine which of these can be considered statistically significant for a given confidence level by employing the proposed test.

An examination of the cross–correlations between annual-scale wind-speed and temperature yields statistically significant values for a number of stations. Two tests were used and compared to determine this significance. The first is the stochastic test introduced in this study. Here, the Hurst parameter is set to 0.8 for all processes based on the suggestion and analysis by Dimitriadis et al. [7]. Additionally, the second test assumes that the timeseries are independent, normally distributed, and with zero autocorrelation, which is similar to the widely used t-test described in [23].

As previously highlighted, only the coefficients identified from the stochastic test can be considered significant under LRD, whereas the rest are indicative of the enhanced variability of the process. For a detailed comparison of all methods and records, see

Table 4. A comparison between statistical significance methods, displaying the number of stations with a significant cross–correlation and their percentage out of the total number of stations reviewed in this study.

	Classic Statistical Test		Stochastic Statistical Test
Cross–Correlations	No. of Stations	% of All Stations	No. of Stations	% of All Stations
Temperature-Wind Speed	683	37.57%	526	28.93%
Temperature-Dew Point	1449	79.70%	1362	74.92%
Precipitation-Temperature	295	24.83%	278	23.40%

.

4. Discussion and Conclusions

From a global-scale analysis of cross–correlations of hydroclimatic processes including precipitation, temperature, wind speed and dew point, the only consistent emerging pattern is the strong positive correlation estimated between temperature and dew point. Generally, a moderately positive is observed around arid areas, and a strong positive cross–correlation near the seafront. However, there are locations where this cross–correlation is zero or even negative, but these occurrences could be related to microclimates or large variability that increase the uncertainty of the estimations. Case-by-case studies are required wherever statistically significant outliers are noted, and then the analysis of similar variables could help explain the causes of a statistically significant cross–correlation occurring. However, when conducting research on these cases, care must be taken to avoid regional or seasonal biases.

Inaccuracies in measurements from the various meteorological stations are expected, but due to the large amount of data and the applied high-quality filters, they are considered to have a small impact. The availability of data has potential for growth, especially as for stations measuring temperature, wind speed and dew point, there are currently only a few records of length greater than 30 years and without significant gaps, which is a relatively lower quality than desired, especially for processes such as these that exhibit long-range dependence.

Comparisons between the other processes show mild cross–correlations, with the average global mean estimated close to zero. This does not mean that the processes are uncorrelated, but only that there is no evidence of a global pattern. On the contrary, significant cross–correlations between any pair of hydroclimatic processes may occur, but the results may be regional, and require further research to assess their statistical significance and spatial dependence. Specifically for wind speed, an important factor that could be expanded upon is the change in direction; this was not included in this study for simplicity but could be important. For example, changes in wind direction could be linked to extreme weather events, indicated by abrupt changes in precipitation or temperature. Another factor that could be expanded upon is the timescale; the available timeseries for temperature, wind speed and dew point have resolutions quite different from precipitation, at approximately 30 min to three hours for some stations. This study focuses on identifying long-term relationships, but there is merit in analyzing hydroclimatic processes on clusters of shorter timescales to study extreme events such as storms. Of course, this would probably require an in-depth study on a location-by-location basis.

Since these processes are not serially independent, standard tests such as the t-test cannot be correctly used. Instead, a stochastic approach using the Monte-Carlo analysis, such as the one introduced in this study, is considered more robust for handling hydroclimatic timeseries. This method can also estimate the statistical significance of a correlation between processes, even if the available timeseries are relatively short in length (however, no less than 20 years). Furthermore, this stochastic test can derive conclusions without requiring the pre-whitening of the timeseries, a procedure which requires careful consideration in order to be applied correctly, and can exacerbate statistical flaws and cause variance inflation. Through the proposed stochastic test, it is evident that a high cross–correlation has a low probability of being outside the confidence limits, especially for large lengths of samples. Thus, any prominent recurrences resulting from a local analysis can be considered statistically significant if the resulting cross–correlations are higher than the values indicated by the stochastic test for a selected confidence interval.

Finally, this study indicates that extreme caution must be exercised when attempting to derive robust conclusions from small samples of processes that are known to exhibit long-range dependence, such as the hydroclimatic ones. Ignoring the enhanced natural variability of hydroclimatic processes and conducting classical statistical tests that disregard long-range dependence may lead to flawed results.