Transformation of Water Wave Spectra into Time Series of Surface Elevation
Abstract
:1. Introduction
2. Fourier Analysis Background
- Axiom 1:
- x is a real-valued function if and only if the Fourier transform of x is Hermitian;
- Axiom 2:
- x is a Hermitian function if and only if the Fourier transform of x is real-valued.
3. Transformation of the Spectrum
Oleinik, P.H.; Tavares, G.P.; Machado, B.N.; Isoldi, L.A. Transformation of Water Wave Spectra into Time Series of Surface Elevation: base implementation. Earth 2021, 1, 1–9. Available online: https://gist.github.com/PhelypeOleinik/39803f2385a18d0e86dc3ff8fe02af7b (accessed on 18 September 2021).
4. Verification of the Method
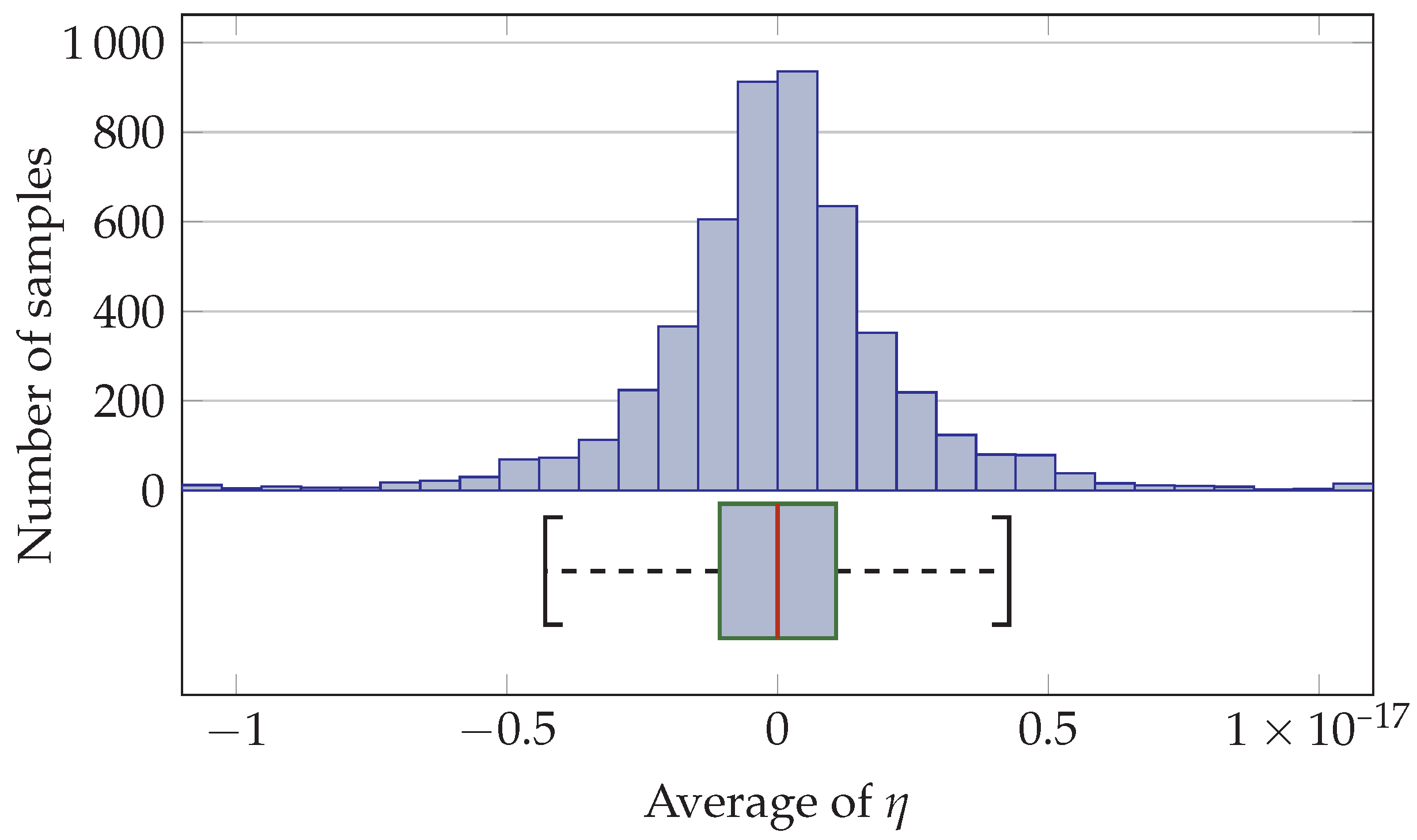
4.1. Verification of Average Values
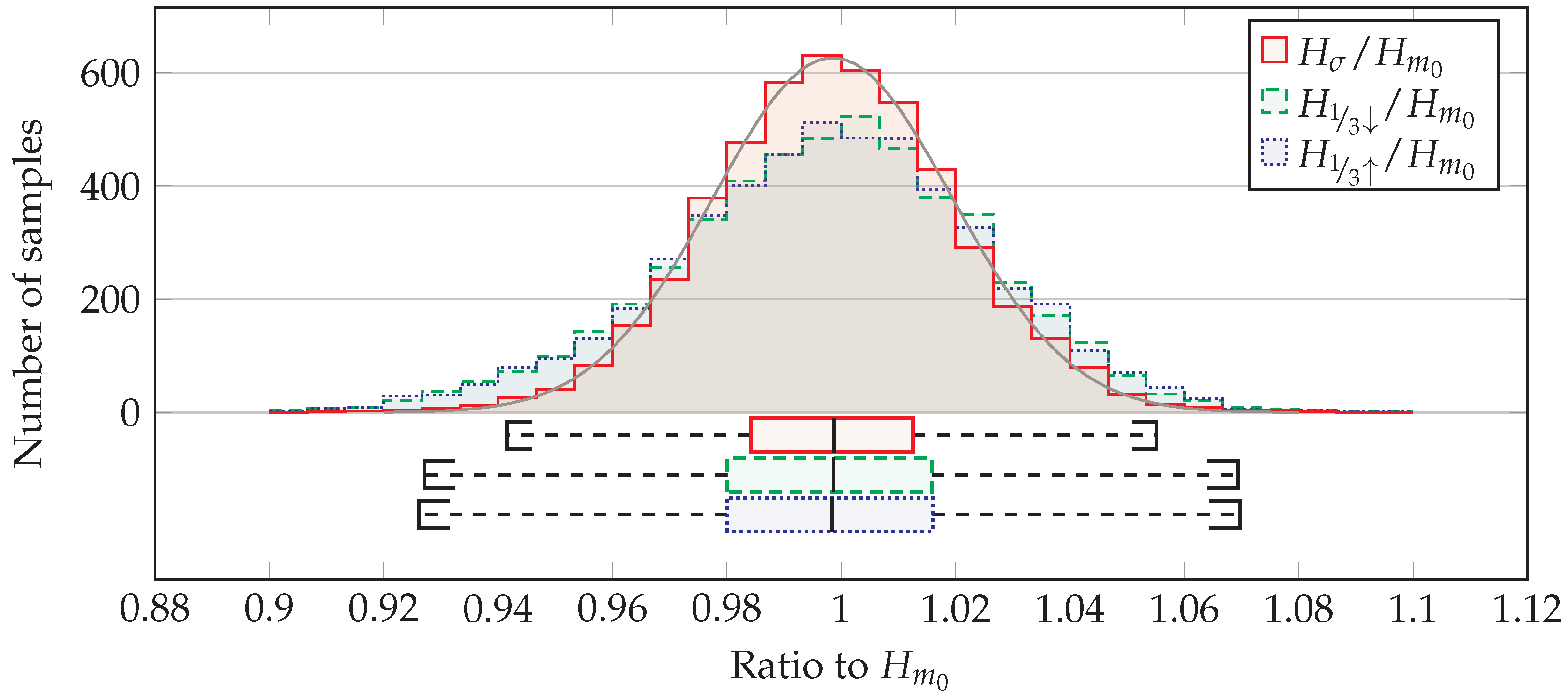
4.2. Reversing the Process to Obtain the Spectrum from
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goda, Y. Random Seas and Design of Maritime Structures, 2nd ed.; Advanced Series on Ocean Engineering; World Scientific: Singapore, 2000; Volume 15. [Google Scholar]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters, 1st ed.; Cambridge University Press: Cambridge, UK, 2007; p. 387. [Google Scholar]
- Boussinesq, J.V. Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 1872, 17, 55–108. [Google Scholar]
- Golden, K.M.; Bennetts, L.G.; Cherkaev, E.; Eisenman, I.; Feltham, D.; Horvat, C.; Hunke, E.; Jones, C.; Perovich, D.K.; Ponte-Castaneda, P.; et al. Modeling Sea Ice. Not. Am. Math. Soc. 2020, 67, 1. [Google Scholar] [CrossRef]
- Voermans, J.J.; Rabault, J.; Filchuk, K.; Ryzhov, I.; Heil, P.; Marchenko, A.; Collins, C.O., III; Dabboor, M.; Sutherland, G.; Babanin, A.V. Experimental evidence for a universal threshold characterizing wave-induced sea ice break-up. Cryosphere 2020, 14, 4265–4278. [Google Scholar] [CrossRef]
- Chen, W.; Dolguntseva, I.; Savin, A.; Zhang, Y.; Li, W.; Svensson, O.; Leijon, M. Numerical modelling of a point-absorbing wave energy converter in irregular and extreme waves. Appl. Ocean. Res. 2017, 63, 90–105. [Google Scholar] [CrossRef]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M. Survivability of wave energy converters using CFD. Renew. Energy 2017, 109, 235–247. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.R.; Ye, H.X.; Wan, D.C. URANS simulations of ship motion responses in long-crest irregular waves. J. Hydrodyn. 2014, 26, 436–446. [Google Scholar] [CrossRef]
- Ferguson, T.M.; Fleming, A.; Penesis, I.; Macfarlane, G. Improving OWC performance prediction using polychromatic waves. Energy 2015, 93, 1943–1952. [Google Scholar] [CrossRef]
- Ferguson, T.M.; Penesis, I.; Macfarlane, G.; Fleming, A. A PIV investigation of OWC operation in regular, polychromatic and irregular waves. Renew. Energy 2017, 103, 143–155. [Google Scholar] [CrossRef]
- Horvat, C.; Tziperman, E. A prognostic model of the sea-ice floe size and thickness distribution. Cryosphere 2015, 9, 2119–2134. [Google Scholar] [CrossRef] [Green Version]
- Didenkulova, E.; Slunyaev, A.; Pelinovsky, E. Numerical simulation of random bimodal wave systems in the KdV framework. Eur. J. Mech. B/Fluids 2019, 78, 21–31. [Google Scholar] [CrossRef]
- Merigaud, A.; Ringwood, J.V. Free-Surface Time-Series Generation for Wave Energy Applications. IEEE J. Ocean. Eng. 2018, 43, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Benoit, M.; Marcos, F.; Becq, F. Development of a Third Generation Shallow-Water Wave Model with unstructured spatial meshing. In Proceedings of the 25th International Conference on Coastal Engineering: Book of Abstracts, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: New York, NY, USA, 1996; pp. 465–478. [Google Scholar]
- Awk, T. Tomawac User Manual Version 7.2. The Telemac-Mascaret Consortium. 2017. Available online: http://opentelemac.org (accessed on 18 September 2021).
- Machado, B.N.; Oleinik, P.H.; Kirinus, E.d.P.; dos Santos, E.D.; Rocha, L.A.O.; Gomes, M.d.N.; Paixão Conde, J.M.; Isoldi, L.A. WaveMIMO Methodology: Numerical Wave Generation of a Realistic Sea State. J. Appl. Comput. Mech. 2021, 7, 2129–2148. [Google Scholar] [CrossRef]
- Tavares, G.P.; Maciel, R.P.; dos Santos, E.D.; Gomes, M.N.; Rocha, L.A.O.; Machado, B.N.; Oleinik, P.H.; Isoldi, L.A. Estudo Numérico Comparativo da Potência Disponível Entre Ondas Regulares e Irregulares: Estudo de Caso de um Dispositivo de Coluna de Água Oscilante na Costa de Rio Grande–RS. Int. J. Dev. Res. 2021, 11, 23001. [Google Scholar] [CrossRef]
- Gentleman, W.M.; Sande, G. Fast Fourier Transforms—For Fun and Profit. In Proceedings of the Fall Joint Computer Conference on XX—AFIPS ’66, San Francisco, CA, USA, 7–10 November 1966; ACM Press: New York, NY, USA, 1966; p. 563. [Google Scholar] [CrossRef]
- Cavaleri, L.; Alves, J.H.; Ardhuin, F.; Babanin, A.; Banner, M.; Belibassakis, K.; Benoit, M.; Donelan, M.; Groeneweg, J.; Herbers, T.; et al. Wave modelling—The state of the art. Prog. Oceanogr. 2007, 75, 603–674. [Google Scholar] [CrossRef] [Green Version]
- Oleinik, P.H.; Kirinus, E.d.P.; Cristiano, F.; Marques, W.C.; Costi, J. Energetic Potential Assessment of Wind-Driven Waves on the South-Southeastern Brazilian Shelf. J. Mar. Sci. Eng. 2019, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Marsaglia, G. Xorshift RNGs. J. Stat. Softw. 2003, 8. [Google Scholar] [CrossRef]
- Knop, R.E. Remark on algorithm 334 [G5]: Normal random deviates. Commun. ACM 1969, 12, 281. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A Note on the Generation of Random Normal Deviates. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Mackay, E. Resource Assessment for Wave Energy. In Comprehensive Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2012; Volume 8, pp. 11–77. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oleinik, P.H.; Tavares, G.P.; Machado, B.N.; Isoldi, L.A. Transformation of Water Wave Spectra into Time Series of Surface Elevation. Earth 2021, 2, 997-1005. https://doi.org/10.3390/earth2040059
Oleinik PH, Tavares GP, Machado BN, Isoldi LA. Transformation of Water Wave Spectra into Time Series of Surface Elevation. Earth. 2021; 2(4):997-1005. https://doi.org/10.3390/earth2040059
Chicago/Turabian StyleOleinik, Phelype Haron, Gabriel Pereira Tavares, Bianca Neves Machado, and Liércio André Isoldi. 2021. "Transformation of Water Wave Spectra into Time Series of Surface Elevation" Earth 2, no. 4: 997-1005. https://doi.org/10.3390/earth2040059
APA StyleOleinik, P. H., Tavares, G. P., Machado, B. N., & Isoldi, L. A. (2021). Transformation of Water Wave Spectra into Time Series of Surface Elevation. Earth, 2(4), 997-1005. https://doi.org/10.3390/earth2040059







