Electro-Thermal Modeling and Thermal Analysis of High-Inertia Synchronous Condenser Converters
Abstract
1. Introduction
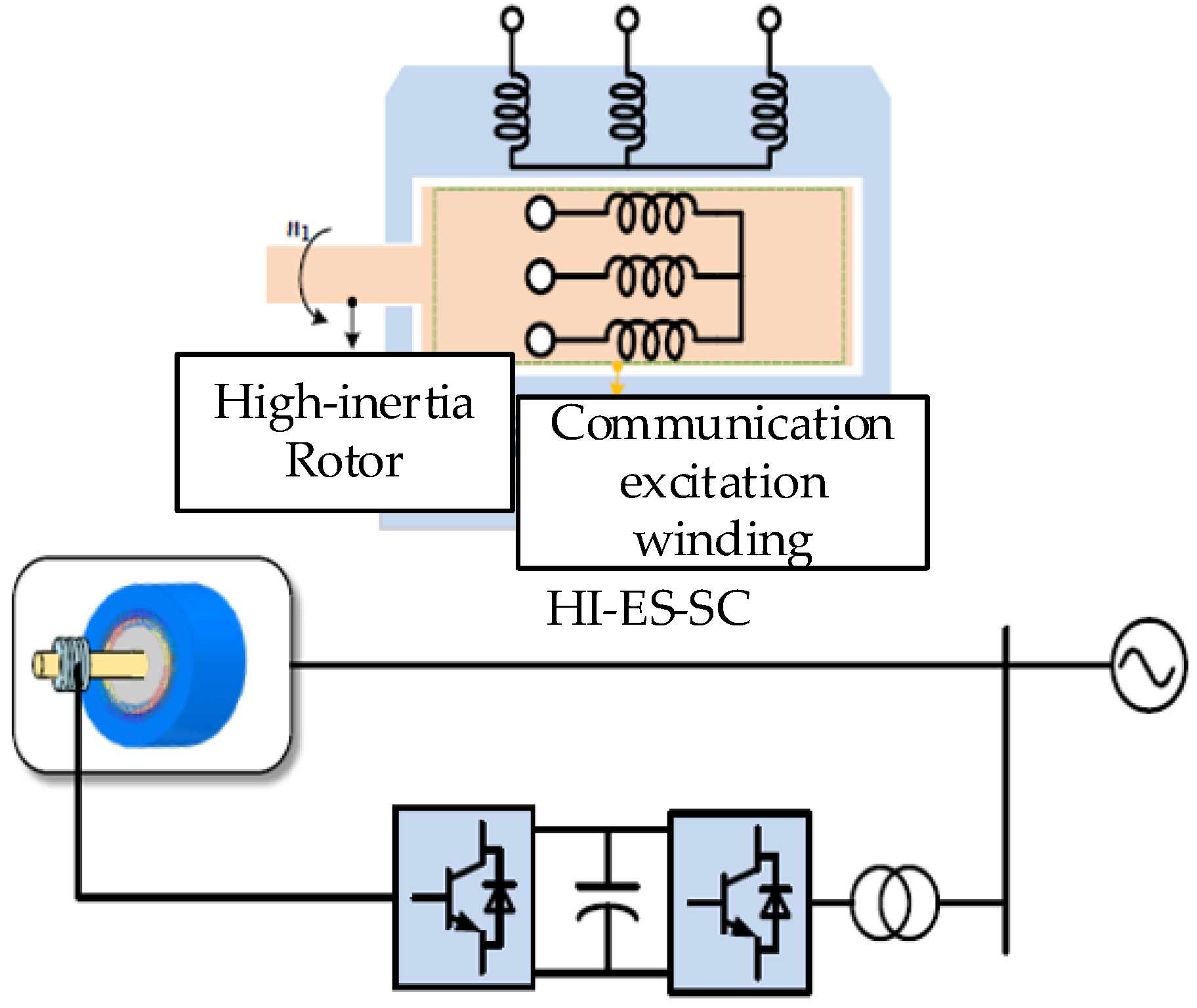
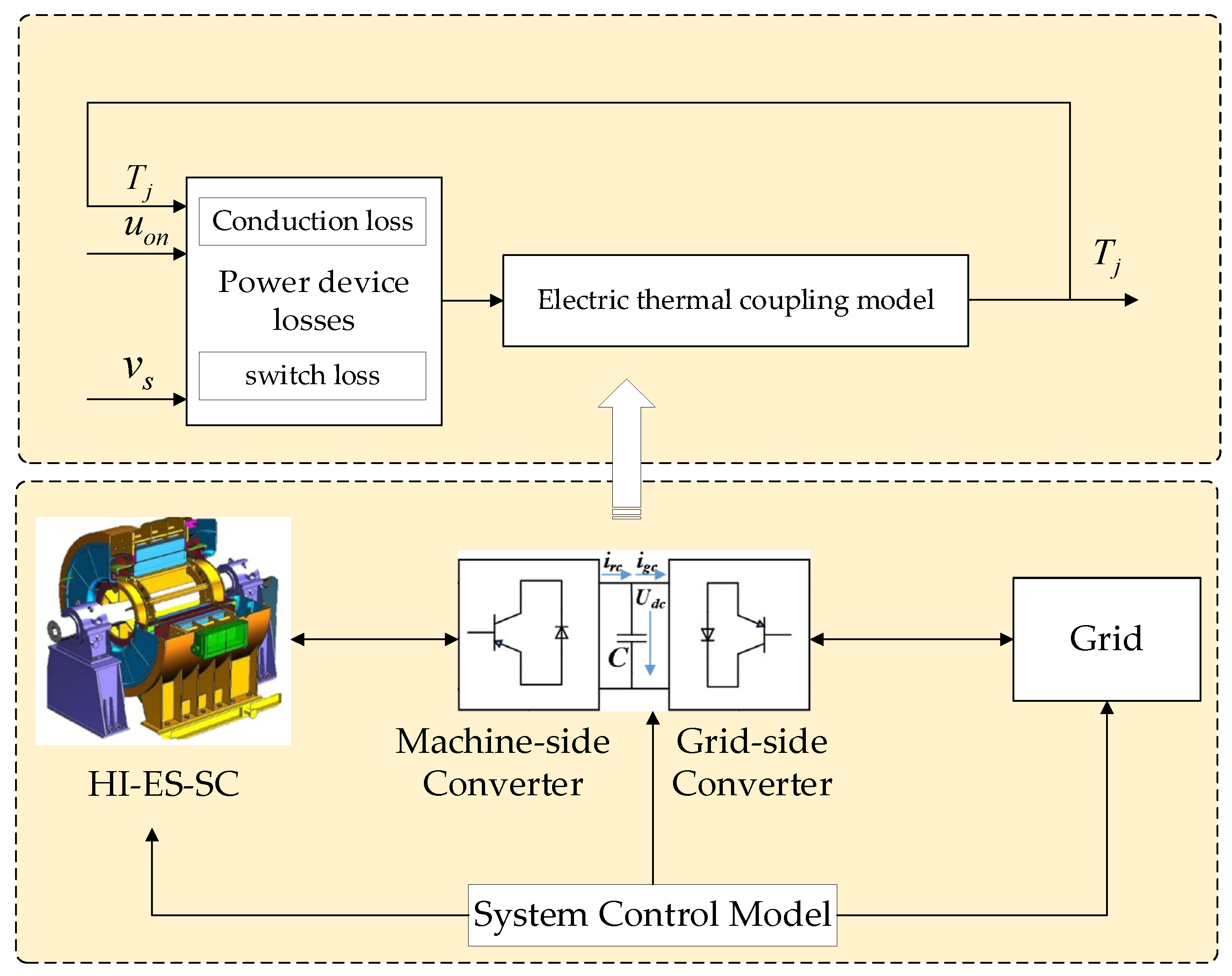
2. Operating Characteristics of HI-ES-SC
3. Electro-Thermal Coupling Modeling of the HI-ES-SC Converter
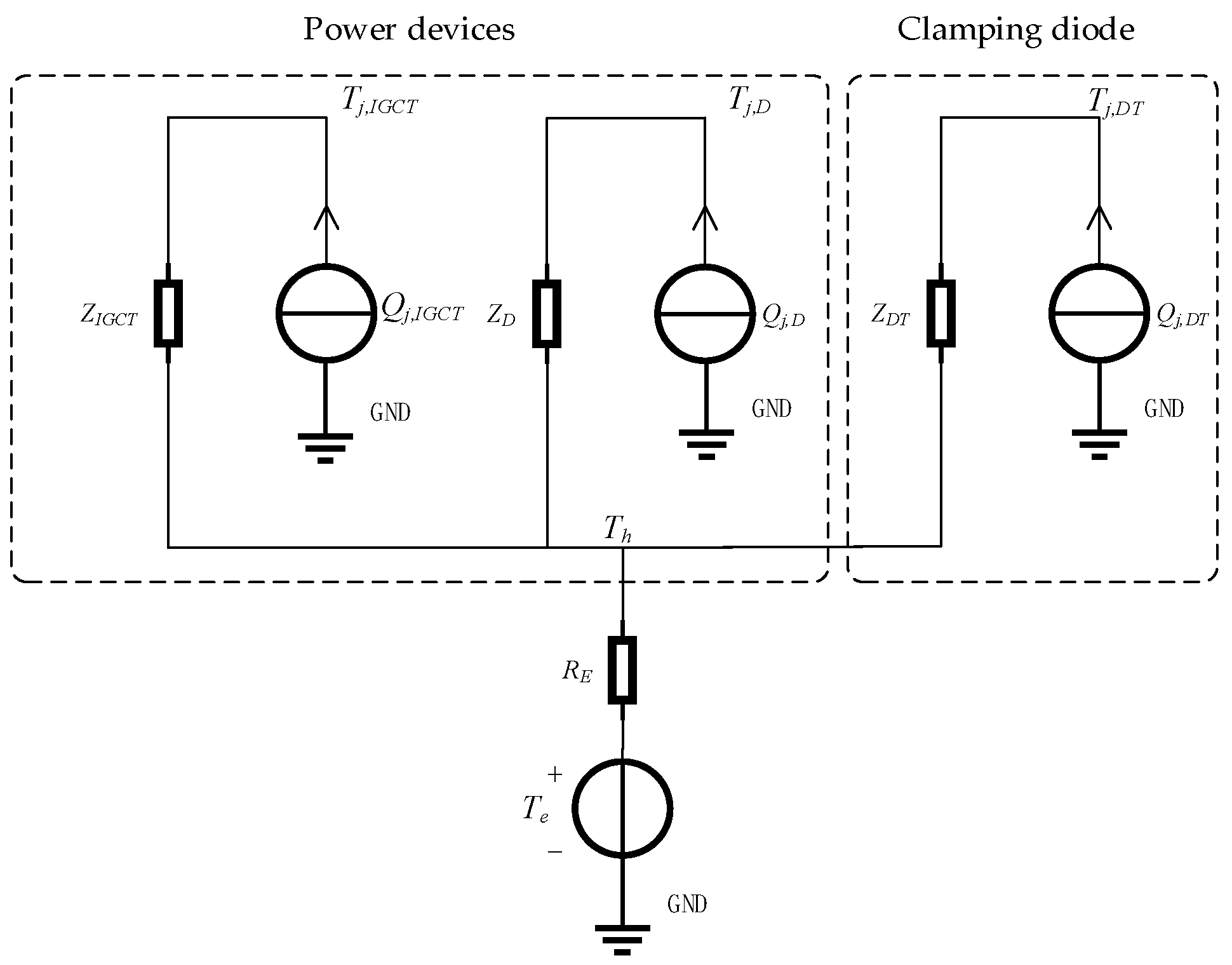
3.1. Calculation Model of Converter Junction Temperature
3.2. Calculation Method of Converter Thermal Network Parameters
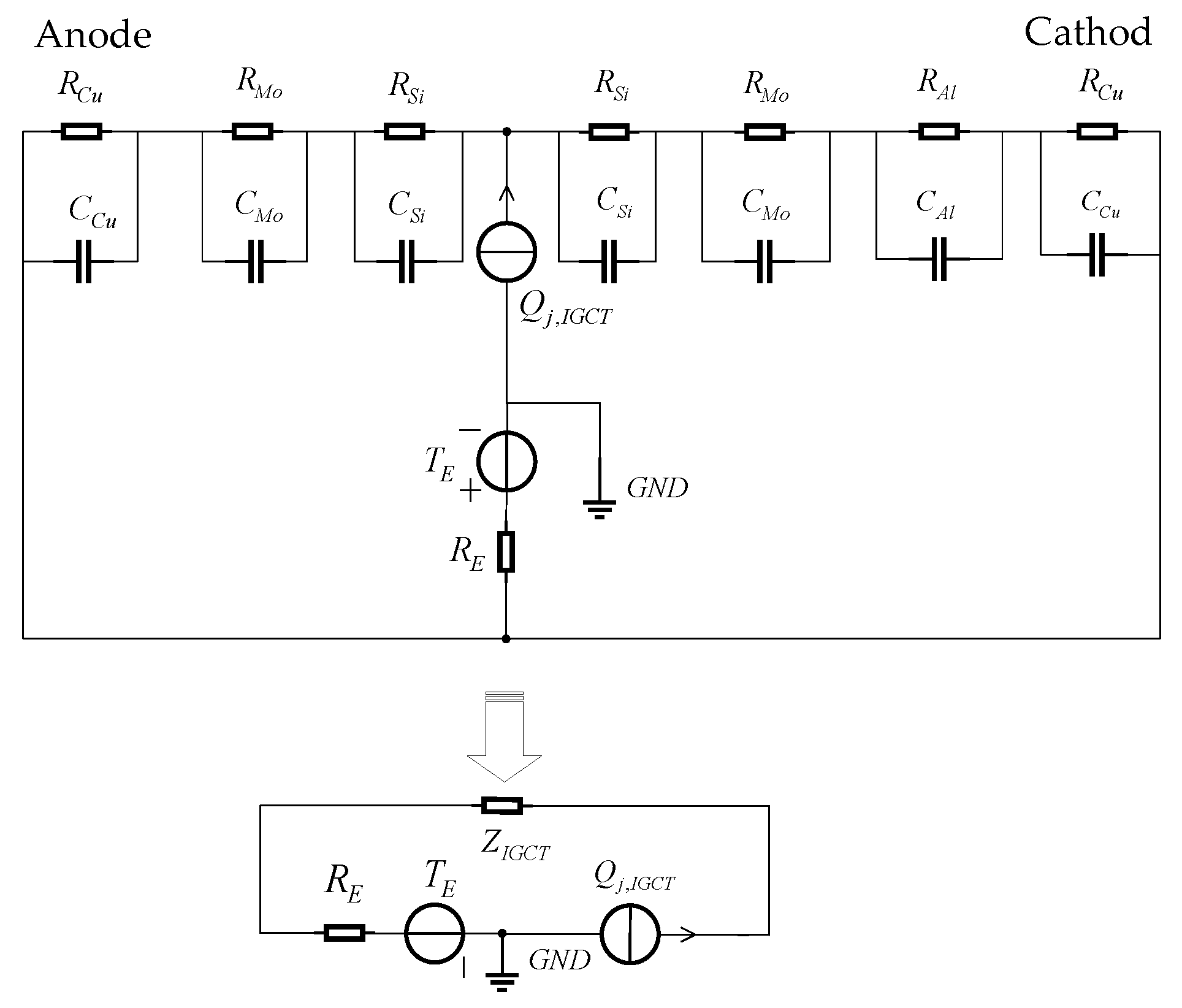
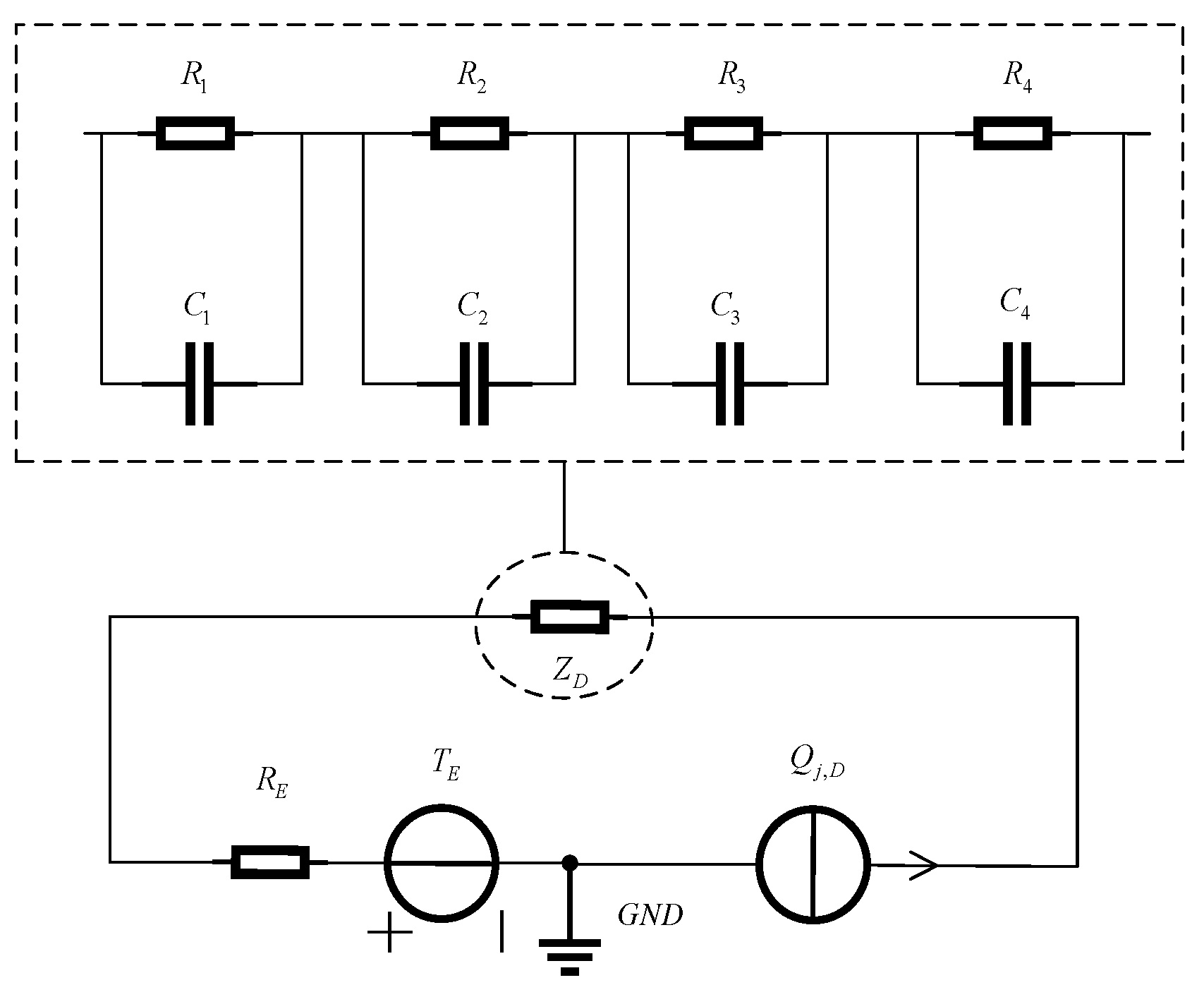
3.2.1. Heat Parameters
3.2.2. Thermal Capacitance Parameters
3.2.3. Thermal Resistance Parameters
3.3. Real-Time Calculation Method of Junction Temperature of Converter Electro-Thermal Coupling Model
4. Simulation of Electro-Thermal Coupling Model and Temperature Rise in HI-ES-SC
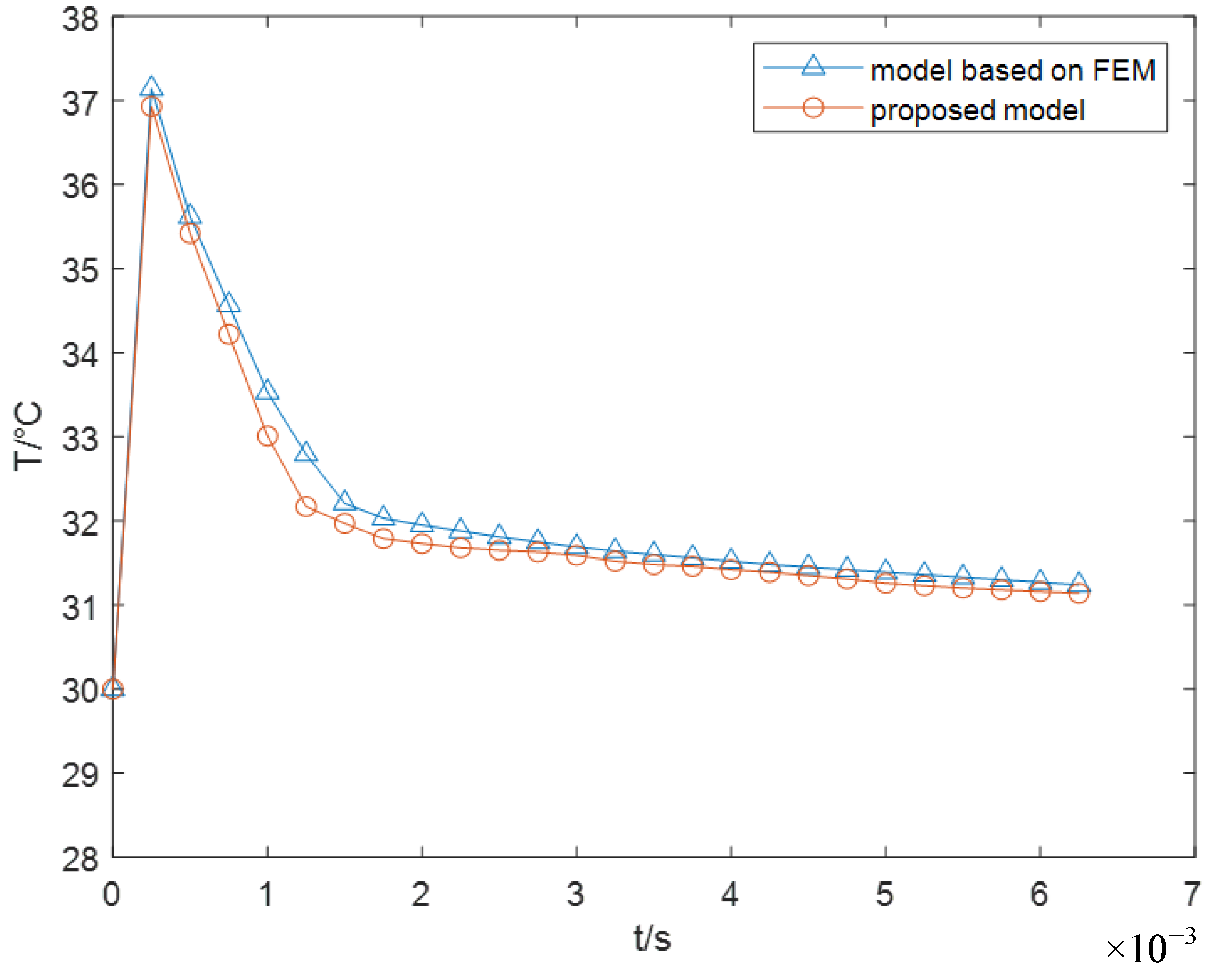
4.1. Validation of the Electrical-Thermal Coupling Model of the Converter
4.2. Model Validity Verifications of Junction Temperature
4.2.1. Single Switch Test
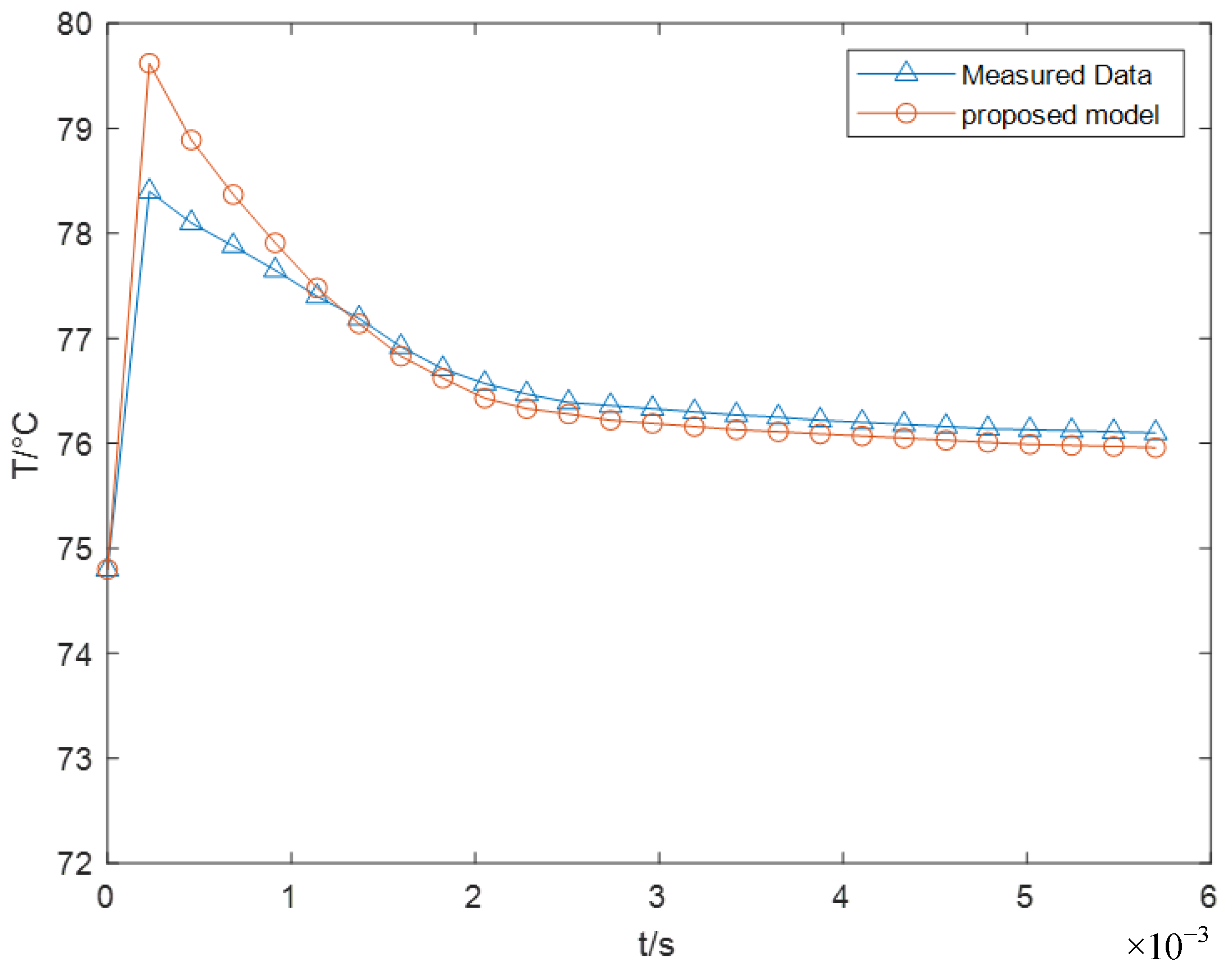
4.2.2. 3-H Junction Temperature Test
4.3. Analysis of Converter Loss and Junction Temperature
5. Conclusions
- The proposed model demonstrates low sensitivity to parameter variations and achieves high simulation accuracy across multiple time scales. Although the thermal resistance and thermal capacitance parameters exhibit errors in the range of approximately 2.8% to 9.6%, experimental results indicate a simulation deviation of about 1.6% in the single switching test. Under a prolonged 3 h test at rotor currents of 3.5 kA and 4 kA, the simulation deviations are approximately 0.5% and 3.3%, respectively. The model performs consistently well across different studies and parameter sets, demonstrating its strong potential to serve as a theoretical basis for device parameter selection in practical converter design.
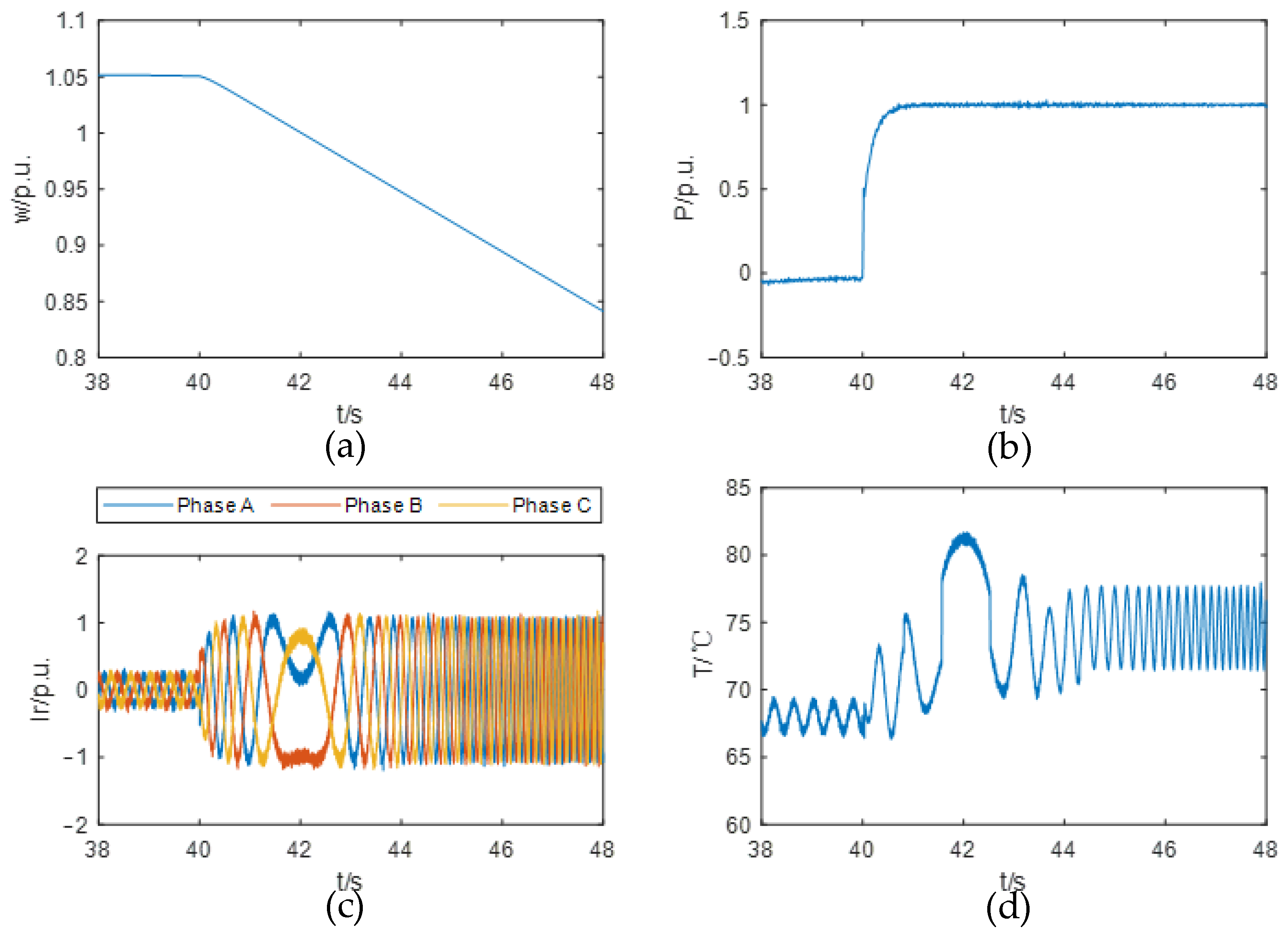
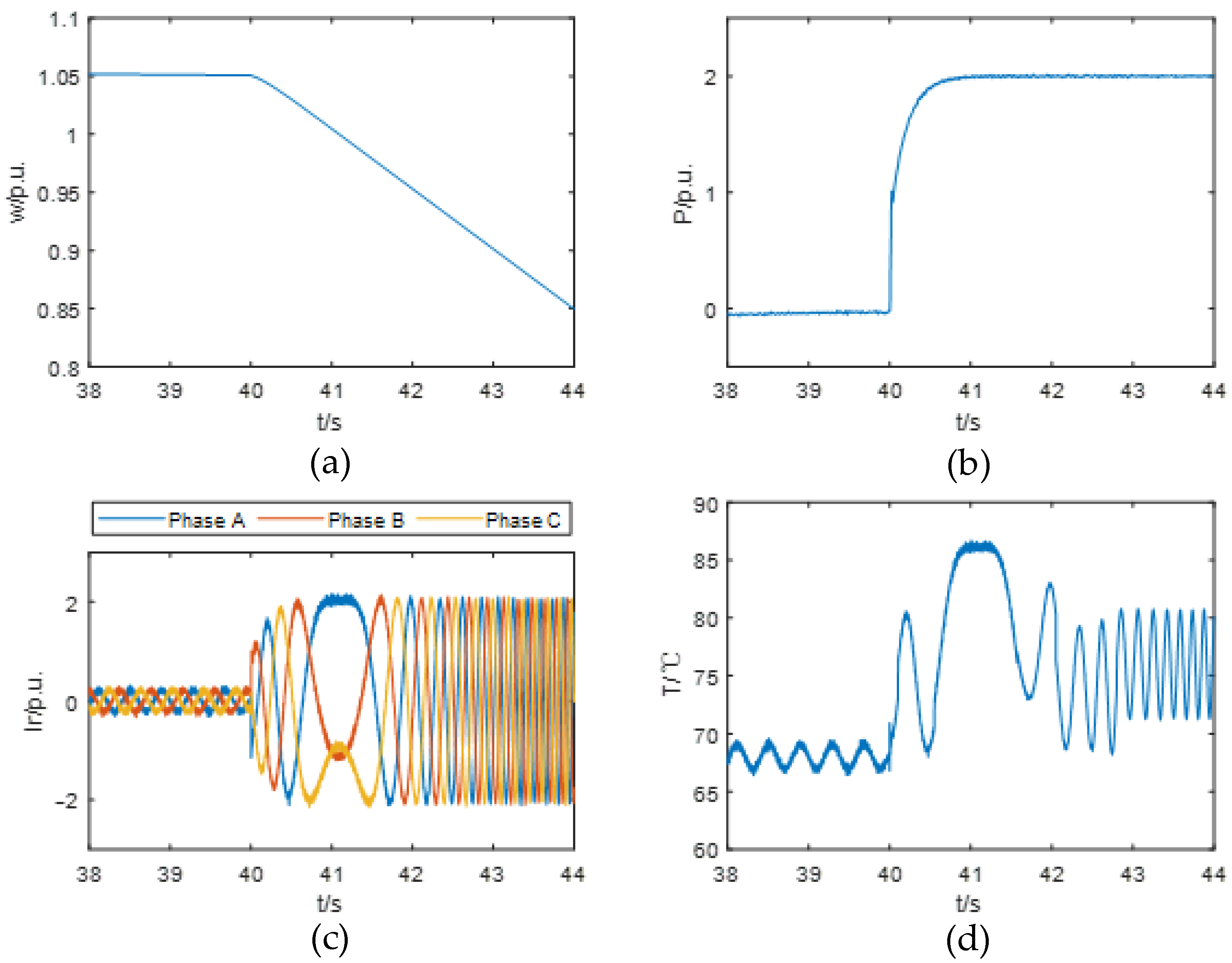
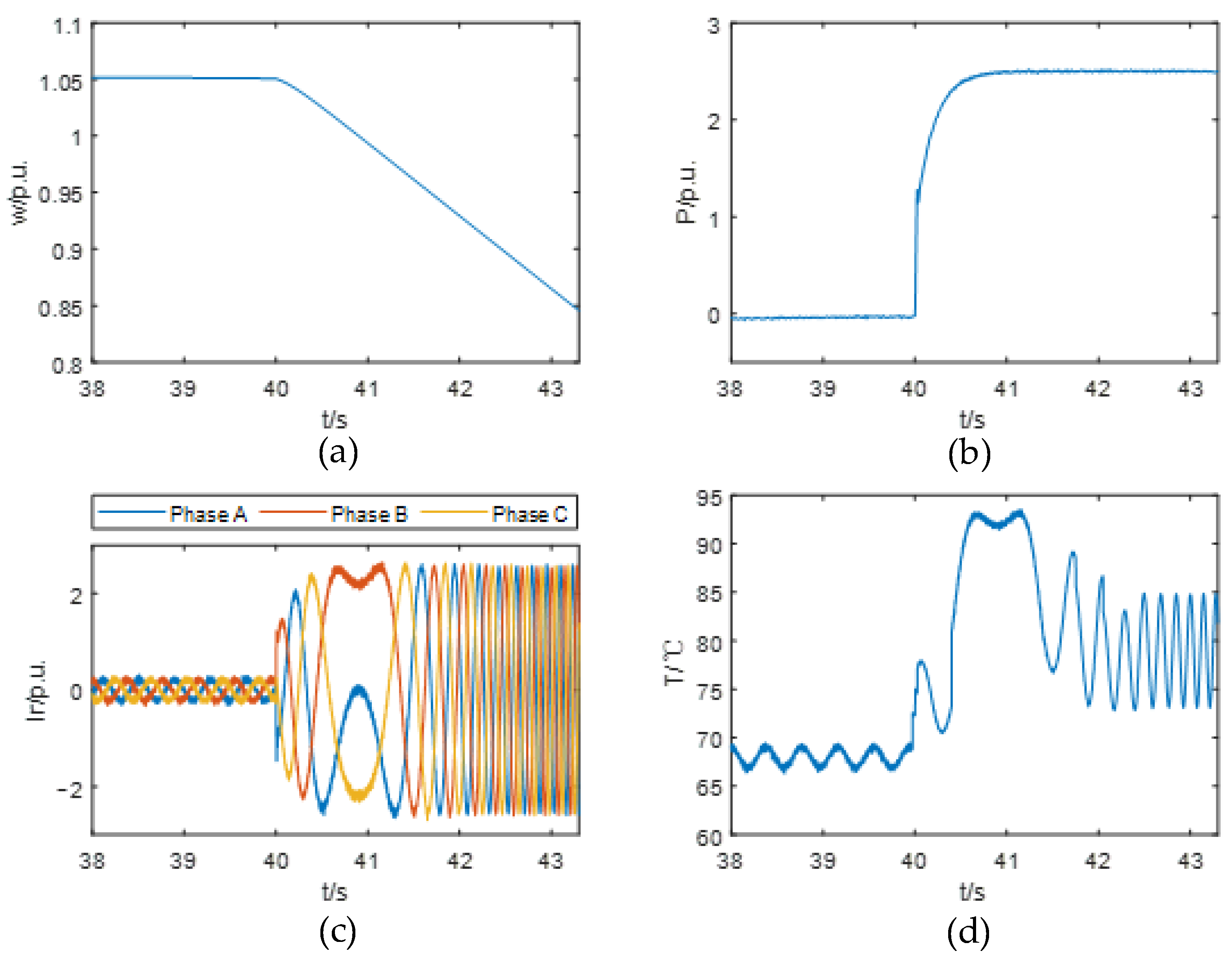
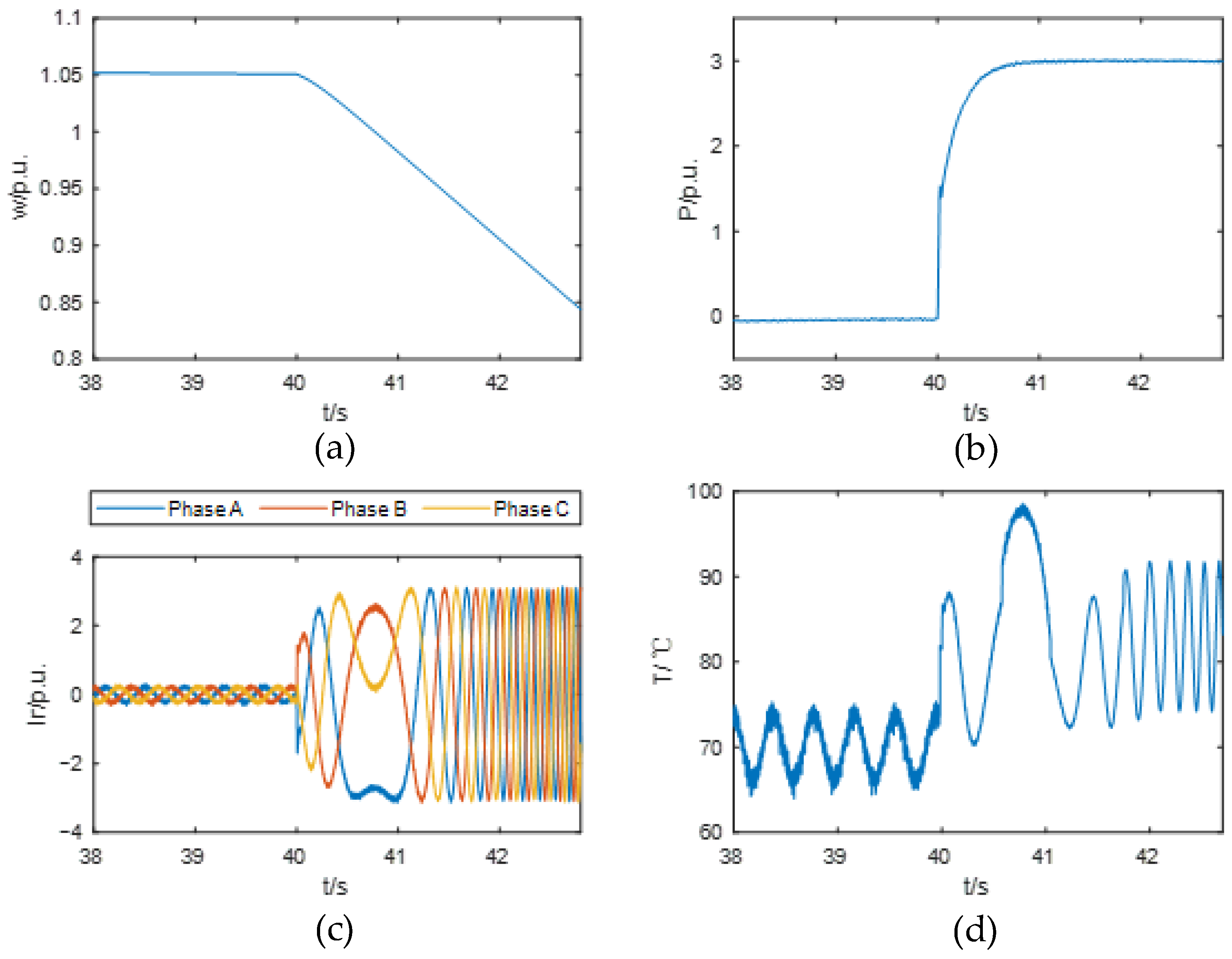
- When the HI-ES-SC provides high-level active power support (e.g., up to 3.0 p.u.), the junction temperature rises significantly as the rotor speed crosses the synchronous speed. This phenomenon is primarily caused by thermal accumulation effects in the converter during low-frequency operation. Under 3.0 p.u. active power support, the peak junction temperature reaches 98.50 °C.
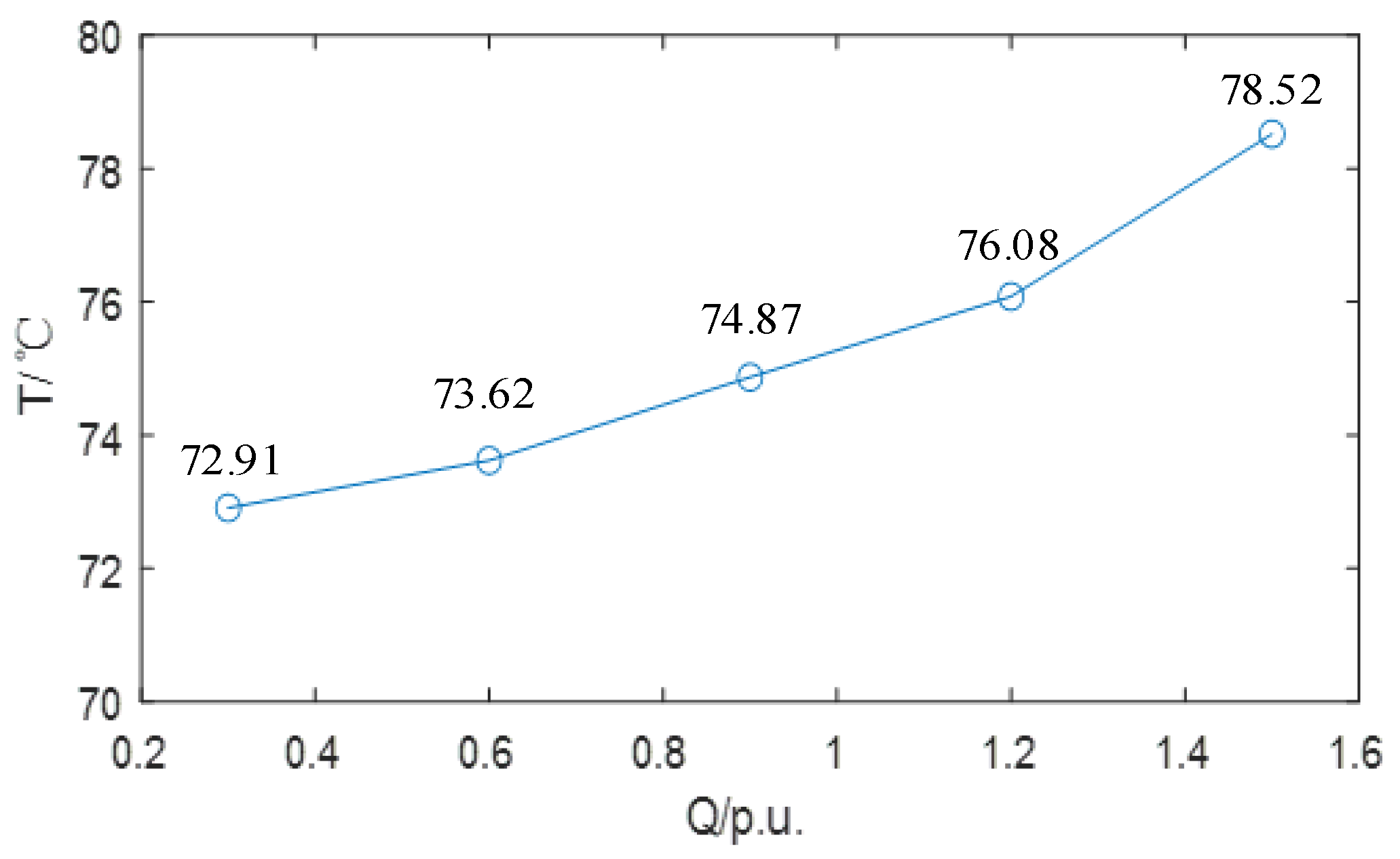
- In contrast, reactive power support has a minor impact on the junction temperature variation in the converter. Since the HI-ES-SC can maintain a relatively constant speed during reactive power output, it avoids low-frequency operation of the converter, which is the main contributor to significant temperature rise. Under 1.5 p.u. reactive power support, the peak junction temperature is only 78.52 °C.
- It is applicable only to air-cooled heat sinks. For water-cooled systems, modeling and analysis must account for specific thermal dissipation structures.
- Further research is needed to investigate the impact of more factors on the accuracy of the model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HI-ES-SC | High-Inertia Energy Storage Synchronous Condensers |
| UHVDC | Ultra-High Voltage Direct Current |
| NPC | Mid-Point Clamped |
| ANPC | Active Mid-Point Clamped |
| IGCT | Integrated Gate-Commutated Thyristor |
| IGBT | Insulated Gate Bipolar Transistors |
| FEM | Finite Element Model |
| TSEP | Temperature-Sensitive Electrical Parameter |
References
- Ouyang, J.; Pan, X.; Ye, J.; Xiao, C.; Diao, Y.; Zhang, Q. An Improved Prediction Method of Subsequent Commutation Failure of an LCC-HVDC Considering Sequential Control Response. Prot. Control. Mod. Power Syst. 2023, 8, 1–11. [Google Scholar] [CrossRef]
- Ouyang, J.; Chen, J.; Li, A.; Chen, Y.; Xiao, C. Fault Ride-Through Control Method for VSC-HVDC Balancing between DC Voltage Security and Reactive Power Support. Trans. China Electrotech. Soc. 2024, 39, 6129–6144. [Google Scholar] [CrossRef]
- Muniappan, M. A Comprehensive Review of DC Fault Protection Methods in HVDC Transmission Systems. Prot. Control. Mod. Power Syst. 2021, 6, 1–20. [Google Scholar] [CrossRef]
- Xu, G.; Wang, L.; Li, Z.; Li, Z.; Zhao, H.; Zhan, Y.; Zhang, Y. Improvement of Reactive Power Consumption Ability for Dual-Excited Synchronous Condenser. IEEE Trans. Ind. Appl. 2024, 60, 6056. [Google Scholar] [CrossRef]
- Guo, Q.; Li, Z. Summarization of Synchronous Condenser Development. Proc. CSEE 2023, 43, 6050–6064. [Google Scholar]
- Lee, I.; Lee, K. Junction Temperature Estimation of SiC MOSFETs in Three-Level NPC Inverters. J. Electr. Eng. Technol. 2024, 19, 1607–1617. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Wang, Y.; Li, W.; Li, C.; Xian, Z. Key Technical Parameters and Optimal Design of New Types of Large Capacity Synchronous Condenser. Large Electr. Mach. Hydraul. Turbine 2017, 4, 15–22. [Google Scholar]
- Zhang, B.; Wang, Z.; Gu, M. An Improved Si/SiC Hybrid Three-Level ANPC Inverter with Optimized Thermal Distribution-Based Modulation Scheme. In Proceedings of the 27th International Conference on Electrical Machines and Systems, Fukuoka, Japan, 26–29 November 2024; pp. 1012–1017. [Google Scholar]
- Woldegiorgis, D.; Mantooth, H. Precise Electro-thermal Power Loss Model of a Three-level ANPC Inverter with Hybrid Si/SiC Switches. Chin. J. Electr. Eng. 2022, 8, 76–89. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, J.; Zhou, S.; Li, S.; Wen, Z.; Ji, Y. Loss Analysis and Junction Temperature Prediction for Modular Multilevel Converters. In Proceedings of the 9th International Conference on Power And Renewable Energy, Guangzhou, China, 20–23 September 2024; pp. 156–161. [Google Scholar] [CrossRef]
- Musarrant, M.N.; Islam, M.R.; Muttaqi, K.; Sutanto, D.; Rahman, M.A. Improving the Thermal Performance of Rotor-Side Converter of Doubly Fed Induction Generator Wind Turbine While Operating Around Synchronous Speed. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 298–307. [Google Scholar] [CrossRef]
- Charalambous, A.; Hadjidemetriou, L.; Polycarpou, M.M. Junction Temperature Control for Lifetime Extension of Multi-Functional Photovoltaic Inverters. IEEE Trans. Ind. Appl. 2024, 60, 4125–4137. [Google Scholar] [CrossRef]
- Ding, S.; Jiang, X.; Zhu, M.; Liu, W. Starting and Steady Temperature Rise Investigation for Permanent Magnet Synchronous Motor Based on Lumped-Parameter Thermal-Network. Electr. Mach. Control. 2020, 24, 143–150. [Google Scholar] [CrossRef]
- Xu, G.; Hu, P.; Li, Z.; Zhan, Y.; Zhao, H. Influence of Different Steady State Conditions on Transient Temperature Rise of Synchronous Condenser After Single-phase Short-circuit. Proc. CSEE 2024, 44, 1587–1597. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Wen, C.; Qiu, D.; Guo, T.; Li, J. A Real-Time Junction Temperature Evaluation Method Based on the Reduction Thermal Model for IGBT Module of Traction Converter. IEEE Trans. Transp. Electrif. 2025, 11, 9319–9331. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Y.; Wu, Y.; Wang, Z.; Li, X.; Wei, X. Research on Junction Temperature Smooth Control of SiC MOSFET Based on Body Diode Conduction Loss Adjustment. Energies 2024, 17, 6175. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P. A Junction Temperature Smoothing Control Method for SiC MOSFETs Based on the Gate Driving Signal Delay. IEEE Trans. Ind. Electron. 2023, 71, 3122–3132. [Google Scholar] [CrossRef]
- Fu, X.; Jin, M.; Huang, Y.; Du, J.; Wei, K. On-Line Junction Temperature Identification of Converter Power Devices. J. Phys. Conf. Ser. 2025, 2840, 012026. [Google Scholar] [CrossRef]
- Cho, S.; Song, S. A Study on the Power Loss of the High Voltage IGBT for Voltage Type HVDC MMC System. J. Korean Inst. Illum. Electr. Install. Eng. 2021, 35, 31–35. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Z.; Jin, B.; Pang, J. A Thermal Impedance Model for IGBT Modules Considering the Nonlinear Thermal Characteristics of Chips and Ceramic Materials. Electronics 2024, 13, 4465. [Google Scholar] [CrossRef]
- Zhang, X.; Mu, W.; Lv, C.; Shi, M.; Yu, X.; Wu, K.; Li, J. A Thermal Network Model for Monitoring IGBT Chip Solder Degradation Based on Feedback PI Control. Microelectron. Reliab. 2022, 138, 114617. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, B.; Zhang, X.; Chen, Z.; Liu, J.; Zhou, W. Full-Time Junction Temperature Extraction of IGCT Based on Electrothermal Model and TSEP Method for High-Power Applications. IEEE Trans. Ind. Electron. 2021, 68, 47–58. [Google Scholar] [CrossRef]
- Yan, X.; Yu, Z.; Qu, L.; Gan, Z.; Huang, Y.; Feng, J. Electro-Thermo-Mechanical Analysis and Modeling of High-Power Intergrated Gate Commutated Thyristors. IEEE Trans. Power Electron. 2024, 39, 6654–6663. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, J.; Wang, P.; Liu, J.; Chen, Z. Study on Accelerated Aging Test Topology for High Power Semiconductor IGCT Devices Targeting MMC Applications. Proc. CSEE. 2025, 45, 266–277. [Google Scholar] [CrossRef]
- Okilly, A.; Harmony, P.; Kim, C.; Kim, D.; Beak, J. Estimation of Peak Junction Hotspot Temperature in Three-Level TNPC-IGBT Modules for Traction Inverters Through Chip-Level Modeling and Experimental Validation. Energies 2025, 18, 3829. [Google Scholar] [CrossRef]
- Ouyang, J.; Yu, J.; Long, X.; Diao, Y.; Wang, J. Coordination Control Method to Block Cascading Failure of a Renewable Generation Power System Under Line Dynamic Security. Prot. Control. Mod. Power Syst. 2023, 8, 12. [Google Scholar] [CrossRef]
- Liu, H.; Xiang, C.; Du, J.; Zhang, X. Multi-Objective Cooperative Control of a Junction-Temperature-Orientated Three-Level Traction Converter. Transp. Saf. Environ. 2025, 7, tdaf017. [Google Scholar] [CrossRef]
- Guo, C.; Zhu, Y.; Tong, L. Junction Temperature Prediction for Multi-Chip IGBT Modules Based on An Improved 3D Thermal Network Model and Experimental Results. Results Eng. 2025, 27, 106072. [Google Scholar] [CrossRef]
- ABB. IGCT 5SHX 26L4503 datasheet, Doc. No. 5SYA 1230-01; ABB: Lenzburg, Switzerland, 2020; Available online: https://www.5scomponents.com/PDF/5SHX-26L4503_5SYA1230-01Feb-02.pdf (accessed on 1 September 2025).
- Hu, J. An H∞ Observer-based 3-D Thermal Monitoring Method for Multi-chip IGBT Modules with Robustness to Model Parameter and Power Loss Uncertainty. Prot. Control. Mod. Power Syst. 2025, 10, 125–145. [Google Scholar] [CrossRef]





| Device | IGBT | IGCT |
|---|---|---|
| Chip structure | Small-sized chips with complex cells | Whole crystal chip with relatively simple cell structure |
| Package form | Complex multi chip parallel packaging | Simple and reliable whole wafer packaging |
| Production cost | Complex structure and high cost | Simple structure and low cost |
| Switching frequency | High, above several kilohertz | Lower, several hundred hertz |
| Shutdown capability | strong | stronger |
| Dynamic tolerance | di/dt is controllable through driving | di/dt controlled by loop inductance |
| Working loss | High tolerance of dv/d under black start | High tolerance of dw/dt under black start |
| Drive power | High opening and conduction losses | Low opening and conduction losses |
| Capacity characteristics | High shutdown loss after low-frequency optimization | High shutdown loss |
| Security features | lower | Significant decrease at high and low frequencies |
| Switch State | Voltage Level State | Duty Cycle | Conducting Device of Current Switching Path 1 | Conducting Device of Current Switching Path 2 | ||
|---|---|---|---|---|---|---|
| Ir > 0 | Ir < 0 | Ir > 0 | Ir < 0 | |||
| P-O level change | 1/2Udc | m sin(ωit + φ) | VT1, VT2 | VD1, VD2 | VT1, VT2 | VT6, VD3 |
| 0 | 1 − msin(ωit + φ) | VD5, VT2 | VT5, VD2 | VD1, VD2 | VT3, VD6 | |
| O-N level change | 0 | 1 + msin(ωit + φ) | VD5, VT2 | VD6, VT3 | VD3, VT6 | VD2, VT5 |
| −1/2Udc | −m sin(ωit + φ) | VD3, VD4 | VT4, VT3 | VD3, VD4 | VT3, VT4 | |
| IGCT | Si(IGCT Wafer) | Al(Electrode) * | Mo(Mo Piece) | Cu(Case Bolock) | |
|---|---|---|---|---|---|
| Material Parameter | C (J/gK) | 0.7 | 0.76 | 0.25 | 0.39 |
| (g/cm3) | 2.33 | 3.97 | 10.2 | 8.96 | |
| (W/cmK) | 1.48 | 0.36 | 1.38 | 4.01 | |
| Cathode Parameter | D (cm) | 8.9 | 8.9 | 8.9 | 10.16 |
| A (cm2) | 62.21 | 62.21 | 62.21 | 81.07 | |
| L (cm) | 0.05 | 0.0012 | 0.25 | 1.015 | |
| R (K/W) | 0.00054 | 4.47 10−5 | 0.0029 | 0.0031 | |
| C (J/K) | 5.07 | 0.188 | 39.66 | 283.86 | |
| Anode Parameter | D (cm) | 8.9 | / | 8.9 | 9.5 |
| A (cm2) | 62.21 | / | 62.21 | 70.88 | |
| L (cm) | 0.025 | / | 0.25 | 1.015 | |
| R (K/W) | 0.0003 | / | 0.003 | 0.0036 | |
| C (J/K) | 2.54 | / | 39.66 | 248.18 | |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| tb | 13.7 mm | s | 5.6 mm |
| kAl | 255 W/(m K) | 1.0926 kg/m3 | |
| Bcond | 1.312 105 mm2 | 1.961 10−5 kg/ms | |
| 0.89 | 0.7124 | ||
| kf | 0.0277 W/(m K) | 76 mm |
| RC Parameters | Model Based on FEM | Linear Thermal Model | Error of Linear Thermal Model | Model Proposed in This Paper | Error of the Model Proposed |
|---|---|---|---|---|---|
| RSi (K/W) | 5.74 × 10−4 | 1.06 × 10−3 | +84.67% | 5.83 × 10−4 | +1.57% |
| RMo (K/W) | 3.02 × 10−3 | 3.42 × 10−3 | +13.24% | 3.31 × 10−3 | +9.60% |
| RAl (K/W) | 4.65 × 10−5 | 6.20 × 10−5 | +33.33% | 4.91 × 10−5 | +5.59% |
| RCu (K/W) | 3.28 × 10−3 | 4.49 × 10−3 | +36.89% | 3.40 × 10−3 | +3.66% |
| CSi (J/K) | 5.90 | 5.23 | −11.36% | 5.62 | −4.75% |
| CMo (J/K) | 45.23 | 42.97 | −5.00% | 42.26 | −6.57% |
| CAl (J/K) | 0.228 | 0.206 | −9.65% | 0.219 | −3.95% |
| CCu (J/K) | 311.24 | 289.06 | −7.13% | 302.45 | −2.82% |
| UDC | Ir | Junction Temperature (Proposed Method) | Junction Temperature (Experiment) |
|---|---|---|---|
| 2.5 kV | 3.5 kA | 80.7 °C | 81.1 °C |
| 4 kA | 92.3 °C | 95.5 °C |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Solver choice | Fixed-step, ode3 | Stator resistance | 0.074 Ω |
| Signal-exchange rate | 115,200 | Total stator leakage inductance | 6.11 mH |
| Rated capacity | 11.11 MVA | Excitation inductance | 234.93 mH |
| Rated stator voltage | 10.5 kV | Rotor resistance | 0.0275 Ω |
| Rated rotor voltage | 3.3 kV | Total rotor leakage inductance | 6.4 mH |
| Pole-pair number | 1 | Stator/Rotor turns ratio | 0.6 |
| No-load rated rotational speed | 3150 r/min | DC bus voltage | 7000 V |
| Inertia time constant | 20.3 s | DC bus capacitance | 30 mF |
| Rated slew rate | ±0.2% | Inlet reactor inductance | 0.4 mH |
| Maximum slew rate | 3.5 kV | Inlet reactor resistance | 0.00298 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, J.; Lin, Y.; Ye, Z.; Diao, Y. Electro-Thermal Modeling and Thermal Analysis of High-Inertia Synchronous Condenser Converters. Electricity 2025, 6, 53. https://doi.org/10.3390/electricity6030053
Ouyang J, Lin Y, Ye Z, Diao Y. Electro-Thermal Modeling and Thermal Analysis of High-Inertia Synchronous Condenser Converters. Electricity. 2025; 6(3):53. https://doi.org/10.3390/electricity6030053
Chicago/Turabian StyleOuyang, Jinxin, Yaowei Lin, Zhiqi Ye, and Yanbo Diao. 2025. "Electro-Thermal Modeling and Thermal Analysis of High-Inertia Synchronous Condenser Converters" Electricity 6, no. 3: 53. https://doi.org/10.3390/electricity6030053
APA StyleOuyang, J., Lin, Y., Ye, Z., & Diao, Y. (2025). Electro-Thermal Modeling and Thermal Analysis of High-Inertia Synchronous Condenser Converters. Electricity, 6(3), 53. https://doi.org/10.3390/electricity6030053





